CHƯƠNG 7    ƯỚC LƯỢNG KHOẢNG ƯỚC LƯỢNG KHOẢNG
Khoảng tin cậy. Ta gọi khoảng  ( µ a , µ 1 a 2 ) với  
là khoảng tin cậy của tham số a b với độ tin cậy nếu P ( µ a < a < µ a ) = b ( ) b  ƯỚC LƯỢNG KHOẢNG
3 độ tin cậy thương dùng là  b = 90% , 95% , 99%
KHOẢNG TIN CẬY CỦA TỶ LỆ
lGiả sử tỷ lệ các phần tử có dấu hiệu A của
tổng thể U là p chưa biết. 
lLấy ngẫu nhiên n phần tử của tổng thể U
và thấy m phần tử có dấu hiệu A.
lKhi n lớn, khoảng tin cậy đối xứng của p với độ tin c
b ậy là khoảng nghiệm của bất phương trình( f - p) n n  < z(1- b )/2 p (1 - p )
KHOẢNG TIN CẬY CỦA TỶ LỆ
Trong đó z ( 1 - b ) / 2 được xác định bởi   1 + b P( z ) =  (1-b )/2 2
và có thể tra từ bảng A.3 hoặc dò trên máy tính 
KHOẢNG TIN CẬY CỦA TỶ LỆ
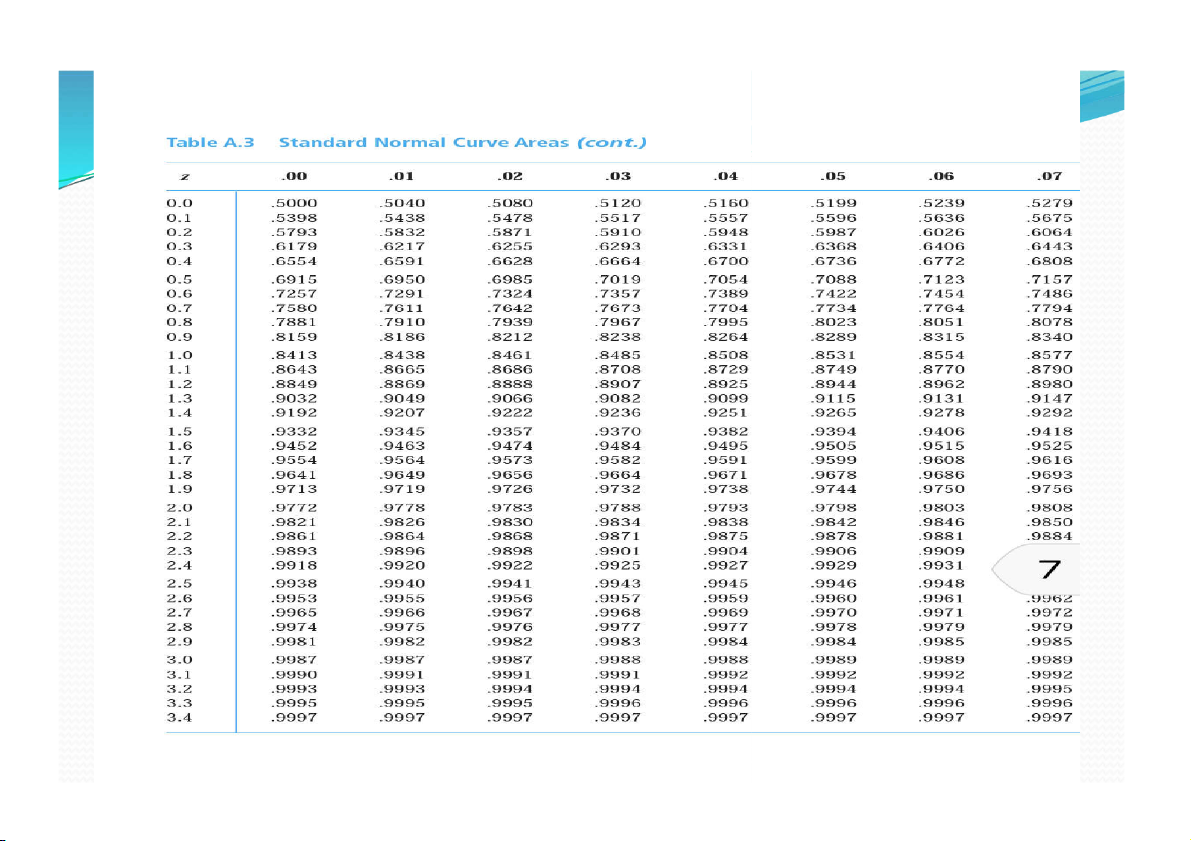
l Tìm z ( 1 - b ) / 2 được thực hiện cụ thể như sau.
l Với b = 0, 95 : P ( z(1 b )/2) = P (z - 0, 02 5 ) = 0, 9 7 5
Trên bảng A.3 tìm giá trị 0,975 ta thấy
giá trị này ứng với cột đầu tiên là 1.9
và hàng đầu tiên 0,06 nên  P (1, 96) = 0, 975 Þ z0,025 = 1, 96
KHOẢNG TIN CẬY CỦA TỶ LỆ
lVới b = 0, 90 : P ( (z1 b )/2 ) = P ( 0 z - , 05 ) = 0, 9 5
Trên bảng A.3 ta thấy giá trị 0,95 nằm
giữa P(1,64) = 0,9495 và P(1,65) =
0,9505 bằng cách thử với P(1,645) =
0,95002 > 0,95; P(1,6449) = 0,95  Þ z0,05 = 1, 6449
KHOẢNG TIN CẬY CỦA TỶ LỆ
Khoảng tin cậy đối xứng xấp xỉ
của p với độ tin bcậy là  ( f - e , f + e ) với  n n  f (1 - f ) n n e = z (1- b ) /2 n
và được gọi là độ chính xác hay
sai số của ước lượng
KHOẢNG TIN CẬY CỦA TỶ LỆ
l Khoảng tin cậy (xấp xỉ) bên trái của p với độ tin c b ậy là æ f (1 - f ) ö  0, n n fn + ç ( z 1- b ) ÷ n è ø
l Hay giá trị tối đa của p với độ tin cậy b là f (1 - f ) n n f + z  n (1- b ) n 