


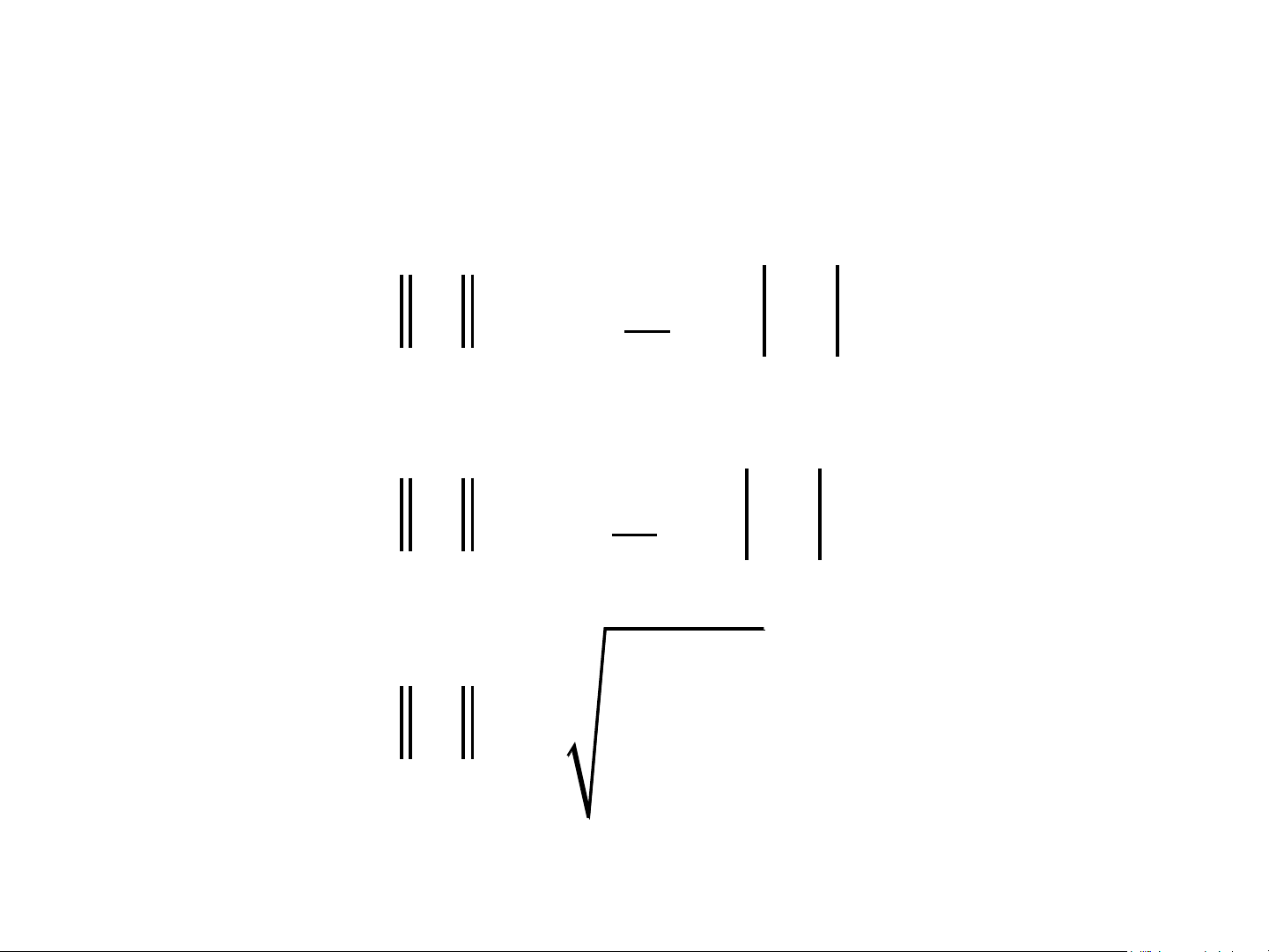

Preview text:
PP LẶP ĐƠN
GIẢI GẦN ĐÚNG HỆ ĐSTT Ý tưởng phương pháp
- Đưa về phương trình tương đương
Ax = b x = Bx + d - Lập dãy véctơ x = Bx + d, n x n n 1 − 0
- Nếu dãy hội tụ thì giới hạn là nghiệm của phương trình Chuẩn của véctơ
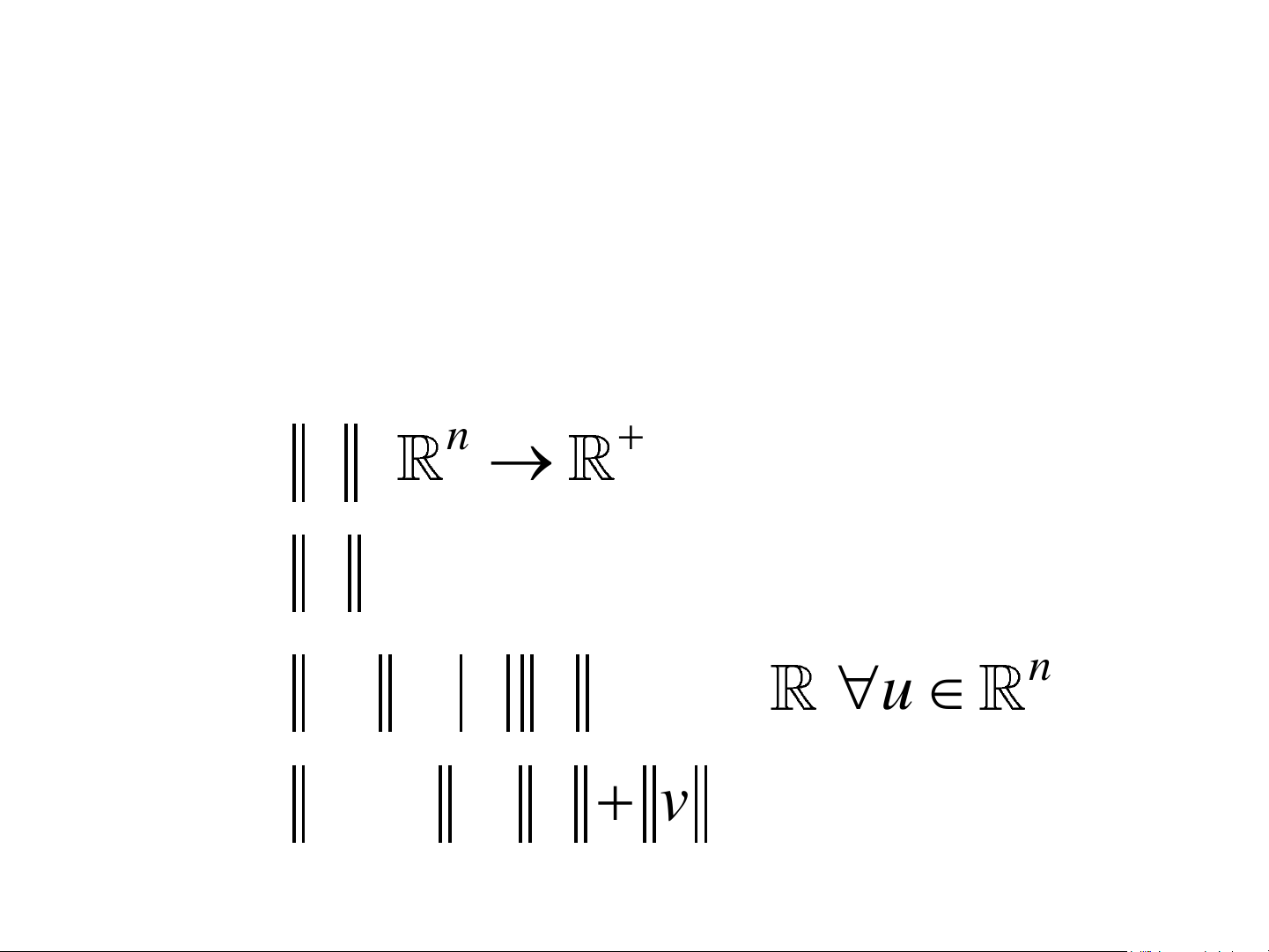
• Định nghĩa: chuẩn là một ánh xạ thỏa mãn các tính chất sau: + . : n →
u 0, " = " u = 0 n ku = k u k u
u + v u + v Chuẩn véctơ
• Các chuẩn thường gặp x = max xi i 1, = n n x = x 1 i i 1 = n 2 x = x 2 i i 1 =
Sự hội tụ của dãy véctơ • Định nghĩa: n→ → x ⎯⎯⎯ → *
x x − x * n ⎯⎯⎯→0 n n n→
x ⎯⎯⎯→ x * i =1,n ni i
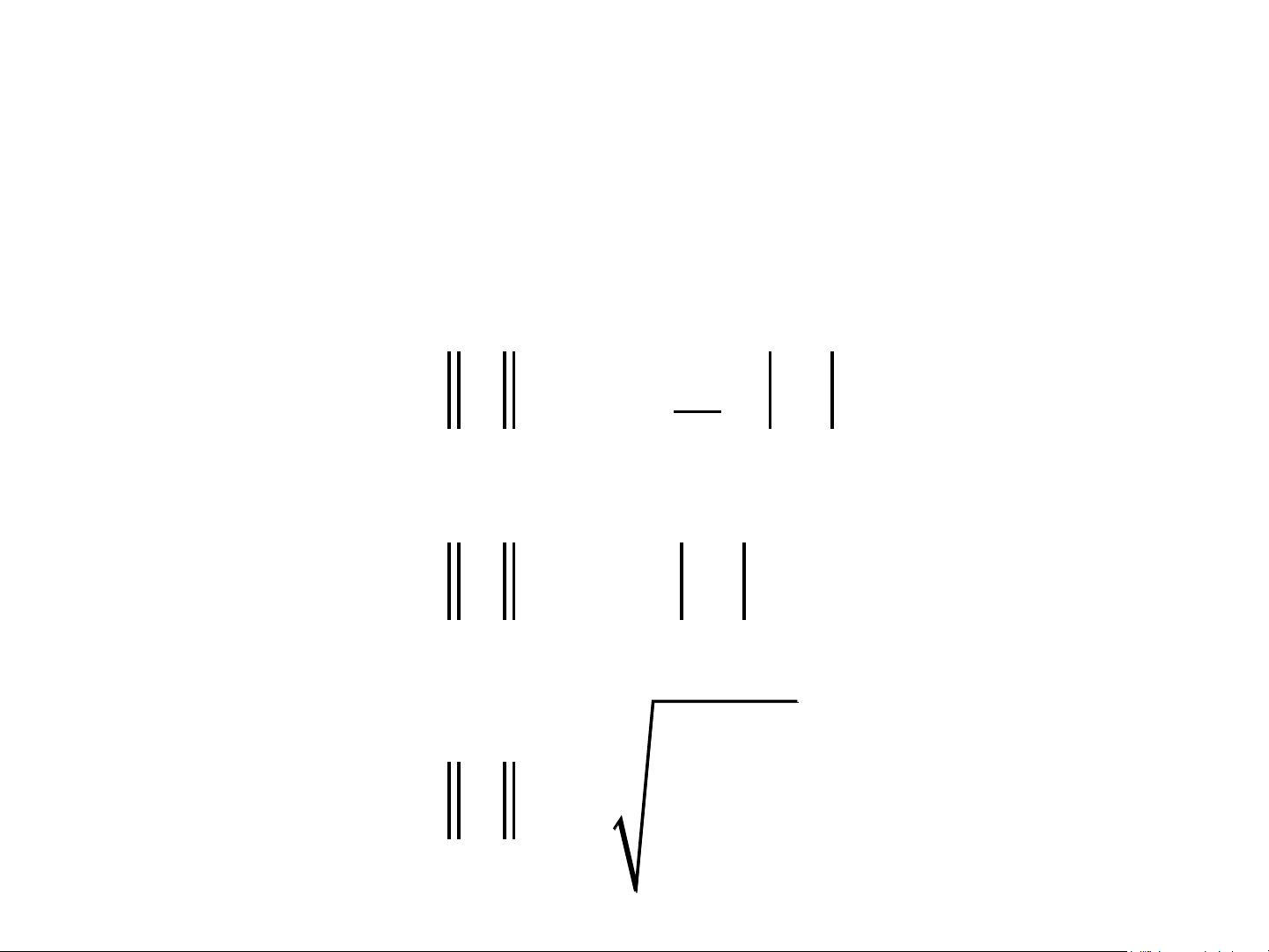
• Chuẩn tương đương: Hai chuẩn p và q
được gọi là tương đương nếu C
,C 0, C x x C x 1 2 1 2 p q p
Sự hội tụ của dãy véctơ
• Nếu hai chuẩn p và q tương đương thì
dãy véctơ hội tụ theo chuẩn p khi và chỉ
khi nó hội tụ theo chuẩn q
• Mọi chuẩn trong không gian véctơ hữu
hạn chiều đều tương đương Chuẩn của ma trận n A = max a ij i 1, = n j 1 = n A = max a 1 ij j 1, = n i 1 = n 2 A = a 2 ij i, j 1 =
Sự hội tụ của PP lặp đơn • Nếu B 1 thì dãy x = B x + d, x n n n 1 − 0
hội tụ tới nghiệm đúng duy nhất của phương trình x = Bx + d theo đánh giá n B x − x * x − x n 1 0 1 − B B x − x * x − x n n n 1 − 1 − B Ví dụ




