lOMoAR cPSD| 49831834
CHƢƠNG VI. PHƢƠNG TRÌNH VI PHÂN
I. PHƢƠNG TRÌNH VI PHÂN CẤP I 1. Ñịnh nghĩa
• Phöông trình vi phaân laø moät phöông trình chöùa moái
lieân heä giöõa hai bieán x, y (maø trong ñoù ta xem y laø
moät haøm khaû vi cuûa x) vaø caùc ñaïo haøm cuûa y.
• Caáp cuûa phöông trình vi phaân laø caáp cao nhaát cuûa
ñaïo haøm cuûa y xuaát hieän trong phöông trình.
• Phöông trình vi phaân caáp 1 laø phöông trình coù daïng: F(x; y, y’) = 0 (1) hay y’ = f(x; y) (2)
• Nghieäm toång quaùt – Nghieäm rieâng: 1 lOMoAR cPSD| 49831834
* Nghieäm toång quaùt cuûa (1) (hoaëc (2)) trong mieàn D R2 laø haøm y (x; C) sao cho :
- Thoaû phöông trình ñaõ cho vôùi moïi giaù trò cuûa haèng soá C
baát kyø thuoäc moät taäp naøo ñoù.
- Vôùi moïi ñieàu kieän ban ñaàu y(x2) 2) 0) = y0 sao cho
(x ; y ) D chæ coù moät giaù trò duy nhaát C0 thoaû maõn 0 0 ñieàu kieän ban ñaàu. * Moïi nghieäm y
(x; C ) nhaän ñöôïc töø nghieäm toång 0 quaùt y
(x; C) öùng vôùi giaù trò cuï theå C0 ñöôïc goïi laø nghieäm rieâng. 2 lOMoAR cPSD| 49831834
Baøi toaùn 1: Phöông trình vi phaân caáp 1 coù bieán phaân ly
Dạng tổng quát : f(x)dx = g(y)dy
Phương pháp giải :
Ñeå tìm nghieäm cuûa phöông trình treân, ta laáy tích phaân baát ñònh 2 veá: f(x)dx g(y)dy Khi
ñoù ta coù: F(x) = G(y) + C
trong ñoù F laø nguyeân haøm cuûa f, G laø nguyeân
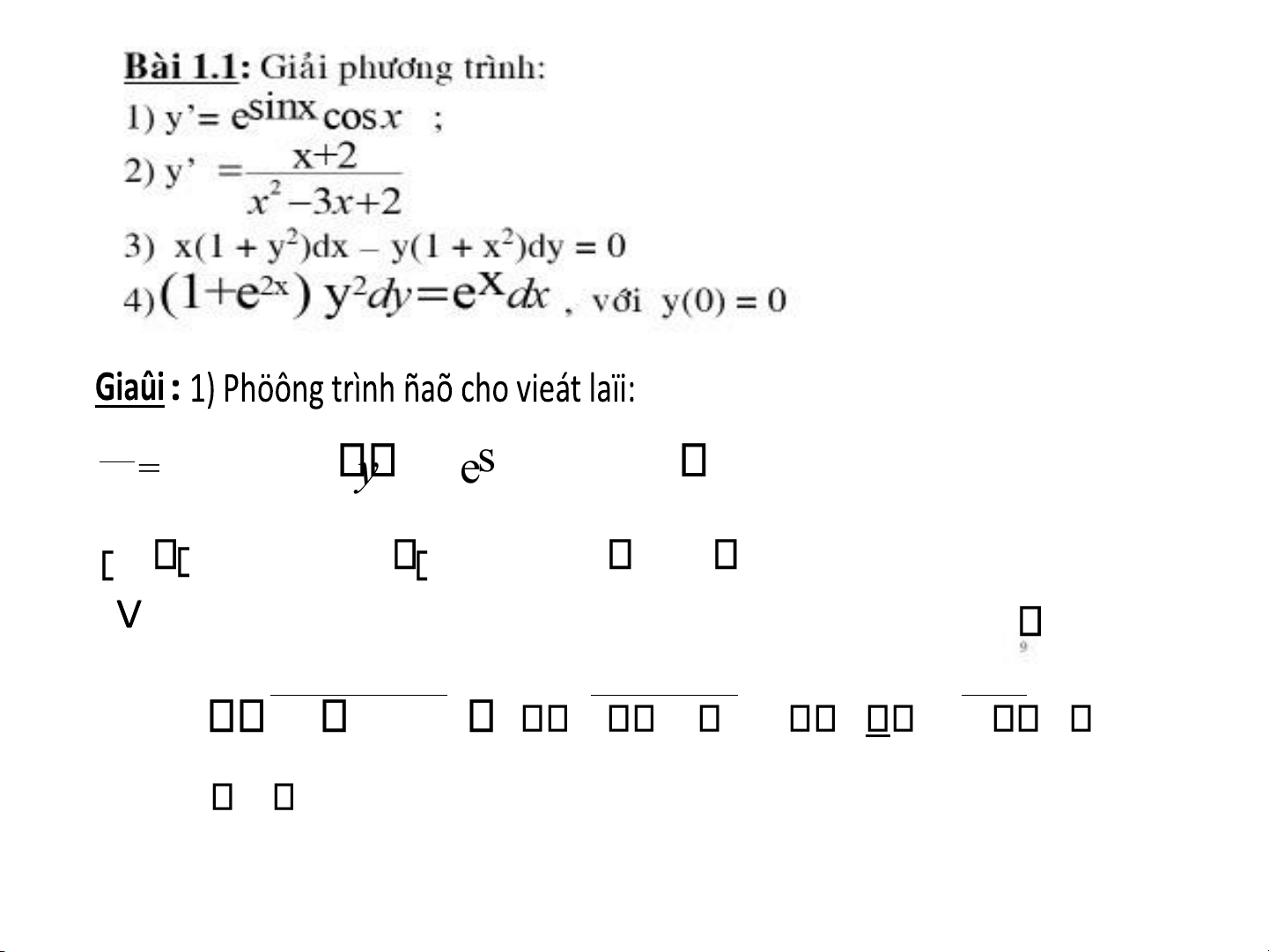
haøm cuûa g vaø C laø haèng soá baát kyø. 3 lOMoAR cPSD| 49831834 dy= sinx sinx e cosxdy xdx e cos dx sinx sinx sinx dy e cos xdx e dsin x e c
ậy nghiệm tổng quát của phương trình là sinx : y=f(x)=e c 2) y
x2 x+23x 2 dy 2x 2 dx x 31dx x 42dx x 3x 2 4 lOMoAR cPSD| 49831834
3lnx 1 4lnx 2 C
Vậy nghiệm tổng quát của phương trình là:
y 3lnx 1 4lnx 2 C 3) x(1 + y2)dx = y(1 + x2)dy x y x2 dx 1 y2 dy vì (1 x 2),(1 y2) 0 1
Tích phaân baát ñònh 2 veá ta coù: 1ydy y2 1xdx x2 1 2 ln(1 y2) ln(1 x2) ln C (C 0) ln(1 y2) ln(1 x2) lnC2 (C 0) 1 y2 C2(1 x2) (C 0) 5 lOMoAR cPSD| 49831834
Vaäy nghieäm toång quaùt cuûa phöông trình ñaõ cho laø: 1 + y2 = C2(1 + x2) C 0 x
d) (1+e )2x y2dy e dx (1) vôùi y(0) = 0 2x 2 (1) (1+e2x) y2dy ex dx y dy 1+ eex2 1+e y3 arctgex C 3 y3 x 6 lOMoAR cPSD| 49831834 vì y(0)=0 arctge
, nên ta có nghiệm riêng là 3 4
Baøi toaùn 2: Phöông trình vi phaân tuyeán tính caáp 1
Daïng: y’ + P(x)y = Q(x) (1) trong ñoù P(x), Q(x) laø
caùc haøm soá lieân tuïc trong moät khoaûng naøo ñoù.
Böôùc 1: Xeùt phöông trình vi phaân thuaàn nhaát töông öùng: dy y’ + P(x)y = 0 (2) P(x)y. dx
Ngoaøi nghieäm y = 0, ta coøn coù: Lny P(x)dx C y e .eC P(x)dx B.e P(x)dx,B 0
Keát hôïp nghieäm y = 0, ta coù nghieäm toång quaùt cuûa (2) laø: 7 lOMoAR cPSD| 49831834 P(x)dx y C.e (C: haèng soá baát kyø)
Bài toán 2: Giải phƣơng trình 1/ Giải phương trình: y' ysinx sinx.cosx
( Ñ.S y=-cosx+1+c.e-cosx)
2/Giả sử y = f(x) là nghiệm của phương trình vi phân y
xy sinx thỏa điều kiện Đề Câu 08 thi K.39 : Giả sử y = f(x) là nghiệm của
phƣơng f( ) 1 . Khi đó f 2 có giá trị
trình vi phân thỏa iều kiện . Khi ó có giá trị 2 là 2 2 là A.
1 B. AC. . 1 C. D. Một kết quả khácB. D. 2 Đề thi K.39 8 lOMoAR cPSD| 49831834
Câu 08 : Giả sử y = f(x) là nghiệm của phương trình vi phân y
xy 2 0 thỏa iều kiện f(1) 2 . Khi ó f 2 có giá trị là 3 x A. 3 B. 5 C. 2
D. Một kết quả khác
Baøi toaùn 3 Phöông trình Bernouilly
Dạng tổng quát: y’+ P(x)y = Q(x)yn (n 0; n 1) vôùi P(x),
Q(x) laø caùc haøm soá lieân tuïc trong moät khoaûng naøo ñoù.
Phương pháp giải : Chia 2 veá cuûa phöông trình cho yn (y 0):
y–n.y’+ P(x)y1–n = Q(x) Ñaët z = y1–n z’ = (1 – n).y–n.y’.
Thay vaøo phöông trình ñaõ cho, ta seõ coù phöông trình vi phaân caáp 1 tuyeán tính. 9 lOMoAR cPSD| 49831834
1) Giaûi caùc phöông trình Bernouilly; x y' y e 2 .y a) y' 2xy 2x y3 3 ; b) y' yx y2 4 y' 4 y x y c) x ; d) x 10 lOMoAR cPSD| 49831834 Giaûi: :
a) Nhaän xeùt raèng y = 0 laø nghieäm cuûa (1) Vôùi
y 0, ta chia 2 veá cuûa pt cho y3: y’.y–3 +2x y–2 = 2x3
Ñaët z = y–2 z’ = – 2.y–3.y’ y–3.y’=- z’/2. Khi ñoù thay vào(1) ta
có phương trình: -z’/2+2xZ=2x3
z’- 4xz = – 4x3 (2) Xeùt z’- 4xz = 0 (3)
dz 4xz z Ce2x2 nghieäm toång quaùt cuûa (3) dx
Xem C = C(x) thì z C xe( ) 2x2. Thay vaøo (2), ta coù: C'(x).e + 4xC(x).e2x2 2x2 -4xC(x)e .= - 4x2x2 3 C'(x) 4x3e-2x 2
C(x) 2x2e-2x e-2x C
Vaäy nghieäm toång quaùt cuûa 11 lOMoAR cPSD| 49831834 (1) laø: 1 2 2x 2 y = 0 hay 2x 1 Ce y2
II .PHÖÔNG TRÌNH VI PHAÂN CAÁP 2 1.Ñònh nghóa:
Phöông trình vi phaân caáp 2 coù daïng: F(x; y; y’;y”) = 0 (1)
Hay y” = f(x; y; y’) (2) Nghieäm
toång quaùt – Nghieäm rieâng:
Nghieäm toång quaùt cuûa phöông trình vi phaân caáp 2 laø moät haøm y
(x;C ;C )thoaû maõn : Khi thay vaøo 1 2
phöông trình ñaõ cho ta coù moät ñaúng thöùc ñuùng với mọi giá trị của C ;C . 12 lOMoAR cPSD| 49831834 1 2
Moïi nghieäm nhaän ñöôïc töø nghieäm toång quaùt öùng
vôùi giaù trò cuï theå C1, C2 ñöôïc goïi laø moät nghieâm rieâng
cuûa phöông trình vi phaân caáp 2.
2. Phƣơng pháp giải : Baøi toaùn 4
Phöông Trình Vi Phaân Tuyeán Tính Caáp 2 • Ñònh nghóa:
Phöông trình vi phaân tuyeán tính caáp 2 coù daïng:
y”+ a(x).y’+ b(x).y = c(x) (1)
Trong ñoù a(x); b(x); c(x) laø caùc haøm soá lieân tuïc trong moät khoaûng
naøo ñoù. 2. Phƣơng pháp giải :
Ta goïi phöông trình sau ñaây laø phöông trình vi phaân tuyeán tính caáp 2
thuaàn nhaát töông öùng vôùi (1):
y”+ a(x).y’+ b(x).y = 0 (2) 13 lOMoAR cPSD| 49831834 • Ñònh nghóa:
Hai haøm f(x) vaø g(x) ñöôïc goïi laø phuï thuoäc tuyeán tính trong α,β
neáu c1,c2 khoâng ñoàng thôøi baèng 0 sao cho c1.f(x) + c2.g(x) = β 0, x α,
Hai haøm khoâng phaûi laø phuï thuoäc tuyeán tính ñöôïc goïi laø ñoäc laäp tuyeán tính.
• Ñònh lyù 1: Neáu bieát moät nghieäm rieâng cuûa (2) laø
y1(x) 0 thì ta tìm ñöôïc nghieäm rieâng thöù hai ñoäc laäp
tuyeán tính vôùi y1(x) laø: a(x)dx y (x) y (x) e 2 dx. • Ñònh lyù 2: 2 1 y (x)1 14 lOMoAR cPSD| 49831834
* Neáu y1(x); y2(x) laø hai nghieäm ñoäc laäp tuyeán tính cuûa
(2) thì nghieäm toång quaùt cuûa (2) laø: Y(x) =
c1.y1(x) + c2.y2(x) Ñònh lyù 3:
* Neáu y0 laø nghieäm cuûa (1) vaø Y(x) laø nghieäm toång
quaùt cuûa (2) thì nghieäm toång quaùt cuûa (1) laø : y(x) = y0 + Y(x)
Bái toán 5: Phƣơng trình vi phân cấp 2 tuyến tính
có hệ số là hằng Dạng tổng quát: : y”+ ay’+ by = f(x) (1)
❖Phương trình thuần nhất: y”+ ay’+ by = 0 (2) 15 lOMoAR cPSD| 49831834
❖ Phương trình ặc trưng: k2 + ak + b = 0 (*) Số Phức : + Giải PT : x2+1=0
Nếu xét trên R (Số thực) thì PT vô nghiệm
Nếu ặt -1=i2, ta có PT : x2=-1=i2
x i i là số ảo
Tổng quát : ax2+bx+c=0: b2-4ac +TH1:
b2-4ac>0 thì Pt có hai nghiệm +TH2:
b2-4ac=0 thì PT có 1 nghiệm kép 16 lOMoAR cPSD| 49831834 +TH3:
b2-4ac<0 , ặt i2=-1, PT có hai nghiệm ảo: b .i = i ( nghiệm ảo), x1,2 2a
- ược gọi là phần thực, ược gọi là phần ảo
* Neáu (*) coù 2 nghieäm thöïc k k thì (2) coù 2 1 2
nghieäm rieâng ñoäc laäp tuyeán tính laø:
y (x) e k1x;y (x) e k2x 1 2 17 lOMoAR cPSD| 49831834
* Neáu (*) coù nghieäm keùp k thì (2) coù 2 nghieäm 0`
rieâng ñoäc laäp tuyeán tính laø: k x k x
y (x) e 0 ;y (x) x.e 0 . 1 2
* Neáu (*) coù 2 nghieäm phöùc k α iβ thì (2) coù
2 nghieäm rieâng ñoäc laäp tuyeán tính laø:
y1(x) = e x.cos x; y2(x) = e x.sin x
Baøi 5.1: Giaûi phöông trình: 1/ y” – 5y’ + 6y = 0 2/ y”+ 2y’+ y = 0 18 lOMoAR cPSD| 49831834 3 / y”+ 9y = 0
Giaûi: 1/ Xeùt phöông trình ñaëc tröng: k2 – 5k + 6 = 0 k 3;k 2
Do ñoù phöông trình coù 2 nghieäm rieâng ñoäc laäp tuyeán tính laø: y1(x) = e3x ; y2(x) = e2x
Vaäy nghieäm toång quaùt laø: y = C1e3x + C2e2x
2/ Giaûi phöông trình: y”+ 2y’+ y = 0
Giaûi: Xeùt phöông trình ñaëc tröng: k2 + 2k + 1 = 0 k -1 (keùp)
Do ñoù phöông trình coù 2 nghieäm rieâng ñoäc laäp tuyeán tính laø: y1(x) = e-x ; y2(x) = x.e-x 19 lOMoAR cPSD| 49831834
Vaäy nghieäm toång quaùt laø: y = C1e-x + C2e-x.x
3/ Giaûi phöông trình: y”+ 9y = 0
Xeùt phöông trình ñaëc tröng: k2 + 9 = 0 k 3i
Do ñoù phöông trình coù 2 nghieäm rieâng ñoäc
laäp tuyeán tính laø: y1(x) = cos3x ; y2(x) = sin3x
Vaäy nghieäm toång quaùt laø: y = C1.cos3x + C2.sin3x
Bái toán 6: Phƣơng trình vi phân cấp 2 tuyến tính có
hệ số là hằng, vế phải có dạng ặc biệt
Dạng tổng quát: : y”+ ay’+ by = f(x) (1) 20