












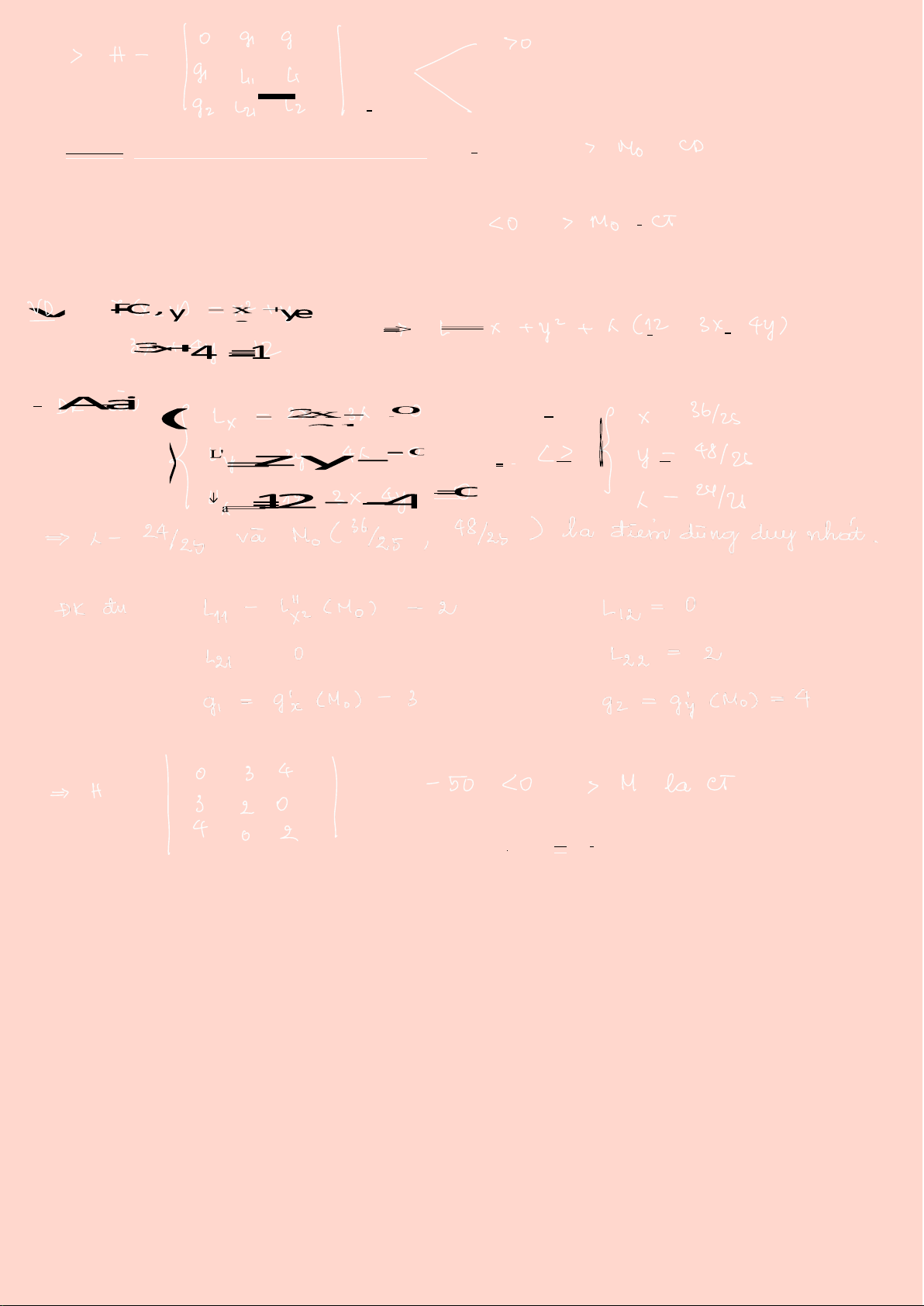
Preview text:
lOMoAR cPSD| 49519085 STT 39 lOMoAR cPSD| 49519085
Changof. Ling dung kind tohain a blen
& Gia' ti hietai +trong laicia tier.
tai:Guiistien A varugain hang, lai sud't u Bai ↳) 1dueke. Hai -
saw a cheekie' od give valid bar alieve? +r". =>A= An Ctrn
Baind:Not thing qui ngainlng wtr, v 12% rain. = Saw 42 thing co'bar nhien? lOMoAR cPSD| 49519085 tre- x voi daie tui =
a Gid tee carbien. 4 xC) < y Bintan = = limt+)Cx0) -'Cx0) = f(xo+1)-fCx) - = Ax-> 0 X
f'(xo):gtre can bien Syla gtei can be diax tal 40). -> Tai Yo, nil bien x=dv the bienyse w ↑ Long = 13C40) / dvc. VD Q= 100 1.5. MPPL12022) =? - lOMoAR cPSD| 49519085 of noocLoisfoarrain .
Tai this dimmeic s dung law dong tang them scalltun,
sai long thing I'll sai plain.
3 Quy lot loi ich can bien grandi.
FCX) nghich bien voi x tillion. · · F"(x) s0 vai x dillion. UD: Q=100.16 =>0= 1001.1 Q" 100 = (d-1). 18-2 = lOMoAR cPSD| 49519085 It 24 He .x. is'co gian (9) 'co He is gian clay a
the x taixo. -> T itian to, new blew & x
↑ 1% the bienyse they do I long bring 121%
UD. Hair cai D= Gp-DF. Hay time his soco gian aid caie the gtes tai milc gid $4. Cp+P=ga .p oop =- => 24 (%1 = nil > Tai muic gid $4, thing girl
bain them 4% the cases gran 140. 5 Toi vin ham a bien.
chingsNext sis van tomis ring ham + bi.ie lOMoAR cPSD| 49519085 K. lOMoAR cPSD| 49519085 AL Choy -
= 7Cx) cs do hair caps a thi (a, b). *= (a, b). FCx) = EcxoTEcxoscicos,incx0) (x-401" .. + X · (x-XS"; x - - RnCx) = 7 fri(Y (x-Xo)"h Chung3:Tien plan.
① Ving dungtich plan along point. F'(x) f(x) = lOMoAR cPSD| 49519085
the the this gran CtER). lamic dai titait. kleongpliailu now ching not voin. -> # -- ECt
#SICt) Ot => Neil isgrid that K(t) 10 the hig = &c dvoic xotinh => KC+) drocxtins. SIC dt Sloot"sdt = nor is+c - ot" - a -
K) (0) 200.015+c 55 =>c = 05. = = Vay: KCt) 200t15 + 85. = lOMoAR cPSD| 49519085
12 xtins him ting the bit him can bless. U2, Cho MR 10-4.. Vaius = hair cir TR. A R SC10-40) do = R (0) = C 0 =) = => ② Ving dung tide plan xtink.
Hamcai QD D(P), bill dien long can the p. =>P=D"(E). = Hamclurges 3(P). - lung-- ->P=SH(0)· = G
Daig Ni SP" CR3de-Po.Qo CS Eqtri = = >Ps - Nsx 10.00- * 5"Cada = = 2
Choham cauctai P35eo.G => G=4...in lOMoAR cPSD| 49519085 9" CS (35-42 dCK) 4.29 · = - IsroloOilHI- ⑤ Tiel plan say song. D cho laim s'+ + C SECXdx= EECXdx (t> a). · Chong4. Hm alive bein ① Gioi has kep - AN:Cho EMnCXnc Yn)3+8 n=1. # Acab neil: timAMn= 3Mn1;t33tn= 1 va ACoil). AMn CLE-12 = lOMoAR cPSD| 49519085 aintno In it*memimra m s: ammen o UClim 2x3 + => M011;3). x -> 1 -3
Lay day them tayy'MrCxniyn) saw cho lim Mn = Mo (123]. Slim => xn= 1 lim yn 3 = lOMoAR cPSD| 49519085
vs limit. Muchin), lmMn =0(oi0). Y -> 0 = timECMn 0 lim timoC1) = = Lay NCIifC"IPo, Eni LinECNG = lim = -> limy khing co gio; han kee & =
7Cxy) xdinhtren D, Mo (40,yo) ED. Fl (oigo) tim y)-E(xoiy c · = Ax Eycxoiyss=tim Ey-Es(xino · Ay lOMoAR cPSD| 49519085 1 FCx,y) 244+ = y; M1273). -E12is 25: Fx12i3 tim is = #X-0 -1 -O 32-2.2.srsn lim = Ax #X - lim #x->0 him FIAT-s - Eccis Laic: Fg12is) Luma - = =--- tim RTC = lim C4Ay 253 25 + = Alto lOMoAR cPSD| 49519085 8=0l.=o.KOLO.K=0. 29 =
0.8 => Neil (190 + voi coust -> 51018%. # aic tel. If Chic teethis do. Cho z=F(x,y) = 7CM), MCX, Y). (m) lOMoAR cPSD| 49519085 SCMocr) GM: MMo= 5 CMo.r) GM: MMoxr] Cding) =
Mo (40%) dioe goil diemonic dai ni Fr · >0 saw cho: FCM) > FCM) FSCMoirs (CM3
Mo (40%) dioe goita diemectianell Fr>0 sa0 cho: FCM) < FCM) FSCMoirs (CM3 dii: Mo ladin doing. an 7'x[Mo), and Fxy (Mos D=/a" = = = = => Flya (MO), ac2 Fip (Mo) l New to = being loaictei. a
AC0DO => No tadicatic. Tan <0=>Motcricdai > - 70 an No laarction.
)0 -> sir dung #L de'check. = X U = n0X+42-6xy-24x ~AK can: UI =c0x-by-24 =Cy 6X 0 - = lOMoAR cPSD| 49519085 MC12; 36) too" ding => AR di:Vixz c0 - = Hyx 6 =-
=>D=/- ) = 430 -> Mo radicicter.
Ma au = 2030 => Mo lad' are tell. #Neel '
free tap D haim soas I ciction Mo va khong dat ascic dai now theham si GTNN1D tai gial' tri 0. = t ECxcys -BK can:L= + x (D-g(xcys). M otactantlyCMOs 1, CMOs 0 = = o A 'ding
AK ai: No lad' diving:hi L"x2 (Mo) G2= Y" CMos - = = 21 L"yx (Mos Lzz v"Y2(Mos = 9=g'x (Mo) 92 gy CMos = lOMoAR cPSD| 49519085 a.ge a) - => > # - 010 ano-a 10 Mo-ct x"+y= x (12-3x-44) + x= 36125 ( FI = 40125 x= 2125 13s I **= =- 50 <0=> Molact.




