Lý thuyết chương 3: Systems of linear equations | Môn toán cao cấp

lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU
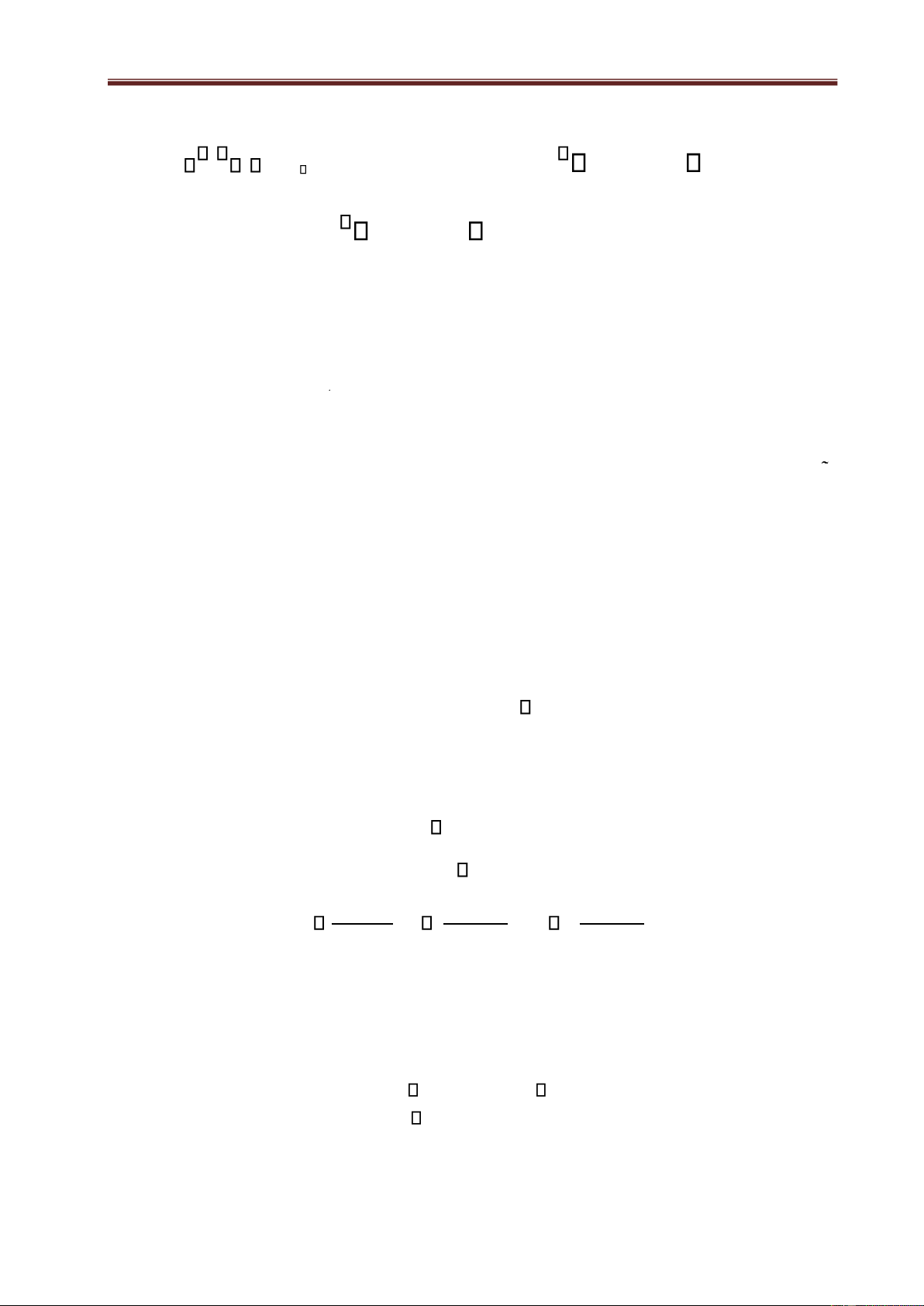
Chapter 3. Systems of linear equations 3.1 Concepts
A system of linear equations (or, more briefly, a linear system) of m equations and n
unknowns x ,x ,...,x1 2 n can be written as
a x11 1 + a12x2 + ... + a1nxn = b1
a x21 1 + a22x2 + ... + a2nxn = b2 (3.1)
..................................................
am1x1 + am2x2 + ... + amnxn = bm
where aij and bi are constants. The aij is the coefficient of the unknown x j in the ith
equation and the number bi is the constant of the ith equation.
The system (3.1) is called a square system if m = n, that is, if the number m of
equations is equal to the number n of unknowns.
The system (3.1) is said to be homogeneous if all the constant term are zero, that is,
if b1 = 0, b2 = 0, …, bm = 0.
A solution of the system (3.1) is a sequence of n numbers c ,c ,...,c1 2 n for which the substitution x1 c ,x12 c ,...,x2 n cn
makes each equation a true statement.
The set of all solutions of the system is called the solution set or general solution of the system.
We say that a system of linear equations is consistent if it has at least one solution
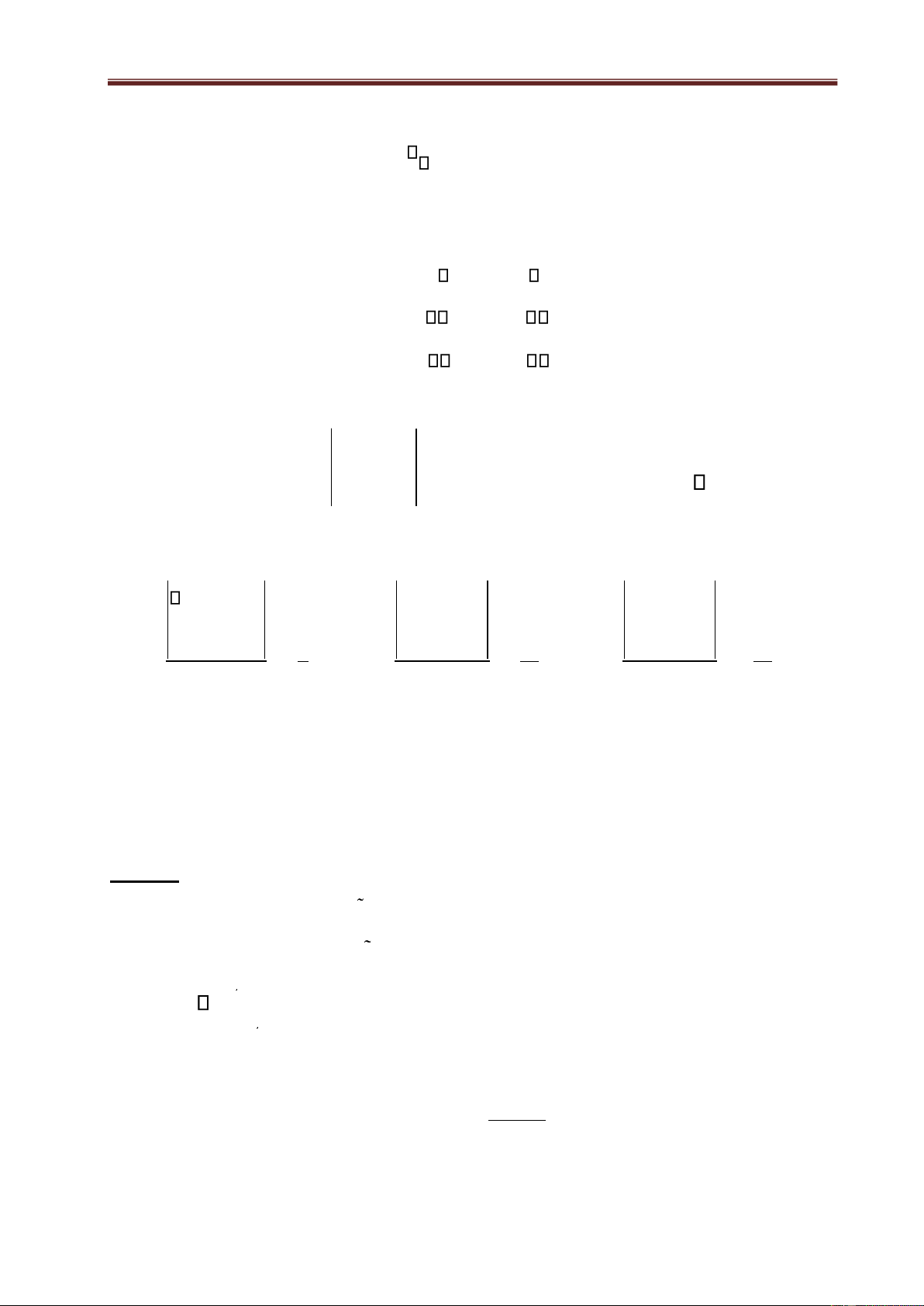
(it has either one solution or infinitely many solutions) and inconsistent if it has no solutions. The matrix a11 a ... a12 1n 1 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU A a21 a22 ... a2n ... am1 am2 ... amn
is called the coefficient matrix for the system (3.1). The matrix a11 a ... a b12 1n 1 A = a21 a 22 ... a2n b2 ... am1 am2 ... amn bm
is called the augmented matrix for the system (3.1).
Each row of the augmented matrix consists of the coefficients and constant on the
right of the equal sign form a given equation in the system. The first row is for the
first equation, the second row is for the second equation etc. Likewise each of the
first m columns of the matrix consists of the coefficients from the unknowns. The
first column contains the coefficients of x1 , the second column contains the
coefficients of x2, etc. The final column (the m+1st column) contains all the constants
on the right of the equal sign.
The system (3.1) of m linear equations in n unknowns is equivalent to the matrix equation a11 a ... a 12 1n x1 b 1
a21 a22 ... a2n . x2 = b2 or AX = b. (3.2) ... ... ... am1 a m2 ... amn xn b m 2 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU where A a T
ij m n is the coefficient matrix, X x ,x ,...,x1 2 n is the column vector of unknowns and b b ,b ,...,b T 1 2 m
is the column vector of constants.
3.2 Condition for existence and uniqueness of solution
Theorem 1 (Kronecker-Capelli theorem). The system of linear equations (3.1) is
is consistent if and only if the rank of its coefficient matrix A is equal to the rank of its augmented matrix A.
Định lý 2. The system of linear equations (3.1) has unique solution if and only if the
rank of its coefficient matrix A is equal to the rank of its augmented matrix A and
equals the number of unknowns (= n).
3.3 Methods for solving system of linear equations
3.3.1 Methods for solving Cramer system of linear equations
a) Definition. The Cramer system of linear equations is a system of square linear
equations (the number of equations is equal to the number of unknowns) in which
its coefficient matrix is non-singular (det(A) 0).
b) Theorem. The Cramer system has a unique solution. c) Formula of solution
Theorem (Cramer’s rule). Let Ax b be the Cramer system of linear equations
with n unknowns. Then, its solution Ax b is given by the folowing formulars
x1 det(A )1 ,x2 det(A )2 ,...,xn det(A )n , det(A) det(A) det(A)
where Aj is the matrix received by replacing the jth column of A by b. Example.
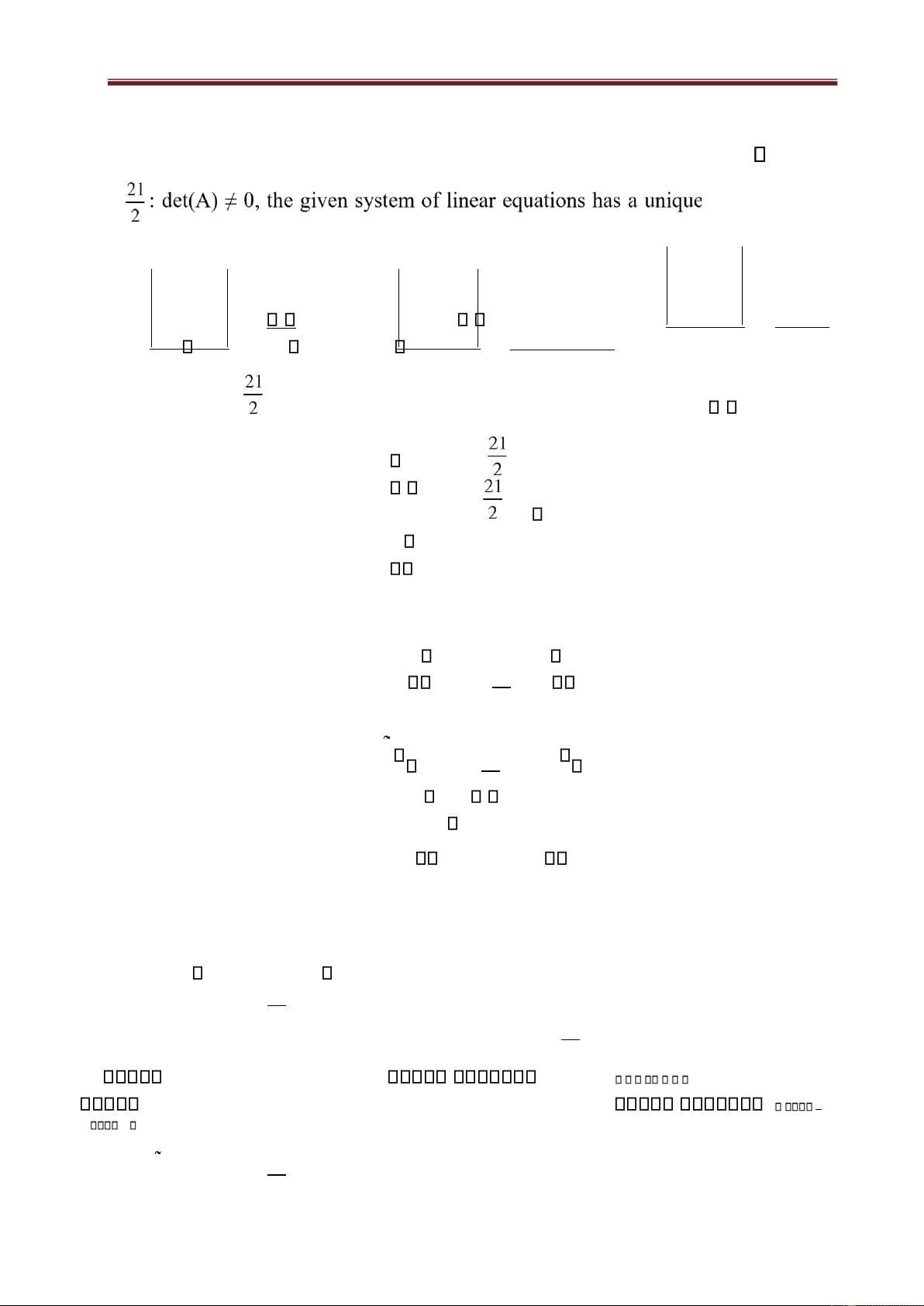
Solve the following system of equations + y + 2z = -1x 2x - y + 2z = -4 3 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU 4x + y + 4z = -2
Solution. The coefficient matrix is 1 1 2 A= 2 -1 2 4 1 4 We have 1 1 2 det(A) = 2 -1 2 = -4 + 8 + 4 + 8 – 2 – 8 = 6 0 4 1 4
Therefore, the given system of linear equations is the Cramer system. We obtain that
1 1 2 1 -1 2 1 1 -1 -4 -1 2 2 -4 2 2 -1 -4 -2 1 4 6 4 -2 4 12 4 1 -2 12 x = = = 1, y = = = 2, z = = - = -2 det(A) 6 det(A) 6 det(A) 6
Then, the unique solution to the system is (1, 2, -2).
3.3.2 Method for solving the general system of linear equations
Suppose that we solve a general system of linear equations of m equations and n unknowns (3.1): Method: • Compute r(A) and r(A). • Compare r(A) with r(A):
+) If r(A) r(A) then the system of linear equations (3.1) has no solution.
+) If r(A) = r(A) = the number of unknowns (=n) then the system of linear equations
(3.1) (3.1) has unique solution defined by Cramer’s rule: det(A )j xj = (j = 1, 2, …, n). det(A) 4 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU
+) If r(A) = r(A) = r < n then the system of linear equations (3.1) has infinitely many solutions:
Show a sub-determinant of size r and not zero of A, denoted by Dr. Then, the
given system of linear equations is equivalent to the system of r equations of the
given system that has the coefficient of the unknowns that make Dr. r these equations
are called the r main equations of the system (3.1). r unknowns of the system (3.1)
has the coefficient forming r columns of Dr called r main unknowns, (n - r) the
remaining unknowns are called the sub-unknowns. We solve the system of r main
equations and r main unknowns by moving (n - r) sub-unknowns to the right side
and considering them as parameters, we get the Cramer system. Solving that Cramer
system, we get the formulas that represent r main unknowns through (n - r) sub- unknowns.
Example. Solve and argue the following system of linear equations x1 + 2x + ax = 32 3 3x - x - ax = 1 2 3 2 2x + x + 3x = b1 2 3
Solution. The coefficient matrix for the given system is 1 2 a 1 2 a
A = 3 -1 -a det(A) = 3 -1 -a = 2a – 21. 2 1 3 2 1 3
The augmented matrix of this system is 1 2 a 3 = 3 -1 -a 2 . A 2 1 3 b 5 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU * The case a solution, that is: 3 2 a 1 3 a 1 2 3 2 -1 -a 3 2 -a 3 -1 2
b 1 3 5a ab 21 2 b 3 4ab 10a 21 2 1 b 21 - 7b x = = , y = = , z = =
det(A) 2a 21 det(A) 2a 21 det(A) 2a 21
* The case a = : the given system of linear equations has become x1 + 2x + 2x = 33 3x - x - 12x = 23 2x + x + 3x = b1 2 3
So, the augmented matrix of the system is 21 1 2 2 : 3 21 A = 3 -1 - 2 : 2 . 2 1 3 : b
Use elementary operators to transform the augmented matrix into Echelon matrix 21 = 13 2 -1 - 2122 : 2 : 3 R ( 3) RR ( 2) R11 23 RR32
100 2 -7 -42 : -3 -18 : b - 212 : 3-76 R2 73 R3 R3 A 6 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU 2 1 3 : b 1 2 : 3 0 -7 -42 : -7 0 0 0 : b - 3 We see that r(A) = 2.
- If b ≠ 3 then r(A) = 3 r(A) ≠ r(A) the given system has no solution.
- If b = 3 then r(A) = 2 r(A) = r(A) = 2 < 3 the given system has 1 21 2 infinitely many solutions. We see is sub- determinant of A and 7 0 3 -13 -1
. Then, the given system of linear equations is equivalent to the following system: 3 x1 + 2x = 3 - 2212 x3 x1 = 1 + 23 x3 xx12 = 1 + = 1 - 6t2 t , t R. 3x - x = 2 + 1 2 212 x3 x 2 = 1 - 6x3 x = t3
, b is arbitrary: the given system has a unique solution, that is 5a ab 21 4ab 10a 21 21 - 7b x = , y = , z = 2a 21 2a 21 2a 21 21 a = 7 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU - The case
2 : the given system has no solution. b 3 21 a =
- The case 2 : the given system has infinitely many solutions with the formula of b 3 solution is: x1 = 1 + t x2 = 1 - 6t , t R. x = t3
3.3.3 The Gauss-Jordan elimination method
The Gauss-Jordan elimination method including the following steps:
Step 1: We use elementary row operations to transform the augmented matrix A into
Echelon matrix. Suppose the obtained Echelon matrix is A1. Then, the given system
of linear equations is equivalent to the system of linear equations whose the augmented matrix is A1.
Step 2: Solving the system of linear equations whose the augmented matrix is A1 by
starting from the last equation, then substitute the value of the newly found
unknowns into the equation on it and continuing to solve until the first equation, we
will obtain the solution of the given system of equations. 8x1 + 4x + 2x = 242 3 4x + 10x + 5x + 4x = 1 2 3 4 32
Example. Solve the system of linear equations: . 4x + 10x + 13x + 8x = 1 2 3 4 52 8 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU 4x + 4x + 9x = 212 3 4
Solution. The augmented matrix of the given sytem of linear equations is 8 4 2 0 24 A = 4 10 5 4 32 4 10 13 8 52 0 4 4 9 21 1122 R RR11 8 + R 23 R2R3 0 4 2 0 24 8 4 4 20 ( 1)( 12)RR22 RR34 RR34 8 0 4 2 0 24 8 4 4 20 0 8 12 8 40 0 0 8 4 20 0 4 4 9 21 0 0 2 7 11 8 4 2 0 24 ( )R3 R 4 R4 0 8 4 4 20 0 0 8 4 20 0 0 0 6 6
We see that r(A) = r(A) = 4. So, the given system has a unique solution. The
given system of linear equations is equivalent to the system 8x1 + 4x + 2x = 242 3 8x + 4x + 4x = 202 3 4 9 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU 8x + 4x = 203 4 6x = 64 From here, we have
x4 = 1 x3 = (20 – 4x4) = (20 – 4) = 2
x2 = (20 – 4x3 – 4x4) = (20 – 4.2 – 4.1) = 1
x1 = (24 – 4x2 – 2x3) = (24 – 4.1 – 2.2) = 2.
Then, the given system has a unique solution is (2, 1, 2, 1).
3.4 Homogeneous linear systems
3.4.1 Definition. A system of linear equations is said to be homogeneous if all the
constant terms are zero. Thus, a homogeneous system of linear equations of m
equations and n unknowns x ,x ,...,x1 2 n has the form
a x11 1 + a12x2 + ... + a1nxn = 0
a x21 1 + a22x2 + ... + a2nxn = 0 (3.3)
..................................................
am1x1 + am2x2 + ... + amnxn = 0 or
Ax = (0)m 1, where A = (aij)m n, x = (x1, x2, …, xn)T. Note.
* A homogeneous linear system always has the zero vector (0,0,...,0) as a
solution, called the zero or the trivial solution.
* The homogeneous linear system (3.3) has nontrivial solutions (has infinitely many
solutions) if and only if r(A) < the number of unknowns (= n). 10 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU
* Especially, the square homogeneous linear system (the number of equations equal
to the number of unknowns) has nontrivial solutions if and only if det (A) = 0.
Example. Find the value of m such that the following system of linear equations has
nontrivial solutions: 3x + y + 10z = 0 2x +my + 5z = 0 x + 4y + 7z = 0
Solution. This is the square homogeneous linear system. For the given system to
have nontrivial solutions then 3 1 10 det(A) = 2 a 5 = 11(a + 1) = 0. 1 4 7 It means that a = -1.
3.4.2 Structure of solutions of homogeneous linear systems
Theorem. Let A be an m×n matrix of rank r, and consider the homogeneous linear
system in n variables with A as coefficient matrix. Then, the set of all solutions of
this homogeneous linear system is a subspace of the vector space Rn. Furthermore,
the dimension of this subspace is n - r.
This subspace is called the solution space of the homogeneous linear system (3.3).
Definition. Each basis of the solution space of the homogeneous linear system is
called a set of basic solutions of this homogeneous linear system.
Note. A set of solutions of the homogeneous linear system (3.3) is a set of basic
solutions if it satisfies the following conditions
i) This set of solutions has exactly n - r (A) solutions.
ii) This set of solutions is linearly independent.
Example. Find the dimention and a set of basic solutions of the following system of linear equations: 11 lOMoAR cPSD| 49519085
Lecturer: Nguyen Duong Nguyen, Mathematics Department, Faculty of Basic Science, FTU 2x1 - x + 5x + 7x = 02 3 4 4x - 2x + 7x + 5x = 1 2 3 4 0 2x - x + x - 5x = 1 2 3 4 0
Solution. We have A = 24 -2 7 -1 5 75 R ( 2) RR ( 1) R 11 32 RR32 02 0 -3 -1 5 7-9 R2 () R3 2 R3 -1 5 7 0 0 -3 -9 2 -1 1 -5 0 0 -4 -12 0 0 0 0 Therefore, r(A) 2.
From this, we obtain the dimension of the solution space is 4 2 2 .
The given system of linear equations is equivalent to the system of linear equations 2x 1 x2 5x + 7x = 3 4 0 x 2x 8x2 1 4 3x3 9x = 4 0 x3 3x4
Choose x1 = 1, x4 = 0, we have a solution of the given system: x(1) = (1, 2, 0, 0)
Choose x1 = 0, x4 = 1, we have a solution of the given system: x(2) = (0, -8, -3, 1)
The set {x(1), x(2)} is linearly independent, so {x(1), x(2)} is a set of basic solutons of
the given system of linear equations. 12