



Preview text:
lOMoAR cPSD| 47305584
Đại Số Tuyến T nh CH O H A MA TRẬN
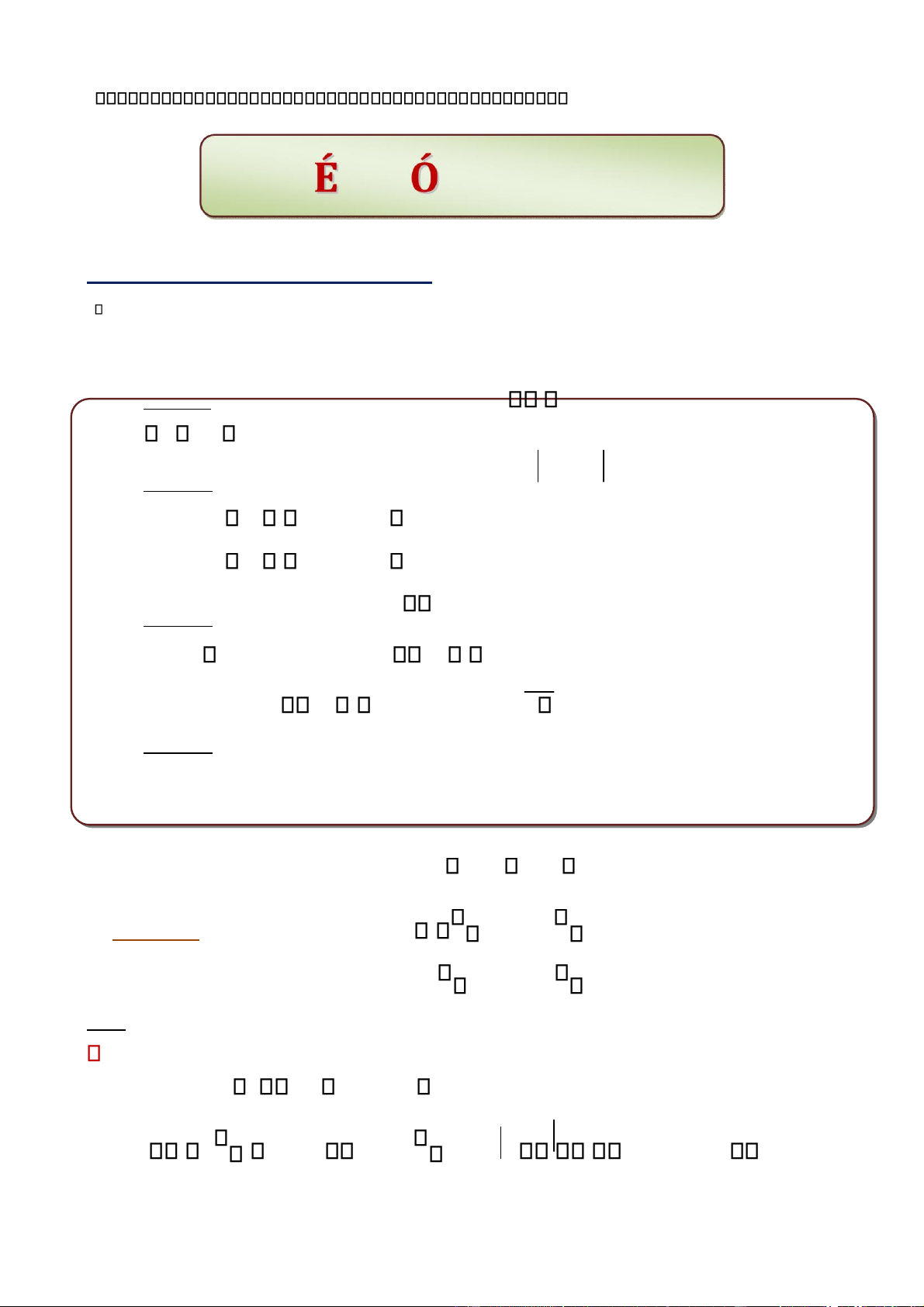
B i toÆn CH O H A MỘT MA TRẬN (Diagonalizable) : Cho ma tra n vu ng An
n . Hªy chØo h a ma tra n n y.
Thuật toÆn :
✓ Bước 1 : Xé t phương trnh đa c trưng A
I 0. Gia i ra cÆc giÆ tri riŒng 1, 2, ,
k c bo i tương ư ng l n1, n2, , nk
✓ Bước 2 : Kié m tra • n 1 n2 ...
nk n : A không chéo hóa được. • n 1 n2 ...
nk n : A chéo hóa được.
✓ Bước 3 : T nh cÆc rank A( kI) •
j sao cho rank A( jI) n
nj : A kh ng chØo hóa được. • rank A( jI) n
nj vơ i mo i i 1,n : A chéo hóa được.
✓ Bước 4 : T m cÆc véctor ta o tha nh cơ sơ cu a cÆc kh ng gian con riŒng
tương ư ng cÆc giÆ tri riŒng. La p ma tra n S c co t l như ng véctor vư a t m đươ c. 3 2 0
B i tập 1 : ChØo h a ma tra n A 2 3 0 0 0 5 Giải : Bước 1 : 3 2 0 Ta c A I 2 3 0 nŒn A I ( 1)( 5)2 ThS.Đào-Bảo-Dũng Trang 1 lOMoAR cPSD| 47305584
Đại Số Tuyến T nh 0 0 5
Xé t phương trnh đa c trưng A I 0 ( 1)( 5)2 0 1 (bo i n 1 1) , 5 (bo i n2 2) Bước 2 : Ta c : n 1 n2
1 2 3 n (ca p cu a ma tra n A) A chØo hóa được. Bước 3 : 2 2 0 2 2 0 ➢ Vơ i 1 : A I 2 20 d2 d2 d1 00 0 0 0 4 0 0 4 2 2 0 d2 d3 0 0 4 nŒn R A( I) 2 n n1 0 0 0 2 2 0 2 2 0 ➢ Vơ i 5 :A 5I 2 20 d2 d2 d1 0 0 0 0 0 0 0 0 0
nŒn R A( 5 )I 1 n n2
A chéo hóa được. Bước 4 : x y
➢ XØt (A I X). 0, ta c nghié m to ng quÆt y . Kh ng gian con z 0 ThS.Đào-Bảo-Dũng Trang 2 lOMoAR cPSD| 47305584
Đại Số Tuyến T nh y 1 riŒng ư ng vơ i 1 l W1 y / y , né n co cơ sơ l u1 1 . 0 0 x y
➢ XØt (A 5 ).I X 0, ta c nghié m to ng quÆt
y . Kh ng gian con z y riŒng ư ng vơ i 5 l W2 y / y z, , né n co cơ sơ l z 1 0 u 2 1 ,u3 0 . 0 1 1 1 0 1 0 0 Khi đo , đa t P 1 1 0 th P AP 1 0 5 0 0 0 1 0 0 5
(đé vé thư tư cu a cÆc giÆ tri riŒng trong ma tra n P AP 1 phu thuo c
v o thư tư ca c véctor rié ng tương ư ng đươ c sa p trong ma tra n P) ThS.Đào-Bảo-Dũng Trang 3 lOMoAR cPSD| 47305584
Đại Số Tuyến T nh Lưu : 1 1 0 5 0 0
▪ Né u ta vié t ma tra n P 1 1 0 th P AP 1 0 1 0 0 0 1 0 0 5 1 0 1 5 0 0
▪ Né u ta vié t ma tra n P 1 0 1 th P AP 1 0 5 0 0 1 0 0 0 1 5 0 0
B i tập 2 : ChØo h a ma tra n A 1 5 0 0 1 5 Giải : Bước 1 : 5 0 0 Ta c A I 1 5 0 nŒn A I ( 5)3 0 1 5
Xé t phương trnh đa c trưng A I 0 ( 5)3 0 5 (bo i n 1 3)
Bước 2 : (tho a mªn, v c n 1 3 n) Bước 3 : Vơ i 5 ta c ThS.Đào-Bảo-Dũng Trang 4 lOMoAR cPSD| 47305584
Đại Số Tuyến T nh 0 0 0 1 0 0 1 0 0 A 5I 1 0 0 d1 d2 00 0 d2 d3 01 0 0 1 0 0 1 0 0 0 0
nŒn R A( 5 )I 2 n n 1 0
A không chéo hóa được. Ké t lua n
: ma tra n A kho ng ché o ho a đươ c. ThS.Đào-Bảo-Dũng Trang 5




