lOMoAR cPSD| 49519085
CH¯ƠNG IV: GIàI H¾N
BÀI 1: GIàI H¾N CĀA DÃY SÞ
I. GIàI H¾N HĀU H¾N CĀA DÃY SÞ 1. Đßnh ngh*a
ĐÞNH NGH)A 1 (Giái h¿n 0)
Ta nói dãy số (un) có giái h¿n là 0 khi n dần tới dương vô cực, nếu un có thể bé hơn một số dương bé tùy ý,
kể từ một số hạng nào ó trở i.
Kí hißu: lim u ý n 0 hay un 0 khi n . n Chú ý: lim u ý n limun. n
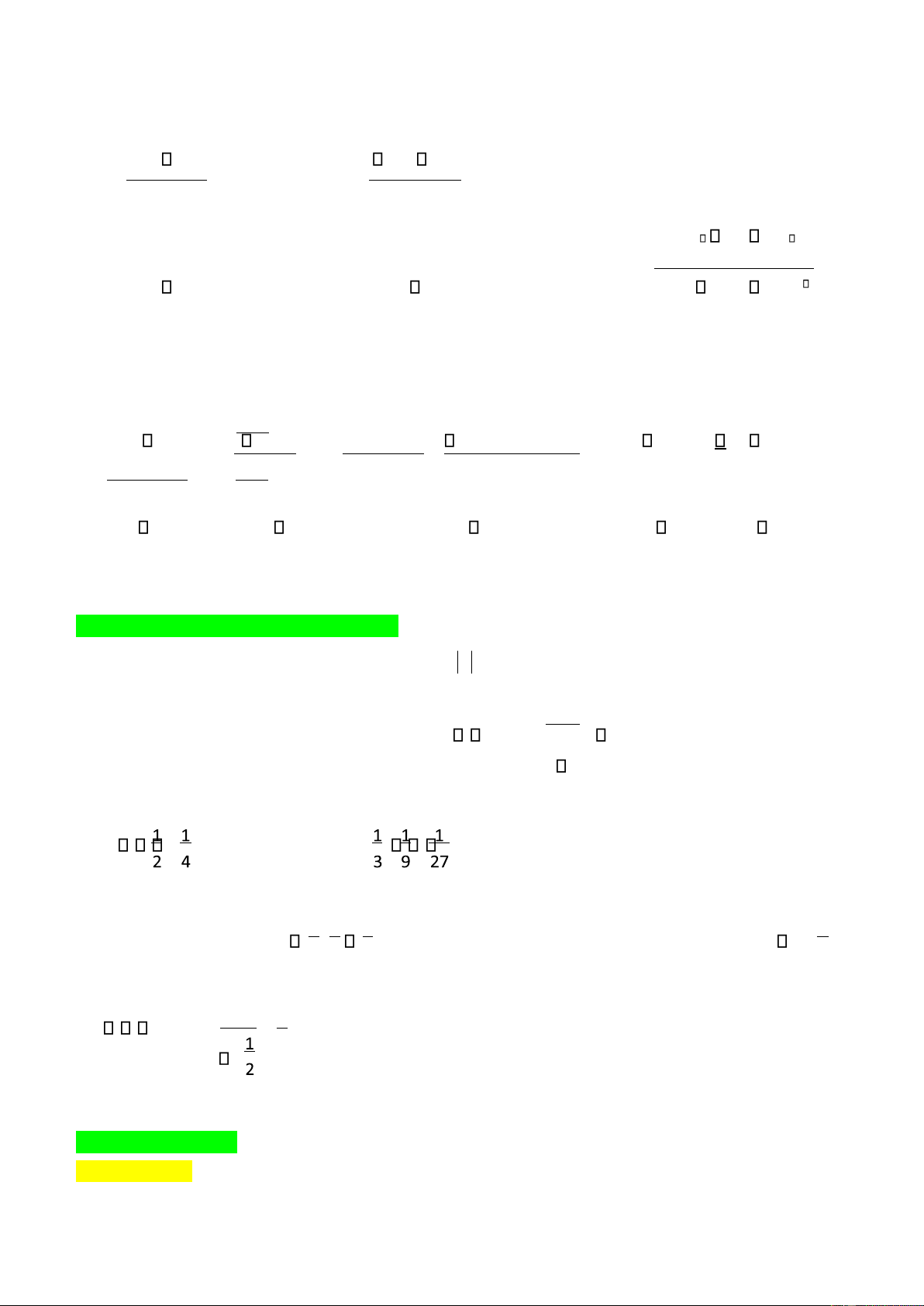
❖ Mßt sß giái h¿n 0 1 1 1 c) limý 0 a) 3 lim ý 0 b) lim ý 0 n n n
ĐÞNH NGH)A 2 (Giái h¿n hāu h¿n) Ta nói dãy số (v ùý
n)có giới hạn là số a (hay vn a ) khi n , nếu lim øv an 0 n
Kí hißu: lim v ý n a hay vn a khi n . n
2. Mßt sß giái h¿n ặc bißt
Từ ịnh nghĩa suy ra các kết quả sau: a) lim 1 ý 0 ; lim 1 ý k
0 với k nguyên dương. n n
b) limqn ý 0 nếu q ü1. c) Nếu u ý ý
n c (c là hằng số) thì limun limc cý
II. ĐÞNH LÍ VỀ GIàI H¾N HĀU H¾N ĐÞNH LÍ 1 a) Nếu limu ý ý
n a và limv bn thì ✓ lim(u v ý n n) a b lOMoAR cPSD| 49519085
✓ limøu vn n. ùýab
✓ limun ý a (b 0) vn b b) Nếu u ý n
0 với mọi n và limun a thì a 0 và lim u ý n a.
D¿ng 1: Tìm giới hạn của P n( ) lim với P n Qn( ),
( ) là hai a thức theo n. Q n( )
PP: Chia cả tử và mẫu của phân thức cho số hạng có chứa lũy thừa bậc cao nhất của n. Ví
dÿ 1: Tìm các giới hạn sau: 2n n2 1 (2n 1)(3 n)2 2n 13 ý 2 0 0 ý 2 a) lim 2 b) lim 3 c) lim 2 3 0 0 3 3n 5n 7 ø4n 5ù (n 5) Gi¿i
a) Chia cả tử và mẫu cho n2 ta ược ö 1 1 ÷ö lim 2÷ö 11 ÷ö lim 2n n22
1 ý lim÷÷ 2 n n2 ÷ý ø
n n2 ø ý lim2 lim 1n lim n12 3n 5n 7 ø÷ 3 5
72 ø÷ lim 3÷øö 5 72 ÷øö lim3 lim
n5 lim n72 n n n n
H¯àNG DẪN BÀM MÁY TÍNH 2n n2 1 a) lim 2 3n 5n 7 B1: Nhập hàm số
B2: Calc 99999999 (hoặc 106) B3: Bấm =
Câu b) c) học sinh tự giải
D¿ng 2: D¿ng sÿ dÿng công thức limqn ý 0 vái q ü1.
PP: Chia tử và mẫu của phân thức cho an với a là hệ số lớn nhất. lOMoAR cPSD| 49519085
Ví dÿ 2: Tìm các giới hạn sau: 5.2n 6.3n 3.5n 4.7n a) lim b) lim c) lim
32 1n 15n 52 2n 3.2n 2.3n 8.5n 2.7n
4.32n 2.15n 7.52 1n Gi¿i:
a) Chia cả tử và mẫu cho 3n
5.2nn 6.3nn5.23nnn 6 ý lim 5.ö ö÷ ÷ø ø32 nn 6 ý lim5.ö öø ø÷ ÷32 nn lim6 ý 0 6 ý 3 lim ý lim 3.2 2.3
3.23n 2 3.÷ ÷ø øö ö23 2lim3.ö ö÷ ÷ø ø23 lim2 0 2
Câu b) c) học sinh tự giải
III. TỔNG CĀA CÀP SÞ NHÂN LÙI VÔ H¾N q Cho (u ü
n) là cấp số nhân với công bội q thỏa mãn
1 là cấp số nhân lùi vô hạn thì có tổng S u uq uqý 2 ý 1 1 1 ... u1 1 q
Ví dÿ: Tính tổng vô hạn các số hạng của cấp số nhân sau: a) Sý 1... b) Sý ... Gi¿i ý
a) Các số hạng của tổng S: 1; 1 1; ; 1;... lập thành một cấp số nhân lùi vô hạn có công bội q 1 2 4 8 2 S ý ý1 1 1 ... 1 ý 2 2 4 1 3 IV. GIàI H¾N VÔ CĂC 1. Đßnh ngh*a ĐÞNH NGH)A lOMoAR cPSD| 49519085
Ta nói dãy số (un) có giới hạn
, nếu un có thể lớn hơn một số dương tùy ý bất kỳ, kể từ một số hạng nào ó trở i.
Kí hißu: limu ý n
Dãy số (un) ược gọi là có giới hạn khi n nếu lim( ý
un) . Kí hißu: limu ý n
Nh¿n xét: limu ý n lim( ý un)
2. Mßt vài giái h¿n ặc bißt a) limnk ý
với k nguyên dương b) limqn ý nếu qþ1. 3. Đßnh lí ĐÞNH LÍ 2 a) u Nếu limu ý ý n ý n a và limvn thì lim 0. vn u b) Nếu limu ý þ ý þ n ý n
a 0, limvn 0 và vn 0 với mọi n thì lim . vn c) Nếu limu ý ý þ n và limvn
a 0 thì limu vn n. ý .
Bảng tính limu vn n.
limun limvn limu ýa vn n. aþ0 aü0 aþ0 aü 0
Ví dÿ: Tìm các giới hạn sau: c) 2n 5 lim(n3 d)lim( a) lim 2n n b) n2 lim(n2 2n 1) n2 5n 2) n.3 1) Gi¿i
a) Chia tử và mẫu cho n lOMoAR cPSD| 49519085 5n 5n 2n ý ö÷ø n5 2 n lim 2ö÷ø n lim ý lim n.3 3 lim3
Vì üÿýlim 2ö÷ø 5nö÷øý 2 lim 2n n5 ý 0 ÿlim3n ý n.3 þ
b) lim(n2 2n ý1)
limn2ö÷ø1 n n2 1 öø÷ý ö÷ø 2
limn2.lim 1ö÷ø n n2 12 ülimn2 ý ÿ
lim(n2 2n ý 1)
Vì ýÿþlim 1ö÷ø n n2 12
ö÷øý þ1 0 Câu c), d) học sinh tự làm lOMoAR cPSD| 49519085
PHIẾU BÀI T¾P TĂ LUYÞN
Bài 1: Tính các giới hạn sau: 22n 1
n2ö÷øn n2 12 ö÷ø ý lim n n2 12 ý 0 0 ý 0 a) lim ý lim n 2n 4 n2øö1 n n2 42 ÷øö1 n n2 42 1 0 0 ÷ 3ö 12 53 ö÷ n 5 n ÷ b) lim 3 ý lim øn
n ø ý 0 3n 1 n ö÷ 3 3 13 ö÷ ø n ø
: Giới hạn của hai a thức P n( ) lim
có bậc tử nhỏ hơn bậc mẫu thì giới hạn Chú ý bằng 0. Q n( )
Bài 2: Tính các giới hạn sau: 5n23 3n32 6
n3ö÷ø5 n n363 ø÷ö ý 5 0 0 ý 5 a) lim ý lim 4n 3n 7n n ÷ö 3 4 372 ÷ö 0 3 0 3 øn n ø
b) lim 6n4 22n2 41 ý lim n4ö÷ø6 n22 n14 ö÷ø ý 6 0 0 ý 2 1 5 n 3n n ö÷ 4 14 52 3ö÷ 0 0 3 øn n ø
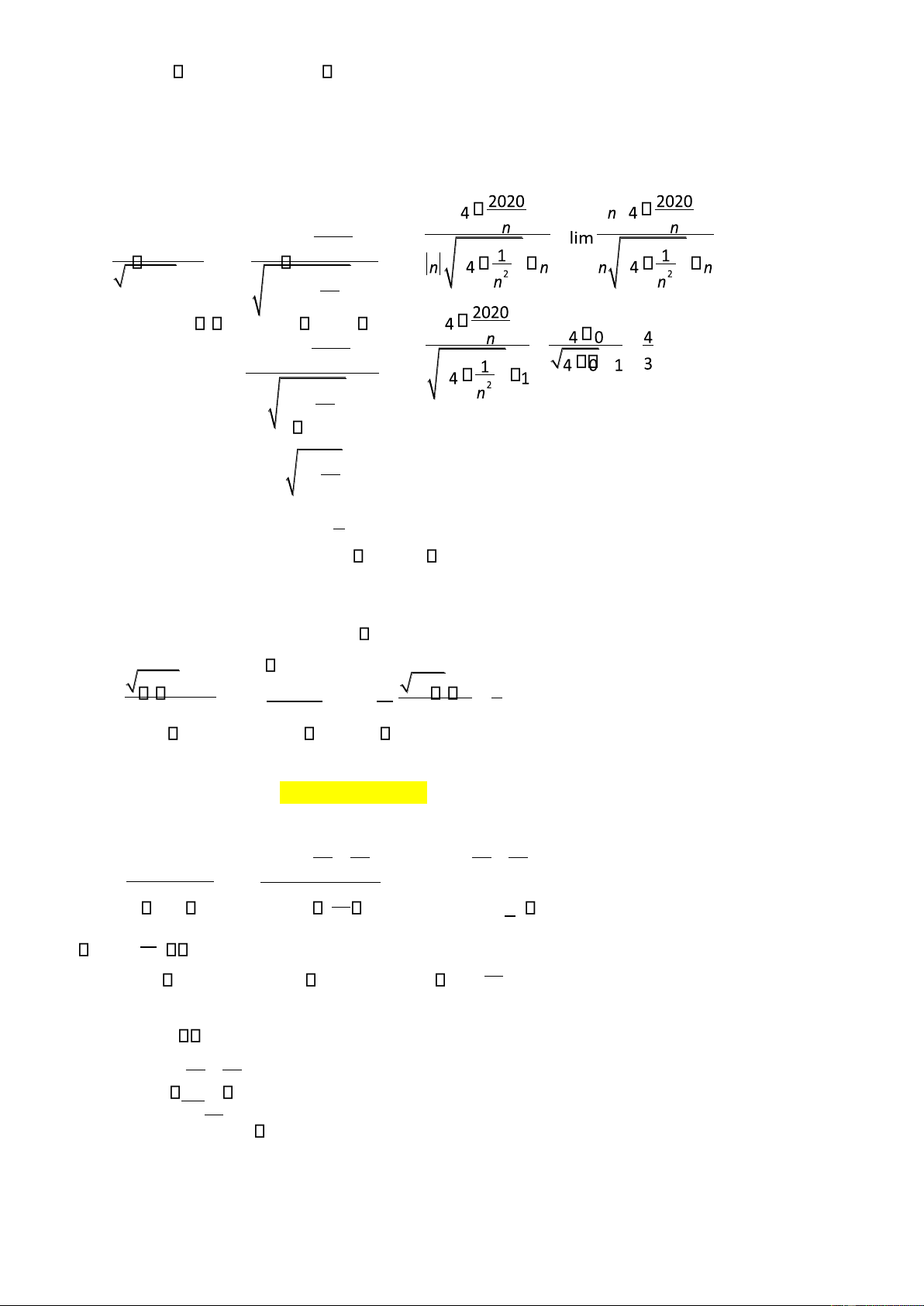
c) lim 2n n22 3 ý lim n2÷øö2 1n n32 øö÷ ý 2 3n 2n 1 n ö÷ 2 3 212 ö÷ 3 ø n n ø 2n 3n 1 n2÷ö 2 3 1 ö÷ d) lim 22 ý lim ø n nø ý 2 lOMoAR cPSD| 49519085 n 1 n ö÷ 2 12 ö÷ 1 ø n ø e) ö ö ö ö ÷ ÷ ÷ ÷ ø ø ø ø ý ö ö ö ö lim 4n 2020 ý lim
n÷öø4 2020n ö÷ø ý ÷ ÷ ÷ ÷ ø ø ø ø ö ö
lim n 4n2 1 n n ö÷ ÷ 2 4 12 ö÷ n ÷ ø ø ý ý ö ö ø n ø ÷ ÷ ø ø ö 2020ö÷ n÷4 ý lim ø n ø ý lim
nø÷÷ö ø÷ö4 n12 ø÷ö 1ø÷÷ö ö 1 ö n÷ 1 4÷ f) lim n2 1 4n ý lim ø n2 ø ý 1 0 4 ý 5 3n 2 ö 2ö÷ 3 0 3 n÷3 ø nø
Bài 3: Tính các giới hạn sau: (bậc tử > bậc mẫu) ö ö ö a) lim n4 ø÷1 ø÷ ý ÷ø 33n2 2 ý lim n4 n32 n24 lim n 1 n32 n24 ÷öø ý n 2 3øö n23 ÷øö 1 n23 n ÷1 ülimný ÿ
Vì ÿýlim1 n n32 24 ý þ1 0 ÿ 2 ÿ 1 þ n3 lOMoAR cPSD| 49519085 4 2 n4ö÷8 32 23 14 ö÷ n ÷ö 2 8 32 23 14 ÷ö
b) lim8n 32n 2n 1 ø n n n ø ý lim ø n n n ø ý ý lim 2n 4n 3 2ö
n ÷ 2 ÷ ø n n ø n n2 2 4 3 ö 2 4 3 ülimn2 ý ÿ ÿ 3 2 1 Vì ýlim8 n n n2 3 4 ý ü4 0 ÿ 4 3 ÿ 2 þ n n2 c) lim
2n n34 22 3 lim n4÷øö2 n12 3n 2n 1 ö 2 1 ö 3 2
n34 ÷öø ý lim nö÷ø2 n12 n3÷3 3 ÷ 13 n n34 öø÷ ý ý ü ø limný n n ø n ÿ ÿ 1 3
Vì ý 2 2 4 2 ÿÿlim n n2 1 ý þ3 0 3 þ n n3 4ö 2 5 ö ö 2 5 ö
3n4 3 2n 5 n ÷ø 3 n3
n4 ÷ø ý lim nø÷ 3 n3 n4 ÷ø ý d) lim ý lim 2n 4 3ö 4 ö 2 n ÷2 ÷ ø n 3 3 4 ülimný ÿ n ø ÿ 2 5 lOMoAR cPSD| 49519085
Vì ýlim 3 n n3 4 ý ü3 0 ÿ 4 2 ÿ 2 þ n3
Bài 4: Tính các giới hạn sau: a) ø ø ùø
lim n2 2n n ùý lim n2 2n n 2
n2 2n n ù ý lim n2 2 2n n 2 ý lim2 2n n 2n n n 2n n n 2n n 2n 2 2 ý lim ý lim ý
ý1 n÷ö 1 2 1÷ö 1 2 1 1 0 1 ø n ø n D¿ng:
(A-B) l°ợng liên hợp là (A+B): (A-B)(A+B) = A2 - B2 b) ø ù lim
n2 2n 3 n ø ùø ù
n2 2n 3 n
n2 2n 3 n
n2 2n 3 n2 ý limý lim
n2 2n 3 n
n2 2n 3 n ö 2n 3
nö÷ø2 n3 ÷ø
ý lim 2 n3 ý1 ý limý lim
n2 2n 3 n n÷ö 1 2 32 1÷ö 1 2 32 1 ø n n ø n n d) ø ù lim
n 1 n2 2n 5 ý lim 4 ý lim 4 n 1 n 1 2 52 nö÷1 1 1 2 52 ö÷ n n ø n n n ø lOMoAR cPSD| 49519085 ý lim 1.lim 4 ý 0 n ö 1 2 5 ö ÷1 1 ÷ ø 2 n n n ø
Vì üÿÿÿýlimlim 1n ý 0 4 ý 2 ÿ ö 1 2 5 ö ÿ ÷1 1 ÷ ÿþ ø 2 n n n ø e) lOMoAR cPSD| 49519085 ý ù ø ù ý ø ù ø ù ö ö ÷ ÷ ø ø ø ùø ù ö ö ÷ ÷ ø ø ö ö ö ö ÷ ÷ ÷ ÷ ø ø ø ø ö ö ÷ ÷ ø ø ö ö ö ö ÷ ÷ ÷ ÷ ÷ . ÷ ø ø ø 1 ø ö ö ÷ ÷ . ø ø 1 ý ý ø ý lim ý lim ý lim ý lim lOMoAR cPSD| 49519085 ý lim ý lim Dạng ø ù f) lim
3 3n n 43 9n2 6n 1