lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân Gv: Phan Ngô Tuấn Anh
Khoa Toán – Thống Kê, UEH
Chương 5. Đạo hàm & vi phân I. Đạo hàm (derivative) 1.1 Định nghĩa
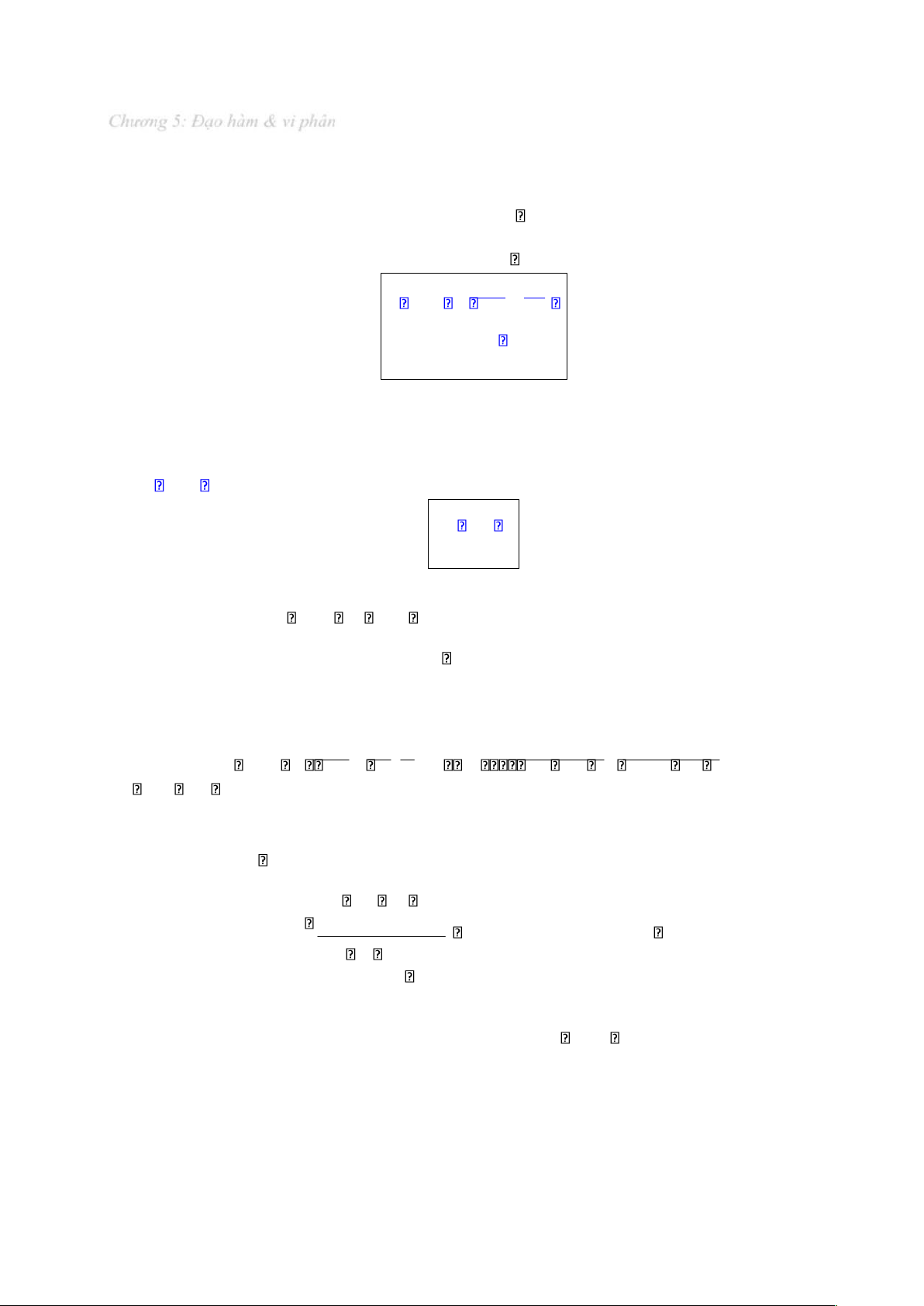
Đạo hàm của hàm số f(x) tại x , ký hiệu là 0
f (x ) 0 , ược ịnh nghĩa là giới hạn: f (x ) 0 xlim x0 f(x)x f(x )x0 0
Nếu giới hạn trên tồn tại hữu hạn thì ta nói hàm số f(x) có ạo hàm (khả vi – differentiable) tại x 0
Ví dụ: Cho f(x) x 2 , chứng minh rằng f (x) 2x x Lấy x0 , theo ịnh nghĩa: f (x ) 0 xlim x0 f(x)x f(x )x0 0 xlim x0 xx2 xx02 00 0 lim (x x )(x0 x )0 x x x x 0 0 xlim(x x x ) 0 0 2x0
Vì x tùy ý nên ta kết luận 0 f (x) 2x x Trang | 1 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân ln(1 3x 2 ) Ví dụ: Cho f(x) x khi x 0 0 khi x 0
Hàm số f(x) có khả vi tại 0 hay không? Nếu có, tính f (0)
Để hàm số f(x) khả vi tại 0 thì giới hạn sau phải tồn tại hữu hạn: f (0) lim f(x) f(0) x 0 x 0 ln(1 3x 2 ) x 0 0 lim x 0 x 0 limx ln(1x 23x 2 ) 00 0 ln(1 3x2 ) limx 0 3x2 3 3 (chú ý rằng ln(1 3x2 ) x 0 1 vì ln(1 t) t 0 1) 3x2 t
Vậy, hàm số f(x) khả vi tại 0 và f (0) 3 1 Ví dụ: Cho f(x) x khi x 0 xsin 0 khi x 0
a) Hàm số f(x) có liên tục tại 0 hay không?
Để hàm số f(x) liên tục tại 0 thì limf(x) f(0) x 0 Trang | 2 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân Trong ó, 1 limf(x)x 0 limxsinx 0 x 0 limf(x)x 0 f(0) f(0) 0 1 (chú ý rằng, xsin x1 x 0 0 vì xsin x
là tích của một ại lượng
tiến về 0 và một ại lượng bị chận)
Vậy hàm số f(x) liên tục tại 0.
b) Hàm số f(x) có khả vi tại 0 hay không?
Để hàm số f(x) khả vi tại 0 thì giới hạn sau phải tồn tại hữu hạn: f (0) lim f(x) f(0) x 0 x 0 x 0 lim xsin 1x 0 x 0 x 0 1 limsinx 0 x 1 Giới hạn limsinx 0 x1
không tồn tại vì khi x 0 thì sin x
không hội tụ về bất cứ giá trị nào cả.
Vậy, hàm số f(x) không khả vi tại 0 (dù rằng liên tục tại 0).
Nhận xét: Ví dụ trên cho ta thấy, hàm số liên tục nhưng chưa chắc có ạo hàm (khả vi). Trang | 3 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân Ghi chú: df(x) Ngoài ký hiệu f (x) , ta còn dùng ký hiệu ể chỉ ạo
hàm của hàm số f(x) : dx f (x) df(x) dx d(x )
Chẳng hạn, thay vì viết (x 2 ) 2x, ta có thể viết là 2 2x dx Đặt
x x x0 ( ộ biến thiên của x) f
f(x) f(x )0 f(x0 x) f(x )0 ( ộ biến thiên của f(x) ) thì f (x ) 0 limx 0 xf lim f(x0 x) f(x )0 x 0 x f Tỉ số
có ý nghĩa là ộ biến thiên (tăng, giảm) trung bình của hàm số f(x) khi biến số x tăng x
thêm 1 ơn vị. Trong kinh tế, nó chính là biên tế của ại lượng f(x) . Chẳng hạn, nếu x là sản lượng f
và f(x) là chi phí sản xuất (hàm chi phí) thì tỉ số
chính là mức tăng chi phí trung bình khi tăng x
sản lượng thêm 1 ơn vị, ược gọi là chi phí biên (marginal cost). f Đẳng thức f (x ) 0 limx0
x nói lên rằng, khi ộ biến thiên của x khá nhỏ, nghĩa là x 0, thì ộ f 0 : biến thiên trung bình
có giá trị rất gần f (x ) Trang | 4 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân x xf f (x ) khi x 0 0
Vậy, khi ộ biến thiên của biến số khá nhỏ thì ộ biến thiên trung bình có thể xấp xỉ với ạo hàm.
Kế tiếp, ta ịnh nghĩa các ạo hàm một phía (one-sided derivatives) của hàm số.
Đạo hàm bên phải (right-hand derivative) của hàm số f(x) tại x là giới hạn bên phải: 0 f (x ) 0 lim f(x) f(x )0 x x x x 0 0
và ạo hàm bên trái (left-hand derivative) của hàm số f(x) tại x là giới hạn bên trái: 0 f (x ) 0 lim f(x) f(x )0 x x x x 0 0
Áp dụng kết quả trong phần giới hạn hàm số (chương 4 - giới hạn & sự liên tục), ta có:
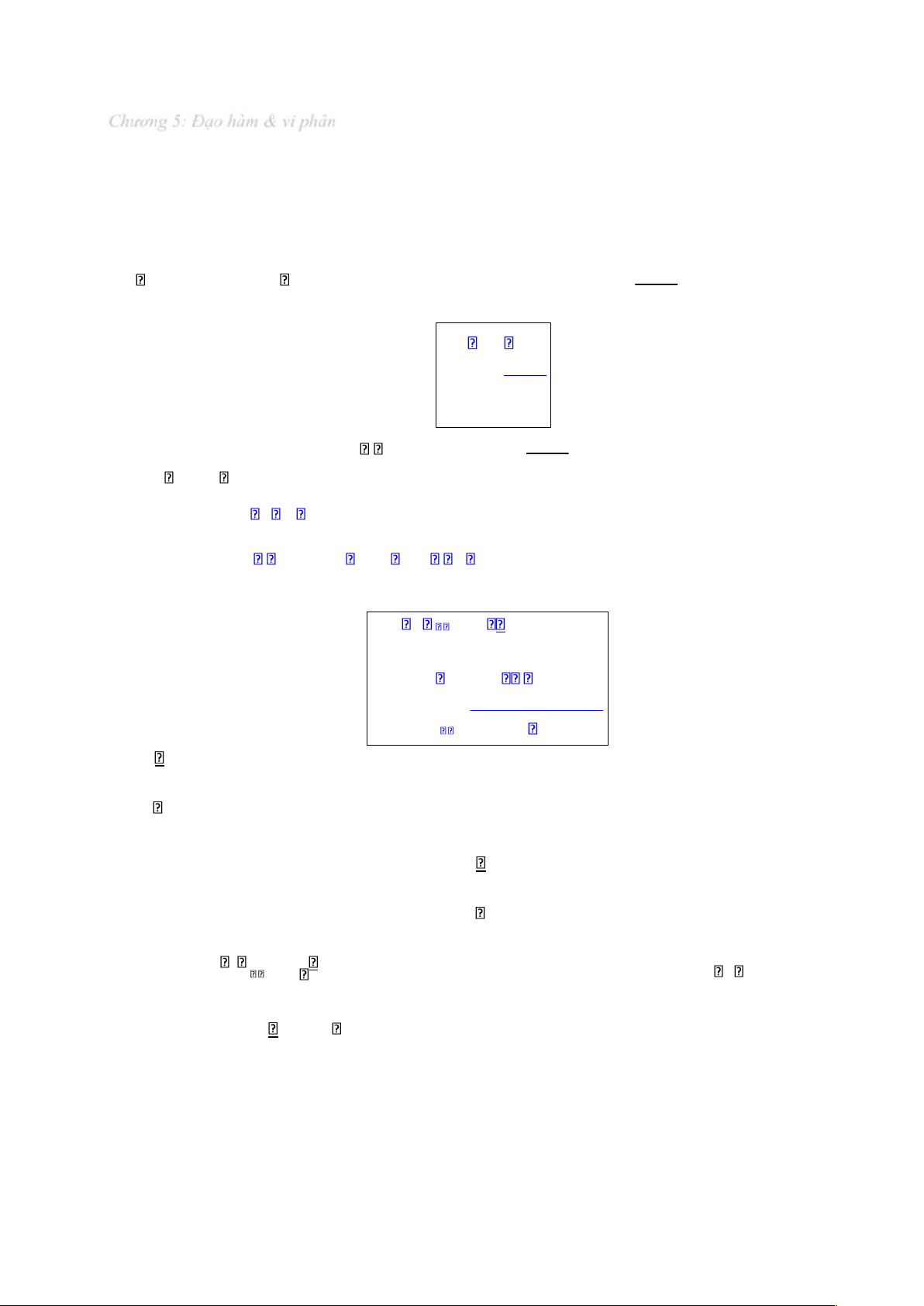
Mệnh ề. Để hàm số f(x) có ạo hàm (khả vi) tại x thì iều kiệu cần và ủ là 0 f (x ) 0 f (x ) 0 Khi ó: f (x ) 0 f (x ) 0 f (x ) 0
Ghi chú: Đẳng thức f (x ) 0 f (x ) 0 f (x )
0 nói lên rằng, khi hàm số f(x) khả vi
tại x thì ồ thị 0 của hàm số tại iểm (x ,y ) là trơn (smooth), không bị gãy: 0 0 Trang | 5 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
Ví dụ: Hàm số sau ây có ạo hàm (khả vi) tại 0 không? ln(1 x )2 f(x) x khi x 0 sin x khi x 0
Để hàm số f(x) có ạo hàm tại 0 thì f (0 ) f (0 ) f (0 ) lim f(x) f(0) x 0 x 0 ln(1 x )2 x 0 sin0 lim x 0 x 0 x 0lim ln(1x 2x )2 1 (chú ý rằng sin0 0 và ln(1 x )2 x 0 1 vì ln(1 t) t 0 1) x 2 t f (0 ) lim f(x) f(0) x 0 x 0 x 0 sin x sin0 lim x 0 x 0 lim sin x x 0 x 1 sin t (chú ý rằng sin0 0 và t 0 1) t Trang | 6 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
Ta thấy f (0 ) f (0 ) 1, do ó hàm số f(x) có ạo hàm tại 0 và f (0) f (0 ) f (0 ) 1
Ví dụ: Hàm số f(x) x có ạo hàm (khả vi) tại 0 không? Ta có: f (0 ) lim f(x) f(0) x 0 x 0 x 0 x 0 lim x 0 x 0 1 f (0 ) lim f(x) f(0) x 0 x 0 x 0 ( x) 0 lim x 0 x 0 1
Ta thấy f (0 ) f (0 ) nên không có ạo hàm (không khả vi) tại 0, nghĩa là f (0) không tồn tại.
Nhận xét: Hàm số f(x) | x | liên tục tại 0 ( ồ thị là ường nét liền), nhưng không có ạo hàm tại 0.
Khi i băng ngang qua iểm 0, ồ thị bị gãy.
Giữa tính khả vi (có ạo hàm) và tính liên tục của hàm số có mối liên hệ như sau:
Mệnh ề. Nếu hàm số f(x) khả vi tại x thì liên tục tại 0 x (ngược lại thì sai) 0
Hệ quả. Nếu hàm số f(x) không liên tục tại x thì không khả vi tại 0 x 0
Tính khả vi bảo ảm ồ thị hàm số là ường cong liên tục ( ường nét liền) và trơn. Do ó, hàm số khả vi
còn ược gọi là hàm trơn (smooth function). Trang | 7 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
Ta nói hàm số f(x) khả vi trên khoảng (a,b) nếu hàm số có ạo hàm tại mọi iểm thuộc khoảng (a,b).
Ta nói hàm số f(x) khả vi trên oạn [a,b] nếu hàm số khả vi trên khoảng (a,b) và có ạo hàm bên phải a
(tồn tại f (a ) ), có ạo hàm bên trái b (tồn tại f (b ) ).
1.2 Ý nghĩa kinh tế của ạo hàm
a) Biên tế (Marginal functions)
Giả sử x và y là các ại lượng kinh tế có mối quan hệ hàm số y y(x). Biên tế của y theo x là biểu thức: My y (x) dy dx
Giá trị của biên tế cho ta biết, khi ại lượng x tăng thêm 1 ơn vị thì ại lượng y tăng thêm (hoặc giảm i)
trung bình (xấp xỉ) bao nhiêu ơn vị.
Biên tế My có cùng ơn vị o với ại lượng y.
Ghi chú: Nếu y ax b thì My y (x) a và do ó hệ số góc a (slope – ộ dốc) cho ta biết khi ại lượng
x tăng 1 ơn vị thì ại lượng y sẽ tăng thêm (hoặc giảm i) a ơn vị.
Ví dụ: Một nhà sản xuất ộc quyền cửa nhôm hiện tại ang bán ược 500 cửa nhôm với mức giá
80$/cửa nhôm (trong một tuần). Nếu giá giảm xuống còn 75$/cửa nhôm thì số cửa nhôm bán ược
tăng thêm 50 cửa (trong một tuần). Hãy thiết lập hàm cầu của loại cửa nhôm này với giả thiết mối
quan hệ giữa mức giá và lượng cầu là tuyến tính.
Gọi q là lượng cầu (demand quantity) về loại cửa nhôm (trong một tuần) và p (price) là mức giá. D
Do giả thiết q và D p có quan hệ tuyến tính nên ta có: qD ap b
Tại mức giá p 80, lượng cửa nhôm bán ược là qD 500 nên ta có 500 80a b (1)
Khi giá giảm i 5$ (từ 80$ giảm xuống còn 75$) thì số cửa nhôm bán ược tăng thêm là 50. Vậy, khi giá
giảm i 1$ thì số cửa nhôm bán ược tăng thêm là 10 (chú ý là q và D p có quan hệ nghịch biến).
Suy ra biên tế của q theo p là D MqD 10. Mà MqD (qD ) a nên a 10 (2) Từ (1),(2) ta có hệ 80a b 500 (1) a 10 a 10 (2) b 1300 Trang | 8 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
Vậy hàm cầu của loại cửa nhôm này là: qD 10p 1300
Ví dụ: Chi phí biên (Marginal Cost)
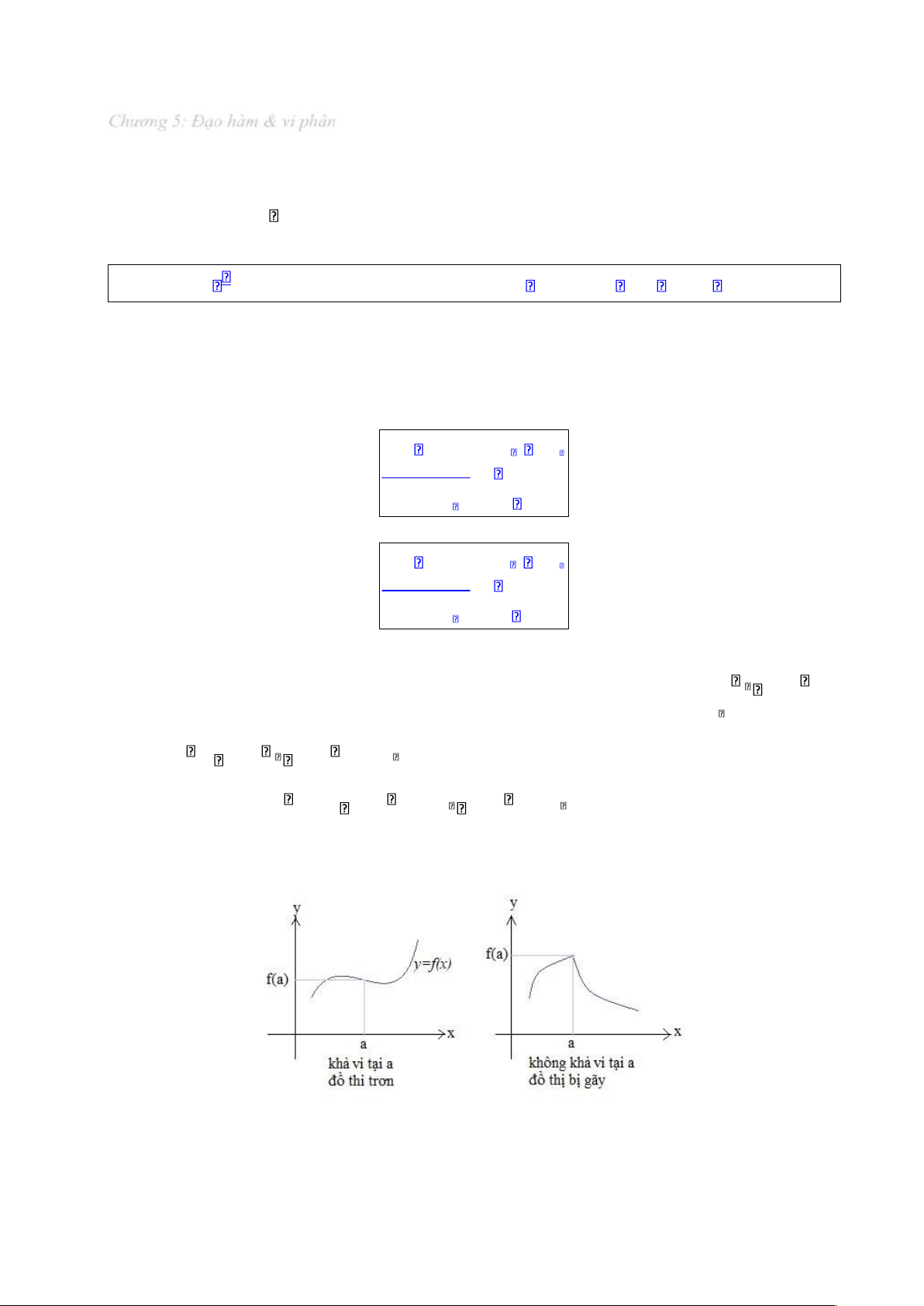
Gọi q (quantity) là sản lượng và C (Cost) là tổng chi phí sản xuất thì C C(q)(hàm chi phí – cost function). Chi phí biên: MC C (q) dC dq
Giá trị của chi phí biên cho ta biết, khi tăng sản lượng thêm 1 ơn vị thì chi phí sản xuất sẽ tăng thêm
trung bình bao nhiêu ơn vị.
Về mặt hình học, chi phí biên là hệ số góc ( ộ dốc – slope) của tiếp tuyến với ường cong chi phí. Chi
phí biên càng lớn thì tiếp tuyến càng dốc ứng.
Áp dụng: Một xí nghiệp có sản lượng trung bình mỗi ngày là q 25 và hàm chi phí sản xuất của xí
nghiệp là C q2 20q 10. Hãy tính chi phí biên tại mức sản lượng này và nêu ý nghĩa.
Ta có: MC C (q) 2q 20 (hàm chi phí biên)
Tại q 25 thì MC 2 25 20 70 ( ơn vị tiền)
Vậy, tại mức sản lượng thường ngày của xí nghiệp là q 25, nếu xí nghiệp tăng sản lượng thêm 1 (
ơn vị hàng) thì chi phí sản xuất tăng thêm xấp xỉ 70 ơn vị tiền.
Chú ý: Tại mức sản lượng q 25, nếu tăng sản lượng thêm 1 ( ơn vị hàng) thì chi phí tăng thêm một lượng chính xác là
C C(26) C(25) (262 20.26 10) (252 20.25 10) 71 ( ơn vị tiền) Trang | 9 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
Ví dụ: Doanh thu biên (Marginal Revenue)
Giả sử giá (price) của sản phẩm phụ thuộc vào sản lượng: p p(q) Biểu
thức R pq p(q)q ược gọi là hàm doanh thu (revenue function). Doanh thu biên: MR R (q) dR dq
Giá trị của doanh thu biên cho ta biết, khi tăng sản lượng thêm 1 ơn vị thì doanh thu sẽ tăng thêm
(hoặc giảm i) trung bình bao nhiêu ơn vị.
Áp dụng: Biết giá của sản phẩm tuân theo quy luật p p(q) 400 q và mức sản lượng thường
ngày của xí nghiệp là q 120 . Hãy tính doanh thu biên tại mức sản lượng này và nêu ý nghĩa.
Ta có hàm doanh thu: R pq (400 1 q)q 400q 1 q2 2 2
Doanh thu biên: MR R (q) (400q q )2 400 q
Tại q 120 thì MR 400 120 280 ( ơn vị tiền)
Vậy, tại mức sản lượng thường ngày q 120 , nếu xí nghiệp tăng sản lượng thêm 1 ơn vị thì doanh
thu tăng thêm trung bình 280 ( on vị tiền).
Chú ý: Khi sản lượng tăng quá nhiều so với nhu cầu tiêu thụ thì giá bán của sản phẩm sẽ giảm mạnh
và hậu quả là doanh thu có thể giảm. Ví dụ: Lợi nhuận biên (Marginal Profit)
Gọi C C(q) là hàm chi phí và R R(q) là hàm doanh thu thì hàm R C ược gọi là hàm lợi nhuận (profit function).
Biên tế của lợi nhuận theo q ược gọi là lợi nhuận biên, ký hiệu là MP: d MP (q) dq R (q) C (q) MR MC
(lợi nhuận biên = doanh thu biên – chi phí biên) Trang | 10 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
Giá trị của lợi nhuận biên cho ta biết, khi tăng sản lượng thêm 1 ơn vị thì lợi nhuận sẽ tăng hoặc
giảm trung bình bao nhiêu ơn vị tiền.
Áp dụng: Giá bán của sản phẩm là p 460 0.5q với q là sản lượng. Hàm chi phí là: C q2 10q 40
Mức sản lượng thường ngày là q 50
Hãy tính lợi nhuận biên tại mức sản lượng này và nêu ý nghĩa.
Doanh thu: R pq (460 0.5q)q 460q 0.5q2
Lợi nhuận: R C (460q 0.5q )2 (q2 10q 40) 1.5q2 450q 40 Lợi nhuận biên: MP (q) 3q 450
Tại mức sản lượng q 50 thì lợi nhuận biên có giá trị là: MP 3 50 450 300 ( ơn vị tiền)
Điều này có nghĩa là tại mức sản lượng q 50 , nếu tăng sản lượng thêm 1 ơn vị thì lợi nhuận tăng
thêm xấp xỉ 300 ơn vị tiền.
Nhận xét: Nếu lợi nhuận biên có giá trị dương thì khi tăng sản lượng, lợi nhuận vẫn còn tăng thêm,
suy ra lợi nhuận chưa ạt cực ại. Tương tự, khi lợi nhuận biên có giá trị âm, nếu giảm sản lượng thì lợi
nhuận vẫn còn tăng thêm, do ó lợi nhuận chưa ạt cực ại. Ví dụ: Năng suất biên theo lao ộng
(Marginal Productivity of Labor)
Giả sử mức sản lượng q (quantity) phụ thuộc vào lượng lao ộng l (labor): q q(l)
Ta gọi hàm q q(l) là hàm sản xuất (production function). Biên tế của hàm sản xuất theo lượng lao
ộng ược gọi là năng suất biên theo lao ộng (Marginal Productivity of Labor), ký hiệu là MPL : MPL q (l) dq dl
Giá trị của năng suất biên theo lao ộng cho ta biết, khi lượng lao ộng tăng thêm 1 ơn vị thì sản lượng
sẽ tăng thêm trung bình bao nhiêu ơn vị.
Áp dụng: Sản lượng của xí nghiệp ược cho bởi hàm năng suất q q(l) 120l l và lượng lao ộng
hiện tại của xí nghiệp là l 625 . Hãy tính năng suất biên theo lao ộng hiện tại và nêu ý nghĩa. Ta có: 1 MPL q (l) (120l l) 120 Trang | 11 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân 2 l Tại l 625 thì 1 1 MPL 120 120 120.02 2 625 2.25
Vậy, với lượng lao ộng hiện tại, nếu tăng lượng lao ộng thêm 1 ơn vị thì sản lượng sẽ tăng thêm xấp
xỉ 120.02 ơn vị sản phẩm.
Ví dụ: Hữu dụng biên (Marginal Utility)
Khi mua một mặt hàng với số lượng là x, người mua sẽ nhận ược lợi ích (có thể o ược hoặc không o
ược). Để nghiên cứu các quy luật liên quan ến lợi ích chi tiêu, người ta ưa ra hàm hữu dụng U U(x) (Utility function)
Biên tế của hàm hữu dụng này ược gọi là hữu dụng biên (Marginal Utility), ký hiệu là MU: MU U (x) dU dx
Giá trị của MU là phần lợi ích tăng thêm khi chi tiêu thêm cho 1 ơn vị hàng.
Áp dụng: Giả sử hàm hữu dụng của một loại sản phẩm là U U(x) 2lnx , tính hữu dụng biên tại x 10 và nêu ý nghĩa. Ta có: MU U (x) 2 x Tại x 10 thì MU U (10) 0.2
Vậy, với lượng hàng ược mua hiện tại là x 10, nếu mua thêm 1 ơn vị hàng nữa thì lợi ích tăng thêm trung bình là 0.2 ơn vị.
Ví dụ: Khuynh hướng tiêu dùng biên MPC (Marginal Propensity to Consume) và khuynh hướng tiết
kiệm biên MPS (Marginal Propensity to Save) Ta gọi •
I (Income) là tổng thu nhập •
C (Consume) là lượng tiêu dùng •
S (Saving) là lượng tiết kiệm của một cá nhân, một hộ gia ình, hoặc của một quốc gia
(tính bằng ơn vị tiền). Rõ ràng, lượng tiêu dùng C và lượng tiết kiệm S phụ thuộc vào thu nhập I: Trang | 12 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
C C(I) (hàm tiêu dùng – consumption function)
S S(I) (hàm tiết kiệm – saving function)
Biên tế của C và S theo I ược gọi là khuynh hướng tiêu dùng biên (Marginal Propensity to Consume)
và khuynh hướng tiết kiệm biên (Marginal Propensity to Save), ký hiệu là MPC và MPS: dC MPC C (I) dI MPS S (I) dS dI
Giá trị của MPC và MPS cho ta biết, khi mức thu nhập tăng thêm 1 ơn vị tiền thì lượng tiêu dùng và
lượng tiết kiệm sẽ tăng thêm trung bình bao nhiêu. Vì I C(I) S(I) I
nên lấy ạo hàm 2 vế theo biến số I thì ta ược 1 C (I) S(I) MPC MPS Vậy, ta có ẳng thức: MPC MPS 1
Đẳng thức này nói lên rằng, khi thu nhập tăng thêm 1 ơn vị tiền thì tổng của lượng tiêu dùng tăng
thêm và lượng tiết kiệm tăng thêm bằng 1.
Áp dụng: Biết C C(I) 2I 1, hãy tính MPC và MPS tại I 7 và nêu ý nghĩa. I 3 Ta có: MPC C (I) 2II 31 2(I (3)I 3)(22 I 1) (I 73)2 Tại I 7 thì MPC 0.07 và MPS 1 MPC 1 0.07 0.93
Vậy, tại mức thu nhập I 7 , nếu thu nhập tăng thêm 1 ( ơn vị tiền) thì lượng chi tiêu tăng thêm xấp
xỉ 0.07 ( ơn vị tiền), lượng tiết kiệm tăng thêm xấp xỉ 0.93 ( ơn vị tiền). b) Độ co giãn (Elasticity) Trang | 13 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
Giả sử x và y là các ại lượng kinh tế có quan hệ hàm số y y(x)
Độ co giãn (hệ số co giãn) của y theo x, ký hiệu Ey (hoặc yx ), là biểu thức: x Ey y (x) dy x y(x) dx y
(chú ý là ộ co giãn không có ơn vị o)
Giá trị của ộ co giãn cho ta biết, khi ại lượng x tăng thêm 1% thì ại lượng y sẽ tăng thêm (hoặc giảm i)
trung bình bao nhiêu phần trăm. Vì My y (x) nên x Ey My y
(mối quan hệ giữa ộ co giãn và biên tế)
Ví dụ: Cho hàm chi phí C C(q) q2 20q 50 với q là sản lượng.
Tính ộ co giãn của chi phí tại mức sản lượng q 40 và nêu ý nghĩa.
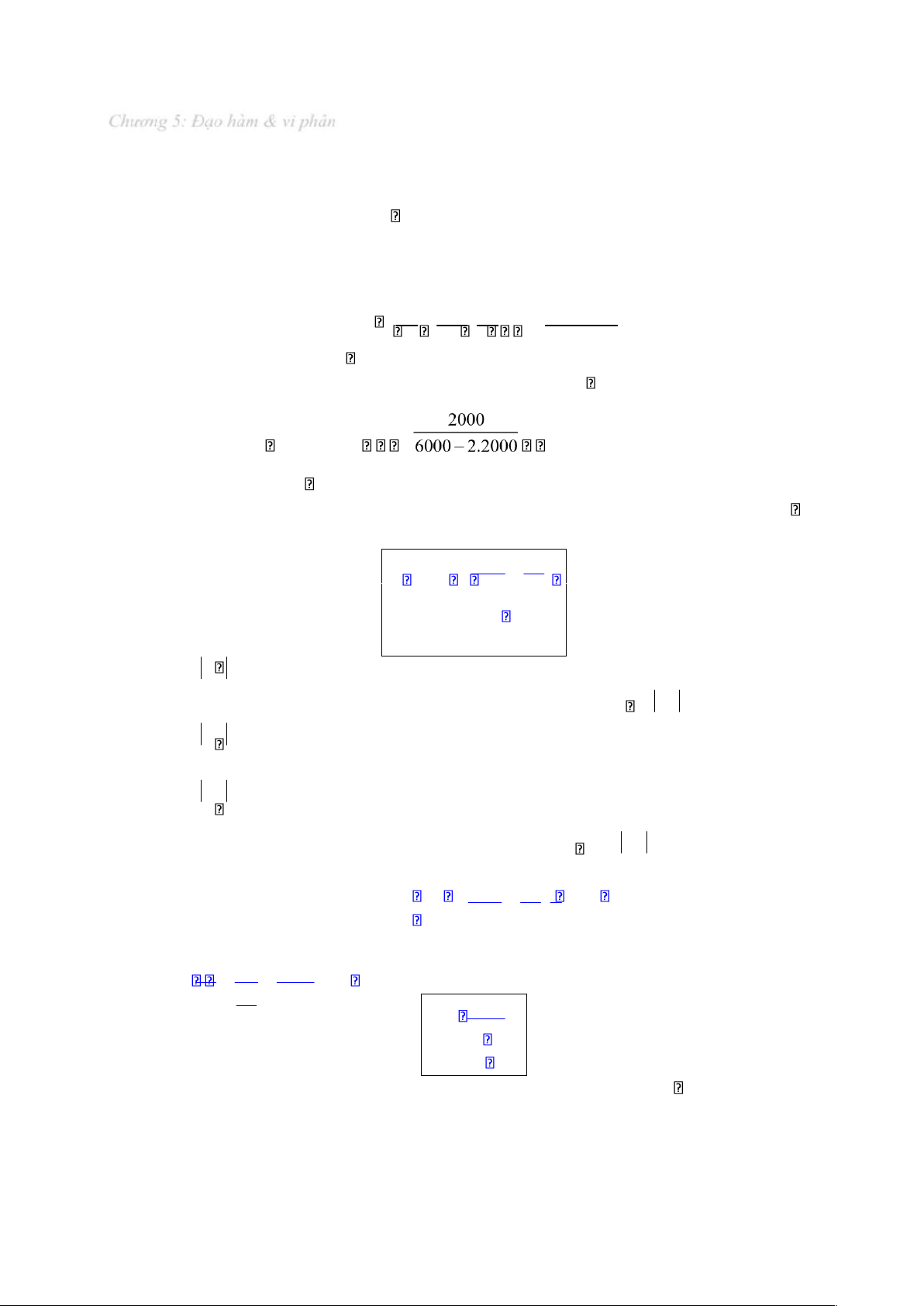
Độ co giãn của chi phí theo sản lượng là: EC C (q) MC C(q)q dC qdq C (2 qMC 20) q2 20qq 50 q22 q220 q20 q50
Tại mức sản lượng q 40 thì giá trị của ộ co giãn là: 2 402 20 40 EC
2 1.63 (không có ơn vị o) 40 20 40 50
Điều này có nghĩa là tại mức sản lượng q 40, nếu tăng sản lượng thêm 1% (nghĩa là tăng sản lượng
thêm 0.4 ơn vị) thì chi phí tăng thêm xấp xỉ 1.63%
Ví dụ: Cho hàm cầu (demand function) của một mặt hàng là qD 6000 2p, trong ó p (price) là giá của
mặt hàng, q (demand quantity) là lượng cầu tương ứng. D Trang | 14 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
Mức giá hiện tại của mặt hàng này là p 2000. Tính ộ co giãn của lượng cầu tại mức giá hiện tại và nêu ý nghĩa.
Ta có biểu thức của ộ co giãn lượng cầu: D p dqD p 2 p ED q qD dp qD 6000 2p
Tại mức giá hiện tại p 2000 thì ED 2 2 (không có ơn vị o)
Vậy, ở mức giá hiện tại là p 2000, nếu giá tăng thêm 1% (nghĩa là giá tăng thêm 20 ơn vị tiền) thì
lượng cầu giảm trung bình 2% ( ây là mặt hàng không thiết yếu, xa xỉ). Ghi chú: Cho hàm cầu q
q(p) với p là giá, q là lượng cầu thì ộ co giãn của cầu là p ED q (p) dq p q(p) dp q
• Nếu ED 1 thì ta nói lượng cầu là co giãn (elastic), khi ó nếu giá tăng thêm 1% thì lượng cầu
giảm i nhiều hơn 1%, chẳng hạn mặt hàng không thiết yếu có ED 1
• Nếu ED 1 thì ta nói lượng cầu có ộ co giãn ơn vị (unit elasticity) hay là ẳng co giãn, khi ó nếu
giá tăng thêm 1% thì lượng cầu giảm i 1%
• Nếu ED 1 thì ta nói lượng cầu là ít co giãn (inelastic), khi ó nếu giá tăng thêm 1% thì lượng
cầu giảm i ít hơn 1%, chẳng hạn mặt hàng thiết yếu có ED 1 Chú ý: Trong công thức D p dq p E q (p) q(p) dp q dq 1 1
nếu ta thay thì ược dp dp p (q) dq ED 1 p p (q) q
Công thức hữu ích này thường ược sử dụng khi hàm cầu ược cho dưới dạng p p(q) Trang | 15 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân
Ví dụ: Cho hàm cầu của một mặt hàng là p 40 0.15q2 , tính hệ số co giãn cầu theo giá khi p 30
Xem q là hàm theo p, nghĩa là q q(p) thì hệ số co giãn cầu theo giá cho bởi: p dq ED q (p) p q(p) dp q Từ giả thiết, ta có q2 40 p 40 p q 0.15 0.15 Vậy 1 1 1 1 q (p) ( ) 40 p 0.15 0.3 40 p 2 0.15 0.15 Do ó ED q (p) p 1 1 p 1 p 1 p q(p) 0.3 40 p 40 p 0.3 40 p 2 40 p 0.15 0.15 0.15 Tại p 30 thì: ED 1 30 1.5 2 40 30
Điều này có nghĩa là tại mức giá p 30 , nếu giá tăng thêm 1% (tăng thêm 0.3 ơn vị tiền) thì lượng
cầu giảm i xấp xỉ 1.5%. Vì ED 1.5 1 nên lượng cầu là co giãn (elastic). 1 p
Cách khác: Trong ví dụ này, ta dùng công thức: ED
sẽ thuận tiện hơn vì hàm cầu ược p (q) q
cho dưới dạng p p(q) . Cách làm như sau: Trang | 16 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân Ta có: p 40 0.15q2 p (q) 0.3q Vậy ộ co giãn cầu là: ED 1 p 1 p p 2 p (q) q 0.3q q 0.3q Tại p 30 thì 30 40 0.15q2 q2 10 0.15 Do ó p 30 30 ED 2 10 1.5 0.3q 0.3 0.15 20
Bây giờ, ta hãy khảo sát ộ co giãn của hàm cầu có ảnh hưởng thế nào ến doanh thu.
Giả sử hàm cầu của một loại sản phẩm là q q(p) hay p p(q) , doanh thu là: R pq p(q)q Doanh thu biên: dR q dp q 1 1 p (q)q p(q) p(q)(1 p (q) ) p(1 ) p(1 ) p(1 ) dq p(q) dq p dq p ED dp q dR 1 p(1 ) dq ED dR
Nếu ED 1 (cầu là co giãn) trên một khoảng nào ó thì
0, do ó R tăng khi q tăng, nghĩa là dq
khi lượng cầu q tăng thì doanh thu tăng. Trong tình huống này, nếu giá sản phẩm giảm thì lượng cầu
tăng, kéo theo doanh thu tăng. Trang | 17 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân dR
Tương tự, ED 1 (cầu là ít co giãn) trên một khoảng nào ó thì
0, do ó R giảm khi q tăng, dq
nghĩa là khi lượng cầu q tăng thì doanh thu giảm. Trong tình huống này, nếu giá sản phẩm giảm thì
lượng cầu tăng, kéo theo doanh thu giảm. Còn nếu ED 1 thì doanh thu thay ổi rất ít khi giá giảm.
Ta có thể thấy iều này trực tiếp nếu xét ẳng thức: dR p q pq (p) q(1 q (p) ) q(1 E )D dp q dR q(1 E ) dp D 1.3 Quy tắc tính ạo hàm
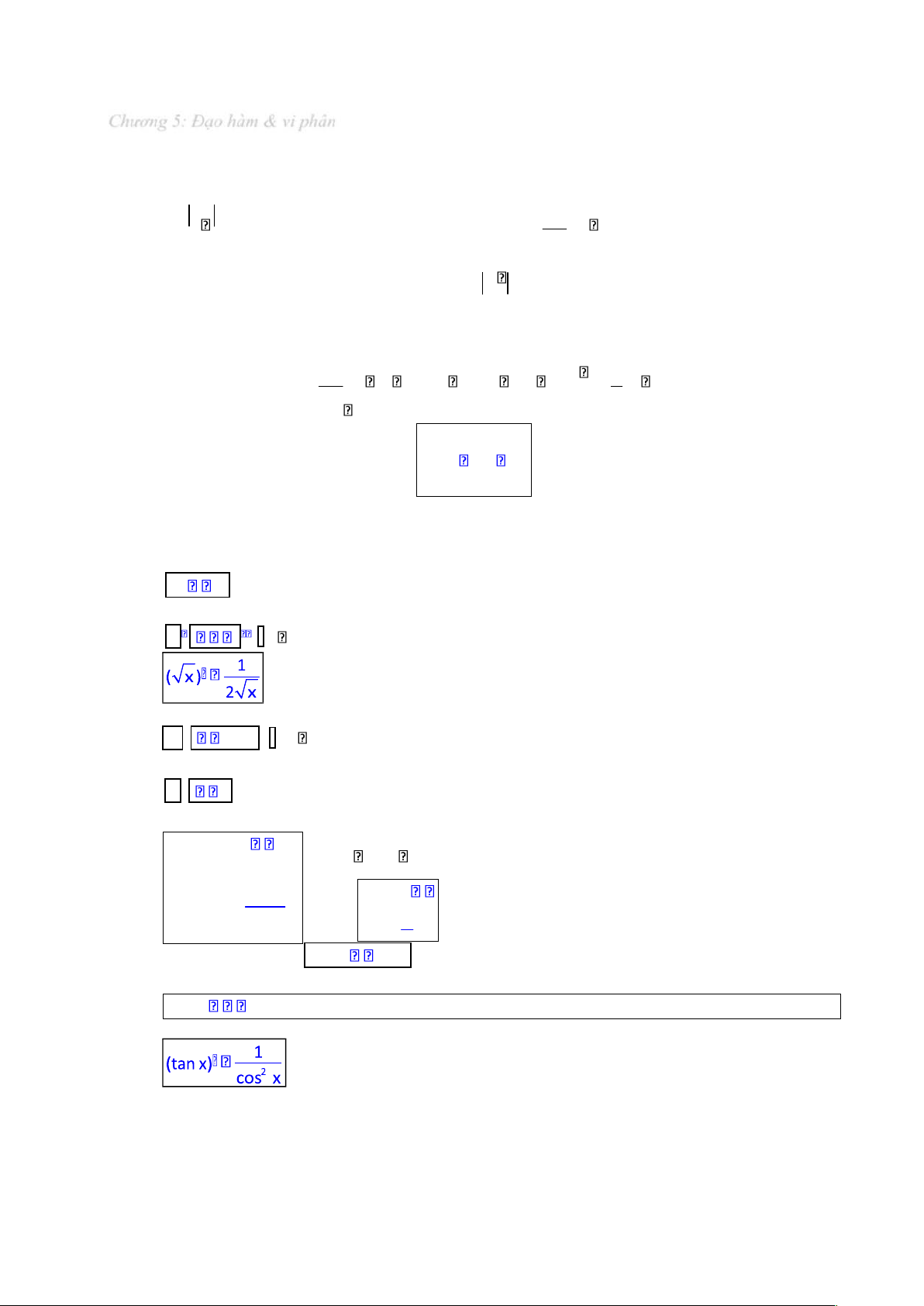
a) Đạo hàm của các hàm số sơ cấp cơ bản (C) 0 (C là hằng số) (x ) x 1 ( là hằng số)
(a x ) a lnax (a 0 là hằng số) (ex ) ex (log xa ) (a 0, a 1 là hằng số) 1 (ln x) 1 x xlna (sin x) cosx (cosx) sinx Trang | 18 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân (cot x) 12 sin x
Ví dụ: Áp dụng công thức (x ) x 1 , ta có (x3 ) 3x 2 ( 3
x) (x1/3) 13 x13 1 13 x 32 3x132 331x2 1 1 (x 1) 1.x 2 2 x x 1 x 12 1 x 12 1 1 x 23 21x 3 1 3 2 2 2 2 x
Ví dụ: Áp dụng công thức (a x ) a lnax , ta có (3 )x 3x ln3
Ví dụ: Áp dụng công thức (log xa ) 1, ta có (log x4 ) 1 xlna xln4
b) Đạo hàm của tổng, hiệu, tích, thương
Nếu các hàm số u u(x); v v(x) có ạo hàm thì (u v) u v ( u) u (uv) u v v u Trang | 19 lOMoAR cPSD| 47206071
Chương 5: Đạo hàm & vi phân u u v 2v u v v Ví dụ: Tính 1 1 2 5 4 x 3ex 5ln x 6cosx 7) 4 3ex 5 6.( sin x) 3ex 6sin x 2 x x x (x e 5x ) (
x ) .e5 x (e ) .xx 5 5x e4 x e xx 5 x e (54 x x) uv u v v u 2ln x
(2ln x) .(3ln x 1) (3ln x2 1) .(2 ln x) 3ln x 1 (3ln x 1) u u v v u v v2 2 3 (3ln x 1) (2ln x) x (3ln x 1)x 2 x(3ln x2 1)2
c) Đạo hàm của hàm số hợp
Giả sử các hàm số u u(x) (biến số là x) và z f(u) (biến số là u) có ạo hàm. Khi ó, hàm số hợp
(composite function) z f(u(x)) (biến số là x) có ạo hàm và: z (x) f (u)u (x) Trang | 20