Lý thuyết cực trị nhiều biến | Môn toán cao cấp

lOMoAR cPSD| 49519085
3.6.1. Cực trị không có iều kiện
1) Định nghĩa. Cho hàm số f(x1, x2, …, xn) =f(M) xác ịnh trong một miền D, M 0
0 = (x1 , x 02 , ..., x 0n ) là một iểm trong của D.
Ta gọi là hình tròn tâm M bán kính r là tập hợp S(M, r)={N: MN-
Nếu f(M) < f(M0) với mọi iểm M trong S(M0, r)\{ M0} thì M0 ược gọi là iểm cực ại và f(M0)
ược gọi là giá trị cực ại. -
Nếu f(M) > f(M0) với mọi iểm M trong S(M0, r)\{ M0} thì M0 ược gọi là iểm cực tiểu và
f(M0) ược gọi là giá trị cực tiểu. Nhận xét:
Nếu trong mọi hình tròn tâm M0 ều tồn tại hai iểm N, P sao cho f(N) > f(M0) và f(P) < f(M0) thì M0
không phải là iểm cực trị. 2)
Điều kiện cần ể tồn tại cực trị: Định lý. Nếu hàm số f(x 0
1, x2, …, xn) ạt cực trị tại iểm M0 = (x1 , x 02 , ..., x 0n ) D và các ạo hàm riêng cấp 1
M0 ều tồn tại thì tất cả các ạo hàm riêng cấp 1 ó triệt tiêu: f 'xi M0 0 * i 1,n Định nghĩa. Điểm M 0
0 = (x1 , x02, ..., x0n ) thoả mãn iều kiện (*) ược gọi là iểm dừng của hàm số f(x1, x2, …, xn). 3)
Điều kiện ủ ể có cực trị: a) Hàm hai biến:
Định lý. Giả sử M0(x0, y0) là một iểm dừng của hàm f(x, y) và trong một lân cận nào ó của iểm này
hàm f(x, y) có các ạo hàm riêng ến cấp 2 liên tục và a 11 a12 D = a21 a 22 trong ó a11 = f xx (M0); a12 = f xy (M0) ; a21 = f yx (M0); a22 = f yy (M0); Định lý: lOMoAR cPSD| 49519085
i) Nếu D > 0 thì iểm dừng M0 là iểm cực trị của hàm số f(x, y):
+) M0 là iểm cực ại nếu a11 < 0. +) M0 là iểm cực tiểu nếu a11 > 0. ii)
Nếu D < 0 thì iểm M0 không phải là iểm cực trị của hàm f(x, y). iii) Nếu
D = 0 thì M0 là iểm nghi vấn, cần có những khảo sát bổ sung.
Ví dụ 1. Tìm cực trị của hàm số f(x, y) = x2 + xy + y2 -2x – 3y Giải. Hàm
số ã cho xác ịnh khắp nơi trên mặt phẳng Oxy. Ta có
Ta có: f x = 2x + y -2; f y = x + 2y – 3; Đk cần: x 1 f =2x + y -2 = 0x 3 f =x + 2y - 3 = 0y y 4 3
Hệ có nghiệm duy nhất M0( , ).
Đó là iểm dừng duy nhất +)ĐK ủ
f’’xx = 2; f’’xy=1; f’’yx=1; f’’yy=2 a11 = 2; a12 = 1=a21; a22 = 2 2 1 Do ó D= 3 0và a11 >0 1 2
nên hàm số ã cho có iểm cực tiểu là M0
Ví dụ. Tìm cực trị của hàm số u(x,y) 18xy 8x3 27y3 u x 18y 24x2 0 lOMoAR cPSD| 49519085 u y 18x 91y2 0
Ví dụ 2. Tìm cực trị của hàm số f(x, y) = x4 + y4 Giải.
Hàm số xác ịnh với mọi (x, y) R2.
Hàm có iểm dừng là nghiệm của hệ 4x3 0 4y3 = 0 M0(0, 0) Dễ dàng thấy rằng f xx(0, 0) = f xy(0, 0) = f yy(0, 0) = 0 nên D = 0.
Điều này có nghĩa là M0 = (0, 0) là iểm nghi vấn.
f(M) = x4 + y4 >0= f(M0) , M(x, y) thuộc S(M0, 1)\{M0}.
Suy ra M0 là iểm cực tiểu của hàm số
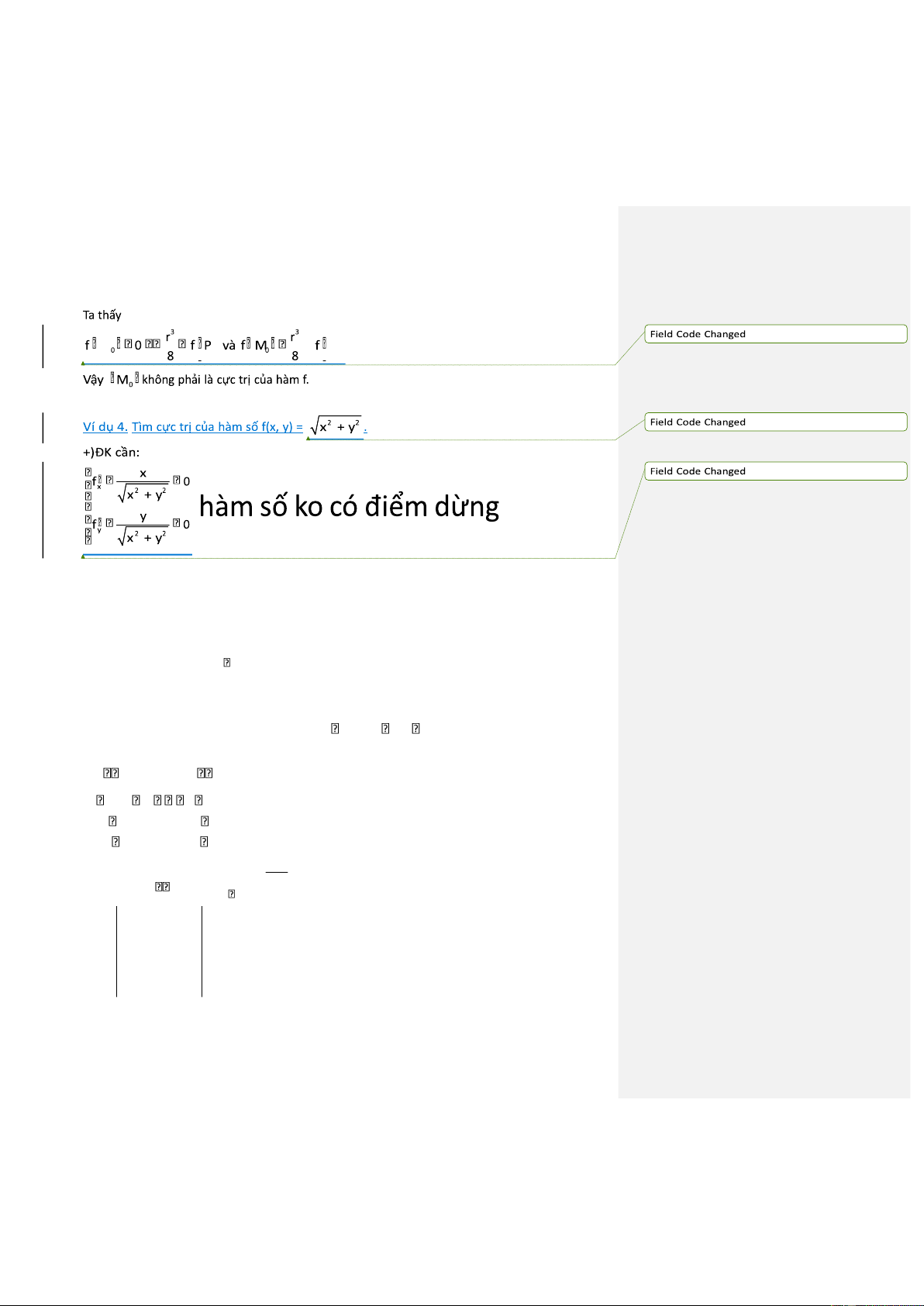
Ví dụ 3. Tìm cực trị của hàm f(x, y) = x3 + y3 Giải. Hàm xác ịnh (x, y) R2.
Hàm có iểm dừng là nghiệm của hệ 3x2 = 0 3y = 2 0 M0 (0, 0)
Tại iểm M0, ta có f x2 (M0) = f xy (M0) = f y2 (M0) = 0
Do ó D = 0, tức là ta gặp trường hợp ịnh lý iều kiện ủ không giải quyết ược, phải sử dụng
ịnh nghĩa ể kiểm tra xem iểm M0 có phải là cực trị hay không.
Trong mọi hình tròn tâm S(M0 ; r) bất kỳ bán kính r (r dương tùy ý) lOMoAR cPSD| 49519085
ta lấy 2 iểm N(r/2;0) và P(-r/2;0)
O(0,0) ktra ĐN thì nó là iểm cực tiểu giống VD2
b) Đk ủ cho Hàm n biến (n 3) Định lý. Giả sử M 0
0 = (x1 , x 02 , ..., x 0n ) là một iểm dừng của hàm w =
f(x1, x2, …, xn) và trong một lân cận nào ó của iểm này hàm f(x1, x2,
…, xn) có các ạo hàm riêng liên tục tới cấp 2 và a11 a 12 a1n H = a21 a ... a22 2n (Ma trận Hessian) a a ... an1 n2 nn trong ó a ij = f xxi j (M0), i, j = 1, n a11 a ... a12 1k a21 a ... a22 2k Hk = lOMoAR cPSD| 49519085 ..................... ak1 a ... ak2 kk
( ịnh thức tạo bởi k dòng ầu và k cột ầu của ma trận H) Khi ó
i) Nếu Hk > 0, k = 1, n thì M0 là iểm cực tiểu của hàm số f(x1, x2, …, xn).
ii) Nếu (-1)k.Hk > 0, k = 1, n thì M0 là iểm cực ại của hàm số f(x1, x2, …, xn).
Chú ý. Với giả thiết về sự tồn tại các ạo hàm riêng liên tục tới cấp 2, ta luôn có
a ij = a ji ( i, j = 1, n, i j) y2 z2 2
Ví dụ. Tìm cực trị của hàm số sau f(x, y, z) = x + + + 4x y z
Giải. Trước hết ta tìm các iểm dừng của f(x, y, z) f'x = 1 - 4yx22 = 0 y = 2x x = +)ĐK cần: f' = 2yx - yz22 = 0 y = 2xzy = z 3 3 2 z = y = 11 y f = 'z 2yz - z22 = 0 M1 = 12, 1, 1 , M2 = 12, -1, -1 Tại iểm M1 12, 1, 1 y2 f xx = 2x3 a11 = 4 lOMoAR cPSD| 49519085 y f xy = f yx = - 2x2 a12 = a21 = -2 f xz = f zx = 0 a13 = a31 = 0 1 2z2 f yy = 2x + y3 a22 = 3 2z f yz = f zy = - y2 a23 = a32 = -2 2 4 f zz = y + z3 a33 = 6 4 -2 0 H(M1) = -2 3 -2 0 -2 6 4 -2 0
4 -2 H1 = |4| = 4 > 0; H2 = = 8 > 0; H3= -2 3 -2 = 32 > 0 -2 3 0 -2 6 Vậy iểm M1
là iểm cực tiểu của hàm số ã cho - -1, -1 1,
: ta làm tương tự như trên. Tại iểm M2 2 lOMoAR cPSD| 49519085 y2 f xx = 2x3 a11 = -4 y f xy = f yx = -
2x2 a12 = a21 = 2 f xz = f zx = 0 a13 = a31 = 0 1 2z2 f yy = 2x + y3 a22 = -3 2z f yz = f zy = - y2 a23 = a32 = 2 2 4 f zz = y + z3 a33 = -6 4 2 0 H M 2
2 -3 2 H1=-4, H2=8; H3=-32 M2 iểm cực ại 0 2 -6 Cực trị có iều kiện
1) Định nghĩa. Người ta gọi cực trị của hàm số
w = f(M) = f(x1, x2, …, xn), (1)
trong ó các biến số x1, x2, …, xn bị ràng buộc bởi hệ thức
g(x1, x2, …, xn) = b (2) là cực trị có iều kiện.
VD Tìm cực trị của hàm số f(x,y)=x2+y2 với k 3x+4y=5 f(0,0)=?
Tìm iểm M trên ường thẳng 3x+4y=5 sao cho MO bé nhất. lOMoAR cPSD| 49519085
2) Phương pháp nhân tử Lagrange Bài
toán: Tìm cực trị của hàm số
w = f(x1, x2, …, xn) với iều kiện g(x1, x2, …, xn) = b
Bài toán này ược giải quyết theo phương pháp Lagrange, gồm các bước sau:
Bước 1: Lập hàm số Lagrange
L(x1, x2, …, xn, ) = f(x1, x2, …, xn) + [b - g(x1, x2, …, xn)] (3) Biến phụ
ược gọi là nhân tử Lagrange. Bước 2: Tìm các iểm M 0
0 = (x1 , x02, ..., x0n ) mà tại ó hàm số (1) có thể có cực trị với iều kiện Field Code Changed Field Code Changed
ràng buộc (2) bằng cách áp dụng iều kiện cần sau Field Code Changed
Định lý. Cho M0 là iểm cực trị của hàm số f(x1, x2, …, xn) với k: g(x1, x2, …, xn)=b và ạo hàm riêng
của L tại M0 ều tồn tại thì các ạo hàm riêng ó ều bằng 0: g(x , x , ..., x ) = b1 2 n L = 0, i = 1, n xi (4)
Chú ý: M0 thỏa mãn (4) ược gọi là iểm dừng
Bước 3: (Định lý iều kiện ủ) g (M ) xi0 gi L x xij (M ) = L0 ij 0 g1 g2 ... gn g1 L11 L12 ... L1n lOMoAR cPSD| 49519085 H g2 L21 L22 ... L2n (Ma trận Hessian) ... ... ... ... ... gn Ln1 Ln2 ... Lnn 0 g1 g2 ... gk g1 L11 L12 ... L1k 2 L21 L22 ...
L2k, k=2,…,n (k+1 dòng và k+1 cột ầu tiên) ... ... ... ... ... gk Lk1 Lk2 ... Lkk
( ịnh thức tạo bởi k+1 dòng ầu và k+1 cột ầu của ma trận H)
i) Nếu Hk 0, k 2,3,...,n thì M0 là iểm cực tiểu của f(x1, x2, …, xn). ii) Nếu ( 1) k.Hk 0, k
2,3,...,n thì M0 là iểm cực ại của f(x1, x2, …, xn).
VD. Tìm cực trị của hàm số f(x,y)=x2+y2 với k 3x+4y=5. Giải. Lập hàn Lagrange: L= x2+y2 + (5-3x-4y). Điều kiện cần: x 15 7 Lx 2x 3 0 Ly 2y 4 0 y 207 M0 157; 207 3x 4y 5 107 g x 3;g y 4 lOMoAR cPSD| 49519085 L xx 2;L yx 0;L xy 0;L yy 2 0 3 4 H 3 2 0 4 0 2 0 3 4 2
0 50 0 Vậy M0 là iểm cực tiểu. 4 0 2
Chú ý với bài toán cực trị của hàm dạng Cobb-Douglas f(x,y)
100.x0,6.y0,4 tìm cực trị
- Giải k cần: chuyển lamda sang vế phải, chía 2 pt vế theo vế, suy ra tỷ lệ x/y=…
Thay vào pt k g(x,y)=b ể giải
- Đk ủ, ko thay M0 vào L’’ vì sẽ ra nhận giá trị gần úng, nên chỉ xét
dấu H2 dựa vào dấu của Lij.
Điều kiện ể cực trị trở thành giá trị lớn nhất, nhỏ nhất trên 1 miền D:
Định lý: Nếu hàm f thỏa mãn các iều kiện sau ây: - D là một tập mở
- Trên D có duy nhất 1 iểm cực ại M0 và không có iểm cực tiểu nào
- Định lý iều kiện ủ úng với mọi iểm trong D Thì hàm f ạt cực GTLN trên D tại M0.
Ví dụ. Tìm giá trị NN của hàm số sau trên R2 : f(x, y) = x2 + xy + y2 – 2x – 3y Giải. Hàm
số ã cho xác ịnh khắp nơi trên mặt phẳng Oxy. Ta có
Ta có: f x = 2x + y –2; f y = x + 2y – 3; Đk cần: lOMoAR cPSD| 49519085 3 f =2x + y -2 = 0x x 1 f =x + 2y - 3 = 0y y 4
3 Hệ có nghiệm duy nhất M0(ଵ ǡ ସ ሻ ). ଷ ଷ
Đó là iểm dừng duy nhất +)ĐK ủ
f’’xx = 2; f’’xy=1; f’’yx=1; f’’yy=2 a11 = 2; a12 = 1=a21; a22 = 2 2 1 Do ó D= 3 0và a11 >0 1 2
nên hàm số ã cho có iểm cực tiểu là M0 Xét trên miền D=R2 - D là tập mở
- Trên D có duy nhất 1 iểm cực tiểu và không có cực ại nào.
- Định lý iều kiện ủ úng với mọi iểm M trên D
Duy ra hàm f ạt GTNN trên D tại M0
VD. Tìm giá trị nhỏ nhất của hàm số f(x,y)=x2+y2 với k 3x+4y=5.
Theo kq phía trên, ta chứng minh ược M0 là iểm cực tiểu. Xét trên miền D=R2 - D là tập mở
- Trên D có duy nhất 1 iểm cực tiểu và không có cực ại nào.
- Định lý iều kiện ủ úng với mọi iểm M trên D
Duy ra hàm f ạt GTNN trên D tại M0 và GTNN của hàm f với k 2x+4y=5 là f(M0).