Lý thuyết Giới hạn hàm số liên tục | Môn toán cao cấp
Cho y = f(x) là hàm 1 - 1 với miền xác định D và miền giá trị E. Hàm ngược của y = f(x) là hàm từ E vào D, ký hiệu x = f ^ - 1 * (y) xác định bởi x=f^ -1 (y) Leftrightarrow y = f(x).Vì a=f^ -1 (b) Leftrightarrow b = f(a) nên (a,b) thuộc đồ thị y = f(x) khi và chỉ khi (b,a) thuộc đồ thị của f ^ -!. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem !
Môn: Toán Cao Cấp (KTHCM)
Trường: Đại học Kinh tế Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Tài liệu liên quan:
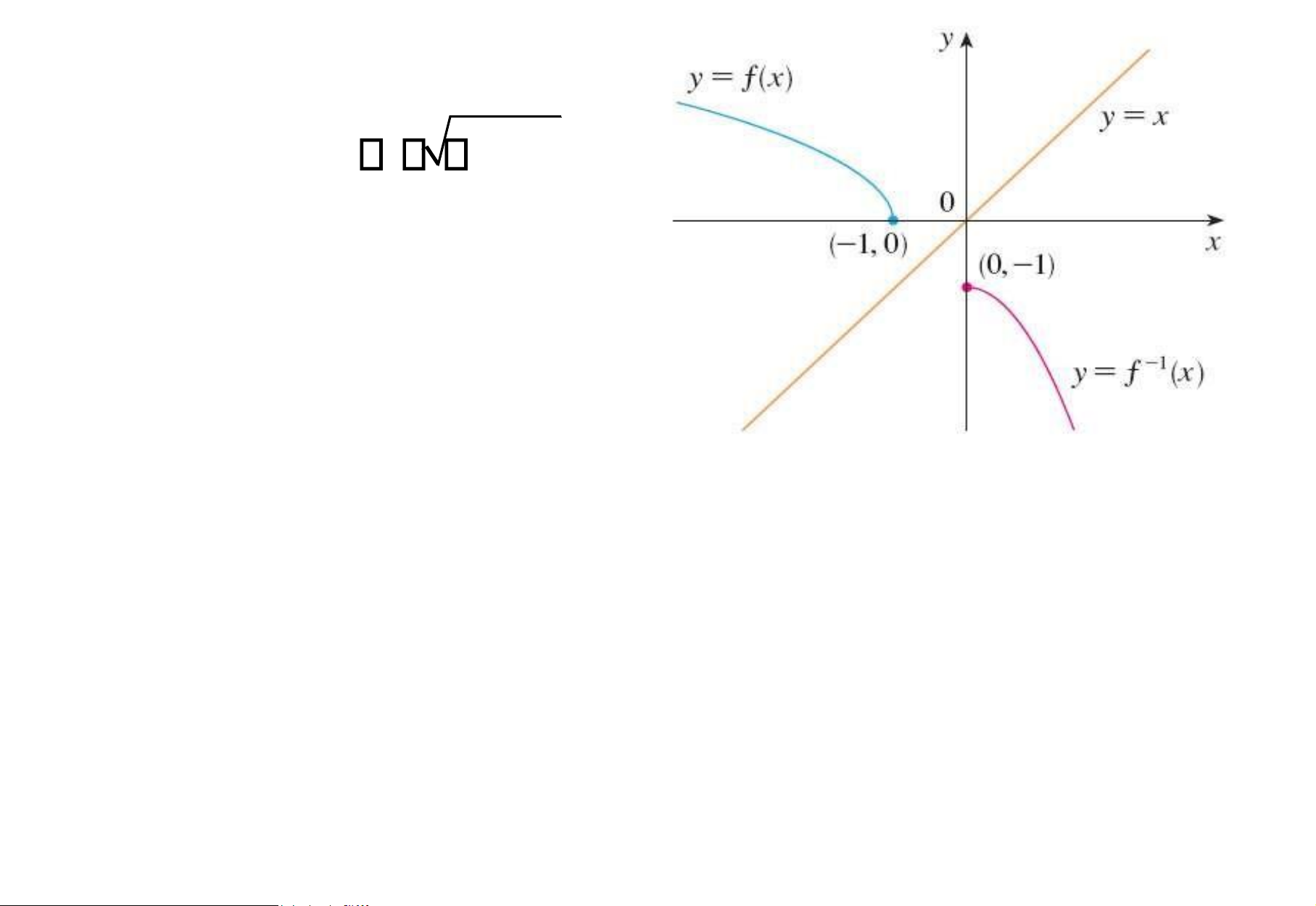
Preview text:
lOMoAR cPSD| 49519085 Nội dung
---------------------------------------------------------------------------------------------------------------------------
I.2 – Giới hạn của hàm số – Hàm số.
– Giới hạn của hàm số. lOMoAR cPSD| 49519085
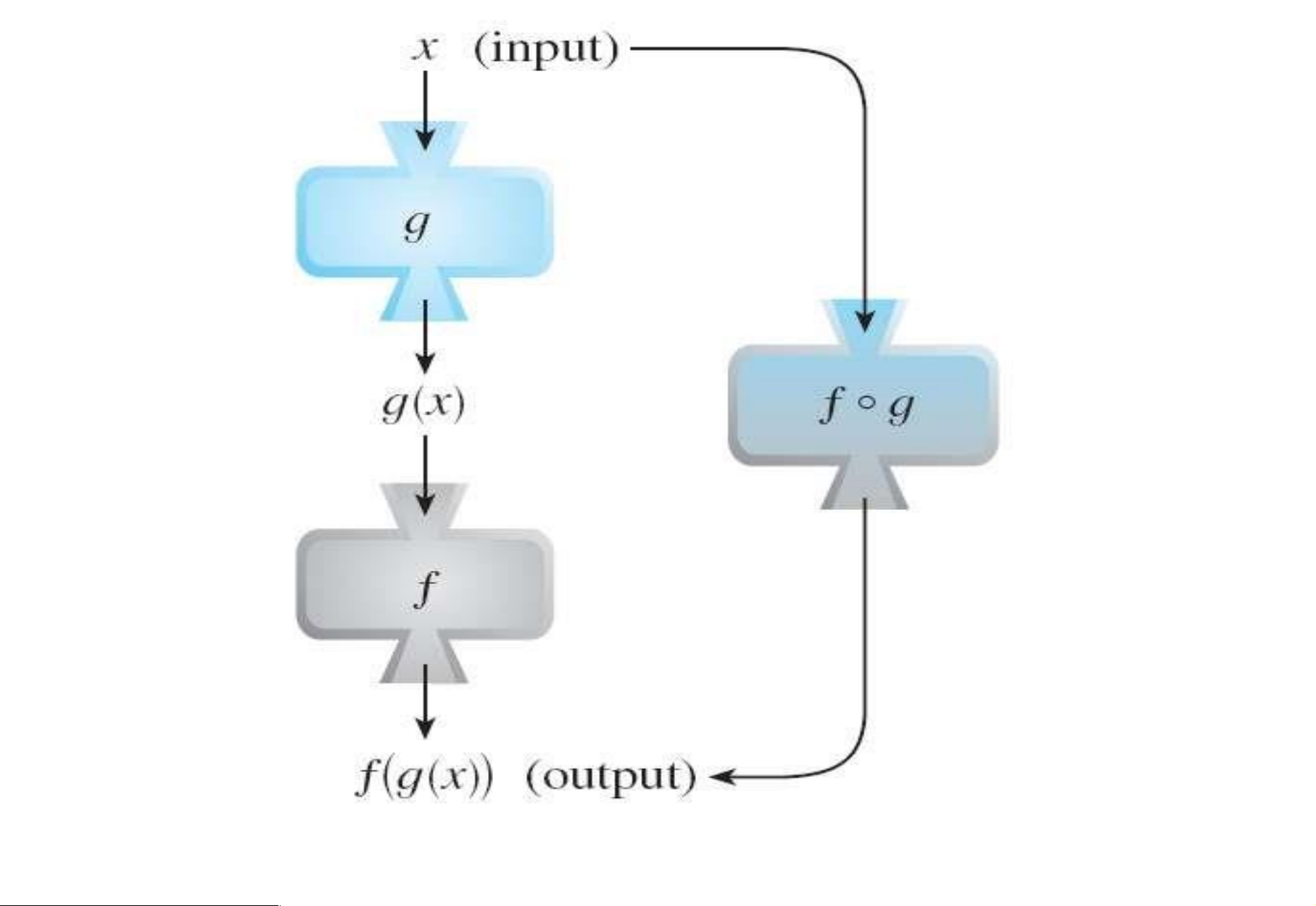
– Vô cùng bé, Vô cùng lớn. 1. Hàm số Định nghĩa (hàm hợp) Cho hai hàm . g X:
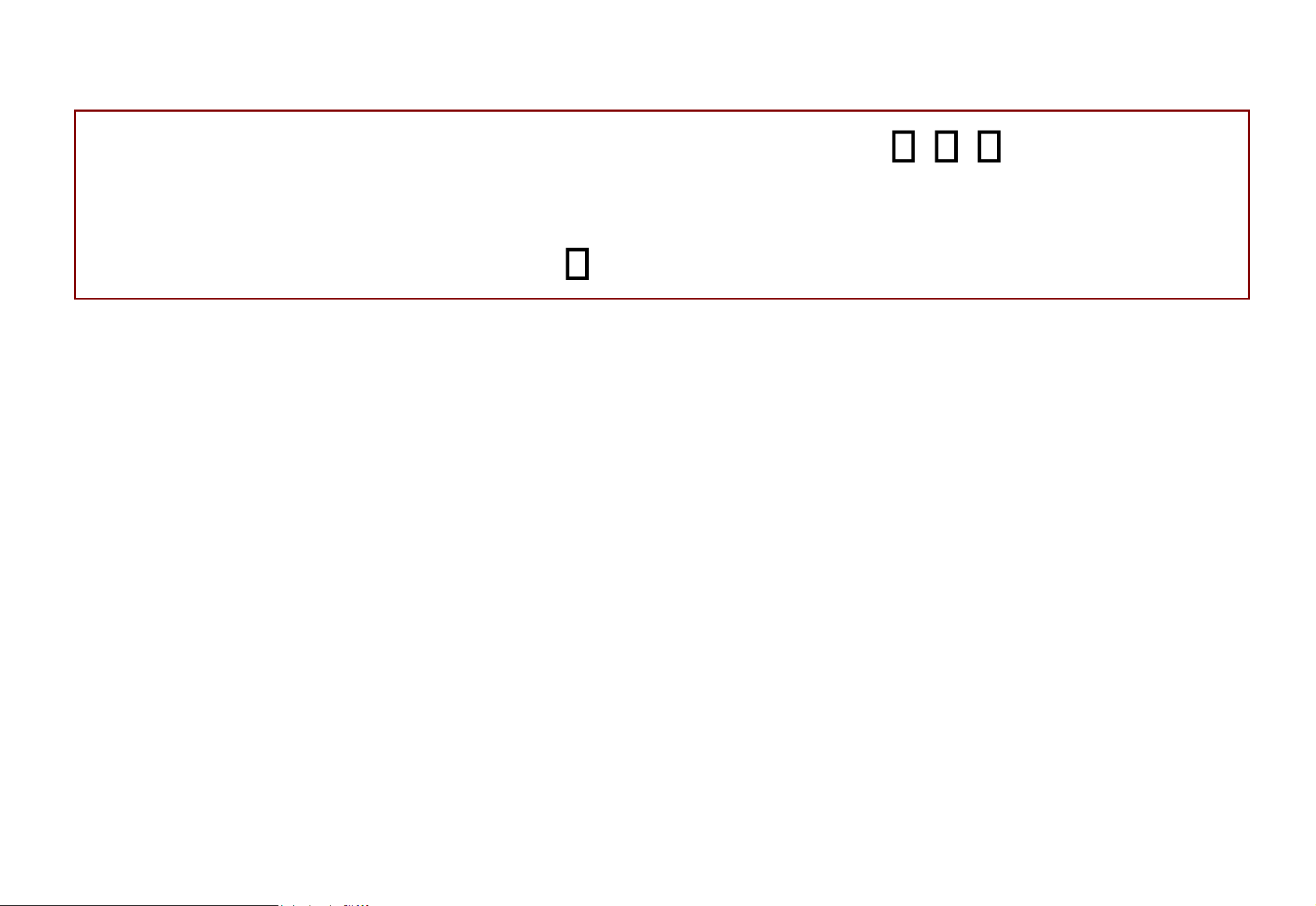
Y f Y; : Z Khi ó tồn tại hàm hợp . f g X: Z h f g f g x( ( )) Ví dụ.
g x( ) x 3; f x( ) x2 lOMoAR cPSD| 49519085 f
g x( ) f g x( ( ) f x( 3) x3 2 g
f x( ) g f x( ( )) g x( 2) x2 3 Ví dụ.
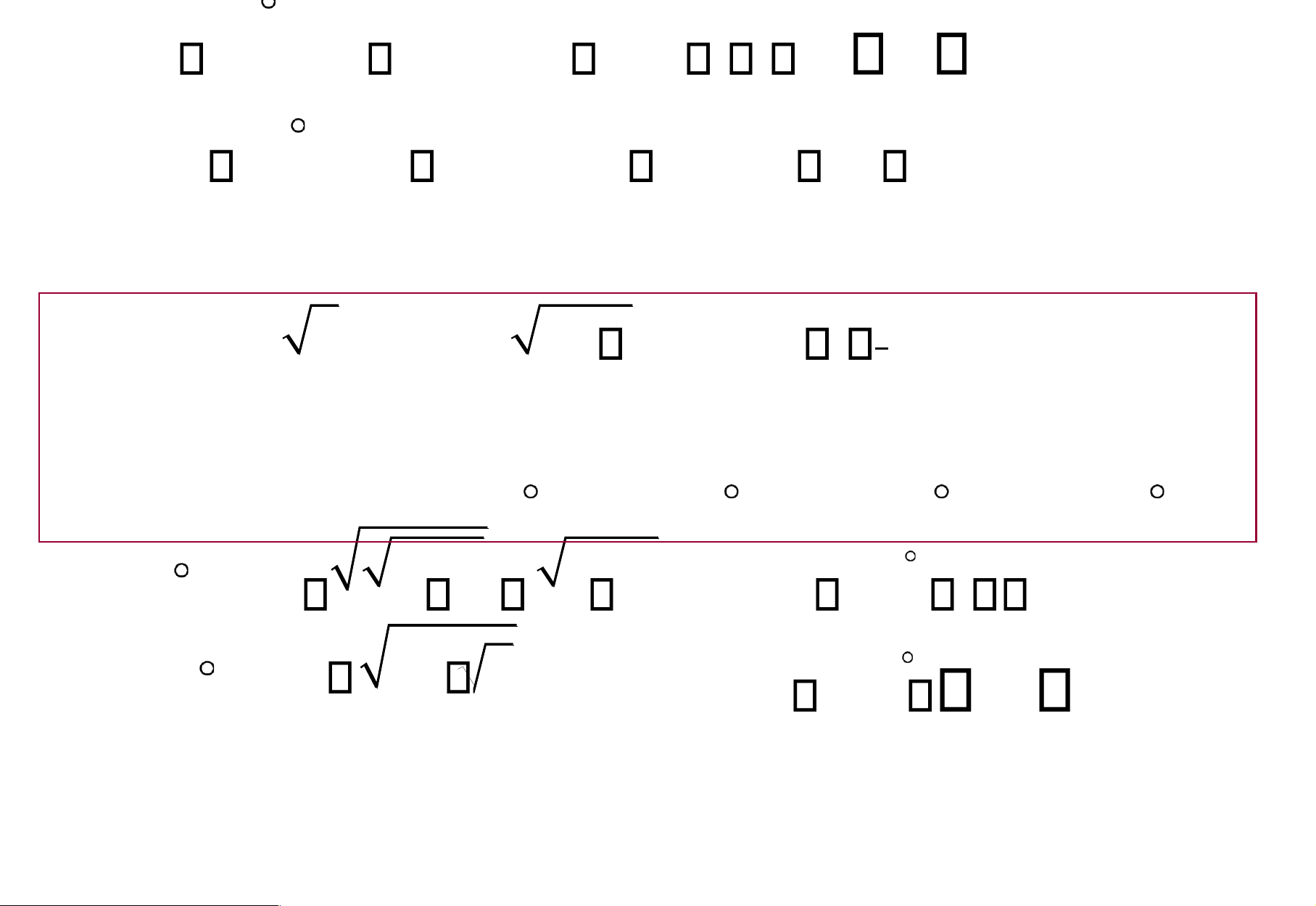
Cho f x( ) x; g x( ) . Tìm các hàm sau và 2 x miền
xác ịnh của nó: a) f
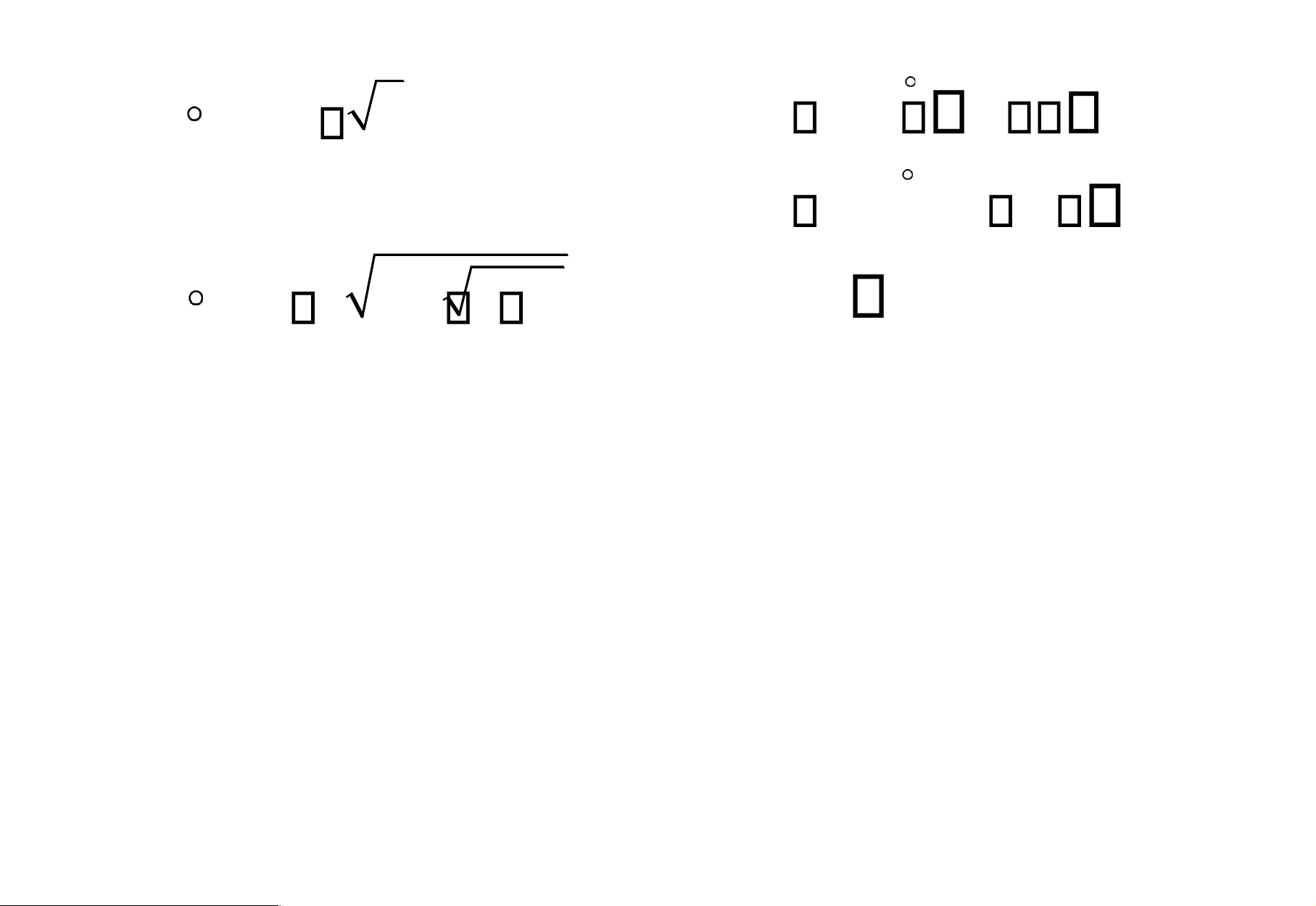
g; b) g f ; c) f f ; d) g g. ,2 a) f g x( ) 2 x 4 2 x Df g ( ]
b) g f x( ) 2 x Dg f 0,4 lOMoAR cPSD| 49519085
c) f f x( ) 4 x Df f 0, Dg g d) g g x( ) 2 2 x 2,2 lOMoAR cPSD| 49519085 Đầu vào Đầu ra lOMoAR cPSD| 49519085
Định nghĩa (hàm 1 – 1)
Hàm y = f(x) ược gọi là hàm 1 – 1, nếu x1 x2 Df
thì . f x( )1 f x( )2
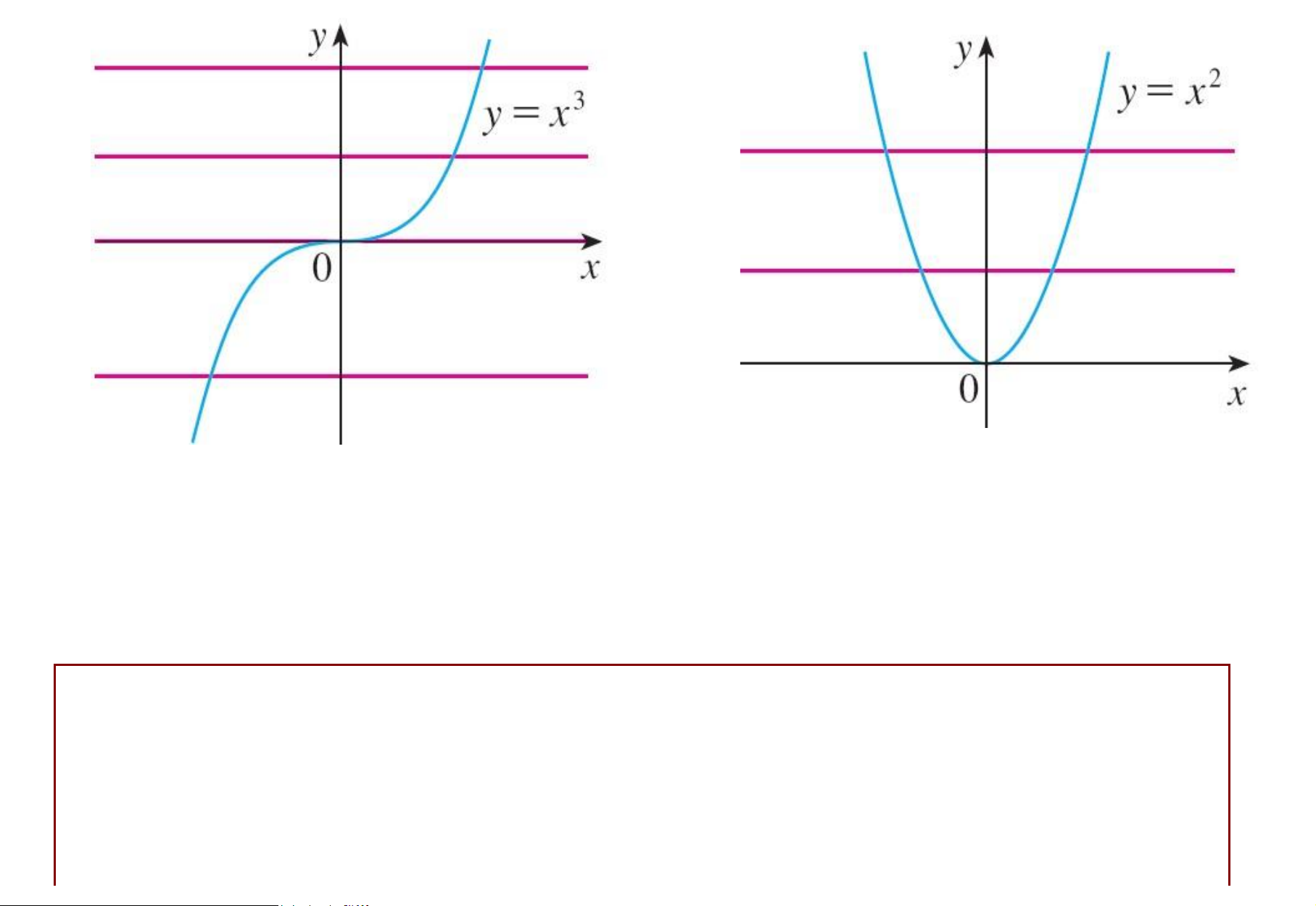
Hàm y = f(x) là hàm 1 – 1 khi và chỉ khi không tồn tại
ường thẳng nằm ngang cắt ồ thị nhiều hơn một iểm. Ví dụ. lOMoAR cPSD| 49519085 Hàm 1 – 1 Không là hàm 1 – 1
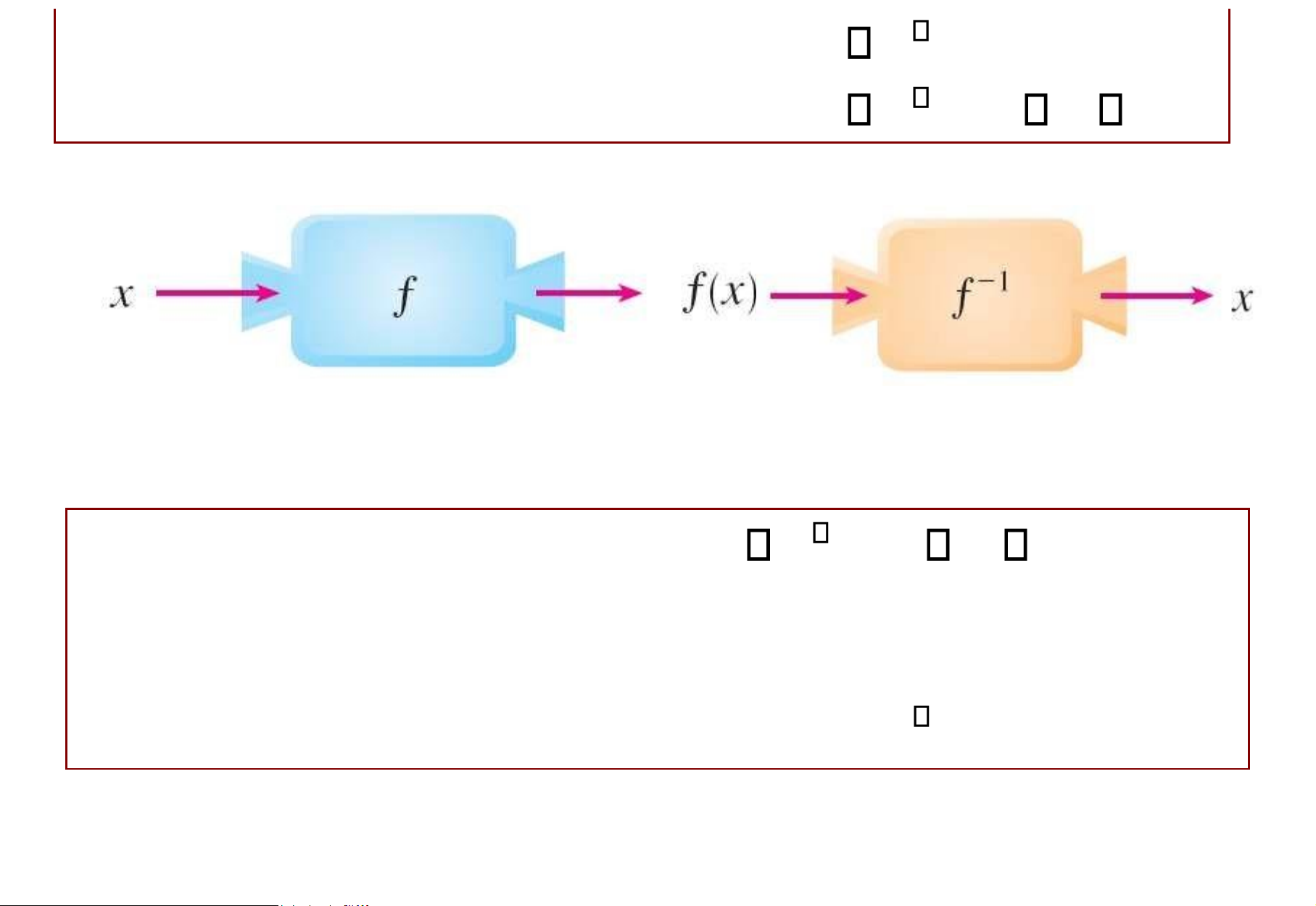
Định nghĩa (hàm ngược)
Cho y = f(x) là hàm 1 – 1 với miền xác ịnh D và miền
giá trị E. Hàm ngược của y = f(x) là hàm từ E vào D, lOMoAR cPSD| 49519085
ký hiệu , xác x f 1( )y ịnh bởi
. x f 1( )y y f x( ) Chú ý:
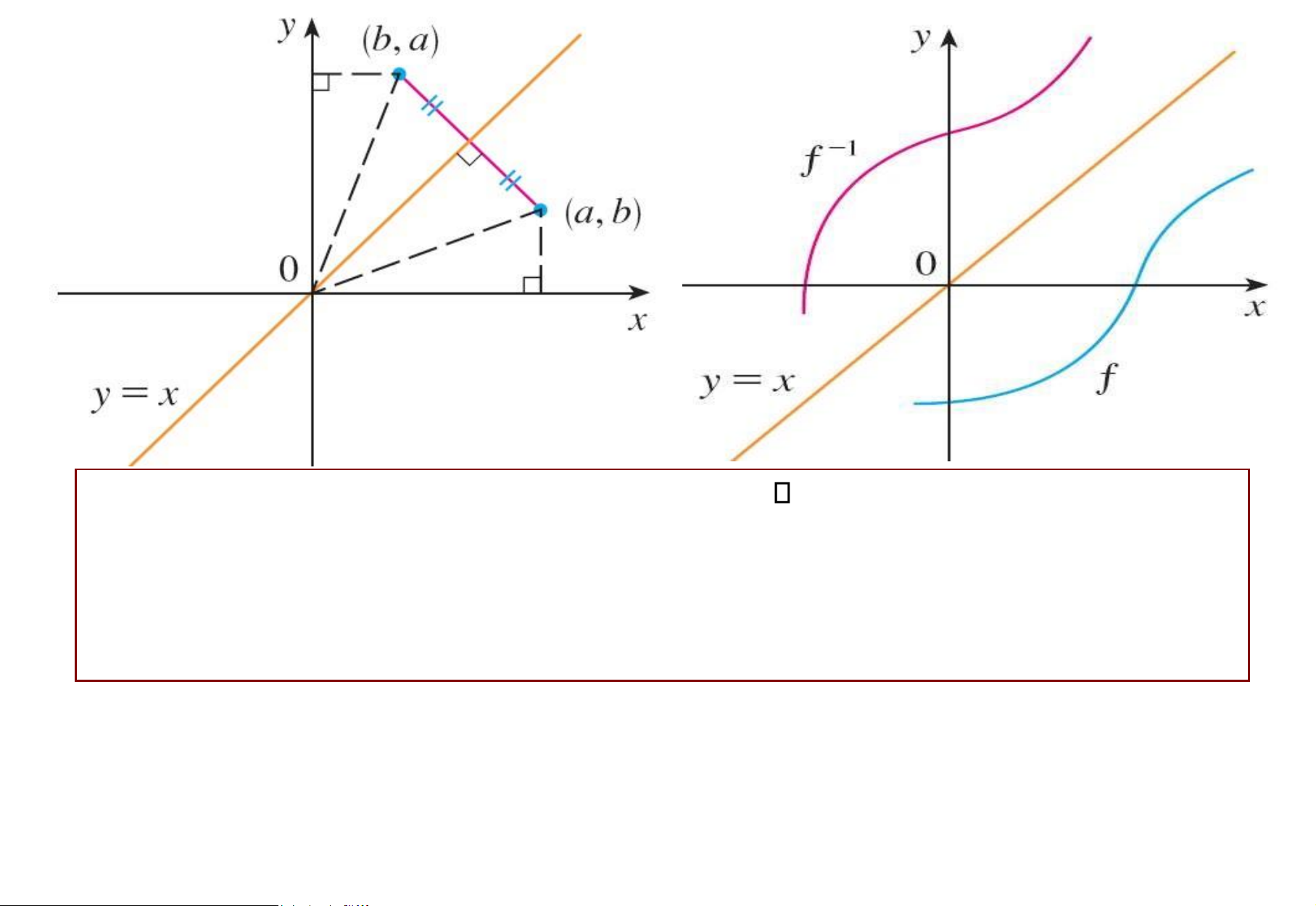
Vì , nên (a f 1( )b b f a( ) a,b)
thuộc ồ thị y = f(x)
khi và chỉ khi (b,a) thuộc ồ thị của . f 1 lOMoAR cPSD| 49519085
Đồ thị y = f(x) và ồ thị của f 1 ối xứng nhau qua qua ường thẳng y = x. lOMoAR cPSD| 49519085
Ví dụ. Vẽ ồ thị của
Vẽ ồ thị của y x 1 và ồ thị hàm ngược.
Định nghĩa (hàm lượng giác ngược)
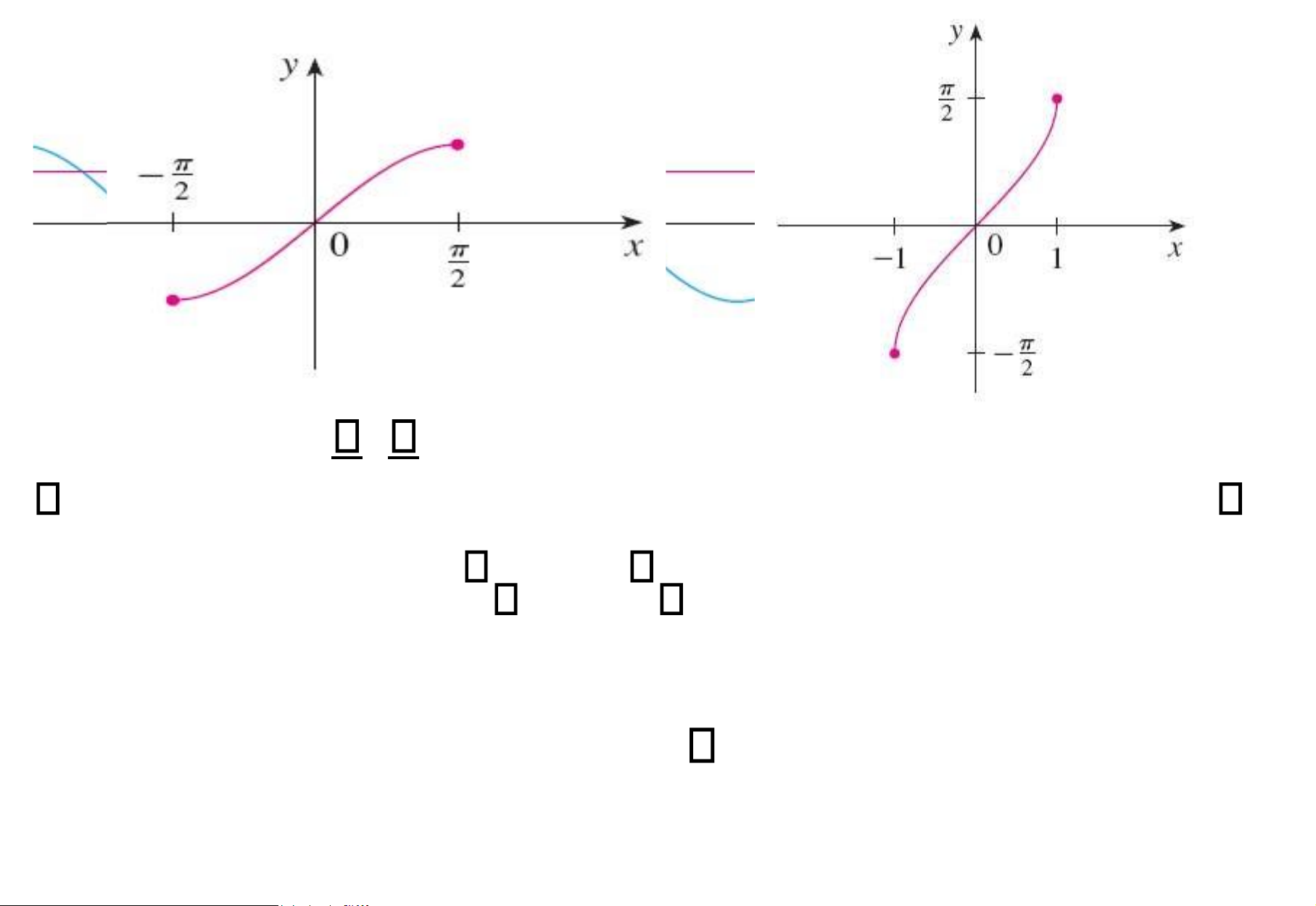
Xét hàm lượng giác y = sin x lOMoAR cPSD| 49519085 - Trên oạn , 2 , 2
y = sin x là hàm 1 – 1.
Tồn tại hàm ngược, ký hiệu y arcsinx lOMoAR cPSD| 49519085
Định nghĩa (hàm lượng giác ngược)
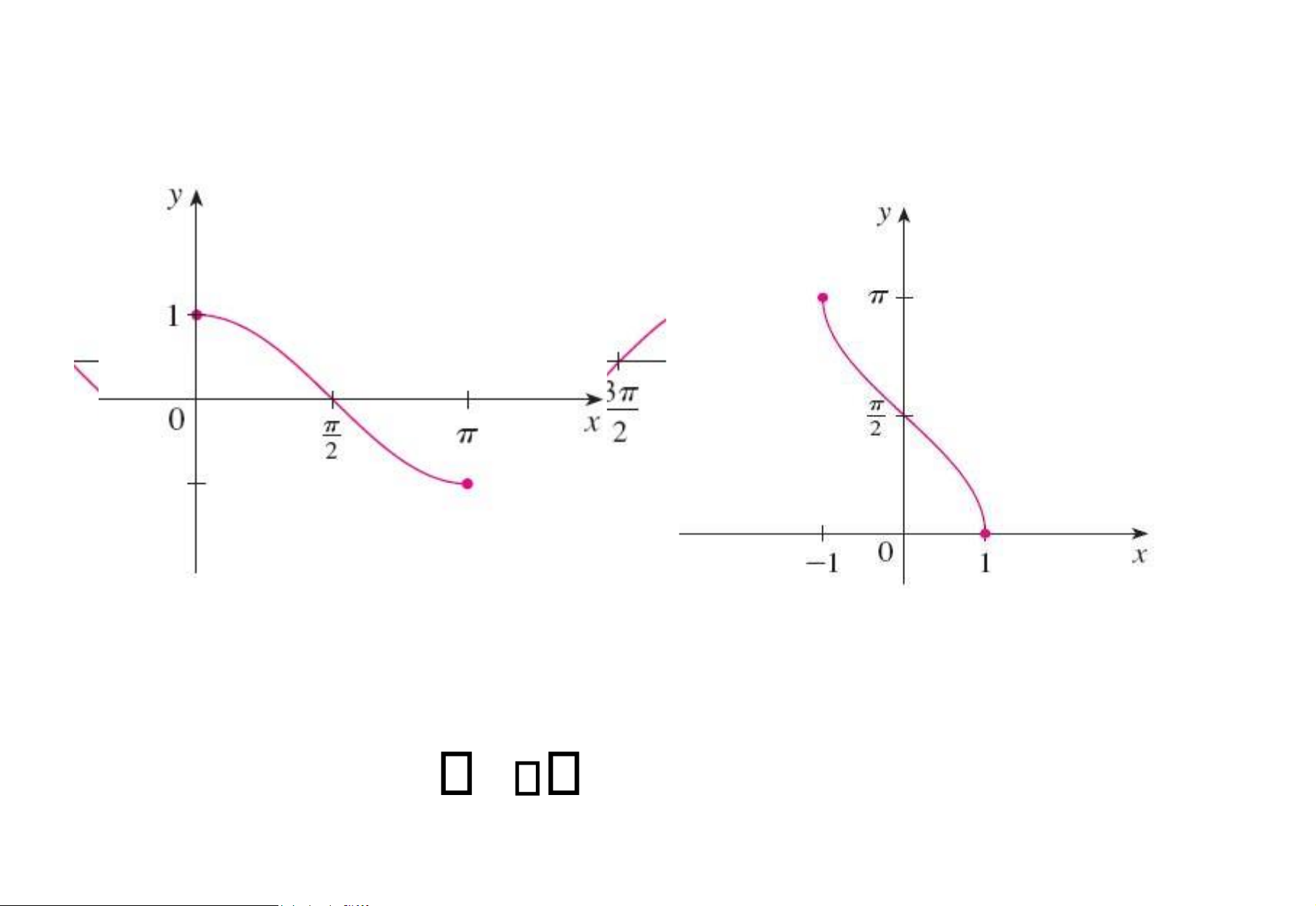
Xét hàm lượng giác y = cos x Trên oạn , 0,
y = cos x là hàm 1 – 1. lOMoAR cPSD| 49519085
Tồn tại hàm ngược, ký hiệu y arccosx Hàm arcsin x Miền xác ịnh: [-1,1] Miền giá trị: - 2 , 2
Hàm luôn luôn tăng. Hàm arccos x
Miền xác ịnh: [-1,1]
Hàm luôn luôn giảm. lOMoAR cPSD| 49519085 Miền giá trị: 0,
Định nghĩa (hàm lượng giác ngược)
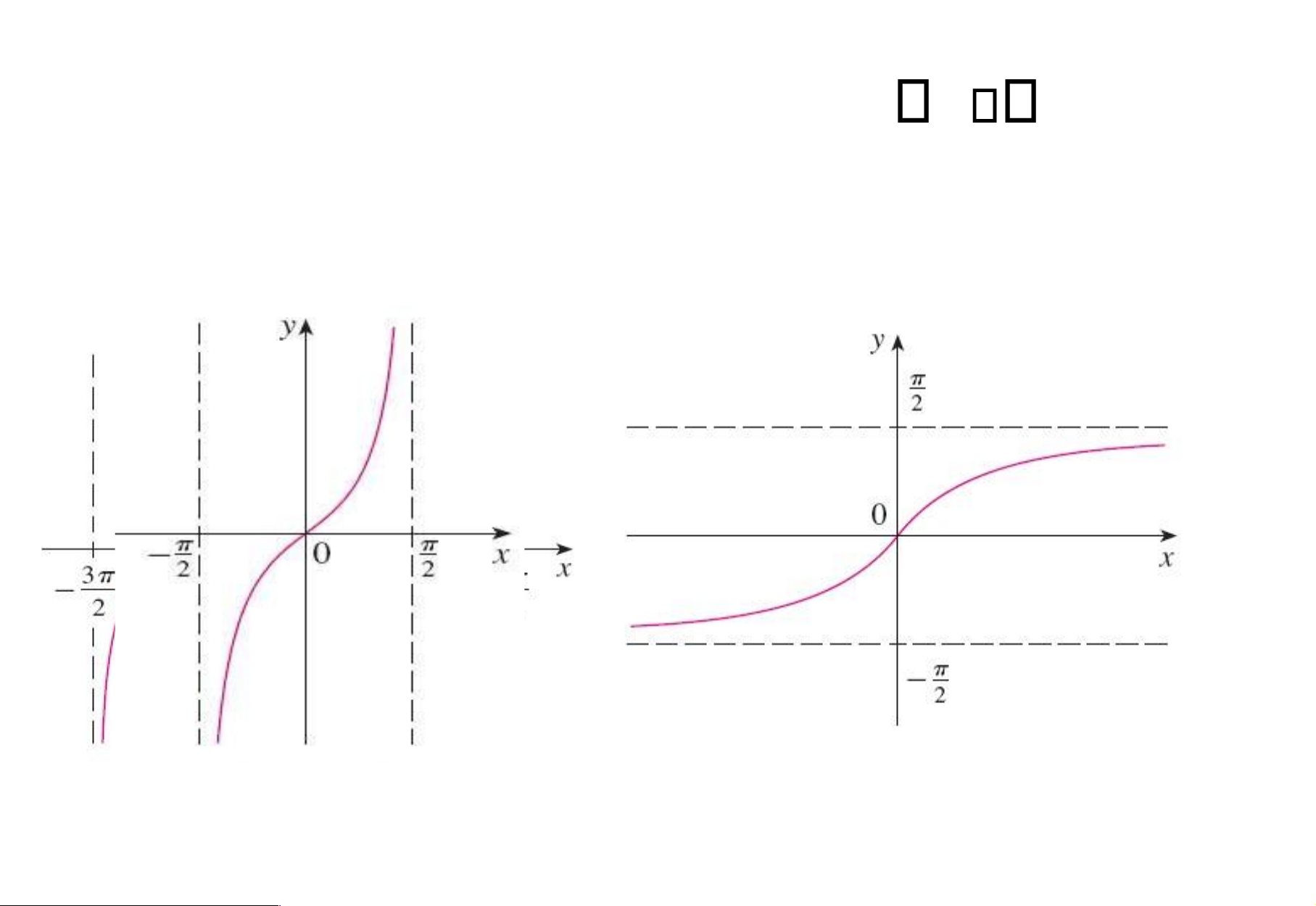
Xét hàm lượng giác y = tanx lOMoAR cPSD| 49519085 Trên khoảng , , y = tan x là hàm 1 – 1. 2 2
Tồn tại hàm ngược, ký hiệu y arctanx
Định nghĩa (hàm lượng giác ngược)
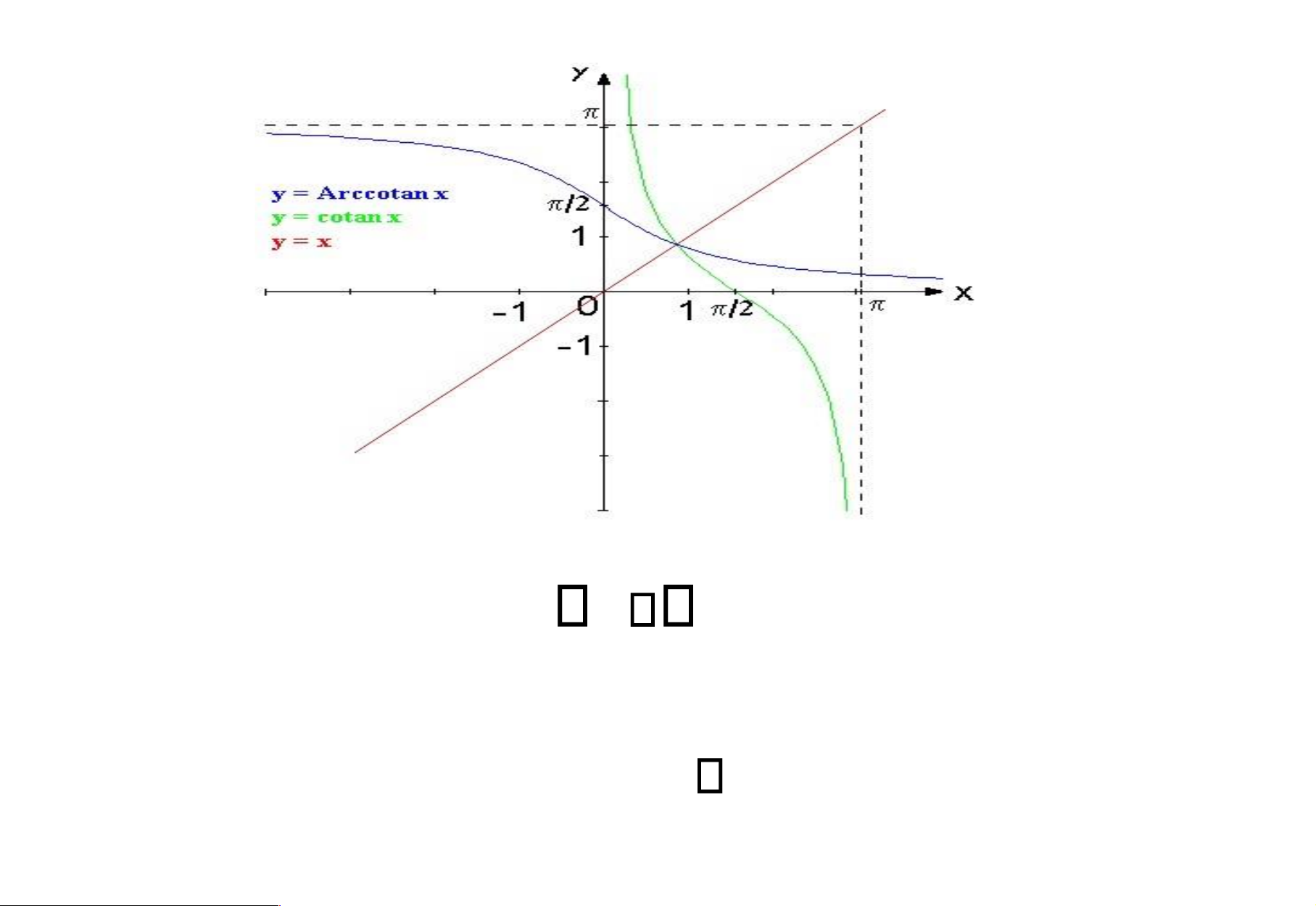
Xét hàm lượng giác y = cot x lOMoAR cPSD| 49519085 Trên khoảng , 0, y = cot x là hàm 1 – 1.
Tồn tại hàm ngược, ký hiệu y arccot x lOMoAR cPSD| 49519085 Hàm arctan x Miền xác ịnh: R Miền giá trị: - , 2 2
Hàm luôn luôn tăng. Hàm arccotan x Miền xác ịnh: R lOMoAR cPSD| 49519085
Hàm luôn luôn giảm. Miền giá trị: 0,
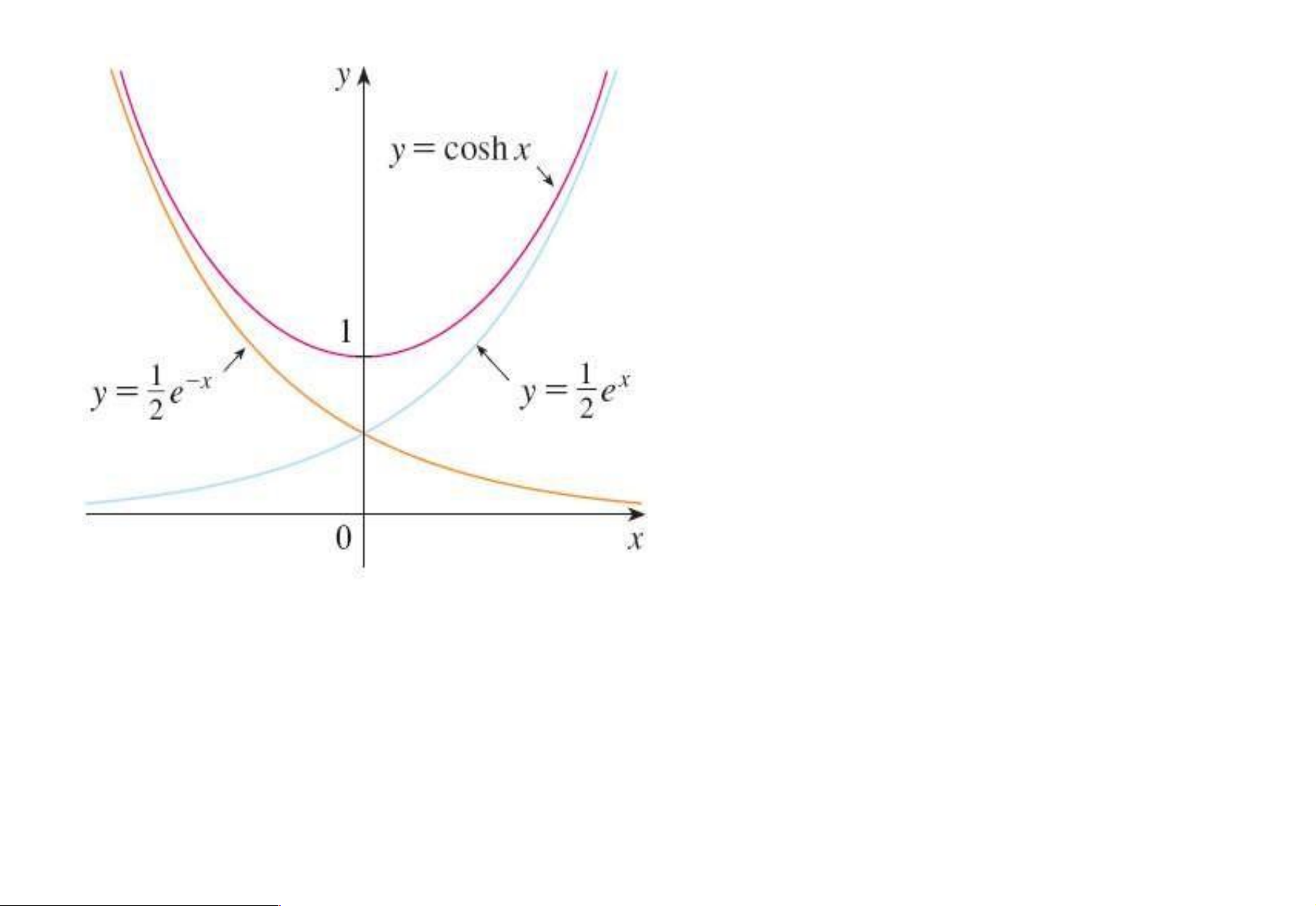
Định nghĩa (hàm Hyperbolic) ex e x sinh( )x sin hyperbolic 2 ex e x cos hyperbolic cosh( )x 2 lOMoAR cPSD| 49519085 tan hyperbolic tanh( )x cotan hyperbolic coth( )x lOMoAR cPSD| 49519085