Lý thuyết giới hạn hàm số | Môn toán cao cấp

lOMoAR cPSD| 49519085
Giới hạn hàm sô
Shortlink: http://wp.me/P8gtr-1bc
I. Các định nghĩa: 1. Định nghĩa 1:
Nếu f là một hàm số, khi đó ta nói:
A là giới hạn của hàm số f khi x dần tiến đến a
nếu giá trị của hàm số f(x) nhận các giá trị rất gần giá trị A khi x dần tiến đến a. Điều này được viết lim f x( ) A
theo ký hiệu Toán học như sau: x a lim x2 9 2 Ví dụ: x 3
do x nhận các giá trị rất gần 9 khi x tiến đến 3. limx 1 xx2 11 12 vì:
Mặc dù khái niệm giới hạn đã tiềm ẩn trong sự phát triển của ngành Giải tích từ thế kỷ thứ 17 và 18,
nhưng, khái niệm hiện đại về giới hạn của hàm số mới được đề cập đầu tiên vào năm 1817 bởi nhà
toán học Bolzano. Ông đã đưa ra khái niệm epsilon - delta khi đề cập đến khái niệm hàm số liên tục.
Tuy nhiên, thật đáng tiếc, công trình này đã không được mọi người biết đến trong suốt cuộc đời của
ông. (Felscher, Walter (2000), "Bolzano, Cauchy, Epsilon, Delta", American Mathematical Monthly
(Mathematical Association of America), 107).
Năm 1821, Cauchy đã thảo luận về vấn đề giới hạn trong quyển Cours d'analyse, trong đó ông đã
dùng thuật ngữ “approaches indefinitely” để mô tả khái niệm giới hạn. Việc mô tả này gần giống với
định nghĩa giới hạn hiện tại. Dẫu vậy, điều này cũng không được công nhận vì ông mô tả nó bằng lời.
(theo Grabiner, 1983, "Who Gave You the Epsilon? Cauchy and the Origins of Rigorous Calculus",
American Mathematical Monthly (Mathematical Association of America), 90).
Mãi sau này, đến năm 1840, Weierstrass mới được biết đến như là người đầu tiên đưa ra thuật ngữ
"epsilon - delta" để định nghĩa cho khái niệm giới hạn. Và đây cũng chính là khái niệm giới hạn mà
ta biết như ngày nay. Bên cạnh đó, ông cũng là người đề xuất ký hiệu lim (1840) và limx->x0.
(1854).(theo Burton, The History of Mathematics: An Introduction, p.616 - 617, 1997, McGrawHill).
Còn ký hiệu giới hạn như ngày nay, đặt dấu mũi tên phía dưới ký hiệu lim, là do nhà Toán học
Hardy đưa ra vào năm 1908 trong quyển sách có tựa đề A Course of Pure Mathematics. (theo Miller, 2004) lOMoAR cPSD| 49519085
Định nghĩa như trên hoàn toàn theo ngôn ngữ nói bình thường. 2. Định nghĩa 2:
Cho hàm số y f x( ) xác định trong một lân cận v(a) của a, số thực L hữu hạn được gọi là giới hạn
của hàm số f(x) khi x a nếu: ò 0, 0 : 0 x a
(1) f x( ) L (2)
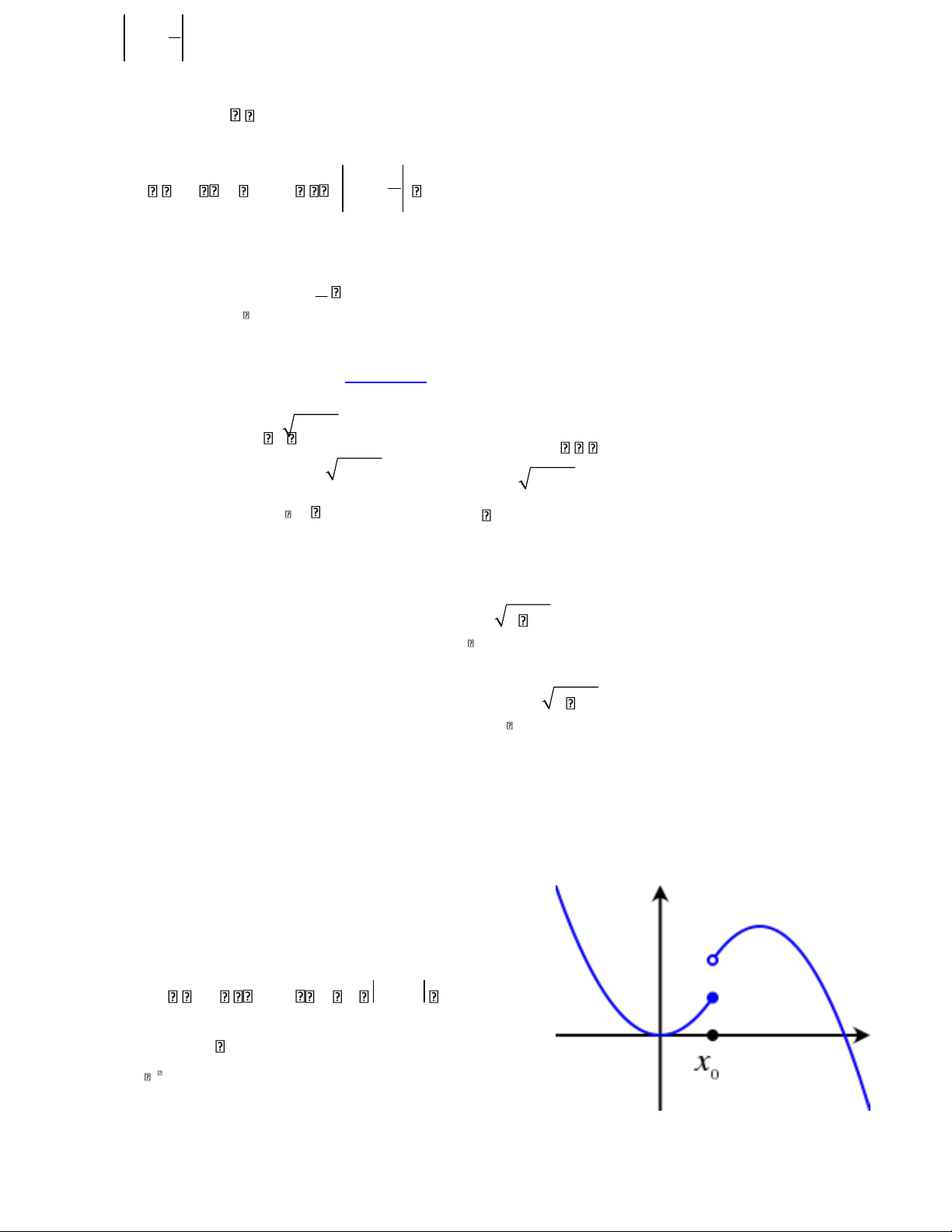
Ý nghĩa: Với khoảng sai khác rất bé ε được định
trước ta luôn tìm được 1 khoảng lân cận v(a) của
a sao cho với mỗi giá trị x nằm trong lân cận của
v(a) ta luôn có giá trị f(x) sai khác L 1 khoảng bé hơn ε.
Nói cách khác: nếu ta muốn f(x) gần với L đến
mức nào mà bạn muôn (sai khác một khoảng ε
khá bé (để bất đẳng thức (2) xảy ra), thì bạn có
thể tìm được δ thích hợp để x đủ gần a (để có bất đẳng thức (1)).
Khi đó, bất cứ khi nào x ≠ a thỏa mãn (1), giả sử tại x0 thì sẽ có giá trị f(x) thỏa mãn (2), và giá trị đó
là f(x0). Như vậy, giới hạn hàm số f(x) khi x tiến đến a không phụ thuộc vào việc hàm số y = f(x) có
xác định tại x = a hay không! 1 lim .cosx 0
Ví dụ: Chứng minh x 0 x 1 ( )f x x.cos Nhận xét: hàm số
x không xác định tại x = 0 nhưng xác định trong lân cận của 0. 1 f x( ) 0 x.cos ò
Với mỗi số ε > 0 nhỏ tùy ý, ta có: x
Ta cần tìm giá trị sao cho: 0 |x| 1 1 x.cos | x |. cos | x| lOMoAR cPSD| 49519085 Ta có: x x
Vậy ta chỉ cần chọn ò 1 ò 0, =ò 0:|x-0| x.cos ò Khi đó: x 1 lim .cosx 0
Vậy theo định nghĩa: x 0 x
3. Giới hạn 1 bên: (Left limit and right limit) f x( ) Ví dụ: Xét hàm số
9 x2 có miền xác định trong đoạn 3 x 3 . Nếu a là 1 giá trị bất kỳ nằm
trong khoảng (-3;3) thì limx a 9 x2 tồn tại và bằng 9 a2 . Tuy nhiên, tại x = 3: lim 9 x2
Cho x tiến đến 3 từ phía bên trái (x < 3): Khi đó: x 3 tồn tại và bằng 0. lim 9 x2
Nhưng cho x tiến đến 3 từ phía bên phải (x > 3): thì x 3 không tồn tại ( do x không thuộc MXD của hàm số)
Vậy, chỉ có những giá trị x < 3 mới tồn tại giới hạn nên xuất hiện khái niệm giới hạn trái.
Tương tự, xét x dần tiến về -3, sẽ xuất hiện khái niệm giới hạn phải. Giới hạn trái: ò 0, 0 : a- x a f (x)-L ò lim f x( ) L
Ký hiệu: x a Giới hạn phải: lOMoAR cPSD| 49519085 ò 0, 0 : a x
a+ f (x)-L ò Image via Wikipedia lim f x( ) L
Ký hiệu: x a Nhận xét:
lim f x( ) L lim f x( ) lim f x( ) L Từ định nghĩa ta có: x a x a x a
4. Giới hạn vô cùng: (Infinity limit) 1 lim Xét: x 0 x
Trong trường hợp này, khi x càng dẩn tiến đến 0, thì giá trị f(x) càng ngày càng lớn, lớn hơn bất kỳ 1
số thực dương nào cho trước, nói chung là Vô cùng lớn. lim f x( )
M 0, 0: 0 |x-a| f (x) M Do đó: x a
lim f x( ) L ò 0, 0N R :|x| N f(x)-L ò Tương tự: x
Ký hiệu được nhà toán học John Wallis sử dụng đầu tiên vào năm 1665 trong quyển sách có tựa đề
"Arithmetica Infinitorum".
Ký hiệu này bắt nguồn từ việc người La Mã dùng nó để chỉ số 1000. Cũng giống như ngày nay, từ
"myriad" (vô số) được dùng để chỉ một số lượng lớn mặc dù tiếng Hy Lạp cổ, nó có nghĩa là 10.000
II. Các định lý và tính chất: 1. Định lý:
Các định lý sau đây được chứng minh khá dễ dàng. Xem như đây là bài tập.
1. Nếu f x( ) là hàm số sơ cấp và f a( ) c - hằng số thì limx a f x( ) f a( ) c
Nếu không để ý điều kiện f(x) là hàm sơ cấp sẽ dẫn đến sai lầm sau: lOMoAR cPSD| 49519085 1 ;x 0 f x( ) Xét 0 ;x 0 lim f x( ) 1 0 f (0) Khi đó: x 0
lim f x( ) A;lim ( )g x B
Trong các định lý sau đây, giả sử x a x a (A, B hữu hạn).
lim . ( )c f x c.lim f x( ) c A.
2. x a x a
lim f x( ) g x( ) AB 3. x a
limx a f x g x( ). ( ) limx a f x( ).limx a g x( ) AB. 4. 5. lim g xf x( )( ) limlimxx aa g
xf x( )( ) BA;(B 0) x a 6.limx a a
n f x( ) n limx f x( ) n A (nếu n A xác định )
7. limx a f x( )g x( ) AB (B 0) 1 1 lOMoAR cPSD| 49519085 Ví dụ: limx ;lim 0 x2 x 0 x4
Nhưng: limx 0 11// xx24 x 0 2 0
lim x lim f x( ) lim f x( )
Lưu ý: ta nói x a hoặc x là tồn tại nếu giá trị của giới hạn là số thực hữu hạn nhưng không nói tồn tại nếu giới hạn là ; ;
lim f x( );lim g x( )
lim[ ( )f x g x( )]
Mở rộng: Tìm ví dụ sao cho x a x a
không tồn tại nhưng tồn tại x a
2. Định lý giới hạn kẹp: (pinching theorem or sandwich theorem or squeeze theorem)
Cho I là một khoảng lân cận của a. Và f, g, h là các hàm số xác định trên I (có thể không xác định tại a)
Giả sử rằng: g x( ) f x( ) h x( ); x I
lim ( )g x lim ( )h x L Và nếu: x a x a
lim f x( ) L Khi đó: x a
Định lý giới hạn kẹp được nhà Toán học Archimedes và Eudoxus sử dụng lần đầu tiên dưới dạng biểu
diễn hình học; trong một nỗ lực để tính toán số Pi.
Sau đó, nó được nhà Toán học Gauss thể hiện theo ngôn ngữ Toán học hiện đại như ngày nay.
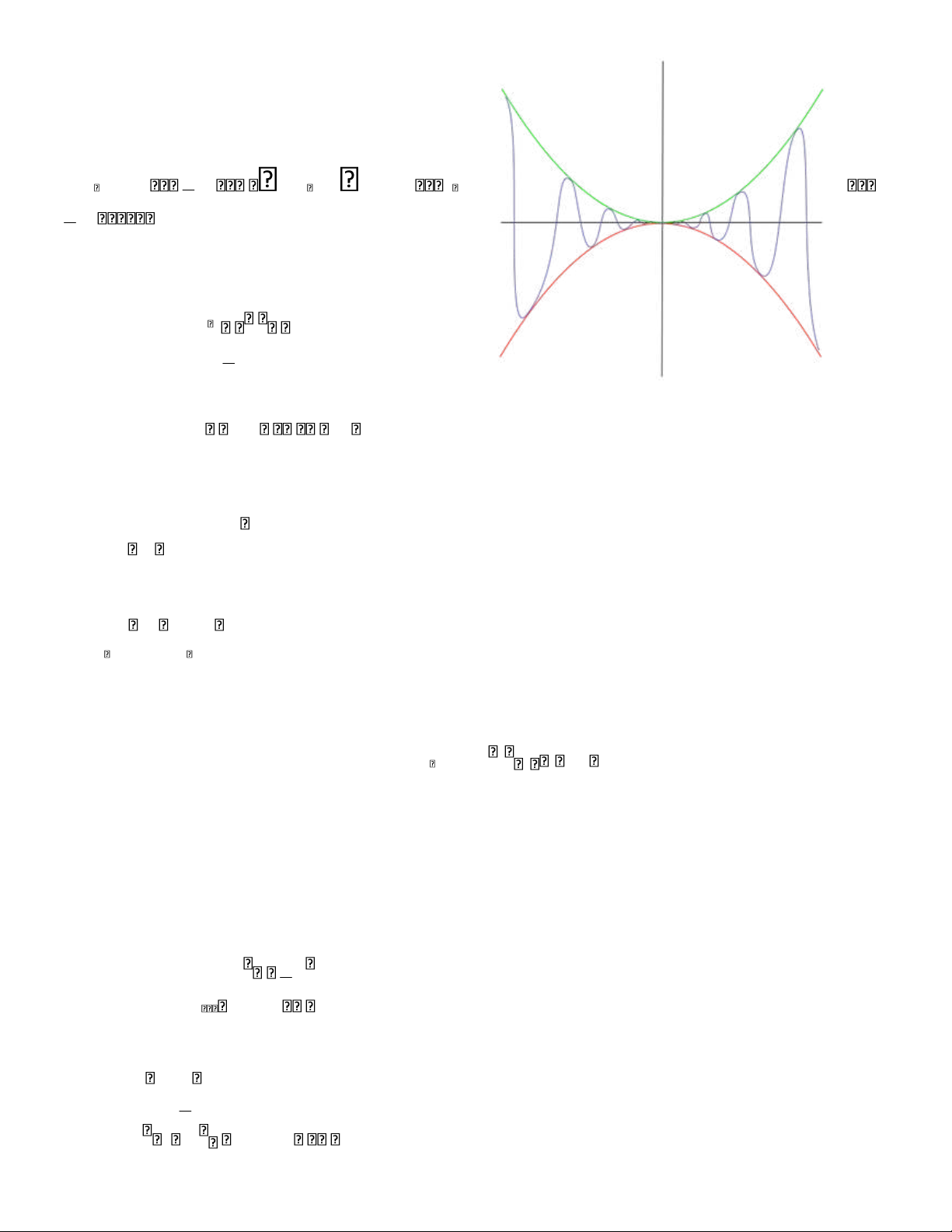
Ví dụ: Tìm giới hạn của: limx 0 x2.sin 1x lOMoAR cPSD| 49519085
Nhận xét: giới hạn trên không thể tính toán thông qua
các tính chất giới hạn: limx 0 x2.sin 1x
limx 0 x2 . limsin x 0 1x
vì giời hạn limsinx 0 1x không tồn tại.
Tuy nhiên, ta có: 1sin 1x 1 2 x2.sin 1 x2 x Từ đó: x lim x2 lim x2 0 Do: x 0 x 0
Do đó, theo định lý giới hạn kẹp ta có: 1 limx 0 x2.sin x 0 3. Sô e: x lim 1 1 Ta chứng minh: x x e n 1
Ta đã có: 1 n e khi n (n N) lOMoAR cPSD| 49519085 - Xét x :
Với x > 0 và khá lớn, ta luôn tìm được n N sao cho: n x n 1 1 1 1 1 1 1 1 1 1 Khi đó, ta có: n 1 x n Hay: n 1 x n n x x 1 1 1 1 Suy ra: n 1 1 n 1 1 x (1) 1 x 1 n 1 1 n 1 Mặt khác: 1 x 1 x 1 n (2) n x n 1 1 1 1 Từ (1) và (2) ta có: 1 n 1 1x 1n e 1 1 n 1 n 1 1 n e nlim 1 n 1 nlim 1 1 1
Khi x thì n và: n 1 n n 1 1 nlim 1 n nlim 1 n 1 . 1 n e.1 e 1 x xlim 1 x
e &fg ff 0000(3)
Vậy theo định lý giới hạn kẹp ta có: Xét x :
Ta đặt: x (t 1) t x 1;(t R) (t 1)
Khi x thì t . Khi đó: 1 x 1 (t 1) t lOMoAR cPSD| 49519085 lim 1 x tlim 1 t 1 tlim t 1 x t 1 tlim t t 1 t 1 tlim 1 1t t t e1 e(4)
Vậy, từ (3) và (4) ta có điều phải chứng minh. 1 1/ò x
ò ta có: lim 1ò 0 ò e Hệ quả: Đặt
III. Khử dạng vô định: 0 f x( ) lim
3.1. x x0 g x( ) có dạng vô định 0 : biến đổi để tử và mẫu số xuất hiện nhân tử chung (x x0) Ví dụ 3.1: limx 4 x2 x x 412 Ta có: limx 4
2 x x 412 limx 4
(x x3)( x4 4) limx 4 x1 3 17 x
Nhận xét: ta có thể khử x - 4 ở tử và mẫu trước khi lấy giới hạn vì x 4 khi x 4 4 x2 lim Ví dụ 3.2: x 2 3 x2 5
Do ở mẫu có chứa căn bậc hai, nên ta nhân lượng liên hợp để khử căn bậc 2 trước. Ta có: lim 4 x2
lim (4 x2 )(3 x2 5) lim 3 x2 5 6 x 2 2 3 x2 5 x 9 (x2 5) x 2 lOMoAR cPSD| 49519085 3.2. Dạng vô định
Chia phân thức cho số hạng có bậc cao nhất của tử số và mẫu số. 1 x 3 x3 2 13 2x
xlim x2 1 xlim x2 1 12 Ví dụ 3.3: x 3.3. Dạng vô định
Nhân thêm lượng liên hợp để đưa về dạng lim x
x2 1 Ví dụ 3.4: x
(x x2 1)(x x2 1) 1 lim lim 0 Ta có: x x x2 1 x x x2 1
3.4. Công thức L'Hospital - Bernulli:
lim f x( ) g x( )
3.5. Giới hạn dạng: x x0
lim f x( ) a a( 0); lim g x( ) b lim[ ( )]f x g x( ) ab 3.5.1. Nếu x x0 x x0 (a, b
hữu hạn) thì x x0
lim f x( ) 1; lim g x( )
3.5.2. Nếu x x0 x x0 thì kết quả được suy ra ngay một cách trực tiếp. (Bạn đọc thử suy nghĩ) lOMoAR cPSD| 49519085 lim[ ( )]f x g x( )
3.5.3. Nếu x x có dạng 1 . Khi đó: 0
u x( ) f x( ) 1 lim u x( ) 0 Đặt x x0 1 lim 1 u x( ) u x( ) e Khi đó: x x0 1 lim 1 ( ( )f x 1)
f x( ) 1 e Suy ra: x x0 Do vậy: g x( ) 1 ( f x( ) 1). ( )
g xx xlim ( 0 f x( ) 1) g x( )
lim f x( ) lim 1 ( ( )f x 1) f x( ) 1 e &fg ff 0000 x x0 x x0 sinx
x2 2x 1 2x lim
Ví dụ 3.5: Tính giới hạn: x 0 2x2 2x 1 x2 2x 1 1
Do limx 0 2x2 2x 3 3 sinx 1 lim Và: x 0 2x 2 sinx Nên: limx 0 2xx22 22xx 11 2x 13 1/2 33 sinx
x2 2x 1 2x
Ví dụ 3.6: Tính giới hạn: lim 2x2 2x 3 x x2 2x 1 1 lOMoAR cPSD| 49519085
Ta có: limx 2x2 2x 3 2 sinx lim 0 Và: x 2x
(sử dụng giới hạn kẹp) sinx Vậy: lim 2xx22 22xx 13 2x 12 0 1 x 1 x2 x2
Ví dụ: Tính giới hạn: limx x2
Nhận xét: Do f x( ) 1 x2x x x 2 1;g x( ) x2
nên giới hạn có dạng vô định 1 1 x2 lim ( x x f x( ) 1) ( ) g x L limx 2 e Do đó: x
lim( ( )f x 1). ( )g x lim 1 x2 2 lim x2 1 x x x2 1 . x x x2 Xét:
Vậy: L e1 e
3.5.4 Dạng vô định 00; 0
Với giới hạn dạng vô định này, ta xét: y f x( )g x( ) lny g x ln f x( ). ( ( )) lOMoAR cPSD| 49519085 lim lny Khi đó: x x0 có dạng vô định 0.
Khử dạng vô định của lny. lim lny A
Giả sử x x0
lim f x( )g x( ) eA Khi đó: x x0