






Preview text:
lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
BÀI 1: HÀM SÞ MÞT BI¾N SÞ
1.1. Mßt sß khái niệm cơ bản về hàm mßt bi¿n
1.1.1. Định nghĩa hàm sß mßt bi¿n
Cho X, Y là các tập con của tập số thực R. Ta gọi quy tắc f cho tương ứng
với mỗi số x X có một giá trị duy nhất y Y là hàm số một biến. -
Ký hiệu hàm số là: y = f(x) (Ta gọi y là hàm số của x, hay f là hàm số của x) -
Tập X gọi là tập xác ịnh của hàm số -
Tập f(X):= y Y y, = f x x( ), X gọi là tập giá trị của hàm số
Ví dụ 1. quy tắc cho tương ứng giữa một số thực với một số thực xác ịnh
bßi các công thức y= x ; y=cosx là những hàm số một biến
Ví dụ 2. Doanh số bán hàng S phụ thuộc vào thßi gian t ược cho bßi bảng sau: Tháng t 1 2 3 4 5 6 7 8 9 10 11 12
Doanh số S 57 54 59 62 65 63 70 71 68 76 69 71
Mỗi giá trị của tháng t cho ta một giá trị doanh số S, chẳng hạn S(2) = 54.
Ta nói S là một hàm số của t.
Ví dụ 3. Chi phí C phải bỏ ra khi i taxi phụ thuộc vào ộ dài quãng ưßng di
chuyển d như sau: Giá mß cửa 10000 VNĐ/0,3 km; Giá ến km thứ 32 là 14000
VNĐ/km; Giá từ km thứ 33 trß i là 11000 VNĐ/km. Với một ộ dài quãng ưßng di
chuyển d, ta sẽ phải trả một số tiền C tương ứng tính theo quy tắc trên. Ta nói C
là một hàm số của d.
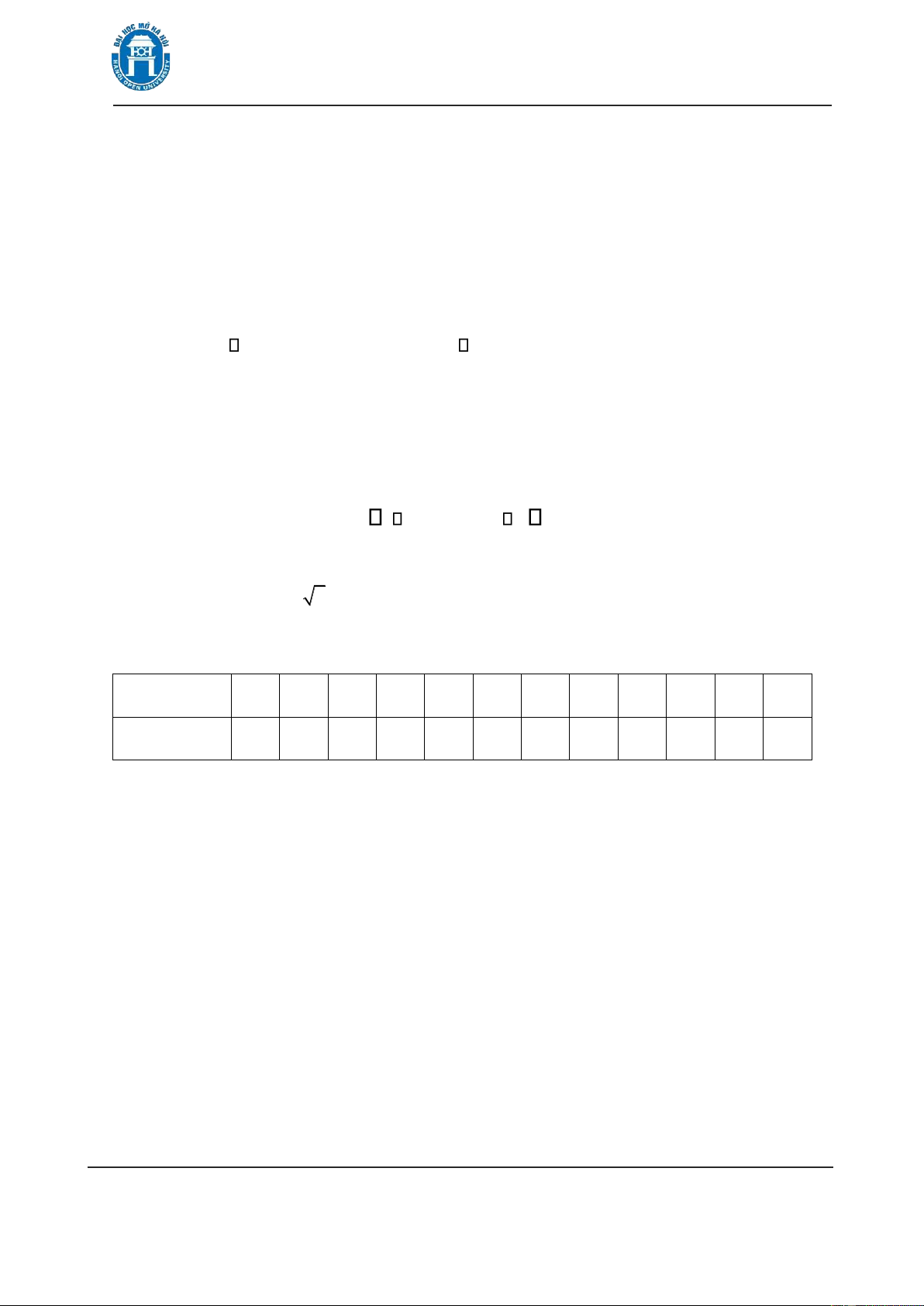
Ví dụ 4. Sự phụ thuộc giữa giá P và số lượng Q của một loại sản phẩm ược
mô tả trên hình 1.1. Với mỗi một số Q cho trước ta có một giá trị P tương ứng, Ta
nói P là một hàm số của Q.
Toán ứng dụng trong kinh tế – Bài 1 1 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
Hình 1.1. Mối liên hệ giữa P và Q
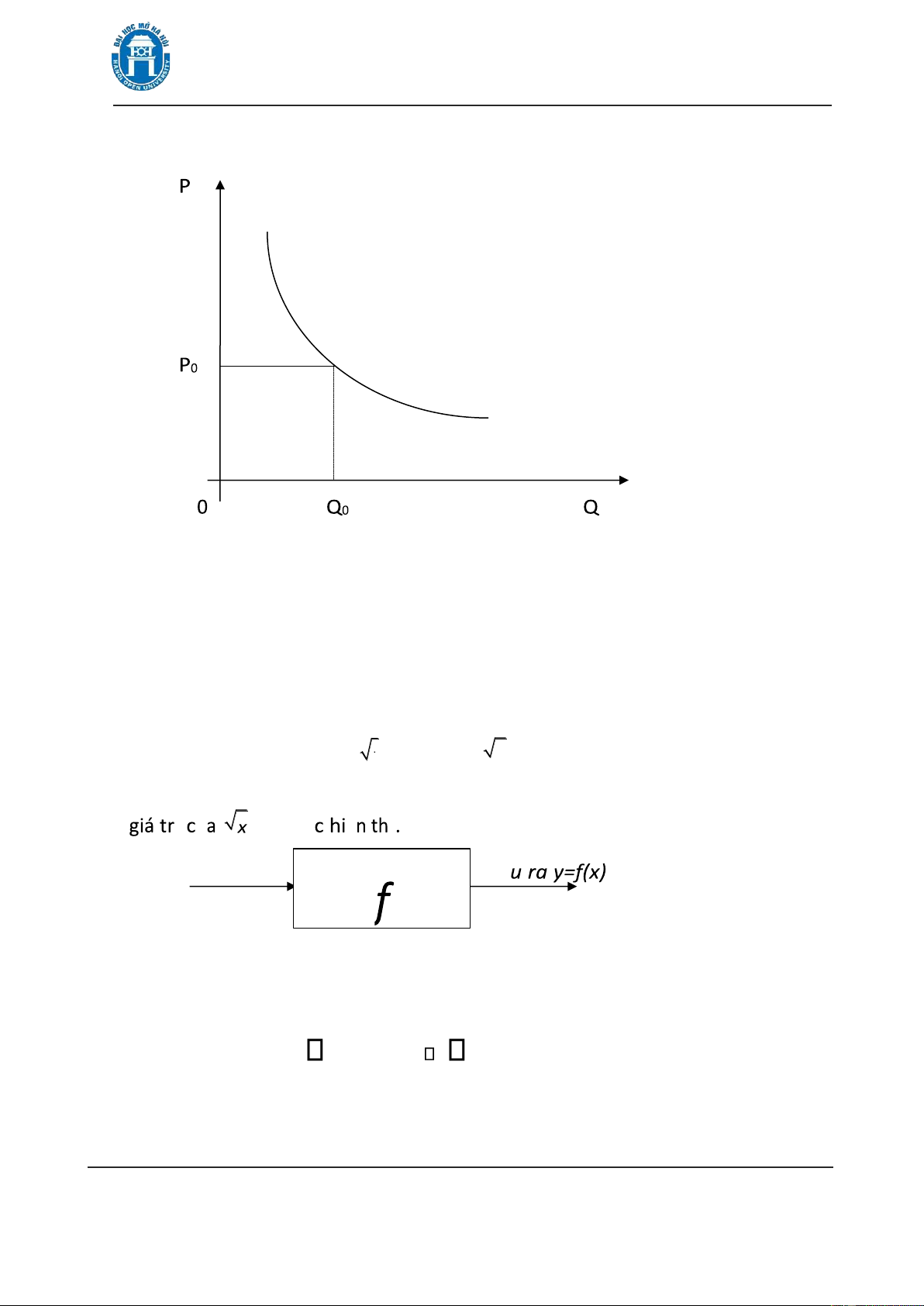
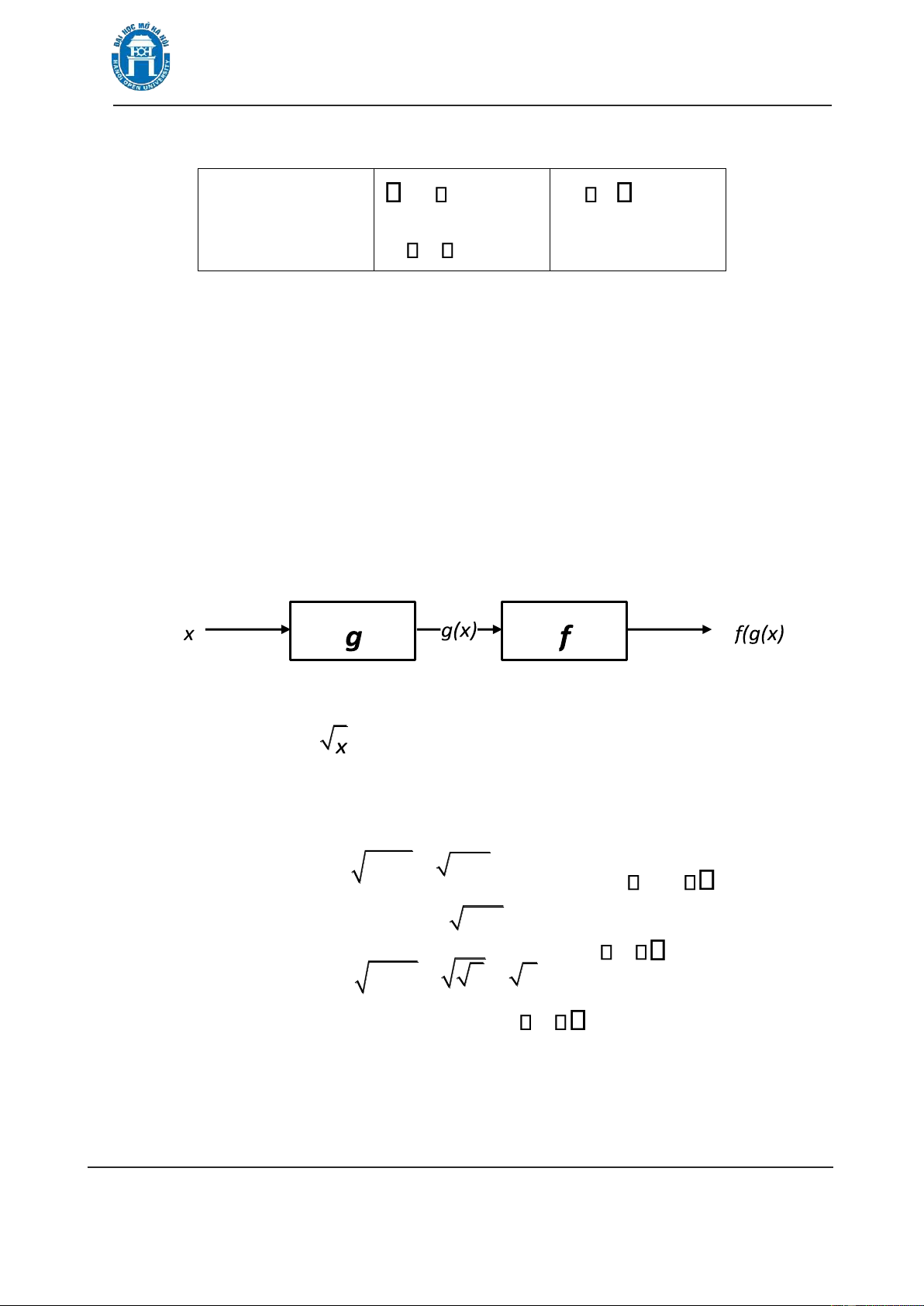
* Nhận xét: 1) Có thể coi hàm số như một cái máy sản xuất mà ầu vào của máy
là giá trị x và ầu ra của máy là giá trị y=f(x) (xem hình 1.2). Các hàm lập trình
sẵn trên máy tính bỏ túi là ví dụ minh hoạ dễ hiểu cho việc coi hàm số như là
một cái máy. Chẳng hạn, có thể coi phím căn bậc hai trên máy tính như là một
hàm số. Ta ấn phím có nhãn (ho
ặc x ) và nhập vào giá trị ầu vào x.
Nếu x<0 thì máy tính báo lỗi (vì giá trị này không thuộc tập xác ịnh).Nếu x ≥ 0 ị ủ s ẽ ượ ể ị Đầ u vào x Đầ
Hình 1.2. Hàm số như một máy sản xuất
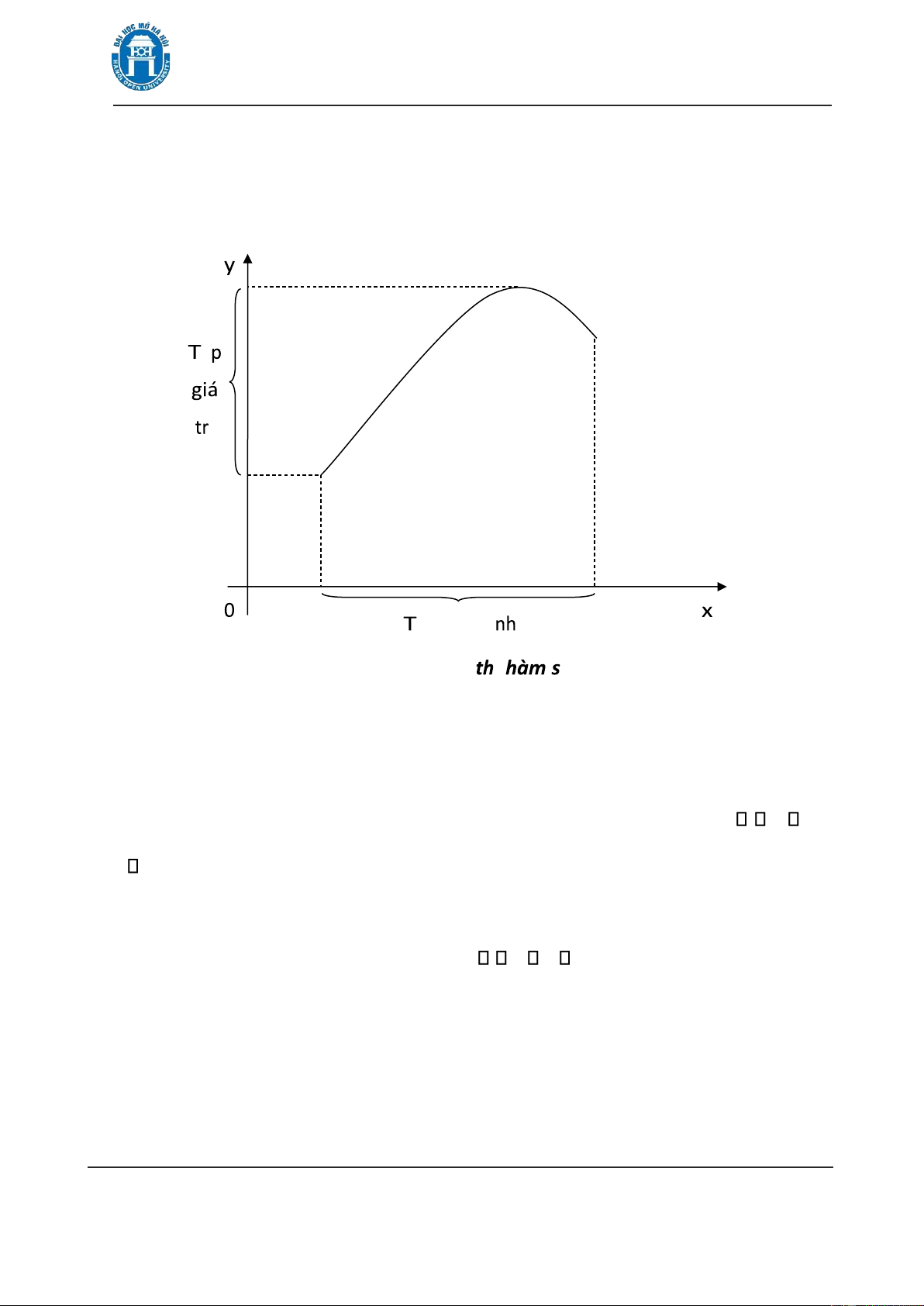
2) Để trực quan hoá hàm số, ngưßi ta sử dụng ồ thị của nó. Đồ thị của hàm số là
tập hợp tất cả các cặp (x f x, ( ))| x D . Nói cách khác, ồ thị hàm số f bao
gồm tất cả các iểm (x,y) trong mặt phẳng toạ ộ sao cho y=f(x) với x thuộc tập xác
Toán ứng dụng trong kinh tế – Bài 1 2 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
ịnh của hàm số f. Có thể nói ồ thị là ta có thể thấy rõ ược tập xác ịnh và tập giá trị của hàm số (xem hình 1.3). ậ ị ập xác ị
Hình 1.3. Đồ ị
ố
1.1.2. Các loại hàm sß.
a) Hàm chẵn, hàm lẻ
Nếu một hàm số f thoả mãn f(-x) = f(x) với mọi x thuộc tập xác ịnh của
nó thì f ược gọi là hàm chẵn. Chẳng hạn, hàm số f(x)=x2 là hàm chẵn vì −
+ x ( , ) ta có: f (− = − = =x) ( x)2 ( ) x2 f x
Nếu f thoả mãn f(-x) = - f(x) với mọi x thuộc tập xác ịnh thì f ược gọi là hàm
lẻ. Chẳng hạn, hàm số f(x) = x3 là hàm lẻ vì − + x ( , ) ta có: f (− = − =− =−x) ( x)3 ( ) x3 f x
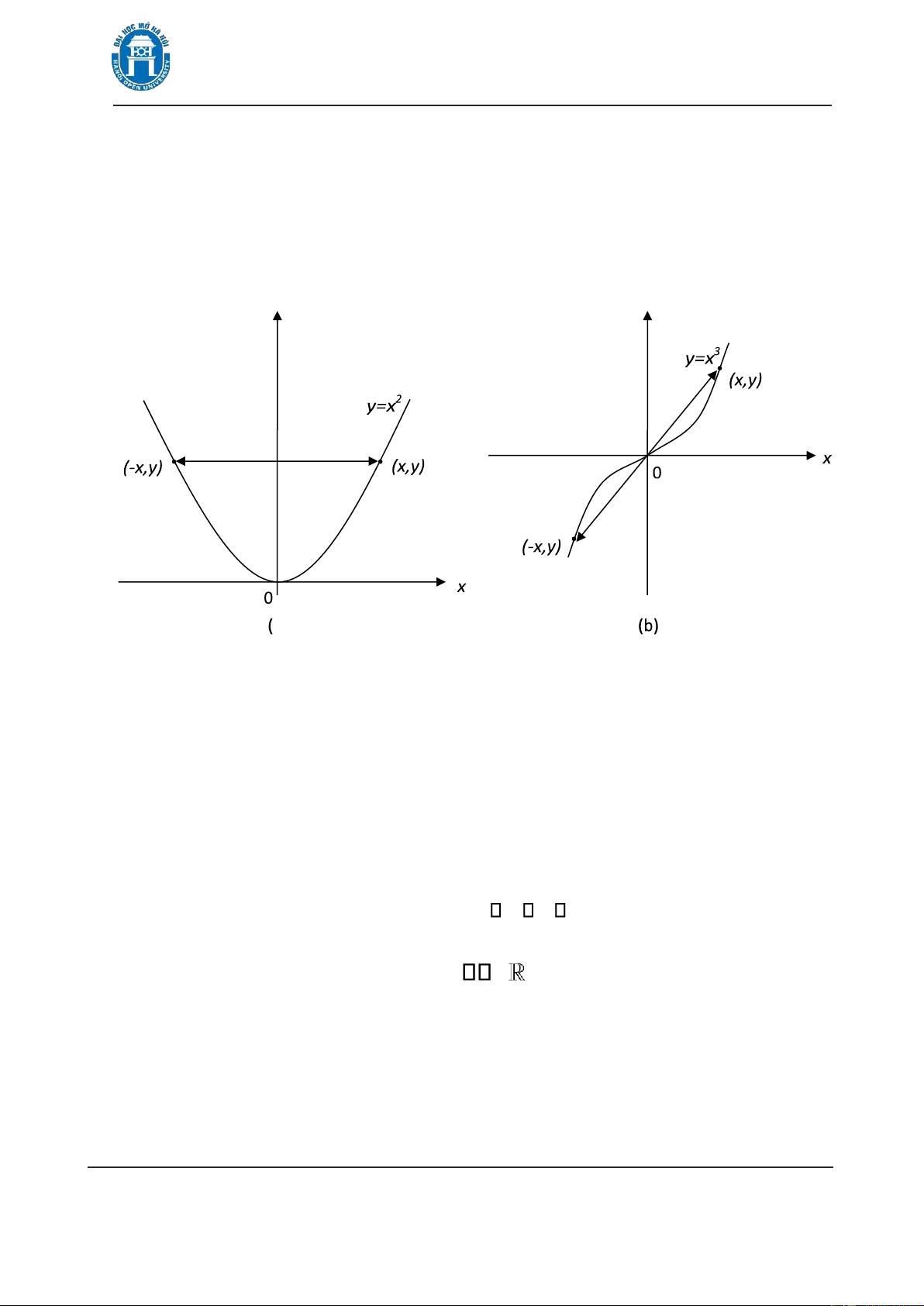
Đồ thị của hàm số chẵn nhận trục tung là trục ối xứng, ồ thị của hàm lẻ
nhận gốc toạ ộ làm tâm ối xứng (xem hình 1.4).
Toán ứng dụng trong kinh tế – Bài 1 3 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i y y a)
Hình 1.4. Tính ối xứng của ồ thị hàm số chẵn a) và hàm số lẻ b)
Ví dụ 1. Xét tính chẵn lẻ của các hàm số sau ây:
1) f x( )= +x7 2x
2) g x( ) = −3 x6
3) h x( ) =5x2 −4x Lời giải:
Các hàm số trên ều có tập xác ịnh x − + ( , ) . f x 1) Hàm
( )= +x7 2x là lẻ vì x , ta luôn có f (− =
− + − =− +x) ( x)7 2( x) (x7 2x)=− f x( )
Toán ứng dụng trong kinh tế – Bài 1 4 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i g x 2) Hàm
( ) = −3 x6là chẵn vì x , ta luôn có g(− = − − = − =x) 3 ( x)6 3 x6 g x( ) h x 3) Hàm
( ) =5x2 −4x không chẵn cũng không lẻ vì chẳng hạn với x=1, ta có:
h(− = − − − =1) 5( 1)2
4( 1) 9 h( )1 = 5 1( )2 −4 1( )=1
Rõ ràng, h(−1) h( )1 và h(−1) −h( )1
b) Hàm ồng bi¿n và hàm nghịch bi¿n
Ta kí hiệu các khoảng, oạn: (a b, ); a b, ; (a b, ; a b, ) là I. Một hàm
số f ược gọi là ồng biến (tăng) trên tập I nếu f x( ) ü f x( ) ü 1 2 khi x1
x2 x x1, 2 I
Một hàm số f ược gọi là nghịch biến (giảm) trên I nếu f x( ) þ f x( ) ü 1 2 khi x1
x2 x x1, 2 I y y x
Ví dụ. Xét hàm số = x2 và = 3 (xem hình 1.4), ta có: Hàm số Đoạn tăng Đoạn giảm
Toán ứng dụng trong kinh tế – Bài 1 5 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i y = x2 y 0,− ) ( − ,0 x= 3 ( Không tồn tại − + ,) c) Hàm hợp g x .
Cho hai hàm số f x( ) và
( ). Hàm hợp f g x ( ) ược xác ịnh bßi f g x. ( ) = f g x[ ( )]
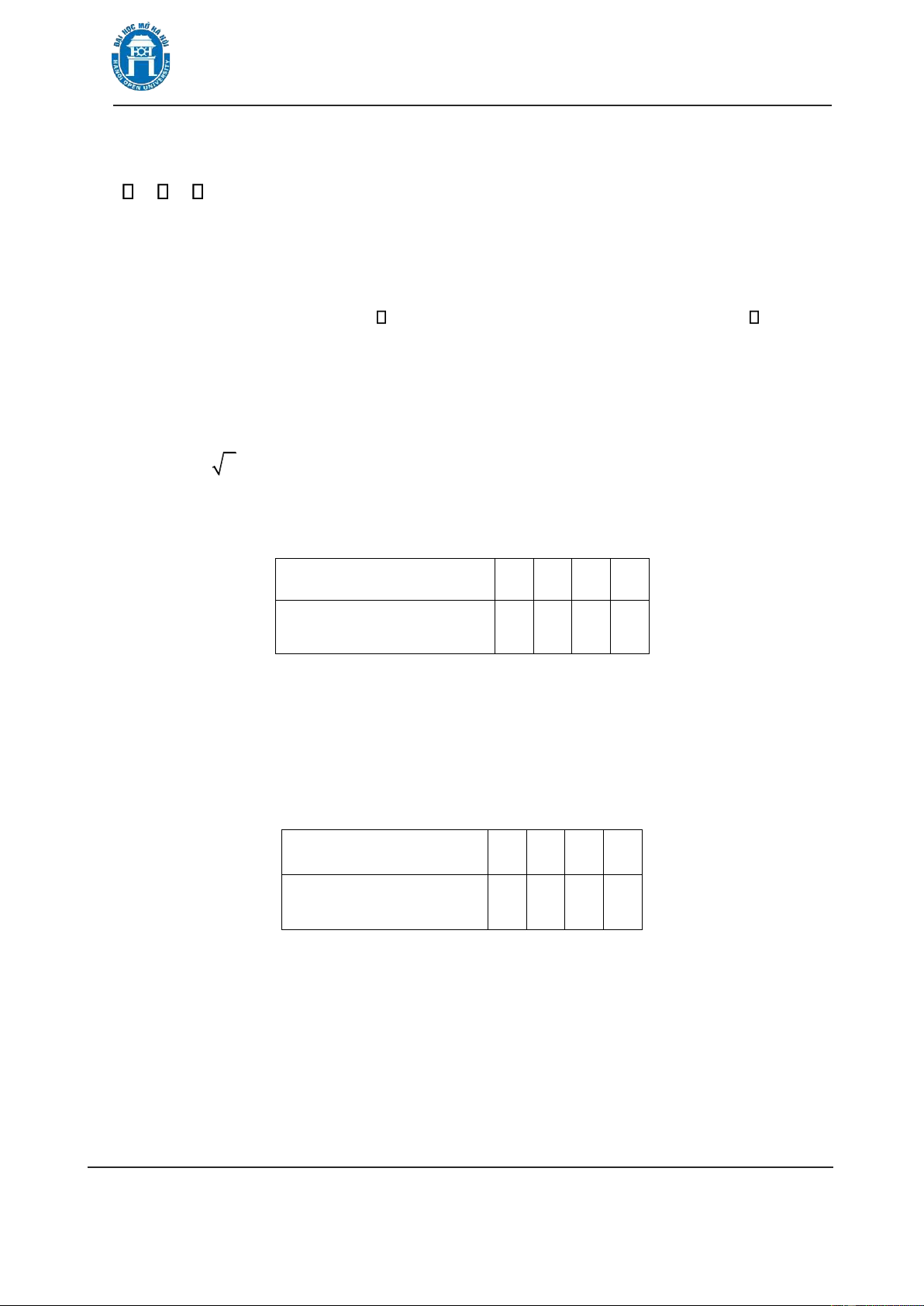
Để cho ơn giản, có thể coi hàm hợp là tổ hợp của hai máy như ược minh hoạ trên hình 1.5.
Hình 1.5. Hàm hợp như là tổ hợp của hai máy f x
Ví dụ . Cho hàm ( )=
và g x( ) = +x 1. Hãy tìm các hàm hợp sau ây: a/ f g. b/ g f. c/ f f. d/ g g. Lời giải:
a/ f g. = f g x( ( ))= g x( ) = +x 1 với tập xác ịnh x − + 1, ) b/
g f. = g f x( ( ))= f x( )+ = +1 x 1 với tập xác ịnh là x +
0, ) c/ f f. = f
( f x( ))= f x( ) = x = 4 x với tập xác ịnh là x + 0, ) d/ g g. = g g x( (
))= g x( )+ = + + = +1 (x 1) 1 x 2 với tập xác ịnh là
Toán ứng dụng trong kinh tế – Bài 1 6 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i x − + ( , )
d) Hàm ngược
* Định nghĩa hàm ngược: Cho y = f(x) là hàm số có tính chất tương ứng (1 – 1)
khi ó hàm số xác ịnh bßi mỗi y f X( )có một giá trị tương ứng duy nhất x X gọi
là hàm ngược của hàm y = f(x) và ký hiệu là x = f −1( )y
Ví dụ 1: hàm số y = f x( ) = x3 là hàm tương ứng 1 – 1, nên có hàm ngược là
x = f −1( )y = 3 y
Ví dụ 2: Giả sử ta có bảng GNP của một quốc gia (tổng sản phẩm quốc gia) phụ
thuộc theo thßi gian t như sau: t (năm) 2 5 10 20 GNP = f t( ) 12 16 27 74 (tỷ USD)
Ta thấy, GNP là hàm của thßi gian GNP = f t( ) . Trong thực tế, ta còn
quan tâm ến câu hỏi khi nào ể GNP ạt tới một ngưỡng nào ó. Nói cách khác, ta
ang nghĩ ến biểu diễn thßi gian như là một hàm số của GNP. Hàm số này gọi là
hàm ngược của hàm GNP = f t( ) , kí hiệu f −1. Vậy là t = f −1( )x là số năm cần
có ể GNP ạt ngưỡng x . GNP (tỷ USD) 12 16 27 74
t = f −1(GNP) (năm) 2 5 10 20 Chú ý: 1)
Không phải hàm số nào cũng có hàm ngược. Chỉ những hàm số có tương
ứng (một – một) mới có hàm ngược. 2)
Ngưßi ta thưßng dùng x ể chỉ biến ộc lập và y ể chỉ biến phụ thuộc nên ta
có các bước ể tìm hàm ngược của hàm y = f x( ) như sau:
Toán ứng dụng trong kinh tế – Bài 1 7 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
Bước 1: Từ hàm y = f x( ) , biểu diễn x theo y
Bước 2: Thay vai trò của x và y .
Ví dụ 3. Tìm hàm ngược của hàm y x= +3 2 Lời giải:
Bước 1: Từ y x= +3 2 ta có x = −3 2 y .
Bước 2: Hàm ngược sẽ là y = f −1( )x = −3 2 x .
1.2. Āng dụng cÿa hàm tuy¿n tính trong phân tích cung, cầu và xác ịnh thu nhập qußc dân 1.2.1. Hàm tuy¿n tính
Hàm tuyến tính hay hàm bậc nhất là hàm số có dạng y = f x( )= +ax b ,
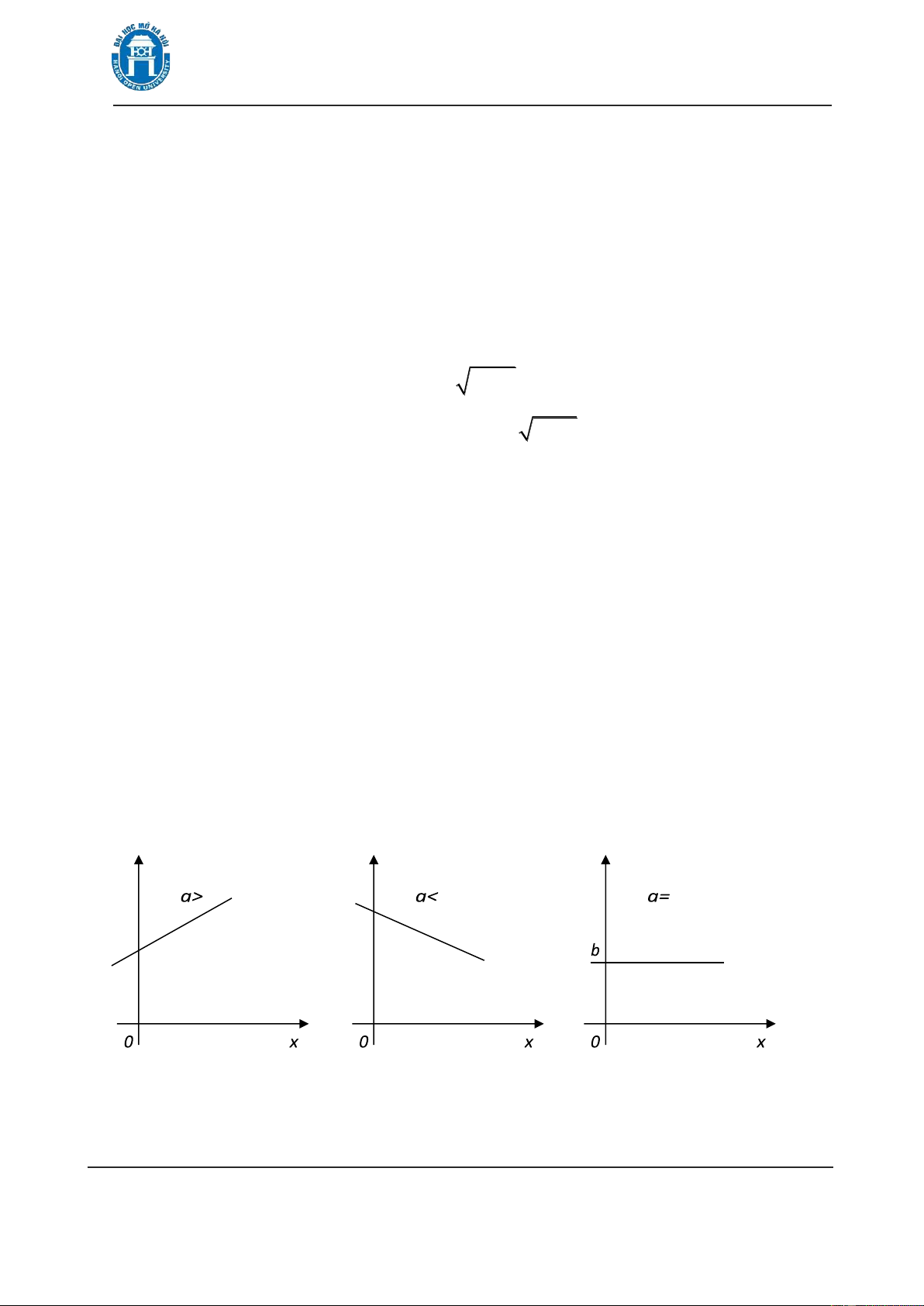
trong ó a và b là các hằng số. Đồ thị của hàm tuyến tính là ưßng thẳng. Hệ số a
ược gọi là hệ số góc của ưßng thẳng. Hàm số là hàm tăng nếu a þ0; hàm giảm a y a
nếu ü0 và là hàm = b nếu =0(xem hình 1.7). y y y
Hình 1.7. Đồ thị hàm y = +ax b
Toán ứng dụng trong kinh tế – Bài 1 8 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
Chú ý: Hàm tuyến tính có tính chất ặc trưng, ó là giá trị hàm thay ổi ều khi
biến số thay ổi. Chẳng hạn, xét hàm số y = f x( )= −3x
2. Mỗi khi x tăng một
lượng là 1 ơn vị thì f x( ) tăng một lượng là 3 ơn vị. 1.2.2.
Āng dụng cÿa hàm tuy¿n tính trong phân tích cung, cầu
và xác ịnh thu nhập qußc dân
Xét mßi quan hệ giữa giá cả ( )P và sß lượng ( )Q cÿa mßt loại sản phẩm.
Giả sử mßi quan hệ này là tuy¿n tính, tāc là ta có: P = aQ+b
Mối quan hệ này sẽ khác nhau tuỳ thuộc vào việc ta là ngưßi tiêu dùng hay nhà sản xuất:
a) Với ngưßi tiêu dùng: Hàm số P = aQ+b ược gọi là hàm cầu. Khi giá cả
tăng thì nhu cầu (số lượng sản phẩm) có xu hướng sẽ giảm và ngược
lại. Nói cách khác hàm số P = aQ+b là hàm giảm (a<0).
b) Với nhà sản xuất: Hàm số P = aQ+b ược gọi là hàm cung. Khi giá cả tăng
thì nhà sản xuất có xu hướng sản xuất thêm sản phẩm và ngược lại khi
giá giảm, nhà sản xuất sẽ hạn chế quy mô. Nói cách khác hàm số P =
aQ+b là hàng tăng (a>0)
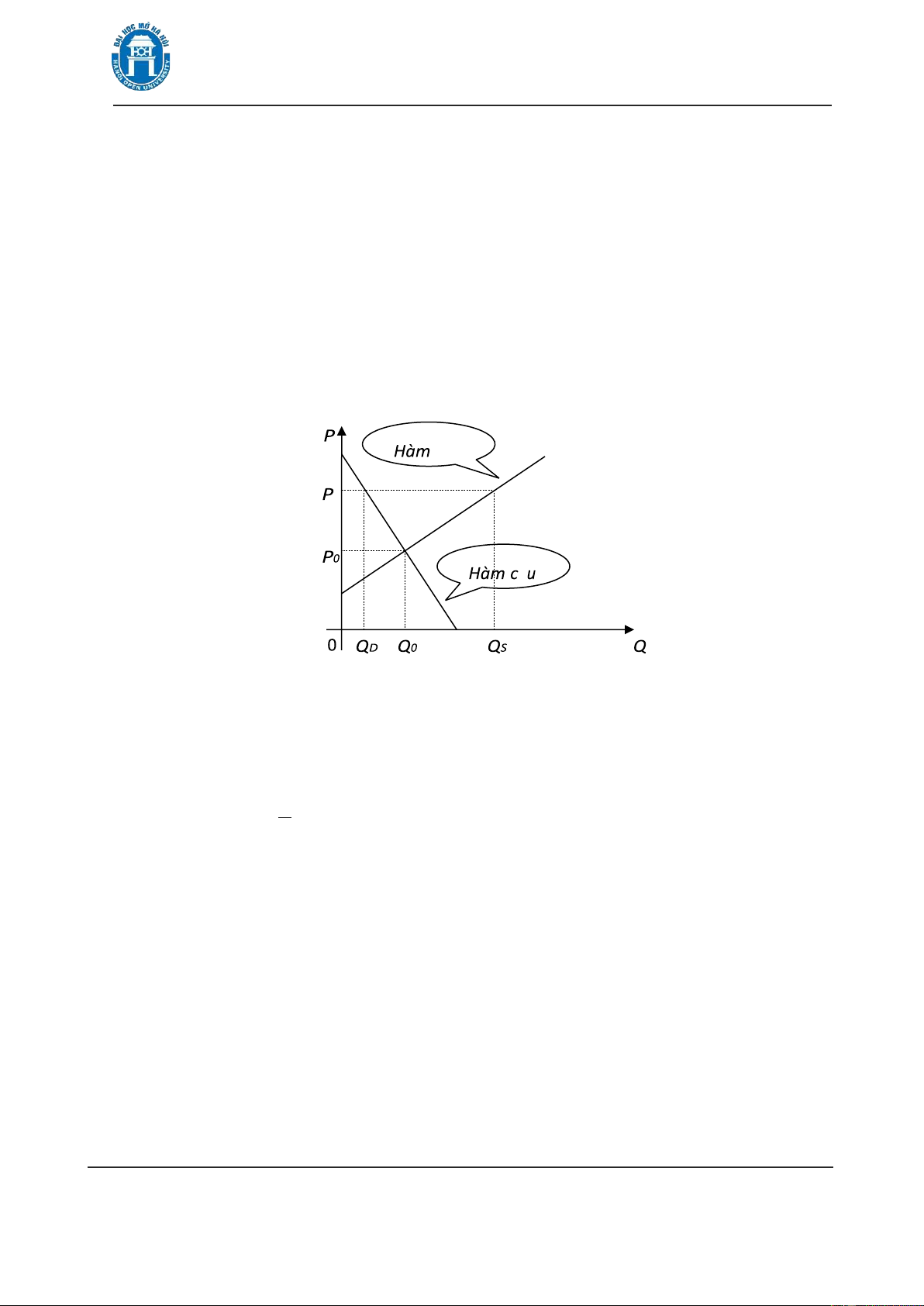
Xét sự tương tác cung cầu trong kinh tế vi mô. Hình 1.8 là ồ thị của hàm
cung và hàm cầu trên cùng một hệ trục toạ ộ. Giao iểm giữa ưßng cung và ưßng cầu (P Q )
0, 0 gọi là iểm cân bằng của thị trưßng bßi tại ó lượng cung chính xác
bằng lượng cầu. Trong thực tế, ta thưßng hay quan tâm ến trưßng hợp giá thị
trưßng bị lệch khỏi iểm cân bằng giá P0. Giả sử giá cả thị trưßng là
Toán ứng dụng trong kinh tế – Bài 1 9 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i P P* þ þ
0 từ hình 1.8, ta thấy QS
QD . Khi ó Lượng cung lớn hơn lượng cầu dẫn tới
việc hàng sẽ bị tồn kho không bán ược. Các công ty sẽ có xu hướng cắt giảm sản
xuất. Hệ quả là, thị trưßng bị kéo lại về iểm cân bằng. Tương tự, nếu giá của thị
trưßng nhỏ hơn giá tại iểm cân bằng, cầu sẽ vượt cung. Sự thiết hụt hàng hoá sẽ
ẩy giá lên và khuyến khích các công ty sản xuất nhièu hơn và do ó thị trưßng cũng quay về iểm cân bằng. * ầ
Hình 1.8. Cân bằng cung cầu
Ví dụ . Hàm cung và hàm cầu của một loại sản phẩm ược cho bßi công thức: = P =−2Q + 1 + D 50; P QS 25 2
Trong ó P, QD, và QS lần lượt tương ứng là giá, số lượng cầu và số lượng cung.
a/ Xác ịnh iểm cân bằng giá cả và số lượng
b/ Nếu chính phủ ánh thuế 5 USD trên mỗi ơn vị sản phẩm, iểm cân
bằng thị trưßng thay ổi thế nào? Lời giải:
Toán ứng dụng trong kinh tế – Bài 1 10 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
a/ Tại iểm cân bằng thị trưßng Q = ) S
QD . Vậy là, iểm cân bằng (P Q0, 0 là nghiệm
của hệ phương trình üP =− +2Q 50 ÿ ýÿþP 12 +25 = Q
Giải hệ phương trình ta ược P =30 và Q =10.
b/ Nếu chính phủ ánh thuế 5 USD trên mỗi ơn vị sản phẩm, số tiền mà công ty P
thực tế nhận ược khi bán mỗi sản phẩm với giá P , chỉ còn là −5. Vậy là
trong hàm cung cầu ban ầu, P ược thay bằng P−5; P− =5 1Q + S 25 2 = hay P 1Q + S 30 2
Tại iểm cân bằng Q = = S
QD Q. Vậy là iểm cân bằng mới là nghiệm của
hệ phương trình üP =− +2Q 50 ÿ ýÿþ P
P = 12Q+30 Giải hệ ta ược Q = 8 và =34.
Đườ ng cung ế
Đườ ng cung rướ ế Đườ ầ
Hình 1.9. Điểm cân bằng trước và sau thuế
Toán ứng dụng trong kinh tế – Bài 1 11 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
Trên hình 1.9, ưßng cung sau thuế thu ược từ ưßng cung trước thuế bằng
cách tịch tiến lên trên 5 ơn vị. Chú ý rằng, khi chính phủ ánh thuế 5 USD trên mỗi
ơn vị sản phẩm, iểm cân bằng của thị trưßng thay ổi. Ta thấy iểm cân bằng giá
tăng từ 30 USD lên 34 USD. Vậy là, khách hàng phải chịu 4 USD tiền thuế, 1 USD
còn lại ược trả bßi công ty.
1.2.3. Xác ịnh thu nhập qußc dân
Ta giả sử nền kinh tế chia ra hai thành phần: doanh nghiệp và hộ gia ình.
Hộ gia ình có nguồn thu nhập ( )Y ược sử dụng vào hai việc, ó là tiêu dùng ( )C
và tiết kiệm ( )S : Y = +C S
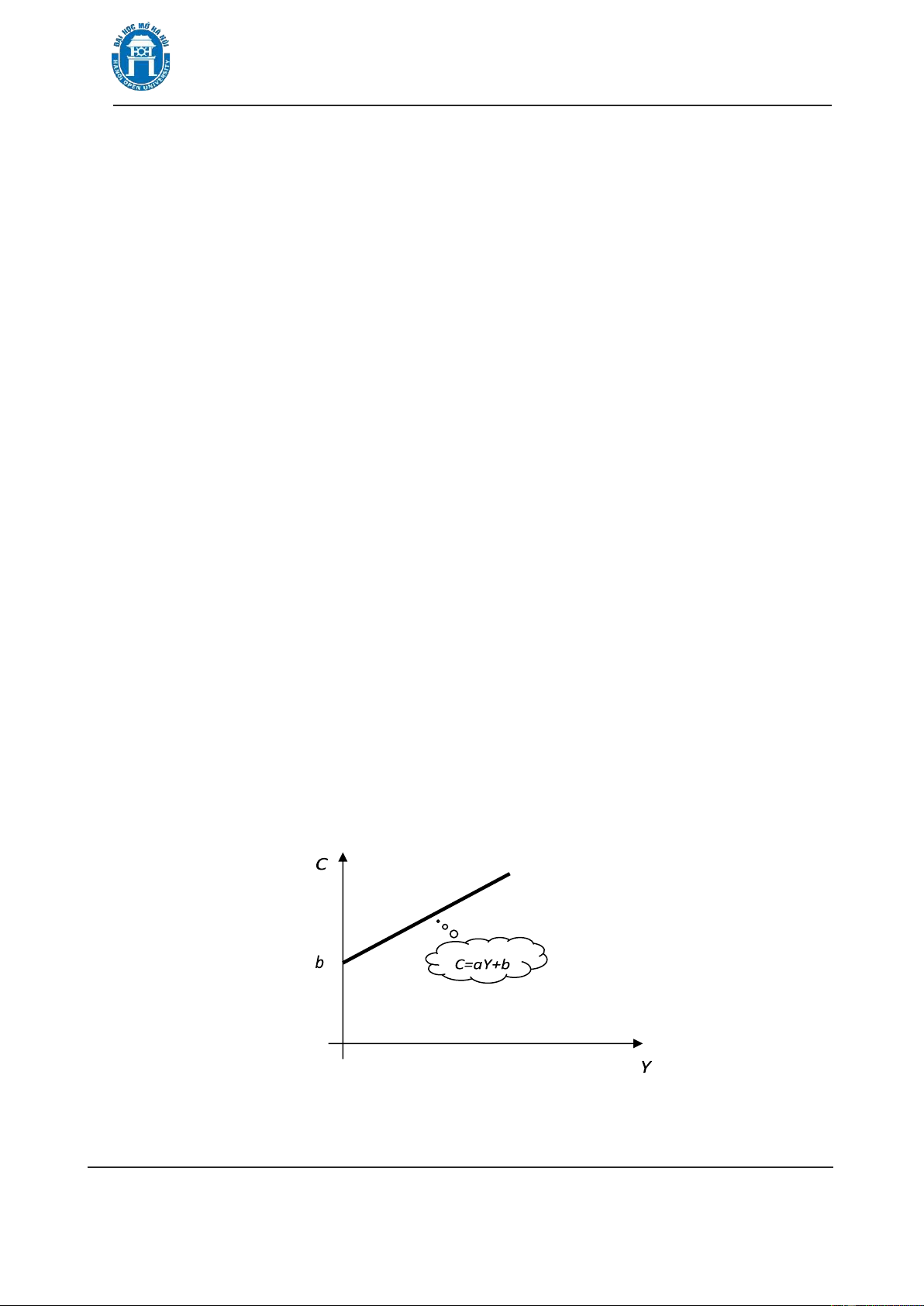
Tiêu dùng nói chung là hàm của nguồn thu nhập C = f Y( ) . Giả sử mối
quan hệ này là tuyến tính, tức C = +aY b. Thực tế, khi nguồn thu (Y) tăng, các
hộ gia ình có xu hướng chi tiêu (C) nhiều hơn. Vậy là hàm C = +aY b là hàm tăng,
tức a>0. Khi không có nguồn thu (Y=0), ta vẫn phải có tiêu dùng (lấy tiền tiết kiệm
ể tiêu) (C>0) nên C= a(0) + b = b > 0 (xem hình 1.10).
Toán ứng dụng trong kinh tế – Bài 1 12 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
Hình 1.10. Hàm tiêu dùng
Như ã biết trong phần hàm tuyến tính, vì a là hệ số góc của hàm tuyến tính
nên khi tăng Y lên 1 ơn vị, C sẽ tăng a ơn vị. Ta có aü1vì từ C = aY + = − b suy ra a
C b (C Y ; b þ ü0) a 1 ( Tức khi nguồn thu tăng 1 ơn vị thì Y Y Y
một phần a sẽ tăng vào tiêu dùng C còn phần còn lại sẽ tăng vào tiết kiệm S). Ta cũng có:
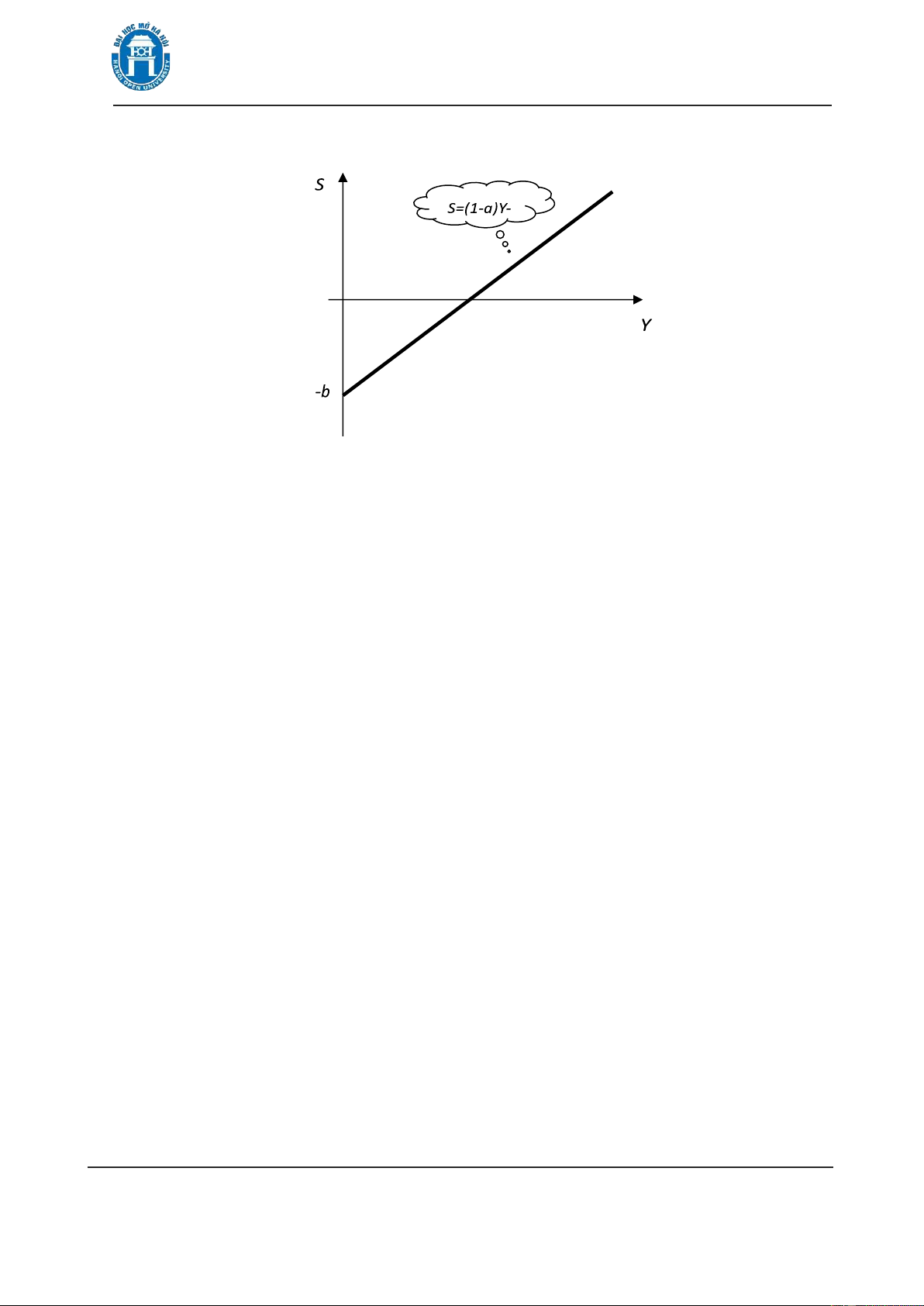
S = Y – C = Y – (aY + b) = (1 – a)Y – b
Vậy là tiết kiệm S cũng là hàm tuyến tính của nguồn thu Y. Bßi aü1 ồng
nghĩa với hệ số góc (1 – a) dương nên hàm này cũng là hàm tăng (xem hình 1.11).
Chú ý rằng khi nguồn thu Y =0 thì khoản tiết kiệm S =−bü0. Điều này có nghĩa
là khi tiêu dùng C lớn hơn nguồn thu Y , hộ gia ình phải rút tiết kiệm.
Toán ứng dụng trong kinh tế – Bài 1 13 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
Hình 1.11. Hàm tiết kiệm
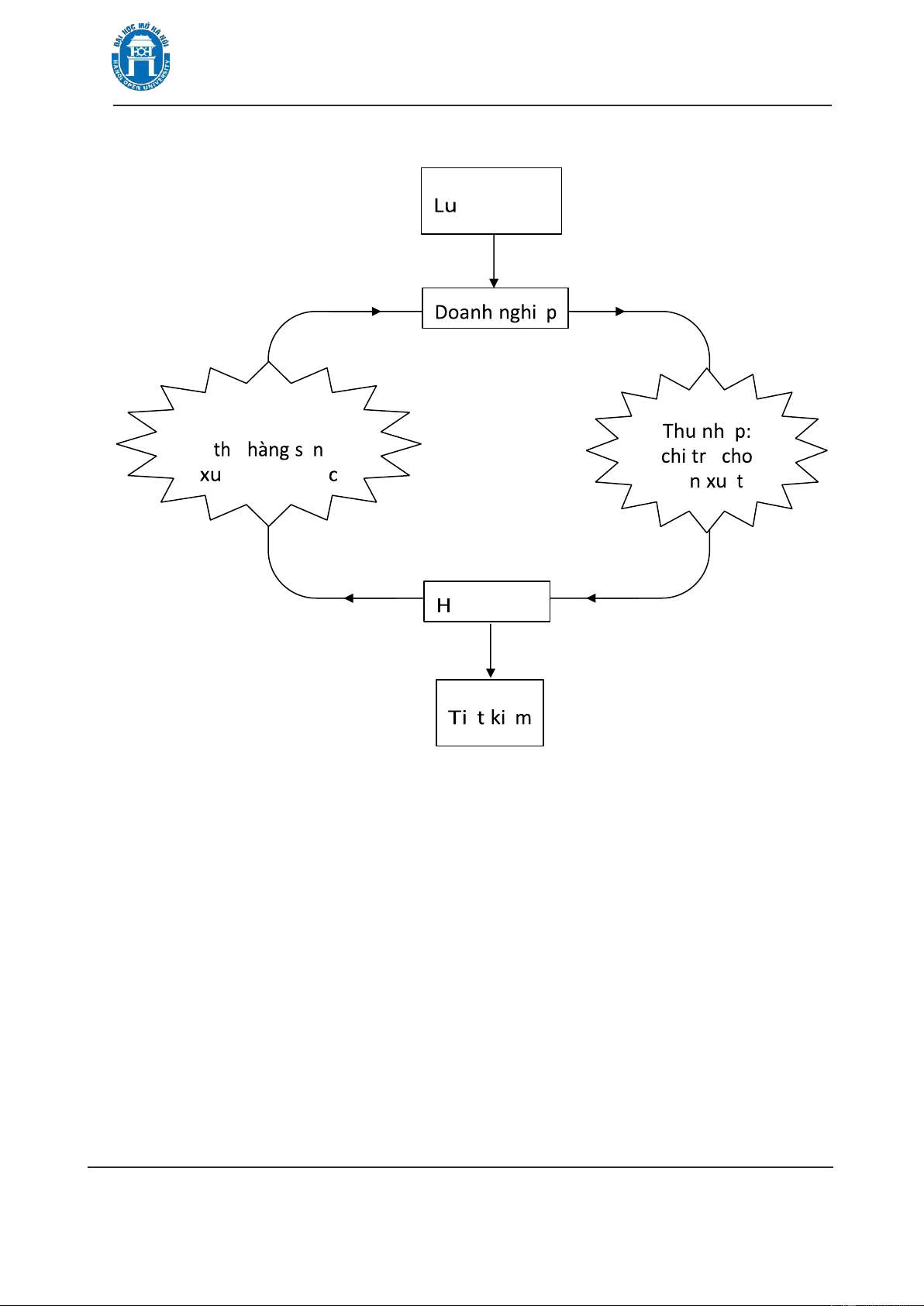
Mô hình ơn giản nhất của nền kinh tế quốc dân ược thể hiện trên hình 1.12.
Trong sơ ồ này, nguồn ầu tư ( )I vào doanh nghiệp và tiền các hộ gia ình sử dụng
cho tiêu dùng ( )C chính là nguồn thu ( )Y của doanh nghiệp. Y = +C I
Giả sử rằng việc ầu tư là có kế hoạch từ trước, tức giá trị I = I* cố ịnh, ta sẽ có: Y = +C I*
Từ phương trình trên và phương trình hàm tiêu dùng C = +aY b, ta có thể tính
ược giá trị C và Y cụ thể.
Toán ứng dụng trong kinh tế – Bài 1 14 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i ồng ầu tư ệ Chi tiêu: tiêu ậ ụ ả ả ất trong nướ s ả ấ ộ gia ình ế ệ
Hình 1.12. Mô hình kinh tế quốc dân
Ví dụ 1. Tính nguồn thu và mức tiêu dùng biết hàm tiêu dùng cho bßi C
= 0,6Y +10 và lượng ầu tư ược hoạch ịnh là I =12. Lời giải:
Từ phương trình Y = +C I ta có Y = +C 12.
Kết hợp với phương trình hàm tiêu dùng C = 0,6Y +10, ta có hệ; üY C= +12
ýþC = 0,6Y +10
Toán ứng dụng trong kinh tế – Bài 1 15 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
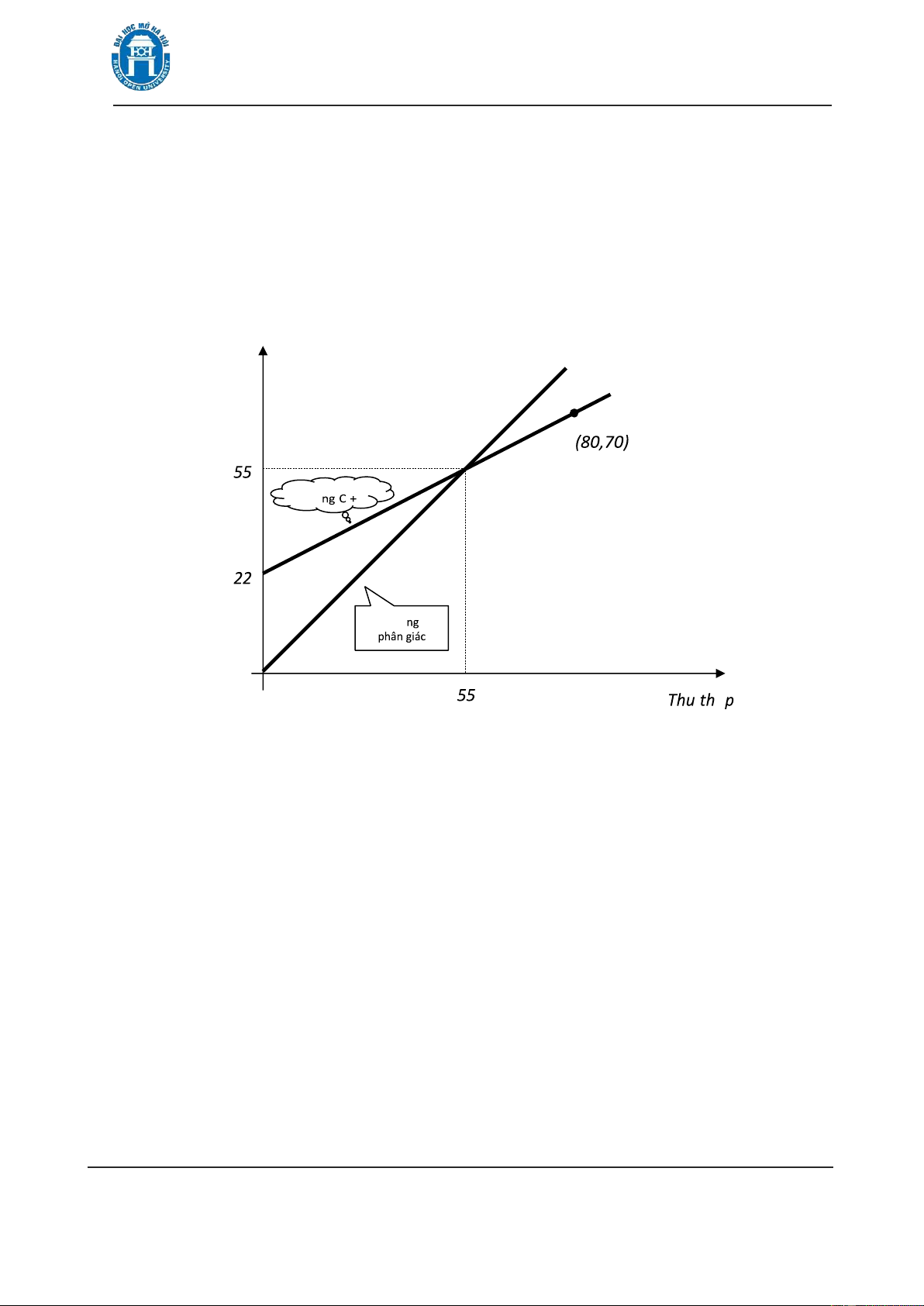
Giải hệ ta ược Y =55 và C =43. Tiêu dùng Đưß Đưß ậ
Hình 1.13. Điểm cân bằng nguồn thu và tiêu dùng
Ta có thể mô tả hình học về kết quả tìm ược qua hình 1.13 với chú ý rằng
trong hệ trục toạ ộ mà trục hoành là nguồn thu và trục tung là tiêu dùng, mọi iểm
trên ưßng phân giác của góc phần tư thứ nhất ều có ặc iểm là tiêu dùng và nguồn
thu bằng nhau. Giao iểm của ưßng phân giác này với ưßng C+I thoả mãn phương
trình Y = +C I hay Y = 0, 6Y + + =10 12 0, 6Y + 22 . Từ ó có Y =55 và C = 0,6Y + =10 43.
Trong mô hình trước, ta mới chỉ tính ến tiêu dùng của các hộ gia ình. Để mô
hình úng với thực tế hơn, ta tính ến cả tiêu dùng của chính phủ (G), và thuế
(T). Trên hình 1.12, nguồn thu Y của doanh nghiệp giß sẽ có 3 thành phần:
Toán ứng dụng trong kinh tế – Bài 1 16 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i Y = + +C
G I (C- tiêu dung HGĐ; G – tiêu
dùng Chính phủ; I lượng ầu tư)
Giả sử tiêu dùng chính phủ và lượng ầu tư ược cố ịnh là G* và I* , khi ó ta có:
Y = + +C G* I*
Nếu mô hình quan tâm ến cả thuế T, thì thu nhập sau thuế Yd của các hộ gia ình là: Y = − d
Y T và vậy là tiêu dùng C phụ thuộc vào thu nhập sau thuế Yd: C = aY + d b
Trong thực tế ngưßi ta thưßng cho thuế là cố ịnh T T= * hoặc thuế tỷ lệ với
thu nhập trước thuế T =tY , với t là một số nào ó hoặc là tổ hợp của hai phương
án trên T = +tY T* .
Ví dụ 2. Cho G = 20; I = 35; C = 0.9Yd + 70 và T = 0.2Y + 25. Tính mức thu
nhập quốc dân cân bằng? Lời giải:
Ta có Y = + + = + +C G* I* C 20 35 = C + 55 Từ C = 0,9Y + = − d
70; T = 0,2Y + 25 và Yd Y T ta có:
C = 0,9(Y − + =T ) 70 0,9Y −0,9 0.2( Y + 25)+70 = 0,72Y + 7,5
Giải hệ phương trình üY C= +55
ýþC = 0,72Y + 47,5 ta thu ược Y = 366
*Phác ồ IS và phác ồ LM:
Toán ứng dụng trong kinh tế – Bài 1 17 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i Y
Xét mô hình kinh tế hai thành phần: = +C I (Y nguồn thu của doanh
nghiệp, C tiêu dùng của hộ GĐ, I là nguồn ầu tư vào doanh nghiệp); C = +aY b
Thực tế, lượng ầu tư I thưßng không phải là hằng số như ta ã xét lúc trước,
mà nó phục thuộc vào lãi suất ngân hàng r. Giả sử giá trị ầu tư phụ thuộc tuyến
tính vào lãi suất, tức I = +cr d với c, d là hằng số nào ó. Chú ý rằng vì khi lãi suất
tăng thì lượng ầu tư sẽ giảm nên c < 0 và vì lượng ầu tư luôn là số dương nên d > 0.
Ta có Y =(aY + +b (cr +d)) do ó (1−a Y) − = +crb d
Phương trình trên mô tả mối liên quan của Y và r trong kinh tế vĩ mô ược
gọi là phác ồ IS.
Để xác ịnh giá trị cụ thể của Y và r lúc này ta cần thêm thông tin về thị
trưßng tiền tệ. Thị trưßng tiền tệ ược gọi là cân bằng khi nguồn cung tiền MS và nguồn cầu tiền tệ M = D bằng nhau: MS MD
Lượng tiền MS bao gồm cả tiền ang lưu thông trên thị trưßng và tiền gửi
trong tài khoản ngân hàng. Giá trị của MS ược kiểm soát bßi ngân hàng trung
ương và thưßng ược cố ịnh một giá trị: M M = * S S
Lượng tiền MD bao gồm 3 khoản:
i) nhu cầu tiền tệ ể giao dịch trao ổi hàng hoá hàng ngày ii)
nhu cầu tiền ể dự phòng cho tiêu dùng phát sinh iii) nhu cầu tiền ể ầu cơ
Tổng nhu cần tiền ể giao dịch và dự phòng, ký hiệu L1, tỉ lệ với thu nhập L quốc dân Y: =kY 1
1 (với k1 là một hằng số dương)
Toán ứng dụng trong kinh tế – Bài 1 18 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
Nhu cần tiền ầu cơ, ký hiệu L2 tỷ lệ nghịch với lãi suất r, giả sử mối quan hệ L k
này là tuyến tính: = +k r 2
2 3 (trong ó hằng số k2 < 0 và k3 > 0)
Vậy là tổng nhu cầu tiền tệ là: M = + + D kY1 k r2 k3
Thị trưßng tiền tệ cân bằng M = S
MD dẫn ến phương trình kY k r k + + = * + = * − 1
23 MS hay kY k r M1 2S k3
Trong kinh tế vĩ mô, phương trình trên mô tả mối quan hệ của Y và r ược
gọi là phác ồ LM. Từ các phác ồ IS và LM, ta có thể tìm ược chính xác giá trị cân bằng của Y và r.
Ví dụ 3. Xác ịnh giá trị cân bằng của thu nhập quốc dân và lãi suất biết
thông tin về thị trưßng hàng hoá là: C = 0,8Y +100 ; I =− +20 100r và thị trưßng tiền tệ là: M = =− + S 2375; L1 = 0,1Y; L2 25 2000r
Nếu nguồn cung tiền tệ MS giảm thì thu nhập quốc dân Y và lãi suất r sẽ bị
ảnh hưßng như thế nào? Lời giải: Nhu cầu tiền tệ là M = + = D
L1L2 0,1Y −25r +2000
Vì lượng cung tiền tệ là MS = 2375 nên ta có phác ồ LM ược thể hiện trong phương trình sau:
0,1Y −25r + 2000 = 2375 suy ra 0,1Y −25r = 375
Từ Y = +C I ; C = 0,8Y +100 và I =− +20 1000r , ta có:
Y =(0,8Y +100) (+ −20r +1000)
Toán ứng dụng trong kinh tế – Bài 1 19 lOMoAR cPSD| 49519085
Trường Đạ i h ọ c M ở Hà N ß i M ở cơ hộ i h ọ c t ậ p cho m ọi ngườ i
Do ó, phác ồ IS có phương trình là: 0,2Y + 20r =1100 Ta có
hệ 2 phương trình phác ồ LM và IS:
ü0,1Y −25r = 375
ýþ0,2Y + 20r=1100
Giải hệ trên, ta thu ược Y =5000 và r =5
Ta biểu diễn Y theo r từ phương trình của phác ồ LM, cụ thể: kY k r k + + = * 1 23 MS hay ö k2 ö MS* −k3 Y = −÷ ÷r+ ø k ø 1 k1
Ta biểu diễn các ưßng phác ồ LM và IS trên cùng hệ trục tạ ộ với trục hoành
là lãi suất r và trục tung là thu nhập quốc dân Y (xem hình 1.14). Toạ ộ giao iểm
của hai ưßng LM và IS chính là nghiệm (5000,5). Khi M *
S giảm, ưßng IS không thay
ổi trong khi ưßng LM sẽ bị tịnh tiến song song xuống dưới. Ta có thể giải thích từ
phương trình trên, khi M *S giảm, hệ số góc của ưßng
LM không ổi, trong khi giao iểm của ưßng LM với trục tung sẽ ß vị trí thấp hơn.
Trên hình 1.14, ta biểu diễn ưßng LM mới bằng ưßng thẳng ứt oạn. Nhìn giao iểm
mới của ưßng LM và IS, ta có thể kết luận lãi suất r sẽ tăng trong khi thu nhập quốc dân Y sẽ giảm.
Toán ứng dụng trong kinh tế – Bài 1 20




