Lý thuyết một vài ứng dụng của chương trình vi phân | Môn toán cao cấp

lOMoAR cPSD| 49519085
MỘT VÀI ỨNG DỤNG
CỦA PHƯƠNG TRÌNH VI PHÂN
❑ Quy luật làm lạnh của Newton (Newton’s Law of Cooling).
Nếu có một vụ giết người xảy ra, thì nhiệt độ cơ thể của nạn nhân sẽ giảm dần từ 370 C (nhiệt độ
bình thường trong cơ thể) đến nhiệt độ của môi trường xung quanh. Nghĩa là nhiệt độ của nạn
nhân lạnh dần với tốc độ tỷ lệ với sự chênh lệch giữa nhiệt độ của cơ thể và nhiệt độ của môi
trường xung quanh. Đây chính là quy luật làm lạnh của Newton. Giả sử T t( ) là nhiệt độ của cơ
thể tại thời điểm t và gọi a là nhiệt độ của môi trường xung quanh. Thì quy luật làm lạnh của
Newton sẽ là phương trình vi phân dT k T a( )
(*) dt Ta sẽ giải phương trình (*) như sau. dT k dt
Phương trình trên tương đương : T a
Lấy tích phân bất định hai vế, ta sẽ có : ln(T a
)kt C (chú ý rằng T a )
T a e kt C e kt.eC
Đặt A eC 0, thì ta có : T a
Ae kt T a Ae kt
Như vậy, nhiệt độ của cơ thể theo quy tắc làm lạnh Newton là
T t( ) a Ae kt
❑ Bài toán 1 (Thời gian của vụ giết người)
Một người gọi điện thoại báo với cảnh sát : đã phát hiện có một nạn nhân bị sát hại trong chính
căn nhà của nạn nhân. Cảnh sát đến hiện trường lúc 23 20h . Tại thời điểm đó, cảnh sát đo được
nhiệt độ cơ thể của nạn nhân là 310 C, và một giờ sau thì cảnh sát lại đo được nhiệt độ cơ thể của
nạn nhân là 300 C. Nhiệt độ căn phòng mà xác nạn nhân được tìm thấy là 220 C. Hãy ước lượng
thời gian mà nạn nhân bị sát hại. Giải :
Vì nhiệt độ căn phòng là 220 C nên nhiệt độ cơ thể của nạn nhân sau khi bị sát hại là : T t( ) 22 Ae kt
Tại thời điểm mà cảnh sát đến hiện trường, nhiệt độ cơ thể của nạn nhân là 310 C nên T(0) 31 22 A 31 A 9
Nên T t( ) 229e kt
Sau một giờ tính từ lúc cảnh sát có mặt tại hiện trường, nhiệt độ cơ thể của nạn nhân đo được là 300 C nên
ThS. Đào Bảo Dũng Trang 1 lOMoAR cPSD| 49519085 T(1) 30
22 9e k 30 e k
Như vậy : T t( ) 22 9 8 t 9
Lúc nạn nhân vừa bị sát hại thì nhiệt độ cơ thể của nạn nhân là 370 C. Ta tìm t để T t( ) 37 22 9 8 t
37 8 t 15 t log8 15 4,34 9 9 9 9 9
Ta đổi 4,34 sang giờ, thì 4,34 xấp xỉ 4 giờ 20 phút. Nghĩa là vụ giết người đã xảy ra trước lúc cảnh
sát đến hiện trường khoảng 4 giờ 20 phút. Do cảnh sát đến hiện trường lúc 23 20h , nên nạn nhân
bị sát hại vào khoảng 19 00h .
❑ Mô hình tăng trưởng (Exponential Growth Model).
Ta ký hiệu y t( ) là số lượng của một đại lượng tại thời điểm t . Nếu tốc độ tăng trưởng của số
lượng tỷ lệ với số lượng, thì có phương trình vi phân dy k y. (**) dx
Phương trình (**) là một phương trình vi phân cấp 1 tách biến. Với kiến thức đã biết, ta dễ dàng
tìm được nghiệm tổng quát của phương trình (**) là
y t( ) A e. kt
Nếu k 0 , ta gọi là tăng trưởng theo quy luật hàm mũ. Nếu k 0 , ta gọi là phân rã theo quy
luật hàm mũ. Ngoài ra, công thức nghiệm nói trên cũng rất hữu ích trong khoa khảo cổ học, được
các nhà khảo cổ dùng nhiều trong việc tính tuổi của một cổ vật (người đọc có thể tìm thấy các ví dụ
trong các sách về khảo cổ học).
❑ Bài toán 2 (Tăng trưởng dân số)
Trong một thành phố, các nhà dân số học quan sát thấy rằng tốc độ tăng trưởng của dân số thành
phố tỷ lệ với cỡ của dân số tại mọi thời điểm. Cách đây hai mươi năm, dân số của thành phố này
là 125000 người. Năm nay, dân số của thành phố này là 140000 người. Sau hai mươi năm, dân số
của thành phố này sẽ là bao nhiêu ? Giải :
Gọi y t( ) là dân số của thành phố này tại thời điểm t .
Vì tốc độ tăng trưởng của dân số thành phố tỷ lệ với cỡ của dân số tại mọi thời điểm nên
ThS. Đào Bảo Dũng lOMoAR cPSD| 49519085 dy
k y. dx Nghĩa là y t( ) A e. kt
Cách đây hai mươi năm, dân số của thành phố này là 125000 người nên y(0) 125000 A 125000
Tức là y t( ) 125000.ekt
Năm nay, dân số của thành phố này là 140000 người nên y(20) 140000
125000.e20t 140000 e20k 1,12
Do đó, dân số của thành phố này tại thời điểm t là :
y t( ) 125000.ekt 125000. e20k 20t 125000.(1,12)20t
Vậy, dân số của thành phố này sau hai mươi năm sẽ là : y(40) 125000.(1,12) 156800
❑ Hàm Logistic (Logistic Funtion).
Phương trình vi phân có đóng góp rất lớn trong thực tiễn. Một trong những phương trình vi phân
có tính ứng dụng rộng rãi trong các bài toán về mô hình tăng trưởng là
dy k y M y. .( ) (***) dx
trong đó y y t( ) là hàm chứa một biến t và các số k , M là những hằng số dương thỏa 0 y t( ) M ,
t (0, ) . Nghiệm tổng quát của phương trình (***) được gọi là hàm Logistic.
Ta giải phương trình (***) như sau. Ta có : (***) y M( dy k dt 1 1 y Mk dt y) y M
Lấy tích phân bất định hai vế, ta sẽ có : ln y y
Mk t. C (chú ý điều kiện 0 y t( ) M , t (0, ) ). M y e Mk t C.
eMk t. .eC () M y
Ta xem eC A 0, thì ta có :
y AeMk t. . Khi đó, () tương đương y AeMk t.
ThS. Đào Bảo Dũng Trang 3 lOMoAR cPSD| 49519085 M y M y
y (M y Ae) Mk t. MAeMk t. AeMk t. y
y MAeMk t. AeMk t. y (1 AeMk t. )y MAeMk t. y MAeMk tMk t.. 1 Ae MAeMk t.
y AeMk tMk t. . 1 Ae AeMk t. y M 1 e Mk t. 1 A 1
Để đơn giản cách viết, ta có thể thay chữ b cho
và chữ c cho Mk , thì ta có hàm Logistic : A y t( ) M ct 1 be
Người ta còn gọi hàm Logistic là hàm Logistic Verhulst – Pearl. Hàm này có ứng dụng thực tiễn
rất lớn, liên quan đến nhiều mô hình thực tế (chẳng hạn như mô hình tăng trưởng Logistic, mô
hình tin đồn lan truyền, mô hình lây lan bệnh dịch, …). Hàm Logistic có một tiệm cận ngang là y M .
Ta sẽ khảo sát hình dáng đồ thị của hàm Logistic này. ct
Trước hết, ta có : y t ( ) M
bc e be. ct)2 . Vì M b c, , 0 nên rõ ràng y t ( ) 0 t 0 , do đó hàm (1
Logistic đồng biến trong (0, ) . ct ( ) M bc e2. be(be 1) ct ct)3
nên hoành độ điểm uốn là nghiệm của phương
Mặt khác, ta lại có : y t
ThS. Đào Bảo Dũng lOMoAR cPSD| 49519085 (1
trình be ct 1 0 ect b t
lnb . Với hoành độ điểm uốn là t lnb U , thì ta tìm được tung c c
độ điểm uốn là y M U . 2 ▪ y t
( ) 0 với t tU : đồ thị lõm phía bên trái điểm uốn. ▪ y t
( ) 0 với t tU : đồ thị lồ phía bên phải điểm uốn.
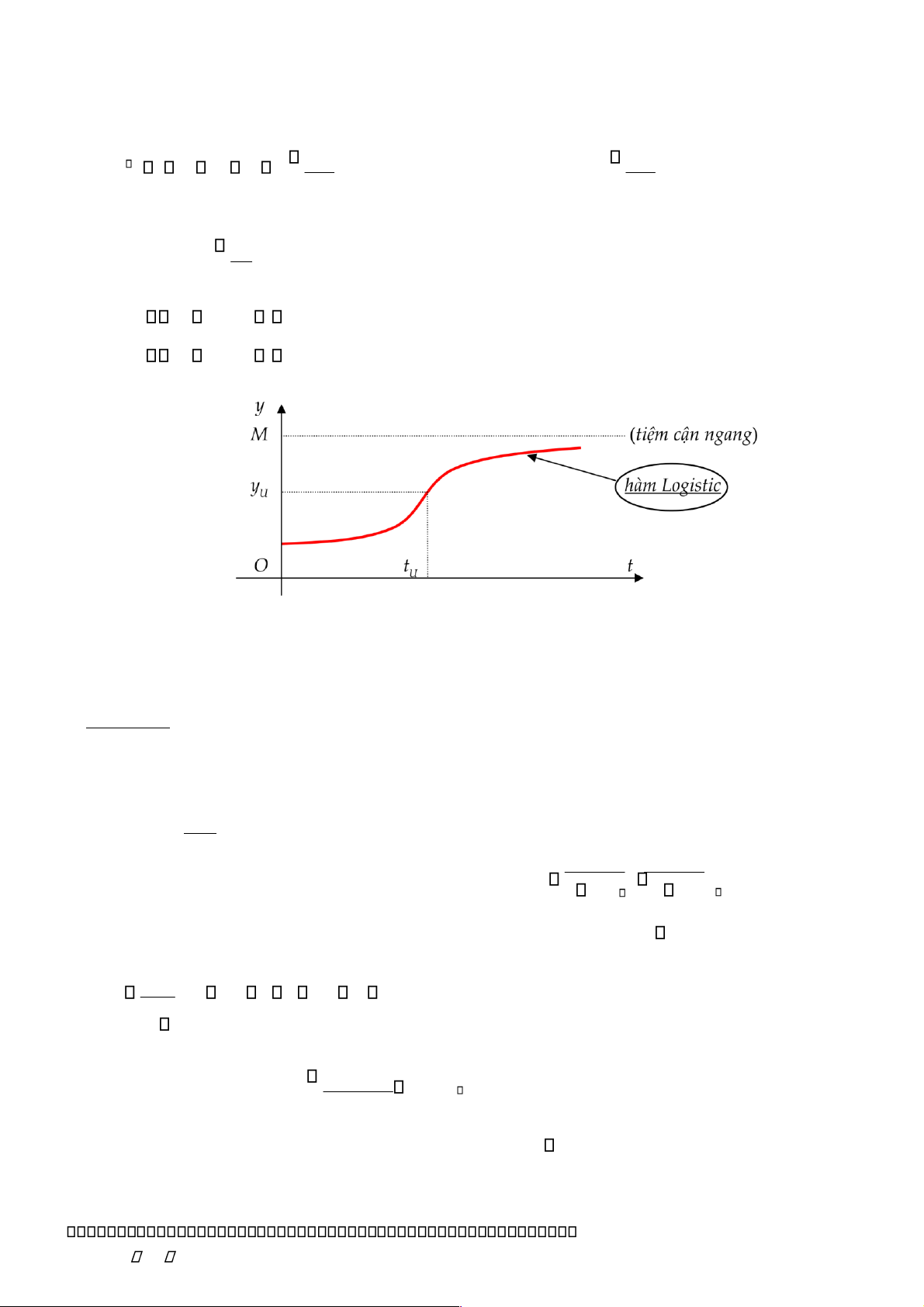
Đồ thị của hàm Logistic được gọi là đường cong Logistic, có dạng tổng quát như sau
Sau đây, chúng ta sẽ làm quen một số ứng dụng của hàm Logistic trong thực tiễn.
❑ Bài toán 3 (Thành viên câu lạc bộ) :
Một câu lạc bộ có số thành viên tối đa là 800 . Một năm trước, số thành viên ban đầu của câu lạc
bộ này là 50 . Hiện nay, số thành viên của câu lạc bộ này là 200 . Cho biết sự gia nhập của các
thành viên tuân theo quy luật Logistic. Sau ba năm kể từ bây giờ, số thành viên của câu lạc bộ này
là bao nhiêu ? Giải :
Vì số thành viên tối đa là 800 nên ta xét hàm logistic : y t( ) 1 Mbe ct 1 800be ct
Một năm trước, số thành viên ban đầu của câu lạc bộ này là 50 nên y(0) 50
800 50 1 b 16 b 15 1 b
Do đó, hàm Logistic là : y t( ) 80015e ct 1
Hiện nay, số thành viên của câu lạc bộ này là 200 nên y(1) 200
ThS. Đào Bảo Dũng Trang 5 lOMoAR cPSD| 49519085
80015e c 200 1 15e c 4 e c 153 0,2
1 Vậy, hàm hàm Logistic là : y t( ) 800 t 1 15. 0,2
Do đó, sau ba năm kể từ bây giờ, số thành viên của câu lạc bộ này là y(4) 800 4 3125 781 1 15. 0,2 4
❑ Bài toán 4 (Lan truyền của tin đồn) :
Các nhà xã hội học đã chứng minh được sự lan truyền của tin đồn sẽ tuân theo quy luật Logistic.
Giả sử tại một trường đại học có 45000 sinh viên. Ban đầu có 300 sinh viên biết về tin đồn X . Sau
một tuần, có 900 sinh viên biết tin đồn nay. Hỏi : sau ba tuần thì có bao nhiêu sinh viên sẽ biết tin
đồn X nói trên ? Giải :
Vì số sinh viên trong trường đại học là 45000 nên ta xét hàm logistic : y t( ) M ct 145000 be ct
1 be Ban đầu có 300 sinh viên biết tin đồn, nên y(0) 300
45000 300 1 b 150 b 149 1 b
Do đó, hàm Logistic là : y t( ) 45000149e ct 1
Sau một tuần có 900 sinh viên biết tin đồn, nên y(1) 900
45000149e c 900 1 149e c 50 e c 14949 1
Vậy, hàm hàm Logistic là : y t( ) 45000 t 1 149. 49 149
Do đó, sau ba tuần, số sinh viên biết tin đồn là y(4) 45000 3 7143 1 149. 49 149
ThS. Đào Bảo Dũng