


Preview text:
lOMoAR cPSD| 47305584
Bai 2: Tập hợp và các phép toán trên tập hợp
1. Các khái niệm cơ bản về tập hợp 1.1. Tập hợp
Có thể mô tả một tập hợp bằng một trong hai cách sau:
- Cách 1. Liệt kê các phần tử của tập hợp;
- Cách 2. Chỉ ra tính chất
ặc trưng cho các phần tử của tập hợp.
+ a ∈ S: phần tử a thuộc tập hợp S.
+ a ∉ S: phần tử a không thuộc tập hợp S.
Chú ý: Số phần tử của tập hợp S ược kí hiệu là n(S). Ví dụ:
- Cho tập hợp A là tập hợp các số tự nhiên chia hết cho 2, lớn hơn 5 và nhỏ hơn 15.
+ Ta mô tả tập hợp A bằng hai cách như sau:
Cách 1: Liệt kê các phần tử của tập hợp: A = {.........................................................};
Cách 2: Chỉ ra tính chất ặc trưng của các phần tử: A = {.........................................................};
+ Tập hợp A có 5 phần tử, ta viết: n(A) = …
+ 10 thuộc tập hợp A, ta viết ……….
+ 15 không thuộc tập hợp A, ta viết ……….
• Tập hợp không chứa phần tử nào ược gọi là tập rỗng, kí hiệu là ∅ . Ví dụ:
+ Tập hợp các nghiệm của phương trình x^2 + 1 = 0 là tập rỗng;
+ Tập hợp những người sống trên Mặt Trời là tập rỗng. 1.2. Tập hợp con
Nếu mọi phần tử của tập hợp T
ều là phần tử của tập hợp S thì ta nói T là một tập hợp con
(tập con) của S và viết là T ⊂ S ( ọc là T chứa trong S hoặc T là tập con của S). -
Thay cho T ⊂ S, ta còn viết S ⊃ T ( ọc là S chứa T). -
Kí hiệu T ⊄ S ể chỉ T không là tập con của S. Nhận xét: - Từ
ịnh nghĩa trên, T là tập con của S nếu mệnh ề sau úng: ∀ x, x ∈ T ⇒ x ∈ S. -
Quy ước tập rỗng là tập con của mọi tập hợp. -
Người ta thường minh họa một tập hợp bằng một hình phẳng ược bao quanh bởi
một ường kín, gọi là biểu ồ Ven.
Ví dụ: Cho các tập hợp: T = {2; 3; 5}, S = {2; 3; 5; 7; 9}, M = {2; 3; 4; 5}. -
Tập hợp …. là tập con của tập hợp ….. -
Tập hợp …. không là tập hợp con của tập hợp ….
1.3. Hai tập hợp bằng nhau - Hai tập hợp S và T
ược gọi là hai tập hợp bằng nhau nếu mỗi phần tử của T cũng là
phần tử của tập hợp S và ngược lại. Kí hiệu là S = T.
- Nếu S ⊂ T và T ⊂ S thì S = T. Ví dụ:
Cho 2 tập hợp: S = {n | n là bội chung của 2 và 3; n < 20} và T = {n | n là bội của 6; n < 20}. lOMoAR cPSD| 47305584 2. Các tập hợp số
2.1. Mối quan hệ giữa các tập hợp số
- Tập hợp các số tự nhiên N={0;1;2;3;4;…} .
- Tập hợp các số nguyên Z gồm các số tự nhiên và số nguyên âm:
Z={…;−3;−2;−1;0;1;2;3;…}.
- Tập hợp các số hữu tỉ Q gồm các số
ược viết dưới dạng phân số a/b , với a,b ∈Z, b≠0 .
Số hữu tỉ còn ược biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn. - Tập
hợp các số thực R gồm các số hữu tỉ và các số vô tỉ. Số vô tỉ là các số thập phân vô hạn không tuần hoàn.
- Mối quan hệ giữa các tập hợp số: N…Z…Q…R
Ví dụ: Cho tập hợp B = {– 1; 2; 4; 10}.
- Tập hợp B chứa số – 1 không phải là số tự nhiên nên B không là tập con của ...
- Tập hợp B gồm các số nguyên: – 1; 2; 4; 10 nên B là tập con của …
- Số nguyên cũng là các số hữu tỉ và cũng là các số thực, nên B cũng là tập con của …, …..
2.2. Các tập con thường dùng của R
- Một số tập con thường dùng của tập số thực R:
Kí hiệu + ∞: Đọc là dương vô cực (hoặc dương vô cùng).
Kí hiệu – ∞: Đọc là âm vô cực (hoặc âm vô cùng).
a, b gọi là các ầu mút của oạn, khoảng hay nửa khoảng. + Khoảng: (a;b) (a;+∞) (-∞;b) (-∞;+∞) + Đoạn [a;b] + Nửa khoảng [a;b) (a;b] [a;+∞) (-∞;b]
3. Các phép toán trên tập hợp
3.1. Giao của hai tập hợp
Tập hợp gồm các phần tử thuộc cả hai tập hợp S và T gọi là giao của hai tập hợp S và T.
S ∩ T ={x | x ∈ S và x ∈ T}.
3.2. Hợp của hai tập hợp
Tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc tập hợp T gọi là hợp của hai tập hợp S và T.
S ∪ T = {x | x ∈ S hoặc x ∈ T}.
3.3. Hiệu của hai tập hợp
- Hiệu của hai tập hợp S và T là tập hợp gồm các phần tử thuộc S nhưng không thuộc T. lOMoAR cPSD| 47305584
S \ T = {x | x ∈ S và x ∉ T}.
BÀI TẬP: TẬP HỢP VÀ CÁC PHÉP TOÁN TRÊN TẬP HỢP
Bài 1: Điền Đ vào ô trống nếu mệnh ề úng, iền S vào ô trống nếu mệnh ề sai. a) ∅⊂ℕ □ b) ℕ⊂ℚ □ c) ∅ = {0} □ d) {∅} ⊂ℝ □
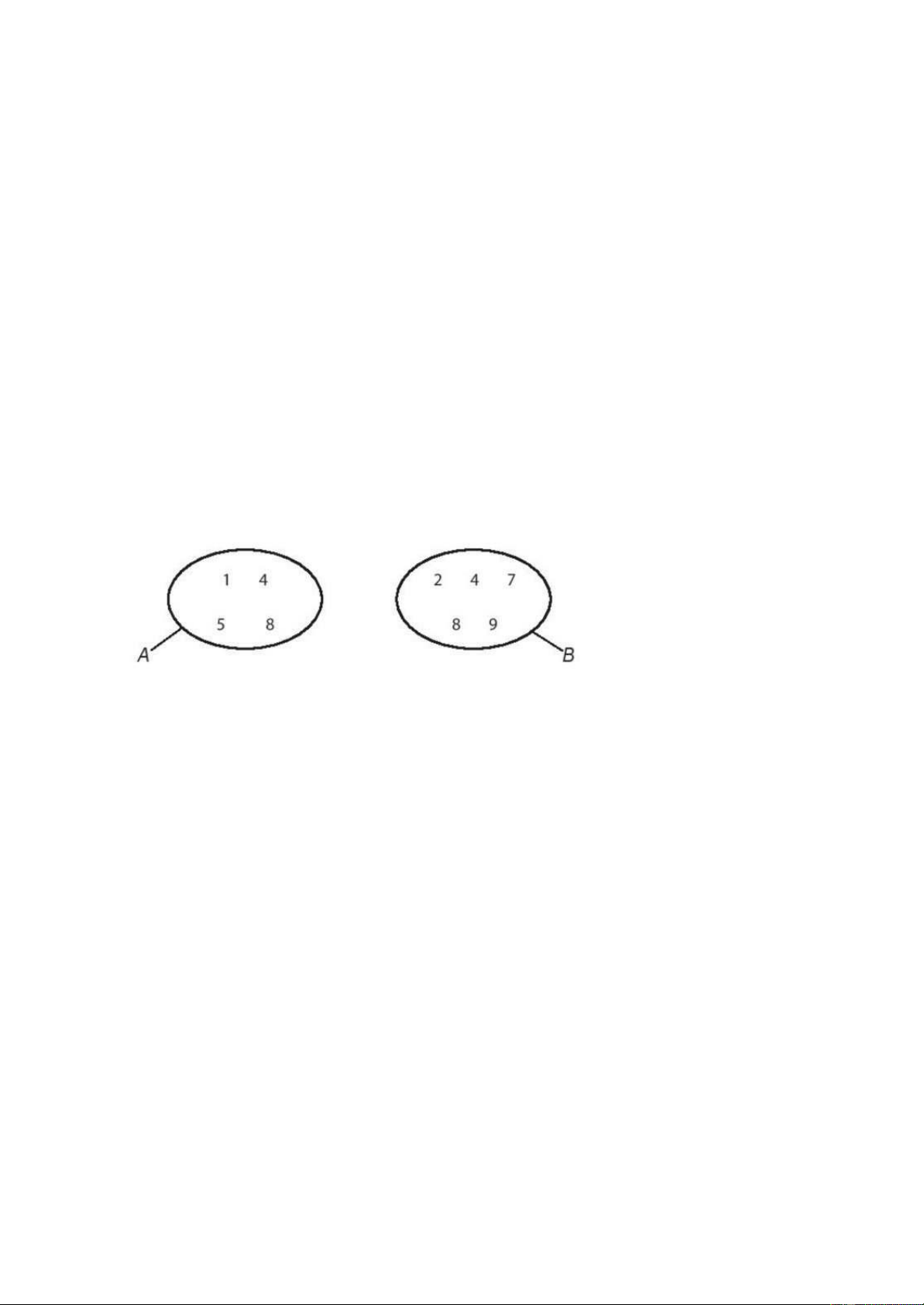
Bài 2: Cho hai tập hợp A, B ược mô tả bởi biểu ồ Ven như sau:
a) Hãy chỉ ra các phần tử của tập hợp A, tập hợp B. b) Tính n (A ∪ B).
c) Hãy chỉ ra các phần tử thuộc tập hợp A mà không thuộc tập hợp B.
d) Hãy chỉ ra các phần tử thuộc tập hợp B mà không thuộc tập hợp A. Bài 3: Xác
ịnh các tập hợp sau bằng cách nêu tính chất ặc trưng cho phần tử của tập hợp. A = {0; 4; 8; 12; 16}; B = {-3; 9; -27; 81}; C là
ường thẳng trung trực của oạn thẳng AB.
Bài 4: Trong các tập hợp sau, tập nào là tập rỗng? lOMoAR cPSD| 47305584 A = {x ∈ℕ | x ≤ 0};
B = {x ∈ℕ | 2x^2 - 3x - 5 = 0}.
Bài 5: Trong các mệnh
ề sau, mệnh ề nào úng? Mệnh ề
nào sai? a) Tập rỗng là tập con của mọi tập hợp;
b) Nếu X = {a; b} thì a ⊂ X;
c) Nếu X = {a; b} thì {a; b} ⊂ X. Bài 6: Xác
ịnh các tập hợp sau và biểu diễn chúng trên trục số. a) (4; 7) ∩ (-1; 3); b) (-2; 1] ∩ (-∞; 1); c) (-2; 6) \ (3; 10); d) (-3; 5] \ [2; 8).
Bài 7: Trong một cuộc phỏng vấn 56 người về những việc họ thường làm vào ngày nghỉ cuối
tuần, có 24 người thích tập thể thao, 15 người thích i câu cá và 20 người không thích cả hai hoạt ộng trên.
a) Có bao nhiêu người thích chơi thể thao hoặc thích câu cá?
b) Có bao nhiêu người thích cả câu cá và chơi thể thao?
c) Có bao nhiêu người chỉ thích câu cá, không thích chơi thể thao?
Bài 8. Hãy viết tập hợp sau và cho biết mỗi tập hợp có bao nhiêu phần tử.
A là tập hợp các số tự nhiên chia hết cho 3 và nhỏ hơn 20.
Bài 9. Cho các tập hợp: A={x∈N ∣ x⋮3, x<10} và B={x∈N ∣ x⋮2, x<10} . a) Viết
tập hợp A và B bằng cách liệt kê các phần tử của tập hợp.
b) Xác ịnh các tập hợp A ∩ B, A ∪ B, A \ B, B \ A.




