











Preview text:
lOMoAR cPSD| 47207194 ĐỀ SỐ 1 A. A. Câu 3: Cho lOMoAR cPSD| 47207194 A. A. 0 B. m2 C. m D. m3
Câu 6: Cho A là ma trận vuông cấp 10, trong ó phần tử ở dòng i cột j là ( 1)i j . Phần tử ở dòng 1 cột
2 của ma trận A2 là A. 10 B. -10 C. 0 D. 1 Câu 7: Cho ma trận
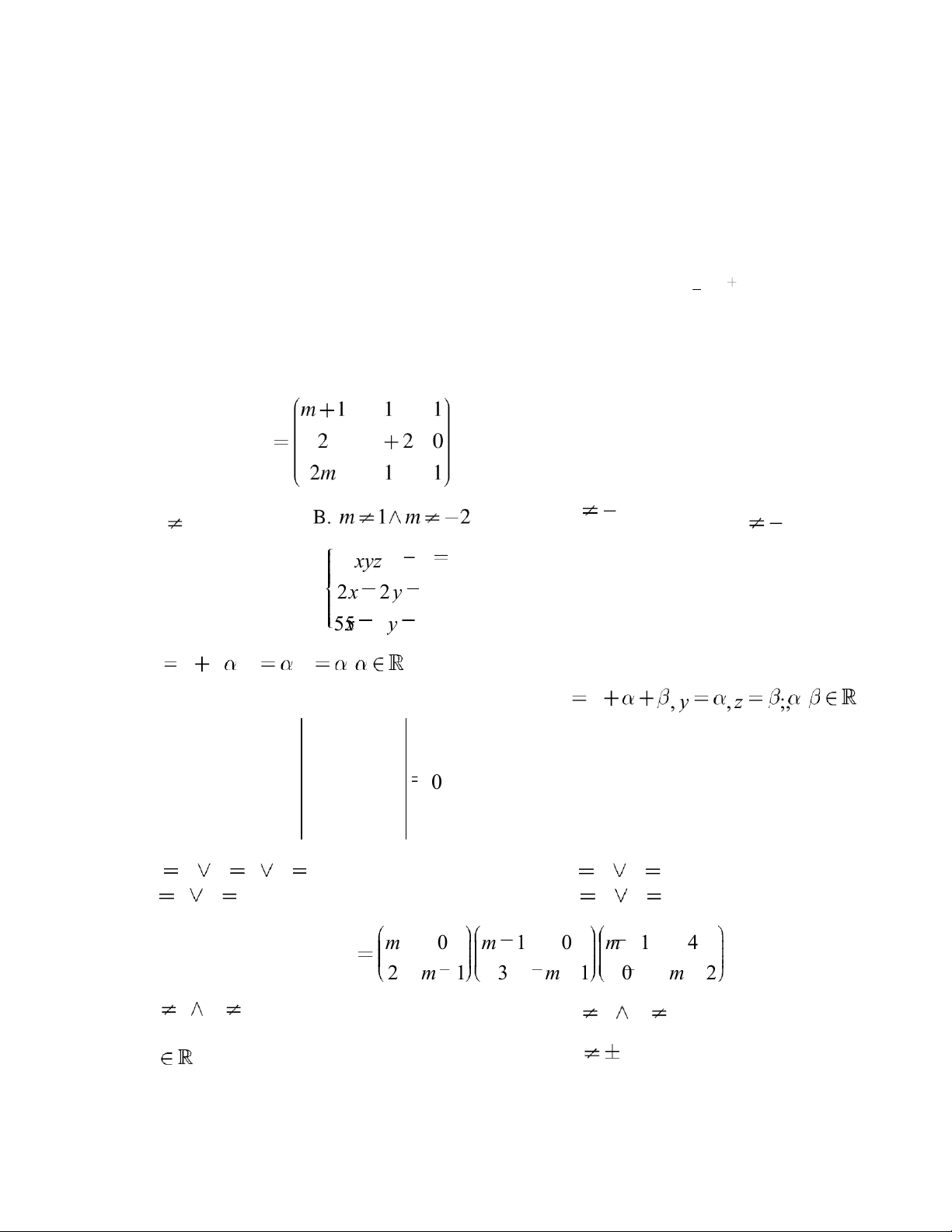
Am 2 0 . Tìm m ể A khả nghịch. A. m 1 C. m 1 D. m 2 xyz 3
Câu 8: Gi ả i h ệ phương trình 2 x 2 y 2 z 6 55x y 5 z 15 3 2 , y , z ; A.
x B. x = 3, y = 0, z = 0 C. Hệ vô nghiệm D. x 3 , y , z ;, xx 10 1211
Câu 9: Gi ải phương trình 0 2212 xx 2 x
A. x 0 x 1 x 4 B. x 0 x 1 C. x 1 x 4 D. x 0 x 4 m 0 m 1 0 m 1 4
Câu 10: Số thực m ể ma trận A khả nghịch là 2 m 1 3 m 1 0 m 2 A. m 1 m 2 B. m 0 m 1 C. m \ 0,1,2 D. m 1 lOMoAR cPSD| 47207194 2 x 3 yz 1
( m 5) y ( m 3) z m
Câu 11: Tìm m ể hệ phương trình tuyến tính 8 x ( m 11) y ( m 5) z m 44 x1 có nghiệm A. m 0 B. m 1 C. m tùy ý D. Không có giá trị m Câu 12: Cho hai ma trận A A. X C. X Câu 13: Cho phương trình ma trận 18
b . Tìm iều kiện của a, b, c ể phương trình có nghiệm. A. 3a – 5b – 4c = 0 B. 3a + 5b – 4c = 0 C. 3a + 5b + 4c = 0 D. 3a – 5b + 4c = 0 0 1 0 0 0 m 1 0 1
Câu 14: Cho ma trận A 2
. Phần tử dòng 1 cột 4 của A là 0 m m 1 4 0 0 0 A. m B. -1/4 C. -m D. 1/4 1 2 1 1 2 2 4 1 0 2
Câu 15: Tìm hạng r(A) của ma trận A 4 8 1 2 2 7 15 9 8 18 A. r(A) = 4 B. r(A) = 2 C. r(A) = 1 D. r(A) = 3
Câu 16: Cho A là ma trận vuông cấp n khả nghịch, có ịnh thức bằng a. Định thức của ma trận lOMoAR cPSD| 47207194 3 A 3 1 là: A. 9 .n a 3 3 3 B. (3. )a C. 3. a D. 3 .n a 3
Câu 17: Giá trị của m ể hạng của ma trận A bằng 2 là: A. m 0 B. m 0 m 1 D. m 2 m 0 1 2 3 2 4
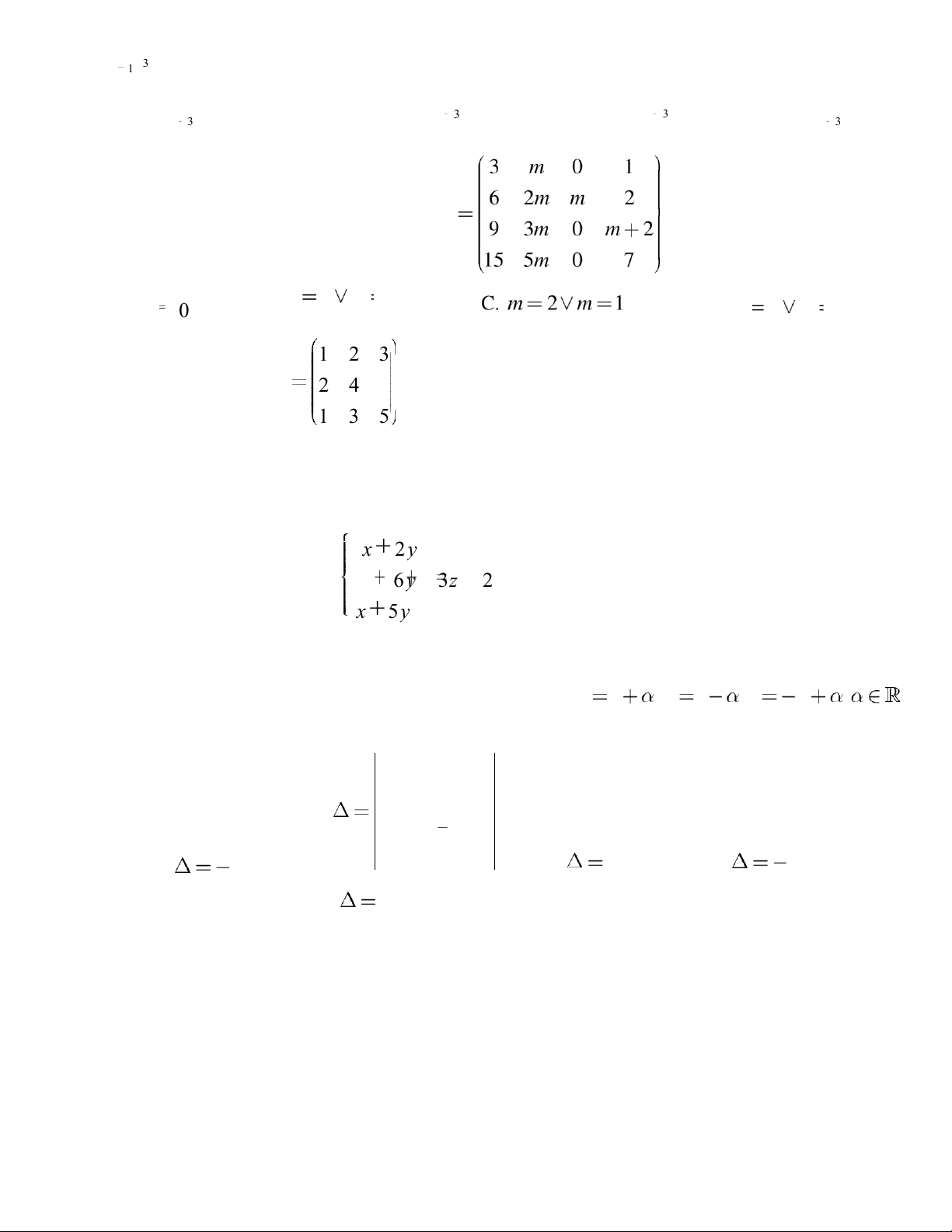
Câu 18: Cho ma trận A
1 3 5 6 . Khẳng ịnh nào sau ây úng?
A. A có ịnh thức bằng 0 B. A có hạng bằng 1 C. A có hạng bằng 3 D. A khả nghịch x 2 yz 1 6 y 3 z 2
Câu 19: Giải hệ phương trình: x 5 y 3 z 0 2x
A. Hệ phương trình vô số nghiệm B. x = 1, y = 1, z = -2
C. Hệ phương trình vô nghiệm D. x 1 , y 1 , z 2 ;
Câu 20: Giá trị của ịnh thức 7 3 4 1 0 1 2 0 là: 5 1 3 1 0 4 4 0 A. 8 B. 4 C. 8 D. 4 lOMoAR cPSD| 47207194 ĐỀ SỐ 2 lOMoAR cPSD| 47207194 úng? A. A. A lOMoAR cPSD| 47207194 A. A. A. x A. X 2 10 2 10 C. X 1 6 D. X 1 6
Câu 7: Cho A là ma trận vuông cấp n có ịnh thức bằng a. Định thức của ma trận A AT 2 là A. a B. a3 C. a2 D. a4 2 1 2 0 1 a 1 6 8 1. X
Câu 8: Cho phương trình ma trận 21 2 6 10 2
c 18 b . Tìm iều kiện của a, b, c ể phương trình có nghiệm. A. 3a + 5b + 4c = 0 B. 3a + 5b – 4c = 0 lOMoAR cPSD| 47207194 C. 3a – 5b + 4c = 0 D. 3a – 5b – 4c = 0 Câu 9: Xét hai ịnh thức , khẳng ịnh nào sau ây úng? A. 2 1 D. 2 4 1 Câu 10: Tìm m ể hệ phương trình tuyến tính có vô số nghiệm A. m = 2 B. m = -2 C. m = 1 D. m = -1 1 1 1 2 2 2 1 0 4 2
Câu 11: Tìm hạng r(A) của ma trận A 4 1 2 8 2 7 9 8 14 18 A. r(A) = 4 B. r(A) = 1 C. r(A) = 2 D. r(A) = 3 là 1 1 25 1 1 A. 0 D. 0 0 1 0 Câu 13: Cho hai ma
trận A . Khẳng ịnh nào sau ây úng? A. AB = BA
B. AB xác ịnh nhưng BA không xác ịnh lOMoAR cPSD| 47207194 D. BA m . Tìm m ể C. m 0 D. m 0 m 4 A. A có hạng bằng 3 B. A khả nghịch C. A có hạng bằng 1
D. A có ịnh thức bằng 0
x 3 y 4 z 1
Câu 16: Gi ả i h ệ ph ươ ng trình 25x yz 2 51x3 y 6 z 5 1 ,y 0 , z 0 B. x B. Hệ phương trình vô nghiệm 1 17 , y 7 , z ; D. x C. x 1 17 , y 7 , z ;
Câu 17: Giá trị của m ể hạng
của ma trận A bằng 2 là: A. m 2 m 0
B. m D. m 2 m 1 Câu 18: Hệ phương trình tuyến tính vô nghiệm khi và chỉ khi: A. m = -1 B. m = 1 C. m = 0 D. m = 2 lOMoAR cPSD| 47207194 Câu 19: Giá tr 4 0012 7134 là: 1027 0044 A. 4 B. 8 C. 8 D. ị của ịnh thức
Câu 20: Cho A và B là các ma trận vuông cấp n. Biết ịnh thức của A bằng a và AB. n I . Tính ịnh
thức của ma trận ABA2 T : A. a B. a4 C. a2 D. a3 lOMoAR cPSD| 47207194 ĐỀ SỐ 3 0 3 7 m 2 Câu 2: Tìm ma trận nghịch ảo của ma trận A 9 Câu 3: Tìm m ể hạng của ma trận A A. m 2 m 11 B. m = 11 C. m 2 m 9 D. m 2 m 11 1 n
Câu 4: Cho A là ma trận vuông cấp n. Biết det(A) = 2 và A A n I
. Tính det(A2 I ) là A. 0 B. 2 C. 4 D. 3 0 1 0
Câu 5: Cho ma trận A 0 0 1 . Số nguyên dương n nhỏ nhất thỏa An 0( ma trận không) là 0 0 0 B. 4 B. 5 C. 3 D. 2 0 1 0 0 0 m 1 0 1 A Câu 6: Cho ma trận
2 , phần tử ở dòng 4 cột 1 của A là 0 m m 1 4 0 0 0 lOMoAR cPSD| 47207194 A. m m3 B. m C. m3 m D. m 1
x 3 y 4 z 1
Câu 7: Gi ả i h ệ phương trình 25 x yz 2 51x3 y 7 z 5 1 17 , y 7 , z ; A.
x B. x 1 17 , y 7 , z ; C. x = 1, y = 0, z = 0 D. Hệ vô nghiệm phương trình có nghiệm. A. C = 8a – 2b B. c = 8a + b C. b = 8a - 2c D. a = 8b - 2c
2 x 2 y 4 z m 3 x 5 yz 3
Câu 12: Tìm m ể hệ phương trình tuyến tính
4 x 4 y 8 z 2 có vô s ố nghiệm lOMoAR cPSD| 47207194 A. m = -1 B. m = 1 C. m = 2 D. m = -2 A. lOMoAR cPSD| 47207194 A. m 3 C. x = 3, y = 0, z = -2 D. x 3( ) /2, y , z ;, 1 0 20 ) A I
Câu 18: Cho ma trận A. Ma trận ( 2 là: 1 1 A. 20 1 1 20 T 7 7 1 A. D. 1 7 7 lOMoAR cPSD| 47207194 A. r(A) = 3 B. r(A) = 2 C. r(A) = 1 D r(A) = 4




