Ôn tập biến ngẫu nhiên và bài tập môn xác xuất thống kê về biến ngẫu nhiên | Trường Đại học sư phạm kỹ thuật TP Hồ Chí Minh

Biến ngẫu nhiên rời rạc.1. Tập giá trị. 2. Hàm xác suất 𝑝𝑋(𝑢) = 𝑃(𝑋 = 𝑢) . Bài tập: Một đồng xu không cân đối (hay đồng xu thiên vị ) với xác suất xuất hiện mặt có hình gấp 4 lần xác suất xuất hiện mặt không có hình. Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Xác suất thống kê (Toán 2)

Trường: Đại học Sư phạm Kỹ thuật Thành phố Hồ Chí Minh

Thông tin:

23 trang 2 tháng trước

Tác giả:

Profile Lê Kim Dung
Phân bi t ệ
Biến ng u nhiên rẫ ời rạc
1. Tập giá trị
2. Hàm xác suất 𝑝
𝑋
(𝑢) = 𝑃(𝑋 = 𝑢)
3.
𝑃
(
𝑎 ≤ 𝑋 ≤ 𝑏
)
=
= ∑ 𝑝
𝑋
(𝑢)
𝑎≤𝑢≤𝑏
4.
∑
𝑝
𝑋
(𝑢)
𝑢
= 1
5. Hàm phân ph ối tích lũy
𝐹
𝑋
( (
𝑐
)
= 𝑃 𝑋 ≤ 𝑐
)
= ∑𝑝
𝑋
(𝑢)
𝑢≤𝑐
6.
𝐸𝑋 =
∑
𝑢.𝑝
𝑋
( )
𝑢
𝑢
;
V(X)
= 𝐸
(
𝑋
2
)
− ( )𝐸𝑋
2
Biến ng u nhiên liên tẫ ục
1. Tập giá trị
2. Hàm m xác suật độ ất 𝑓(𝑥)
3.
𝑃
( (
𝑎 ≤ 𝑋 ≤ 𝑏
)
= 𝑃 𝑎 < 𝑋 ≤ 𝑏
)
=
𝑃
( (
𝑎 ≤ 𝑋 < 𝑏
)
= 𝑃 𝑎 < 𝑋 < 𝑏
)
=
∫𝑓(𝑥)𝑑𝑥
𝑏
𝑎
Vì 𝑃(𝑋 = 𝑎) = 0
4.
∫
𝑓(𝑥)𝑑𝑥
∞
−∞
= 1
5. Hàm phân ph ối tích lũy
𝐹
𝑋
( (
𝑐
)
= 𝑃 𝑋 ≤ 𝑐
)
= ∫𝑓(𝑥)𝑑𝑥
𝑐
−∞
6. E(X)=
∫
𝑥𝑓(𝑥)𝑑𝑥
∞
−∞
V(X)=
∫
𝑥
2
𝑓(𝑥)𝑑𝑥
∞
−∞
− ( (𝑥)
∫
𝑥𝑓 𝑑𝑥
∞
−∞
)
2
Bài tập: Cho BNN X có t p các giá tr có th có là 0, 1, 3 và 5. ậ ị ể
u
0
1
3
5
P
X
(u)
0,1
0,15
P
0,35
1) p?
2) P(1<X<=5)= ?
3) P(X
2
>1)= ?
4) P((X>1)/(X<5)) ?
5) E(X)=?
6) V(X)=?
Giải Bài t p: ậ
1) 0,1+0,15+p+0,35=1 Nên p=0,4
2) P(1<X<=5)= P(X=3)+P(X=5)=0,4+0,35=0,75
3) P(X
2
>1)= P(X>1)+P(X<-1)=P(X=3)+P(X=5)=0,75
P(A/B)=
𝑃(𝐴𝐵)
𝑃(𝐵)
4) P((
X>1 X<5)/( )) =
𝑃(1<𝑋<5)
𝑃(𝑋<5)
=
𝑃(𝑋=3)
𝑃
( ) ( )
𝑋=0 +𝑃 𝑋=1 +𝑃(𝑋=3)
=
0,4
0,
65
=
40
65
=
8
13
5) E(X)=0.0,1+1.0,15+3.0,4+5.0,35=3,1
6) V(X)=E(X )-(E(X)) .0,1+1 .0,15+3 .0,4+5
2 2
= 0
2 2 2 2
.0,35 - 3,1 = 2,89
2
Bài tập Cho BNN X có E(X)=4 và b ng phân ph i xác su t có d ng ả ố ấ ạ
U
0
2
6
P
X
(u)
P
0,2
0,4
a/ (p, q) =.
b/
𝑃(
𝑋 > 0
𝑋 < 3
⁄ ).
Giải
a/P+0,2+q+0,4=1 nên p+q=0,4
Do E(X)=0.p+2.0,2+4.q+6.0,4=4 suy ra q=0,3 và p=0,1
b/
𝑃(
𝑋 > 0
𝑋 < 3
⁄ ) ==
𝑃(0<𝑋<3)
𝑃(𝑋<3)
=
𝑃(𝑋=2)
𝑃 𝑋=0 +𝑃 𝑋=2
( ) ( )
=
0,2
0,3
=
2
3
Phân bi ệt:
1) BNN X có Phân phối Bernoulli có 2 giá trị có th có 0; 1. ể
X là s l n xu t hi n t/c S khi th c hi n TNNN. ố ầ ấ ệ ự ệ 1
2) BNN X có Phân ph i nhố ị thức
𝑋 là s l n xu t hi n tính ch t S khi th c hi n ố ầ ấ ệ ấ ự ệ n TNNN độc lập có xs xuất
hiện t/c S trong m và bỗi TNNN là như nhau ằng p.
Hàm xác su t ấ
𝑝
𝑋
( (
𝑢
)
= 𝑃 𝑋 = 𝑢
)
= 𝐶
𝑛
𝑢 𝑢
𝑝 (1 − 𝑝)
𝑛−𝑢
;𝑢 = 0;1;2;…;𝑛
𝐸(𝑋) = (1 − 𝑝)𝑛𝑝; 𝑉(𝑋) = 𝑛𝑝
3) BNN X có Phân phối nhị thức âm v i 2 tham s là r và p ớ ố :
Thực hiện các TNNN độc lập có xs xuất hiện t/c S trong mỗi TNNN là
như nhau và bằng p cho đến khi xu t hi n t/c S r l n thì dấ ệ ầ ừng.
S Phân ph i hình h c là pp nh c âm v i r=1. ố ọ ị thứ ớ
Lưu ý:
*) X là s l n ko xh t/c S ố ầ cho đến khi S xuất hiện r lần thì dừng.
Hàm xác su t ấ
𝑝
𝑋
( (
𝑢
)
= 𝑃 𝑋 = 𝑢
)
= 𝐶
𝑢+𝑟−1
𝑟−1
𝑝
𝑟
(1 − 𝑝)
𝑢
;𝑢 = 0;1;2;…
VD1: c hi n khi xu t hi n S 3 l n thì d Thự ện TNNN cho đế ấ ệ ầ ừng.
Giả s d ng l l n th 7. ử ừ ại ở ầ ứ
Gọi X là s l n ố ầ ko xu t hi n S ấ ệ cho đến khi x/h S 3 lần thì dừng
𝑝
𝑋
( (
4
)
= 𝑃 𝑋 = 4
)
= 𝐶
4+3−1
3−1
𝑝
3
(1 − 𝑝)
4
= 𝐶
6
2
𝑝
3 4
(1 − 𝑝)
*) Y là s l n th c hi n TNNN ố ầ ự ệ cho đến khi S xuất hiện r lần thì dừng.
Hàm xác su t ấ
𝑝
𝑌
(
𝑢
)
= 𝑃
(
𝑌 = 𝑢
)
= 𝐶
𝑢−1
𝑟−1 𝑢−𝑟
𝑝
𝑟
( )
1 − 𝑝 = 𝐶
𝑢−1
𝑢−𝑟 𝑢−𝑟
𝑝
𝑟
( )
1 − 𝑝
𝑢 = 𝑟; 𝑟 + 1;𝑟 + 2; …
VD2: c hi n khi xu t hi n S 3 l n thì d Thự ện TNNN cho đế ấ ệ ầ ừng.
Giả s d ng l l n th 7. ử ừ ại ở ầ ứ
Gọi Y là số l n th c hi n TNNN ầ ự ệ cho n khi xh S 3 l n thì d ng đế ầ ừ
𝑝
𝑌
( (
7
)
= 𝑃 𝑌 = 7
)
= 𝐶
7−1
3−1 7−3
𝑝
3
(1 − 𝑝) = 𝐶
6
2
𝑝
3
(1 − 𝑝)
4
4) Phân phối siêu bội L y ng u nhiên n ph n tấ ẫ ầ ử từ N ph n tầ ử trong đó có M
phần tử có tính ch t Sấ . Gọi 𝑋 là s phố ần t có tính chử ất S trong n phần t ử
lấy ra. có phân ph i siêu b i v 𝑋 ố ộ ới 3 tham s n; M; Nố
Hàm xác suất
𝑝
𝑋
( (
𝑢
)
= 𝑃 𝑋 = 𝑢
)
=
𝐶
𝑀
𝑢
𝐶
𝑁−𝑀
𝑛−𝑢
𝐶
𝑁
𝑛
𝐸
(
𝑋
)
= 𝑛
𝑀
𝑁
; 𝑉
(
𝑋
)
= 𝑛
𝑀
𝑁
(1 −
𝑀
𝑁
)
𝑁 − 𝑛
𝑁 − 1
5) Phân phối Poisson Phân phối nhị thức có n r t l n và p r t nh là phân ấ ớ ấ ỏ
phối Poisson v i tham sớ ố 𝜆 = 𝑛𝑝
Hàm xác su t c có phân ph i Poisson v i tham s ấ ủa 𝑋 ố ớ ố 𝜆
𝑝
𝑋
( (
𝑢
)
= 𝑃 𝑋 = 𝑢
)
=
𝒆
−𝜆
𝜆
𝒖
𝒖!
;𝒖 = 𝟎, 𝟏,𝟐,…
𝐸(𝑋) = 𝑉(𝑋) = 𝜆
Bài tập: M ng xu thiên v ) v i xác su t xu t hi n ột đồng xu không cân đối (hay đồ ị ớ ấ ấ ệ
mặt có hình g p 4 l n xác su t xu t hi n m t không có hình. ấ ầ ấ ấ ệ ặ
1) Xác su t xu t hi n m t có hình là bao nhiêu? ấ ấ ệ ặ
2) Tung m ng xu này. X là sột đồ ố l n xu t hiầ ấ ện m t có hình. X có phân phặ ối
gì?
3) Tung đồng xu cho đến khi xuất hiện mặt có hình 3 lần thì dừng. X là số lần
thự ốc hiện TNNN. Hỏi X có phân ph i gì?
4) Tung đồng xu này 20 lần. X là số lần xuất hiện mặt có hình. X có phân phối
gì? Trung bình c a X b ng bao nhiêu? ủ ằ
Giải Bài tập: M ng xu thiên v ) v i xác su t xuột đồng xu không cân đối (hay đồ ị ớ ấ ất
hiện m t có hình g p 4 l n xác su t xu t hi n m t không có hình. ặ ấ ầ ấ ấ ệ ặ
1) Xác su t xu t hi n m t có hình là bao nhiêu? 4/5=0,8 ấ ấ ệ ặ
2) Tung m ng xu này. X là sột đồ ố l n xu t hiầ ấ ện m t có hình. X có phân phặ ối
gì? X có pp Bernoulli v i tham s 0,8. ớ ố
3) Tung đồng xu cho đến khi xuất hiện mặt có hình 3 lần thì dừng. X là số lần
không xu t hi n m t có hình. ấ ệ ặ
Hỏi X có phân ph i gì? X có pp nhố ị thức âm v i r=3 và p=0,8. ớ
4) Tung đồng xu này 20 lần. X là số lần xuất hiện mặt có hình. X có phân phối
gì? Trung bình c a X b ng bao nhiêu? X có pp nh c v i n=20 và p=0,8. ủ ằ ị thứ ớ
E(X)=20.0,8=16.
Bài t p áp d ậ ụng
Bài 1 Lấy ng u nhiên t ng s n ph m t lô hàng có 3 s n ph m lo i I và 2 s n ph m lo i II ẫ ừ ả ẩ ừ ả ẩ ạ ả ẩ ạ
cho đến khi số sản phẩm loại I và loại II còn l ng nhau thì d ng. G i X là s s n phại bằ ừ ọ ố ả ẩm
lấy ra. Tìm hàm xác su t c a X, tính E(X) và V(X) ấ ủ .
Gợi ý:
B1: X/Đ TNNN L y ng u nhiên tấ ẫ ừng s n ph m t lô hàng có ả ẩ ừ 3 s n ph m lo i I và sả ẩ ạ 2 ản
phẩm lo i II n khi sạ cho đế ố s n ph m lo i I và lo i II còn l i b ng nhau thì dả ẩ ạ ạ ạ ằ ừng
B2: Xác định các giá trị có thể có của X là 1; 3; 5
B3: Tính xs X nh n giá tr có th ng ậ ị ể có tương ứ
Giải
T
ập các giá tr có th có c a X là ị ể ủ 𝑈
𝑋
=
{
1,3,5
}
𝑝
𝑋
( (
1
)
= 𝑃 𝑋 = 1
)
=
3
5
𝑝
𝑋
( (
3
)
= 𝑃 𝑋 = 3
)
=
2.3.2
5.4.3
=
1
5
𝑝
𝑋
( (
5
)
= 𝑃 𝑋 = 5
)
=
2. .3.2.1 + .3. .2.11 2 1
5!
=
1
5
Hàm xác su t c a X có d ng
ấ ủ ạ 𝑝
𝑋
(
𝑢
)
=
{
3
5
𝑘ℎ𝑖 𝑢 = 1
1
5
𝑘ℎ𝑖 𝑢 = 3
1
5
𝑘ℎ𝑖 𝑢 = 5
𝐸
(
𝑋
)
=
11
5
;𝑉
(
𝑋
)
=
64
25
Bài 2 Có 10 lô hàng, mỗi lô chứa 8 sản phẩm loại 1 và 2 sản phẩm loại 2. Lấy ngẫu nhiên
từ mỗi lô 2 sản phẩm và gọi X là số sản phẩm loại 1 trong 20 sản phẩm lấy ra. Tính kỳ
vọng, phương sai của X và P(X = 1).
Giải
Gọi 𝑋
𝑖
là s s n ph m lo i 1 trong 2 s n ph m l y ra t lô s n ph m th ố ả ẩ ạ ả ẩ ấ ừ ả ẩ ứ i. i=1, 2, …, 10.
Hàm xác su t cấ ủa 𝑋
𝑖
có d ng ạ
𝑝
𝑋
𝑖
(
𝑢
)
=
{
𝐶
8
2
𝐶
10
2
=
28
45
𝑘ℎ𝑖 𝑢 = 2
2.8
𝐶
10
2
=
16
45
𝑘ℎ𝑖 𝑢 = 1
1
𝐶
10
2
=
1
45
𝑘ℎ𝑖 𝑢 = 0
𝐸
(
𝑋
𝑖
)
=
72
45
;𝑉 𝑋
(
𝑖
)
=
64
225
Gọi X là s s n ph m lo i 1 trong 20 s n ph m l y ra ố ả ẩ ạ ả ẩ ấ
𝑋 = 𝑋
1
+ 𝑋
2
+ ⋯+ 𝑋
10
𝐸
(
𝑋
)
= 𝐸 𝑋
(
1
)
+ 𝐸 𝑋
(
2
)
+ ⋯+ 𝐸
(
𝑋
10
)
= 10.
72
45
= 16
Vì các 𝑋
𝑖
độc lập nên
𝑉
(
𝑋
)
= 𝑉 𝑋
(
1
)
+ 𝑉
(
𝑋
2
)
+ ⋯+ 𝑉
(
𝑋
10
)
= 10.
64
225
=
128
45
𝑃
(
𝑋 = 1
)
= 𝐶
10
1
𝑝
𝑋
𝑖
( )
1 (1 − 𝑝
𝑋
𝑖
(
1
)
)
9
= 10.
16
45
.(
29
45
)
9
=
Bài 3 Một đồng xu thiên vị với xác su t xu t hi n m t có hình g t không có hình. ấ ấ ệ ặ ấp đôi mặ
1) Tung đồng xu này 10 lần, tính xác suất số lần xuất hi n mệ ặ ầt có hình từ 3 đến 6 l n.
B1: Nh n di n TNNN: ậ ệ Tung đồng xu này 10 lần
B2: Nh n di n BNN xu t hi bài ậ ệ ấ ện trong đề
G i X là s l n xu t hi n m t có hình ng xu 10 l n. ọ ố ầ ấ ệ ặ khi tung đồ ầ
X có phân ph i nh c v i n=10 và p=2/3 ố ị thứ ớ
Hàm xác su t ấ
𝑝
𝑋
( (
𝑢
)
= 𝑃 𝑋 = 𝑢
)
= 𝐶
10
𝑢
(2/3)
𝑢
(1 − 2/3)
10−𝑢
;𝑢 = 0; 1;2;…; 10
B3: xác suất số l n ầ xuất hi n m t có hình tệ ặ ừ 3 đến 6 lần
P(3<=X<=6)=
∑
𝑃
(
𝑋 = 𝑢
)
6
𝑢=3
=
∑
𝐶
10
𝑢
(2/3)
𝑢
(1 − 2/3)
10−𝑢
6
𝑢=3
2) Tung đồng xu này cho đến khi xu t hi n m t có hình thì d ng lấ ệ ặ ừ ại. Tính xác suất cần tung
5 l n thì dầ ừng.
B1: Nh n di n TNNN: ậ ệ Tung đồng xu này cho đến khi xuất hiện mặt có hình thì dừng lại
B2: Nh n di n BNN xu t hi bài ậ ệ ấ ện trong đề
G i Y là s l n khi xu t hi n m t có hình thì d ng. ọ ố ần tung đồng xu cho đế ấ ệ ặ ừ
Y có phân ph i hình h c v i p=2/3 hay nh c âm v i r=1; p=2/3. ố ọ ớ ị thứ ớ
Hàm xác su t c a Y là ấ ủ
𝑝
𝑌
( (
𝑢
)
= 𝑃 𝑌 = 𝑢
)
= 𝐶
𝑢−1
𝑟−1 𝑢−𝑟
𝑝
𝑟
(1 − 𝑝) ; 𝑢 = 𝑟; 𝑟 + 1;𝑟 + 2
𝑝
𝑌
( (
𝑢
)
= 𝑃 𝑌 = 𝑢
)
= ( )(1 − ) ;𝑢 = 1;2;3; …2/3 2/3
𝑢−1
B3: xác su . ất cần tung 5 l n thì dầ ừng
P(Y=5) = (2/3)(1 − )2/3
5−1
3) M ng xu thiên v v i xác su t xu t hi n m t có hình gột đồ ị ớ ấ ấ ệ ặ ấp đôi mặt không có hình.Tung
đồng xu này cho đến khi xuất hi n m t có hình 3 l n thì d ng lệ ặ ầ ừ ại. Tính xác suất cần tung ít
nh iất 5 l n thì dầ ừng lạ .
B1: Nh n di n TNNN:ậ ệ Tung đồng xu này cho đến khi xuất hiện m t có hình 3 l n thì dặ ầ ừng
lại
B2: Nh n di n BNN xu t hi bài ậ ệ ấ ện trong đề
G i T là s l n khi xu t hi n m t có hình 3 l n thì d ng ọ ố ần tung đồng xu cho đế ấ ệ ặ ầ ừ
T có phân ph i nh c âm v i r=3 và p=2/3 ố ị thứ ớ
Hàm xác su t c a T là ấ ủ
𝑝
𝑇
(
𝑢
)
= 𝑃 𝑇 = 𝑢 = 𝐶
( )
𝑢−1
𝑟−1 𝑢−𝑟
𝑝
𝑟
(1 − 𝑝) ;𝑢 = 𝑟; 𝑟 + 1; 𝑟 + 2;…
𝑝
𝑇
(
𝑢
)
= 𝑃 𝑇 = 𝑢 = 𝐶
( )
𝑢−1
2
(
2
3
)
3
(1 −
2
3
)
𝑢−3
;𝑢 = 3; 4;5; ….
B3: xác su ất cần tung ít nh t 5 l n thì d ng lấ ầ ừ ại.
𝑃
( ( (
𝑇 ≥ 5
)
= 1 − 𝑃 𝑇 ≤ 4
)
= 1 − 𝑃 3 ≤ 𝑇 ≤ 4
)
= 1 − ∑ 𝐶
𝑢−1
2
(
2
3
)
3
(1 −
2
3
)
𝑢−3
4
𝑢=3
= 1 − ∑ 𝐶
𝑢−1
2
(
2
3
)
3
(
1
3
)
𝑢−3
4
𝑢=3
=
Xác su t c n tung không quá 5 l n ấ ầ ầ
𝑃
(
3 ≤ 𝑇 ≤ 5
)
= ∑ 𝐶
𝑢−1
3−1
(
2
3
)
3
(1 −
2
3
)
𝑢−3
5
𝑢=3
= ∑ 𝐶
𝑢−1
2
(
2
3
)
3
(
1
3
)
𝑢−3
5
𝑢=3
=
Giải Gọi p là xác suất xuất hi n m t không có hình thì 2p là xác su t xu t hi n m t có ệ ặ ấ ấ ệ ặ
hình.
Vì đồng xu chỉ xuất mặt có hình hoặc không có hình nên theo tính chất hàm xác
suất ta có suy ra 3𝑝 = 1 𝑝 =
1
3
. Xác su t xh m t có hình là 2/3. ấ ặ
Gợi ý:
B1: Xác đị đó Nhậ ủa BNN x/h trong đềnh TNNN từ n diện dạng phân phối xs c bài.
B2: Bi u di n b/c c n tính xác suể ễ ầ ất qua BNN đã x/đ ở B1
B3: Áp d ng các CT XS và hàm xs c ụ ủa BNN để tính
1) G i X là s l n xu t hi n m ng xu này. X có phân ph i Bernoulli ọ ố ầ ấ ệ ặt có hình khi tung đồ ố
với tham số 𝑝
0
=
2
3
.
Hàm xác su t c a X có d ng ấ ủ ạ
𝑝
𝑋
( (
𝑢
)
= 𝑃 𝑋 = 𝑢
)
= {
2
3
𝑘ℎ𝑖 𝑢 = 1
1
3
𝑘ℎ𝑖 𝑢 = 0
2) ng xu này 10 l n, g i Y là s l n xu t hi n m t có hình Tung đồ ầ ọ ố ầ ấ ệ ặ
Y có phân ph i nh c v i n=10 và ố ị thứ ớ 𝑝
0
=
2
3
.
Hàm xác su t c a bi n ng u Y có d ng ấ ủ ế ẫ ạ
𝑝
𝑌
( (
𝑢
)
= 𝑃 𝑌 = 𝑢
)
= 𝐶
10
𝑢
(
2
3
)
𝑢
(1 −
2
3
)
10−𝑢
Xác su t s l n xu t hi n m t có hình t n 6 ấ ố ầ ấ ệ ặ ừ 3 đế
𝑷
( ( )
𝟑 ≤ 𝒀 ≤ 𝟔
)
= ∑ 𝑃 𝑌 = 𝑢
𝟔
𝒖=𝟑
= ∑ 𝐶
10
𝑢
(
2
3
)
𝑢
(1 −
2
3
)
10−𝑢
𝟔
𝒖=𝟑
=
2) Tung đồng xu này cho đến khi xuất hiện mặt có hình thì dừng lại, gọi Z là số lần tung.
Z có phân ph i hình h c v i tham s ố ọ ớ ố 𝑝
0
=
2
3
Hàm xác su a Z có d ng ất củ ạ
𝑝
𝑍
( (
𝑢
)
= 𝑃 𝑍 = 𝑢
)
= (
2
3
)(1 −
2
3
)
𝑢−1
Tính xác su . ất cần tung 5 l n thì dầ ừng
𝑃
(
𝑍 = 5
)
= (
2
3
)(1 −
2
3
)
5−1
3) Tung đồng xu này cho đến khi xu t hi n m t có hình 3 l n thì d ng l i, T là s l n tung. ấ ệ ặ ầ ừ ạ ố ầ
T có phân ph i nh c âm v i tham s r=3 và ố ị thứ ớ ố 𝑝
0
=
2
3
.
Hàm xác t c a T có d ng
suấ ủ ạ 𝑝
𝑇
(
𝑢
)
= 𝑃 𝑇 = 𝑢 = 𝐶
( )
𝑢−1
3−1
(
2
3
)
3
(1 −
2
3
)
𝑢−3
Xác su ất cần tung ít nh t 5 l n thì d ng lấ ầ ừ ại.
𝑃
( ( (
𝑇 ≥ 5
)
= 1 − 𝑃 𝑇 ≤ 4
)
= 1 − 𝑃 3 ≤ 𝑇 ≤ 4
)
= 1 − ∑ 𝐶
𝑢−1
3−1
(
2
3
)
3
(1 −
2
3
)
𝑢−3
4
𝑢=3
= 1 − ∑ 𝐶
𝑢−1
2
(
2
3
)
3
(
1
3
)
𝑢−3
4
𝑢=3
=
Xác su t c n tung không quá 5 l n ấ ầ ầ
𝑃
(
3 ≤ 𝑇 ≤ 5
)
= ∑ 𝐶
𝑢−1
3−1
(
2
3
)
3
(1 −
2
3
)
𝑢−3
5
𝑢=3
= ∑ 𝐶
𝑢−1
2
(
2
3
)
3
(
1
3
)
𝑢−3
5
𝑢=3
=
Bài 4 Thống kê cho thấy % khách hàng tới cửa hàng S mua bột giặt chọn loại bột giặt E 60
và số còn lại chọn loại bột giặt H. Trên kệ của cửa hàng lúc này còn 10 gói bột giặt E và 8
gói bột giặt H. Tính xác suất số bột giặt này đáp ứng được nhu cầu của 12 khách hàng mua
bột giặt tiếp theo.
Hướng dẫn:
B1: Xác định TNNN đề bài: Quan sát 12 khách hàng mua bột giặt
B2: Xác định BNN x/h trong giả thuyết
Gọi X là số khách hàng mua bột giặt E trong 12 khách hàng tiếp theo.
X có phân phối phân phối nhị thức với n=12 và p=0,6
Hàm xác suất của X là
𝑝
𝑋
(
𝑢
)
= 𝑃
(
𝑋 = 𝑢
)
= 𝐶
12
𝑢
0,6
𝑢
(1 − 0,6)
12−𝑢
;𝑢 = 0;1; 2;…; 12
B3: Biểu diễn biến cố đề bài yêu cầu theo giá trị của BNN đã x/đ ở bước 2
4 ≤ 𝑋 ≤ 10
B4: Tính 2 xác suất số bột giặt này đáp ứng được nhu cầu của 1 khách hàng mua bột giặt
tiếp theo
𝑃
(
4 ≤ 𝑋 ≤ = ∑ 𝑃(𝑋 = 𝑢)10
)
10
𝑢=4
= ∑ 𝐶
12
𝑢
0,6
𝑢
(1 − 0,6)
12−𝑢
10
𝑢=4
=
Bài 5 Trong kho hàng có 1000 sp trong đó có 200 sp của nhà máy A. Lấy ngẫu
nhiên 100 sp t kho hàng. ừ
1/ Tính xác su t trong 100 s n ph m l y ra có ít nh t 20 s n ph m c a nhà máy A. ấ ả ẩ ấ ấ ả ẩ ủ
2/ Trong 100 s n ph m l y ra trung bình có bao nhiêu s n ph m c a nhà máy A? ả ẩ ấ ả ẩ ủ
Hướng dẫn:
B1: Xác định TNNN đề bài: Lấy ng u nhiên 100 sp tẫ ừ kho hàng có 1000 sp .
B2: Xác định BNN x/h trong giả thuyết
Gọi X là số sản phẩm của nhà máy A trong 100 sản phẩm lấy ra
X có phân phối siêu bội với n= 100 ; M=200 ; N=1000
Hàm xác suất của X là 𝑝
𝑋
(
𝑢
)
= 𝑃
(
𝑋 = 𝑢
)
=
𝐶
200
𝑢
𝐶
800
100−𝑢
𝐶
1000
100
B3: Biểu diễn biến cố đề bài yêu cầu theo giá trị của BNN đã x/đ ở bước 2
Trong 100 sản phẩm lấy ra có ít nhất 20 sản phẩm của nhà máy A
20 100≤ 𝑋 ≤
B4: Tính
𝑃
( ( )
𝑋 ≥ = ∑20
)
𝑃 𝑋 = 𝑢
100
𝑢=
20
= ∑
𝐶
200
𝑢
𝐶
800
100−𝑢
𝐶
1000
100
100
𝑢=
20
=
2/Trong 100 sản phẩm lấy ra trung bình có bao nhiêu sản phẩm của nhà máy A
E(X)=n.M/N=20 (s n ph ả ẩm)
Bài 6: Số khách đến quầy dịch vụ S trong 5 phút là bi n ng u nhiên có phân ph i Poisson ế ẫ ố
với trung bình là 3. Tính xác su có ít nh n qu y S có ất trong 10 phút ất 5 khách đế ầ bi ngết rằ
không quá 8 khách đến quầy S trong 10 phút.
Giải
B1: X/đ TNNN: Quan sát số khách đế n quầy dịch vụ S trong 10 phút
B2: X/đ BNN xuấ ện trong đềt hi bài
G i X là s n qu y d ch v S trong 5 phút
ọ ố khách đế ầ ị ụ 𝑋~𝑃
(
3
)
G i Y là s n qu y d ch v S trong 10 phút
ọ ố khách đế ầ ị ụ 𝑌~𝑃
(
6
)
Hàm xác su t c a Y là
ấ ủ 𝑝
𝑌
( (
𝑢
)
= 𝑃 𝑌 = 𝑢
)
=
𝑒
−6
.6
𝑢
𝑢!
;𝑢 = 0;1; 2;…
B3: Bi u di n bi n c c c 2 ể ễ ế ố ần tính qua BNN bướ
Xác su t trong 10 phút có ít nh n qu y S ấ ất 5 khách đế ầ biết r ng ằ có không quá 8 khách đến
quầy S trong 10 phút là
𝑃 (
𝑌 ≥ 5
𝑌 ≤ 8
⁄ ) =
𝑃(5 ≤ 𝑌 ≤ 8)
𝑃(𝑌 ≤ 8)
=
∑
𝑝
𝑌
(𝑢)
8
𝑢=5
∑
𝑝
𝑌
(𝑢)
8
𝑢=0
=
∑
𝑒
−6
.6
𝑢
𝑢!
8
𝑢=5
∑
𝑒
−6
.6
𝑢
𝑢!
8
𝑢=0
=
1134
1709
Bài 7 Gieo đồ ắc đồng thời 10 con xúc x ng chất.
1/ Tính xác su t có ít nh t 2 xúc s c xu t hi n m t có s m chia h t cho 3. ấ ấ ắ ấ ệ ặ ố chấ ế
2/ Tính xác su t có không quá 3 xúc s c xu t hi n m t có s m chia h t cho 3. ấ ắ ấ ệ ặ ố chấ ế
3/ Tính xác su có ít nh t 2 xúc s c xu t hi n m t có s m chia h t cho 3 biất để ấ ắ ấ ệ ặ ố chấ ế ết đã có
1 m t chia h t cho 3 xu t hi n. ặ ế ấ ệ
Bài 8 M t lô hàng ch a 10000 s n phộ ứ ả ẩm, trong đó có 8000 sản phẩm tốt và 2000 s n phả ẩm
xấu. Chọn ng u nhiên t lô hàng ra 10 s n ph m. Gẫ ừ ả ẩ ọi X là s s n ph m tố ả ẩ ốt trong 10 sản
phẩm đượ ọng, phương sai củ ọn được chọn. Tính kỳ v a X và xác suất ch c 7 sản phẩm tốt.
Bài 9 Số khách đến mua hàng tại một quầy hàng trong 1 phút là biến ngẫu nhiên có phân
phối Poisson v i tham s ớ ố λ=3. Tính xác suất trong khoảng thời gian t 7 gi 18 phút n 7 ừ ờ đế
giờ 20 phút có ít nh n cất 5 khách đế ửa hàng bi t có nhi u nh n cế ề ất là 8 khách đế ửa hàng
trong kho ng th i gian này. ả ờ
Bài 10 Số cuộc g n H trong các khung giọi đến trung tâm tư vấ ờ 8 đến 9 giờ, 9 đến 10 giờ
và 10 đế ần lượn 11 giờ là các biến ngẫu nhiên có phân phối Poisson với các tham số l t là
8; 9 và 9. Tính xác su t trong kho ng th i gian t n 11 gi có không quá 30 cu c gấ ả ờ ừ 8 đế ờ ộ ọi
đến trung tâm tư vấn H.
Bài 11 Trong kho hàng có 30% sản phẩm là của công ty A, 45% sản phẩm là của công ty
B và 25% sản phẩm là của công ty C. Tỷ lệ sản phẩm của công ty A, B, C đạt chuẩn tương
ứng là 0,97; 0,94 và 0,91.
1) Tính tỷ lệ phế phẩm của kho hàng.
2) Lấy ngẫu nhiên một sản phẩm từ kho hàng này và thấy nó là sản phẩm đạt chuẩn.
Tính xác suất lấy được sản phẩm của công ty B.
3) Lấy ngẫu nhiên từ kho hàng ra 30 sản phẩm. Tính xác suất có không quá 3 sản phẩm
là phế phẩm trong số xác sản phẩm lấy ra.
4) Lấy ngẫu nhiên lần lượt từng sản phẩm từ kho hàng cho đến khi lấy được sản phẩm
là phế phẩm thì dừng. Tính xác suất không phải lấy ra quá 10 sản phẩm.
5) Lấy ngẫu nhiên lần lượt từng sản phẩm cho đến khi lấy được 3 phế phẩm thì dừng.
Xác suất phải lấy ra ít nhất 15 sản phẩm là bao nhiêu?
Bài t p áp dậ ụng biến ngẫu nhiên liên t c ụ
Bài 1 i gian c n thiThờ ầ ết để s n xu t m t s n ph m M là bi n ng u nhiên X ả ấ ộ ả ẩ ế ẫ (đơn vị : phút)
có hàm m xác suật độ ất 𝑓(𝑥) =
𝐴
𝑥
2
n u ế 𝑥 ∈ [8 ; 10], f(x)= 0 n u xế ∉ [8 ; 10].
1/ Tìm A.
2/ Tính s n xu t m t s n ph m thời gian trung bình để ả ấ ộ ả ẩ M.
3/ Tính t l s n ph m có th i gian s n xu t nh i gian trung bình ( . ỷ ệ ả ẩ ờ ả ấ ỏ hơn thờ E(X))
4/ Quan sát quá trình s n xu t m t s n ph m M i gian s n xu t m ít nh t 8 phút ả ấ ộ ả ẩ thấy thờ ả ấ ất ấ
30 giây xác su t c n ít nh t 9 phút 30 giây s n xu t s n ph m này. . Tính ấ ầ ấ để ả ấ ả ẩ
5/ Quan sát ng u nhiên th i gian s n xu t 30 s n ph m này. Tính xác su t có t n 25 ẫ ờ ả ấ ả ẩ ấ ừ 12 đế
sản ph m có th i gian s n xu t ít nh t là 8 phút 30 giây. ẩ ờ ả ấ ấ
Giải
1/
∫ 𝑓(𝑥)𝑑𝑥
∞
−∞
= 1 ⟺ ∫
𝐴
𝑥
2
𝑑𝑥
10
8
= 1 ⟺ 𝐴 = 40
2/ Th s n xu t m t s n ph m M ời gian trung bình để ả ấ ộ ả ẩ
𝐸
(
𝑋
)
= ∫ 𝑥𝑓(𝑥)𝑑𝑥
∞
−∞
= ∫
40𝑥
𝑥
2
𝑑𝑥
10
8
= 40(𝑙𝑛
5
4
)~8,925742053
3/ T l s n ph m có th i gian s n xu t nhỷ ệ ả ẩ ờ ả ấ ỏ hơn thời gian trung bình
𝑃(𝑋 < 𝐸
(
𝑋
)
) = ∫ 𝑓
(
𝑥
)
𝑑𝑥
𝐸
(
𝑋
)
−∞
= ∫
40
𝑥
2
𝑑𝑥
40
(𝑙𝑛
5
4
)
8
= 0,5185798823
4/ Quan sát quá trình s n xu t m t s n ph m M ả ấ ộ ả ẩ thấy thời gian s n xu t m ít nh t 8 phút ả ấ ất ấ
30 giây xác su t c n ít nh t 9 phút 30 giây s n xu t s n ph m này.. Tính ấ ầ ấ để ả ấ ả ẩ
𝑃
(
𝑋 ≥ 9,5
𝑋 ≥ 8,5
⁄
) =
𝑃(𝑋 ≥ 9,5)
𝑃(𝑋 ≥ 8,5)
=
∫
40
𝑥
2
𝑑𝑥
10
9,5
∫
40
𝑥
2
𝑑𝑥
10
8,5
=
17
57
5/ Quan sát ng u nhiên th i gian s n xu t 30 sẫ ờ ả ấ ả ẩn ph m này. Tính xác su t có t ấ ừ 12 đến 25
sản ph có th i gian s n xu t ít nh t là 8 phút 30 giây. ẩm ờ ả ấ ấ
B1: X/đ TNNN xuất hiện: Quan sát ng u nhiên th i gian s n xu t 30 s n ph m ẫ ờ ả ấ ả ẩ
B2: X/đ BNN xuất hiện trong giả thuyết
Gọi Y là số sản ph có th i gian s n xu t ít nh t là 8 phút 30 giây sẩm ờ ả ấ ấ trong 30 ản
phẩm.
Y có phân ph i nh c v i n=30 và ố ị thứ ớ 𝑝 = 𝑃(𝑋 ≥ 8,5) =
∫
40
𝑥
2
𝑑𝑥
10
8,5
= 12 17/
Hàm xác su ất
𝑝
𝑌
(
𝑢
)
= 𝑃
(
𝑌 = 𝑢
)
= 𝐶
30
𝑢
.( / )12 17
𝑢
(1 − / )12 17
30−𝑢
B3: Xác su t có t n 25 s n ph m có th i gian s n xu t ít nh t là 8 phút 30 giây. ấ ừ 12 đế ả ẩ ờ ả ấ ấ
𝑃
(
12 25≤ 𝑌 ≤
)
=
∑
𝑃
( )
𝑌 = 𝑢
25
𝑢=12
= ∑ 𝐶
30
𝑢
( / )12 17
𝑢
(1 − / )12 17
30−𝑢
25
𝑢=
12
= 0,948603208
Bài 2 : Theo dõi th c t ng c a m t lo i s n ph nh là có tr ng ự ế trọng lượ ủ ộ ạ ả ẩm được quy đị ọ
lượng 2,5 gam, có thể coi tr ng này là m t biọng lượ ộ ến ngẫ ậu nhiên X liên tục có hàm m t
độ
𝑓
(
𝑥
)
= {
𝑘
(
1 + 𝑥
2
)
; 2 ≤ 𝑥 ≤ 4
0; 𝑥 > 2 ℎ 𝑥 < 4𝑎𝑦
a/ Tính k
b/ Tính E(X) (X) , V
c/ Tính t l s n ph m này có tr ng l nh. ỷ ệ ả ẩ ọng lượ ớn hơn trọng lương quy đị
d/ Tính xác su t chênh l a tr ng trong th c t so v i tr nh ấ ệch giữ ọng lượ ự ế ớ ọng lượng quy đị
của loại sản ph m này nh ẩ ỏ hơn 0.25 gam.
Giải
∫
𝑓
(
𝑥
)
𝑑𝑥
∞
−∞
= 1 ⟺ 1 + 𝑥∫ 𝑘
(
2
)
𝑑𝑥
4
2
= 1 ⟺ 𝑘 =
3
62
𝐸
(
𝑋
)
= ∫ 𝑥𝑓
(
𝑥
)
𝑑𝑥
∞
−∞
= ∫ 𝑥.
3
62
(
1 + 𝑥
2
)
𝑑𝑥
4
2
=
99
31
𝑉
(
𝑋
)
= ∫ 𝑥
2
𝑓
(
𝑥
)
𝑑𝑥
∞
−∞
−
(∫ 𝑥𝑓
(
𝑥
)
𝑑𝑥
∞
−∞
)
2
= ∫ 𝑥
2
.
3
62
(
1 + 𝑥
2
)
𝑑𝑥
4
2
− (
99
31
)
2
= 0,3044745057
3/ T l s n ph m này có tr ng lỷ ệ ả ẩ ọng lượ ớn hơn trọng lượng quy định là
𝑃
(
𝑋 > 2,5
)
= ∫ 𝑓
(
𝑥
)
𝑑𝑥
∞
2,5
= ∫
3
62
(
1 + 𝑥
2
)
𝑑𝑥
4
2,5
=
4/ Xác su t chênh l ch gi a tr ng trong th c t so v i tr nh c a loấ ệ ữ ọng lượ ự ế ớ ọng lượng quy đị ủ ại
sản ph m này nhẩ ỏ hơn 0,25 gam là
𝑃( 𝑋 − 2,5 < 0, = 𝑃(2,5 − 0, < 𝑋 < 2,5 + 0,
| |
25 25 25) = ∫ 𝑓
(
𝑥
)
𝑑𝑥
2,75
2,25
= ∫
3
62
(
1 + 𝑥
2
)
𝑑𝑥 =
2,75
2,
25
Bài 3 Một tr c cung c n trong 1 tu ng kho chạm xăng đượ ấp xăng 1 lầ ần. Dung lượ ứa của
trạm là 10 m3. Dung lượng xăng được yêu cầu bán ra trong 1 tuần của trạm là biến ngẫu
nhiên X (đơn vị ật độ
: m
3
) có hàm m xác suất 𝑓
(
𝑥
)
= 𝑘( − 𝑥)17
4
nếu , và 𝑥 ∈ [0; 17]
𝑓(𝑥) = 0 𝑥 ∉ [0; n u ế 17]. Tính k và xác su t h t tu n c a tr m này. ấ ết xăng trong mộ ầ ủ ạ
Giải:
Ta có
∫
𝑓(𝑥)𝑑𝑥
∞
−∞
= 1 𝑘( − 𝑥) Nên
∫
17
4
𝑑𝑥
17
0
= 1 Suy ra 𝑘 =
5
1419857
Xác su t h t tu n c a tr m này là ấ ết xăng trong mộ ầ ủ ạ
P(X>10)=
∫
𝑓(𝑥)𝑑𝑥
∞
10
=
∫
5
1419857
.( − 𝑥)17
4
𝑑𝑥
17
10
= 0,01183710754
Phân lo i bi n ng u nhiên liên t c ạ ế ẫ ụ
Biến ng u nhiên X có phân ph u trên [A; B]ẫ ối đề
X có hàm m xác su t có d ng ật độ ấ ạ
𝑓
(
𝑥
)
= {
1
𝐵 − 𝐴
𝑘ℎ𝑖 [𝐴; 𝐵]𝑥𝜖
0 𝑘ℎ𝑖 𝑥 ∉ [𝐴;𝐵]
E(X)=
𝐴+𝐵
2
; V(X)=
(𝐵−𝐴)
2
12
X nh n giá tr c [A; B] v i kh i mậ ị thuộ ớ ả năng là như nhau tạ ọi
điể ịm và khả năng nhận giá tr ngoài [A; B] là bằng 0.
Bài 2 Thời gian c n thi s n xu t m t s n ph i M là bi n ngầ ết để ả ấ ộ ả ẩm loạ ế ẫu nhiên X (đơn vị :
phút) có hàm m xác su u [8; B] u ật độ ất 𝑓(𝑥) = 𝑘 nế 𝑥 ∈ , 𝑓(𝑥) = 0 nế 𝑥 ∉ [8 ; 𝐵].
1/ Tìm 𝑘,𝐵 và thời gian trung bình để s n xu t m t s n ph m i này t xác suả ấ ộ ả ẩ loạ , biế ất để một
sản ph m M có th i gian s n xu t không quá 9 phút là 0,25. ẩ ờ ả ấ
2/ Tính t l s n ph m có th i gian s n xu i gian s n xu t trung bình. ỷ ệ ả ẩ ờ ả ất ít hơn thờ ả ấ
Giải
X là bi n ng u nhiên có phân ph u trên [8; B] ế ẫ ối đề
X có hàm m xác su t có d ng ật độ ấ ạ
𝑓
(
𝑥
)
= {
1
𝐵 − 8
𝑘ℎ𝑖 [8;𝐵]𝑥𝜖
0 𝑘ℎ𝑖 𝑥 ∉ [8; 𝐵]
nên ta có 𝑘 =
1
𝐵−8
Xác su m t s n ph m có th i gian s n xu t không quá 9 phút là ất để ộ ả ẩ ờ ả ấ
𝑃
(
𝑋 ≤ 9
)
= ∫ 𝑓(𝑥)𝑑𝑥
9
−∞
= ∫ 𝑘𝑑𝑥
9
8
=
1
4
Suy ra 𝑘 =
1
4
dẫn đến B=12
Vậy th s n xu t 1 s n ph m lo i M là ời gian trung bình để ả ấ ả ẩ ạ
𝐸
(
𝑋
)
=
8 + 12
2
= 10
(
𝑝ℎú𝑡
)
.
2/ T l s n ph m có th i gian s n xu i gian s n xu t trung bình. ỷ ệ ả ẩ ờ ả ất ít hơn thờ ả ấ
𝑃
(
𝑋 ≤ 10
)
= ∫ 𝑓(𝑥)𝑑𝑥
10
−∞
= ∫ 𝑘𝑑𝑥
10
8
=
1
2
3/ Quan sát ng u nhiên th i gian s n xu t c a 50 s n ph m này tính xác su t có ít nh t 20 ẫ ờ ả ấ ủ ả ẩ ấ ấ
sản ph có th i gian s n xu i gian s n xu t trung bình. ẩm ờ ả ất ít hơn thờ ả ấ
Gọi Y là s s n ph m có th i gian s n xu i gian s n xu t trung bình trong 50 ố ả ẩ ờ ả ất ít hơn thờ ả ấ
sản ph ẩm.
Y có phân ph i nh c v i n=50 và p=0,5 ố ị thứ ớ
Hàm xác su t ấ
𝑝
𝑌
(
𝑢
)
= 𝑃
(
𝑌 = 𝑢
)
= 𝐶
50
𝑢
0,5
𝑢
(1 − 0,5)
50−𝑢
;𝑢 = 0;1; 2;…; 50
Xác su t có ít nh t 20 s n ph có th i gian s n xu i gian s n xu t trung bình. ấ ấ ả ẩm ờ ả ất ít hơn thờ ả ấ
𝑃( ≤ 𝑋 ≤ ) = ∑20 50 𝑃
(
𝑌 = 𝑢
)
50
𝑢=
20
= ∑ 𝐶
50
𝑢
0,5
𝑢
(1 − 0,5)
50−𝑢
50
𝑢=
20
4/ Quan sát ng u nhiên th i gian s n xu t c a các s n ph n khi g c 10 s n ẫ ờ ả ấ ủ ả ẩm cho đế ặp đượ ả
phẩm có th i gian s n xu t không quá 9 phút thì d ng. ờ ả ấ ừ Biết đã quan sát được 20 s n ph m. ả ẩ
Tính xác su i này quan sát không quá 45 s n ph ất ngườ ả ẩm.
Giải: Gọi T là số sản phẩm c n khi g c 10 sần quan sát cho đế ặp đượ ản phẩm có thời gian
sản xu t không quá 9 phút thì dấ ừng
T có phân ph i nh c âm v i r=10 và p=0,25. ố ị thứ ớ
Hàm xác su t ấ
𝑝
𝑇
( (
𝑢
)
= 𝑃 𝑇 = 𝑢
)
= 𝐶
𝑢−1
9
0,25
10
(
1 − 0,25
)
𝑢−10
𝑢 = ; …10 11 12; ;
Xác su i này quan sát không quá 45 s n ph m ất ngườ ả ẩ bi tế đã quan sát được 20 sản phẩm là
𝑃 (
𝑇 ≤ 45
𝑇 ≥ 20
⁄ ) =
𝑃( ≤ 𝑇 ≤ )20 45
𝑃(𝑇 ≥
20)
=
𝑃( ≤ 𝑇 ≤ )20 45
1 − 𝑃(𝑇 <
20)
=
∑
𝑃
(
𝑇 = 𝑢
)
45
𝑢=20
1 −
∑
𝑃
(
𝑇 = 𝑢
)
20
𝑢=10
=
∑
𝐶
𝑢−1
9
0,25
10
(
1 − 0,25
)
𝑢−10
45
𝑢=20
1 −
∑
𝐶
𝑢−1
9
0,25
10
(
1 − 0,25
)
𝑢−10
20
𝑢=
10
Bài 3: Thời gian đi đến trườ ủa sv H là bnn X (đơn vịng c : phút) có phân phối đều trên [10;
15]. Sinh viên H đi từ ất sv H đến trường trướ nhà lúc 6h48 phút. Tính xác su c 7h.
X có hàm m có d ng ật độ ạ
𝑓
(
𝑥
)
= {
1
5
𝑘ℎ𝑖 𝑥𝜖 [10 15; ]
0 𝑘ℎ𝑖 𝑥 ∉ [10 15; ]
Xác su c 7h là ất sv H đến trường trướ
𝑃
(
𝑋 < 12
)
= 𝑃
(
10 ≤ 𝑋 < 12
)
= ∫
1
5
12
10
𝑑𝑥 = 0,4
Biến ng u nhiên có phân ph i tham s ẫ ối mũ vớ ố 𝝀
Hàm m xác su t c a BNN ật độ ấ ủ T có phân ph i tham s ối mũ vớ ố 𝝀 > 𝟎
𝑓
(
𝑥;𝝀
)
= {
𝝀𝒆
−𝝀𝒙
𝑘ℎ𝑖 𝑥 ≥ 0
0 𝑘ℎ𝑖 𝑥 < 0
Hàm phân phối xác suất (tích lũy )
𝐹
( (
𝑥; 𝝀
)
= 𝑃 𝑇 ≤ 𝑥
)
= {
𝟏 − 𝒆
−𝝀𝒙
𝑘ℎ𝑖 𝑥 ≥ 0
0 𝑘ℎ𝑖 𝑥 < 0
Hàm phân phối xác suất bù
𝐹
𝑐
( (
𝑥; 𝝀
)
= 𝑃 𝑇 > 𝑥
)
= {
𝒆
−𝝀𝒙
𝑘ℎ𝑖 𝑥 ≥ 0
1 𝑘ℎ𝑖 𝑥 < 0
Tính ch t không nh
ấ ớ 𝑃(
𝑇 > 𝑠 + 𝑡
𝑇 > 𝑠
⁄ ) = 𝑃(𝑇 > 𝑡)
Kỳ vọng, phương sai
𝐸
(
𝑇
)
=
1
𝝀
; 𝑉
(
𝑇
)
=
1
𝝀
2
Bài 3 Thời gian tr l n tho i (nghe máy) cả ời điệ ạ ủa m ột người ở vùng A khi nhân viên tư vấn
tiếp th s n ph m gị ả ẩ ọi đến là bi n ngế ẫu nhiên X (đơn vị: phút) có phân phối mũ với 𝝀 = 𝟏,𝟓
(1/phút). =40 giây).(hoặc là với thời gian nghe điện thoại trung bình là 2/3 phút
1/ Nhân viên tiếp thị gọi đến cho một người, tính xác suất người này nhận cuộc gọi ít nhất
2 phút.
2/ Nhân viên iếp thị gọi đến cho một người và người này đã nhận cuộc gọi được 1 phút.
Tính xác suất người này nhận cuộc gọi ít nhất 1 phút nữa.
3/ Tính xác suất thời gian nhận cuộc gọi khi nhân viên tiếp thị gọi đến của 1 người vùng A
là từ 2 đến 3 phút?
4/ Tính xác suất trong 30 người mà nhân viên tiếp thị gọi đến có ít nhất 10 người có thời
gian nhận cuộc gọi ít nhất 2 phút.
5/ Nhân viên tiếp thị gọi lần lượt từng người người có thời gian nhận cho đến khi được 5
cuộc gọi ít nhất 2 phút . Tính xác suất nhân viên này không cần gọi quá 20 người. thì dừng
Giải
1/ Xác suất người này nhận cuộc gọi ít nhất 2 phút
𝑃
(
𝑋 ≥ 2
)
= 𝒆
−𝝀.𝟐
= 𝒆
−𝟑
2/ Nhân viên tiếp thị gọi đến cho một người và người này đã nhận cuộc gọi được 1 phút.
Xác suất người này nhận cuộc gọi ít nhất 1 phút nữa.
𝑃 (
𝑋 ≥ 1 + 1
𝑋 ≥ 1
⁄ ) = 𝑃
(
𝑋 ≥ 1
)
= 𝒆
−𝟏,𝟓
3/ Tính xác suất thời gian nhận cuộc gọi khi nhân viên tiếp thị gọi đến của 1 người vùng A
là từ 2 đến 3 phút?
𝑃
( ( ( ( (
2 ≤ 𝑋 ≤ 3
)
= 𝑃 𝑋 ≤ 3
)
− 𝑃 𝑋 ≤ 2
)
= 𝐹 3; 𝝀
)
− 𝐹 2;𝝀
)
=
(
𝟏 − 𝒆
−𝟏,𝟓.𝟑
)
−
(
𝟏 − 𝒆
−𝟏,𝟓.𝟐
)
= 𝑒 − 𝑒
−3 −4,5
4/ Tính xác suất trong 30 người mà nhân viên tiếp thị gọi đến có ít nhất 10 người có thời
gian nhận cuộc gọi ít nhất 2 phút.
B1: TNNN xuất hiện trong bài: Gọi tới cho 30 người vùng A.
B2: Bnn xuất hiện:
Gọi Y là số người có thời gian nhận cuộc gọi ít nhất 2 phút trong 30 người
Y có phân phối nhị thức n=30 và p=P(X>=2)= 𝒆
−𝟑
Hàm xác suất của Y có dạng
𝑃
(
𝑌 = 𝑢
)
= 𝐶
30
𝑢
(𝒆
−𝟑 −𝟑 −𝑢
)
𝑢
(1 − 𝒆 )
30
;𝑢 = 0,1,2, …,30
B3: Xác suất trong 30 người mà nhân viên tiếp thị gọi đến có ít nhất 10 người có thời gian
nhận cuộc gọi ít nhất 2 phút là
𝑃
(
𝑌 ≥ 10
)
= ∑ 𝑃 𝑌 = 𝑢
( )
30
𝑢=
10
= ∑ 𝐶
30
𝑢
(𝒆
−𝟑 −𝟑 −𝑢
)
𝑢
(1 − 𝒆 )
30
30
𝑢=
10
=
5/ Nhân viên tiếp thị gọi lần lượt từng người người có thời gian nhận cho đến khi được 5
cuộc gọi ít nhất 2 phút . Tính xác suất nhân viên này không cần gọi quá 20 người. thì dừng
2
3
B1: TNNN xuất hiện:
Nhân viên tiếp thị gọi lần lượt từng người người có thời gian cho đến khi được 5
nhận cuộc gọi ít nhất 2 phút thì dừng
B2: Bnn xuất hiện:
Gọi Z là số người ở vùng A cần gọi cho đến được 5 người có thời gian nhận khi
cuộc gọi ít nhất 2 phút thì dừng.
Z có phân phối nhị thức âm với r=5 và p=P(X>=2)= 𝒆
−𝟑
Hàm xác suất của Z có dạng
𝑃
(
𝑍 = 𝑢
)
= 𝐶
𝑢−1
4
(
𝒆
−𝟑 −𝟑
)
5
(1 − 𝒆 )
𝑢−5
;𝑢 = 5; 6;7;…..
B3: xác suất nhân viên này không cần gọi quá 20 người là
𝑃
(
𝑍 ≤ 20
)
= ∑ 𝑃(𝑍 = 𝑢)
20
𝑢=5
= ∑ 𝐶
𝑢−1
4
(
𝒆
−𝟑
)
5
(1 − 𝒆
−𝟑
)
𝑢−5
20
𝑢=5
=
Biến ng u nhiên X có phân ph i chu ẫ ố ẩn 𝑵(𝝁; 𝝈
𝟐
)
Hàm m
ật độ 𝒇
(
𝒙
)
=
𝟏
√
𝟐𝝅 𝝈
𝒆
−
(𝒙−𝝁)
𝟐
𝟐𝝈
𝟐
𝑬
( (
𝑿
)
= 𝝁; 𝑽 𝑿
)
= 𝝈
𝟐
Phân ph i chu n t c
ố ẩ ắ 𝒁~𝑵 𝟎; 𝟏
( )
Hàm m
ật độ 𝒇
(
𝒙
)
=
𝟏
√
𝟐𝝅
𝒆
−
𝒙
𝟐
𝟐
Hàm
phân phối của phân phối chuẩn tắc ∅
( (
𝒄
)
= 𝑷 𝒁 ≤ 𝒄
)
=
∫
𝟏
√
𝟐𝝅
𝒆
−
𝒙
𝟐
𝟐
𝒅𝒙
𝒄
−∞
Bài 4 Cho Z là biến ngẫu nhiên có phân phối chuẩn tắc N(0; 1). Tính:
1.
𝑃
(
𝑍 < 1,54
)
2. P(Z>1,65) 3. 𝑃
(
1,51 23≤ 𝑍 ≤ 2,
)
4. 𝑃
(
𝑍 ≥ 2/𝑍 ≤ 2,4
)
𝑃
(
𝑍 < 1,54
)
= ∅(1,54)=
𝑃
(
𝑍 > 1,65
)
= 1 − 𝑃 𝑍 ≤ 1,
(
65
)
= 1 − ∅(1,65)=
𝑃
(
1,51 ≤ 𝑍 ≤ 2,23
)
= ∅ 2,
(
23
)
− ∅(1,51)=
𝑃
(
𝑍 ≥ 2/𝑍 ≤ 2,4
)
=
𝑃(2≤𝑍≤2,4)
𝑃(𝑍≤2,4)
=
∅(2,4 −∅(2))
∅(2,4)
=
X
~ 𝑁
(
𝜇; 𝜎
2
)
thì biến ng u nhiên chu n t c hóaẫ ẩ ắ 𝒁 =
𝑿−𝝁
𝝈
~𝑵(𝟎;𝟏)
𝑷 𝒂 < 𝑿 < 𝒃 = 𝑷(
( )
𝒂 − 𝝁
𝝈
< 𝒁 <
𝒃 − 𝝁
𝝈
) = ∅(
𝒃 − 𝝁
𝝈
) − ∅(
𝒂 − 𝝁
𝝈
)
𝑷 𝑿 < 𝒃 = ∅ (
( )
𝒃 − 𝝁
𝝈
); 𝑷
(
𝑿 > 𝒂
)
= 𝟏 − ∅ (
𝒂 − 𝝁
𝝈
)
Bài 4 Cho X là bi n ng u nhiên có phân ph i chu n v ế ẫ ố ẩ ới 𝜇 = 16; 𝜎 = 5. Tính:
1.
𝑃
(
𝑋 ≥ 24
)
2. 𝑃
(
15 22≤ 𝑋 ≤
)
3. 𝑃
(
𝑋 ≥ 20 24/𝑋 ≤
)
𝑿~𝑵
(
𝟏𝟔; 𝟓
𝟐
)
suy ra Bi n ng u nhiên chu n t c hóaế ẫ ẩ ắ 𝒁 =
𝑿−𝟏𝟔
𝟓
~𝑵(𝟎;𝟏)
1/
𝑃
(
𝑋 ≥ 24
)
= 𝑃 (𝑍 ≥
24−16
5
) = = 1 − 𝑃 𝑍 < 1,6𝑃
(
𝑍 ≥ 1,6
) ( )
= 1 − ∅ 1,6
( )
= 0,0548
2/
𝑃
(
15 22≤ 𝑋 ≤
)
= 𝑃 (
15−16
5
≤ 𝑍 ≤
22−16
5
) = 𝑃(−0,2 ≤ 𝑍 ≤ 1,2) = ∅ 1,2 −
( )
∅
(
−0,2
)
= 0,46419
3/
𝑃
(
𝑋 ≥ 20 24/𝑋 ≤
)
=
𝑃( ≤𝑋≤ )20 24
𝑃(𝑋≤
24)
=
∅(
24 16−
5
)−∅(
20 16−
5
)
∅(
24 16−
5
)
= 0,1661658908
Bài 5 Tuổi th s n ph m c a nhà máy M là bi n ngọ ả ẩ ủ ế ẫu nhiên X (đơn vị: năm) có phân phối
chuẩn 𝑁(4; 1). Nhà máy M bảo hành sản phẩm trong 3 năm.
1/ Tính tỷ lệ sản phẩm phải bảo hành của nhà máy M.
2/ Quan sát ngẫu nhiên một sản phẩm M đã sử dụng được 1 năm, tính xác suất sản phẩm
này sử dụng được thêm 2 năm nữa.
3/ Quan sát ngẫu nhiên thời gian sử dụng của 10 sản phẩm M, thấy có ít nhất 1 sản phẩm
phải bảo hành. Tính xác suất có không quá 5 sản phẩm phải bảo hành trong số 10 sản phẩm
này.
4/ Tính xác suất có không quá 0 sản phẩm phải bảo hành trong số 10000 sản phẩm M 120
này.
𝑿~𝑵
(
𝟒; 𝟏
)
suy ra Bi n ng u nhiên chu n t c hóaế ẫ ẩ ắ 𝒁 =
𝑿−𝟒
𝟏
~𝑵(𝟎;𝟏)
1/ Tỷ lệ sản phẩm phải bảo hành của nhà máy M
𝑃
(
𝑋 < 3
)
= 𝑃 (𝑍 <
3 − 4
1
) = ∅(
3 − 4
1
) = ∅
(
−1
)
= 0,15866
2/ Quan sát ngẫu nhiên một sản phẩm M đã sử dụng được 1 năm, tính xác suất sản phẩm
này sử dụng được thêm 2 năm nữa.
𝑃 (
𝑋 ≥ 3
𝑋 ≥ 1
⁄ ) =
𝑃(𝑋 ≥ 3)
𝑃(𝑋 ≥ 1)
=
1 − 𝑃 (𝑍 <
3 − 4
1
)
1 −
𝑃(𝑍 <
1 − 4
1
)
=
1 −
∅
(
−1
)
1 −
∅
(
−3
)
= 0,8424773444
3/ Quan sát ngẫu nhiên thời gian sử dụng của 10 sản phẩm M, thấy có ít nhất 1 sản phẩm
phải bảo hành. Tính xác suất có không quá 5 sản phẩm phải bảo hành trong số 10 sản phẩm
này.
B1: X/đ TNNN: Quan sát ngẫu nhiên thời gian sử dụng của 10 sản phẩm M
B2: X/đ BNN
Gọi Y là số máy phải bảo hành trong 10 sp
Y có phân phối nhị thức với n=10; p=0,15866
Hàm xác suất của Y là
𝑝
𝑌
( (
𝑢
)
= 𝑃 𝑌 = 𝑢
)
= 𝐶
10
𝑢
.0,15866
𝑢
(1 − 0, )15866
10−𝑢
;𝑢 = 0;1; 2;…;10
B3: Tính xác suất
𝑃 (
𝑌 ≤ 5
𝑌 ≥ 1
⁄ ) =
𝑃(1 ≤ 𝑌 ≤ 5)
𝑃(1 ≤ 𝑌 ≤
10)
=
∑
𝐶
10
𝑢
.0,15866
𝑢
(1 − 0, )15866
10−𝑢
𝟓
𝒖=𝟏
∑
𝐶
10
𝑢
.0,15866
𝑢
(1 − 0, )15866
10−𝑢
𝟏𝟎
𝒖=𝟏
Định lý xấp xỉ phân phối
X có phân ph i nh c v i 2 tham s n và p v i n r t lố ị thứ ớ ố ớ ấ ớn thì ta xem như
X có phân ph i chu n v ố ẩ ới 𝝁 = (𝟏 − 𝒑)𝒏𝒑; 𝝈
𝟐
= 𝒏𝒑
4/ Tính xác suất có không quá 1 00 sản phẩm trong số 10000 sản phẩm M 5 phải bảo hành
này.
B1: X/đ TNNN: Quan sát ngẫu nhiên thời gian sử dụng của 10000 sản phẩm M
B2: X/đ BNN
Gọi T là số máy phải bảo hành trong 10000 sp
T có phân phối nhị thức với n=10000; p=0,15866
Hàm xác suất của T là
𝑝
𝑇
(
𝑢
)
= 𝑃 𝑇 = 𝑢 = 𝐶
( )
10000
𝑢
.0,1538
𝑢
( )
1 − 0,15866
10000−𝑢
;
𝑢 = 0;1; 2;… ;10000
| 1/23
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Phân biệt
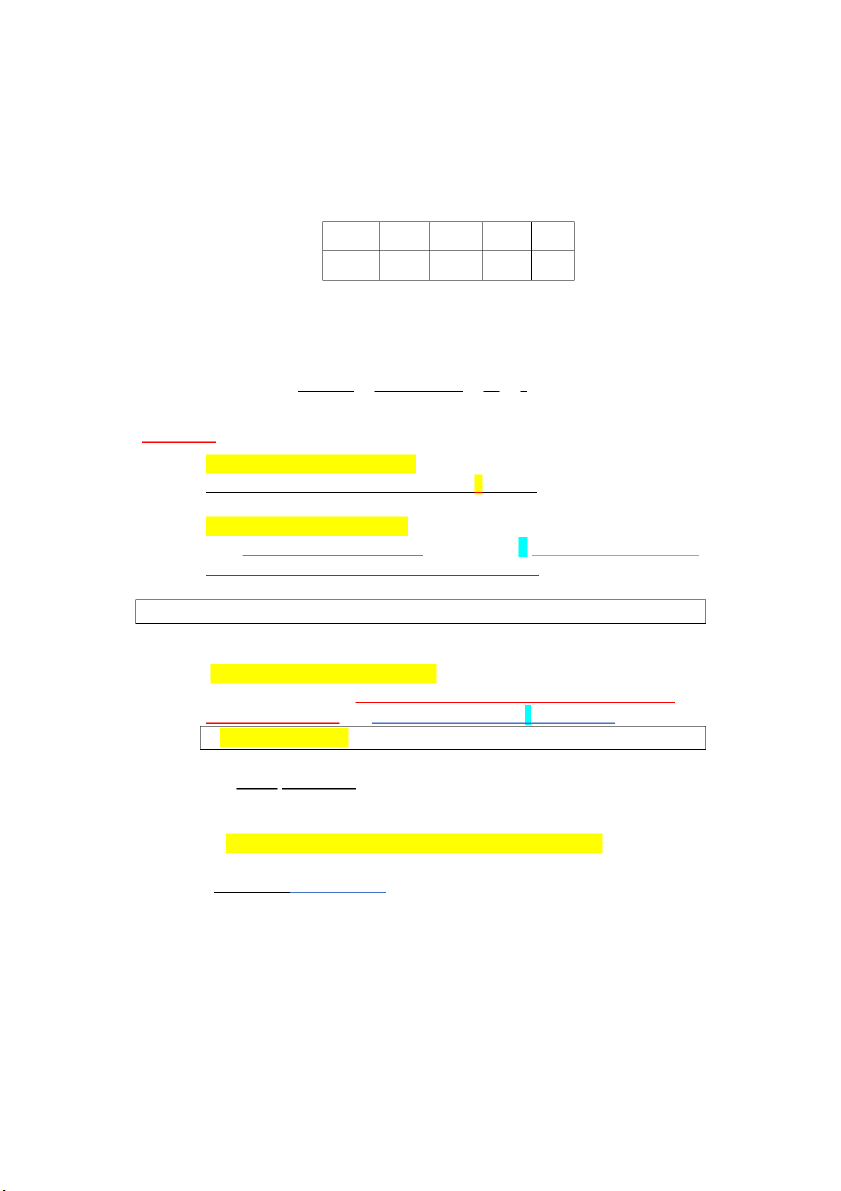
Biến ngẫu nhiên rời rạc
Biến ngẫu nhiên liên tục 1. Tập giá trị 1. Tập giá trị
2. Hàm xác suất 𝑝𝑋(𝑢) = 𝑃(𝑋 = 𝑢)
2. Hàm mật độ xác suất 𝑓(𝑥)
3. 𝑃(𝑎 ≤ 𝑋 ≤ 𝑏) =
3. 𝑃(𝑎 ≤ 𝑋 ≤ 𝑏) = 𝑃(𝑎 < 𝑋 ≤ 𝑏) =
𝑃(𝑎 ≤ 𝑋 < 𝑏) = 𝑃(𝑎 < 𝑋 < 𝑏) = = ∑ 𝑝𝑋(𝑢) 𝑏 𝑎≤𝑢≤𝑏 ∫ 𝑓(𝑥)𝑑𝑥 𝑎 Vì 𝑃(𝑋 = 𝑎) = 0 4. ∑ ∞ 𝑢 𝑝𝑋(𝑢) = 1 4. ∫ 𝑓(𝑥)𝑑𝑥
5. Hàm phân phối tích lũy −∞ = 1
5. Hàm phân phối tích lũy 𝐹 𝑐
𝑋(𝑐) = 𝑃(𝑋 ≤ 𝑐) = ∑ 𝑝𝑋(𝑢) 𝑢≤𝑐
𝐹𝑋(𝑐) = 𝑃(𝑋 ≤ 𝑐) = ∫𝑓(𝑥)𝑑𝑥 −∞ 6. 𝐸𝑋 = ∑ ∞ 𝑢 𝑢. 𝑝𝑋(𝑢) ;
6. E(X)= ∫ 𝑥𝑓(𝑥)𝑑𝑥
V(X)= 𝐸(𝑋2) − (𝐸𝑋)2 −∞
V(X)= ∫∞ 𝑥2𝑓(𝑥)𝑑𝑥 ∞ −∞
− (∫ 𝑥𝑓(𝑥)𝑑𝑥 −∞ )2
Bài tập: Cho BNN X có tập các giá trị có thể có là 0, 1, 3 và 5. u 0 1 3 5 PX(u) 0,1 0,15 P 0,35 1) p? 2) P(13) P(X2>1)= ? 4) P((X>1)/(X<5)) ? 5) E(X)=? 6) V(X)=? Giải Bài tập:
1) 0,1+0,15+p+0,35=1 Nên p=0,4
2) P(13) P(X2>1)= P(X>1)+P(X<-1)=P(X=3)+P(X=5)=0,75 P(A/B)= 𝑃(𝐴𝐵) 𝑃(𝐵)
4) P((X>1)/(X<5)) =𝑃(1<𝑋<5)= 𝑃(𝑋=3) = 0,4 = 40 = 8 𝑃(𝑋<5)
𝑃(𝑋=0)+𝑃(𝑋=1)+𝑃(𝑋=3) 0,65 65 13
5) E(X)=0.0,1+1.0,15+3.0,4+5.0,35=3,1
6) V(X)=E(X2)-(E(X))2= 02.0,1+12.0,15+32.0,4+52.0,35 - 3,12 = 2,89
Bài tập Cho BNN X có E(X)=4 và bảng phân phối xác suất có dạng U 0 2 4 6 PX(u) P 0,2 q 0,4 a/ (p, q) =. b/ 𝑃(𝑋 > 0 𝑋 ⁄ < 3). Giải a/P+0,2+q+0,4=1 nên p+q=0,4
Do E(X)=0.p+2.0,2+4.q+6.0,4=4 suy ra q=0,3 và p=0,1
b/ 𝑃(𝑋 > 0⁄𝑋 < 3)== 𝑃(0<𝑋<3) = 𝑃(𝑋=2) = 0,2 = 2 𝑃(𝑋<3) 𝑃 (𝑋=0)+𝑃(𝑋=2) 0,3 3 Phân biệt:
1) BNN X có Phân phối Bernoulli có 2 giá trị có thể có 0; 1.
X là số lần xuất hiện t/c S khi thực hiện 1 TNNN.
2) BNN X có Phân phối nhị thức
𝑋 là số lần xuất hiện tính chất S khi thực hiện n TNNN độc lập có xs xuất
hiện t/c S trong mỗi TNNN là như nhau và bằng p. Hàm xác suất 𝑝 𝑢 𝑢
𝑋(𝑢) = 𝑃(𝑋 = 𝑢) = 𝐶𝑛𝑝 (1 − 𝑝)𝑛−𝑢; 𝑢 = 0; 1; 2; … ; 𝑛
𝐸(𝑋) = 𝑛𝑝; 𝑉(𝑋) = 𝑛𝑝(1 − 𝑝)
3) BNN X có Phân phối nhị thức âm với 2 tham số là r và p:
Thực hiện các TNNN độc lập có xs xuất hiện t/c S trong mỗi TNNN là
như nhau và bằng p cho đến khi xuất hiện t/c S r lần thì dừng.
S Phân phối hình học là pp nhị thức âm với r=1. Lưu ý:
*) X là số lần ko xh t/c S cho đến khi S xuất hiện r lần thì dừng. Hàm xác suất 𝑝 𝑟−1
𝑋(𝑢) = 𝑃(𝑋 = 𝑢) = 𝐶𝑢+𝑟−1𝑝𝑟(1 − 𝑝)𝑢; 𝑢 = 0; 1; 2; …
VD1: Thực hiện TNNN cho đến khi xuất hiện S 3 lần thì dừng.
Giả sử dừng lại ở lần thứ 7.
Gọi X là số lần ko xuất hiện S cho đến khi x/h S 3 lần thì dừng 𝑝 3−1 2
𝑋(4) = 𝑃(𝑋 = 4) = 𝐶4+3−1𝑝3(1 − 𝑝)4 = 𝐶6 𝑝3 4 (1 − 𝑝)
*) Y là số lần thực hiện TNNN cho đến khi S xuất hiện r lần thì dừng. Hàm xác suất 𝑝 𝑟−1 𝑢−𝑟 𝑢−𝑟 𝑢−𝑟
𝑌(𝑢) = 𝑃(𝑌 = 𝑢) = 𝐶𝑢−1𝑝𝑟(1 − 𝑝)
= 𝐶𝑢−1 𝑝𝑟(1 − 𝑝)
𝑢 = 𝑟; 𝑟 + 1; 𝑟 + 2; …
VD2: Thực hiện TNNN cho đến khi xuất hiện S 3 lần thì dừng.
Giả sử dừng lại ở lần thứ 7.
Gọi Y là số lần thực hiện TNNN cho đến khi xh S 3 lần thì dừng 𝑝 3−1 7−3 2
𝑌(7) = 𝑃(𝑌 = 7) = 𝐶7−1𝑝3(1 − 𝑝) = 𝐶6𝑝3(1 − 𝑝)4
4) Phân phối siêu bội Lấy ngẫu nhiên n phần tử từ N phần tử trong đó có M
phần tử có tính chất S. Gọi 𝑋 là số phần tử có tính chất S trong n phần tử
lấy ra. 𝑋 có phân phối siêu bội với 3 tham số n; M; N Hàm xác suất 𝐶𝑢𝐶𝑛−𝑢 𝑝 𝑀 𝑁−𝑀
𝑋(𝑢) = 𝑃(𝑋 = 𝑢) = 𝐶𝑛 𝑁 𝑀 𝑀 𝑀 𝑁 − 𝑛
𝐸(𝑋) = 𝑛 𝑁 ; 𝑉(𝑋) = 𝑛𝑁 (1 − 𝑁) 𝑁 − 1
5) Phân phối Poisson Phân phối nhị thức có n rất lớn và p rất nhỏ là phân
phối Poisson với tham số 𝜆 = 𝑛𝑝
Hàm xác suất của 𝑋 có phân phối Poisson với tham số 𝜆
𝑝𝑋(𝑢) = 𝑃(𝑋 = 𝑢) = 𝒆−𝜆𝜆𝒖;𝒖 = 𝟎, 𝟏,𝟐, … 𝒖!
𝐸(𝑋) = 𝑉(𝑋) = 𝜆
Bài tập: Một đồng xu không cân đối (hay đồng xu thiên vị) với xác suất xuất hiện
mặt có hình gấp 4 lần xác suất xuất hiện mặt không có hình.
1) Xác suất xuất hiện mặt có hình là bao nhiêu?
2) Tung một đồng xu này. X là số lần xuất hiện mặt có hình. X có phân phối gì?
3) Tung đồng xu cho đến khi xuất hiện mặt có hình 3 lần thì dừng. X là số lần
thực hiện TNNN. Hỏi X có phân phối gì?
4) Tung đồng xu này 20 lần. X là số lần xuất hiện mặt có hình. X có phân phối
gì? Trung bình của X bằng bao nhiêu?
Giải Bài tập: Một đồng xu không cân đối (hay đồng xu thiên vị) với xác suất xuất
hiện mặt có hình gấp 4 lần xác suất xuất hiện mặt không có hình.
1) Xác suất xuất hiện mặt có hình là bao nhiêu? 4/5=0,8
2) Tung một đồng xu này. X là số lần xuất hiện mặt có hình. X có phân phối
gì? X có pp Bernoulli với tham số 0,8.
3) Tung đồng xu cho đến khi xuất hiện mặt có hình 3 lần thì dừng. X là số lần
không xuất hiện mặt có hình.
Hỏi X có phân phối gì? X có pp nhị thức âm với r=3 và p=0,8.
4) Tung đồng xu này 20 lần. X là số lần xuất hiện mặt có hình. X có phân phối
gì? Trung bình của X bằng bao nhiêu? X có pp nhị thức với n=20 và p=0,8. E(X)=20.0,8=16. Bài t p áp d ậ ụng
Bài 1 Lấy ngẫu nhiên từng sản phẩm từ lô hàng có 3 sản phẩm loại I và 2 sản phẩm loại II
cho đến khi số sản phẩm loại I và loại II còn lại bằng nhau thì dừng. Gọi X là số sản phẩm
lấy ra. Tìm hàm xác suất của X, tính E(X) và V(X). Gợi ý:
B1: X/Đ TNNN Lấy ngẫu nhiên từng sản phẩm từ lô hàng có 3 sản phẩm loại I và 2 sản
phẩm loại II cho đến khi số sản phẩm loại I và loại II còn lại bằng nhau thì dừng
B2: Xác định các giá trị có thể có của X là 1; 3; 5
B3: Tính xs X nhận giá trị có thể có tương ứng Giải
Tập các giá trị có thể có của X là 𝑈𝑋 = {1, 3, 5} 3
𝑝𝑋(1) = 𝑃(𝑋 = 1) = 5 2.3.2 1
𝑝𝑋(3) = 𝑃(𝑋 = 3) = 5.4.3 = 5 2.1.3.2.1 + 2.3.1.2.1 1
𝑝𝑋(5) = 𝑃(𝑋 = 5) = 5! = 5 3 𝑘ℎ𝑖 𝑢 = 1 5
Hàm xác suất của X có dạng 𝑝 1 𝑋(𝑢) = 𝑘ℎ𝑖 𝑢 = 3 5 1 { 𝑘ℎ𝑖 𝑢 = 5 5 11 64
𝐸(𝑋) = 5 ;𝑉(𝑋) = 25
Bài 2 Có 10 lô hàng, mỗi lô chứa 8 sản phẩm loại 1 và 2 sản phẩm loại 2. Lấy ngẫu nhiên
từ mỗi lô 2 sản phẩm và gọi X là số sản phẩm loại 1 trong 20 sản phẩm lấy ra. Tính kỳ
vọng, phương sai của X và P(X = 1). Giải
Gọi 𝑋𝑖 là số sản phẩm loại 1 trong 2 sản phẩm lấy ra từ lô sản phẩm thứ i. i=1, 2, …, 10.
Hàm xác suất của 𝑋𝑖 có dạng 𝐶28 28 𝐶2 = 10 45 𝑘ℎ𝑖 𝑢 = 2 𝑝 2.8 16 𝑋 (𝑢) = 𝑖 𝐶2 = 10 45 𝑘ℎ𝑖 𝑢 = 1 1 1 {𝐶2 = 10 45 𝑘ℎ𝑖 𝑢 = 0 72 64 𝐸( 𝑋𝑖) = ( 45 ; 𝑉 𝑋𝑖) = 225
Gọi X là số sản phẩm loại 1 trong 20 sản phẩm lấy ra
𝑋 = 𝑋1 + 𝑋2 + ⋯ + 𝑋10 72
𝐸(𝑋) = 𝐸(𝑋1) + 𝐸(𝑋2) + ⋯ + 𝐸(𝑋10) = 10.45 = 16
Vì các 𝑋𝑖 độc lập nên 64 128
𝑉(𝑋) = 𝑉(𝑋1) + 𝑉(𝑋2) + ⋯ + 𝑉(𝑋10) = 10.225 = 45 16 29 9
𝑃(𝑋 = 1) = 𝐶110𝑝𝑋 (1)(1 − 𝑝 (1))9 = 10. = 𝑖 𝑋𝑖 45 . (45)
Bài 3 Một đồng xu thiên vị với xác suất xuất hiện mặt có hình gấp đôi mặt không có hình.
1) Tung đồng xu này 10 lần, tính xác suất số lần xuất hiện mặt có hình từ 3 đến 6 lần.
B1: Nhận diện TNNN: Tung đồng xu này 10 lần
B2: Nhận diện BNN xuất hiện trong đề bài
Gọi X là số lần xuất hiện mặt có hình khi tung đồng xu 10 lần.
X có phân phối nhị thức với n=10 và p=2/3 Hàm xác suất 𝑝 𝑢
𝑋(𝑢) = 𝑃(𝑋 = 𝑢) = 𝐶10(2/3)𝑢(1 − 2/3)10−𝑢; 𝑢 = 0; 1; 2; … ; 10
B3: xác suất số lần xuất hiện mặt có hình từ 3 đến 6 lần P(3<=X<=6)=∑6 6 𝑢
𝑢=3 𝑃(𝑋 = 𝑢)= ∑ 𝑢= 𝐶
3 10 (2/3)𝑢(1 − 2/3)10−𝑢
2) Tung đồng xu này cho đến khi xuất hiện mặt có hình thì dừng lại. Tính xác suất cần tung
5 lần thì dừng.
B1: Nhận diện TNNN: Tung đồng xu này cho đến khi xuất hiện mặt có hình thì dừng lại
B2: Nhận diện BNN xuất hiện trong đề bài
Gọi Y là số lần tung đồng xu cho đến khi xuất hiện mặt có hình thì dừng.
Y có phân phối hình học với p=2/3 hay nhị thức âm với r=1; p=2/3. Hàm xác suất của Y là 𝑝 𝑟−1 𝑢−𝑟
𝑌(𝑢) = 𝑃(𝑌 = 𝑢) = 𝐶𝑢−1𝑝𝑟(1 − 𝑝)
; 𝑢 = 𝑟; 𝑟 + 1; 𝑟 + 2 𝑝 𝑢−1
𝑌(𝑢) = 𝑃(𝑌 = 𝑢) = (2/3)(1 − 2/3) ; 𝑢 = 1; 2; 3; …
B3: xác suất cần tung 5 lần thì dừng.
P(Y=5) = (2/3)(1 − 2/3)5−1
3) Một đồng xu thiên vị với xác suất xuất hiện mặt có hình gấp đôi mặt không có hình.Tung
đồng xu này cho đến khi xuất hiện mặt có hình 3 lần thì dừng lại. Tính xác suất cần tung ít
nhất 5 lần thì dừng lại.
B1: Nhận diện TNNN: Tung đồng xu này cho đến khi xuất hiện mặt có hình 3 lần thì dừng lại
B2: Nhận diện BNN xuất hiện trong đề bài
Gọi T là số lần tung đồng xu cho đến khi xuất hiện mặt có hình 3 lần thì dừng
T có phân phối nhị thức âm với r=3 và p=2/3 Hàm xác suất của T là 𝑝 𝑟−1 𝑢−𝑟
𝑇(𝑢) = 𝑃(𝑇 = 𝑢) = 𝐶𝑢−1𝑝𝑟(1 − 𝑝)
; 𝑢 = 𝑟; 𝑟 + 1; 𝑟 + 2; … 2 3 2 𝑢−3 𝑝 2
𝑇(𝑢) = 𝑃(𝑇 = 𝑢) = 𝐶𝑢−1( ) (1 − ) ; 𝑢 = 3; 4; 5; …. 3 3
B3: xác suất cần tung ít nhất 5 lần thì dừng lại. 4 2 3 2 𝑢−3
𝑃(𝑇 ≥ 5) = 1 − 𝑃(𝑇 ≤ 4) = 1 − 𝑃(3 ≤ 𝑇 ≤ 4) = 1 − ∑ 𝐶 2 𝑢−1 (3) (1 − 3) 𝑢=3 4 2 3 1 𝑢−3 = 1 − ∑ 𝐶 2 𝑢−1 (3) ( 3) = 𝑢=3
Xác suất cần tung không quá 5 lần 5 2 3 2 𝑢−3 5 2 3 1 𝑢−3
𝑃(3 ≤ 𝑇 ≤ 5) = ∑ 𝐶 3−1 2 𝑢−1
(3) (1 − 3) = ∑𝐶𝑢−1 (3) (3) = 𝑢=3 𝑢=3
Giải Gọi p là xác suất xuất hiện mặt không có hình thì 2p là xác suất xuất hiện mặt có hình.
Vì đồng xu chỉ xuất mặt có hình hoặc không có hình nên theo tính chất hàm xác
suất ta có 3𝑝 = 1 suy ra 𝑝 = 1. Xác suất xh mặt có hình là 2/3. 3 Gợi ý:
B1: Xác định TNNN từ đó Nhận diện dạng phân phối xs của BNN x/h trong đề bài.
B2: Biểu diễn b/c cần tính xác suất qua BNN đã x/đ ở B1
B3: Áp dụng các CT XS và hàm xs của BNN để tín h
1) Gọi X là số lần xuất hiện mặt có hình khi tung đồng xu này. X có phân phối Bernoulli với tham số 𝑝0 = 2. 3
Hàm xác suất của X có dạng 2 𝑝 3 𝑘ℎ𝑖 𝑢 = 1
𝑋(𝑢) = 𝑃(𝑋 = 𝑢) = {1 3 𝑘ℎ𝑖 𝑢 = 0
2) Tung đồng xu này 10 lần, gọi Y là số lần xuất hiện mặt có hình
Y có phân phối nhị thức với n=10 và 𝑝0 = 2. 3
Hàm xác suất của biến ngẫu Y có dạng 2 𝑢 2 10−𝑢 𝑝 𝑢
𝑌(𝑢) = 𝑃(𝑌 = 𝑢) = 𝐶10( 3) (1 − 3)
Xác suất số lần xuất hiện mặt có hình từ 3 đến 6 𝟔 𝟔 2 𝑢 2 10−𝑢
𝑷(𝟑 ≤ 𝒀 ≤ 𝟔) = ∑ 𝑃(𝑌 = 𝑢) = ∑ 𝐶 𝑢 10 (3) (1 − 3) = 𝒖=𝟑 𝒖=𝟑
2) Tung đồng xu này cho đến khi xuất hiện mặt có hình thì dừng lại, gọi Z là số lần tung.
Z có phân phối hình học với tham số 𝑝0 = 2 3
Hàm xác suất của Z có dạng 2 2 𝑢−1
𝑝𝑍(𝑢) = 𝑃(𝑍 = 𝑢) = (3)(1 − 3)
Tính xác suất cần tung 5 lần thì dừng. 2 2 5−1 𝑃(𝑍 = 5) = (3)(1 − 3)
3) Tung đồng xu này cho đến khi xuất hiện mặt có hình 3 lần thì dừng lại, T là số lần tung.
T có phân phối nhị thức âm với tham số r=3 và 𝑝0 = 2. 3 3 𝑢−3
Hàm xác suất của T có dạng 𝑝 3−1
𝑇(𝑢) = 𝑃(𝑇 = 𝑢) = 𝐶𝑢−1(2 ) (1 − 2) 3 3
Xác suất cần tung ít nhất 5 lần thì dừng lại. 4 2 3 2 𝑢−3
𝑃(𝑇 ≥ 5) = 1 − 𝑃(𝑇 ≤ 4) = 1 − 𝑃(3 ≤ 𝑇 ≤ 4) = 1 − ∑ 𝐶 3−1 𝑢−1 (3) (1 − 3) 𝑢=3 4 2 3 𝑢−3 = 1 − ∑ 𝐶 2 1 𝑢−1 (3) (3) = 𝑢=3
Xác suất cần tung không quá 5 lần 5 2 3 2 𝑢−3 5 2 3 1 𝑢−3
𝑃(3 ≤ 𝑇 ≤ 5) = ∑ 𝐶 3−1 2 𝑢−1 ( (
3) (1 − 3) = ∑ 𝐶𝑢−1 3) (3) = 𝑢=3 𝑢=3
Bài 4 Thống kê cho thấy 60% khách hàng tới cửa hàng S mua bột giặt chọn loại bột giặt E
và số còn lại chọn loại bột giặt H. Trên kệ của cửa hàng lúc này còn 10 gói bột giặt E và 8
gói bột giặt H. Tính xác suất số bột giặt này đáp ứng được nhu cầu của 12 khách hàng mua bột giặt tiếp theo. Hướng dẫn:
B1: Xác định TNNN đề bài: Quan sát 12 khách hàng mua bột giặt
B2: Xác định BNN x/h trong giả thuyết
Gọi X là số khách hàng mua bột giặt E trong 12 khách hàng tiếp theo.
X có phân phối phân phối nhị thức với n=12 và p=0,6 Hàm xác suất của X là 𝑝 𝑢
𝑋(𝑢) = 𝑃(𝑋 = 𝑢) = 𝐶120,6𝑢(1 − 0,6)12−𝑢; 𝑢 = 0; 1; 2; … ; 12
B3: Biểu diễn biến cố đề bài yêu cầu theo giá trị của BNN đã x/đ ở bước 2 4 ≤ 𝑋 ≤ 10
B4: Tính xác suất số bột giặt này đáp ứng được nhu cầu của 12 khách hàng mua bột giặt tiếp theo 10 10
𝑃(4 ≤ 𝑋 ≤ 10) = ∑ 𝑃(𝑋 = 𝑢) = ∑ 𝐶 𝑢
12 0,6𝑢(1 − 0,6)12−𝑢= 𝑢=4 𝑢=4
Bài 5 Trong kho hàng có 1000 sp trong đó có 200 sp của nhà máy A. Lấy ngẫu nhiên 100 sp từ kho hàng.
1/ Tính xác suất trong 100 sản phẩm lấy ra có ít nhất 20 sản phẩm của nhà máy A.
2/ Trong 100 sản phẩm lấy ra trung bình có bao nhiêu sản phẩm của nhà máy A? Hướng dẫn:
B1: Xác định TNNN đề bài: Lấy ngẫu nhiên 100 sp từ kho hàng có 1000 sp.
B2: Xác định BNN x/h trong giả thuyết
Gọi X là số sản phẩm của nhà máy A trong 100 sản phẩm lấy ra
X có phân phối siêu bội với n= 100 ; M=200 ; N=1000 𝑢 𝐶100−𝑢
Hàm xác suất của X là 𝑝 800
𝑋(𝑢) = 𝑃(𝑋 = 𝑢) = 𝐶200𝐶100 1000
B3: Biểu diễn biến cố đề bài yêu cầu theo giá trị của BNN đã x/đ ở bước 2
Trong 100 sản phẩm lấy ra có ít nhất 20 sản phẩm của nhà máy A 20 ≤ 𝑋 ≤ 100 B4: Tính 100 1 𝐶00 𝑢 𝐶100−𝑢
𝑃(𝑋 ≥ 20) = ∑ 𝑃(𝑋 = 𝑢) = ∑ 200 800 = 𝐶100 𝑢=20 𝑢=20 1000
2/Trong 100 sản phẩm lấy ra trung bình có bao nhiêu sản phẩm của nhà máy A E(X)=n.M/N=20 (sản phẩm)
Bài 6: Số khách đến quầy dịch vụ S trong 5 phút là biến ngẫu nhiên có phân phối Poisson
với trung bình là 3. Tính xác suất trong 10 phút có ít nhất 5 khách đến quầy S biết rằng có
không quá 8 khách đến quầy S trong 10 phút. Giải
B1: X/đ TNNN: Quan sát số khách đến quầy dịch vụ S trong 10 phút
B2: X/đ BNN xuất hiện trong đề bài
Gọi X là số khách đến quầy dịch vụ S trong 5 phút 𝑋~𝑃(3)
Gọi Y là số khách đến quầy dịch vụ S trong 10 phút 𝑌~𝑃(6)
Hàm xác suất của Y là 𝑝𝑌(𝑢) = 𝑃(𝑌 = 𝑢) = 𝑒−6.6𝑢; 𝑢 = 0; 1; 2; … 𝑢!
B3: Biểu diễn biến cố cần tính qua BNN bước 2
Xác suất trong 10 phút có ít nhất 5 khách đến quầy S biết rằng có không quá 8 khách đến quầy S trong 10 phút l à 𝑃(5 ≤ 𝑌 ≤ 8) ∑ 8 8 𝑢=𝑝 ∑ 𝑒−6.6𝑢 1134 𝑃 (𝑌 ≥ 5 5 𝑌(𝑢) 𝑢=5 𝑢! 𝑌
⁄ ≤ 8) = 𝑃(𝑌 ≤ 8) = ∑8 = = 𝑢=0 𝑝𝑌(𝑢) ∑8 𝑒−6.6𝑢 1709 𝑢=0 𝑢!
Bài 7 Gieo đồng thời 10 con xúc xắc đồng chất.
1/ Tính xác suất có ít nhất 2 xúc sắc xuất hiện mặt có số chấm chia hết cho 3.
2/ Tính xác suất có không quá 3 xúc sắc xuất hiện mặt có số chấm chia hết cho 3.
3/ Tính xác suất để có ít nhất 2 xúc sắc xuất hiện mặt có số chấm chia hết cho 3 biết đã có
1 mặt chia hết cho 3 xuất hiện.
Bài 8 Một lô hàng chứa 10000 sản phẩm, trong đó có 8000 sản phẩm tốt và 2000 sản phẩm
xấu. Chọn ngẫu nhiên từ lô hàng ra 10 sản phẩm. Gọi X là số sản phẩm tốt trong 10 sản
phẩm được chọn. Tính kỳ vọng, phương sai của X và xác suất chọn được 7 sản phẩm tốt.
Bài 9 Số khách đến mua hàng tại một quầy hàng trong 1 phút là biến ngẫu nhiên có phân
phối Poisson với tham số λ=3. Tính xác suất trong khoảng thời gian từ 7 giờ 18 phút đến 7
giờ 20 phút có ít nhất 5 khách đến cửa hàng biết có nhiều nhất là 8 khách đến cửa hàng
trong khoảng thời gian này.
Bài 10 Số cuộc gọi đến trung tâm tư vấn H trong các khung giờ 8 đến 9 giờ, 9 đến 10 giờ
và 10 đến 11 giờ là các biến ngẫu nhiên có phân phối Poisson với các tham số lần lượt là
8; 9 và 9. Tính xác suất trong khoảng thời gian từ 8 đến 11 giờ có không quá 30 cuộc gọi
đến trung tâm tư vấn H.
Bài 11 Trong kho hàng có 30% sản phẩm là của công ty A, 45% sản phẩm là của công ty
B và 25% sản phẩm là của công ty C. Tỷ lệ sản phẩm của công ty A, B, C đạt chuẩn tương
ứng là 0,97; 0,94 và 0,91.
1) Tính tỷ lệ phế phẩm của kho hàng.
2) Lấy ngẫu nhiên một sản phẩm từ kho hàng này và thấy nó là sản phẩm đạt chuẩn.
Tính xác suất lấy được sản phẩm của công ty B.
3) Lấy ngẫu nhiên từ kho hàng ra 30 sản phẩm. Tính xác suất có không quá 3 sản phẩm
là phế phẩm trong số xác sản phẩm lấy ra.
4) Lấy ngẫu nhiên lần lượt từng sản phẩm từ kho hàng cho đến khi lấy được sản phẩm
là phế phẩm thì dừng. Tính xác suất không phải lấy ra quá 10 sản phẩm.
5) Lấy ngẫu nhiên lần lượt từng sản phẩm cho đến khi lấy được 3 phế phẩm thì dừng.
Xác suất phải lấy ra ít nhất 15 sản phẩm là bao nhiêu?
Bài tập áp dụng biến ngẫu nhiên liên tục
Bài 1 Thời gian cần thiết để sản xuất một sản phẩm M là biến ngẫu nhiên X (đơn vị : phút)
có hàm mật độ xác suất 𝑓(𝑥) = 𝐴 nếu 𝑥 ∈ [8 ; 10], f(x)= 0 nếu x∉ [8 ; 10]. 𝑥2 1/ Tìm A.
2/ Tính thời gian trung bình để sản xuất một sản phẩm M.
3/ Tính tỷ lệ sản phẩm có thời gian sản xuất nhỏ hơn thời gian trung bình (E(X)).
4/ Quan sát quá trình sản xuất một sản phẩm M thấy thời gian sản xuất mất ít nhất 8 phút
30 giây. Tính xác suất cần ít nhất 9 phút 30 giây để sản xuất sản phẩm này.
5/ Quan sát ngẫu nhiên thời gian sản xuất 30 sản phẩm này. Tính xác suất có từ 12 đến 25
sản phẩm có thời gian sản xuất ít nhất là 8 phút 30 giây. Giải 1/ ∞ 1𝐴0
∫ 𝑓(𝑥)𝑑𝑥= 1 ⟺ ∫ = 1 ⟺ 𝐴 = 40 −∞ 8 𝑥2 𝑑𝑥
2/ Thời gian trung bình để sản xuất một sản phẩm M ∞ 1040𝑥 5
𝐸(𝑋) = ∫ 𝑥𝑓(𝑥)𝑑𝑥 = ∫ 𝑑𝑥 = 40 (𝑙𝑛 𝑥2 4) ~8,925742053 −∞ 8
3/ Tỷ lệ sản phẩm có thời gian sản xuất nhỏ hơn thời gian trung bình 𝐸(𝑋) 40(𝑙𝑛54) 40
𝑃(𝑋 < 𝐸(𝑋)) = ∫ 𝑓(𝑥)𝑑𝑥 = ∫ = 𝑥2 𝑑𝑥 0,5185798823 −∞ 8
4/ Quan sát quá trình sản xuất một sản phẩm M thấy thời gian sản xuất mất ít nhất 8 phút
30 giây. Tính xác suất cần ít nhất 9 phút 30 giây để sản xuất sản phẩm này. 10 𝑃(𝑋 ≥ 9,5) ∫ 40 𝑃 (𝑋 ≥ 9,5 9,5 𝑥2 𝑑𝑥 17 𝑋
⁄ ≥ 8,5) = 𝑃(𝑋 ≥ 8,5) = = ∫10 40 57 8,5 𝑥2 𝑑𝑥
5/ Quan sát ngẫu nhiên thời gian sản xuất 30 sản phẩm này. Tính xác suất có từ 12 đến 25
sản phẩm có thời gian sản xuất ít nhất là 8 phút 30 giây.
B1: X/đ TNNN xuất hiện: Quan sát ngẫu nhiên thời gian sản xuất 30 sản phẩm
B2: X/đ BNN xuất hiện trong giả thuyết
Gọi Y là số sản phẩm có thời gian sản xuất ít nhất là 8 phút 30 giây trong 30 sản phẩm. 10
Y có phân phối nhị thức với n=30 và 𝑝 = 𝑃(𝑋 ≥ 8,5) = ∫ 40𝑑𝑥 8,5 = 12/17 𝑥2 Hàm xác suất 𝑝 𝑢 𝑢 30−𝑢
𝑌(𝑢) = 𝑃(𝑌 = 𝑢) = 𝐶30. (1 / 2 17) (1 − 1 / 2 17)
B3: Xác suất có từ 12 đến 25 sản phẩm có thời gian sản xuất ít nhất là 8 phút 30 giây.
𝑃(12 ≤ 𝑌 ≤ 25) = ∑ 25 𝑢=12𝑃(𝑌 = 𝑢) 25 = ∑ 𝐶 𝑢 𝑢 30 (1 / 2 17) (1 − 12/1 ) 7 30−𝑢= 0,948603208 𝑢=12
Bài 2 : Theo dõi thực tế trọng lượng của một loại sản phẩm được quy định là có trọng
lượng 2,5 gam, có thể coi trọng lượng này là một biến ngẫu nhiên X liên tục có hàm mật độ
𝑓(𝑥) = {𝑘(1 + 𝑥2); 2 ≤ 𝑥 ≤ 4
0; 𝑥 > 2 ℎ𝑎𝑦 𝑥 < 4 a/ Tính k b/ Tính E(X), V(X)
c/ Tính tỷ lệ sản phẩm này có trọng lượng lớn hơn trọng lương quy định.
d/ Tính xác suất chênh lệch giữa trọng lượng trong thực tế so với trọng lượng quy định
của loại sản phẩm này nhỏ hơn 0.25 gam. Giải ∞ 4 3
∫ 𝑓(𝑥)𝑑𝑥 = 1 ⟺ ∫ 𝑘(1 + 𝑥2)𝑑𝑥 = 1 ⟺ 𝑘 = −∞ 2 62 ∞ 4 3 99
𝐸(𝑋) = ∫ 𝑥𝑓(𝑥)𝑑𝑥= ∫ 𝑥. = −∞ 2 62 (1 + 𝑥2)𝑑𝑥 31 ∞ ∞ 2 4 3 99 2
𝑉(𝑋) = ∫ 𝑥2𝑓(𝑥)𝑑𝑥− (∫ 𝑥𝑓(𝑥)𝑑𝑥 ) = ∫ 𝑥2. − ( −∞ −∞ 2 62 (1 + 𝑥2)𝑑𝑥 31) = 0,3044745057
3/ Tỷ lệ sản phẩm này có trọng lượng lớn hơn trọng lượng quy định l à ∞ 34
𝑃(𝑋 > 2,5) = ∫ 𝑓(𝑥)𝑑𝑥 = ∫ (1 + 𝑥2)𝑑𝑥= 2,5 2,5 62
4/ Xác suất chênh lệch giữa trọng lượng trong thực tế so với trọng lượng quy định của loại
sản phẩm này nhỏ hơn 0,25 gam l à 2,75
𝑃(|𝑋 − 2,5| < 0,25 = 𝑃(2,5 − 0,25 < 𝑋 < 2,5 + 0,25) = ∫ 𝑓(𝑥)𝑑𝑥 2,25 2,735 = ∫ ( 2,25 62 1 + 𝑥2)𝑑𝑥 =
Bài 3 Một trạm xăng được cung cấp xăng 1 lần trong 1 tuần. Dung lượng kho chứa của
trạm là 10 m3. Dung lượng xăng được yêu cầu bán ra trong 1 tuần của trạm là biến ngẫu
nhiên X (đơn vị: m3) có hàm mật độ xác suất 𝑓(𝑥) = 𝑘(17 − 𝑥)4 nếu 𝑥 ∈ [0; 17], và
𝑓(𝑥) = 0 nếu 𝑥 ∉ [0; 17]. Tính k và xác suất hết xăng trong một tuần của trạm này. Giải:
Ta có ∫∞ 𝑓(𝑥)𝑑𝑥 17 4 −∞
= 1 Nên ∫ 𝑘(17 − 𝑥) 𝑑𝑥 0 = 1 Suy ra 𝑘 = 5 1419857
Xác suất hết xăng trong một tuần của trạm này là
P(X>10)= ∫∞ 𝑓(𝑥)𝑑𝑥 17 4 10 = ∫ 5 . (17 − 𝑥) 𝑑𝑥 10 = 0,01183710754 1419857
Phân loại biến ngẫu nhiên liên tục
Biến ngẫu nhiên X có phân phối đều trên [A; B]
X có hàm mật độ xác suất có dạng 1
𝑓(𝑥) = {𝐵 − 𝐴 𝑘ℎ𝑖 𝑥𝜖 [𝐴; 𝐵]
0 𝑘ℎ𝑖 𝑥 ∉ [𝐴; 𝐵]
E(X)= 𝐴+𝐵; V(X)= (𝐵−𝐴)2 2 12
X nhận giá trị thuộc [A; B] với khả năng là như nhau tại mọi
điểm và khả năng nhận giá trị ngoài [A; B] là bằng 0.
Bài 2 Thời gian cần thiết để sản xuất một sản phẩm loại M là biến ngẫu nhiên X (đơn vị :
phút) có hàm mật độ xác suất 𝑓(𝑥) = 𝑘 nếu 𝑥 ∈[8; B] , 𝑓(𝑥) = 0 nếu 𝑥 ∉ [8 ; 𝐵].
1/ Tìm 𝑘, 𝐵 và thời gian trung bình để sản xuất một sản phẩm loại này, biết xác suất để một
sản phẩm M có thời gian sản xuất không quá 9 phút là 0,25.
2/ Tính tỷ lệ sản phẩm có thời gian sản xuất ít hơn thời gian sản xuất trung bình. Giải
X là biến ngẫu nhiên có phân phối đều trên [8; B]
X có hàm mật độ xác suất có dạng 1
𝑓(𝑥) = {𝐵 − 8 𝑘ℎ𝑖 𝑥𝜖 [8;𝐵]
0 𝑘ℎ𝑖 𝑥 ∉ [8; 𝐵] nên ta có 𝑘 = 1 𝐵−8
Xác suất để một sản phẩm có thời gian sản xuất không quá 9 phút là 9 9 1
𝑃(𝑋 ≤ 9) = ∫ 𝑓(𝑥)𝑑𝑥 = ∫ 𝑘𝑑𝑥 = −∞ 8 4
Suy ra 𝑘 = 1 dẫn đến B=12 4
Vậy thời gian trung bình để sản xuất 1 sản phẩm loại M là 8 + 12
𝐸(𝑋) = 2 = 10 (𝑝ℎú𝑡).
2/ Tỷ lệ sản phẩm có thời gian sản xuất ít hơn thời gian sản xuất trung bình. 10 10 1
𝑃(𝑋 ≤ 10) = ∫ 𝑓(𝑥)𝑑𝑥 = ∫ 𝑘𝑑𝑥 = −∞ 8 2
3/ Quan sát ngẫu nhiên thời gian sản xuất của 50 sản phẩm này tính xác suất có ít nhất 20
sản phẩm có thời gian sản xuất ít hơn thời gian sản xuất trung bình.
Gọi Y là số sản phẩm có thời gian sản xuất ít hơn thời gian sản xuất trung bình trong 50 sản phẩm.
Y có phân phối nhị thức với n=50 và p=0,5 Hàm xác suất 𝑝 𝑢
𝑌(𝑢) = 𝑃(𝑌 = 𝑢) = 𝐶500,5𝑢(1 − 0,5)50−𝑢; 𝑢 = 0; 1; 2; … ; 50
Xác suất có ít nhất 20 sản phẩm có thời gian sản xuất ít hơn thời gian sản xuất trung bình. 50 50
𝑃(20 ≤ 𝑋 ≤ 50) = ∑ 𝑃(𝑌 = 𝑢) = ∑ 𝐶 𝑢 50 0,5𝑢(1 − 0,5)50−𝑢 𝑢=20 𝑢=20
4/ Quan sát ngẫu nhiên thời gian sản xuất của các sản phẩm cho đến khi gặp được 10 sản
phẩm có thời gian sản xuất không quá 9 phút thì dừng. Biết đã quan sát được 20 sản phẩm.
Tính xác suất người này quan sát không quá 45 sản phẩm.
Giải: Gọi T là số sản phẩm cần quan sát cho đến khi gặp được 10 sản phẩm có thời gian
sản xuất không quá 9 phút thì dừng
T có phân phối nhị thức âm với r=10 và p=0,25. Hàm xác suất 𝑝 9
𝑇(𝑢) = 𝑃(𝑇 = 𝑢) = 𝐶𝑢−10,2510(1 − 0,25)𝑢−10 𝑢 = 10; 11; 1 ; 2 …
Xác suất người này quan sát không quá 45 sản phẩm biết đã quan sát được 20 sản phẩm là 𝑃(20 ≤ 𝑇 ≤ 45) ∑45 𝑢=20 𝑃(𝑇 = 𝑢) 𝑃 (𝑇 ≤ 45 𝑃(20 ≤ 𝑇 ≤ 45) 𝑇 ⁄ ≥ 20) = 𝑃(𝑇 ≥ 20)
= 1 − 𝑃(𝑇 < 20) = 1 − ∑20𝑢=10 𝑃(𝑇 = 𝑢) ∑45 𝑢=20 𝐶9 0,2510(1 − 0,25)𝑢−10 = 𝑢−1 1 − ∑20
𝑢=10 𝐶9𝑢−1 0,2510(1 − 0,25)𝑢−10
Bài 3: Thời gian đi đến trường của sv H là bnn X (đơn vị: phút) có phân phối đều trên [10;
15]. Sinh viên H đi từ nhà lúc 6h48 phút. Tính xác s ấ
u t sv H đến trường trước 7h.
X có hàm mật độ có dạng 1
𝑓(𝑥) = { 5 𝑘ℎ𝑖 𝑥𝜖 [10; 15]
0 𝑘ℎ𝑖 𝑥 ∉ [10; 15]
Xác suất sv H đến trường trước 7h là 1 1 2
𝑃(𝑋 < 12) = 𝑃(10 ≤ 𝑋 < 12) = ∫ 𝑑𝑥 = 0,4 10 5
Biến ngẫu nhiên có phân phối mũ với tham số 𝝀
Hàm mật độ xác suất của BNN T có phân phối mũ với tham số 𝝀 > 𝟎
𝑓(𝑥; 𝝀) = {𝝀𝒆−𝝀𝒙 𝑘ℎ𝑖 𝑥 ≥ 0 0 𝑘ℎ𝑖 𝑥 < 0
Hàm phân phối xác suất (tích lũy)
𝐹(𝑥; 𝝀) = 𝑃(𝑇 ≤ 𝑥) = {𝟏 − 𝒆−𝝀𝒙 𝑘ℎ𝑖 𝑥 ≥ 0 0 𝑘ℎ𝑖 𝑥 < 0
Hàm phân phối xác suất bù
𝐹𝑐(𝑥; 𝝀) = 𝑃(𝑇 > 𝑥) = { 𝒆−𝝀𝒙 𝑘ℎ𝑖 𝑥 ≥ 0 1 𝑘ℎ𝑖 𝑥 < 0
Tính chất không nhớ 𝑃(𝑇 > 𝑠 + 𝑡⁄𝑇 > 𝑠)= 𝑃(𝑇 > 𝑡) Kỳ vọng, phương sai 1 1
𝐸(𝑇) = 𝝀; 𝑉(𝑇) = 𝝀2
Bài 3 Thời gian trả lời điện thoại (nghe máy) của một người ở vùng A khi nhân viên tư vấn
tiếp thị sản phẩm gọi đến là biến ngẫu nhiên X (đơn vị: phút) có phân phối mũ với 𝝀 = 𝟏, 𝟓
(1/phút). (hoặc là với thời gian nghe điện thoại trung bình là 2/3 phút=40 giây).
1/ Nhân viên tiếp thị gọi đến cho một người, tính xác suất người này nhận cuộc gọi ít nhất 2 phút.
2/ Nhân viên iếp thị gọi đến cho một người và người này đã nhận cuộc gọi được 1 phút.
Tính xác suất người này nhận cuộc gọi ít nhất 1 phút nữa.
3/ Tính xác suất thời gian nhận cuộc gọi khi nhân viên tiếp thị gọi đến của 1 người vùng A là từ 2 đến 3 phút?
4/ Tính xác suất trong 30 người mà nhân viên tiếp thị gọi đến có ít nhất 10 người có thời
gian nhận cuộc gọi ít nhất 2 phút.
5/ Nhân viên tiếp thị gọi lần lượt từng người cho đến khi được 5 người có thời gian nhận
cuộc gọi ít nhất 2 phút thì dừng. Tính xác suất nhân viên này không cần gọi quá 20 người. Giải
1/ Xác suất người này nhận cuộc gọi ít nhất 2 phút
𝑃(𝑋 ≥ 2) = 𝒆−𝝀.𝟐 = 𝒆−𝟑
2/ Nhân viên tiếp thị gọi đến cho một người và người này đã nhận cuộc gọi được 1 phút.
Xác suất người này nhận cuộc gọi ít nhất 1 phút nữa. 𝑃 (𝑋 ≥ 1 + 1 𝑋
⁄ ≥ 1) = 𝑃(𝑋 ≥ 1) = 𝒆−𝟏,𝟓
3/ Tính xác suất thời gian nhận cuộc gọi khi nhân viên tiếp thị gọi đến của 1 người vùng A là từ 2 đến 3 phút?
𝑃(2 ≤ 𝑋 ≤ 3) = 𝑃(𝑋 ≤ 3) − 𝑃(𝑋 ≤ 2) = 𝐹(3; 𝝀) − 𝐹(2; 𝝀)
= (𝟏 − 𝒆−𝟏,𝟓.𝟑) − (𝟏 − 𝒆−𝟏,𝟓.𝟐) = 𝑒−3 − 𝑒−4,5 2 3
4/ Tính xác suất trong 30 người mà nhân viên tiếp thị gọi đến có ít nhất 10 người có thời
gian nhận cuộc gọi ít nhất 2 phút.
B1: TNNN xuất hiện trong bài: Gọi tới cho 30 người vùng A. B2: Bnn xuất hiện:
Gọi Y là số người có thời gian nhận cuộc gọi ít nhất 2 phút trong 30 người
Y có phân phối nhị thức n=30 và p=P(X>=2)= 𝒆−𝟑
Hàm xác suất của Y có dạng
𝑃(𝑌 = 𝑢) = 𝐶𝑢30(𝒆−𝟑 −𝟑 −𝑢
)𝑢(1 − 𝒆 )30 ;𝑢 = 0,1,2, … ,30
B3: Xác suất trong 30 người mà nhân viên tiếp thị gọi đến có ít nhất 10 người có thời gian
nhận cuộc gọi ít nhất 2 phút là 30 30
𝑃(𝑌 ≥ 10) = ∑ 𝑃(𝑌 = 𝑢) = ∑ 𝐶 𝑢 30 (𝒆−𝟑 −𝟑 −𝑢 )𝑢(1 − 𝒆 )30 = 𝑢=10 𝑢=10
5/ Nhân viên tiếp thị gọi lần lượt từng người cho đến khi được 5 người có thời gian nhận
cuộc gọi ít nhất 2 phút thì dừng. Tính xác suất nhân viên này không cần gọi quá 20 người. B1: TNNN xuất hiện:
Nhân viên tiếp thị gọi lần lượt từng người cho đến khi được 5 người có thời gian
nhận cuộc gọi ít nhất 2 phút thì dừng B2: Bnn xuất hiện:
Gọi Z là số người ở vùng A cần gọi cho đến khi được 5 người có thời gian nhận
cuộc gọi ít nhất 2 phút thì dừng.
Z có phân phối nhị thức âm với r=5 và p=P(X>=2)= 𝒆−𝟑
Hàm xác suất của Z có dạng
𝑃(𝑍 = 𝑢) = 𝐶4𝑢−1(𝒆−𝟑 −𝟑
)5(1 − 𝒆 )𝑢−5;𝑢 = 5; 6;7; … .
B3: xác suất nhân viên này không cần gọi quá 20 người là 20 20
𝑃(𝑍 ≤ 20) = ∑ 𝑃(𝑍 = 𝑢) = ∑ 𝐶 4 𝑢−1
(𝒆−𝟑)5(1 − 𝒆−𝟑)𝑢−5= 𝑢=5 𝑢=5
Biến ngẫu nhiên X có phân phối chuẩn 𝑵(𝝁; 𝝈𝟐)
Hàm mật độ 𝒇(𝒙) = 𝟏 𝒆−(𝒙−𝝁)𝟐 𝟐𝝈𝟐 √𝟐𝝅 𝝈
𝑬(𝑿) = 𝝁; 𝑽(𝑿) = 𝝈𝟐
Phân phối chuẩn tắc 𝒁~𝑵(𝟎; 𝟏)
Hàm mật độ 𝒇(𝒙) = 𝟏 𝒆−𝒙𝟐𝟐 √𝟐𝝅
Hàm phân phối của phân phối chuẩn tắc ∅(𝒄) = 𝑷(𝒁 ≤ 𝒄) = ∫𝒄 𝟏 𝒆−𝒙𝟐𝟐𝒅𝒙 −∞ √𝟐𝝅
Bài 4 Cho Z là biến ngẫu nhiên có phân phối chuẩn tắc N(0; 1). Tính:
1. 𝑃(𝑍 < 1,54) 2. P(Z>1,65) 3. 𝑃(1,51 ≤ 𝑍 ≤ 2,23) 4. 𝑃(𝑍 ≥ 2/𝑍 ≤ 2,4)
𝑃(𝑍 < 1,54) = ∅(1,54)=
𝑃(𝑍 > 1,65) = 1 − 𝑃(𝑍 ≤ 1,65) = 1 − ∅(1,65)=
𝑃(1,51 ≤ 𝑍 ≤ 2,23) = ∅(2,23) − ∅(1,51)=
𝑃(𝑍 ≥ 2/𝑍 ≤ 2,4) = 𝑃(2≤𝑍≤2,4)= ∅(2,4)−∅(2)= 𝑃(𝑍≤2,4) ∅(2,4)
X ~ 𝑁(𝜇; 𝜎2) thì biến ngẫu nhiên chuẩn tắc hóa 𝒁 = 𝑿−𝝁 ~𝑵(𝟎; 𝟏) 𝝈 𝒃−𝝁 𝒃 − 𝝁 𝒂 − 𝝁 𝑷(𝒂 < 𝑿 < 𝒃) 𝒂 − 𝝁
= 𝑷 ( 𝝈 < 𝒁 < 𝝈 ) = ∅( 𝝈 )−∅( 𝝈 ) 𝒂 − 𝝁 𝑷(𝑿 < 𝒃) 𝒃 − 𝝁
= ∅ ( 𝝈 ); 𝑷(𝑿 > 𝒂) = 𝟏− ∅( 𝝈 )
Bài 4 Cho X là biến ngẫu nhiên có phân phối chuẩn với 𝜇 = 16; 𝜎 = 5. Tính:
1. 𝑃(𝑋 ≥ 24) 2. 𝑃(15 ≤ 𝑋 ≤ 22) 3. 𝑃(𝑋 ≥ 20/𝑋 ≤ 24)
𝑿~𝑵(𝟏𝟔; 𝟓𝟐) suy ra Biến ngẫu nhiên chuẩn tắc hóa 𝒁 = 𝑿−𝟏𝟔~𝑵(𝟎; 𝟏) 𝟓
1/ 𝑃(𝑋 ≥ 24) = 𝑃 (𝑍 ≥ 24−16) = 𝑃(𝑍 ≥ 1,6) = 1 − 𝑃(𝑍 < 1,6) = 1 − ∅(1,6) = 0,0548 5
2/ 𝑃(15 ≤ 𝑋 ≤ 22) = 𝑃 (15−16 ≤ 𝑍 ≤ 22−16 ) = 𝑃(−0,2 ≤ 𝑍 ≤ 1,2) = ∅(1,2) − 5 5 ∅(−0,2) = 0,46419 − − 20 24 )−∅(20 16
3/ 𝑃(𝑋 ≥ 20/𝑋 ≤ 24) = 𝑃( ≤𝑋≤ ) = ∅(24 16 5 5 ) = 0,1661 𝑃(𝑋≤24) 658908 ∅(24−16 5 )
Bài 5 Tuổi thọ sản phẩm của nhà máy M là biến ngẫu nhiên X (đơn vị: năm) có phân phối
chuẩn 𝑁(4; 1). Nhà máy M bảo hành sản phẩm trong 3 năm.
1/ Tính tỷ lệ sản phẩm phải bảo hành của nhà máy M.
2/ Quan sát ngẫu nhiên một sản phẩm M đã sử dụng được 1 năm, tính xác suất sản phẩm
này sử dụng được thêm 2 năm nữa.
3/ Quan sát ngẫu nhiên thời gian sử dụng của 10 sản phẩm M, thấy có ít nhất 1 sản phẩm
phải bảo hành. Tính xác suất có không quá 5 sản phẩm phải bảo hành trong số 10 sản phẩm này.
4/ Tính xác suất có không quá 1200 sản phẩm phải bảo hành trong số 10000 sản phẩm M này. 𝑿~𝑵(𝟒; 𝟏)
suy ra Biến ngẫu nhiên chuẩn tắc hóa 𝒁 = 𝑿−𝟒 ~𝑵(𝟎; 𝟏) 𝟏
1/ Tỷ lệ sản phẩm phải bảo hành của nhà máy M 3 − 4
𝑃(𝑋 < 3) = 𝑃 (𝑍 < 3 − 4
1 ) = ∅ ( 1 ) = ∅(−1) = 0,15866
2/ Quan sát ngẫu nhiên một sản phẩm M đã sử dụng được 1 năm, tính xác suất sản phẩm
này sử dụng được thêm 2 năm nữa. 𝑃(𝑋 ≥ 3) 1 − 𝑃 (𝑍 < 3 − 4 1 − ∅(−1) 𝑃 (𝑋 ≥ 3 1 ) 𝑋
⁄ ≥ 1) = 𝑃(𝑋 ≥ 1) = = 1 − 𝑃 (𝑍 < 1 − 4
1 − ∅(−3) = 0,8424773444 1 )
3/ Quan sát ngẫu nhiên thời gian sử dụng của 10 sản phẩm M, thấy có ít nhất 1 sản phẩm
phải bảo hành. Tính xác suất có không quá 5 sản phẩm phải bảo hành trong số 10 sản phẩm này.
B1: X/đ TNNN: Quan sát ngẫu nhiên thời gian sử dụng của 10 sản phẩm M B2: X/đ BNN
Gọi Y là số máy phải bảo hành trong 10 sp
Y có phân phối nhị thức với n=10; p=0,15866 Hàm xác suất của Y là 𝑝 𝑢 10−𝑢
𝑌(𝑢) = 𝑃(𝑌 = 𝑢) = 𝐶10. 0,15866𝑢(1 − 0,15866) ; 𝑢 = 0; 1; 2; … ; 10 B3: Tính xác suất 𝑃(1 ≤ 𝑌 ≤ 5)
∑𝟓𝒖=𝟏𝐶 𝑢 . 0,15866𝑢(1 − 0,15866)10−𝑢 𝑃 (𝑌 ≤ 5 10 𝑌
⁄ ≥ 1) = 𝑃(1 ≤ 𝑌 ≤ 10) = ∑𝟏𝟎 𝒖=𝟏 𝐶𝑢 10−𝑢 10. 0,15866𝑢(1 − 0,15866)
Định lý xấp xỉ phân phối
X có phân phối nhị thức với 2 tham số n và p với n rất lớn thì ta xem như
X có phân phối chuẩn với 𝝁 = 𝒏𝒑; 𝝈𝟐 = 𝒏𝒑(𝟏 − 𝒑)
4/ Tính xác suất có không quá 1500 sản phẩm phải bảo hành trong số 10000 sản phẩm M này.
B1: X/đ TNNN: Quan sát ngẫu nhiên thời gian sử dụng của 10000 sản phẩm M B2: X/đ BNN
Gọi T là số máy phải bảo hành trong 10000 s p
T có phân phối nhị thức với n=10000; p=0,15866 Hàm xác suất của T là 𝑝 𝑢 10000−𝑢
𝑇(𝑢) = 𝑃(𝑇 = 𝑢) = 𝐶10000. 0,1538𝑢(1 − 0,15866) ; 𝑢 = 0; 1; 2;… ; 10000