lOMoAR cPSD| 49519085
Đ¾ I H â C UEH
TR¯à NG KINH DOANH UEH
KHOA KINH DOANH QU Þ C T ¾
N T ¾ P TO`N D NH CHO KINH T
¾ V QU À N TR à Gi Á ng viŒn phā trÆch: Th Å y Nguy ß n Thanh V n
Ng°å i th ā c hi án: 1. Ngô Văn Đính 2. L°¢ng Thá L á c B nh Kh a – L ã p: K47 – CT2 lOMoAR cPSD| 49519085
CH¯¡NG 1: MA TRÀN VÀ ĐàNH THĄC I, KH`I NIàM V MA TRÀN: 1. ĐàNH NGH)A:
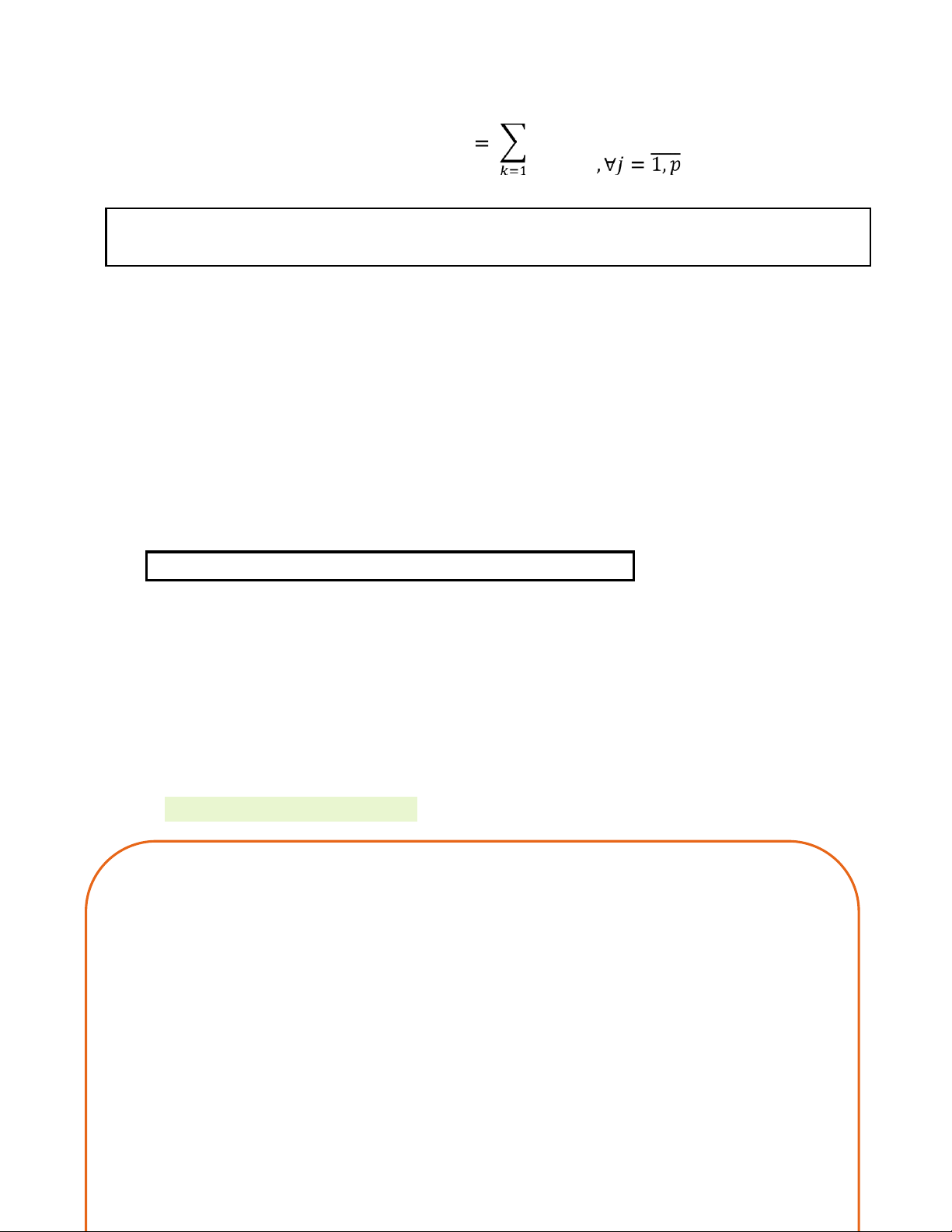
- Cho m v n l 2 sá nguyên d°¢ng. Mát ma trÁn A cÃp m x n l mát bÁng gồm m x n
sá °ÿc xÁp th nh m h ng v n cát, ngh*a là: ÿ11 ï ÿ1Ā
A = ( î ⋱ î ) ÿÿ1 ï ÿÿĀ
Ta k hiáu: A = [ÿÿĀ] Čßÿ ÿ = 1,2,3, & ă ; Ā = 1,2,3, & Ą.
2. C`C PH P TO`N VÂ MA TRÀN:
a, PhØp cộng hai ma trÁn: ý = (ÿÿĀ)(ÿ,Ā); þ = (ĀÿĀ)(ÿ,Ā)
ý + þ = (ÿÿĀ + ĀÿĀ )(ÿ,Ā) V dụ: ý = (1 2) ; þ = (4 5) 3 4 6 7 5 7
Ąÿ āó: ý + þ = ( ) 9 11
b, PhØp nh n ma trÁn vßi một sß thực: āý = (ā. ÿÿĀ)(ÿ,Ā)
V dụ: Cho ma trÁn: ý = (1 2) . ĄíĄ/ 2ý. 3 4 Ta c : 2ý = 2. (1 2) = (2 4) 3 4 6 8
c, PhØp nh n hai ma tr¿n: ý = (ÿÿĀ)(ÿ,Ā); þ = (ĀÿĀ)(Ā,㕝) Ā lOMoAR cPSD| 49519085
ý. þ = (āÿĀ)(ÿ,㕝)Čßÿ āÿĀ ÿÿā . ĀāĀ
Tips: Tổng d ng n y nh n cát kia t°¢ng ąng
ĐiÃu kián: Sá cát căa A bÅng sá h ng căa B.
V dụ: ÿ/ą ăÿ ĊĈậĄ ý = (1
2) ; þ = (1 4) . ĄíĄ/ ý. þ 3 4 0 1 1 2 1 4 1 6 ýþ = ýþ = ( ) . ( ) = ( ) 3 4 0 1 3 16
d, PhØp chuyển vá căa ma trÁn:ÿ/ą ăÿ ĊĈậĄ ý = (ÿÿĀ)(ÿ,Ā)
Ma trÁn chuyển vá căa A, k hiáu l ýĀ.
Chuyển h ng th nh cát, chuyển cát th nh h ng t°¢ng ąng. V dụ: ý = (1 2) => ýĀ = (1 3) 3 4 2 4
e, Lũy thừa ma trÁn:
ýĀ = ýĀ21. ý ( Ą Ăà ĉố Ċự Ą/ÿêĄ g 1) 3. MàT Sà LO¾I MA TRÀN:
a, Ma tr¿n h ng ( cột) l ma trÁn chß c mát h ng ( cát) b, Ma
tr¿n kh ng l ma trÁn m mọi phÅn tử Ãu bÅng kh ng c, Ma
tr¿n vu ng l ma trÁn c sá h ng bÅng sá cát ↔ ă = Ą
d, Ma tr¿n chØo l ma trÁn vu ng m mọi phÅn tử nÅm ngo i °ång chØo ch nh bÅng 0 lOMoAR cPSD| 49519085
e, Ma tr¿n ¡n vá l ma trÁn chØo m mọi phÅn tử trên °ång chØo ch nh bÅng 1 f,
Ma tr¿n tam giÆc l ma trÁn vu ng m mọi phÅn tử nÅm phía trên/ d°ãi °ång chØo ch nh Ãu bÅng 0.
g, Ma tr¿n b¿c thang l ma trÁn mà các hàng khác 0 Ãu ç trŒn cÆc h ng bÅng
kh ng, phÅn tử c¢ sç căa hàng d°ãi nÅm bŒn phÁi phÅn tử c¢ sç căa h ng trŒn. II. TÍNH ĐàNH THĄC:
1.QUY TÂC TÍNH ĐàNH THĄC:
a, Cấp 2: Ā = |ÿÿ1121 ÿÿ1222| = ÿ11. ÿ22 2 ÿ21ÿ12 V dụ: Ā = |1 2| = 1.4 2 2.3 = 22 3 4
b, Cấp 3: G a trá căa ánh thąc cÃp 3 bÅng tổng ¿i sá căa 2 nh m:
+, Nh m 1 (mang dấu +) t ch cÆc phÅn tử nÅm trên °ång chØo ch nh, t ch cÆc
phÅn tử song song vãi °ång chØo ch nh vãi phÅn tử ç góc ái dián.
+, Nh m 2 (mang dấu -): t ch căa cÆc phÅn tử nÅm trên °ång chØo phā, t ch cÆc
phÅn tử song song vãi °ång chØo phā vãi phÅn tử ç góc ái dián. 1 2 3 V dụ: ÿ = |4 3
2| = (1.3.1 + 2.2.2 + 4.6.3) 2 (3.3.2 + 2.6.1 + 2.4.1) = 45 2 6 1
2.T˝NH CHÂT CĂA ĐàNH THĄC:
+, Đánh thąc không thay ổi qua phØp chuyển vá ↔ [ý] = |ýĀ|
+, Đánh thąc ổi dấu nÁu ổi chß 2 d ng/ cát vãi nhau trong ánh thąc
+, C thể rœt thừa sá chung căa mát d ng/ cát ra ngoài ánh thąc
+, Đánh thąc c giÆ trá bằng 0 nÁu c 2 d ng tỷ lá nhau ho¿c 1 d ng/ cát 0.
+, Đánh thąc căa ma trÁn tam giÆc bÅng t ch cÆc phÅn tử nÅm trên °ång chØo ch nh. lOMoAR cPSD| 49519085
+, NÁu cÆc phẩn tử thą i nh n ā b 0 thì ánh thąc cũng nhân ā
3.MàT Sà PH¯¡NG PHÁP TÍNH ĐàNH THĄC:
*Ph°¡ng pháp 1- Bi¿n ổi: Døng cÆc t nh chÃt căa ánh thąc ể °a và ma trÁn tam
giÆc. [Cáng, trừ, nh n, chia cÆc cát / cÆc d ng phø hÿp] 3 2 1 1 1 2 1 3 1 2 1 3 2ý1+ý3 V dụ: ÿ = [2
1 2 0] →(ÿ1;ÿ4 ) 2 [0 1 2 2 ] →23 ý1+ý 4 2 [0 1 2 2 ] 3 1 2 1 1 1 2 3 0 21 1 0 4 2 0 3 3 2 0 4 0 24 23 25 1 2 1 3 1 2 22 3 1 2 22 3 2ý2+ý3
→4 ý2+ý 4 2 [0 1 2 2] (→2 ÿ4+ÿ 1) 2 [0 1 0 2] (→22 ý3+ý 4) 2 [0 1 0 2 ] 0 0 3 2 0 0 1 2 0 0 1 2 0 0 5 3 0 0 2 3 0 0 0 21 = 1
*Ph°¡ng pháp 2: Khai triển ánh thąc theo d ng/ cát:
+, Khai triển theo d ng i: ĀĀ = ÿÿ1. ýÿ1 + ÿÿ2. ýÿ2 + ï . + ÿÿĀ. ýÿĀ +,
Khai triển theo cột j: ĀĀ = ÿ1Ā. ý1Ā + ÿ2Ā. ý2Ā + ï . + ÿĀĀ. ýĀĀ
ĄĈąĄą đó: ýÿĀ = (21)ÿ+Ā. āÿĀ
āÿĀ Ăà đߥ/ Ċ/ÿā āąĄ ā¿Ć (Ą 2 1) āÿÿ Ā, āó đ±ÿā ĀằĄą āáā/:
Ďóÿ ĂòĄą ÿ, āßĊ Ā ĊĈąĄą Ā. V dụ: 2 23 4 1 lOMoAR cPSD| 49519085 4 22 3 2
þ = | | [Ąÿ Ċ/¿ď ĂòĄą 3 ā/ÿÿ Ċ/ÿă ĉố ĄêĄ Ąếċ ĂùĄą āáā/ 2 ā/ą Ą/¿ Ą/àĄą. ÿ Ā ā Ă 3 21 4 3
+, ÿ/ÿÿ ĊĈÿểĄ đߥ/ Ċ/ÿā Ċ/ăą ĂòĄą 3 Ċÿ āó: Ā = ÿ. ý31 + Ā. ý32 + ā. ý33 + Ă. ý34 23 4 1
+, ĄíĄ/ Ć/¿Ą Āù đ¿ÿ ĉố: ý31 = (21)3+1. [22
3 2] = 8 ; Ą±¡Ąą Ċự: 3 21 4
ý32 = 15; ý33 = 12; ý34 = 219 => Ā = 8ÿ + 15Ā + 12ā 2 19Ă III, MA TRÀN NGHàCH ĐÀO:
- Ma trÁn vu ng A cÃp n °ÿc gọi l khÁ nghách nÁu tồn t¿i ma trÁn B cÃp n sao cho: AB = B = 㕰Ā.
-B °ÿc gọi l ma tr¿n nghách Áo căa A. KH: ý21
A c ma trÁn nghách Áo khi v chß khi A kh ng suy bi¿n ↔ |ý| b ÿ 11 21 ý ý ï ýĀ1 1 ý 12 22 Ā2 21 = .ý∗ ý∗= ( ) | 㔴| î î ⋱ î ý ý ï ý .
ĄĈąĄą đó. ýÿĀ = (21)ÿ+Ā. āÿĀ ý1Ā ý2Ā ï ýĀĀ
A* °ÿc gọi l ma tr¿n phụ hợp căa A, KH: ý 1 2 21 0 V dụ: ÿ/ą ā = |2 1 0
3 | . Ąìă ă để ā ā/ôĄą ĉċď ĀÿếĄ. 3 ă 25 23 3 3 21 1 lOMoAR cPSD| 49519085 1 2 21 0 1 0
Để ā ā/ôĄą ĉċď ĀÿếĄ ↔ |ā| b 0 → ā = |2 3 ă 25 (ă 2 9) b 0 3 3 21 | = 4. 3 23 1 ↔ ă b 9 IV, H¾NG CĂA MA TRÀN:
- H¿ng căa A l cấp cao nhất căa cÆc ánh thąc con khÆc kh ng căa A.
- Để t m h¿ng căa mát ma trÁn A, ta døng cÆc phØp biÁn ổi s¢ cÃp °a ma trÁn vÃ
d¿ng bÁc thang v h¿ng căa A ch nh l sá h ng khÆc 0.
V dụ: T m h¿ng căa ma trÁn: 1 ý = 4 0 ý12ý2 1 4 0 3ý222ý3 1 4 0 (1 2 0 ) → (0 2 0 ) → (0 2 0 ) 0 3 18 0 3 18 0 0 236
=> ÿ¿Ąą āÿÿ ăÿ ĊĈậĄ ý = 3 Čì āó 3 /àĄą b 0 V, MàT Sà C NG THĄC:
D¿ng 1: ĐiÃu kián tồn t¿i ý21:
ý ā/¿ Ąą/ßā/ ↔ |ý| b 0
D¿ng 2: T m ma trÁn ý21: lOMoAR cPSD| 49519085
+, n = 1: NÁu A =(a), a ≠0 th ý21 = 1 㕎 +, n = 2: NÁu ý = (ÿ
Ā) → ý21 = 1 . ( Ă ā 2Ā Ă |㔴| 2ā ) +, n >3: Døng c ng thąc ÿ
D¿ng 3: T nh chÃt căa ý21 +, (ý21)21 = ý +, (ýĀ)21 = (ý21)Ā +, (ýþ)21 = þ21ý21
D¿ng 4: GiÁi ph°¢ng tr nh ma trÁn
+, AX = B ↔ ý21. ý. 㕋 = ý21. þ ↔ ÿ = ý2Ā. þ
+, XA=B ↔ X.A.ý21 = þ. ý21↔ X = B.ý2Ā
D¿ng 5: T m h¿ng căa ma trÁn
D¿ng 6: T nh chÃt căa phØp toÆn trŒn ma trÁn: A+B = B+A *(A+B)+C=A+(B+C) 0+A = A+ 0 = A * A+ (-A) = 0 m(A+B) = mA+Mb * (m+t)A =mA A(BC)=(AB).C * A(B+C) = A (AB)T = BTAT
CH¯¡NG 2: Hà PH¯¡NG TRÌNH
I, Hà PH¯¡NG TRÌNH TUYÀN T˝NH: lOMoAR cPSD| 49519085 1. KH`I NIàM:
- Há ph°¢ng trình tuyÁn t nh gồm m ph°¢ng trình, n ẩn sá l há c d¿ng:
ÿ11Ď1 + ÿ12Ď2 + ï + ÿ1ĀĎĀ = Ā1
{ ÿ21Ď1 + ÿ22Ď2 + ï + ÿ2ĀĎĀ = Ā2 (1) /ÿď ý. 㕋 = þ (2)
& & & & & & & & & & & & & & &
ÿÿ1Ď1 + ÿÿ2Ď2 + ï + ÿÿĀĎĀ = Āÿ ÿ11 ÿ12 & ÿ1Ā ÿ ÿ22 & ÿ2Ā
ý = ( &21 ÿÿ1 & &
. . . ) đ±ÿā ąßÿ Ăà ÿÿ āÿậĀ Ăệ Āố ÿÿĀ & ÿÿ2 ÿ11 ÿ12 & ÿ1Ā Ā1 ÿ ÿ22 & ÿ ý ̅ = ( & 2Ā Ā 21 2 & &
. . . | Ā3) đąĂ ÿÿ āÿậĀ Ăệ Āố ÿở ÿßĀā (Āổ ĀĂĀā) ÿÿĀ & ÿ Ā ÿ1 ÿÿ2 4
ĐiÃu kián há ph°¢ng trình có nghiám: ↔ r(A) = r(ý ̅)
N¿u r(A) = r(ý) = n: Há c nghiám duy nhÃt.
N¿u r(A) < n: Há c v sá nghiám phā thuác v o (n-r) tham sá.
Để cùng 1 lúc tìm °ÿc h¿ng A v ý ̅ ta sử dāng cÆc phØp biÁn ổi s¢ cÃp theo d ng trŒn ma trÁn mç ráng ý ̅ 2Ď1 + 3Ď2 + Ď3 2 Ď4 = 1 V dụ: 3Ď {
1 + Ď2 2 2Ď3 + Ď4 = 2 Tìm m ể há ph°¢ng trình sau có nghiám: Ď1 2 2Ď2 + Ď3 + 2Ď4 = 1 4Ď1 2 Ď2 2 Ď3 + 3Ď4 = ă 2 3 1 21 1 1 22 1 2 1 ý ̅ = (3 1 22 1 |2 ) (→ý1,ý3 ) (3 1 22 1 |2 ) →23 ý1+ý 2 1 22 1 2 1 2 3 1 21 1 4 21 21 3 ă 4 21 21 3 ă 1 22 1 2 1 1 22 1 2 1 lOMoAR cPSD| 49519085 0 7 25 25 21 0 7 25 25 21 ( | ) → ( | ) 0 7 21 25 21 0 0 4 0 0 0 7 25 25 ă 2 4 0 0 0 0 ă 2 3
*ÿệ āó Ąą/ÿệă ↔ Ĉ(ý) = Ĉ(ý ̅) = 3 ↔ ă 2 3 = 0 ↔ ă = 3
2. PH¯¡NG PHÁP GIÀI Hà PH¯¡NG TRÌNH TUYÀN T˝NH:
2.1 Ph°¡ng pháp ma tr¿n:
Cho há ph°¢ng trình tuyÁn t nh AX = B, vãi A l ma trÁn vu ng cÃp n khÁ nghách:
Ta có: AX = B ↔ X = ý21. þ
2.2: Ph°¡ng pháp Cramer: *ĐiÃu kián:
Ā = |A| b 0 → ÿệ āó Ąą/ÿệă Ăċď Ą/¿Ċ:
Ď1 = ĀĀ1 ; Ď2 = ĀĀ2 ; & ; ĎĀ = ĀĀ㕗
NÁu r(A) < r(ý ̅) : Há v nghiám
NÁu r(A) = r(ý ̅) = n: Há c nghiám duy nhÃt.
NÁu r(A) = r(ý ̅) = k < n: Há c v sá nghiám. Ď1 2 Ď2 + Ď3 = 6
V dụ: GiÁi há pt sau: {2Ď1 + Ď2 + Ď3 = 3 Ď1 + Ď2 + 2Ď3 = 5 1 21 1 → ý = |2 1
1| = 5 b 0 => ÿệ āó Ąą/ÿệă Ăċď Ą/¿Ċ. 1 1 2 6 21 1 1 6 1 1 21 6 Ā1 = |3 1 1| = 5 ; Ā2 = |2 3 1| = 210; Ā3 = |2 1 3| = 15 5 1 2 1 5 2 1 1 5 Ā1 Ď1 = = 1 Ā lOMoAR cPSD| 49519085 Ā Ā Ā3 { Ď3 = Ā = 3
2.3 Ph°¡ng pháp Gauss:
Đ°a ma trÁn mç ráng ý ̅ và d¿ng bÁc thang bçi PhØp biÁn ổi s¢ cÃp trŒn d ng.
ViÁt l¿i há ph°¢ng trình và giÁi ng°ÿc từ d ng cuái cøng lŒn trŒn.
V dụ: GiÁi v bián luÁn ph°¢ng trình bÅng ph°¢ng pháp Gauss theo tham sá m: ăĎ + ď + Đ = 1 { Ď + ăď + Đ = ă Ď + ď + ăĐ = ă2
GiÁi: Døng cÆc phØp biÁn ổi Gauss trŒn ma trÁn há sá mç ráng. ý ̅ = (ă1
ă1 11| ă1 ) →(ý2,ý1 ) (ă1 ă111| ă1 ) →2 ÿý1+ ýý12ý2 2 (10 1 2ăă2 1 21 ă|1 2ăă2 ) 1 1 ă ă2 1 1 ă ă2 0 1 2 ă ă 2 1 ă2 2 ă
ý2→ 2ý2ý2↔ý3 1 ă 1 ă 2) ý3→ý3+→ (ÿ+1 )ý2 (10 ăă21 121ă | ă2ăă 2 ) → (0 ă21 12ă|ă2ă 0 12ă2 12ă 12ă2 0 0 (12ă)(ă+2)(12ă2)(12ă) *Biện lu¿n: ÿ+1 Ď = 2 ÿ+2 1
m ≠1, m≠-2: há c nghiám duy nhÃt ď = ÿ+2 2 { ÿ+2 lOMoAR cPSD| 49519085 1 1 1 1 m= 1: ta c ý ̅ = (0 0
0|0) → r(A) = r(ý ̅) =1 ≠ sá ẩn nŒn há c v sá nghiám v 0 0 0 0 Đ = (ÿ+1)
nghiám tổng quÆt X =(1 2 ď 2 Đ; ď; Đ) 0 22 1 22 m= -2: ta c ý ̅ = (0 23
3|26) → Ĉ(ý) = 2 b Ĉ(ý ̅) = 3 ĄêĄ /ệ Čô Ąą/ÿệă. 0 0 0 3
Chœ : Trong quÆ tr nh thāc hián b°ãc 1, nÁu:
• C 2 d ng tß lá thì xóa i 1 dòng
• C d ng n o bÅng0 thì xóa i dòng ó
• C 1 d ng d¿ng (0&0 |b) b≠ 0 → Hà V NGHIàM.
II. Hà PH¯¡NG TRÌNH TUYÀN T˝NH THUÄN NHÂT: 1. ĐàNH NGH)A:
ÿ11Ď1 + ÿ12Ď2 + ï + ÿ1ĀĎĀ = 0
{ ÿ21Ď1 + ÿ22Ď2 + ï + ÿ2ĀĎĀ = 0 (1)
& & & & & & & & & & & & & & &
ÿÿ1Ď1 + ÿÿ2Ď2 + ï + ÿÿĀĎĀ = 0 *NhÁn xØt:
• Há ph°¢ng trình tuyÁn t nh thuÅn nhÃt lu n c nghiám (0,0,0&0)
• Há muán c nghiám khác (0,0..,0) thì r(A) < n, khi ó há vô ánh, nghiám tổng
quÆt phā thuác v o (n –r) tham sá. 2. Hà NGHIàM C¡ BÀN:
- Đánh nghĩa: XØt (1 )c r (A) < n lOMoAR cPSD| 49519085
- CÆch t m hệ nghiệm c¡ bÁn: NÁu há pt c v sá nghiám th c nhiÃu cÆch chọn sá
ẩn ch nh v ẩn phā. Do ó, có nhiÃu nghiám c¢ bÁn t°¢ng ąng vãi mßi cÆch chọn
ẩn ch nh v ẩn phā. Cā thể nh°: NÁu há pt thuÅn nhÃt c n ẩn sá v h¿ng l r th c ÿ 㕟 Ā
cÆch chọn ẩn ch nh v c (Ą 2 Ĉ)ÿ 㕟 Ā nghiám c¢ bÁn. Ď 2 2ď + 3Đ = 0
V dụ: Cho há ph°¢ng trình: {2Ď 2 4ď + 7Đ = 0 . Ąìă /ệ Ąą/ÿệă ā¡ Ā¿Ą āÿÿ /ệ 2Ď + 2ď 2 Đ = 0 1 22 3 0 2ý12ý2 1 22 3 0 2ý2+ý3 1 22 3 0 ̅ = ( 2 24 7 |0) →ý1+ý3 (0 0 21|0) → (0 0 21|0) ý 21 2 21 0 0 0 2 0 0 0 0 0
Ta có: r(A) = 2 → Há t°ng °¢ng {Ď 2 2ď + 3Đ = 0 ↔ {Ď + 3Đ = 2ď ↔ {Ď = 2ď 2Đ = 0 Đ = 0 Đ = 0
Há vô ánh, phā thuác 1 tham sá, nghiám tổng quÆt (2y, y, 0) . Há nghiám c¢ bÁn (2,1,0) III, MàT V
I ĄNG DĀNG TRONG PH´N T˝CH KINH TÀ: 1. M
H NH C´N BÄNG THà TR¯äNG:
- Để tìm iểm c n bÅng thá tr°ång, ta giÁi há ph°¢ng trình tuyÁn t nh āÿÿ = āĀÿ
{ā1 =& & &āÿ1 2 āĀ1 (1) hay {2ÿÿ1121. Ā. Ā1122 ÿ ÿ1222. Ā. Ā22++ï 2 ÿï 2 ÿ12ĀĀ. Ā. ĀĀĀ==ĀĀ12 (2) & . āĀ = āÿĀ 2 āĀĀ
ÿĀ1. Ā1 2 ÿĀ2. Ā2 + ï 2 ÿĀĀ. ĀĀ = ĀĀ
- Để t m giÆ của cÆc lo¿i h ng h a t¿i iểm c n bÅng thá tr°ång, ta phÁi giÁi há
ph°¢ng tr nh tuyÁn t nh (2).
- Låi giÁi căa (2) có ý nghĩa kinh t¿ khi cÆc th nh phÅn căa nghiám phÁi d°¢ng
và khi thay nhÿng giÆ trá ó vào các hàm cung và cÅu, giÆ trá các hàm ó cũng phÁi d°¢ng.
K hiáu căa ma trÁn há (2): lOMoAR cPSD| 49519085 ÿ11 2ÿ12 Ā 2ÿ1Ā Ā1 Ā1 2ÿ ÿ22 ā Ā 2ÿ ý = ( 2Ā Ā2 ; þ = (Ā2) 21 ā 2ÿ ÿ Ā2 ) ; Ā = ( ) 2ÿ Ā Ā1 ā ā ā ÿĀĀ ĀĀ ĀĀ
(2) ↔ A.P = B ( 2’) V dụ: Låi giÁi: ā1 = āÿ1 2 āĀ11 = 0 24 Ā1 2 3Ā2 2 Ā3 = 175
{ ā2 = āÿ2 2 āĀ2 = 0 ↔ {23Ā1 + 20Ā2 2 2 Ā3 = 230 (∗) ā3 = āÿ3 2 āĀ3 = 0 2Ā1 2 4Ā2 + 15Ā3 = 230
GiÁi há ph°¢ng trình (*) bÅng ph°¢ng pháp Cramer, ta có: 24 23 21 Ā=|23 20 22|=6835 b0 21 24 15 175 23 21 24 175 21 24 23 175
Ā1 =|230 20 22|=68350 ; Ā2 =|23 230 22|=102525; Ā3 =|23 20 230|=136700 230 24 230 21 230 15 21 24 230 VÁy nghiám căa há l : Ā1
Ā1 = Ā = 10 → āĀ1 = 100 Ā2 Ā2 = = 15 → ā
{ Ā3 = ĀĀĀ3 = 20 → āĀ3Ā2 == 145155 → Do ó iểm c n bÅng thá tr°ång l (10;15;20) 2. M
H NH INPUT – OUTPUT Mæ LEONTIEF: lOMoAR cPSD| 49519085
- M h nh: “Xác ịnh ầu ra của mỗi ng nh trong n ng nh sao cho vừa ủ ể thỏa mªn to n
bộ nhu cầu của cả nền kinh tế ó ( kể cÁ dā trÿ v xuÃt khẩu)
- K hiáu ÿÿĀ l giÆ trá căa l°ÿng nguyŒn liáu m ng nh j nhÁn °ÿc từ ngành i ể sÁn
xuÃt ra mát l°ÿng sÁn phẩm c giÆ trá mát ¢n vá tiÃn. ÿ11 ÿ12 ÿ ÿ1Ā
Ma trÁn ý=(ÿ21 ÿ22 ÿ ÿ2Ā)đ±ÿā ąßÿ Ăà ăÿ ĊĈậĄ /ệ ĉố đ¿ċ Čàą /ÿď ăÿ ĊĈậĄ /ệ ĉố āỹ Ċ/ċậĊ ā ā ÿ ā ÿĀ1 ÿĀ2 ÿ ÿĀĀ
X = (Ď1; Ď2; Ď3) Ăà ĊổĄą ĉ¿Ą ñÿĄą ( đ¿ċ Ĉÿ)āÿÿ āáā ĄąàĄ/.
Y = (ď1; ď2; ď3 ) Ăà ĊổĄą ĄąċďêĄ Ăÿệċ ( đ¿ċ Čàą)āÿÿ Āÿ ĄąàĄ/.
Ta c há ph°¢ng trình tuyÁn t nh: A.X = Y
+, Gọi yŒu cÅu cuái cùng cho Åu ra căa ng nh i l :
Khi ó, ta có há ph°¢ng trình: (㕰 Ā 2 ý). ÿ = 㕫 ↔ X = (㕰 Ā 2 ý) 2Ā .D
(1 2 ÿ11)Ď1 2 ÿ12Ď2 2 ï 2 ÿ1ĀĎĀ = Ă1
{2ÿ21Ď1 + (1 2 ÿ22)Ď2 2 ï 2 ÿ2ĀĎĀ = Ă2 &
2ÿĀ1Ď1 2 ÿĀ2Ď2 2 ï + (1 2 ÿĀĀ)ĎĀ = ĂĀ
V dụ: XØt m h nh Input – Output Mç Leontief, gồm ba ng nh vãi ma trÁn há sá 0,1 0,3 0,2 Åu v o l : ý = (0,4 0,2 0,1) 0,2 0,3 0,3
a, T m giÆ trá sÁn l°ÿng căa ba ng nh, biÁt rÅng nhu cÅu căa ng nh mç ái vãi ba ng nh l (75,90,81).
b, T m giÆ trá sÁn l°ÿng căa ba ng nh vãi iÃu kián bổ sung: do cÁi tiÁn kỹ thuÁt ç ng
nh 1 tiÁt kiám °ÿc 25% nguyŒn liáu căa ng nh 2, c n nhu cÅu cuái cøng căa ng nh mç
ái vãi ba ng nh l v¿n l (75,90,81). lOMoAR cPSD| 49519085
c, GiÁ sử nhu cÅu cuái cøng căa ng nh mç ái vãi ba ng nh lÅn l°ÿt l Ă1, Ă2, Ă3. NÁu Ă1
tăng 2 ¢n vá, Ă2 giÁm 1, Ă3 giÁm 1 th giÆ trá sÁn l°ÿng căa ba ngành thay ổi nh° thÁ n o? Låi giÁi:
a, Gọi X l vecto biểu thá giÆ trá sÁn l°ÿng căa ba ng nh, ta c : 0,9 20,3 20,2 Ď1 75
(Ā3 2 ý). 㕋 = Ā ↔ (20,4 0,8 20,1) . (Ď2) = (90) (∗) 20,2 20,3 0,7 Ď3 81
GiÁi há (*) bÅng ph°¢ng pháp Cramer, ta tìm °ÿc giÆ trá sÁn l°ÿng căa ba ng nh l :
(Ď1; Ď2; Ď3) = (240, 270, 300)
b, Do cÁi tiÁn kỹ thuÁt ng nh 1 nŒn nguyŒn liáu ng nh thą 2 cøng cÃp cho ngành 1
°ÿc giÁm 25%. Nh° vÁy, lúc Åu ch°a cÁi tiÁn ÿ21 = 0,4 sau khi cÁi tiÁn kỹ thuÁt th ÿ21 = 0,3.
Ta c ma trÁn cÆc há sá Åu v o mãi nh° sau ( sau khi ã cÁi tiÁn kỹ thuÁt) 0,1 0,3 0,2 0,9 20,3 20,2 Ď1 75 ý = (0,3 0,2
0,1) . Ąÿ āó: (Ā3 2 ý). 㕋 = Ā ↔ (20,3 0,8 20,1) . (Ď2) = (90) (∗∗) 0,2 0,3 0,3 20,2 20,3 0,7 Ď3 81
GiÁi há (**) bÅng ph°¢ng pháp Cramer, ta tìm °ÿc giÆ trá sÁn l°ÿng căa ba ng nh l : Ď1 = 221,899 {Ď2 = 230,477 Ď3 = 277,877 &Ď1
c, Ta gọi: Sā thay ổi căa ba ngành là &X = (&Ď2) &Ď3 &Ă1 2
Sā thay ổi căa nhu cÅu cuái cøng căa ng nh mç là: &D =(&Ă2) = (21)
Thì &X = (ĀĀ 2 ý)21. &D = &Ă3 21 lOMoAR cPSD| 49519085 0,53 0,27 0,19 2 1,676
. (0,23 0,59 0,15) . (21) = (20,782) 0,25 0,33 0,63 21 21,284
CH¯¡NG 3: HÀM MàT BIÀN – GIâI H¾N V LI˚N TĀC I – GIâI H¾N:
1. ĐIÂU KIàN CÄN VÀ ĐĂ:
- Để h m sá lim Ą(Ď) Ăà: :
lim Ą(Ď) = lim Ą(Ď) ý → ý → ý0 ý0+ ý → ý02 - Ta xØt 2 b i toÆn sau:
*B i toÆn 1: ÿ/ą Ą(Ď) = |Ď| .ĄíĄ/ Ăÿă Ą(Ď) ? ý → ý0 Ta c : lim Ą(Ď) = lim Ď =0 ; lim Ą(Ď) = lim 2Ď = 0 ý → ý0+
ý → ý0+ ý → ý02 ý → ý02 → lim Ą(Ď) = lim Ą(Ď) = lim Ą(Ď) = 0 ý → ý0+ ý → ý02 ý → ý0
*B i toÆn 2: Cho h m số Ą(Ď)=
. T nh Ăÿă Ą(Ď) 1+þ㕥ý → ý0 Ta c : lim Ą(Ď) = lim
1 1 = 0 (ÿ/ÿ Ď → 0+Ăą đó:
ý → ý0+ ý → ý0+ 1+þ㕥 ý lim0 Ą(Ď) = lim 1 0 ý1 2Ăą đó: Ď → 0) lOMoAR cPSD| 49519085 = 1 (ÿ/ÿ Ď → 0 ý → ý 2 ý → ý 2 1 + ă
VÁy: lim Ą(Ď) b lim Ą(Ď) → lim Ą(Ď) ā/ôĄą āó ąÿßÿ /¿Ą. ý → ý0+ ý → ý02 ý → ý0 2. GIâI H¾N Đ¾C BIàT: 3. QUY TÂC L’HOPITAL: lOMoAR cPSD| 49519085
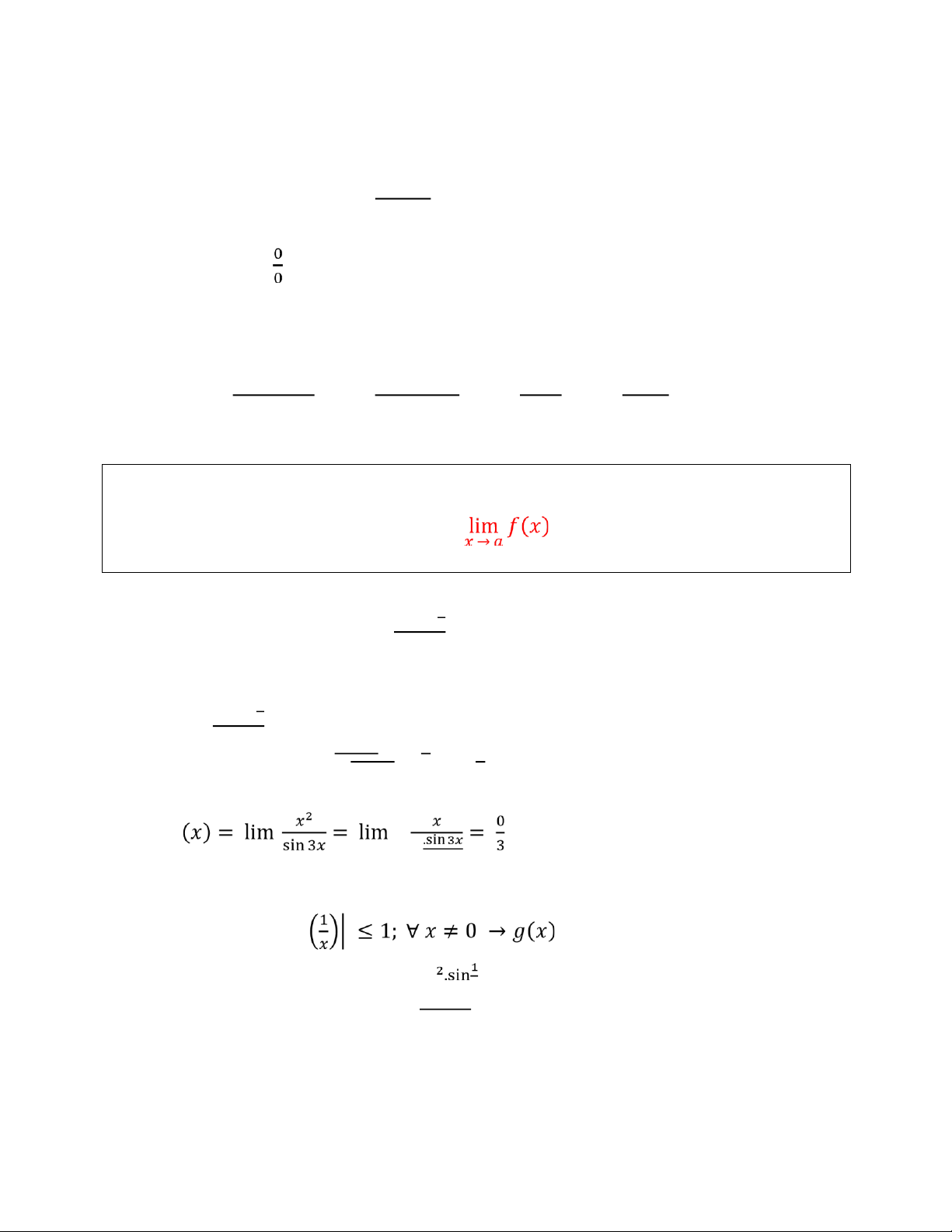
*B i toÆn 3: ĄíĄ/: lim 2ý3 ý → 0 ý2sin ý Thay x =0 v o ta c d¿ng
`p dāng L’Hopital 3 lÅn ta c : 2Ď3 6Ď2 12Ď 12 lim = lim = lim = lim = 12 ý → 0
Ď 2 sin Ď ý → 0 1 2 cos Ď ý → 0 ĉÿĄĎ ý → 0 cos Ď
Mánh Ã: ą(Ď) ≤ Ą(Ď) ≤ /(Ď)∀x.
V lim ą(Ď) = lim /(Ď) =Ā . Khi ó = Ā ý → 㕎 ý → 㕎 ý2.sin1
*B i toÆn 4: ĄíĄ/ lim㕥 ý → 0 sin 3ý ý2.sin㕥1 ý2 1 ý2 1 Ta c : lim = lim . sin = lim
. lim sin ý → 0 sin 3ý ý → 0 sin 3ý ý ý → 0 sin 3ý ý → 0 ý Ta c : Ą = 0 ý → 0 ý → 0 3. 3㕥 Ta l¿i c : ą(Ď) = |ăÿĄ Ăà /àă Āß ā/¿Ą. ý
VÁy Áy lim Ą(Ď).ą(Ď) = 0 ↔ lim 㕥 = 0 ý→0 ý → 0 sin 3ý lOMoAR cPSD| 49519085 II. T˝NH LI˚N TĀC: 1.ĐàNH NGH)A:
- H m sá f °ÿc gọi l liŒn tục tại Ď Ą(Ď) = Ą(Ď0) 0 Ąếċ lim ý → ý0
- Ą(Ď02) = lim 2 Ą(Ď) = Ą(Ď0) : f liŒn tục trÆi t¿i iểm Ď0 ý → ý0
- Ą(Ď0+) = lim + Ą(Ď) = Ą(Ď0) : f liŒn tục phải t¿i iểm Ď0 ý → ý0
- H m sá f °ÿc gọi l liŒn tục trong (a,b) khi f liŒn tāc t¿i mọi x ∈ (a,b)
- H m sá f °ÿc gọi l liŒn tục trŒn [a,b] khi f liŒn tāc trong (a,b), liŒn tāc bŒn phÁi a, liŒn tāc bŒn trÆi b.
- NÁu f kh ng liŒn tục tÁi iểm Ď0 th Ď0 °ÿc gọi l iểm gián oạn căa f. 2. ĐàNH L˝:
a, Điều kiện cần và ủ ể h m f liŒn tāc t¿i Ď0: Ą(Ď0+) = Ą(Ď02) = Ą(Ď0) b,
NÁu h m f v h m g liŒn tāc t¿i Ď0 th cÆc h m f– g; f.g ; Āÿ (ą(Ď0) b 0) cũng liŒn tāc t¿i Ď0.
c, NÁu h m f liŒn tāc t¿i Ď0 v g liŒn tāc t¿i ď0=Ą(Ď0) thì hàm g cũng liên tāc t¿i Ď0
*Đặc biệt: CÆc h m sá s¢ cÃp s¿ liŒn tāc trŒn khoÁng mç mà nó xác ánh. 3.C`C T˝NH CHÂT CĂA H M LI˚N TĀC:
*Cho h m f liŒn tāc trên o¿n [a,b], ta c :
a, H m f GTLN v GTNN trŒn [a,b]