Ôn tập xác suất thống kê ứng dụng – Bộ môn Xác suất thống kê | Trường đại học sư phạm kỹ thuật TP. Hồ Chí Minh

Lê Thị Mai Trang 2022– Ôn tập XSTK
ÔN TẬP XÁC SUẤT THỐNG KÊ ỨNG DỤNG (MATH132901)
CHƯƠNG 1: TỔNG QUAN và THỐNG KÊ MÔ TẢ
Thống kê bao gồm Thống kê mô tả và Suy luận thống kê. A. Thống kê mô tả:
1. Phương pháp trực quan (hình ảnh)
1.1 Biểu đồ gốc – lá (Stem-leaf)
1.2 Biểu đồ chấm (Dotplot)
1.3 Biểu đồ cột (Histogram)
- Histogram cho biến rời rạc
- Histogram cho biến liên tục: chia lớp [a;b)
+ Biến liên tục có độ rộng lớp bằng nhau
+ Biến liên tục có độ rộng lớp khác nhau
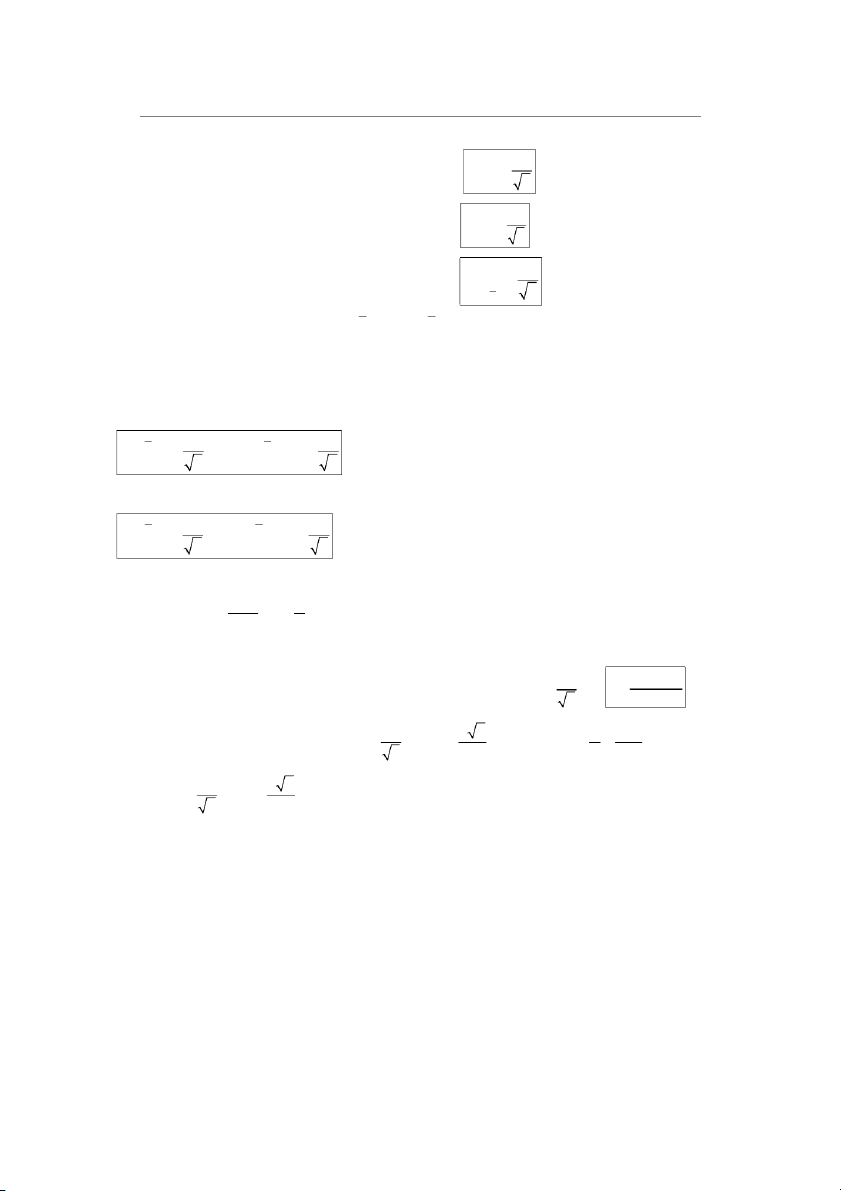
+ Hình dạng biểu đồ: 1 đỉnh, 2 đỉnh, nhiều đỉnh, đối xứng, nghiêng dương, âm. + Dữ liệu định tính 2. Đo lường tính toán 2.1 Đo lường vị trí: n xi - Trung bình (Mean): i1 x  n
- Trung vị (Median x ): sắp xếp các giá trị quan sát của mẫu từ nhỏ đến lớn ( với bất
kì giá trị quan sát nào lặp lại trong mẫu). Khi đó : n1
+ Nếu n là số lẻ thì x là giá trị chính giữa thứ . 2 n n
+ Nếu n là số chẵn thì x là trung bình của hai giá trị ở giữa thứ và 1 2 2 1
Lê Thị Mai Trang 2022– Ôn tập XSTK
Trung bình và trung vị đều để miêu tả sự tập trung. Tuy nhiên trung bình là giá trị
trung bình của mẫu, trung vị là giá trị ở giữa của tổng thể.
- Trung bình thu gọn (trimmed mean): a% ( trường hợp có giá trị ngoại lai, giảm
được các hạn chế của trung bình và trung vị)
- Tứ phân vị, phân vị mức phần trăm: Trung vị chia dữ liệu thành 2 phần có kích
thước bằng nhau. Tham số tứ phân vị chia dữ liệu thành bốn phần bằng nhau. Tương
tự cho tham số phần trăm. m - Tỉ lệ mẫu: f  n
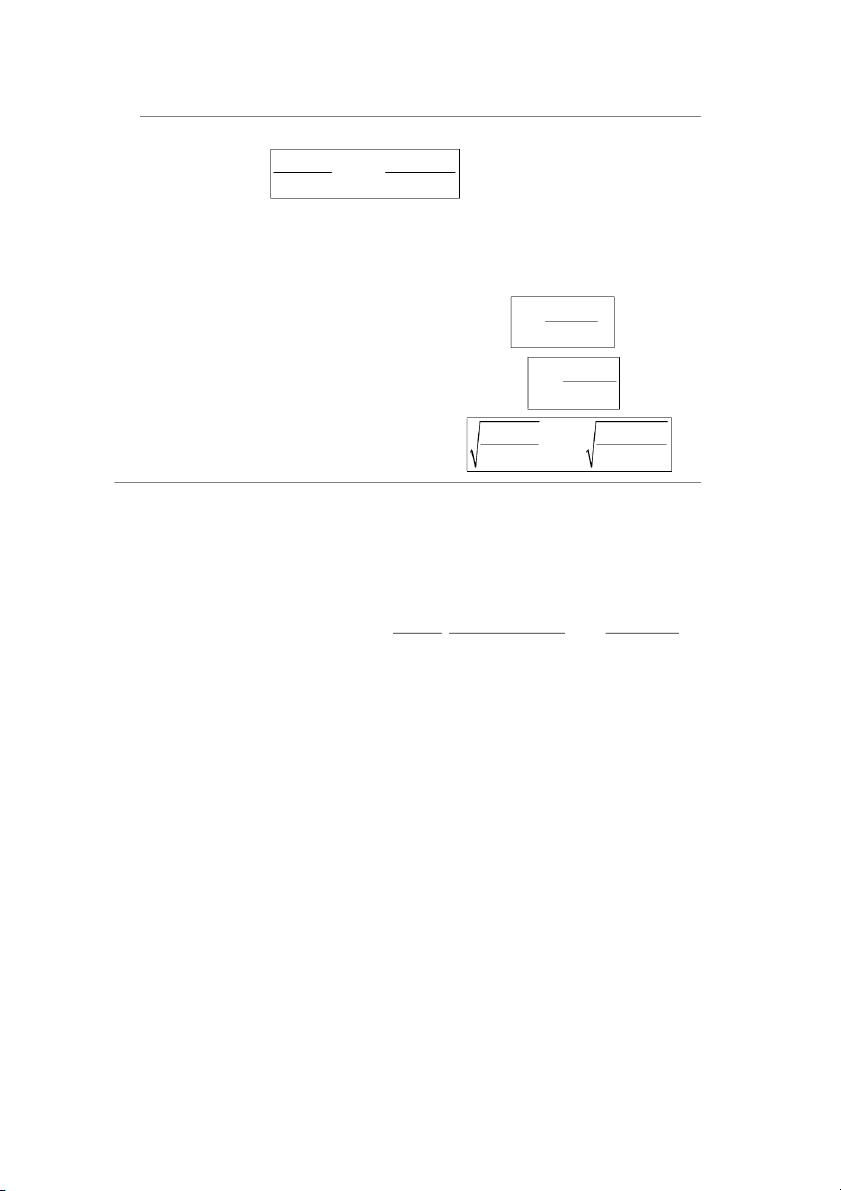
2.2 Độ đo độ biến thiên của mẫu: n 2 ( x  x)  i S x  2 i1 xx 2  i 2 - Phương sai: s    x   n 1 n 1 i n - Độ lệch chuẩn: 2 s  s
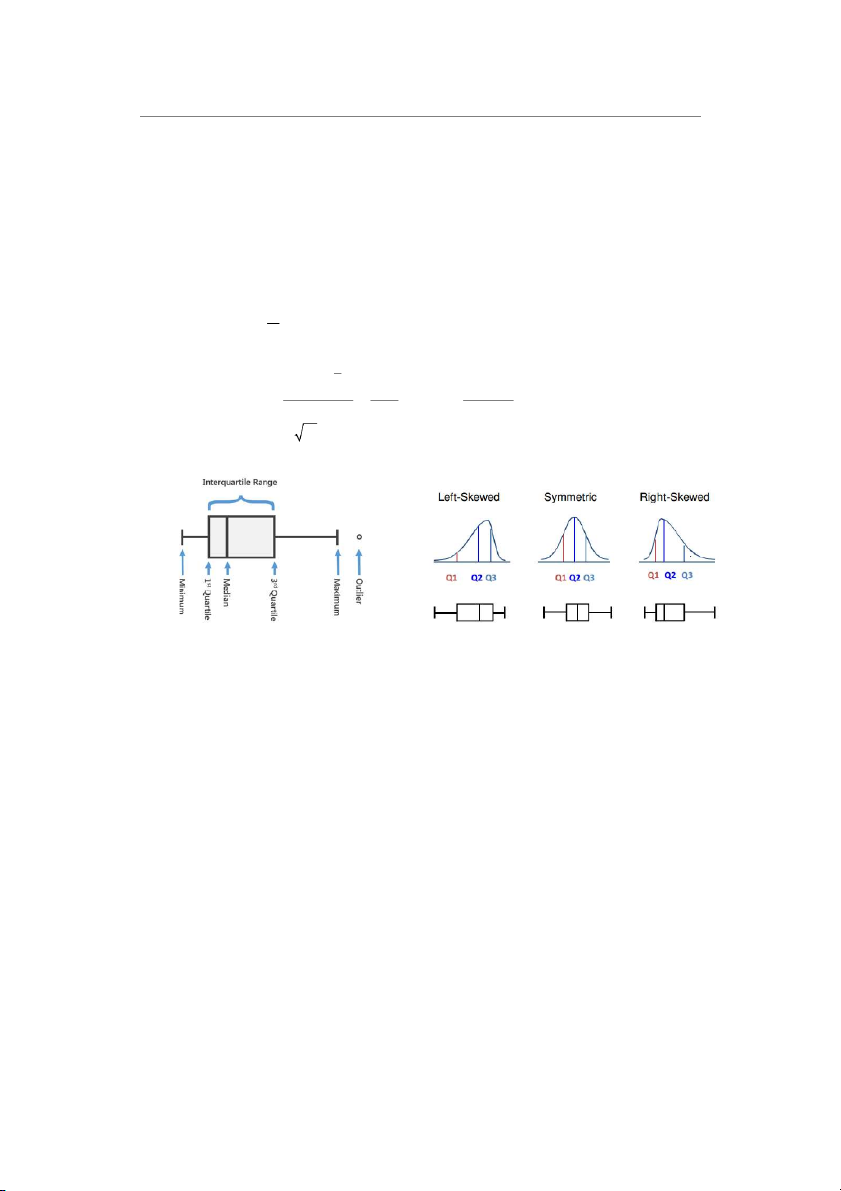
2.3 Biểu đồ hộp (boxplot )
Có 2 cách vẽ biểu đồ hộp gồm cách cho trung vị nằm trong 2 khoảng chia hoặc không.
- Boxplot có ngoại lai (outlier)
B. Thống kê suy luận : kiểm định, ước lượng, hồi quy.
C. Phần mềm: Minitab, R, SAS, S-plus 2
Lê Thị Mai Trang 2022– Ôn tập XSTK
CHƯƠNG 2: PHÉP TÍNH XÁC SUẤT
2.1 Không gian mẫu và biến cố:
- Phép thử: là một nhóm các hành động hoặc thí nghiệm do ta tiến hành hoặc dự định
tiến hành nhằm nghiên cứu một vấn đề nào đó.
- Không gian mẫu : Tập hợp tất cả các kết quả của một phép thử
- Biến cố: một tập hợp con của không gian mẫu . Thường kí hiệu bằng chữ in: A, B,…
Biến cố sơ cấp : kết quả đơn giản nhất có thể xảy ra khi thực hiện phép thử .
Biến cố chắc chắn: là biến cố luôn xảy ra khi thực hiện phép thử. Kí hiệu : 
Biến cố không thể: là biến cố không thể xảy ra. Kí hiệu là 
Biến cố kép: là biến cố chứa nhiều hơn một kết quả.
- Mối quan hệ của lý thuyết tập hợp:
a. Hợp của hai biến cố: Kí hiệu: C = A + B hay C  A B ( chỉ cần ít nhất một biến cố xảy ra)
Công thức cộng xác suất: P(A  B)  P(A)  P(B)  P(AB)
Mở rộng : P(A  B+C)  P(A)  P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
Nếu A, B là hai biến cố xung khắc thì P(A  B)  P(A)  P(B) .
b. Giao của hai biến cố: Kí hiệu : C = A.B hay C  AB (hai biến cố đồng thời xảy ra)
c. Đối lập (phần bù) :. Kí hiệu A A   A : . A A  
d. Xung khắc (rời nhau) : . A B  .
e. Độc lập: Biến cố A độc lập với biến có B khi khả năng xảy ra của biến cố này
không ảnh hưởng đến biến cố kia và ngược lại.
A  A    A  
f. Hệ đầy đủ: Hệ A ,A ,…,A gọi là hệ đầy đủ nếu  1 2 n  1 2 n
A A     i  j  n  i j 1 
2.2 Các tiên đề và tính chất của xác suất: m
- Định nghĩa xác suất theo lối cổ điển: ( P ) A A  n 3
Lê Thị Mai Trang 2022– Ôn tập XSTK
- Tính chất: A : 0  ( P )
A  1 ; P ( )  1, P ( )  0 ; P(A)  1 P(A) 2.3 Giải tích tổ hợp:
a. Quy tắc nhân: ( các giai đoạn phụ thuộc nhau) n  n .n ...n 1 2 k
b. Quy tắc cộng: (các phương pháp ko phụ thuộc nhau) m  m  m  ... m 1 2 k ! n c. Hoán vị: P  ! n . Hoán vị lặp , sao cho k  l  n . n k !l!
d. Chỉnh hợp ( k- hoán vị) : (lấy ra k phần tử có quan tâm thứ tự) n! k A  P  ,k n n k, n (n k)! n n k ! e.  
Tổ hợp: (lấy ra k phần tử không quan tâm thứ tự) C    k  n n ,  k   k!(n ) k !
2.4 Xác suất có điều kiện: P(AB)
- Công thức xác suất điều kiện: P(A|B)  P(B)
(Xác suất xảy ra A với điều kiện B đã xảy ra).
- Công thức nhân xác suất: P(AB)  P(A) . P(B|A)
Mở rộng :P(ABC)  P(A) . P(B|A) . P(C|AB)
Hai biến cố A và B gọi là độc lập thì : P(AB) P(A)P(B) - Công thức Bernoulli: k k nk ( P X  k)  C p (1 ) p , k  0,1,2,...,n n
- Công thức xác suất đầy đủ (toàn phần): n
P (B )  P (A )P(B | A )  P (A )P (B | A )  P(A )P(B | A ) . i i 1 1 n n i1 - Công thức Bayes: P(A )P(B | A ) P(A | B) i i  ,  i 1, ,n i P (B) 4
Lê Thị Mai Trang 2022– Ôn tập XSTK
CHƯƠNG 3: BIẾN NGẪU NHIÊN RỜI RẠC VÀ PHÂN PHỐI XÁC SUẤT
3.1 Biến ngẫu nhiên ( đại lượng ngẫu nhiên): 2 loại ĐLNN (BNN)
- BNN rời rạc: tập giá trị của nó là hữu hạn hay vô hạn đếm được.
- BNN liên tục: tập giá trị của nó lấp đầy một khoảng nào đó tên trục số và xác suất của
một điểm bất kì luôn là 0.
3.2 Phân phối xác suất của biến ngẫu nhiên rời rạc:
a/ Hàm phân phối xác suất của biến rời rạc X ( hay hàm khối lượng xác suất) là n p( x)  P( X  x) với ( p ) x 0 ; ( p x ) 1  . i i 1 
Bảng phân phối xác suất: X x1 …. x n p(x ) p (x ) p x i 1 … ( ) n
b/ Hàm phân phối tích luỹ (CDF) : kí hiệu F (x )
(cả biến rời rạc và biến liên tục đều có hàm phân phối xác suất tích luỹ) F (x)  P( X  x)
Chú ý: với X là biến rời rạc thì F (x)  P(X  x)  p (y) ; x     y x
3.3 Kỳ vọng và phương sai:
a/ Kỳ vọng (trung bình) : E(X )     .xp(x)  x p(x ) x ( p x )  ... x p(x ) X 1 1 2 2 n n x D  Tính chất: 1/ ( E ) c  c , c  const 2 / ( E . c ) X  . c ( E ) X 3/ ( E X  ) Y  ( E ) X  ( E ) Y 4/ ( E . X Y)  ( E X). (
E Y) nếu như X và Y độc lập. 5 / E [ ( h X)]   ( h ) x . ( p x) x D  5
Lê Thị Mai Trang 2022– Ôn tập XSTK b/ Phương sai: 2 2 2
V ( X )   E( X )  (EX ) với 2 2 ( E X )   x ( p x) . x D 
Độ lệch chuẩn:   V (X ) Chú ý: 2 2 2 2
V ( X )  (xEX) .p(x)  [ E (XEX) ]  E( X ) (  EX) D Tính chất : 1 / V ( X )  0 2 / V (c) 0 , c  const 2 3 / V ( . c X )  c .V (X ) 4 / V ( X Y ) V ( X ) V  (Y) neu X ,Y doc lap
3.4 -3.6 Các phân phối xác suất ( biến rời rạc)
1/ Phân phối nhị thức: Kí hiệu: X  Bin( , n ) p
X là số phép thử xảy ra trong n phép thử, xs của mỗi phép thử xảy ra là p.(mỗi phép thử chỉ có hai kết quả).
Hàm khối lượng xác suất của X kí hiệu là b(x, n, p) : x x C p (1 p)n x    ,  x  0,1,2,...,n ( b ; x ; n ) p  P(X  )  n x  (công thức Bernoulli) 0  , khac 
Hàm phân phối tích luỹ của X là B( ; x ; n p) : x B(x; ; n p)  P(X  x)  b(y;n; p) ; x  0,1,..., n  y 0 EX   np Tính chất: 2 V (X )  npq ( voi q  1 p)
2/ Phân phối siêu bội: X có phân phối siêu bội thì x C . nx C M N  n P(X  x)  h( ; x , n M , N) M N M  và EX  . n ; V ( X )  . n . p (1 ). p n C N N 1  N
3/ Phân phối nhị thức âm: (khác với trong sách)
Y là số phép thử thực hiện cho đến khi nào có r phép thử xuất hiện thì dừng. 6
Lê Thị Mai Trang 2022– Ôn tập XSTK r 1  r 1
P(Y n) C .p  .(1  )n r p  . p for n r . n 1  r r(1 p) Tính chất: EY  ; V(Y)  2 p p
4/ Phân phối Poisson: Kí hiệu : X  P() tham số  0
X là số phép thử xảy ra.   . x e  p(x; )   P(X  x)  (x  0,1,2,...) x!
Tính chất: EX  V ( X )   Nhận biết pp Poisson:
- X  Bin (n, p ) , biết n và p . Trong đó n lớn ( n > 50) ; p nhỏ; tích np    5. Xem X  P( ) 
- X  Bin (n , p ) , chưa biết n và p mà chỉ biết trung bình np   . Xem X  ( P ) 7
Lê Thị Mai Trang 2022– Ôn tập XSTK
CHƯƠNG 4: BIẾN NGẪU NHIÊN LIÊN TỤC và PHÂN PHỐI XÁC SUẤT
4.1 Hàm mật độ của biến ngẫu nhiên liên tục (pdf) : kí hiệu f X
X là biến ngẫu nhiên liên tục có hàm mật độ thoả 1/ f (x)  0 ,x  R  2/ f (x)dx 1   3/
P(a  X  b)  P(a  X  b)  P(a  X b) b  P(a  X b)  f (x)dx a 4/ P (X  a) 0
4.2 Hàm phân phối tích luỹ và các đặc trưng
a/ Hàm phân phối tích luỹ F(x) của biến ngẫu nhiên liên tục X là : x F(x)  ( P X  x)  f (y)dy   Chú ý: / F (x)  f (x)
Tính chất: P( X  a) 1  F( ) a ; P( a  X  ) b  F( ) b  F(a)
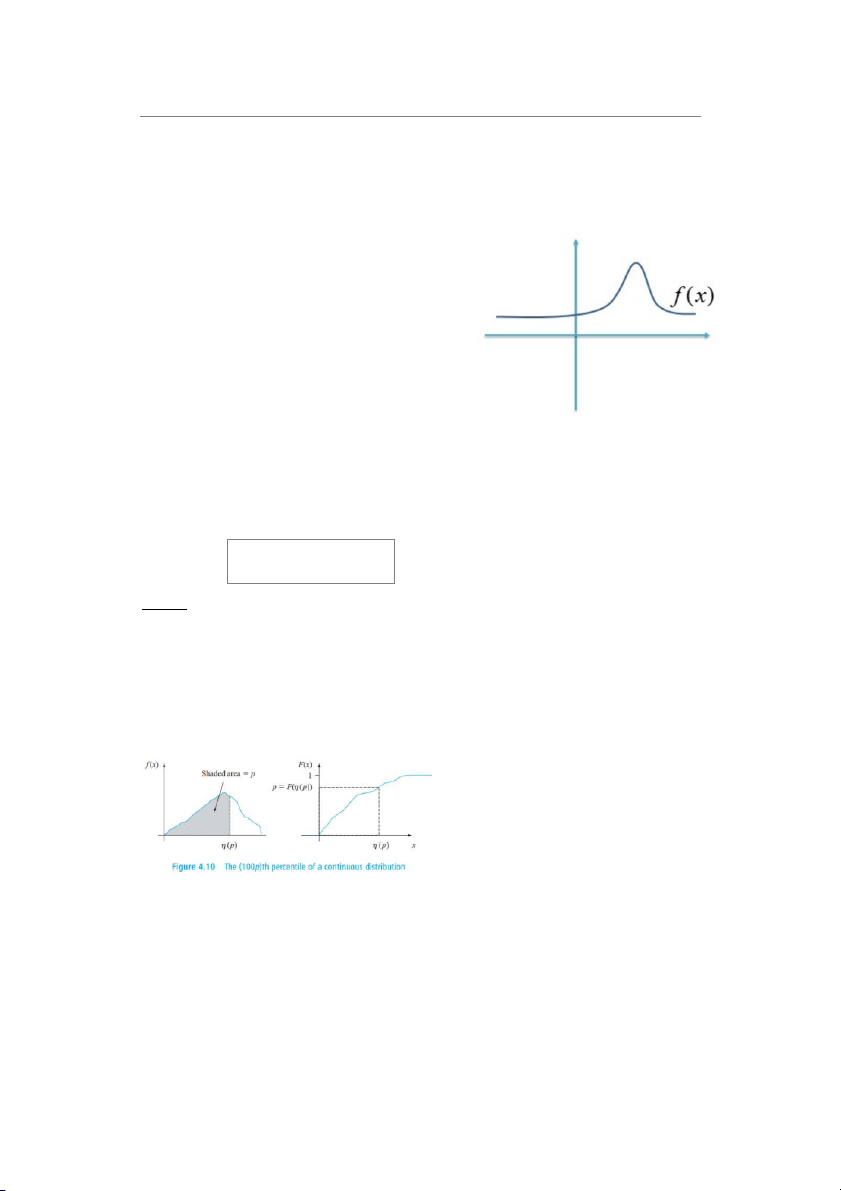
b/ Phân vị của phân phối liên tục: Cho p là một số thuộc khoảng [0;1]. Phân vị
thứ (100p) của một hàm phân phối của một biến ngẫu nhiên liên tục X, kí hiệu là ( ) p ( p)
được xác định bởi p  F ( (p ))  f (y )dy   8
Lê Thị Mai Trang 2022– Ôn tập XSTK
c/ Trung vị của một phân phối liên tục, kí hiệu  , là phân vị thứ 50, sao cho  thoả mãn 
F()  0.5 . Hay trung vị là giá trị chia phân phối thành 2 phần bằng nhau. 
d/ Kì vọng ( trung bình):   ( E X)  x . f (x)dx X  .   Đặc biệt   E[h(X )] h(x).f (x)dx h( X )   2     e/ Phương sai: 2 2 2 2  
  V ( X )  E( X ) (EX )  x . f (x)dx x. f ( ) x dx X        
Chú ý: Có thể dùng công thức 2 2 V( X) E ( X )      (x )  . f ( ) x dx    
f/ Độ lệch chuẩn:   V (X ) .
4.3 Các phân phối xác suất ( biến liên tục): 1/ Phân phối đều:
X có phân phối đều trên đoạn [a;b] nếu  1  a  u  b f (u )    X b a 0 khac  . 2 a  b (a  ) b Tính chất: EX  ; Var X  2 12 2/ Phân phối chuẩn:
a/ Phân phối chuẩn chuẩn tắc: Kí hiệu: Z  N (0;1) ,   0 ;  1 1
- Hàm mật độ có dạng: 2  z /2 f (z;0,1)  e 2 z
- Hàm phân phối của Z là: P (Z  z )  f (y ;0,1)dy  (z )   9
Lê Thị Mai Trang 2022– Ôn tập XSTK P(Z a)  (a) P(Z b) 1  (b) - Tính chất: ( P a  Z  ) b  ( ) b  ( ) a (z)  1  when z 3.49 (z)  0 when z  3.49 
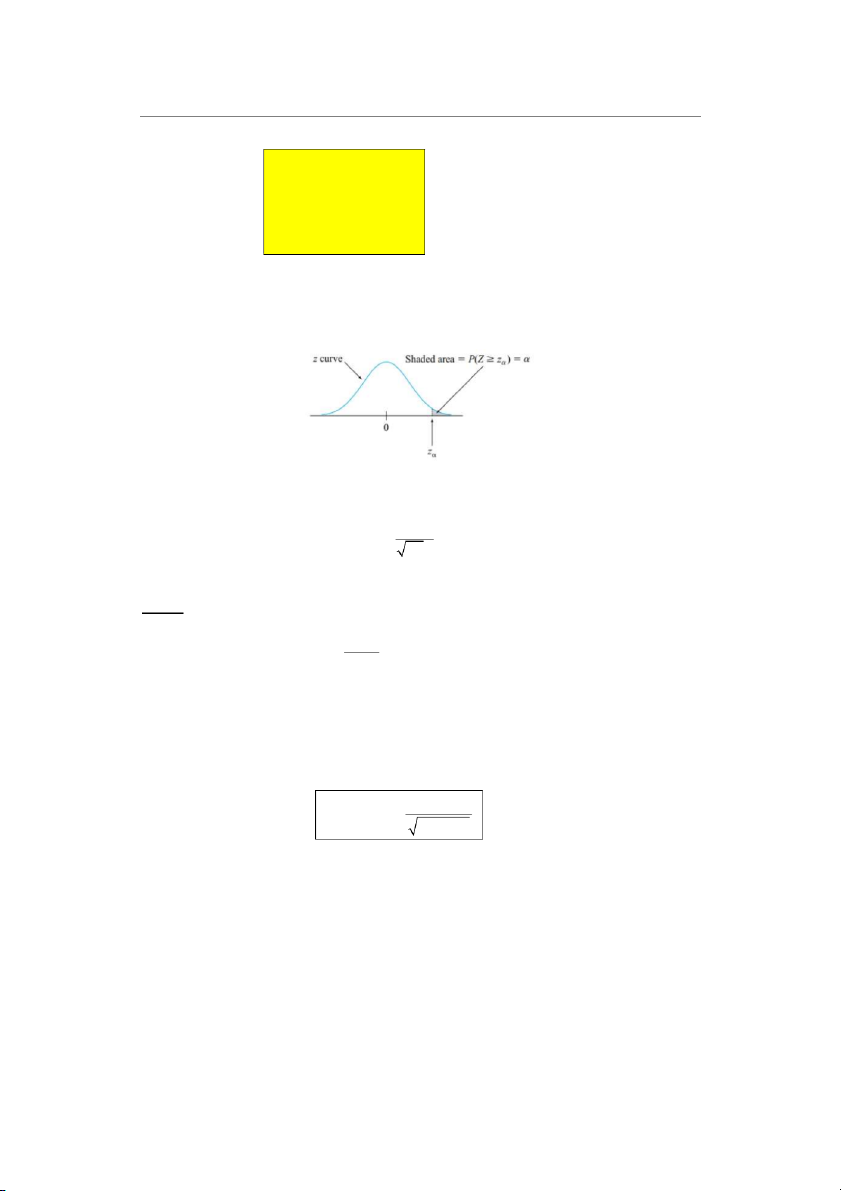
b/ Phân vị của phân phối chuẩn: z biểu thị giá trị trên trục z mà   là diện tích vùng
dưới đường cong z nằm bên phải z . Khi đó chính là phân vị thứ 100(1-  z  ) của phân phối chuẩn.
c/ Phân phối chuẩn: Kí hiệu: 2 X N(   , ) 1
- Hàm mật độ có dạng: 2 2  (x  ) /(2 ) f ( ; x , )  e     2 - Tính chất: 2 EX   ; V ( X )  
Chú ý: Chuyển từ phân phối chuẩn về dạng chuẩn chuẩn tắc :  Với X  2 X  (
N , ) ; ta đặt : Z   N(0,1) 
d/ Sự hội tụ của phân phối nhị thức về phân phối chuẩn: X  Bin (n ,p )
Nếu đồ thị của phân phối nhị thức không quá lệch ( không quá mất đối xứng)
( np  10 ; n(1  p)  10 ) thì có thể xấp xỉ X như một phân phối chuẩn 2 X  N (, ) bằng   np  x  0.5 np  cách đặt và ( P X  ) x 2       npq  . np (1 p )     3/ Phân phối mũ :
- X có phân phối mũ với tham số   0 , thì hàm mật độ của X là 10
Lê Thị Mai Trang 2022– Ôn tập XSTK   . t e ; x  0 f (x)   . 0  ; neu khac 1   x   e ; x  0
- Hàm phân phối xác suất của X là F (x; )  P(X  x)   0 ; x   0 1 1 - Tính chất: 2   ;  . 2  
4/ Phân phối Gamma: (đọc thêm) 
- Cho   0 , khi đó hàm gamma  1 ( )   x  x e dx  0
- Biến ngẫu nhiên liên tục X có phân phối gamma nếu hàm mật độ của X là  1  1 x x e ; x   0 f ( ; x ,  )     ()
trong đó  ;  là hai tham số dương. 0  ; neu khac  - Tính chất: 2 2 E( X )     ; V ( X )      1  1 x x e ; x  0
- Hàm gamma chuẩn tắc: khi   1 thì f ( ; x ,  1)   (   ) 0  ; neu khac  x  1  y y e
Hàm phân phối của X có phân phối gamma chuẩn tắc là: F (x;)  dy ; x  0  --  ( ) 0
- Mệnh đề 4.4.4: Cho X là biến ngẫu nhiên có hàm phân phối gamma với tham số  x 
 ; . Khi đó, với x>0, hàm phân phối của X là P(X  x)  F (x; , ) F ;  với    
F ( ; ) là hàm gamma không đầy đủ.
5/ Phân phối Chi-bình phương: 2 X   bậc tự do 
X có phân phối chi- bình phương với tham số  nếu hàm mật độ xác suất của X là hàm
mật độ gamma có tham số   / 2 ;   2 . Hàm mật độ của X có phân phối Chi-bình  1  /2 1  x/ 2 x e ; x  0 phương là  /2 f ( ; x )  2 (    / 2) 0  ; x   0 11
Lê Thị Mai Trang 2022– Ôn tập XSTK
4.3 Một số phân phối liên tục khác : ( đọc sách) Phân phối Weibull ; Phân phối lô-ga chuẩn; phân phối Bê ta.
CHƯƠNG 5: PHÂN PHỐI XÁC SUẤT ĐỒNG THỜI VÀ MẪU NGẪU NHIÊN (đọc sách) CHƯƠNG 6,7: ƯỚC LƯỢNG
- Tổng thể: tập hợp tất cả các phần tử mà từ các phần tử đó ta có thể thu thập, khảo sát những
thông tin về các dấu hiệu ta cần nghiên cứu được gọi là tổng thể (population).
- Mẫu ngẫu nhiên: Cho đại lượng ngẫu nhiên X với quy luật phân phối xác suất nào đó. Một mẫu
ngẫu nhiên kích thước n được thành lập từ đại lượng ngẫu nhiên X là n đại lượng ngẫu nhiên độc
lập X ,X ,...,X , có cùng phân phối xác suất với đại lượng ngẫu nhiên X. 1 2 n
+ Chọn ngẫu không hoàn lại.
+ Chọn mẫu có hoàn lại.
- Các tham số của tổng thể:
N : số phần tử của tổng thể - Các tham số của mẫu: M n: kích thước mẫu
A : số phần tử có tính chất A của tổng thể
m : số phần tử có tính chất A của mẫu. A M  m m A A A p  hay f p 
: tỷ lệ của tổng thể về tính chất  : tỷ lệ mẫu về tính N n n A. chất A.
 : trung bình của tổng thể x : trung bình mẫu. 2 2
s : phương sai của mẫu hiệu chỉnh.
 : phương sai của tổng thể
 : Độ lệch chuẩn của tổng thể
s : Độ lệch chuẩn mẫu hiệu chỉnh ( hoặc kí hiệu  ) n1 12
Lê Thị Mai Trang 2022– Ôn tập XSTK  Calculator fx570 ES :
Bước 1: (gọi cột tần số) Shift Mode 4 1.on Bước 2: Mode 3.STAT 1.
Nhập dữ liệu rồi nhấn AC . Bước 3: Shift 1. 5.Var 1.n 2. x 4. x or s n 1  Chú ý:
Shift 1. 3.Edit 2. Del (xoá dữ liệu) Mode 1. ( thoát)  Calculator fx580 :
Bước 1: (gọi cột tần số) Shift Menu 3. Tần số 1 Bước 2: Mode 6 1
Nhập dữ liệu rồi nhấn AC .
Bước 3: OPTN 2 Sẽ thấy n, x , x or s n 1 
1. Phương pháp ước lượng điểm: (ước lượng không chệch)
Dùng trung bình mẫu x để ước lượng cho trung bình tổng thể  . Dùng phương sai mẫu 2
s để ước lượng cho phương sai tổng thể 2  .
Dùng tỷ lệ mẫu p để ước lượng cho tỷ lệ tổng thể p
2. Phương pháp ước lượng khoảng:
- Độ tin cậy : kí hiệu  với   1 (  là mức ý nghĩa)
2.1. Ước lượng khoảng cho trung bình của tổng thể  :
a/ Khoảng ước lượng đối xứng :
Gọi  là trung bình của tổng thể (  chưa biết), ta cần tìm ước lượng khoảng đối xứng của
 với độ tin cậy   1  . - Trung bình mẫu: x
- Độ chính xác ( sai số) của ước lượng: 13
Lê Thị Mai Trang 2022– Ôn tập XSTK  TH1 : 2  đã biết : Sai số là   z /2 n s TH2 : 2
 chưa biết , mẫu lớn (n > 40):  z /  2 (tra bảng Z) n s TH3 : 2  t
 chưa biết , mẫu nhỏ ( tra bảng T - Student) ;  n 1  n 2
- Khoảng ước lượng cho trung bình : (x    x )
( Xem giới thiệu về phân phối Student trong giáo trình)
b/ Khoảng ước lượng 1 phía :
- Giá trị ước lượng tối đa cho trung bình tổng thể  là: s s  x z ;  x t  ;  n 1 n  n
- Giá trị ước lượng tối thiểu cho trung bình tổng thể  là: s s  x z ;  xt  ; n 1 n  n Chú ý:  1 Với (z )   1  
 ; (z      được tra từ bảng Z- chuẩn tắc  ) 1 /  2 2 2
c/ Tìm cỡ mẫu, độ tin cậy : s 2 2 4.z .s
- Tìm cỡ mẫu n : Cho chiều rộng cỡ mẫu w  2 , mà w  2  2.z   /2 n  /  2 n 2 w s  n   1
- Tìm độ tin cậy khi biết sai số:   z  z  (z )  1     ? /2 /2 /2 n s 2 2 s  n Hoặc   z  z   (  z )  ?    ?  n  s  14
Lê Thị Mai Trang 2022– Ôn tập XSTK
2.2. Ước lượng khoảng cho tỷ lệ của tổng thể p :
a/ Khoảng ước lượng đối xứng :
Gọi p là tỷ lệ các phần tử có tính chất A của tổng thể ( p chưa biết), ta cần tìm ước lượng
khoảng đối xứng của p với độ tin cậy   1  . m - Tìm tỷ lệ mẫu  A p  n p(  1  p)
- Sai số ước lượng ( độ chính xác) :  z (tra bảng Z) /  2 n
- Khoảng ước lượng (khoảng tin cậy): (p    p   p )
b/ Khoảng ước lượng 1 phía : p (1 ) p
- Giá trị ước lượng tối đa cho tỉ lệ tổng thể p là:  p  p z n p (1p)
- Giá trị ước lượng tối thiểu cho tỉ lệ tổng thể p là:  p p z   n
c/ Tìm cỡ mẫu, độ tin cậy : - Tìm cỡ mẫu n :  p (1   ) p
Cho chiều rộng cỡ mẫu w  2 , mà 2 n 4z /2 2 w
- Tìm độ tin cậy khi biết sai số:   p (1 p)  z z  ... (z )  ....   ?  /2  /2  /2 n p(1 p )  z
z  ...  (z ) ....    ?  n  
2.3. Ước lượng khoảng cho phương sai của tổng thể 2  :
a/ Khoảng ước lượng đối xứng : Gọi 2
 là phương sai của tổng thể ( 2
 chưa biết), ta cần tìm ước lượng khoảng đối xứng của 2
 với độ tin cậy   1  . Ta có : 15
Lê Thị Mai Trang 2022– Ôn tập XSTK 2 2 (n 1) s (n 1) s 2    2 2   / 2; n 1  1 ( / 2) ; n1 Với 2  và 2 
là giá trị của ĐLNN có phân phối Chi bình phương 2 2    ( n 1) (xem /  2 1( / 2) giáo trình)
b/ Khoảng ước lượng 1 phía : 2 2 (n 1  )s
- Giá trị ước lượng tối đa cho phương sai tổng thể 2  là:   2 1    ; n 1  2 ( n 1  )s
- Giá trị ước lượng tối thiểu cho phương sai tổng thể 2 2  là:   2  ;n1 2 2 (n 1) s (n 1) s
c/ Khoảng ước lượng cho độ lệch chuẩn  :    2 2   / 2;n 1  1 (  / 2) ; n 1 
CHƯƠNG 8: KIỂM ĐỊNH DỰA TRÊN MỘT MẪU ĐƠN
1. Một số khái niệm cơ bản:
- Giả thiết thống kê: là những giả thiết về các tham số, phân phối xác suất, hoặc tính độc lập
của các đại lượng ngẫu nhiên.
- Kiểm định giả thiết thống kê: việc tìm ra kết luận bác bỏ hay chấp nhận một giả thiết.
- Giả thiết không : giả thiết cần kiểm định. Ký hiệu là H . 0
- Giả thiết đối : một mệnh đề đối lập với H . Ký hiệu là H . 0 a
- Kiểm định giả thiết hai phía: H :    ; H :    0 0 a 0
(  là tham số nào đó của ĐLNN mà ta đang nghiên cứu;  là giá trị đã biết) 0
- Kiểm định giả thiết một phía : H :  
; H :   (hay H :   ) 0 0 a 0 a 0
( một phía bên phải; một phía bên trái)
- Sai lầm loại 1 và sai lầm loại 2: Từ bài toán thực tế nêu giả thiết H H . 0 và a 16
Lê Thị Mai Trang 2022– Ôn tập XSTK Bản Ho đúng Ho sai chất
Kiểm tra mẫu và kết luận …….. Sai lầm loại 2 Ho đúng Ho sai Sai lầm loại 1 …….. - Mức ý nghĩa  : ( P sai lam loai 1)   ;  1  
( Xác suất không mắc sai lầm loại 2 là  )
- Miền bác bỏ là miền chứa các giá trị làm cho giả thuyết Ho bị bác bỏ.
Miền chấp nhận là miền chứa các giá trị giúp cho giả thuyết Ho không bị bác bỏ (tạm chấp
nhận hoặc chưa đủ cơ sở để bác bỏ Ho)
2. Kiểm định giả thiết về trung bình tổng thể  :
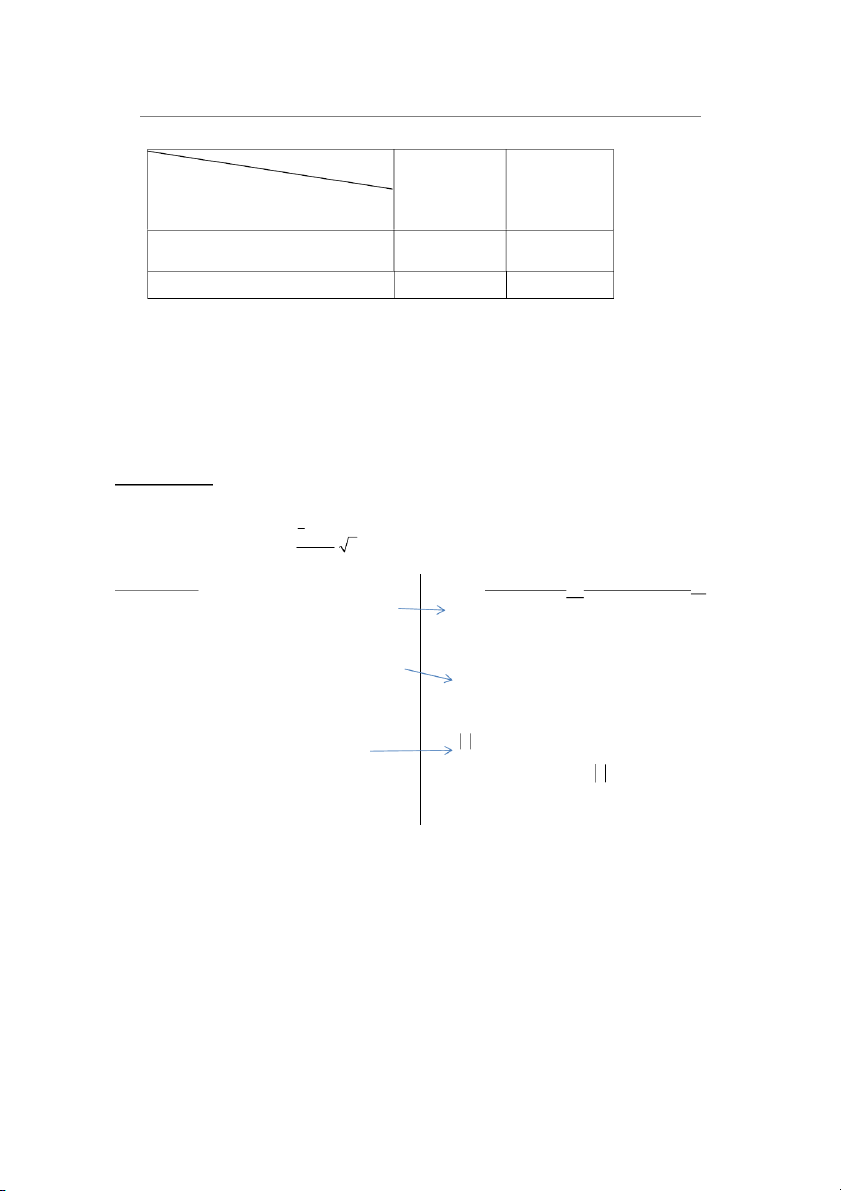
Trường hợp 1: X có phân phối chuẩn; 2  đã biết.
Giả thiết không: H :    0 0 x Tiêu chuẩn kiểm định:  0 z  . n  Giả thiết đối:
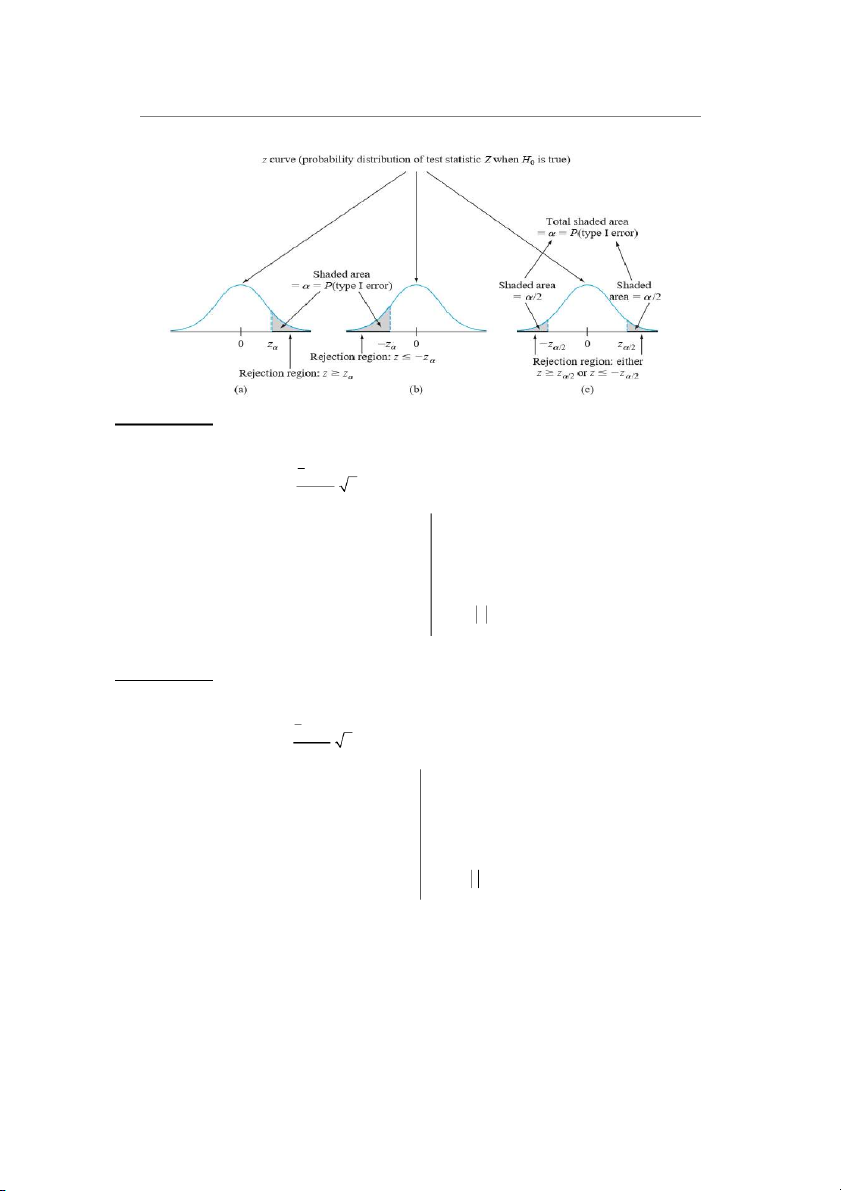
Miền bác bỏ H với mức ý nghĩa  : 0
H :    (kiểm định 1 phía bên phải) a 0 z  z : bỏ H H  0  nhận a Nếu z  z : nhận H  0
H :    ( kiểm định 1 phía bên trái) a 0 z  z  : bỏ H  nhận H  0 a Nếu z  z  : nhận H  0 z  z : bỏ H  nhận H H : 0 a
   (kiểm định 2 phía)  /2 a 0 z  z Nếu : nhận H /2 0 17
Lê Thị Mai Trang 2022– Ôn tập XSTK
Trường hợp 2: Mẫu lớn (n>40) , X có phân phối chuẩn; 2  chưa biết.
Giả thiết không: H :    0 0 x Tiêu chuẩn kiểm định:  0 z  . n s Giả thiết đối:
Miền bác bỏ H với mức ý nghĩa  : 0
H :    (kiểm định 1 phía bên phải) a 0 z  z  H : 
( kiểm định 1 phía bên trái) a  0  z  z  
H :    (kiểm định 2 phía) a 0 z  z /2
Trường hợp 3: Mẫu nhỏ , X có phân phối Student; 2  chưa biết.
Giả thiết không: H :    0 0 Tiêu chuẩn kiểm định: x 0 t  . n s Giả thiết đối:
Miền bác bỏ H với mức ý nghĩa  : 0
H :    (kiểm định 1 phía bên phải) a 0 t t ,n 1 
H :    ( kiểm định 1 phía bên trái) a 0 t t  ,  n 1  H :  (kiểm định 2 phía) a  0  t t   /2,n1 18
Lê Thị Mai Trang 2022– Ôn tập XSTK
Chú ý: Nếu bác bỏ H , nhận H :    . Theo ước lượng điểm ta có 0 a 0
+) Nếu x   thì có thể kết luận  0  0
+) Nếu x   thì có thể kết luận  0  0
3. Kiểm định giả thiết về tỉ lệ tổng thể p: (cho mẫu lớn n.p  10 ; n(1 p ) 10 ) 0 0
Giả thiết không: H : p  p 0 0 (p  p ) n Tiêu chuẩn kiểm định: 0 z  p (1 p ) 0 0 Giả thiết đối:
Miền bác bỏ H với mức ý nghĩa  : 0 H : p  p a 0 z  z : bỏ H , nhận H ;  0 a z  z : nhận H  0 z  z  : bỏ H , nhận H  0 a H : p  p a 0 z  z  : nhận H  0 z  z bỏ H , nhận H H : p  p  /2 0 a a 0 z z : nhận H  /2 0 - Chú ý:
Nếu bác bỏ H , nhận H : p p . Theo ước lượng điểm ta có 0 a 0
+) Nếu p  p thì có thể kết luận  0 p p0
+) Nếu p  p thì có thể kết luận  0 p p0 19
Lê Thị Mai Trang 2022– Ôn tập XSTK P-value:
P-value là xác suất được tính khi giả định giả thiết không H đúng. (chú ý là P-value không 0
phải xác suất để H đúng). P-value là mức ý nghĩa  nhỏ nhất mà H bị bác bỏ. Vì tiêu chuẩn 0 0
kiểm định z khác nhau khi mẫu khác nhau nên cho P-value trong mỗi mẫu khác nhau.
- Mặt khác, nếu quy định trước mức ý nghĩa  thì có thể dùng p-value để kết luận theo  .
Nếu p-value   thì bác bỏ H , thừa nhận H . 0 a
Nếu p-value  thì chưa có cơ sở để bác bỏ H . 0
Tuy nhiên phương pháp dùng p-value để kiểm định cũng giống như dùng miền bác bỏ để kiểm định. 1
 (z) ;kiem dinh phia phai 
- P-value cho kiểm định Z (chuẩn): P value : P    (z ) ;kiem dinh phia trai 2
 1 ( z ) ; kiem dinh hai phia
- P-value cho kiểm định T (Student):
CHƯƠNG 9: KIỂM ĐỊNH DỰA TRÊN 2 MẪU TRƯỜNG HỢP H H MIỀN BÁC BỎ P-VALUE 0 a
1/ Kiểm định so sánh hai trung bình của hai tổng thể 𝑵(𝝁 𝟐 𝟏, 𝝈𝟏); H :    𝜇 0 1  2  0  − 𝜇 ≠ ∆ |𝑧| ≥ 𝑧/ 𝑃 = 2(1− ∅(|𝑧| )) 𝑵(𝝁 𝟐 𝟐, 𝝈𝟐 ) 𝑥 − 𝑦 − ∆
𝜇 − 𝜇 > ∆ 𝑧 ≥ 𝑧 𝑃 = (1− ∅(𝑧)) 𝝈𝟐 𝟐  𝟏 ; 𝝈𝟐 đã biết 𝑧 = 𝜇    − 𝜇 < ∆ 𝑧 ≤ −𝑧 𝑃 = ∅(𝑧) 𝜎 + 𝜎 𝑛 𝑛 H :      𝜇 0 1 2 0  − 𝜇 ≠ ∆ |𝑧| ≥ 𝑧/ 𝑃 = 2(1− ∅(|𝑧| )) Mẫu lớn 𝑛 > 𝑥 − 𝑦 −∆
𝜇 − 𝜇 > ∆ 𝑧 ≥ 𝑧 𝑃 = (1− ∅(𝑧)) 40;  𝑛 𝑧 =  > 40
𝜇 − 𝜇 < ∆ 𝑧 ≤ −𝑧 𝑃 = ∅(𝑧) 𝝈𝟐 𝟐   𝟏; 𝝈𝟐 chưa biết  𝑠 𝑛 + 𝑠  𝑛 Mẫu nhỏ 𝝈𝟐 𝟐
𝟏; 𝝈𝟐 H :      0 1 2 0
𝜇 − 𝜇 ≠ ∆ |𝑡| ≥ 𝑡󰇡 chưa biết  ;󰇢 (*) 𝑃 = 2(1 − 𝑃(𝑇 ≤ |𝑡 |)) (**) 20