Phương pháp giải các dạng toán hàm số bậc nhất

Tài liệu gồm 58 trang, tóm tắt kiến thức trọng tâm và hướng dẫn phương pháp giải các dạng toán hàm số bậc nhất, giúp học sinh lớp 9 tham khảo khi học chương trình Toán 9 phần Đại số chương 2. Mời bạn đọc đón xem.

78 39 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Hàm số bậc nhất

Môn: Toán 9

Thông tin:

58 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
MỤC LỤC
Chương II. HÀM SỐ BẬC NHẤT ................................................................................. 2
§1. NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ .............................. 2
§2.HÀM SỐ BẬC NHẤT ........................................................................................... 2
§3. ĐỒ THỊ CỦA HÀM SỐ 𝑦 = 𝑎𝑥 + 𝑏(𝑎 ≠ 0) .................................................... 18
§4. ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU .............. 31
§5. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
y ax b= +
( )
0a ≠
.................................... 41
ÔN TẬP CHƯƠNG II .............................................................................................. 48
Chương II. HÀM SỐ BẬC NHẤT
§1. NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ
§2.HÀM S
Ố BẬC NHẤT
A. TRỌNG TÂM KIẾN THỨC
1. Khái niệm hàm số
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x, ta luôn
xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x, và x được gọi là
biến số.
Khi y là hàm số của x thì ta có thể viết
( ) ( )
, ,...y fx y gx= =
Khi hàm số được cho bằng công thức
( )
,y fx=
ta hiểu rằng biến số x chỉ lấy những giá
trị mà tại đó
( )
fx
xác định. Tập hợp các giá trị đó được gọi là tập xác định của hàm số, kí
hiệu là D.
Giá trị của
( )
fx
tại
0
x
kí hiệu
( )
0
fx
hay
Khi x thay đổi mà y luôn nhận
một giá trị không đổi thì hàm số y được gọi là hàm hằng.
2. Đồ thị hàm số
Tập hợp
""G
tất cả các điểm biểu diễn các cặp giá trị tương ứng
( )
( )
xfx;
trên mặt
ph
ẳng tọa độ goi là đồ thị của hàm số
( )
.y fx=
( )
00
""Mxy G;∈
hay
""G
đi qua điểm
( )
( )
0
00
00
xD
Mxy
y fx
∈
;⇔
=
3. H
àm số đồng biến, nghịch biến
Cho hàm số
( )
y fx=
xác định trên D trong đó D là một khoảng hoặc đoạn hoặc nửa
khoảng với mọi
12
,.xx D∈
• Nế
u
12
xx<
mà
( ) ( )
12
fx fx<
thì hàm số
( )
y fx=
đồng biến trên D.
• Nế
u
12
xx<
mà
( ) ( )
12
fx fx>
thì hàm số
( )
y fx=
nghịch biến trên D.
4. Hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bởi công thức
,y ax b= +
trong đó
,ab
là các số
cho trước và
0.a ≠
Khi
0,b =
hàm số có dạng
y ax=
(đã học ở lớp 7).
Hàm số bậc nhất
( )
0y ax b a=+≠
xác định với mọi x thuộc
.
Hàm số đồng biến trên
khi
0,a >
hàm số nghịch biến trên
khi
0a <
B. CÁC D
ẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. TÌM TẬP XÁC ĐỊNH (TXĐ) CỦA HÀM SỐ
Phương pháp giải
Hàm số
( )
fx
chứa căn bậc hai
( )
,Ax
điều kiện:
( )
0.Ax≥
Hàm số
( )
fx
chứa biến số ở mẫu
( )
( )
Ax
Bx
(hoặc
( ) ( )
Ax x:Β
), điều kiện:
( )
0.Bx≠
Ví d
ụ 1. Với những giá trị nào của x thì hàm số sau đây xác định?
a)
( )
2
2
1
4
x
y fx
x
+
= =
−
b)
( )
35y gx x x= = −+ −
Gi
ải
a)
( )
fx
xác định khi:
22
4 0 4 2.x xx− ≠ ⇔ ≠ ⇔ ≠±
b)
( )
gx
xác định khi:
30 3
35
50 5
xx
x
xx
−≥ ≥

⇔ ⇔≤≤

−≥ ≤

Ví dụ 2. Tìm tập xác định D của hàm số
( )
2
1
x
y hx x
x
−
= = :
−
Gi
ải
( )
hx
xác định khi:
2
0
0
10
1
0
0
0
0
x
x
x
x
x
x
x
x
x
−≥
≤
−≠
≠±

⇔ ⇔ ∈∅

≥
≥


≠
≠
V
ậy tập xác định của hàm số
.D = ∅
(Tức là không có giá trị nào của x để hàm số xác định).
Ví dụ 3. Tìm tập xác định D của hàm số
2
() .
1
x
y fx
x
= =
+
Giải
()fx
xác định khi:
22
10 1 .x xx+ ≠ ⇔ ≠− ⇔ ∈
Vậy tập xác định
.D =
Ví dụ 4. Tìm tập xác định D của hàm số
2
() 1 1 .y fx x x= = −+ −
Giải
()fx
xác định khi:
2
10
1
1.
11
10
x
x
x
x
x
−≥
≥
⇔ ⇔=

−≤ ≤
−≥
Vậy tập xác định
{ }
1.D =
Chú ý: Tập xác định D của hàm số có thể có một phần tử, một vài phần tử, vô số phần tử hoặc
không có phần tử nào.
D
ạng 2. TÍNH GIÁ TRỊ CỦA HÀM SỐ KHI BIẾT GIÁ TRỊ CỦA BIẾN SÔ.
TÍNH GIÁ TRỊ CỦA BIẾN SỐ KHI BIẾT GIÁ TRỊ CỦA HÀM SỐ
Phương pháp giải
Tìm tập xác định D của hàm số
( ).y fx=
•
Thế giá trị
0
xx D= ∈
vào biểu thức của hàm số rồi tính giá trị biểu thức (đôi khi ta rút gọn
biểu thức, biến đổi
0
x
rồi mới thay vào để tính toán).
•
Thế giá trị
0
yy=
ta được
0
( ).y fx=
Giải phương trình
0
()fx y=
để tìm giá trị biến số
x
(chú ý: chọn
xD∈
).
Ví dụ 1. Tính giá trị của hàm số
2
31
()
44
y fx x= =−−
tại
1; 1.xx= = −
Giải
TXĐ:
Ta có:
2
3 1 31
(1) .1 1;
4 4 44
f =− −=−−=−
2
3 131314
( 1) .( 1) .1 1.
4 444444
f −=− − −=− −=−−=−=−
Ví d
ụ 2. Cho hàm số
2
9
() .
3
x
y fx
x
−
= =
+
Khi đó f(-3) bằng bao nhiêu ?
Giải
Điều kiện
3.x ≠−
Vì
3x = −
không thỏa mãn điều kiện nên không tồn tại
( 3).f −
Ví dụ 3. Cho hàm số
() 1y f x mx m= = +−
, biết
(2) 8.f =
Tính
(3).f
Giải
TXĐ:
Ta có
(2) 8 .2 1 8 3 9 3f mm m m= ⇔ + −= ⇔ = ⇔ =
( ) 3 2 (3) 3.3 2 11.fx x f⇒ = +⇒ = +=
Ví dụ 4. Cho hàm số
( ) (3 2 2) 1.y fx x==−−
Tìm
x
, biết
( ) 0.fx=
Gi
ải
TXĐ:
Ta có
() 0fx=
(3 2 2) 1 0x⇔ − −=
(3 2 2) 1
1
3 2 2.
(3 2 2)
x
xx
⇔− =
⇔= ⇔=+
−
Ví dụ 5. Cho hàm số
() 1 .y fx x x= = +−
a) Tì
m
x
, biết
( ) 1;fx=
b) Tì
m
x
sao cho
( ) 0,5;fx=
c) Tì
m
m
để có giá trị
x
thõa mãn
() .fx m=
Gi
ải
Điều kiện:
0 1.x≤≤
a) Ta có:
22
() 1 1 1 ( 1 ) 1fx xx xx=⇔ +−=⇔ +− =
21 1 121 0xxx x xx⇔ + − +− =⇔ − =
0x⇔=
hoặc
10x−=
0x⇔=
hoặc
1x =
(thỏa mãn điều kiện).
b) Ta có:
22
( ) 0,5 1 0,5 ( 1 ) 0,5 .fx xx xx= ⇔ +−= ⇔ +− =
2 1 1 0,25xxx x⇔ + − +− =
2 1 0,75xx⇔ −=−
(không xảy ra vì
2 1 0).xx−≥
Do đó không có giá trị nào của
x
để
( ) 0,5.fx=
c) Ta có:
22
() 1 () ( 1 )fxxxfxxx= +−⇒ = +−
2
() 2 1 1 1fx x x⇔ = − +≥
(vì
21 0xx−≥
).
Suy ra
() 1fx≥
(dấu bằng xảy ra khi và chỉ khi
0x =
hoặc
1x =
).
Mặt khác:
11
1
22
xx
xx
+−
−≤ =
(dấu bằng xảy ra khi
1
2
x =
).
Do đó
22
( ) 2 2.m fx m= ≤⇒ ≤
Do đó chỉ khi
12m≤≤
thì có giá trị của
x
thỏa mãn
() .fx m=
Chú ý: Ta có thể chứng minh
() 1fx≥
bằng một số cách khác như sau:
Cách 1: Sử dụng bất đẳng thức
A B AB+≥+
với
,0AB≥
(dấu “=” xảy ra khi A = 0
hoặc B = 0 ).
Cách 2: Sử dụng bất đẳng thức
AA≥
với mọi A thỏa mãn điều kiện
0 1.A≤≤
D
ạng 3. BIỂU DIỄN ĐIỂM TRÊN MẶT PHẲNG TỌA ĐỘ.
XÁC ĐỊNH KHOẢNG CÁCH GIỮA HAI ĐIỂM TRÊN MẶT PHẲNG
Phương pháp giải
•
Để biểu diễn điểm
(;)M ab
trên mặt phẳng tọa độ ta làm như sau:
Kẻ đường thẳng vuông góc với trục hoành tại điểm a.
Kẻ đường thẳng vuông góc với trục tung tại điểm b.
Hai đường thẳng cắt nhau tại một điểm đó là điểm M.
•
Xác định khoảng cách giữa hai điểm
(; )
AA
Ax y
và
B( ; )
BB
xy
Ta có:
;
AB AB
AH x x BH y y=−=−
Ta có:
2 22 22
AB AH BH AB AH BH= + ⇒= +
hay:
22
( )( )
BA BA
AB x x y y= − +−
. (*)
Ví dụ 1. Biểu diễn hai điểm
( )
2;1A
và
( )
4;5B
trên cùng một
mặt phẳng tọa độ. Tính khoảng cách giữa hai điểm đó.
Giải
Biểu diễn các điểm A, B như hình vẽ 1.
Trong
ABH∆
, ta có:
90 ; 4 2 2; 5 1 4.H AH BH= ° = − = = −=
x
y
O
a
b
M(a;b)
x
y
A
H
x
B
x
A
y
A
y
B
B
y
x
5
4
2
1
B
A
H
O
Áp dụng định lí Py-ta-go vào
ABH∆
vuông tại H, ta có:
2 2 2 22
2 4 20
20 2 5.
AB AH BH
AB
= + =+=
⇒= =
C
hú ý: Sau này trong thực hành ta sẽ vận dụng ngay công thức (*).
Ta có
( ) ( ) ( ) ( )
2 2 22
4 2 5 1 2 5.
BA BA
AB x x y y= − + − = − +− =
Ví dụ 2. Cho tam giác ABC có A(1;1); B(3;3) và C(5;1).
a) Tính chu
vi tam giác ABC.
b) Ch
ứng minh rằng tam giác ABC vuông cân.
Giải
a) Ta có:
( ) ( )
22
31 31 8 22.AB = − +− = =
( ) ( )
( ) ( )
22 2 2
5 1 1 1 4; 5 3 1 3 4 4 2 2.AC BC= − +− = = − +− = +=
Vậy chu vi tam giác ABC là:
( )
22 22 4 4 2 1AB BC AC+ + = + += +
b) Ta có:
•
22AB BC= =
, suy ra
ABC∆
cân tại B. (1)
•
( )
2
22
22 2
22
22 8
4 16
AB BC
AB BC AC
AC
= = =
⇒+=
= =
ABC⇒∆
vuông tại B. (2)
Từ (1) và (2) suy ra
ABC∆
vuông cân tại B.
Ví dụ 3. Cho các điểm A(2;4), B(-1;0) và C(0;4).
a) Biểu diễn các điểm A, B, C trên mặt phẳng tọa độ.
b) Tính chu
vi và diện tích của tam giác ABC.
Giải
a) Bi
ểu diễn các điểm A(2;4), B(-1;0) và C(0;4) như hình 2.
Hình 1
y
x
Hình 2
4
2
-1
B
A
C
O
b) Ta thấy A, B, C không thẳng hàng nên A, B, C là ba đỉnh của một tam giác. Áp dụng
công th
ức:
( ) ( )
22
NM NM
MN x x y y= − +−
, ta tính được
5; 2; 17.AB AC BC= = =
Chu vi tam giác ABC là:
5 2 17 7 17++ =+
(đvd).
Diện tích tam giác ABC là:
11
. .4.2 4
22
ABC
S BH CA= = =
(đvdt).
Ví dụ 4. Cho hai điểm A(2;4) và B(-1;0) trên hệ trục tọa độ
Oxy.
a) Bi
ểu diễn các điểm A, B trên mặt phẳng tọa độ.
b) Tì
m điểm C trên trục hoành sao cho
ABC∆
cân tại A.
Giải
a) Biểu diễn các điểm A(2;4), B(-1;0) như hình 3.
b) Vì
C nằm trên trục hoành Ox nên tung độ của điểm C
bằng 0, do đó C(x;0) với x
1.≠
Áp dụng công thức:
( ) ( )
22
NM NM
MN x x y y= − +−
, ta
tính được
( ) ( )
22
5; 2 0 4 .AB AC x= = − +−
Ta có
ABC∆
cân tại A
.AB AC⇔=
( ) ( )
( ) ( )
22 2 2
2 0 4 5 2 16 25 2 9x xx⇔ − +− =⇔− +=⇔− =
5x⇔=
hoặc
1x = −
(loại vì điều kiện
1x ≠−
).
Vậy C(5;0) thì
ABC∆
cân tại A.
Chú ý:
• Ta có thể giải cách khác như sau:
ABC∆
cân tại A
3HB HC HC⇔=⇔=
(vì HB = 3)
2 3 5.xx⇔−=⇔=
Do đó, nếu kết hợp với kiến thức hình học thì chúng ta có thể giải bài toán đơn giản
hơn, nhanh hơn.
• Ta có thể thay đổi yêu cầu bài toán thành “Tìm điểm C trên trục hoành sao cho
ABC∆
cân”. Với yêu cầu mới ta phải giải bài toán trong ba trường hợp:
- Trường hợp 1:
ABC∆
cân tại A.
y
x
x
H
Hình 3
4
2
-1
B
A
C
O
- Trường hợp 2:
ABC∆
cân tại B.
- Trường hợp 3:
ABC∆
cân tại C.
Dạng 4. ĐIỂM THUỘC ĐỒ THỊ. ĐIỂM KHÔNG THUỘC ĐỒ THÌ CỦA HÀM SỐ
Phương pháp giải
Cho hàm số
()y fx=
có miền xác định D và có đồ thị G, khi đó:
•
( )
00
;Mxy
thuộc đồ thị G khi và chỉ khi
0
00
()
xD
y fx
∈
∈
•
( )
00
;Mxy
không thuộc đồ thị G khi và chỉ khi
00
()y fx≠
hoặc
0
.xD∉
Ví dụ 1. Cho hàm số
() .y fx x= =
Trong các điểm A(9;3), B(4; -2), M(-1;1) và
( )
4 2 3; 3 1N +−
điểm nào không thuộc và điểm nào thuộc đồ thị (G) của hàm số đã cho ?
Giải
Ta có:
()MG∉
vì khi
1x = −
thì hàm số không xác định
()BG∉
, vì
42 2= ≠−
( )
9;3 ( )AG∈
, vì
(9) 9 3f = =
( )
4 2 3; 3 1 ( )NG+ −∉
vì:
( )
2
(4 23) 4 23 3 1 3 1 3 1.f + = + = + = +≠ −
Ví dụ 2. Điểm
( )
1;1M −
thuộc đồ thị của hàm số nào trong các hàm số dưới đây ?
(A)
2
;yx=
(B)
4
;yx=
(C)
3 2;yx= +
(D)
3
.yx= −
Gi
ải
Loại (A), (B) vì tung độ của M âm.
Loại (D), vì hoành độ và tung độ của M cùng dấu.
Chọn (C).
Ví dụ 3. Khi m thay đổi, tìm tập hợp các điểm M có tọa độ như sau:
a)
( ;3);Mm
b)
(2; ).Mm
Giải
a)
Ta có f(m) = 3, khi m thay đổi f(m) luôn nhận một giá trị không đổi. Hàm số y = f(m) =
3 là
một hà
m hằng.
Đồ thị của hàm số y = 3 là đường thẳng song song với trục hoành và cắt trục tung tại điểm có
tung độ bằng 3 (hình 4).
Tập hợp các điểm M(m;3) là đường thẳng song song với trục hoành và cắt trục tung tại điểm
có tung độ bằng 3 (hình 4).
b)
Tập hợp các điểm M(2; m) là đường thẳng song song với trục tung và cắt trục tung tại điểm
có hoành độ bằng 2 (hình 5)
Ví d
ụ 4. Cho hàm số
( ) ( 1) 2 .y fx m x m= =+−
a) Tìm m để đồ thị của hàm số đã cho đi qua điểm A(1 ; 1).
b) Ch
ứng minh rằng đồ thị của hàm số đã cho luôn đi qua một điểm cố định với mọi m.
Giải
a)
( )
1;1 : ( 1) 2 1 ( 1).1 2 0.A dy m x m m m m∈ =+−⇔=+−⇔=
b)
00 0 0
( ; ) : ( 1) 2 ( 1) 2Mxydymxmymxm∈ =+− ⇔=+ −
0 00
( 2) ( ) 0.mx x y⇔ −+ − =
(1)
d đi qua M với mọi m khi (1) đúng với mọi m, tức là:
00
00 0
20 2
.
02
xx
xy y
−= =

⇔

−= =

Vậy d luôn đi qua điểm (2; 2) cố định với mọi m.
Dạng 5. XÁC ĐỊNH HÀM SỐ BẬC NHẤT
y
x
y = 3
M
m;3
( )
Hình 4
3
m
O
y
x
x = 2
M
2;m
( )
Hình 5
m
2
O
Phương pháp giải
Hàm số bậc nhất là hàm số co dạng
,y ax b= +
trong đó
a
và
b
là các số cho trước và
0.a ≠
Ví dụ 1. Trong các hàm số sau, hàm số nào là hàm số bậc nhất ?
a)
1 3;yx= −
b)
2
2 5;y xx= +−
c)
( )
2
2 3;yx x x=+ −+
d)
( )
2
3 1 1.yx=−+
Giải
a) Hàm số
13yx= −
hay
31yx=−+
có dạng
y ax b= +
, trong đó
3 0,a =−≠
nên
31yx=−+
là hàm số bậc nhất.
b) Hàm
số
2
25y xx= +−
không phải là hàm bậc nhất vì sau khi thu gọn không có dạng
y ax b= +
.
c) Hà
m số
( )
2 22
2 3 2 3 23yx x x x xx x= + − += + − += +
là hàm số bậc nhất vì hàm số
có dạng
y ax b= +
, trong đó
2 0.a = ≠
d) H
àm số
( )
2
31 1yx=−+
là hàm số bậc nhất vì hàm số có dạng
y ax b= +
, trong đó
( )
2
3 1 0.a = −≠
Ví dụ 2. Cho ba hàm số
22
() 3; () 1fxx gxxx= + = −+
và
2
( ) 2 3 1.hx x x= +−
Xét các khẳng định:
(I)
() ()fx gx−
là hàm số bậc nhất;
(II)
() ()hx gx−
là hàm số bậc nhất;
(III)
() () ()f x gx hx+−
là hàm số bậc nhất.
Trong các khẳng định trên, khẳng định đúng là:
(A) Ch
ỉ (I)
(B) Ch
ỉ (II)
(C) Chỉ (I) và (II) (D) Chỉ (I) và (III).
Giải
Ta thực hiện phép tính cộng, trừ các đa thức được kết quả:
() () 2f x gx x−=+
, là hàm số bậc nhất;
2
() () 4 2hx gx x x− =+−
không là hàm số bậc nhất;
() () () 4 5f x gx hx x+ − =−+
là hàm số bậc nhất.
Do đó, chọn (D).
Ví dụ 3. Cho hàm số
2
( ) (1 2 ) 2.y f x mx m= =− ++
Tìm m để hàm số đã cho là hàm số bậc nhất.
Giải
Hàm số
2
( ) (1 2 )y f x mx m==−+
là hàm số bậc nhất khi và chỉ khi:
1
12 0 .
2
mm− ≠⇔ ≠
Ví d
ụ 4. Cho hàm số
22
( ) ( ) 2.y f x m m x mx= = − ++
Tìm m để hàm số đã cho là hàm số bậc nhất.
Giải
Hàm số
22
() ( ) 2y f x m m x mx= = − ++
là hàm số bậc nhất khi và chỉ khi:
2
( 1) 0
0
1 0 1.
0
0
mm
mm
mm
m
m
−=
−=
⇔ ⇔ −= ⇔ =

≠
≠
Khi
1m =
, ta có hàm số
2yx= +
là hàm số bậc nhất.
D
ạng 6. XÁC ĐỊNH TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ
Phương pháp giải
•
Vận dụng định nghĩa: Với mọi
12
,xx
thuộc miền xác định D là một khoảng hoặc đoạn hoặc
nửa khoảng:
Nếu
12
xx>
mà
12
() ()fx fx>
thì hàm số
()y fx=
đồng biến trên D.
Nếu
12
xx>
mà
12
() ()fx fx<
thì hàm số
()y fx=
nghịch biến trên D.
•
Trong thực hành giải toán ta làm như sau: Với mọi
12 1 2
,,x x Dx x∈≠
Nếu
12
12
() ()
0
fx fx
xx
−
>
−
thì hàm số
()y fx=
đồng biến trên D.
Nếu
12
12
() ()
0
fx fx
xx
−
<
−
thì hàm số
()y fx=
nghịch biến trên D.
•
Hàm số
( ) a ( 0)y f x x ba= =+≠
Nếu
0a >
thì hàm số đồng biến trên
Nếu
0a >
thì hàm số đồng biến trên
.
Ví dụ 1. Chứng minh hàm số
() 3y fx x= = +
đồng biến trên tập xác định.
Giải
Hàm số xác định khi
3.x ≥−
Lấy
12
,xx
bất kỳ thõa mản
12 1 2
, 3,xx x x≥− ≠
, ta có:
( ) ( )
12
12 1 2
12 12
1212 12
33
( ) ( ) ( 3) ( 3) 1
0
()33 33
xx
fx fx x x
xx xx
xxxx xx
+− +
− +− +
= = = >
−−
− ++ + ++ +
Do đó hàm số
() 3y fx x= = +
đồng biến trên tập xác định.
Ví dụ 2. Cho hàm số
() 2y fx m x= = −
(
m
là hằng số). Xét sự đồng biến, nghịch biến của hàm
số
()y fx=
trên
.
Giải
Cách 1. Tập xác định:
.
Lấy
12
,xx
thuộc
sao cho
12
xx<
, ta có:
1 2 1 2 1 2 21
( ) ( ) (m 2 ) ( 2 ) 2 2 2( ) 0.fx fx x m x m x m x x x− = − − − =− −+ = − >
Do đó
12
() ()fx fx>
, suy ra hàm số nghịch biến trên
.
Cách 2.
() 2 2y fx m x x m= =− =−+
là hàm số bậc nhất có hệ số
20a =−<
nên hàm số
nghịch biến trên
.
Ví dụ 3. Tìm
m
để hàm số
2
( 2) 1ym x= −+
(
m
là tham số) đồng biến trên
.
Giải
Hàm số
2
( 2) 1ym x= −+
là hàm số bậc nhất khi
2
2m ≠
với hệ số
2
2.am= −
Do đó hàm số đồng biến trên
2
20 2mm⇔ − > ⇔ <−
hoặc
2.m >
Chú ý: Khi
2m = −
hoặc
2m =
thì
0 11yx= +=
nên hàm số là hàm hằng. Khi đó đồ thị
của hàm số là đường thẳng song song với trục hoành và cắt trục tung tại điểm có tung độ bằng
1.
Ví dụ 4. Cho hai hàm số
( ) 2012f x mx= +
và
2
g( ) ( 1) 2011xm x= +−
(
m
là tham số).
Xét tính Đúng, Sai của các khẳng định sau:
(A)
() ()fx gx+
là hàm số đồng biến trên
;
(B)
g() ()x fx−
là hàm số đồng biến trên
;
(C)
() ()fx gx−
là hàm số đồng biến trên
.
Giải
Ta thực hiện phép tính cộng, trừ các đa thức, được kết quả:
2
() () ( 1) 1fx gx m m x+ = ++ +
là hàm số bậc nhất, với hệ số
2
2
13
10
24
am m m

= + += + + >


với mọi m nên khẳng định (A) đúng.
2
g( ) ( ) ( 1) 4023x fx m m x− = −+ −
là hàm số bậc nhất, với hệ số
2
2
13
10
24
am m m

= − += − + >


với mọi m nên khẳng định (B) đúng.
2
( ) ( ) ( 1) 4023fx gx m m x− =− −+ +
là hàm số bậc nhất, với hệ số
2
2
13
( 1) 0
24
a mm m

=− −+=− − −<


với mọi m nên khẳng định (C) đúng.
C. BÀI TẬ
P TỰ LUYỆN
1. Cho hai hàm số
2
()
3
x
y fx
−
= =
và
() 1y gx x x= = +−
a) Tì
m tập xác định của các hàm số đã cho.
b) Tính
11
(2), , (0),g(1),g .
22
ff g
 
 
 
2. Cho các đi
ểm A(2;3), B(-2;0) và C(4;3).
a) Bi
ểu diễn các điểm A, B, C trên mặt phẳng tọa độ.
b) Tính chu
vi và diện tích của tam giác ABC.
c) Tì
m điểm M trên trục hoành sao cho tam giác ABM cân tại A.
d) Tì
m điểm N trên trục tung sao cho tam giác ABN cân tại B.
3. Cho hàm số
( ) 3.y f x mx m= =− +−
Biết
( 2) 6.f −=
Tính
( 3).f −
4. Cho hà
m số
( )
( ) 3 2 2 3.y fx x= = − ++
Tìm
x
sao cho
( ) 3.fx=
5. Cho hàm số
( ) 4.y f x mx= =−+
a) Tì
m
m
để đồ thị của hàm số đã cho đi qua điểm
( 1;1).A −
b) Ch
ứng minh rằng đồ thị của hàm số đã cho luôn đi qua một điểm cố định với mọi
m
.
6. Với các giá trị nào của m thì hàm số sau là hàm số bậc nhất ?
a)
2
(4 1)ymx= −
b)
5 ( 2)y mx=−−
c)
22 2
( 2 4 ) 1 2.y mx mx x x= + + − +−
7. Xác định tính đồng biến, nghịch biến của các hàm số sau:
a)
( ) (1 2 ) 1y fx x==−+
, với
x∈
b)
() 2y fx x= = −
, với
2x ≥
c)
2
() 2y fx x= = +
, với
0.x <
8. Cho hàm số
( ) (1 3) 1y fx x==−−
và
( 1), ( 2 )fm fm++
là hai giá trị tương ứng của
hàm số tại
1, 2.xm xm=+=+
Khi đó:
(A)
( 1) ( 2 )fm fm+> +
(B)
( 1) ( 2)fm fm+< +
(C)
( 1) ( 2)fm fm+= +
(B) Không thể so sánh được vì phụ thuộc vào giá trị của m.
9. Chứng minh rằng không tồn tại đa thức
()fx
bậc ba với hệ số nguyên sao cho
(7) 2010f =
và
(11) 2012.f =
HƯỚNG DẪN GIẢI – ĐÁP SỐ
1. a) Hàm số
2
()
3
x
y fx
−
= =
xác định khi:
2 0 2.xx−≥⇔≥
Hàm số
() 1y gx x x= = +−
xác định khi:
00
0 1.
10 1
xx
x
xx
≥≥

⇔ ⇔≤≤

−≥ ≤

b)
1
(2) 0;
2
ff

=


không xác định;
1 112
(0) 1; g(1) 1; g 2
.
2
222
g

= = =+==


2. a) Biểu diễn các điểm A(2;3), B(-2;0) và C(4;3) như hình 6.
b) Ta th
ấy A, B, C không thẳng hàng nên A,
B, C là
ba đỉnh của một tam giác. Áp dụng công thức:
( ) ( )
22
NM NM
MN x x y y= − +−
, ta tính được
5; 2; 3 5.AB AC BC= = =
Chu vi tam giác ABC là:
5 2 35 7 35.++ =+
Diện tích tam giác ABC là:
11
. .3.2 3
22
ABC
S BH AH= = =
(đvdt)
c) M(6;0).
d)
(0; 21)N
hoặc
(0; 21).N −
3.
( 2) 6 ( 2) 3 6 3 9 3f mm m m− = ⇔− − + − = ⇔ = ⇔ =
( ) 3 ( 3) 9.fx x f⇒ =− ⇒ −=
4.
( )
( )
2
() 3 3 2 2 3 6 2.
32
fx x x
−
= ⇔ − + + ⇔= =− +
−
5. a)
( 1; 1) : 4 1 ( 1) 4 5.A d y mx m m−−∈ =− +⇔−=− −+⇔ =−
b)
00 0 0 0 0
( ; ) : 4 4 4 0.M x y d y mx y mx mx y∈ =− +⇔ =− +⇔ + −=
(1)
d đi qua M với mọi m khi (1) đúng với mọi m, tức là:
00
00
00
40 4
xx
yy
= =

⇔

−= =

y
x
4
2
H
3
Hình 6
-2
B
A
C
O
Vậy d luôn đi qua điểm M(0;4) cố định với m.
6. a)
1
2
m ≠±
b)
5m <
c) m = 0 hoặc m = 4.
7. a) Với mọ
i
12 1 2
,,xx x x∈>
, ta có:
1 2 12
( ) ( ) (1 2 )( ) 0fx fx x x− =− −<
, vì
12
1 2 0, 0.xx− < −>
Do đó
()fx
là hàm số nghịch biến trên
.
b) V
ới mọ
i
12 1 2
, 2,xx x x≥≠
, ta có:
( )
( )
( )
( )
1212
12
12
12 12
12
12 1 2
2222
22
() 1
0.
22
22
xxxx
xx
fx x
xx xx
xx
xx x x
−− − −+ −
−− −
−
= = = >
−−
−+ −
− −+ −
Do đó
()fx
là hàm số đồng biến với mọi
2.x ≥
c) V
ới mọ
i
12 1 2
, 0,xx x x<>
, ta xét:
22
1 2 1 2 1 21 2
( ) ( ) ( 2) ( 2) ( )( ) 0fx fx x x x x x x− = +− += − + <
Vì
12 12
0, 0xx xx−> +<
với mọi
12 1 2
, 0,xx x x<>
, do đó hàm số nghịch biến với mọi
0.x <
8. Hàm số
( ) (1 3) 1y fx x==−−
là hàm số nghịch biến vì
1 3 0.a =−<
Ta có:
( 1) ( 2)fm fm+> +
vì
12mm+< +
. Chọn (A).
9. Giả sử có đa thức
32
() :,,, , 0f x ax bx cx d a b c d a= + ++ ∈ ≠
thỏa mãn
(7) 2010, (1) 2012ff= =
. Ta có:
3 2 32
(11) (7) ( .11 .11 .11 ) ( .7 .7 .7 )f f a b c da b cd− = + + +− + + +
=
33 22 2
4 44
.(11 7 ) .(11 7 ) .(11 7 )abc−+ −+ −

  
Từ đó suy ra:
[ ]
(11) (7) 4.ff−
(*)
Mặt khác
(11) 2012, (7) 2010ff= =
nên
(11) (7) 2.ff−=
(**)
Từ (*) và (**) suy ra
24
(vô lý), suy ra điều giả sử là sai (đpcm).
§3. ĐỒ THỊ CỦA HÀM SỐ 𝒚 = 𝒂𝒙 + 𝒃(𝒂 ≠ 𝟎)
A. TRỌNG TÂM KIẾN THỨC
1. Đ
ồ thị của hàm số 𝒚 = 𝒂𝒙 + 𝒃(𝒂 ≠ 𝟎)
Đồ thị của hàm số
( 0)y ax b a=+≠
là một đường thẳng ( kí hiệu là (d) ):
+ Cắ
t trục tung tại điểm có tung độ bằng b hay (d) luôn đi qua điểm B(0;b)
+
Song so
ng với đường thẳng
y ax=
nếu
0b ≠
; trùng với đường thẳng
y ax=
nếu b = 0.
Chú ý.
b được gọi là tung độ gốc của đường thẳng.
Đồ thị của hàm số
( 0)y ax b a=+≠
còn được gọi là đường thẳng
y ax b= +
hoặc
đường thẳng
0ax y b−+=
.
2. Cách
vẽ đồ thị của hàm số 𝒚 = 𝒂𝒙 + 𝒃(𝒂 ≠ 𝟎)
Trường hợp 1: Khi b = 0 thì
y ax=
. Đồ thị của hàm số
y ax=
là đường thẳng đi qua gốc tọa
độ
(0;0)O
và điểm
(1; ).Aa
Trường hợp 2:
y ax b= +
với
0a ≠
và
0b ≠
Cách 1
. + Xác định hai điểm bất kỳ của đồ thị
Chẳng hạn cho
1x =
thì
.1ya bab= +=+
, ta được
(1; )Bab+
; cho
2x =
thì
.2ya b= +
ta
được điểm
(2;2 ).C ab+
+ Vẽ đường thẳng BC ta được đồ thị hàm số.
Cách 2. + Xác định giao điểm của đồ thị với hai trục tọa độ:
• Cho
0 .0 (0; )x ya bb M b=⇒= +=⇒
thuộc trục tung.
• Cho
0 0 . ( ;0)
bb
y ax b x N
aa
=⇒= +⇔=−⇒ −
thuộc trục hoành
+ Vẽ
đường thẳng MN ta được đồ thị hàm số.
Chú ý. Khi
0b =
thì
y ax=
; đồ thị của hàm số
y ax=
đi qua gốc tọa độ
(0;0).O
Khi
0b ≠
thì đồ thị của hàm số
y ax b= +
đi qua điểm
B(0;b).
Khi
0a >
thì đồ thị của hàm số
y ax b= +
là đường thẳng có chiều đi lên từ trái sang phải
(hàm số đồng biến).
Khi
0a <
thì đồ thị của hàm số
y ax b= +
là đường thẳng có chiều đi xuống từ trái sang phải
(hàm số nghịch biến).
Đường thẳng
yx=
là đường phân giác của góc phần tư thứ (I) và (III).
Đường thẳng
yx= −
là đường phân giác của góc phần tư thứ (II) và (IV).
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. ĐIỂM THUỘC ĐƯỜNG THẲNG.
ĐIỂM KHÔNG THUỘC ĐƯỜNG THẲNG
Phương pháp giải
Cho điểm
00
(; )Mx y
và đường thẳng (d) có phương trình
.y ax b= +
Khi đó:
00
00
()
()
M d y ax b
M d y ax b
∈ ⇔= +
∉ ⇔≠ +
Ví dụ 1. Cho đường thẳng (d):
3 1.yx=−+
Trong các điểm
1
( 1;2), (0;1), ;0 .
3
M NP

−


Hãy xác
định các điểm thuộc và không thuộc đường thẳng (d).
Giải
Ta có:
( 1; 2) ( )Md−∉
vì khi x = -1 thì -3(-1) + 1 = 3 + 1 = 4
≠
2;
(0;1) ( )Nd∈
, vì khi x = 0 thì -3.0 +1 = 0 + 1 = 1;
1
;0 ( )
3
Pd

∈


, vì khi
1
3
x =
thì
1
3. 1 1 1 0.
3
− +=−+=
Ví d
ụ 2. Điểm
( 2;1)M
thuộc đường thẳng nào trong các đường thẳng dưới đây ?
(A)
12yx= +−
(B)
210xy+ − +=
(C)
21 2yx= +−
(D)
20xy+− =
Giải
Kí hiệu các đường thẳng ở các trường hợp (A) , (B) , (C) và (D) lần lượt là
1
( ): 1 2d yx= +−
2
( ): 2 1 0d xy+ − +=
3
( ): 2 1 2dy x= +−
4
( ): 2 0d xy+− =
Ta có:
1
( 2;1) ( )Md∈
, vì khi
2x =
thì
21 21+− =
2
( 2;1) ( )Md∉
, vì khi
2x =
thì
2 21 11− + − =−≠
3
( 2;1) ( )Md∉
, vì khi
2x =
thì
2. 2 1 2 3 2 1+−=−≠
4
( 2;1) ( )Md∉
, vì khi
2x =
thì
2 2 0 1.−+ =≠
Chọn (A).
Ví dụ 3. Cho đường thẳng (d):
2 3.yx=−+
Tìm m để đường thẳng (d) đi qua điểm
( ; 3).Am−−
Giải
Đường thẳng (d):
23yx=−+
đi qua điểm
( ; 3)Am−−
khi:
3 2.( m) 3 2 6 3.mm−=− − + ⇔ =−⇔ =−
V
ậy đường thẳng (d):
23yx=−+
đi qua điểm
( ; 3)Am−−
khi
3.m = −
Ví dụ 4. Cho đường thẳng (d):
( 2) 3 1ym xm=+ +−
. Tìm m để đường thẳng (d) đi qua điểm
( 2;3).M −
Giải
( 2;3) ( )Md−∈
:
( 2) 3 1ym xm=+ +−
khi:
3 ( 2)( 2) 3 1 3 2 4 3 1 8.m m mmm= + − + −⇔ =− −+ −⇔ =
Vậy đường thẳng (d):
( 2) 3 1ym xm=+ +−
đi qua điểm
( 2;3)M −
khi
8.m =
Ví dụ 5. Chứng minh rằng đường thẳng
( 2) 4 3 0m xy m− ++ −=
luôn đi qua một điểm cố định
với mọi giá trị của m.
Giải
Gọi
00
(; )Mx y
là điểm thuộc (d), ta có:
( )
00
2 4 30m xy m+ + + −=
( ) ( )
0 00
4 2 30mx x y⇔ ++ +−=
Đường thẳng
( )
d
luôn đi qua
( )
00
;Mxy
với mọi
m
khi và chỉ khi:
00
00 0
40 4
2 3 0 11
xx
xy y
+= =−

⇔

+ −= =

.
Vậy
( )
d
luôn đi qua điểm cố định
( )
4;11M −
với mọi giá trị của
m
.
D
ạng 2. XÁC ĐỊNH ĐƯỜNG THẲNG.
Phương pháp giải
Gọi hàm số cần cần tìm là:
y ax b= +
( )
0a ≠
, ta phải tìm
a
và
b
.
+ Với điều kiện của bài toán xá định được các hệ số liên hệ giữa
a
và
b
.
+ Giải phương trình để tìm
,ab
.
Ví dụ 1. Cho hàm số bậc nhất
2y xb=−+
. Xác định
b
nếu:
a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng
2
.
b) Đ
ồ thị hàm số đi qua điểm
( )
1; 2A −
.
Lời giải
a) Đ
ồ thị hàm số
2y xb=−+
cắt trục tung tại điểm có tung độ bằng
2
, nên
2b =
.
Vậy đồ thị hàm số cần tìm là
22yx=−+
.
b) Đ
ồ thị hàm số
2y xb=−+
đi qua điểm
( )
1; 2A −
khi:
( ) ( )
2 2. 1 2 2 0b bb=− −+⇔=+⇔=
.
Vậy
0b =
thì
2yx= −
đi qua điểm
( )
1; 2A −
.
Ví dụ 2. Xác định đường thẳng
( )
d
, biết
( )
d
có dạng
4y ax= −
và đi qua điểm
( )
3; 2A −
.
Lời giải
Đường thẳng
( )
:4d y ax= −
đi qua điểm
( )
3; 2A −
khi:
( )
2 .3 4a= −−
3 24 2aa⇔− = + ⇔ =−
.
Vậy
( )
d
có phương trình
24yx=−−
đi qua điểm
( )
3; 2A −
.
Ví dụ 3. Cho hàm số
( )
22y m xm= − ++
. Xác định
m
, biết:
a) Đ
ồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng
2−
.
b) Đ
ồ thị hàm số đi qua gốc tọa độ.
Lời giải
a) Đồ thị
( )
d
của hàm số
( )
22y m xm= − ++
cắt trục hoành tại điểm có hoành độ bằng
2−
nên
( )
2;0A −
thuộc
( )
d
.
Do đó:
( ) ( )
0 2. 2 2mm= − −++
2 4 20 6mm m⇔− + + + = ⇔ =
.
b) Đ
ồ thị
( )
d
của hàm số
( )
22y m xm= − ++
đi qua gốc tọa độ
( )
0;0O
thuộc
( )
d
.
Do đó:
( )
0 2 .0 2mm= − ++
20 2mm⇔ +=⇔ =−
.
Ví dụ 4. Xác định đường thẳng đi qua hai điểm
( )
3;0A −
và
( )
0;2B
.
Lời giải
Gọi phương trình đường thẳng
AB
là:
y ax b= +
.
Ta có:
( )
3;0A AB−∈
( )
0 .3ab⇒= −+
hay
3ba=
.
( )
0;2 2 .0B AB a b∈ ⇒= +
hay
2b =
.
Từ đó suy ra
2
3
a =
.
Vậy phương trình đường thẳng
AB
là:
2
2
3
yx= +
.
Ví dụ 5. Cho đường thẳng
( )
1
: 2012 2dy x= +
. Xác định đường thẳng
( )
2
d
sao cho
( )
1
d
và
( )
2
d
cắt nhau tại một điểm nằm trên trục tung.
Lời giải
y
x
2
-3
Hình 7
B
O
Đồ thị hàm số
2012 2yx= +
cắt trục tung tại điểm có tung độ bằng
2
vì có tung độ gốc là
2b =
⇒
đường thẳng
( )
1
d
luôn đi qua điểm
( )
0;2A
nằm trên trục tung.
Vì
( )
1
d
và
( )
2
d
cắt nhau tại một điểm nằm trên trục tung nên
( )
0;2A
thuộc
( )
2
d
.
Do đó
( )
2
d
có phương trình
2y =
hoặc
0x =
(trục tung) hoặc
2y ax= +
(với
0, 2012aa≠≠
)
Chú ý. Có vô số đường thẳng đi qua điểm
( )
0;2A
.
D
ạng 3. VỀ ĐỒ THỊ CỦA HÀM SỐ
( )
0y ax b a=+≠
Phương pháp giải
+ Tìm hai điểm thuộc đồ thị hàm số bằng cách cho
x
nhận hai giá trị xác định rồi tính hai
giá trị tương ứng của
y
(thông thường ta lấy hai điểm đó là giao điểm của đồ thị với trục
hoành và trục tung)
+ Đường thẳng đi qua hai điểm vừa tìm được là đồ thị hàm số cần vẽ.
Ví dụ 1. Cho các hàm số sau:
2yx=−+
( )
1
;
( )
2 12yx= −
.
a) Vẽ đồ thị các hàm số
( ) ( )
1, 2
trên cùng một mặt phẳng tọa độ.
b) Xác đ
ịnh tọa độ giao điểm
I
của
( )
1
và
( )
2
.
Lời giải
a) Hình 8 * Vẽ đồ thị hàm số
( )
1
:
y
y = 2x-1
D
C
2
I
-1
1
1
2
Hình 8
B
A
O
y = -x+2
x
Cho
0x =
( )
2 0;2y A Oy⇒=⇒ ∈
;
( )
0 2 2;0y x B Ox=⇒=⇒ ∈
.
Đường thẳng
AB
là đồ thị hàm số
2yx=−+
.
* V
ẽ đồ thị hàm số
( )
2
:
Cho
01xy=⇒=−
( )
0; 1C Oy⇒ −∈
;
11
0 ;0
22
y x D Ox

=⇒=⇒ ∈


.
Đường thẳng
CD
là đồ thị hàm số
21yx= −
.
b) Cách 1. Từ giao điểm
I
của hai đồ thị hàm số ta vẽ đường thẳng vuông góc với trục
hoành, cắt trục này tại điểm có hoành độ là
1
. Vậy tọa độ giao điểm là
( )
1;1I
.
Cách 2. Gọi tọa độ giao điểm
I
là
( )
11
;xy
.
Vì
I
là giao điểm của
AB
và
CD
nên
I
vừa thuộc
AB
, vừa thuộc
CD
.
Vì
( )
11
;:2I x y AB y x∈ =−+
nên
11
2yx=−+
.
Vì
( )
11
; : 21I x y CD y x∈=−
nên
11
21yx= −
.
Suy ra ta có:
11 11
22 1 3 3 1xx xx− + = −⇔ = ⇔ =
11
2 121yx⇒ =−+=−+=
.
Vậy tọa độ giao điểm
I
là
( )
1;1I
.
Ví dụ 2. Cho hàm số:
( )
1
1
2
yxd= −
.
a) V
ẽ đồ thị
( )
d
của hàm số đã cho.
b) Tính kh
oảng cách từ gốc
O
của hệ trục tọa độ đến đường thẳng
( )
d
.
Lời giải
a) Cho
01xy=⇒=−
( ) ( )
0; 1 ; 0 2 2;0A Oy y x B Ox⇒ −∈ =⇒=⇒ ∈
.
Đường thẳng
AB
là đồ thị
( )
d
của hàm số
1
1
2
yx= −
.
b) Kẻ
OH
vuông góc với
( )
d
tại
H
. Khi đó
OH
là khoảng cách từ
O
đến đường thẳng
( )
d
(hình 9)
Trong ta
m giác vuông
OAB
, ta có:
2 2 222
1 1 1 115
12 4OH OA OB
= + =+=
.
Từ đó suy ra:
2
4 25
55
OH OH=⇒=
.
Vậy khoảng cách từ
O
đến
( )
d
là
25
5
.
Ví dụ 3. Cho các hàm số sau:
( )
21y =
;
( )
12yx= +
;
( )
2 13y mx m= +−
.
a) Vẽ đồ thị các hàm số
( ) ( )
1, 2
trên cùng mặt phẳng tọa độ.
b) Tì
m
m
để đồ thị hàm số
( )
3
đi qua trong giao điểm của hai đồ thị
( )
1
và
( )
2
.
Lời giải
a) V
ẽ đồ thị của hàm số
2y =
(1);
Đồ thị hàm số
2y =
là đường thẳng song song với trục hoành và cắt trục tung tại điểm có
tung độ bằng
2
.
Vẽ đồ thị của hám số
1yx= +
(2)
y
H
2
-1
Hình 9
B
A
O
x
Ta có:
( )
1 khi 1
1
1 khi 1
xx
yx
xx
+ ≥−
= +=
− + ≤−
.
Từ đó, ta được đồ thị có hình chữ V như hình 10.
Từ hình vẽ ta thấy đồ thị của hai hàm số
( )
1
và
( )
2
cắt nhau tại hai điểm
( )
1; 2M
và
( )
3; 2N −
.
b)
Đồ thị
( )
d
của hàm số
21y mx m= +−
đi qua giao điểm của hai đồ thị hàm số
( )
1
và
đ
ồ thị hàm số
( )
2
khi và chỉ khi
( )
d
đi qua điểm
M
hoặc
N
.
+
Trường h
ợp
( )
d
đi qua
( )
1; 2M
. Kh đó:
2 2 .1 1mm= +−
33m⇔=
1m⇔=
.
+ Trường hợp
( )
d
đi qua
( )
3; 2N −
. Khi đó:
( )
2 2. . 3 1 5 3mm m= − + −⇔ =−
3
5
m⇔=−
.
Vậy với
1m =
hoặc
3
5
m = −
thì đồ thị hàm số
( )
3
đi qua giao điểm của đồ thị hàm số
( )
1
và đ
ồ thị hàm số
( )
2
.
Ví dụ 4. Cho hàm số
3y mx= +
( )
d
. Tìm
m
để khoảng cách từ gốc tọa độ
O
đến đường
thẳng
( )
d
là lớn nhất.
Lời giải
y
M
o
2
-3
Hình 10
N
-1
1
x
Trường hợp 1. Xét
0m =
.
Khi
0m =
thì
( )
d
có phương trình:
0. 3 3yx= +=
hay
3y =
.
Đồ thị hàm số
3y =
là đường thẳng song song với trục hoành và cắt trục tung tại điểm có
tung độ bằng
3
nên khoảng cách từ
O
đến
( )
d
bằng
3
.
Trường hợp 2. Xét
0m ≠
.
Khi đó
( )
:3d y mx= +
luôn đi qua điểm
( )
0;3A
nằm trên trục tung.
Kẻ
OH
vuông góc với
( )
d
tại
H
. Khi đó
OH
là khoảng cách từ
O
đến đường thẳng
( )
d
.
Ta có:
OH OA≤
hay
3OH ≤
(Dấu “=” không xảy ra vì
0m ≠
nên
H
không trùng
A
).
Do đó
3OH <
.
Kết hợp hai trường hợp ta có khi
0m =
thì khoảng cách từ
O
đến đường thẳng
( )
d
là lớn
nhất.
C. BÀI TẬP TỰ LUYỆN
1. Đồ thị của hàm số
21 2yx= +−
đi qua điểm nào sau đây?
A.
( )
1;1M −
B.
( )
1;1N
C.
( )
1; 1P −
D.
( )
2;1Q
2. Đi
ểm
( )
2;0E −
thuộc đường thẳng nào trong các đường thẳng sau đây?
( )
1
:2d yx= +
;
( )
2
: 24dy x=−−
;
( )
3
: 36dyx= +
;
( )
4
24
:
33
dy x= +
.
A. Chỉ thuộc đường thẳng
( )
1
d
B. Chi thuộc
( )
2
d
và
( )
4
d
Hình 11
y
x
H
d
3
y = 3
A
o
C. Chỉ thuộc
( )
2
d
và
( )
3
d
D. Thuộc cả bốn đường thẳng đã cho
3. Cho hai đường thẳng
( )
1
: 2 2012dy x= +
và
( )
2
1
: 2012
2
dy x=−+
. Đường thẳng nào
dưới đây không đi qua giao điểm của
( )
1
d
và
( )
2
d
?
A.
2012yx=
B.
2012yx= +
C.
2012 2012yx= +
D.
2012yx=−+
4. Vẽ đồ thị của các hàm số sau trên cùng một hệ trục tọa độ:
1
2
2
yx= +
;
22yx=−+
;
24yx=−+
.
5. Xác định đường thẳng đi qua hai điểm
( )
2;0A −
và
( )
0;3B
.
6. Cho
( ) ( )
12
: , : 0,5d y xd y x= =
; đường thẳng
( )
d
song song với trục
Ox
và cắt trục tung
Oy
tại điểm
C
có tung độ bằng
2
. Đường thẳng
( )
d
lần lượt cắt
( )
1
d
,
( )
2
d
tại
D
và
E
.
Khi đó, tính diện tích tam giác
ODE
.
7. Với giá trị nào của
m
thì đồ thị của các hàm số
24yx m= +−
và
32y xm= +−
cắt nhau
tại một điểm nằm trên trục tung.
8. Cho hai đường thẳng
( ) ( )
1
: 2 4 10d m x my− + +=
và
( ) ( )
2
: 2 2012 5 0dmx y m− + +− =
(
m
là tham số).
a) Ch
ứng minh rằng
( )
1
d
luôn đi qua một điểm cố định khi
m
thay đổi.
b) Tì
m
m
để hai đường thẳng
( ) ( )
12
,dd
cắt nhau tại một điểm thuộc trục hoành.
9. Cho hàm số
( ) ( )
22y fx m x= =−+
có đồ thị là đường thẳng
( )
d
.
a) Tì
m
m
để
( )
d
đi qua điểm
( )
1;1M −
.
b) Xác định
m
để khoảng cách từ điểm
( )
0;0O
đến
( )
d
có giá trị lớn nhất.
HƯỚNG DẪN GIẢI - ĐÁP SỐ
1. Ta thử cặp giá trị mà triệt tiêu
2
trước. Thử
( )
1;1N
thấy đúng. Chọn
( )
B
.
2. Thử trực tiếp ta thấy tọa độ
( )
2;0−
thỏa mãn cả bốn hàm số. Chọn
( )
D
.
3.
( )
1
d
và
( )
2
d
có cùng tung độ gốc
2012
, hệ số
a
khác nhau. Các đường thẳng có cùng
tung độ
2012
sẽ đi qua giao điểm của
( )
1
d
và
( )
2
d
. Do đó, ta loại (B), (C), (D), vì có
tung độ gốc là
2012
. Chọn (A).
4. (h.12) Vẽ đồ thị của hàm số
1
2
2
yx= +
( )
1
d
.
Cho
( )
0 2 0;2xyA=⇒=⇒
.
Cho
( )
0 4 4;0yx B= ⇒ =−⇒ −
.
Biểu diễn các điểm
,AB
trên mặt phẳng tọa độ.
Vẽ đường thẳng
AB
được đồ thị
( )
1
d
.
Tương tự ta vẽ được:
( )
2
: 22dy x=−+
;
( )
3
: 24dy x=−+
.
5. Gọi phương trình đường thẳng
AB
là:
y ax b= +
. Ta có:
( ) ( )
2;0 0 . 2A AB a b− ∈ ⇒= −+
hay
2ba=
.
( )
0;3 3 .0B AB a b∈ ⇒= +
hay
3b =
. Từ đó suy ra
3
2
a =
.
Vậy phương trình đường thẳng
AB
là:
3
3
2
yx= +
.
6. Vẽ nhanh đồ thị. Từ đồ thị ta thấy:
2, 2DE OC= =
.
4
Hình 12
o
2
x
d
2
(
)
d
1
(
)
d
3
(
)
2
4
1
A
B
y
Do đó diện tích tam giác cần tìm là:
11
. .2.2 2
22
ODE
S OC DE
∆
= = =
(đvdt)
7.
( )
0
0;M Oy M y∈⇒
. Giả sử
M
là giao điểm của
( )
1
d
và
( )
2
d
.
( )
10
: 24 4Mdy x m y m∈ = +− ⇔ =−
;
( )
20
:3 2 2M d y xm y m∈ = + −⇔ = −
.
Suy ra
4 23mm m− = −⇔ =
(Thử lại thấy đúng)
Vậy khi
3m =
thì
( )
1
d
cắt
( )
2
d
tại
( )
0;1M
thuộc
Oy
.
8.
a)
11
;
28
M

−


b) Giao đi
ểm thuộc trục hoành, nên tung độ
0y =
. Vậy:
( )
2 4 .0 1 0m xm− + +=
và
( )
2 2012.0 5 0mx m− + +− =
.
Suy ra:
15 4mm=−⇔=
(thử lại thấy đúng).
9. a)
3m =
.
b)
(h. 13) Khi
2: 2my= =
⇒
Khoảng cách từ
O
đến
( )
d
là
2OH =
.
Khi
2m ≠
:
( )
22ym x=−+
.
Cho
22
0 ;0
22
yx A
mm
−−

=⇒= ⇒

−−

Hình 13
y
x
O
K
d
( )
y = 2
H
A
2
Vẽ
( )
OK d⊥
. Ta có:
( ) ( )
0;2 : 2 2H dy m x∈ =−+
với mọi
m
.
Suy ra:
OK OH<
hay
2OK <
.
Vậy khoảng cách từ điểm
O
đến
( )
d
lớn nhất bằng
2
, đạt được khi
2m =
.
§4.
ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU
A. TR
ỌNG TÂM KIẾN THỨC.
1. Hai
đường thẳng song song.
Hai đường thẳng
( )
0y ax b a=+≠
và
( )
0y ax b a
′ ′′
=+≠
song song với nhau khi và chỉ
khi
,a ab b
′′
= ≠
và trùng nhau khi và chỉ khi
,a ab b
′′
= =
.
2. Hai đ
ường thẳng cắt nhau
Hai đường thẳng
y ax b= +
( )
0a ≠
và
( )
0y ax b a
′ ′′
=+≠
cắt nhau khi và chỉ khi
aa
′
≠
.
Chú ý.
+
Khi
,a ab b
′′
≠=
thì hai đường thảng có cùng tung độ gốc, do đó chúng cắt nhau tại một
đi
ển trên trục tung có tung độ là
b
.
+
Hai đường t
hẳng vuông góc với nhau khi và chỉ khi
.1aa
′
= −
.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. NHẬN DẠNG CẶP ĐƯỜNG THẲNG SONG SONG VỚI NHAU, CẶP
ĐƯỜ
NG THẲNG CẮT NHAU, CẶP ĐƯỜNG THẲNG VUÔNG GÓC VỚI NHAU.
Phương pháp giải
Cho hai đường thẳng
( ) ( )
:0d y ax b a=+≠
và
( ) ( )
:0d y ax b a
′ ′ ′′
=+≠
.
+
( ) ( )
// 'd d aa
′
⇔=
và
'bb≠
.
+
( ) ( )
''d d aa≡ ⇔=
và
'bb=
.
+
( )
d
và
( )
'd
cắt nhau
'aa⇔≠
.
+
( ) ( )
.' 1d d aa
′
⊥⇔=−
.
Ví dụ 1. Hãy chỉ ra hai cặp đường thẳng song song với nhau trong các đường thẳng sau:
( )
1
: 21dy x= +
;
( )
2
3
:
2
x
dy
+
=
;
( )
3
1
:2
2
dy x=−+
;
( )
4
: 0,5 1dy x= −
;
( )
5
: 42dy x= +
;
( )
6
: 12dy x= −
.
Lời giải
Hai cặp đường thẳng song song với nhau là:
( )
( )
15
//dd
vì
( )
'2aa= =
;
( )
'1 4bb≠≠
;
( ) ( )
24
//dd
vì
( )
0,5aa
′
≠=
;
( )
' 1, 5 1bb≠ ≠−
.
Ví dụ 2. Hãy chỉ ra các cặp đường thẳng vuông góc với nhau trong các đường thẳng sau:
( )
1
: 21dy x= +
;
( )
2
3
:
2
x
dy
+
=
;
( )
3
1
:y 2
2
dx=−+
;
( )
4
: 0,5 1dy x= −
;
( )
5
: 45dy x= +
và
( )
6
: 12dy x= −
.
Lời giải
Bốn cặp đường thẳng vuông góc với nhau:
( )
( )
13
dd⊥
;
( )
( )
26
dd⊥
;
( ) ( )
35
dd⊥
;
( )
( )
46
dd⊥
vì đều có
.' 1aa = −
.
Ví dụ 3. Chứng tỏ rằng hai đường thẳng sau luôn cắt nhau với mọi giá trị của
m
:
a)
( )
( )
2
1
: 11dymm x= −+ +
và
( )
2
:y
2
xm
d
−+
=
.
b)
( )
( )
2
3
: 1 2012dym x= ++
và
( )
4
: 2012d y mx=−+
.
Lời giải
a) Xét
( )
1
d
có:
2
2
1 33
10
2 44
am m m

= − += − + ≥ >


;
( )
2
d
có
1
0
2
a
′
=−<
.
Suy ra
'aa≠
với mọi
m
nên
( )
1
d
luôn cắt
( )
2
d
.
b) Ta có:
( )
2
22
1 33
'1 1 0
2 44
aa m m m m m

− = +−− = + + = + + ≥ >


nên
'aa≠
với mọi
m
, suy ra
( )
3
d
luôn cắt
( )
4
d
.
Chú ý: Hai đường thẳng
( )
3
d
và
( )
4
d
có cùng tung độ gốc là
2012
nên chúng cùng đi
qua điểm
( )
0;2012A
nằm trên trục tung.
Ví dụ 4. Chứng minh rằng giao điểm của hai đường thẳng
y mx= −
và
1
4yx
m
= +
luôn nằm
trên mộ
t đường tròn cố định với mọi
0m ≠
.
Lời giải
Kí hiệu đường thẳng
y mx= −
là
( )
d
, đường thẳng
1
4yx
m
= +
là
( )
'd
.
Ta có
( )
:d y mx= −
luôn đi qua gốc tọa độ
( )
0;0O
cố định;
( )
1
:4dy x
m
′
= +
luôn đi qua điểm
( )
0;4B
cố định.
Xét
( )
1
.' . 1aa m
m
=−=−
với
( ) ( )
0'm dd≠⇒ ⊥
tại
A
(
A
là giao điểm của hai đường
thẳng
( )
d
và
( )
'd
)
90OAB⇒=°
.
Do đó giao điểm
A
của
( )
d
và
( )
d
′
luôn nằm trên đường tròn đường kính
OB
cố định,
với
( )
0;0O
và
( )
0;4B
Dạng 2. XÁC ĐỊNH ĐƯỜNG THẲNG VỚI QUAN HỆ SONG SONG.
Phương pháp giải
Viết phương trình đường thẳng đi qua một điểm và song song với một đường thẳng cho
trước: Gọi phương trình đường thẳng cần tìm là
y ax b= +
.
+ Sử dụng điều kiện hai đường thẳng song song với nhau để xác định hệ số
a
.
+ Với
a
vừa tìm được, sử dụng điều kiện còn lại để xác định tung độ gốc
b
.
Ví dụ 1. Tìm
m
để đường thẳng
( )
( )
2
1
:2 5d y mxm= − −−
song song với đường thẳng
( )
2
: 221dy xm=−+ +
.
Lời giải
( ) ( )
2
12
// 2 2dd m⇔− =−
(1) và
( )
52 12mm−−≠ +
.
Giải
( )
22
2
1:2 2 4
2
m
mm
m
=
− =−⇔ = ⇔
= −
.
Giải
( )
2: 5 2 1 3 6 2mm mm− − ≠ + ⇔ ≠ ⇔ ≠−
.
Vậy với
2m =
thì
( ) ( )
12
//dd
.
Ví dụ 2. Cho đường thẳng
( )
:2 3 0d xy+−=
và điểm
( )
1;1M −
. Viết phương trình đường
thẳng
( )
d
′
đi qua điểm
M
và song song với
( )
d
.
Lời giải
Gọi phương trình đường thẳng
( )
d
′
là
y ax b= +
.
Ta có
( )
:2 3 0d xy+−=
hay
23yx=−+
.
Vì
( ) ( )
//dd
′
nên
2a = −
và
3b ≠
. Mặt khác,
( )
d
′
đi qua điểm
( )
1;1M −
nên
( )
1 .1ab= −+
( )
1 21ab b⇔− + = ⇔− − + =
(vì
2a = −
)
( )
13b⇔=−≠
.
Vậy phương trình đường thẳng cần tìm là:
21yx=−−
.
Ví dụ 3. Cho
( ) ( ) ( )
0; 2 , 1; 0 , 1; 1M NP−−
lần lượt là trung điểm của các cạnh
,BC CA
và
AB
c
ủa tam giác
ABC
. Viết phương trình đường thẳng
AB
.
Lời giải
Gọi phương trình đường thẳng
MN
là:
y ax b= +
. Ta có:
( )
1; 0 0 .1N MN a b∈ ⇒= +
hay
ab= −
.
( )
0;2 2 .0M MN a b∈ ⇒= +
hay
22ba=⇒=−
.
Do đó phương trình đường thẳng
MN
là:
22yx=−+
.
Vì
,MN
lần lượt là trung điểm của
CB
và
CA
nên
MN
là đường trung bình của
ABC∆
//MN AB⇒
.
Vì
//AB MN
nên phương trình đường thẳng
AB
có dạng:
( )
22y x bb
′′
=−+ ≠
.
Vì
( )
1; 1P −−
là trung điểm của đoạn
AB
nên đường thẳng
AB
đi qua
( )
1; 1P −−
( )
1 2. 1 ' 3bb
′
⇒− =− − + ⇔ =−
(thỏa mãn).
Vậy phương trình đường thẳng
AB
là:
23yx=−−
.
Ví dụ 4. Cho ba đểm không thẳng hàng
( ) ( )
2; 2 , 0;4AB−−
và
( )
2;02C
. Xác định điểm
D
trên mặ
t phẳng tọa độ sao cho
ABCD
là hình bình hành.
Lời giải
Dễ thấy
: 24BC y x=−+
.
Giả sử có
D
để
ABCD
là hình bình hành.
Khi đó
//AD BC
nên đường thẳng
AD
có phương trình:
26yx=−−
(vì đường thẳng
AD
qua
A
).
Vì
D AD∈
nên
( )
00
;2 6Dx x−−
.
Tứ giác
ABCD
là hình bình hành nên:
22
AD BC AD BC=⇔=
( ) ( )
( )
22
2
2
00
2 242 4xx⇔ + +− − = +−
0
0
0
4
x
x
=
⇔
= −
.
( ) ( )
12
4;2 , 0; 6DD⇒− −
. Từ hình 14 suy ra loại
1
D
vì không đúng thứ tự các đỉnh của tứ
giác
ABCD
.
Vậy
( )
0; 6D −
.
Dạng 3. XÁC ĐỊNH ĐƯỜNG THẲNG VỚI QUAN HỆ VUÔNG GÓC
Phương pháp giải
Viết phương trình đường thẳng đi qua một điểm và vuông góc với một đường thẳng cho
trước:
Gọi phương trình đường thẳng cần tìm là
y ax b= +
.
D
2
A
o
Hình 14
y
4
B
C
-2
-2
x
+ Sử dụng điều kiện hai đường thẳng vuông góc để xá định hệ số
a
.
+ Với
a
vừa tìm được, sử dụng điều kiện điểm thuộc đường thẳng để xác định tung độ
gốc
b
.
Ví dụ 1. Tìm
m
để đường thẳng
( )
2
:1d y mx m= +−
vuông góc với đường thẳng
( )
1
: 2012
4
dy x
′
=−+
.
Lời giải
( ) ( )
2
1
.' 1 . 1
4
d d aa m

′
⊥ ⇔ =−⇔ − =−


2
2
4
2
m
m
m
=
⇔=⇔
= −
.
Vậy
2m = ±
thì
( ) ( )
dd
′
⊥
.
Ví dụ 2. Tìm
a
và
b
, biết đường thẳng
( )
1
:d y ax b= +
vuông góc với đường thẳng
( )
2
1
:
2
dy x= −
và
( )
1
d
đi qua điểm
( )
1; 1P −
.
Lời giải
Vì
( ) ( )
12
dd⊥
nên
1
. 1. 1 3
3
aa a a

′
=−⇔ − =−⇔ =


. Ta có:
( )
1
:3d y xb= +
.
Vì
( )
1
d
đi qua điểm
( )
1; 1P −
nên
3.1 1b+=−
4b⇔=−
.
Vậy
3a =
và
4b = −
.
Ví dụ 3. Cho ba điểm
( )
1; 2A
,
( ) ( )
3;0 , 0;1BC
.
a) Ch
ứng minh rằng
,,ABC
là ba đỉnh của một tam giác.
b) Vi
ết phương trình đường thẳng chứa đường cao
AH
của
ABC∆
.
Lời giải
a) G
ọi phương trình đường thẳng đi qua
( )
3;0B
và
( )
0;1C
là
:BC y ax b= +
.
Ta có:
B BC∈
nên
0 .3 3 0a b ab= +⇔ +=
(1)
C BC∈
nên:
1 .0 1abb= +⇔=
(2)
Từ
( )
1
và
( )
2
suy ra:
11
3 10 :
1
33
a a BC y x+= ⇔ =− ⇒ =− +
.
Vì
A BC∉
nên ba điểm
,,ABC
không thẳng hàng. Vậ ba điểm
,,ABC
là ba đỉnh của một
tam giác.
b) G
ọi phương trình đường cao
AH
là
( )
:d y ax b
′ ′′
= +
.
Vì
AH
là đường cao của tam giác
ABC
nên
( )
.' 1AH BC d BC a a
′
⊥⇔ ⊥⇔ =−
1
'. 1 ' 3
3
aa

⇔ − =−⇔ =


.
Mặt khác:
( ) ( )
1; 2Ad
′
∈
nên
2 .1 2 3.1 1ab bb
′′ ′′
= +⇔= +⇔=−
.
Vậy phương trình đường cao
AH
của
ABC∆
là
31yx= −
.
Ví dụ 4. Cho
( ) ( ) ( )
0; 2 , 1; 0 , 1; 1M NP−−
lần lượt là trung điểm của các cạnh
BC
,
CA
và
AB
c
ủa tam giác
ABC
. Viết phương trình đường trung trực của đoạn thẳng
AB
.
Lời giải
G
ọi phương trình đường thẳng trung trực đoạn
AB
là
( )
:d y mx n= +
.
Gọi phương trình đường thẳng
MN
là:
y ax b= +
. Ta có:
( )
1; 0 0 .1N MN a b∈ ⇒= +
hay
ab= −
.
( )
0;2 2 .0M MN a b∈ ⇒= +
hay
22ba=⇔=−
.
Do đó phương trình đường thẳng
MN
là:
22yx=−+
.
Vì
,MN
lần lượt là trugn điểm của
CB
và
CA
nên
MN
là đường trung bình của
ABC∆
//MN AB⇒
.
Vì
( )
d
là đường trung trực của đoạn
AB
nên
( )
d AB⊥
.
Hình 15
P
-1;-1
( )
N
M
C
B
A
( ) ( )
1
.2 1
2
d MN m m⇒ ⊥ ⇒ − =−⇒ =
.
( )
1
:
2
d y xn⇒=+
.
Vì
( )
1; 1P −−
là trung điểm của đoạn
AB
nên đường thẳng
( )
d
đi qua
( )
1; 1P −−
.
( )
11
1 .1
22
nn⇒− = − + ⇔ =−
.
Vậy phương trình đường trung trực của đoạn thẳng
AB
là:
11
22
yx= −
.
C. BÀI TẬP TỰ LUYỆN
1. Cho đường thẳng
( )
:d y ax b= +
. Tìm giá trị của
a
và
b
trong mỗi trường hợp sau:
A.
( ) ( )
1
// : 2 3d dy x= +
; B.
( )
d
trùng
( )
2
:1dy x=−+
;
C.
( )
d
cắt
( )
3
1
:
2
dy x=
; D.
( ) ( )
4
1
:
2
d dy x⊥=−
.
2. Viết phương trình đường thẳng
( )
d
′
song song với đường thẳng
( )
: 45dy x=−+
và đi
qua điểm
( )
1; 1M −
.
3. Xác định
a
và
b
để đường thẳng
( )
1
:d y ax b= +
vuông góc với đường thẳng
( )
2
1
:
2
dy x= −
và đi qua điểm
( )
1; 2P −
.
4. Đường thẳng
( )
: 2011d y ax=−+
song song với đường phân giác của góc phần tư
( )
I
và
( )
III
thì hệ số
a
của
( )
d
bằng:
A.
1
B.
1−
C.
0
D.
1
2011
−
5.
Cho bốn đường thẳng
( )
1
1
:2
3
dy x= −
;
( )
2
:3dy x= −
;
( )
3
: 34dy x=−+
và
( )
4
1
:2
3
dy x= +
cắt nhau tại bốn điểm phân biệt
,,,M NPQ
.
Khi đó bốn điểm
,,,M NPQ
là bốn đỉnh:
A. Một hình thang B. Một hình bình hành
C. Một hình chữ nhật D. Một tứ giác không có gì đặc biệt.
6. Cho tam giác
ABC
có
( ) ( ) ( )
1;5 , 3;1 , 5;3AB C−
a) Vi
ết phương trình đường trung trực của cạnh
BC
.
b) Vi
ết phương trình đường trung bình
MN
của tam giác
ABC
( )
//MN BC
.
7. Cho
( ) ( ) ( )
0;4 , N 2;0 , 1; 2MP−−
lần lượt là trung điểm của các cạnh
,BC CA
và
AB
của
tam giác
ABC
. Viết phương trình đường thẳng
AB
.
8. Cho hai đường thẳng
( )
1
:d y mx m= +
và
( )
2
2
:3 3d y xm= ++
.
Chứng minh rằng
( )
1
d
và
( )
2
d
không trùng nhau với mọi giá trị của
m
.
9. Cho ba điểm không thẳng hàng
( ) ( )
3;0 , 0; 2AB−
và
( )
1; 0C
. Xác định điểm
D
trên mặt
ph
ẳng tọa độ sao cho
ABCD
là hình bình hành.
HƯ
ỚNG DẪN GIẢI – ĐÁP SỐ
1. a)
( ) ( )
1
// 2; 3dd ab⇔= ≠
b)
( ) ( )
2
1; 1dd a b≡ ⇔=− =
c)
( )
d
cắt
( )
3
1
;
2
dab⇔≠ ∈
.
d)
( ) ( )
4
. ' 1 2;d d aa a b⊥ ⇔ =−⇔ = ∈
2. Gọi phương trình đường thẳng
( )
'd
là
y ax b= +
.
Vì
( ) ( )
' // : 4 5d dy x=−+
nên
4a = −
và
5b ≠
. Mặt khác
( )
d
′
đi qua
( )
1; 1M −
nên
1 .1ab−= +
14 1ab b⇔+=−⇔−+=−
(vì
4a = −
)
3b⇔=
(thỏa mãn)
Vậy
( )
': 4 3dy x=−+
.
3. Vì
( ) ( )
12
dd⊥
nên
1
.' 1 . 1 2
2
aa a a

=−⇔ − =−⇔ =


. Do đó
( )
1
:2d y xb= +
Vì
( )
1
d
đi qua điểm
( )
1; 2P −
nên
( )
2. 1 2 4bb−+=⇔=
.
4.
( )
':d yx=
là đường phân giác của góc phần tư (I) và (III).
( ) ( )
// ' 1 1dd a a⇔− = ⇔ =−
. Chọn B.
5.
( ) ( )
14
//dd
vì
1
'; 2 2 '
3
a ab b= = =−≠ =
; tương tự
( )
( )
( ) ( )
2 32 4
// ;d dd d⊥
vì
( )
1
.3 1
3
−=−
.
Do đó, bốn điểm
,,,M NPQ
là bốn đỉnh của một hình chữ nhật. Chọn (C).
6. a) Gọi phương trình đường thẳng
BC
là:
y ax b= +
.
Vì
( )
3;1B BC−∈
nên
( )
1 3 13 1ab b a=− +⇒=+
;
( )
5;3C BC∈
nên
( )
35 2ab= +
.
Thay (1) vào (2) ta được
17
;
44
ab= =
. Do đó:
17
:
44
BC y x= +
.
Trung trực của
BC
là đường thẳng
( )
d
vuông góc với
BC
tại trung điểm
I
của
BC
.
Tọa độ của điểm
I
là:
1; 2
22
BC BC
II
xx yy
xy
++
= = = =
hay
( )
1; 2I
.
Do đường trung trực
( )
:4d y xm=−+
đi qua
( )
1; 2I
nên ta được
6m =
.
Vậy đường thẳng
( )
d
là:
46yx=−+
.
b) Gọi
,MN
lần lượt là trung điểm của
,AB AC
. Khi đó ta có:
( )
1; 3M −
.
Vì
//MN BC
nên
MN
có dạng:
1
4
y xn= +
7
4
n

≠


. Do đó
( )
1; 3M −
thuộc
MN
nên
13
4
n =
(thỏa mãn).
Vậy
MN
có phương trình:
1 13
44
yx= +
.
7. Phương trình đường thẳng
MN
là:
24yx=−+
.
Vì
//AB MN
nên phương trình đường thẳng
AB
có dạng:
( )
2 ''2y x bb=−+ ≠
.
Vì đường thẳng
AB
đi qua
( )
1; 2P −−
nên
( )
2 2. 1 ' 4bb
′
−=− − + ⇔ =−
.
Vậy phương trình đường thẳng
AB
là:
24yx=−+
.
8. Cách 1.
( ) ( )
( )
( )
12
2
31
'
'
32
m
aa
dd
bb
mm
=
=
≡⇔ ⇔

=
= +
Thay (1) vào (2) ta được:
03=
(vô lí). Dô đó
( )
1
d
không trùng
( )
2
d
với mọi
m
.
Cách 2. Giả sử:
22
11
' 3 30
44
bb mm m m= ⇔ = + ⇔ −++ −=
2
11
30
24
m

⇔− + −=


(vô lí). Do đó điều giả sử là sai.
Vậy
( )
1
d
không trùng
( )
2
d
với mọi
m
.
Chú ý: Chỉ cần
'aa≠
hoặc
'bb≠
thì
( )
1
:d y ax b= +
không trùng
( )
2
:d y ax b
′′
= +
.
9. Đáp số:
( )
2; 2D −−
.
§5. H
Ệ SỐ GÓC CỦA ĐƯỜNG THẲNG
y ax b= +
( )
0a ≠
A.
TRỌNG TÂM KIẾN THỨC
1. H
ệ số góc của đường thẳng
+ Góc
α
tạo bởi tia Ax (A là giao điểm của
đường th
ẳng
y ax b= +
với trục Ox) và tia AB,
trong
đó tia AB là phần của đường thẳn
g
y ax b= +
nằm trong nửa mặt phẳng có bờ x’x
v
à chứa tia Oy được gọi là góc tạo bởi đườn
g
th
ẳng
y ax b= +
và trục Ox (hình 16).
+ Vì có sự liên quan giữa hệ số a với góc tạo bở
i
đường th
ẳng
y ax b= +
và trục Ox nên người
ta g
ọi a là hệ số góc của đường thẳn
g
y ax b= +
Khi góc
α
nhọn thì
tana
α
=
Khi góc
α
tù thì
( )
0
tan 180a
α
=−−
+ Các đường thẳng có cùng hệ số góc a thì tạo với Ox các góc bằng nhau.
Các đường thẳng song song hoặc trùng nhau thì có hệ số góc bằng nhau
+ Khi
0a >
thì góc
α
nhọn, hệ số a càng lớn thì
α
càng lớn.
+ Khi
0a <
thì góc
α
tù, hệ số a càng lớn thì
α
càng lớn.
A
y = ax + b
α
o
Hình 16
y
B
x
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. XÁC ĐỊNH HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
Phương pháp giải
Ví dụ 1. Đường thẳng
( )
15ym x=++
đi qua điểm
( )
1; 3F −
có hệ số góc bằng bao nhiêu?
Giải
Kí hiệu
( )
d
là đường thẳng
( )
15ym x=++
.
Vì
( ) ( )
1; 3Fd−∈
nên
( )( )
3 1 1 5 1.mm= + −+⇔ =
Vậy hệ số góc của đường thẳng
( )
d
là
111 2am= +=+=
Ví dụ 2. Tính hệ số góc của đường thẳng
( ) ( )
: 23dy m x=−+
biết nó song song với đường
thẳng
( )
' :2 1 0d xy− −=
. Vẽ đồ thị
( )
d
vừa tìm được.
Giải
+ Đường thẳng
( )
'd
có phương trình
2 1 0 2 1.
xy y x− −= ⇔ = −
Vì
( ) ( )
// ' 'd d aa⇔=
và
'bb≠
nên
22m −=
và
3 1.≠−
Do đó hệ số góc của đường thẳng
( )
d
là 2.
+ Ta có
( )
: 23dy x= +
. Vẽ đường thẳng đi qua hai
điểm
( )
0;3A
và
3
;0
2
B
−



là đường thẳng
( )
d
cần
vẽ. (h.17)
Ví dụ 3. Tính hệ số góc của đường thẳng
( ) ( )
:1 1d y mx=−+
, biết nó vuông góc với đường
thẳng
( )
': 2 4 0dxy− −=
. Vẽ đồ thị
( )
d
vừa tìm được.
Giải
y
-3
2
A
o
Hình 17
3
B
x
Vận dụng định nghĩa hệ số góc của đường thẳng ; góc giữa
đường thẳng và trục Ox; vận dụng tỉ số lượng giác của góc nhọn.
+ Đường thẳng
( )
'd
có phương trình
1
2 40 2
2
xy y x− −=⇔ = −
Vì
( ) ( )
1
' . ' 1 (1 ). 1 1 2
2
d d aa m m⊥ ⇔ =−⇔ − =−⇔− =−
Do đó h
ệ số góc của đường thẳng
( )
d
là
2−
+ Ta có
( )
: 21dy x−+
. Vẽ đường thẳng đi qua hai điểm
( )
0;1A
và
1
;0
2
B



là đường thẳng
( )
d
cần vẽ (h.18).
Ví dụ 4. Tính hệ số góc của đường thẳng đi qua hai điểm
( )
1;1A −
và
( )
2; 3B −
Giải
Giả sử phương trình đường thẳng đi qua hai điểm
( )
1;1A −
và
( )
2; 3B −
là
:AB y ax b= +
Ta có:
A AB∈
nên:
( )
1 .1 1 1 1a b b ba= −+⇔−+=⇔=+
(1)
B AB∈
nên:
3 .2 2 3abb a−= + ⇔ =− −
(2)
Từ (1) và (2) ta có:
4
23 1
3
aa a− −= +⇔ =−
V
ậy hệ số góc của đường thẳng AB là:
4
3
a = −
.
D
ạng 2. XÁC ĐỊNH GÓC
Phương pháp giải
Vận dụng định nghĩa góc giữa đường thẳng
y ax b= +
( )
0a ≠
và trục Ox; vận dụng
tỉ số lượng giác của góc nhọn; vận dụng tam giác đồng dạng.
Ví dụ 1. Tính góc tạo bởi đường thẳng
23yx=−+
và trục Ox.
Giải
Vẽ đường thẳng
23yx=−+
. Khi đó
BAx
là góc tạo bởi
đường thẳng
23yx=−+
với trục Ox (hình 19)
y
1
2
o
Hình 18
1
x
Vận dụng định nghĩa góc giữa đường thẳng và trục Ox; vận dụng tỉ số
lượng giác của góc nhọn; vận dụng tam giác đồng dạng.
y
x
1,5
A
B
3
o
Hình 19
Xét tam giác vuông ABO, ta có:
0
3
tan 2
63 26'
1, 5
OB
OAB OAB
OA
===⇔≈
00
180 116 34'BAx OAB⇒=− ≈
(Trong đó
2 chính là giá trị tuyệt đối của hệ số góc của đường thẳng
23yx=−+
).
Ví dụ 2. Cho đường thẳng
( )
:3d y mx= +
. Tính góc tạo bởi đường thẳng
( )
d
với trục Ox,
biết
( )
d
đi qua điểm
( )
3;0A −
.
Giải
Vì
( ) ( )
1
3;0 : 3 .
3
A d y mx m− ∈ = + ⇒=
Khi đó
( )
d
có phương trình
1
3.
3
yx= +
Gọi
α
là góc tạo bởi đường thẳng
( )
d
với trục
Ox. Khi đó ta có:
0
1
tan 30 .
3
αα
= ⇒=
Vậy góc tạo bởi đường thẳng
( )
d
với trục Ox
là
0
30
.
Ví dụ 3. Cho hai đường thẳng
( )
1
:2dy x= −
và
( )
2
1
2
dx=
.
( )
d
là đường thẳng song song với
trục Ox và cắt Oy tại điểm có tung độ bằng 3;
( )
d
cắt
( )
1
d
và
( )
2
d
lần lượt tại A và
B. Ch
ứng minh rằng:
0
90AOB =
Giải
Vẽ ba đường thẳng ,
( )
d
,
( )
1
d
,
( )
2
d
như hình 21.
Xét hai tam giác AHO và OHB, ta có:
^^
0
1
90 ; .
2
HA HO
AHO OHB
HO HB
= = = =
Do đó:
AHO∆
∽
OHB AOH OBH∆⇒ =
.
y
Hình 20
3
α
-3
A
o
d
( )
:y =
1
3
x +
3
x
y
x
Hình 21
d
2
(
)
d
1
(
)
H
3
6
-
3
2
O
B
A
Mà
00
90 90AOH HOB AOB+=⇒=
C
hú ý:
( )
1
:2dy x= −
có hệ số góc
1
2a = −
;
( )
2
1
2
dx=
có hệ số góc
2
1
.
2
a =
Ta th
ấy:
( )
12
1
. 2. 1
2
aa=−=−
, do đó:
( ) ( )
12
.dd⊥
Dạng 3. XÁC ĐỊNH ĐƯỜNG THẲNG
Phương pháp giải
Ví dụ 1. Xác định đường thẳng
( )
d
đi qua điểm
( )
2;3A −
và có hệ số góc bằng
2−
.
Giải
Gọi phương trình đường thẳng
( )
d
là:
y ax b= +
.
Vì
( )
d
có hệ số góc là
2−
nên
( )
2 :2a d y xb=−⇒ =− +
Vì
( ) ( )
2;3Ad−∈
nên
( ) ( )
3 2 . 2 1.bb=− −+⇔=−
Do đó phương trình đường thẳng
( )
d
là
21yx=−−
Ví dụ 2. Xác định đường thẳng
( )
d
đi qua điểm
( )
1;1A −
và tạo với trục Ox một góc bằng
0
45
.
Giải
Đường thẳng
( )
d
có dạng
y ax b= +
. Vì
( ) ( )
1;1Ad−∈
nên
( )
1 1 1.a b ba= −+⇔=+
Vì
( )
d
tạo với trục Ox một góc bằng
0
45
nên
0
tan 45 1 2ab= =⇒=
Do đó phương trình đường thẳng
( )
d
là
2yx= +
Ví dụ 3. Xác định đường thẳng
( )
d
đi qua điểm
( )
0;1A
và tạo với đường thẳng
2y =
một
góc bằng
0
60
.
Giải
• Gọi phương trình đường thẳng cần tìm là . Ta cần xác định a và b.
• Chú ý rằng: Gọi là góc tạo bởi đường thẳng với trục Ox.
Ta có:
− Khi góc nhọn thì
− Khi góc tù thì .
Đường thẳng
( )
d
có dạng
y ax b= +
.
Vì
( ) ( )
0;1Ad∈
nên
1 .0 1.abb= +⇔=
Vì đường thẳng
2y =
song song với trục hoành nên từ đề bài ta có
( )
d
tạo với trục
Ox một góc bằng
0
60
.
Ta có:
0
tan tan60 3a
α
= = =
. Vậy
( )
: 31dy x= +
.
C. BÀI TẬ
P TỰ LUYỆN
1
.
Đường thẳng
( )
d
đi qua giao điểm của hai đường thẳng
1yx= +
,
2yx=
và song song với
đường thẳng
2 22yx= ++
là:
(A)
422yx= +−
; (B)
( )
22 1yx=++
;
(C)
222yx= +−
; (D)
2yx= +
.
2
. Đường th
ẳ
ng
13
22
yx= +
vuông góc với đường thẳng nào dưới đây?
(A)
13
22
yx=−−
; (B)
3
2
2
yx= −
;
(C)
3
2
2
yx=−+
; (D)
13
22
yx= −
.
3
. Đường th
ẳng
( )
12ym x=+−
vuông góc với đường thẳng
1
2011
2
yx= +
thì
m
bằng ?
(A)
2−
(B)
3−
(C)
1−
(D)
1
4. Xác đ
ịnh đường thẳng
( )
d
biết nó có hệ số góc bằng 2 và đi qua điểm
( )
3; 2A −
5. Tính h
ệ số góc của đường thẳng đi qua hai điểm
( )
1; 2A
và
( )
3; 4B
6. Cho đường thẳng
( )
:3d mx +
. Tính góc
α
tạo bởi đường thẳng
( )
d
với trục Ox, biết:
a)
( )
d
đi qua điểm
( )
3;0A −
b)
( )
d
đi qua điểm
( )
6; 3B −
.
7. Xác định đường thẳng
( )
d
đi qua điểm
( )
0;3A
và tạo với đường thẳng
2y =
một góc bằng
0
60
.
HƯ
ỚNG DẪN GIẢI – ĐÁP SỐ
1
. (C).
2. (C).
3. (B).
4.
2 8.yx= +
5.
:1AB y x= +⇒
đường thẳng AB có hệ số góc
1.a =
6. a)
0
60 .
α
=
b)
10m =−<
nên
( )
0 00 0
tan 180 1 180 45 135 .
α αα
− − =−⇔ − = ⇔ =
7
.
3 3.yx= +
ÔN TẬP CHƯƠNG II
A. TR
ỌNG TÂM KIẾN THỨC
1. Hà
m số.
+ Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x theo quy tắc f sao cho với mỗi giá
trị x, ta luôn xác định được chỉ một giá trị tương ứng của y mà
( )
y fx=
thì y được gọi
là hàm số của x và x được gọi là biến số.
+ Cách cho hàm số: Hàm số thường được cho bằng công thức.
Chú ý: Có một số cách khác cho hàm số như: Bảng, sơ đồ Ven, đồ thị.
+ Đồ thị của hàm số: Tập hợp các điểm biểu diễn các cặp giá trị tương ứng
( )
( )
;xf x
trên
mặt phẳng tọa độ gọi là đồ thị hàm số
( )
y fx=
+ Tính đồng biến, nghịch biến của hàm số: Cho hàm số
( )
y fx=
xác định trên tập hợp
D là
một khoảng, nửa khoảng hay đoạn, với mọi
12
,xx D∈
:
Nếu
12
xx<
mà
( ) ( )
12
fx fx<
thì hàm số
( )
y fx=
đồng biến trên D
Nếu
12
xx<
mà
( ) ( )
12
fx fx>
thì hàm số
( )
y fx=
nghịch biến trên D
2. Hà
m số bậc nhất
+ Hàm số bậc nhất là hàm số được cho bởi công thức
y ax b= +
, trong đó a, b là các số
cho trước và
0a ≠
.
+ Tập xác định:
+ Khi
0a >
thì hàm số đồng biến trên
; Khi
0a <
thì hàm số nghịch biến trên
+ Đ
ồ thị hàm số là một đường thẳng.
+ Hệ số
( )
0aa≠
được gọi là hệ số góc của đường thẳng
y ax b= +
+ Cho hai đường thẳng
( ):d y ax b= +
( )
0a ≠
và đường thẳng
( ') : ' 'd y ax b= +
( )
'0a ≠
. Ta có:
( ) ( )
// ' 'd d aa⇔=
và
'bb≠
( ) ( )
''d d aa≡ ⇔=
và
'bb=
( )
d
cắt
( )
'd
'aa⇔≠
( )
d
( )
'd⊥
.' 1aa = −
.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. VẼ ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT.
Phương pháp giải
Ví dụ 1. Cho hàm số
( ): 1dyx= −
và
( ') : 3dy x=−+
.
Vẽ đồ thị
( )
d
và
( )
'd
trên cùng hệ trục tọa độ. Xác định tọa độ giao điểm của
( )
d
và
( )
'd
.
Giải
+ TXĐ:
+ V
ẽ
( )
d
:
Cho
( )
0 0 1 1 0; 1xy A= ⇒ = −=−⇒ −
thuộc
trục tung.
Cho
( )
0 0 1 1 1; 0y xxB= ⇒ = −⇒ =⇒
thuộc
trục hoành.
Vẽ đường thẳng AB ta được đồ thị
( )
d
(hình 22).
+ Vẽ
( )
'd
:
Cho
( )
0 0 3 3 0;3
xy C=⇒ =+=⇒
thuộc trục tung.
Bước 1. Tìm tập xác định ( TXĐ của hàm số bậc nhất là ).
Bước 2. Vẽ đồ thị
Cách 1. + Xác định hai điểm phân biết bất kì của đồ thị rồi vẽ đường thẳng đi qua
hai điểm đó.
Cách 2. + Xác định giao điểm của đồ thị với hai trục tọa độ:
• Cho thuộc trục tung.
•
Cho
thuộc trục
hoành.
Vẽ đ ờ hẳ MN đ đồ hị hà ố
Hình 22
O
-1
A
B
d'
d
D
3
I
1
2
1
C
3
y
x
Cho
( )
0 0 3 3 3;0y xxD= ⇒ =−+⇒ = ⇒
thuộc trục hoành.
Vẽ đường thẳng CD ta được đồ thị
( )
'd
.
+ Xác định tọa độ giao điểm I của
( )
d
và
( )
'd
:
Cách 1. Từ giao điểm I ta vẽ các đường vuông góc với hai trục tọa độ ta xác định
được
( )
2;1I
.
Cách 2. Gọi tọa độ giao điểm I là
( )
;
II
xy
Vì là giao điểm của
( )
d
và
( )
'd
nên I vừa thuộc
( )
d
, vừa thuộc
( )
'd
.
Vì
( ) ( )
; :1
II
Ixy d y x∈=−
nên
11
1.yx= −
Vì
( ) ( )
; ': 3
II
Ixy d y x∈ =−+
nên
11
3.yx=−+
Suy ra:
1 1 1 1 11
1 3 2 4 2 3 231x x x x yx−=−+⇔ =⇔ =⇒ =−+=−+=
Vậy tọa độ giao điểm I là
( )
2;1
C
hú ý.
• Hoành độ giáo điểm I là nghiệm của phương trình
13xx−=−+
• Số
giao điểm của
( ) ( )
:d y fx=
và
( ) ( )
':d y gx=
là số nghiệm của phương
trình
( ) ( )
fx gx=
và ngược lại.
Ví dụ 2. Vẽ đồ thị
( )
G
của hàm số
2.yx= −
Giải
Vẽ
( )
2 ( 2) (1)
:2
2 ( 2) (2)
xx
Gyx
xx
−≥
=−=
−+ <
Đ
ồ thị
( )
G
gồm hai nhành (1) và (2).
Nhánh (1) của
( )
G
: điều kiện là
2x ≥
.
Cho
( )
2 2 2 0 2;0xy A=⇒=−=⇒
thuộc
trục hoành
Cho
( )
3 3 2 1 3;1xy B=⇒=−=⇒
.
O
Hình 23
x = 2
1
2
( )
1
( )
B
3
2
A
2
y
x
Vẽ tia AB ta được nhánh (1) của đồ thị
( )
G
.
Tương tự, vẽ nhánh (2) ta thu được đồ thị
( )
G
có hình chữ V như hình 23.
Chú ý. Hai nhánh của
( )
G
đối xứng nhau qua đường thẳng
2x =
Ví dụ 3. Cho hàm số
22yx x=+−
a) V
ẽ đồ thị
( )
G
của hàm số trên.
b) Biện luận theo tham số m số nghiệm của phương trình
22xx m+ −=
.
Giải
a) V
ẽ
( )
( )
3 2 ( 1) (1)
: 22
2 1 (2)
xx
Gyx x
xx
−≥
=+ −=
−+ <
Đ
ồ thị
( )
G
gồm hai nhánh (1) và (2).
Nhánh (1) của
( )
G
: điều kiện là
1x ≥
Cho
( )
1 3.1 2 1 1;1xy A=⇒ = −=⇒
Cho
( )
2 3.2 2 4 2;4xy A=⇒= −=⇒
Vẽ tia AB ta được nhánh (1) của đồ thị
( )
G
.
Tương tự, vẽ nhánh (2) ta thu được đồ thị
( )
G
như hình
24.
b) Số nghiệm của phương trình
2 2 (*)xx m+ −=
là số giao điểm của đường
thẳng
( )
:dym=
và đồ thị
( )
: 22Gyx x=+−
.
Từ đồ thị ta thấy:
+ Nếu
1m <
thì phương trình
( )
*
vô nghiệm.
+ Nếu
1m =
thì phương trình
( )
*
có một nghiệm.
+ Nếu
1m >
thì phương trình
( )
*
hai nghiệm phân biệt.
Ví dụ 4. Với giá trị nào của tham số a thì phương trình
2 1 3 (*)xa x− += +
có nghiệm
duy nhất?
(Thi vào khối PT chuyên Toán – Tin ĐHSPHN năm học 1997-1998)
Giải
y
x
y = m
1( )
2( )
A
m
2
4
1
21
O
Hình 24
+ Ta có:
( )
* 2 3 1 (1)xa x⇔ − =+−
Số
nghiệm của phương trình (1) là số giao
điểm của đồ thị
( )
:2G y xa= −
và đồ thị
( )
': 3 1Gyx=+−
Vẽ hai đồ thị
( )
G
và
( )
'G
như hình 25.
Phương trình
( )
*
có nghiệm duy nhất
( )
1⇔
có nghiệm duy nhất
( )
G⇔
và
( )
'G
có một điểm chung
4
2
a
⇔=−
hoặc
2
2
a
= −
8a⇔=−
hoặc
4.a = −
Dạng 2. XÁC ĐỊNH ĐƯỜNG THẲNG
Phương pháp giải
Ví d
ụ 1. Tìm m và n để đường thẳng
( ) ( )
: 12dy m x n= − +−
đi qua hai điểm
( )
2; 1A −
và
( )
3; 6B −−
.
Giải
Ta có:
( )
Ad∈
nên
( )
1 1 .2 2 2 1 2 1 (1)m n mn n m−= − + − ⇔ − =−⇔ = +
( )
Bd∈
nên
( ) ( )
6 1 . 3 2 3 11 (2)m n mn−= − −+−⇔− −=−
Thay (1) vào (2) ta được:
( )
3 2 1 11 5 10 2mm m m− − + =− ⇔− =− ⇔ =
2 1 2.2 1 5nm⇒ = += +=
1. Viết phương trình đường thẳng đi qua hai điểm cho trước
2. Viết phương trình đường thẳng đi qua một điểm và có hệ số góc cho trước.
3. Viết phương trình đường thẳng đi qua một điểm và song song với một đườ
ng cho
trước
.
4. Viết phương trình đường thẳng đi qua một điểm và vuông góc với một đườ
ng
th
ẳng cho trước.
y
x
Hình 25
-1
G'( )
G( )
y = 2x - a
y = x + 3 - 1
-a
2
a
2
-2
-3
-4
O
Vậy
2m =
và
5n =
thì
( )
:3dyx= −
đi qua hai điểm
( )
2; 1A −
và
( )
3; 6B −−
.
Ví dụ 2. Viết phương trình đường thẳng
( )
d
cắt
( )
'd
tại điểm có tung độ bằng
1−
biết
( )
d
có hệ số góc bằng 2.
Giải
Gọi A là giao điểm của
( )
d
và
( )
'd
. Vì A có tung độ bằng
1−
nên hoành độ của
điểm A là
13x−= −
hay
2x =
. Do đó :
( )
2; 1A −
.
Gọi phương trình đường thằng
( )
d
là:
.y ax b= +
Ta có
( )
d
có hệ số góc là 2 nên
( )
2 :2.a d y xb=⇒=+
Vì
( ) ( )
2; 1Ad−∈
nên
1 2.2 5.bb−= + ⇔ =−
Do đó phương trình đường thẳng
( )
d
là
2 5.yx= −
Ví dụ 3. Cho đường thẳng
( )
: 32dy x= −
và điểm
( )
1;1M −
. Viết phương trình đường thẳng
( )
'd
đi qua và song song với
( )
d
.
Giải
Gọi phương trình đường thẳng
( )
'd
là
.y ax b= +
Vì
( ) ( )
' // : 3 2d dy x= −
nên
3a =
và
2.b ≠−
Mặt khác
( )
'd
đi qua
( )
1;1M −
nên:
( )
1 1 31 4ab bb= −+⇔−+=⇔=
(thỏa mãn)
Vậy phương trình đường thẳng cần tìm là:
3 4.yx= +
Ví dụ 4. Trên mặt phẳng tọa độ Oxy cho
( ) ( )
2;4 , 0;2MN
. Tìm các điểm A trên mặt
phẳng tọa độ Oxy sao cho
.AM AN=
Giải
Cách 1. Tọa độ trung điểm của đoạn MN là:
1; 3
22
MN MN
II
xx yy
xy
++
= = = =
hay
( )
1; 3 .I
Gọi phương trình đường trung trực của MN là
( )
:d y mx n= +
G
ọi phương trình đường thẳng MN là:
y ax b= +
. Ta có
( )
2;4 4 .2M MN a a b∈ ⇒= +
hay
2 4;ba=−+
( )
0;2 2 .0N MN a b∈ ⇒= +
hay
2 1.ba=⇒=
Do đó phương trình đường thẳng MN là:
2.yx= +
Vì AM = AN
A⇒
thuộc đường trung trực của đoạn MN hay
( )
Ad∈
.
Vì
( )
d
là đường trung trực của MN nên
( )
.1 1 1d MN m m⊥ ⇔ =−⇒ =−
( ):d y xn⇒ =−+
Vì
( )
1; 3I
là trung điểm của đoạn MN nên đường thẳng
( )
d
đi qua
( )
1; 3I
( )
3 1 .1 4.nn⇒=− +⇒=
Vậy tập hợp các điểm A là đường thẳng
( )
:4dy x=−+
Cách 2
. Gọi tọa độ A là
( )
;xy
Ta có: AM = AN
( ) ( )
( ) ( )
22 22
24 02xy xy⇔ − +− = − +−
( ) ( ) ( ) ( )
2222
2 22 2
2402
44 168 44
16 4 4
4.
xyxy
xx yy x yy
xy
yx
⇔− +− =− +−
⇔−++−+=+−+
⇔−=
⇔ =−+
V
ậy tập hợp các điểm A trên mặt phẳng Oxy thỏa mãn bài toán là đường thẳng có phương
trình:
4yx=−+
D
ạng 3. CỰC TRỊ
Phương pháp giải
• Vận dụng bất đẳng thức đại số
• Vận dung quan hệ giữa đường xiên và đường vuông góc
• Vận dụng hệ thức lượng trong tam giác vuông
• Vận dụng đồ thị.
Ví dụ 1. Tìm m để khoảng cách từ gốc tọa độ
( )
0;0O
đến đường thẳng
( )
d
có phương trình
22 2
22
m
yx
mm
−
= +
−−
đạt giá trị lớn nhất ( với
2m ≠−
).
Giải
Vì tung độ gốc
2
0
2
b
m
= ≠
−
nên
( )
d
không đi qua gốc tọa độ.
Trường hợp 1: Xét
1m =
. Khi đó
( )
:2dy= −
. Do đó khoảng cách từ
( )
0;0O
đến
( )
d
là 2.
Trường hợp 2. Xét
1m ≠
.
Khi đó
( )
d
cắt trục hoành tại điểm
1
;0
1
A
m
−


−

và cắt trục tung tại điểm
21
0;
21
B OA
mm

⇒=

−−

và
2
2
OB
m
=
−
.
Kẻ OH vuông góc với
( )
d
tại H thì độ dài OH là khoảng cách từ O đến
( )
d
.
Áp dụng hệ thức
2 22
111
hab
= +
vào tam giác vuông ABO ta có:
( ) ( )
22
2
22
2 2 2 22
1 11 . 4
24 1
OA OB
OH
OH OA OB OA OB
mm
=+⇒= =
+
−+ −
22
2 22
5
4
5 12 8
64
5
5
55
OH
mm
m
⇒= = ≤
=
−+

−+


(d
ấu “=” xảy ra khi
6
5
m =
).
Kết hợp hai trường hợp ta có khi
6
5
m =
thì
max
5OH =
.
Ví dụ 2. Trên mặt phẳng tọa độ cho hai điểm A, B đều có hoành độ x và tung độ y thỏa mãn
đẳng thức
1 2 3 (*)xy−+ − =
. Chứng minh khoảng cách
6AB ≤
.
Giải
Điều kiện (*)
( )
( )
( )
( )
6 1; 2
2 1; 2
4 1; 2
0 1; 2
xy x y
xy x y
xy x y
xy x y
+= ≥ ≥
−= ≥ ≤
⇔
−+ = ≤ ≥
−− = ≤ ≤
⇒
Tập hợp các điểm A, B thỏa mãn (*) là hình
vuông MNPQ hình 26
6AB MP⇒≤ ≤
D
ấu “=” xảy ra khi A, B là hai đỉnh đối
nhau của hình vuông MNPQ.
C. BÀI TẬ
P TỰ LUYỆN
1. Hàm số
11
22
y
xx
= +
−−
không xác định với:
(A)
2x =
(B)
2x >
(C)
2x <
(D) Với mọi x thuộc
2.
Với giá trị nào của m thì hàm số
( )
2
21ym x=−+
là hàm số bậc nhất đồng biến?
(A)
22m− <<
; (B)
2m >
hoặc
2m <−
;
(C)
2m ≠±
; (D) Với mọi giá trị của m thuộc
3.
Cho hàm số
( )
53
2007 1y f x ax bx x= =++ +
với
*
,ab∈
, biết
( )
22f =
, tính
( )
2f −
.
4. Cho hàm số
( ) ( )
2
3 1 2.y m x mx= − + −+
a
) Với giá trị nào của m thì hàm số đã cho là hàm số bậc nhất?
b) Với giá trị vừa tìm được của m ở câu a, thì hàm số đã cho đồng biến hay nghịch biến?
5. Cho đường thẳng
( )
3
:3
4
dy x= +
a
) Vẽ đường thẳng
( )
d
.
b) Tính góc tạo bởi đường thẳng
( )
d
và trục Ox.
c) Tính diện tích tam giác do đường thẳng
( )
d
tạo với hai trục tọa độ.
Hình 26
y
x
-2
O
B
A
4
-1
Q
1
5
N
2
P
M
6. Xác định hàm số
y ax b= +
, biết rằng đồ thị của nó song song với đồ thị hàm số
2yx= −
và đi qua điểm
( )
1; 3A −
.
7. Cho các đường thẳng
( ) ( )
( )
1 23
1
:23; : 1; :21
2
dyx dyx dyx=−+ = + =−−
.
Không vẽ đồ thị của các hàm số đó, hãy cho biết vị trí tương đối giữa các đường thẳng đó đối
với nhau như thế nào?
8. Cho các đường thẳng
( ) ( ) ( ) ( )
2
12
: 2 1 1; : 3 3d y m xm d y m x= − +− =+ −
.
a) Tìm các giá trị của m để
( ) ( )
12
//dd
.
b) Tính các giá trị của m để
( )
1
d
đi qua gốc tọa độ.
9. Tìm điểm trên đường thẳng
( )
: 2 25dy x=−+
sao cho khoảng cách OM nhỏ nhất, với
O là gốc tọa độ.
HƯ
ỚNG DẪN GIẢI – ĐÁP SỐ
1. (D)
2. (B)
3.
( )
20f −=
4.
a)
3.m =
b) Đồng biến.
5. b)
0
36 52';
c) 6 (đvdt).
6.
21yx=−−
7.
( )
( )
( ) ( ) ( )
( )
13 12 2 3
// ;dd dd dd⊥⊥
8. a)
4; ) 1m bm= = ±
9.
Gọi tọa độ điểm M là
( )
;ab
. Khoảng cách
22
OM a b= +
.
Ta có
( ) ( )
; : 2 25M ab d y x∈ =−+
nên
2 25 2 25b a ab=− + ⇔ +=
.
Áp dụng bất đẳng thức
( )
( )( )
2
222 2
ax by a b x y+ ≤+ +
với
( ) ( )
; 2;1xy =
, ta có:
( )
( )( )
2
2 2222 22
25 2 2 1 5 5.ab ab ab OM=+≤+ +⇔≤+⇒ ≥
Do đó
( )
min
2 25
10
5 1
0;5 .
5
2
ab
a
OM M
a
b
b
+=
=
=⇔ ⇔⇒

=
=
Chú ý. Ta có thể giải bài toán như sau :
( )
min
OM OM d⇔⊥
tại .
Ta xác định tọa độ điểm M bằng cách:
+ Lậ
p phương trình đường thẳng
( )
'd
đi qua
( )
0;0O
và vuông góc với đường thẳng
( )
d
.
+
M là gia
o điểm của
( )
d
và
( )
'd
| 1/58
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

MỤC LỤC
Chương II. HÀM SỐ BẬC NHẤT ................................................................................. 2
§1. NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ .............................. 2
§2.HÀM SỐ BẬC NHẤT ........................................................................................... 2
§3. ĐỒ THỊ CỦA HÀM SỐ 𝑦 = 𝑎𝑥 + 𝑏(𝑎 ≠ 0) .................................................... 18
§4. ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU .............. 31
§5. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG y = ax + b (a ≠ 0) .................................... 41
ÔN TẬP CHƯƠNG II .............................................................................................. 48
Chương II. HÀM SỐ BẬC NHẤT
§1. NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ
§2.HÀM SỐ BẬC NHẤT
A. TRỌNG TÂM KIẾN THỨC
1. Khái niệm hàm số
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x, ta luôn
xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x, và x được gọi là biến số.
Khi y là hàm số của x thì ta có thể viết y = f ( x), y = g ( x),...
Khi hàm số được cho bằng công thức y = f ( x), ta hiểu rằng biến số x chỉ lấy những giá
trị mà tại đó f ( x) xác định. Tập hợp các giá trị đó được gọi là tập xác định của hàm số, kí hiệu là D.
Giá trị của f ( x) tại x kí hiệu f ( x hay y = f x . Khi x thay đổi mà y luôn nhận 0 ( 0) 0 ) 0
một giá trị không đổi thì hàm số y được gọi là hàm hằng.
2. Đồ thị hàm số
Tập hợp "G" tất cả các điểm biểu diễn các cặp giá trị tương ứng ( x; f ( x)) trên mặt
phẳng tọa độ goi là đồ thị của hàm số y = f ( x).  x ∈ D
M ( x ; y ∈"G" hay "G" đi qua điểm M ( x ; y ⇔  0 0 ) 0 0 0 ) y = f x  0 ( 0)
3. Hàm số đồng biến, nghịch biến
Cho hàm số y = f ( x) xác định trên D trong đó D là một khoảng hoặc đoạn hoặc nửa
khoảng với mọi x , x ∈ . D 1 2
• Nếu x < x mà f (x < f x thì hàm số y = f (x) đồng biến trên D. 1 ) ( 2) 1 2
• Nếu x < x mà f (x > f x thì hàm số y = f (x) nghịch biến trên D. 1 ) ( 2) 1 2
4. Hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b, trong đó a,b là các số
cho trước và a ≠ 0.
Khi b = 0, hàm số có dạng y = ax (đã học ở lớp 7).
Hàm số bậc nhất y = ax + b (a ≠ 0) xác định với mọi x thuộc .
 Hàm số đồng biến trên
 khi a > 0, hàm số nghịch biến trên  khi a < 0
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. TÌM TẬP XÁC ĐỊNH (TXĐ) CỦA HÀM SỐ Phương pháp giải
Hàm số f ( x) chứa căn bậc hai A( x), điều kiện: A( x) ≥ 0. A( x)
Hàm số f ( x) chứa biến số ở mẫu
(hoặc A( x) : Β( x) ), điều kiện: B ( x) ≠ 0. B ( x)
Ví dụ 1. Với những giá trị nào của x thì hàm số sau đây xác định? x +1
a) y = f ( x) 2 =
b) y = g ( x) = x − 3 + 5 − x 2 x − 4 Giải a)
f ( x) xác định khi: 2 2
x − 4 ≠ 0 ⇔ x ≠ 4 ⇔ x ≠ 2. ± x − 3 ≥ 0 x ≥ 3
b) g ( x) xác định khi:  ⇔  ⇔ 3 ≤ x ≤ 5 5  − x ≥ 0 x ≤ 5 −x
Ví dụ 2. Tìm tập xác định D của hàm số y = h( x) = : x 2 1 − x Giải −x ≥ 0  x ≤ 0  2  1 − x ≠ 0  x ≠ 1 ±
h ( x) xác định khi:  ⇔  ⇔ x ∈∅ x ≥ 0 x ≥ 0    x ≠ 0  x ≠ 0
Vậy tập xác định của hàm số D = . ∅
(Tức là không có giá trị nào của x để hàm số xác định). x
Ví dụ 3. Tìm tập xác định D của hàm số y = f (x) = . 2 x + 1 Giải
f (x) xác định khi: 2 2
x +1 ≠ 0 ⇔ x ≠ 1 − ⇔ x ∈ . 
Vậy tập xác định D = . 
Ví dụ 4. Tìm tập xác định D của hàm số 2
y = f (x) =
x −1 + 1 − x . Giải x −1 ≥ 0 x ≥ 1
f (x) xác định khi:  ⇔  ⇔ x = 1. 2 1  − x ≥ 0  1 − ≤ x ≤ 1
Vậy tập xác định D = { } 1 .
Chú ý: Tập xác định D của hàm số có thể có một phần tử, một vài phần tử, vô số phần tử hoặc không có phần tử nào.
Dạng 2. TÍNH GIÁ TRỊ CỦA HÀM SỐ KHI BIẾT GIÁ TRỊ CỦA BIẾN SÔ.
TÍNH GIÁ TRỊ CỦA BIẾN SỐ KHI BIẾT GIÁ TRỊ CỦA HÀM SỐ Phương pháp giải
Tìm tập xác định D của hàm số y = f (x).
• Thế giá trị x = x ∈ D vào biểu thức của hàm số rồi tính giá trị biểu thức (đôi khi ta rút gọn 0
biểu thức, biến đổi x rồi mới thay vào để tính toán). 0
• Thế giá trị y = y ta được y = f (x). 0 0
Giải phương trình f (x) = y để tìm giá trị biến số x (chú ý: chọn x ∈ D ). 0 3 1
Ví dụ 1. Tính giá trị của hàm số 2
y = f (x) = − x −
tại x = 1; x = 1 − . 4 4 Giải TXĐ:  3 1 3 1 Ta có: 2 f (1) = − .1 − = − − = 1 − ; 4 4 4 4 3 1 3 1 3 1 4 2 f ( 1 − ) = − .( 1
− ) − = − .1− = − − = − = 1. − 4 4 4 4 4 4 4 2 x − 9
Ví dụ 2. Cho hàm số y = f (x) =
. Khi đó f(-3) bằng bao nhiêu ? x + 3 Giải Điều kiện x ≠ 3. − Vì x = 3
− không thỏa mãn điều kiện nên không tồn tại f ( 3) − .
Ví dụ 3. Cho hàm số y = f (x) = mx + m −1 , biết f (2) = 8. Tính f (3). Giải TXĐ:  Ta có f (2) = 8 ⇔ .2
m + m −1 = 8 ⇔ 3m = 9 ⇔ m = 3
⇒ f (x) = 3x + 2 ⇒ f (3) = 3.3 + 2 = 11.
Ví dụ 4. Cho hàm số y = f (x) = (3 − 2 2)x −1. Tìm x , biết f (x) = 0. Giải TXĐ: 
Ta có f (x) = 0 ⇔ (3 − 2 2)x −1 = 0 ⇔ (3 − 2 2)x = 1 1 ⇔ x = ⇔ x = 3 + 2 2. (3 − 2 2)
Ví dụ 5. Cho hàm số y = f (x) = x + 1− x.
a) Tìm x , biết f (x) = 1;
b) Tìm x sao cho f (x) = 0,5;
c) Tìm m để có giá trị x thõa mãn f (x) = . m Giải
Điều kiện: 0 ≤ x ≤1. a) Ta có: 2 2 f (x) = 1 ⇔
x + 1 − x = 1 ⇔ ( x + 1 − x ) = 1
⇔ x + 2 x 1− x +1− x = 1 ⇔ 2 x 1− x = 0
⇔ x = 0 hoặc 1− x = 0
⇔ x = 0 hoặc x =1 (thỏa mãn điều kiện). b) Ta có: 2 2 f (x) = 0,5 ⇔
x + 1 − x = 0,5 ⇔ ( x + 1− x ) = 0,5 .
⇔ x + 2 x 1− x +1− x = 0,25
⇔ 2 x 1− x = 0,
− 75 (không xảy ra vì 2 x 1− x ≥ 0).
Do đó không có giá trị nào của x để f (x) = 0,5. c) Ta có: 2 2 f (x) =
x + 1 − x ⇒ f (x) = ( x + 1 − x ) 2
⇔ f (x) = 2 x 1− x +1 ≥ 1 (vì 2 x 1− x ≥ 0 ).
Suy ra f (x) ≥ 1 (dấu bằng xảy ra khi và chỉ khi x = 0 hoặc x = 1). x +1 − x 1 1
Mặt khác: x 1− x ≤
= (dấu bằng xảy ra khi x = ). 2 2 2 Do đó 2 2
m = f (x) ≤ 2 ⇒ m ≤ 2.
Do đó chỉ khi 1 ≤ m ≤ 2 thì có giá trị của x thỏa mãn f (x) = . m
Chú ý: Ta có thể chứng minh f (x) ≥ 1 bằng một số cách khác như sau:
Cách 1: Sử dụng bất đẳng thức A + B ≥ A + B với ,
A B ≥ 0 (dấu “=” xảy ra khi A = 0 hoặc B = 0 ).
Cách 2: Sử dụng bất đẳng thức A ≥ A với mọi A thỏa mãn điều kiện 0 ≤ A ≤ 1.
Dạng 3. BIỂU DIỄN ĐIỂM TRÊN MẶT PHẲNG TỌA ĐỘ.
XÁC ĐỊNH KHOẢNG CÁCH GIỮA HAI ĐIỂM TRÊN MẶT PHẲNG Phương pháp giải
• Để biểu diễn điểm M (a;b) trên mặt phẳng tọa độ ta làm như sau: y M(a;b) b
Kẻ đường thẳng vuông góc với trục hoành tại điểm a.
Kẻ đường thẳng vuông góc với trục tung tại điểm b. O a x
Hai đường thẳng cắt nhau tại một điểm đó là điểm M.
• Xác định khoảng cách giữa hai điểm (
A x ; y ) và B(x ; y ) y A A B B B yB
Ta có: AH = x − x ; BH = y − y A A B A B y H A Ta có: 2 2 2 2 2
AB = AH + BH ⇒ AB = AH + BH x xB x A hay: 2 2
AB = (x − x ) + ( y − y ) . (*) B A B A
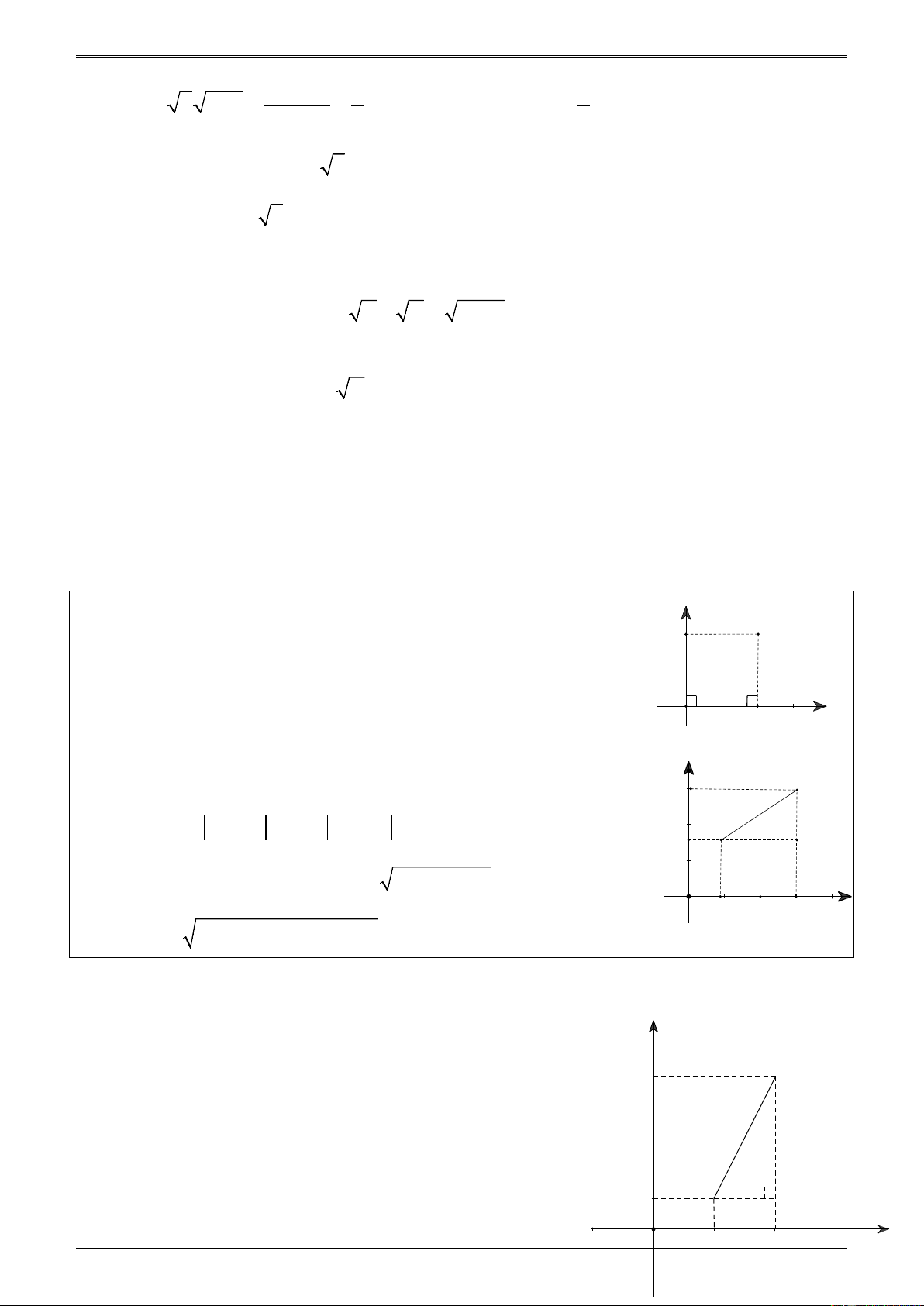
Ví dụ 1. Biểu diễn hai điểm A(2; )
1 và B (4;5) trên cùng một
mặt phẳng tọa độ. Tính khoảng cách giữa hai điểm đó. y Giải 5 B
Biểu diễn các điểm A, B như hình vẽ 1. Trong ABH ∆ , ta có:  H = 90 ;
° AH = 4 − 2 = 2; BH = 5 −1 = 4. 1 A H O x 2 4
Áp dụng định lí Py-ta-go vào ABH ∆ vuông tại H, ta có: 2 2 2 2 2
AB = AH + BH = 2 + 4 = 20 ⇒ AB = 20 = 2 5.
Chú ý: Sau này trong thực hành ta sẽ vận dụng ngay công thức (*). 2 2 2 2
Ta có AB = ( x − x ) + ( y − y ) = (4 − 2) + (5 − ) 1 = 2 5. Hình 1 B A B A
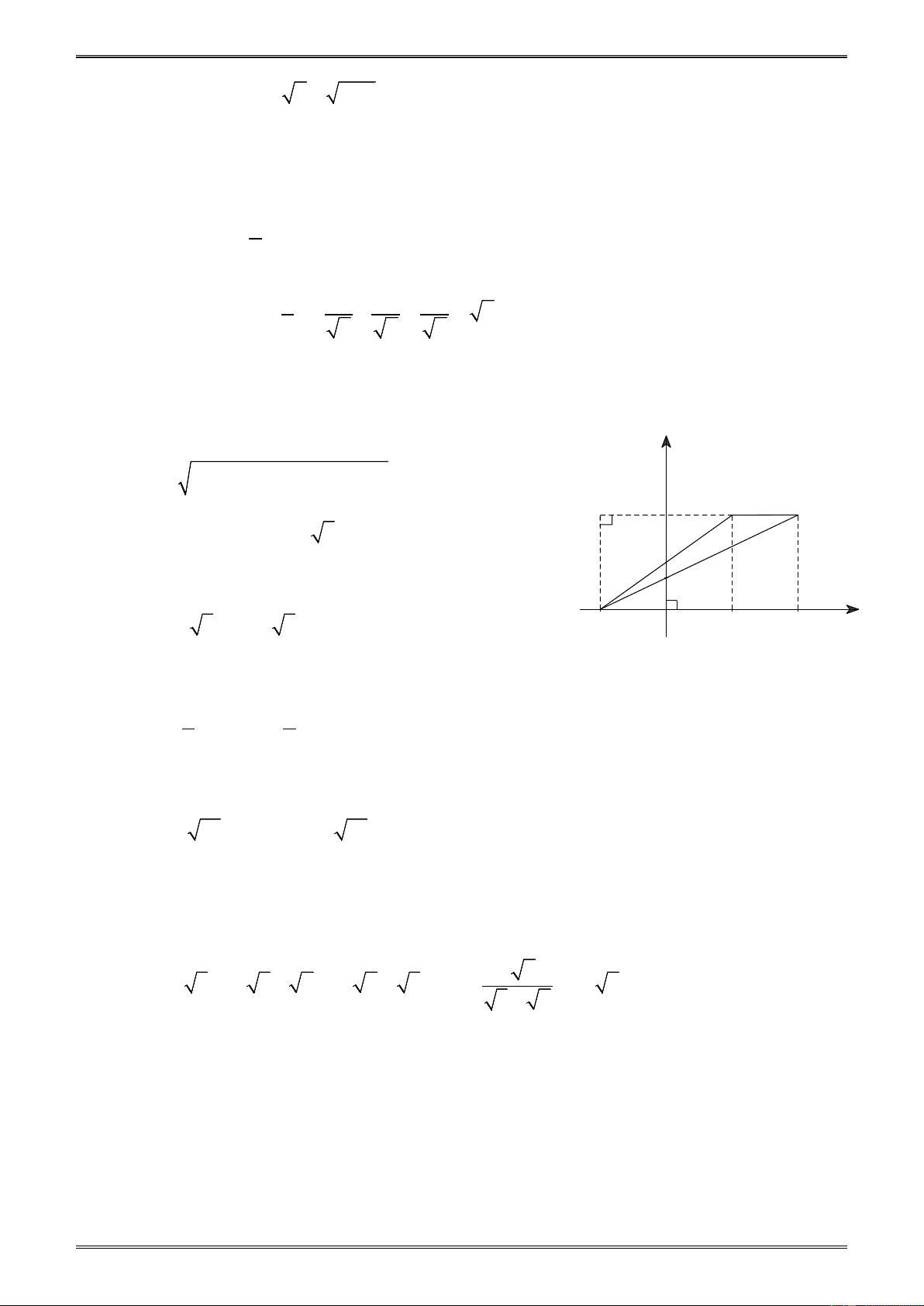
Ví dụ 2. Cho tam giác ABC có A(1;1); B(3;3) và C(5;1). a) Tính chu vi tam giác ABC.
b) Chứng minh rằng tam giác ABC vuông cân. Giải 2 2
a) Ta có: AB = (3 − ) 1 + (3 − ) 1 = 8 = 2 2.
AC = ( − )2 + ( − )2 =
BC = ( − )2 + ( − )2 5 1 1 1 4; 5 3 1 3 = 4 + 4 = 2 2.
Vậy chu vi tam giác ABC là:
AB + BC + AC = 2 2 + 2 2 + 4 = 4( 2 + ) 1 b) Ta có:
• AB = BC = 2 2 , suy ra ABC ∆ cân tại B. (1)
AB = BC = (2 2)2 2 2 = • 8 2 2 2 
⇒ AB + BC = AC 2 2 AC = 4 =16 ⇒ ABC ∆ vuông tại B. (2)
Từ (1) và (2) suy ra ABC ∆ vuông cân tại B.
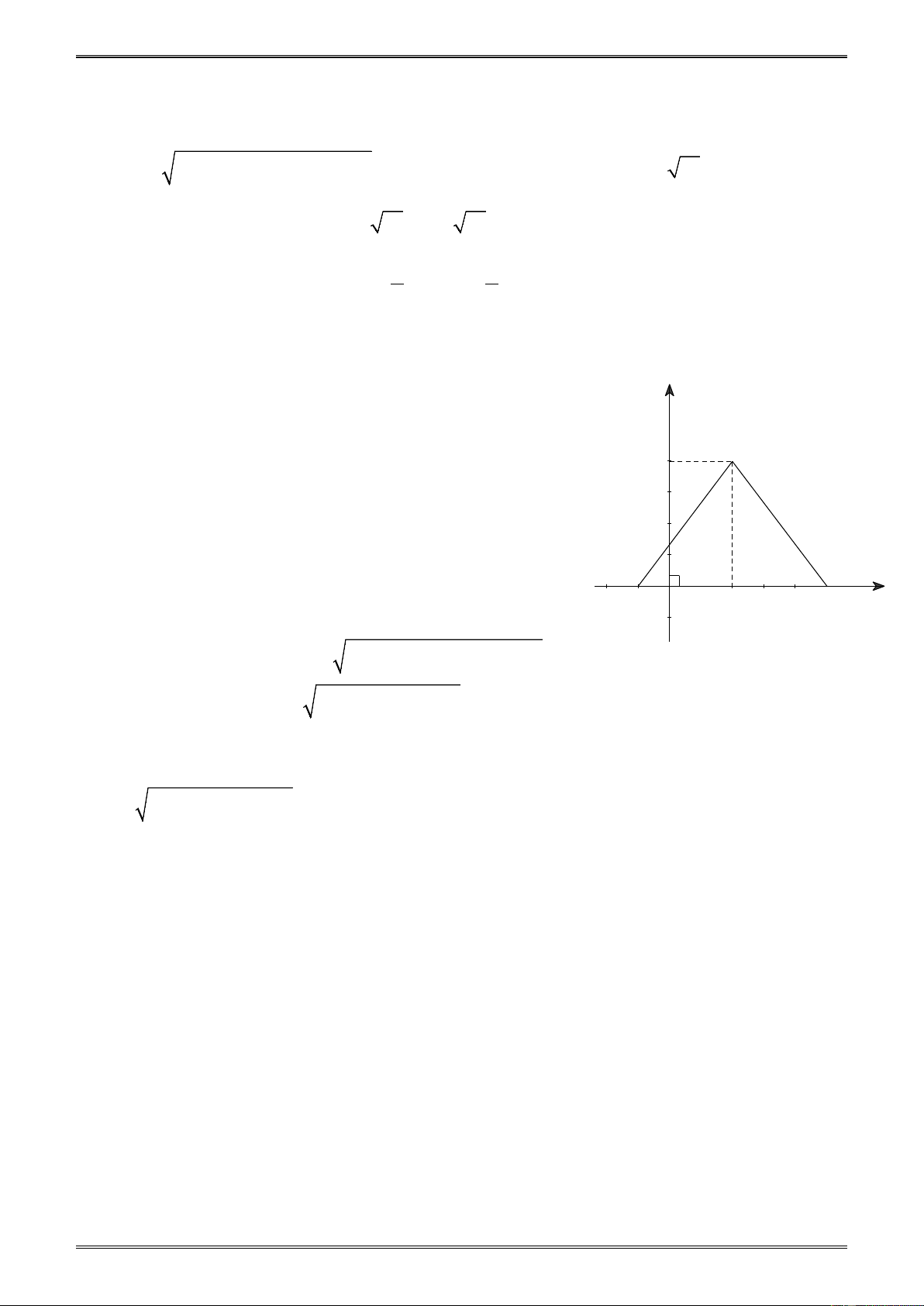
Ví dụ 3. Cho các điểm A(2;4), B(-1;0) và C(0;4).
a) Biểu diễn các điểm A, B, C trên mặt phẳng tọa độ. y
b) Tính chu vi và diện tích của tam giác ABC. 4 C A Giải
a) Biểu diễn các điểm A(2;4), B(-1;0) và C(0;4) như hình 2. B -1 O 2 x Hình 2
b) Ta thấy A, B, C không thẳng hàng nên A, B, C là ba đỉnh của một tam giác. Áp dụng công thức:
MN = ( x − x )2 + ( y − y )2 , ta tính được AB = 5; AC = 2; BC = 17. N M N M
Chu vi tam giác ABC là: 5 + 2 + 17 = 7 + 17 (đvd). 1 1
Diện tích tam giác ABC là: S
= BH.CA = .4.2 = 4 (đvdt). ABC 2 2
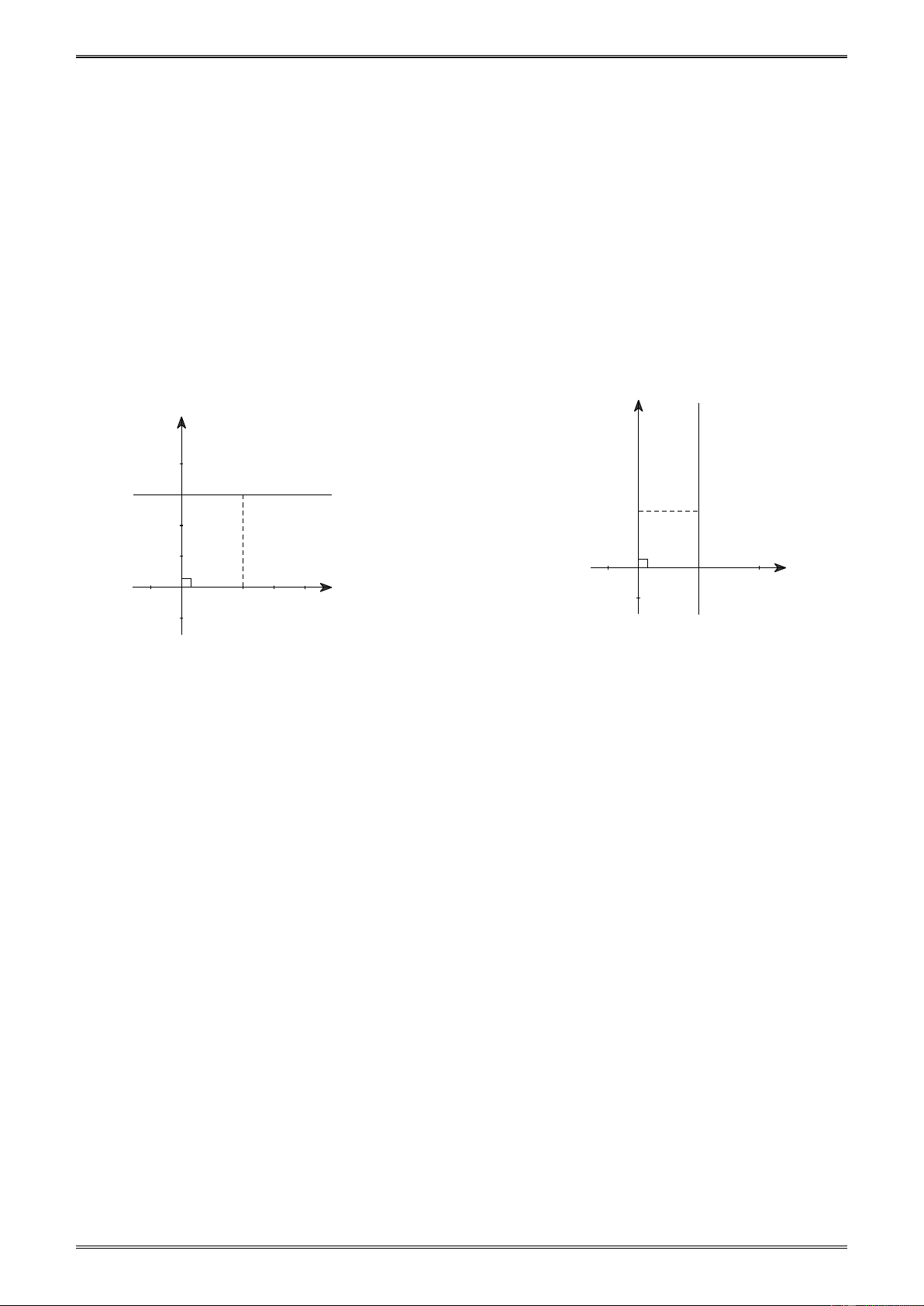
Ví dụ 4. Cho hai điểm A(2;4) và B(-1;0) trên hệ trục tọa độ Oxy. y
a) Biểu diễn các điểm A, B trên mặt phẳng tọa độ.
b) Tìm điểm C trên trục hoành sao cho ABC ∆ cân tại A. A 4 Giải
a) Biểu diễn các điểm A(2;4), B(-1;0) như hình 3.
b) Vì C nằm trên trục hoành Ox nên tung độ của điểm C B H C x -1 O 2 x
bằng 0, do đó C(x;0) với x ≠ 1. 2 2
Áp dụng công thức: MN = ( x − x + y − y , ta N M ) ( N M ) Hình 3 tính đượ 2 2
c AB = 5; AC = ( x − 2) + (0 − 4) . Ta có ABC ∆
cân tại A ⇔ AB = AC.
⇔ (x − )2 + ( − )2 = ⇔ (x − )2 + = ⇔ (x − )2 2 0 4 5 2 16 25 2 = 9
⇔ x = 5 hoặc x = 1
− (loại vì điều kiện x ≠ 1 − ). Vậy C(5;0) thì ABC ∆ cân tại A. Chú ý:
• Ta có thể giải cách khác như sau: ABC ∆
cân tại A ⇔ HB = HC ⇔ HC = 3(vì HB = 3) ⇔ x − 2 = 3 ⇔ x = 5.
Do đó, nếu kết hợp với kiến thức hình học thì chúng ta có thể giải bài toán đơn giản hơn, nhanh hơn.
• Ta có thể thay đổi yêu cầu bài toán thành “Tìm điểm C trên trục hoành sao cho ABC ∆
cân”. Với yêu cầu mới ta phải giải bài toán trong ba trường hợp: - Trường hợp 1: ABC ∆ cân tại A. - Trường hợp 2: ABC ∆ cân tại B. - Trường hợp 3: ABC ∆ cân tại C.
Dạng 4. ĐIỂM THUỘC ĐỒ THỊ. ĐIỂM KHÔNG THUỘC ĐỒ THÌ CỦA HÀM SỐ Phương pháp giải
Cho hàm số y = f (x) có miền xác định D và có đồ thị G, khi đó: x ∈ D
• M (x ; y thuộc đồ thị G khi và chỉ khi 0  0 0 )
y ∈ f (x )  0 0
• M (x ; y không thuộc đồ thị G khi và chỉ khi y ≠ f (x ) hoặc x ∉ . D 0 0 ) 0 0 0
Ví dụ 1. Cho hàm số y = f (x) = x. Trong các điểm A(9;3), B(4; -2), M(-1;1) và N (4 + 2 3; 3 − )
1 điểm nào không thuộc và điểm nào thuộc đồ thị (G) của hàm số đã cho ? Giải
Ta có: M ∉ (G) vì khi x = 1
− thì hàm số không xác định
B ∉ (G) , vì 4 = 2 ≠ 2 −
A(9;3) ∈ (G) , vì f (9) = 9 = 3 N (4 + 2 3; 3 − ) 1 ∉ (G) vì: f + = + = ( + )2 (4 2 3) 4 2 3 3 1 = 3 +1 ≠ 3 −1.
Ví dụ 2. Điểm M ( 1 − ; )
1 thuộc đồ thị của hàm số nào trong các hàm số dưới đây ? (A) 2 y = x ; (B) 4 y = x ; (C) y = 3x + 2; (D) 3 y = −x . Giải
Loại (A), (B) vì tung độ của M âm.
Loại (D), vì hoành độ và tung độ của M cùng dấu. Chọn (C).
Ví dụ 3. Khi m thay đổi, tìm tập hợp các điểm M có tọa độ như sau: a) M ( ; m 3); b) M (2; m). Giải
a) Ta có f(m) = 3, khi m thay đổi f(m) luôn nhận một giá trị không đổi. Hàm số y = f(m) = 3 là một hàm hằng.
Đồ thị của hàm số y = 3 là đường thẳng song song với trục hoành và cắt trục tung tại điểm có
tung độ bằng 3 (hình 4).
Tập hợp các điểm M(m;3) là đường thẳng song song với trục hoành và cắt trục tung tại điểm
có tung độ bằng 3 (hình 4).
b) Tập hợp các điểm M(2; m) là đường thẳng song song với trục tung và cắt trục tung tại điểm
có hoành độ bằng 2 (hình 5) y y x = 2 y = 3 M(m;3) 3 m M(2;m) O 2 x O m x Hình 5 Hình 4
Ví dụ 4. Cho hàm số y = f (x) = (m +1)x − 2 . m
a) Tìm m để đồ thị của hàm số đã cho đi qua điểm A(1 ; 1).
b) Chứng minh rằng đồ thị của hàm số đã cho luôn đi qua một điểm cố định với mọi m. Giải a) A(1; )
1 ∈ d : y = (m +1)x − 2m ⇔ 1 = (m +1).1− 2m ⇔ m = 0.
b) M (x ; y ) ∈ d : y = (m +1)x − 2m ⇔ y = (m +1)x − 2m 0 0 0 0
⇔ m(x − 2) + (x − y ) = 0. (1) 0 0 0
d đi qua M với mọi m khi (1) đúng với mọi m, tức là: x − 2 = 0 x = 2 0 0  ⇔  . x − y = 0 y = 2  0 0  0
Vậy d luôn đi qua điểm (2; 2) cố định với mọi m.
Dạng 5. XÁC ĐỊNH HÀM SỐ BẬC NHẤT Phương pháp giải
Hàm số bậc nhất là hàm số co dạng y = ax + b, trong đó a và b là các số cho trước và a ≠ 0.
Ví dụ 1. Trong các hàm số sau, hàm số nào là hàm số bậc nhất ? a) y = 1 − 3 ; x b) 2
y = 2x + x − 5; c) 2
y = x + x ( 2 − x) + 3; d) y = ( − )2 3 1 x +1. Giải
a) Hàm số y = 1− 3x hay y = 3
− x +1 có dạng y = ax + b , trong đó a = 3 − ≠ 0, nên y = 3
− x +1 là hàm số bậc nhất. b) Hàm số 2
y = 2x + x − 5 không phải là hàm bậc nhất vì sau khi thu gọn không có dạng
y = ax + b . c) Hàm số 2
y = x + x ( − x) 2 2 2
+ 3 = x + 2x − x + 3 = 2x + 3 là hàm số bậc nhất vì hàm số
có dạng y = ax + b , trong đó a = 2 ≠ 0. d) Hàm số y = ( − )2
3 1 x +1 là hàm số bậc nhất vì hàm số có dạng y = ax + b , trong đó a = ( − )2 3 1 ≠ 0.
Ví dụ 2. Cho ba hàm số 2 2
f (x) = x + 3; g(x) = x − x +1 và 2
h(x) = 2x + 3x −1. Xét các khẳng định:
(I) f (x) − g(x) là hàm số bậc nhất;
(II) h(x) − g(x) là hàm số bậc nhất;
(III) f (x) + g(x) − h(x) là hàm số bậc nhất.
Trong các khẳng định trên, khẳng định đúng là: (A) Chỉ (I) (B) Chỉ (II) (C) Chỉ (I) và (II) (D) Chỉ (I) và (III). Giải
Ta thực hiện phép tính cộng, trừ các đa thức được kết quả:
f (x) − g(x) = x + 2 , là hàm số bậc nhất; 2
h(x) − g(x) = x + 4x − 2 không là hàm số bậc nhất;
f (x) + g(x) − h(x) = 4
− x + 5 là hàm số bậc nhất. Do đó, chọn (D).
Ví dụ 3. Cho hàm số 2
y = f (x) = (1 − 2m)x + m + 2.
Tìm m để hàm số đã cho là hàm số bậc nhất. Giải Hàm số 2
y = f (x) = (1 − 2m)x + m là hàm số bậc nhất khi và chỉ khi: 1
1− 2m ≠ 0 ⇔ m ≠ . 2
Ví dụ 4. Cho hàm số 2 2
y = f (x) = (m − m)x + mx + 2.
Tìm m để hàm số đã cho là hàm số bậc nhất. Giải Hàm số 2 2
y = f (x) = (m − m)x + mx + 2 là hàm số bậc nhất khi và chỉ khi: 2 m − m = 0 m(m −1) = 0  ⇔ 
⇔ m −1 = 0 ⇔ m = 1. m ≠ 0 m ≠ 0
Khi m = 1, ta có hàm số y = x + 2 là hàm số bậc nhất.
Dạng 6. XÁC ĐỊNH TÍNH ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ Phương pháp giải
• Vận dụng định nghĩa: Với mọi x , x thuộc miền xác định D là một khoảng hoặc đoạn hoặc 1 2 nửa khoảng:
Nếu x > x mà f (x ) > f (x ) thì hàm số y = f (x) đồng biến trên D. 1 2 1 2
Nếu x > x mà f (x ) < f (x ) thì hàm số y = f (x) nghịch biến trên D. 1 2 1 2
• Trong thực hành giải toán ta làm như sau: Với mọi x , x ∈ D, x ≠ x 1 2 1 2
f (x ) − f (x ) Nếu 1 2
> 0 thì hàm số y = f (x) đồng biến trên D. x − x 1 2
f (x ) − f (x ) Nếu 1 2
< 0 thì hàm số y = f (x) nghịch biến trên D. x − x 1 2
• Hàm số y = f (x) = a x + b(a ≠ 0)
Nếu a > 0 thì hàm số đồng biến trên 
Nếu a > 0 thì hàm số đồng biến trên  .
Ví dụ 1. Chứng minh hàm số y = f (x) = x + 3 đồng biến trên tập xác định. Giải
Hàm số xác định khi x ≥ 3.
− Lấy x , x bất kỳ thõa mản x , x ≥ 3,
− x ≠ x , ta có: 1 2 1 2 1 2
f (x ) − f (x ) x + 3 − x + 3
(x + 3) − (x + 3) 1 1 2 1 2 1 = = = > x − x x − x (x − x )( 2 0 + + + + + + 1 2 1 2 x 3 x 3 x 3 x 3 1 2 1 2 ) ( 1 2 )
Do đó hàm số y = f (x) = x + 3 đồng biến trên tập xác định.
Ví dụ 2. Cho hàm số y = f (x) = m − 2x ( m là hằng số). Xét sự đồng biến, nghịch biến của hàm
số y = f (x) trên .  Giải
Cách 1. Tập xác định: .
 Lấy x , x thuộc  sao cho x < x , ta có: 1 2 1 2
f (x ) − f (x ) = (m− 2x ) − (m − 2x ) = m − 2x − m + 2x = 2(x − x ) > 0. 1 2 1 2 1 2 2 1
Do đó f (x ) > f (x ) , suy ra hàm số nghịch biến trên . 1 2
Cách 2. y = f (x) = m − 2x = 2
− x + m là hàm số bậc nhất có hệ số a = 2 − < 0 nên hàm số nghịch biến trên  .
Ví dụ 3. Tìm m để hàm số 2
y = (m − 2)x +1 ( m là tham số) đồng biến trên  . Giải Hàm số 2
y = (m − 2)x +1 là hàm số bậc nhất khi 2
m ≠ 2 với hệ số 2 a = m − 2.
Do đó hàm số đồng biến trên  2
⇔ m − 2 > 0 ⇔ m < − 2 hoặc m > 2.
Chú ý: Khi m = − 2 hoặc m = 2 thì y = 0x +1 = 1 nên hàm số là hàm hằng. Khi đó đồ thị
của hàm số là đường thẳng song song với trục hoành và cắt trục tung tại điểm có tung độ bằng 1.
Ví dụ 4. Cho hai hàm số f (x) = mx + 2012 và 2
g(x) = (m +1)x − 2011 ( m là tham số).
Xét tính Đúng, Sai của các khẳng định sau:
(A) f (x) + g(x) là hàm số đồng biến trên  ;
(B) g(x) − f (x) là hàm số đồng biến trên  ;
(C) f (x) − g(x) là hàm số đồng biến trên  . Giải
Ta thực hiện phép tính cộng, trừ các đa thức, được kết quả: 2
f (x) + g(x) = (m + m +1)x +1 là hàm số bậc nhất, với hệ số 2  1  3 2
a = m + m +1 = m + + > 0  
với mọi m nên khẳng định (A) đúng.  2  4 2
g(x) − f (x) = (m − m +1)x − 4023 là hàm số bậc nhất, với hệ số 2  1  3 2
a = m − m +1 = m − + > 0  
với mọi m nên khẳng định (B) đúng.  2  4 2
f (x) − g(x) = −(m − m +1)x + 4023 là hàm số bậc nhất, với hệ số 2  1  3 2
a = −(m − m +1) = − m − − < 0  
với mọi m nên khẳng định (C) đúng.  2  4
C. BÀI TẬP TỰ LUYỆN x − 1. Cho hai hàm số 2
y = f (x) =
và y = g(x) = x + 1 − x 3
a) Tìm tập xác định của các hàm số đã cho.  1   1 
b) Tính f (2), f , g(0), g(1), g .      2   2  2.
Cho các điểm A(2;3), B(-2;0) và C(4;3).
a) Biểu diễn các điểm A, B, C trên mặt phẳng tọa độ.
b) Tính chu vi và diện tích của tam giác ABC.
c) Tìm điểm M trên trục hoành sao cho tam giác ABM cân tại A.
d) Tìm điểm N trên trục tung sao cho tam giác ABN cân tại B. 3.
Cho hàm số y = f (x) = −mx + m − 3. Biết f ( 2) − = 6. Tính f ( 3) − . 4.
Cho hàm số y = f (x) = ( 3 − 2 ) x + 2 + 3. Tìm x sao cho f (x) = 3. 5.
Cho hàm số y = f (x) = −mx + 4.
a) Tìm m để đồ thị của hàm số đã cho đi qua điểm ( A 1 − ;1).
b) Chứng minh rằng đồ thị của hàm số đã cho luôn đi qua một điểm cố định với mọi m . 6.
Với các giá trị nào của m thì hàm số sau là hàm số bậc nhất ? a) 2
y = (4m −1)x
b) y = 5 − m (x − 2) c) 2 2 2
y = m x + m(x + 2 − 4x ) +1 − 2 . x 7.
Xác định tính đồng biến, nghịch biến của các hàm số sau:
a) y = f (x) = (1 − 2)x +1, với x ∈ 
b) y = f (x) =
x − 2 , với x ≥ 2 c) 2
y = f (x) = x + 2 , với x < 0. 8.
Cho hàm số y = f (x) = (1− 3)x −1 và f (m +1), f (m + 2) là hai giá trị tương ứng của
hàm số tại x = m +1, x = m + 2. Khi đó:
(A) f (m +1) > f (m + 2)
(B) f (m +1) < f (m + 2)
(C) f (m +1) = f (m + 2)
(B) Không thể so sánh được vì phụ thuộc vào giá trị của m. 9.
Chứng minh rằng không tồn tại đa thức f (x) bậc ba với hệ số nguyên sao cho
f (7) = 2010 và f (11) = 2012.
HƯỚNG DẪN GIẢI – ĐÁP SỐ x − 2 1.
a) Hàm số y = f (x) =
xác định khi: x − 2 ≥ 0 ⇔ x ≥ 2. 3
Hàm số y = g(x) = x + 1− x xác định khi: x ≥ 0 x ≥ 0  ⇔  ⇔ 0 ≤ x ≤ 1. 1  − x ≥ 0 x ≤ 1  1 
b) f (2) = 0; f   không xác định;  2   1  1 1 2 g(0) = 1;g(1) = 1;g = + = = 2.    2  2 2 2 2.
a) Biểu diễn các điểm A(2;3), B(-2;0) và C(4;3) như hình 6.
b) Ta thấy A, B, C không thẳng hàng nên A, B, C là
ba đỉnh của một tam giác. Áp dụng công thức: y
MN = ( x − x )2 + ( y − y )2 , ta tính được N M N M H 3 A C
AB = 5; AC = 2; BC = 3 5. Chu vi tam giác ABC là: B O 5 + 2 + 3 5 = 7 + 3 5. -2 2 4 x Hình 6
Diện tích tam giác ABC là: 1 1 S
= BH.AH = .3.2 = 3 (đvdt) ABC 2 2 c) M(6;0).
d) N (0; 21) hoặc N (0; − 21). 3. f ( 2) − = 6 ⇔ −m( 2)
− + m − 3 = 6 ⇔ 3m = 9 ⇔ m = 3 ⇒ f (x) = 3 − x ⇒ f ( 3) − = 9. − 2 4.
f (x) = 3 ⇔ ( 3 − 2 ) x + 2 + 3 ⇔ x = = −( 6 + 2). 3 − 2 5. a) ( A 1 − ; 1)
− ∈ d : y = −mx + 4 ⇔ 1 − = −m( 1) − + 4 ⇔ m = 5 − .
b) M (x ; y ) ∈ d : y = −mx + 4 ⇔ y = −mx + 4 ⇔ mx + y − 4 = 0. (1) 0 0 0 0 0 0  =  = d đi qua M vớ x 0 x 0
i mọi m khi (1) đúng với mọi m, tức là: 0 0  ⇔  y − 4 = 0 y = 4  0  0
Vậy d luôn đi qua điểm M(0;4) cố định với m. 1 6. a) m ≠ ± b) m < 5 c) m = 0 hoặc m = 4. 2 7.
a) Với mọi x , x ∈ , x > x , ta có: 1 2 1 2
f (x ) − f (x ) = (1 − 2)(x − x ) < 0 , vì 1 − 2 < 0, x − x > 0. 1 2 1 2 1 2
Do đó f (x) là hàm số nghịch biến trên . 
b) Với mọi x , x ≥ 2, x ≠ x , ta có: 1 2 1 2 − − − − − − − − + − f (x x ) x x
( x 2 x 2 x 2 x 2 2 2 1 2 )( 1 2 1 1 2 1 2 ) = = = > 0. x − x x − x x − x x − 2 + x − 2 x − 2 + x − 2 1 2 1 2 ( 1 2)( 1 2 ) 1 2
Do đó f (x) là hàm số đồng biến với mọi x ≥ 2.
c) Với mọi x , x < 0, x > x , ta xét: 1 2 1 2 2 2
f (x ) − f (x ) = (x + 2) − (x + 2) = (x − x )(x + x ) < 0 1 2 1 2 1 2 1 2
Vì x − x > 0, x + x < 0 với mọi x , x < 0, x > x , do đó hàm số nghịch biến với mọi 1 2 1 2 1 2 1 2 x < 0. 8.
Hàm số y = f (x) = (1− 3)x −1 là hàm số nghịch biến vì a = 1− 3 < 0.
Ta có: f (m +1) > f (m + 2) vì m +1 < m + 2 . Chọn (A). 9. Giả sử có đa thức 3 2
f (x) = ax + bx + cx + d : a,b, c, d ∈ , a ≠ 0 thỏa mãn
f (7) = 2010, f (1) = 2012 . Ta có: 3 2 3 2
f (11) − f (7) = ( .11 a + .11 b + .11 c + d) − ( .7 a + .7 b + .7 c + d) = 3 3 2 2 2 . a (11 − 7 ) + . b (11 − 7 ) + . c (11 − 7 )      4  4  4 
Từ đó suy ra: [ f (11) − f (7)]4. (*)
Mặt khác f (11) = 2012, f (7) = 2010 nên f (11) − f (7) = 2. (**)
Từ (*) và (**) suy ra 24 (vô lý), suy ra điều giả sử là sai (đpcm).
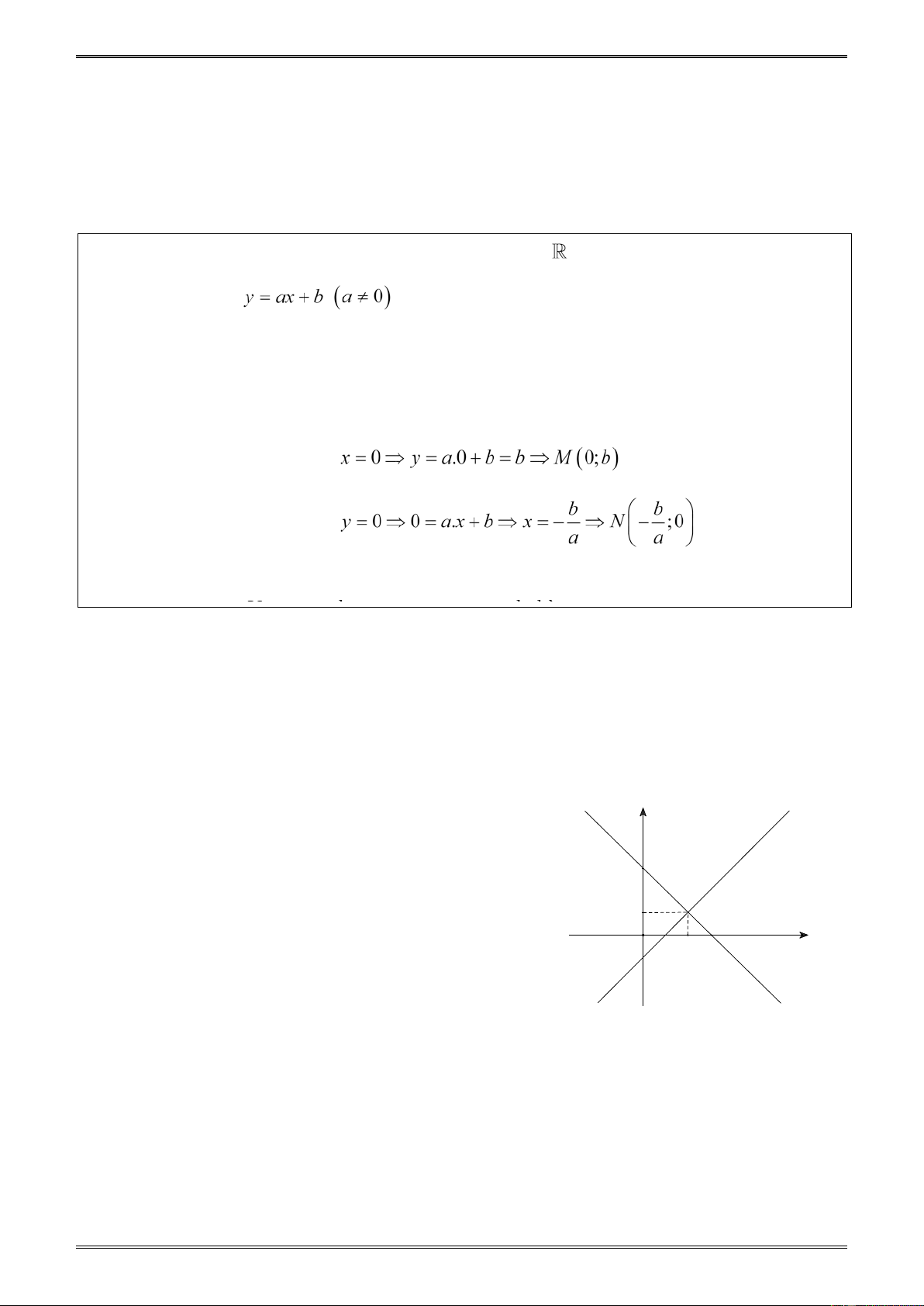
§3. ĐỒ THỊ CỦA HÀM SỐ 𝒚 = 𝒂𝒙 + 𝒃(𝒂 ≠ 𝟎)
A. TRỌNG TÂM KIẾN THỨC
1. Đồ thị của hàm số 𝒚 = 𝒂𝒙 + 𝒃(𝒂 ≠ 𝟎)
Đồ thị của hàm số y = ax + b(a ≠ 0) là một đường thẳng ( kí hiệu là (d) ):
+ Cắt trục tung tại điểm có tung độ bằng b hay (d) luôn đi qua điểm B(0;b)
+ Song song với đường thẳng y = ax nếu b ≠ 0 ; trùng với đường thẳng y = ax nếu b = 0.
Chú ý.  b được gọi là tung độ gốc của đường thẳng.
 Đồ thị của hàm số y = ax + b(a ≠ 0) còn được gọi là đường thẳng y = ax + b hoặc
đường thẳng ax − y + b = 0.
2. Cách vẽ đồ thị của hàm số 𝒚 = 𝒂𝒙 + 𝒃(𝒂 ≠ 𝟎)
Trường hợp 1: Khi b = 0 thì y = ax . Đồ thị của hàm số y = ax là đường thẳng đi qua gốc tọa
độ O(0;0) và điểm ( A 1; a).
Trường hợp 2: y = ax + b với a ≠ 0 và b ≠ 0
Cách 1. + Xác định hai điểm bất kỳ của đồ thị
Chẳng hạn cho x = 1 thì y = .1
a + b = a + b , ta được B(1; a + b) ; cho x = 2 thì y = .2 a + b ta
được điểm C(2;2a + b).
+ Vẽ đường thẳng BC ta được đồ thị hàm số.
Cách 2. + Xác định giao điểm của đồ thị với hai trục tọa độ:
• Cho x = 0 ⇒ y = .
a 0 + b = b ⇒ M (0;b) thuộc trục tung. • b b Cho y = 0 ⇒ 0 = .
a x + b ⇔ x = −
⇒ N(− ;0) thuộc trục hoành a a
+ Vẽ đường thẳng MN ta được đồ thị hàm số.
Chú ý. Khi b = 0 thì y = ax ; đồ thị của hàm số y = ax đi qua gốc tọa độ O(0;0).
Khi b ≠ 0 thì đồ thị của hàm số y = ax + b đi qua điểm B(0; b).
Khi a > 0 thì đồ thị của hàm số y = ax + b là đường thẳng có chiều đi lên từ trái sang phải (hàm số đồng biến).
Khi a < 0 thì đồ thị của hàm số y = ax + b là đường thẳng có chiều đi xuống từ trái sang phải (hàm số nghịch biến).
Đường thẳng y = x là đường phân giác của góc phần tư thứ (I) và (III).
Đường thẳng y = −x là đường phân giác của góc phần tư thứ (II) và (IV).
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. ĐIỂM THUỘC ĐƯỜNG THẲNG.
ĐIỂM KHÔNG THUỘC ĐƯỜNG THẲNG Phương pháp giải
Cho điểm M (x ; y ) và đường thẳng (d) có phương trình y = ax + . b Khi đó: 0 0
M ∈ (d ) ⇔ y = ax + b 0 0
M ∉ (d ) ⇔ y ≠ ax + b 0 0  1 
Ví dụ 1. Cho đường thẳng (d): y = 3
− x +1. Trong các điểm M ( 1
− ;2), N(0;1), P ;0 .   Hãy xác  3 
định các điểm thuộc và không thuộc đường thẳng (d). Giải Ta có: M ( 1
− ;2) ∉(d) vì khi x = -1 thì -3(-1) + 1 = 3 + 1 = 4 ≠ 2;
N (0;1) ∈ (d ) , vì khi x = 0 thì -3.0 +1 = 0 + 1 = 1;  1  1 1 P ;0 ∈ (d )   , vì khi x = thì 3. − +1 = 1 − +1 = 0.  3  3 3
Ví dụ 2. Điểm M ( 2;1) thuộc đường thẳng nào trong các đường thẳng dưới đây ?
(A) y = x +1 − 2
(B) x + y − 2 +1 = 0 (C) y = 2x +1 − 2
(D) x + y − 2 = 0 Giải
Kí hiệu các đường thẳng ở các trường hợp (A) , (B) , (C) và (D) lần lượt là
(d ) : y = x +1 − 2 1
(d ) : x + y − 2 +1 = 0 2 (d ) : y = 2x +1 − 2 3
(d ) : x + y − 2 = 0 4
Ta có: M ( 2;1) ∈ (d ) , vì khi x = 2 thì 2 +1 − 2 = 1 1
M ( 2;1) ∉ (d ) , vì khi x = 2 thì − 2 + 2 −1 = 1 − ≠ 1 2
M ( 2;1) ∉ (d ) , vì khi x =
2 thì 2. 2 +1− 2 = 3 − 2 ≠ 1 3
M ( 2;1) ∉ (d ) , vì khi x = 2 thì − 2 + 2 = 0 ≠ 1. 4 Chọn (A).
Ví dụ 3. Cho đường thẳng (d): y = 2
− x + 3. Tìm m để đường thẳng (d) đi qua điểm ( A − ; m 3) − . Giải
Đường thẳng (d): y = 2
− x + 3 đi qua điểm ( A − ; m 3) − khi: 3 − = 2.(
− − m) + 3 ⇔ 2m = 6 − ⇔ m = 3. −
Vậy đường thẳng (d): y = 2
− x + 3 đi qua điểm ( A − ; m 3) − khi m = 3. −
Ví dụ 4. Cho đường thẳng (d): y = (m + 2)x + 3m −1. Tìm m để đường thẳng (d) đi qua điểm M ( 2; − 3). Giải M ( 2;
− 3) ∈(d) : y = (m + 2)x + 3m −1 khi: 3 = (m + 2)( 2) − + 3m −1 ⇔ 3 = 2
− m − 4 + 3m −1 ⇔ m = 8.
Vậy đường thẳng (d): y = (m + 2)x + 3m −1 đi qua điểm M ( 2; − 3) khi m = 8.
Ví dụ 5. Chứng minh rằng đường thẳng (m − 2)x + y + 4m − 3 = 0 luôn đi qua một điểm cố định
với mọi giá trị của m. Giải
Gọi M (x ; y ) là điểm thuộc (d), ta có: 0 0
(m + 2)x + y + 4m −3 = 0 ⇔ m(x + 4 + 2x + y −3 = 0 0 ) ( 0 0 ) 0 0
Đường thẳng (d ) luôn đi qua M (x ; y với mọi m khi và chỉ khi: 0 0 ) x + 4 = 0 x = 4 − 0 0  ⇔  . 2x + y − 3 = 0 y = 11  0 0  0
Vậy (d ) luôn đi qua điểm cố định M ( 4; − 1 )
1 với mọi giá trị của m .
Dạng 2. XÁC ĐỊNH ĐƯỜNG THẲNG. Phương pháp giải
Gọi hàm số cần cần tìm là: y = ax + b (a ≠ 0) , ta phải tìm a và b .
+ Với điều kiện của bài toán xá định được các hệ số liên hệ giữa a và b .
+ Giải phương trình để tìm a,b .
Ví dụ 1. Cho hàm số bậc nhất y = 2
− x + b . Xác định b nếu:
a) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2.
b) Đồ thị hàm số đi qua điểm A( 1 − ;2). Lời giải
a) Đồ thị hàm số y = 2
− x + b cắt trục tung tại điểm có tung độ bằng 2, nên b = 2 .
Vậy đồ thị hàm số cần tìm là y = 2 − x + 2.
b) Đồ thị hàm số y = 2
− x + b đi qua điểm A( 1 − ;2) khi: 2 = ( 2 − ).(− )
1 + b ⇔ 2 = 2 + b ⇔ b = 0 .
Vậy b = 0 thì y = 2
− x đi qua điểm A( 1 − ;2).
Ví dụ 2. Xác định đường thẳng (d ) , biết (d ) có dạng y = ax − 4 và đi qua điểm A( 3 − ;2) . Lời giải
Đường thẳng (d ) : y = ax − 4 đi qua điểm A( 3 − ;2) khi: 2 = . a ( 3 − ) − 4 ⇔ 3
− a = 2 + 4 ⇔ a = 2 − .
Vậy (d ) có phương trình y = 2
− x − 4 đi qua điểm A( 3 − ;2) .
Ví dụ 3. Cho hàm số y = (m − 2) x + m + 2 . Xác định m , biết:
a) Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng 2 − .
b) Đồ thị hàm số đi qua gốc tọa độ. Lời giải
a) Đồ thị (d ) của hàm số y = (m − 2) x + m + 2 cắt trục hoành tại điểm có hoành độ bằng 2 − nên A( 2; − 0) thuộc (d ) .
Do đó: 0 = (m − 2).( 2 − ) + m + 2 ⇔ 2
− m + 4 + m + 2 = 0 ⇔ m = 6 .
b) Đồ thị (d ) của hàm số y = (m − 2) x + m + 2 đi qua gốc tọa độ O(0;0) thuộc (d ) .
Do đó: 0 = (m − 2).0 + m + 2 ⇔ m + 2 = 0 ⇔ m = 2 − .
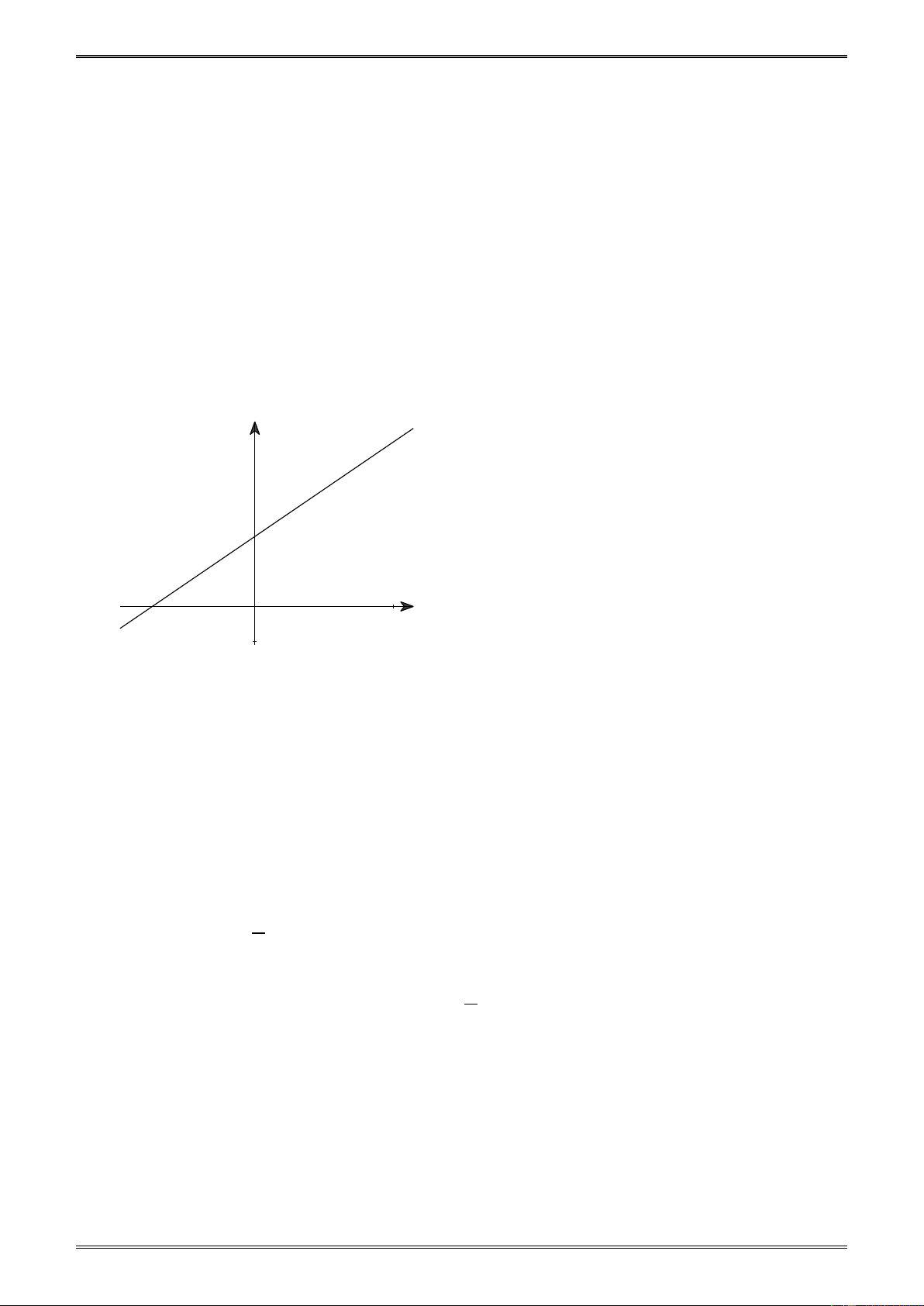
Ví dụ 4. Xác định đường thẳng đi qua hai điểm A( 3 − ;0) và B(0;2) . Lời giải y B 2 O x -3 Hình 7
Gọi phương trình đường thẳng AB là: y = ax + b . Ta có: A( 3
− ;0)∈ AB ⇒ 0 = . a ( 3
− ) + b hay b = 3a .
B (0;2) ∈ AB ⇒ 2 = .
a 0 + b hay b = 2 . Từ đó suy ra 2 a = . 3 2
Vậy phương trình đường thẳng AB là: y = x + 2 . 3
Ví dụ 5. Cho đường thẳng (d : y = 2012x + 2 . Xác định đường thẳng (d sao cho (d và 1 ) 2 ) 1 )
(d cắt nhau tại một điểm nằm trên trục tung. 2 ) Lời giải
Đồ thị hàm số y = 2012x + 2 cắt trục tung tại điểm có tung độ bằng 2 vì có tung độ gốc là
b = 2 ⇒ đường thẳng (d luôn đi qua điểm A(0;2) nằm trên trục tung. 1 )
Vì (d và (d cắt nhau tại một điểm nằm trên trục tung nên A(0;2) thuộc (d . 2 ) 2 ) 1 )
Do đó (d có phương trình y = 2 hoặc x = 0 (trục tung) hoặc y = ax + 2 (với 2 )
a ≠ 0, a ≠ 2012 )
Chú ý. Có vô số đường thẳng đi qua điểm A(0;2) .
Dạng 3. VỀ ĐỒ THỊ CỦA HÀM SỐ y = ax + b(a ≠ 0) Phương pháp giải
+ Tìm hai điểm thuộc đồ thị hàm số bằng cách cho x nhận hai giá trị xác định rồi tính hai
giá trị tương ứng của y (thông thường ta lấy hai điểm đó là giao điểm của đồ thị với trục hoành và trục tung)
+ Đường thẳng đi qua hai điểm vừa tìm được là đồ thị hàm số cần vẽ.
Ví dụ 1. Cho các hàm số sau: y = −x + 2 ( )
1 ; y = 2x −1 (2) .
a) Vẽ đồ thị các hàm số ( )
1 , (2) trên cùng một mặt phẳng tọa độ.
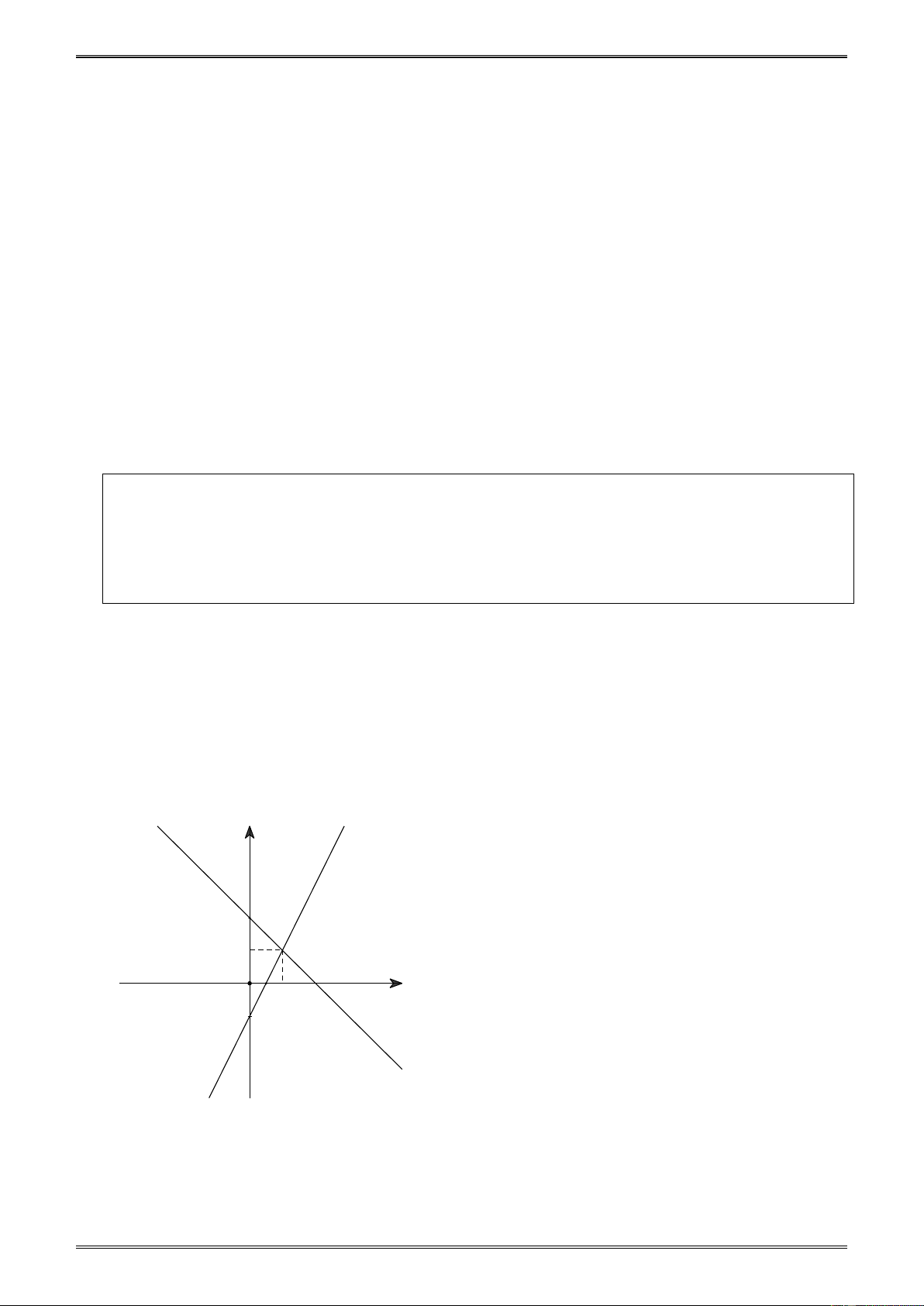
b) Xác định tọa độ giao điểm I của ( ) 1 và (2) . Lời giải y y = 2x-1 A 2 1 I D B O 1 2 x -1 C y = -x+2 Hình 8
a) Hình 8 * Vẽ đồ thị hàm số ( ) 1 :
Cho x = 0 ⇒ y = 2 ⇒ A(0;2) ∈ Oy ;
y = 0 ⇒ x = 2 ⇒ B (2;0) ∈ Ox .
Đường thẳng AB là đồ thị hàm số y = −x + 2 .
* Vẽ đồ thị hàm số (2) :
Cho x = 0 ⇒ y = 1 − ⇒ C (0;− ) 1 ∈ Oy ; 1  1  y = 0 ⇒ x = ⇒ D ;0 ∈ Ox   . 2  2 
Đường thẳng CD là đồ thị hàm số y = 2x −1.
b) Cách 1. Từ giao điểm I của hai đồ thị hàm số ta vẽ đường thẳng vuông góc với trục
hoành, cắt trục này tại điểm có hoành độ là 1. Vậy tọa độ giao điểm là I (1; ) 1 .
Cách 2. Gọi tọa độ giao điểm I là ( x ; y . 1 1 )
Vì I là giao điểm của AB và CD nên I vừa thuộc AB , vừa thuộc CD .
Vì I ( x ; y ∈ AB : y = −x + 2 nên y = −x + 2 . 1 1 ) 1 1
Vì I ( x ; y ∈ CD : y = 2x −1 nên y = 2x −1. 1 1 ) 1 1
Suy ra ta có: −x + 2 = 2x −1 ⇔ 3x = 3 ⇔ x = 1 1 1 1 1
⇒ y = −x + 2 = 1 − + 2 = 1. 1 1
Vậy tọa độ giao điểm I là I (1; ) 1 . 1
Ví dụ 2. Cho hàm số: y = x −1 (d ) . 2
a) Vẽ đồ thị (d ) của hàm số đã cho.
b) Tính khoảng cách từ gốc O của hệ trục tọa độ đến đường thẳng (d ) . Lời giải
a) Cho x = 0 ⇒ y = 1 − ⇒ A(0;− )
1 ∈ Oy; y = 0 ⇒ x = 2 ⇒ B (2;0) ∈ Ox . Đườ 1
ng thẳng AB là đồ thị (d ) của hàm số y = x −1. 2
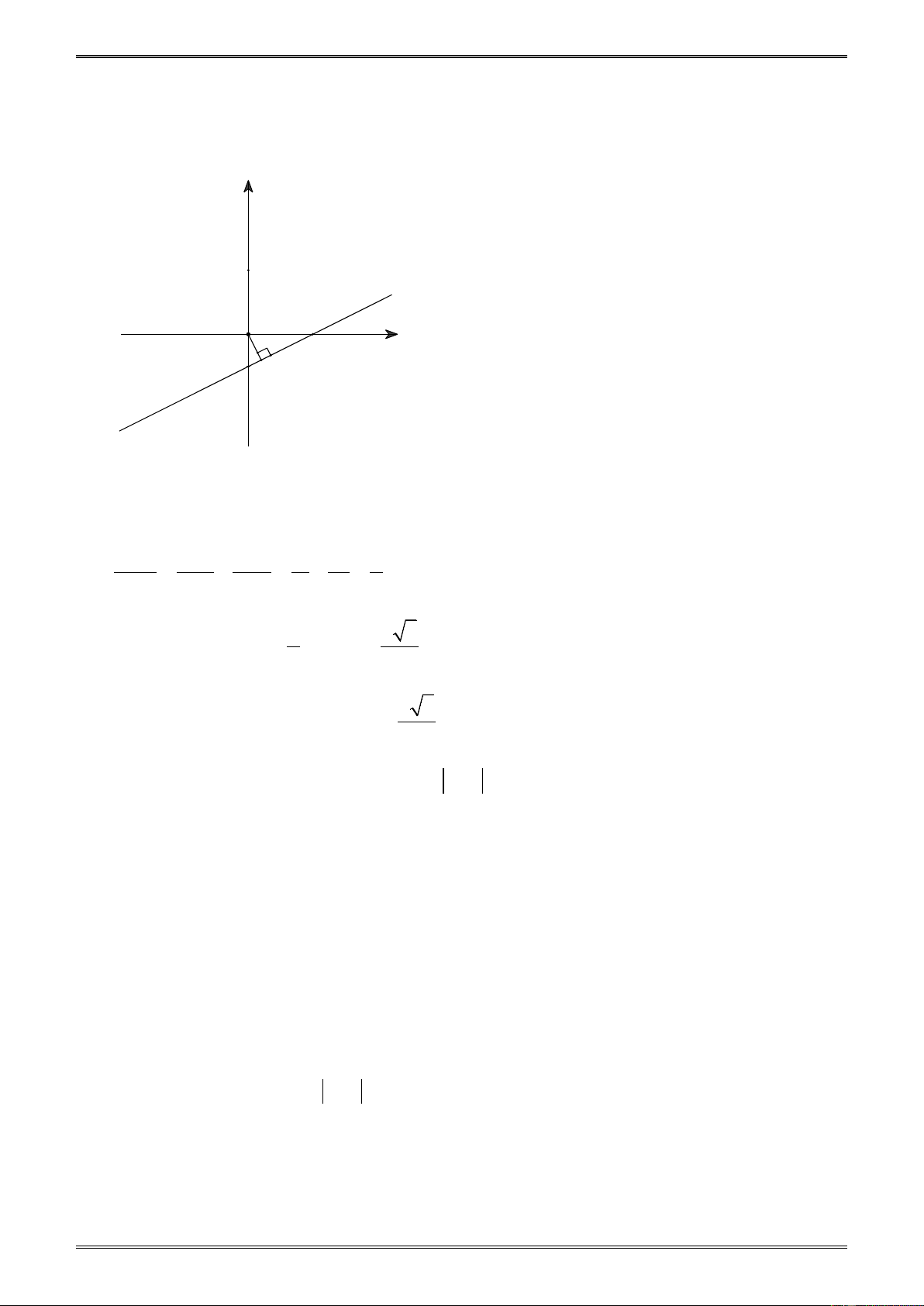
b) Kẻ OH vuông góc với (d ) tại H . Khi đó OH là khoảng cách từ O đến đường thẳng (d) (hình 9) y B O 2 x A H -1 Hình 9
Trong tam giác vuông OAB , ta có: 1 1 1 1 1 5 = + = + = . 2 2 2 2 2 OH OA OB 1 2 4 4 2 5 Từ đó suy ra: 2 OH = ⇒ OH = . 5 5 2 5
Vậy khoảng cách từ O đến (d ) là . 5
Ví dụ 3. Cho các hàm số sau: y = 2 ( )
1 ; y = x +1 (2) ; y = 2mx + m −1 (3) .
a) Vẽ đồ thị các hàm số ( )
1 , (2) trên cùng mặt phẳng tọa độ.
b) Tìm m để đồ thị hàm số (3) đi qua trong giao điểm của hai đồ thị ( ) 1 và (2) . Lời giải
a) Vẽ đồ thị của hàm số y = 2 (1);
Đồ thị hàm số y = 2 là đường thẳng song song với trục hoành và cắt trục tung tại điểm có tung độ bằng 2.
Vẽ đồ thị của hám số y = x +1 (2) y N 2 M -3 -1 o 1 x Hình 10
x +1 khi x ≥ 1 − 
Ta có: y = x +1 =  . −  ( x + ) 1 khi x ≤ 1 −
Từ đó, ta được đồ thị có hình chữ V như hình 10.
Từ hình vẽ ta thấy đồ thị của hai hàm số ( )
1 và (2) cắt nhau tại hai điểm M (1;2) và N ( 3 − ;2) .
b) Đồ thị (d ) của hàm số y = 2mx + m −1 đi qua giao điểm của hai đồ thị hàm số ( ) 1 và
đồ thị hàm số (2) khi và chỉ khi (d ) đi qua điểm M hoặc N .
+ Trường hợp (d ) đi qua M (1;2). Kh đó: 2 = 2 .1
m + m −1 ⇔ 3m = 3 ⇔ m = 1.
+ Trường hợp (d ) đi qua N ( 3 − ;2) . Khi đó: 3 2 = 2. . m ( 3
− ) + m −1 ⇔ 5m = 3 − ⇔ m = − . 5 3
Vậy với m = 1 hoặc m = − thì đồ thị hàm số (3) đi qua giao điểm của đồ thị hàm số ( ) 1 5
và đồ thị hàm số (2).
Ví dụ 4. Cho hàm số y = mx + 3 (d ) . Tìm m để khoảng cách từ gốc tọa độ O đến đường
thẳng (d ) là lớn nhất. Lời giải y A y = 3 3 H o x d Hình 11
Trường hợp 1. Xét m = 0 .
Khi m = 0 thì (d ) có phương trình: y = 0.x + 3 = 3 hay y = 3 .
Đồ thị hàm số y = 3 là đường thẳng song song với trục hoành và cắt trục tung tại điểm có
tung độ bằng 3 nên khoảng cách từ O đến (d ) bằng 3.
Trường hợp 2. Xét m ≠ 0 .
Khi đó (d ) : y = mx + 3 luôn đi qua điểm A(0;3) nằm trên trục tung.
Kẻ OH vuông góc với (d ) tại H . Khi đó OH là khoảng cách từ O đến đường thẳng (d) .
Ta có: OH ≤ OA hay OH ≤ 3 (Dấu “=” không xảy ra vì m ≠ 0 nên H không trùng A). Do đó OH < 3.
Kết hợp hai trường hợp ta có khi m = 0 thì khoảng cách từ O đến đường thẳng (d ) là lớn nhất.
C. BÀI TẬP TỰ LUYỆN
1. Đồ thị của hàm số y = 2x +1− 2 đi qua điểm nào sau đây? A. M ( 1 − ; ) 1 B. N (1; ) 1 C. P (1;− ) 1 D. Q ( 2 ) ;1
2. Điểm E ( 2;
− 0) thuộc đường thẳng nào trong các đường thẳng sau đây? ( 2 4
d : y = x + 2 ; (d : y = 2
− x − 4 ; (d : y = 3x + 6;
(d : y = x + . 4 ) 3 ) 2 ) 1 ) 3 3
A. Chỉ thuộc đường thẳng (d
B. Chi thuộc (d và (d 4 ) 2 ) 1 )
C. Chỉ thuộc (d và (d
D. Thuộc cả bốn đường thẳng đã cho 3 ) 2 ) 1
3. Cho hai đường thẳng (d : y = 2x + 2012 và (d : y = − x + 2012 . Đường thẳng nào 2 ) 1 ) 2
dưới đây không đi qua giao điểm của (d và (d ? 2 ) 1 )
A. y = 2012x
B. y = x + 2012
C. y = 2012x + 2012
D. y = −x + 2012
4. Vẽ đồ thị của các hàm số sau trên cùng một hệ trục tọa độ: 1 y = x + 2 ; y = 2 − x + 2; y = 2 − x + 4. 2
5. Xác định đường thẳng đi qua hai điểm A( 2; − 0) và B(0;3).
6. Cho (d : y = x, d : y = 0,5x ; đường thẳng (d ) song song với trục Ox và cắt trục tung 1 ) ( 2)
Oy tại điểm C có tung độ bằng 2 . Đường thẳng (d ) lần lượt cắt (d , (d tại D và E . 2 ) 1 )
Khi đó, tính diện tích tam giác ODE .
7. Với giá trị nào của m thì đồ thị của các hàm số y = 2x + 4 − m và y = 3x + m − 2 cắt nhau
tại một điểm nằm trên trục tung.
8. Cho hai đường thẳng (d : m − 2 x + 4my +1 = 0 và (d : m − 2 x + 2012 y + 5 − m = 0 ( 2 ) ( ) 1 ) ( ) m là tham số).
a) Chứng minh rằng (d luôn đi qua một điểm cố định khi m thay đổi. 1 )
b) Tìm m để hai đường thẳng (d , d cắt nhau tại một điểm thuộc trục hoành. 1 ) ( 2 )
9. Cho hàm số y = f ( x) = (m − 2) x + 2 có đồ thị là đường thẳng (d ) .
a) Tìm m để (d ) đi qua điểm M ( 1 − ; ) 1 .
b) Xác định m để khoảng cách từ điểm O(0;0) đến (d ) có giá trị lớn nhất.
HƯỚNG DẪN GIẢI - ĐÁP SỐ
1. Ta thử cặp giá trị mà triệt tiêu 2 trước. Thử N (1; )
1 thấy đúng. Chọn ( B) .
2. Thử trực tiếp ta thấy tọa độ ( 2;
− 0) thỏa mãn cả bốn hàm số. Chọn (D) . 3.
(d và (d có cùng tung độ gốc 2012 , hệ số a khác nhau. Các đường thẳng có cùng 2 ) 1 )
tung độ 2012 sẽ đi qua giao điểm của (d và (d . Do đó, ta loại (B), (C), (D), vì có 2 ) 1 )
tung độ gốc là 2012 . Chọn (A).
4. (h.12) Vẽ đồ thị của hàm số 1 y = x + 2 (d . 1 ) 2 y (d )1 4 A 2 B 4 o 1 2 x (d ) (d ) 2 3 Hình 12
Cho x = 0 ⇒ y = 2 ⇒ A(0;2) .
Cho y = 0 ⇒ x = 4 − ⇒ B( 4; − 0) . Biểu diễn các điểm ,
A B trên mặt phẳng tọa độ.
Vẽ đường thẳng AB được đồ thị (d . 1 )
Tương tự ta vẽ được: (d : y = 2
− x + 2 ; (d : y = 2 − x + 4 . 3 ) 2 )
5. Gọi phương trình đường thẳng AB là: y = ax + b . Ta có: A( 2; − 0)∈ AB ⇒ 0 = . a ( 2
− ) + b hay b = 2a .
B (0;3) ∈ AB ⇒ 3 = .
a 0 + b hay b = 3 . Từ đó suy ra 3 a = . 2 3
Vậy phương trình đường thẳng AB là: y = x + 3 . 2
6. Vẽ nhanh đồ thị. Từ đồ thị ta thấy: DE = 2,OC = 2 . Do đó diệ 1 1
n tích tam giác cần tìm là: S
= OC.DE = .2.2 = 2 (đvdt) ODE ∆ 2 2
7. M ∈ Oy ⇒ M (0; y . Giả sử M là giao điểm của (d và (d . 2 ) 1 ) 0 )
M ∈ (d : y = 2x + 4 − m ⇔ y = 4 − m ; 1 ) 0
M ∈ (d : y = 3x + m − 2 ⇔ y = m − 2 . 2 ) 0
Suy ra 4 − m = m − 2 ⇔ m = 3 (Thử lại thấy đúng)
Vậy khi m = 3 thì (d cắt (d tại M (0; ) 1 thuộc Oy . 2 ) 1 )  1 1  8. a) M ; −    2 8 
b) Giao điểm thuộc trục hoành, nên tung độ y = 0 . Vậy:
(m − 2)x + 4 .0
m +1 = 0 và (m − 2) x + 2012.0 + 5 − m = 0 .
Suy ra: 1 = 5 − m ⇔ m = 4 (thử lại thấy đúng). 9. a) m = 3 . b) y (d) H y = 2 2 K A O x Hình 13
(h. 13) Khi m = 2 : y = 2 ⇒ Khoảng cách từ O đến (d ) là OH = 2.
Khi m ≠ 2 : y = (m − 2) x + 2 . 2 −  2 − 
Cho y = 0 ⇒ x = ⇒ A ;0   m − 2  m − 2 
Vẽ OK ⊥ (d ) . Ta có:
H (0;2) ∈ d : y = (m − 2) x + 2 với mọi m .
Suy ra: OK < OH hay OK < 2 .
Vậy khoảng cách từ điểm O đến (d ) lớn nhất bằng 2 , đạt được khi m = 2 .
§4. ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU
A. TRỌNG TÂM KIẾN THỨC.
1. Hai đường thẳng song song.
Hai đường thẳng y = ax + b(a ≠ 0) và y = a x′ + b′(a′ ≠ 0) song song với nhau khi và chỉ khi a = a ,
′ b ≠ b′ và trùng nhau khi và chỉ khi a = a ,′b = b′.
2. Hai đường thẳng cắt nhau
Hai đường thẳng y = ax + b (a ≠ 0) và y = a x′ + b′ (a′ ≠ 0) cắt nhau khi và chỉ khi a ≠ a′ . Chú ý. + Khi a ≠ a ,
′ b = b′ thì hai đường thảng có cùng tung độ gốc, do đó chúng cắt nhau tại một
điển trên trục tung có tung độ là b .
+ Hai đường thẳng vuông góc với nhau khi và chỉ khi . a a′ = 1 − .
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. NHẬN DẠNG CẶP ĐƯỜNG THẲNG SONG SONG VỚI NHAU, CẶP
ĐƯỜNG THẲNG CẮT NHAU, CẶP ĐƯỜNG THẲNG VUÔNG GÓC VỚI NHAU. Phương pháp giải
Cho hai đường thẳng (d ) : y = ax + b(a ≠ 0) và (d′) : y = a x′ + b′ (a′ ≠ 0) .
+ (d ) // (d′) ⇔ a = a ' và b ≠ b ' .
+ (d ) ≡ (d ') ⇔ a = a ' và b = b ' .
+ (d ) và (d ') cắt nhau ⇔ a ≠ a ' .
+ (d ) ⊥ (d′) ⇔ . a a ' = 1 − .
Ví dụ 1. Hãy chỉ ra hai cặp đường thẳng song song với nhau trong các đường thẳng sau: ( x + 3 1
d : y = 2x +1; (d : y = ;
(d : y = − x + 2 ; 3 ) 2 ) 1 ) 2 2
(d : y = 0,5x −1;
(d : y = 4 + 2x ; (d : y =1− 2x. 6 ) 5 ) 4 ) Lời giải
Hai cặp đường thẳng song song với nhau là:
(d // d vì a = a'(= 2); b ≠ b'(1≠ 4); 1 ) ( 5)
(d // d vì a ≠ a′(= 0,5); b ≠ b'(1,5 ≠ − )1. 2 ) ( 4)
Ví dụ 2. Hãy chỉ ra các cặp đường thẳng vuông góc với nhau trong các đường thẳng sau: ( x + 3 1
d : y = 2x +1; (d : y =
; (d : y = − x + 2 ; (d : y = 0,5x −1; (d : y = 4 + 5x 5 ) 4 ) 3 ) 2 ) 1 ) 2 2
và (d : y = 1− 2x . 6 ) Lời giải
Bốn cặp đường thẳng vuông góc với nhau: (d ⊥ d ; (d
⊥ d ; (d ⊥ d ; 3 ) ( 5) 2 ) ( 6) 1 ) ( 3)
(d ⊥ d vì đều có .aa' = 1 − . 4 ) ( 6)
Ví dụ 3. Chứng tỏ rằng hai đường thẳng sau luôn cắt nhau với mọi giá trị của m : −x + m
a) (d ) : y = ( 2
m − m +1 x +1 và (d : y = . 2 ) 1 ) 2
b) (d ) : y = ( 2
m +1 x + 2012 và (d : y = −mx + 2012 . 4 ) 3 ) Lời giải 2  1  3 3 1 a) Xét (d có: 2
a = m − m +1 = m −
+ ≥ > 0 ; (d có a′ = − < 0. 2 ) 1 )    2  4 4 2
Suy ra a ≠ a ' với mọi m nên (d luôn cắt (d . 2 ) 1 ) 2  1  3 3 b) Ta có: 2
a − a ' = m +1 − (−m) 2
= m + m +1 = m + + ≥ > 0  
nên a ≠ a ' với mọi  2  4 4
m , suy ra (d luôn cắt (d . 4 ) 3 )
Chú ý: Hai đường thẳng (d và (d có cùng tung độ gốc là 2012 nên chúng cùng đi 4 ) 3 )
qua điểm A(0;2012) nằm trên trục tung. 1
Ví dụ 4. Chứng minh rằng giao điểm của hai đường thẳng y = −mx và y = x + 4 luôn nằm m
trên một đường tròn cố định với mọi m ≠ 0 . Lời giải 1
Kí hiệu đường thẳng y = −mx là (d ) , đường thẳng y =
x + 4 là (d ') . m
Ta có (d ) : y = −mx luôn đi qua gốc tọa độ O (0;0) cố định; (d′) 1 : y =
x + 4 luôn đi qua điểm B (0;4) cố định. m
Xét a a = (−m) 1 . ' . = 1
− với m ≠ 0 ⇒ (d ) ⊥ (d ') tại A ( A là giao điểm của hai đường m
thẳng (d ) và (d ') ) ⇒  OAB = 90° .
Do đó giao điểm A của (d ) và (d′) luôn nằm trên đường tròn đường kính OB cố định,
với O (0;0) và B (0;4)
Dạng 2. XÁC ĐỊNH ĐƯỜNG THẲNG VỚI QUAN HỆ SONG SONG. Phương pháp giải
Viết phương trình đường thẳng đi qua một điểm và song song với một đường thẳng cho
trước: Gọi phương trình đường thẳng cần tìm là y = ax + b .
+ Sử dụng điều kiện hai đường thẳng song song với nhau để xác định hệ số a .
+ Với a vừa tìm được, sử dụng điều kiện còn lại để xác định tung độ gốc b .
Ví dụ 1. Tìm m để đường thẳng (d ) : y = ( 2 2 − m
x − m − 5 song song với đường thẳng 1 ) (d : y = 2 − x + 2m +1. 2 ) Lời giải (d )//(d ) 2 ⇔ 2 − m = 2
− (1) và −m − 5 ≠ 2m +1 (2) . 1 2 m = 2 Giải ( ) 2 2 1 : 2 − m = 2 − ⇔ m = 4 ⇔  . m = 2 −
Giải (2) : − m − 5 ≠ 2m +1 ⇔ 3m ≠ 6 ⇔ m ≠ 2 − .
Vậy với m = 2 thì (d // d . 1 ) ( 2)
Ví dụ 2. Cho đường thẳng (d ) : 2x + y − 3 = 0 và điểm M ( 1 − ; )
1 . Viết phương trình đường
thẳng (d′) đi qua điểm M và song song với (d ) . Lời giải
Gọi phương trình đường thẳng (d′) là y = ax + b .
Ta có (d ) : 2x + y − 3 = 0 hay y = 2 − x + 3.
Vì (d′) // (d ) nên a = 2
− và b ≠ 3. Mặt khác, (d′) đi qua điểm M ( 1 − ; ) 1 nên 1 = . a (− ) 1 + b
⇔ −a + b = 1 ⇔ −( 2
− ) + b =1 (vì a = 2 − ) ⇔ b = 1 − (≠ 3).
Vậy phương trình đường thẳng cần tìm là: y = 2 − x −1.
Ví dụ 3. Cho M (0;2), N (1;0), P ( 1 − ;− )
1 lần lượt là trung điểm của các cạnh BC,CA và AB
của tam giác ABC . Viết phương trình đường thẳng AB . Lời giải
Gọi phương trình đường thẳng MN là: y = ax + b . Ta có:
N (1;0) ∈ MN ⇒ 0 = .
a 1 + b hay a = b − .
M (0;2) ∈ MN ⇒ 2 = .
a 0 + b hay b = 2 ⇒ a = 2 − .
Do đó phương trình đường thẳng MN là: y = 2 − x + 2.
Vì M , N lần lượt là trung điểm của CB và CA nên MN là đường trung bình của ABC ∆ ⇒ MN //AB .
Vì AB//MN nên phương trình đường thẳng AB có dạng: y = 2
− x + b′(b′ ≠ 2). Vì P ( 1 − ;− )
1 là trung điểm của đoạn AB nên đường thẳng AB đi qua P ( 1 − ;− ) 1 ⇒ 1 − = 2. − (− )
1 + b′ ⇔ b ' = 3 − (thỏa mãn).
Vậy phương trình đường thẳng AB là: y = 2 − x − 3.
Ví dụ 4. Cho ba đểm không thẳng hàng A( 2; − 2
− ), B(0;4) và C (2;02) . Xác định điểm D
trên mặt phẳng tọa độ sao cho ABCD là hình bình hành. Lời giải y 4 B -2 C o 2 x A -2 D Hình 14
Dễ thấy BC : y = 2 − x + 4 .
Giả sử có D để ABCD là hình bình hành.
Khi đó AD//BC nên đường thẳng AD có phương trình: y = 2
− x − 6 (vì đường thẳng AD qua A).
Vì D ∈ AD nên D ( x ; 2 − x − 6 . 0 0 )
Tứ giác ABCD là hình bình hành nên: 2 2
AD = BC ⇔ AD = BC  = ⇔ ( x 0 x + 2)2 + ( 2 − x − 4)2 = 2 + ( 4 − )2 2 0 ⇔ . 0 0 x = 4 −  0 ⇒ D 4; − 2 , D 0; 6
− . Từ hình 14 suy ra loại D vì không đúng thứ tự các đỉnh của tứ 1 ( ) 2 ( ) 1 giác ABCD . Vậy D (0; 6 − ) .
Dạng 3. XÁC ĐỊNH ĐƯỜNG THẲNG VỚI QUAN HỆ VUÔNG GÓC Phương pháp giải
Viết phương trình đường thẳng đi qua một điểm và vuông góc với một đường thẳng cho trước:
Gọi phương trình đường thẳng cần tìm là y = ax + b .
+ Sử dụng điều kiện hai đường thẳng vuông góc để xá định hệ số a .
+ Với a vừa tìm được, sử dụng điều kiện điểm thuộc đường thẳng để xác định tung độ gốc b .
Ví dụ 1. Tìm m để đường thẳng (d ) 2
: y = m x +1 − m vuông góc với đường thẳng (d′) 1 : y = − x + 2012 . 4 Lời giải (   m = 2 d ) ⊥ (d′) 1 2 ⇔ . a a ' = 1 − ⇔ m . − = 1 −   2 ⇔ m = 4 ⇔ .   4  m = 2 − Vậy m = 2
± thì (d ) ⊥ (d′) .
Ví dụ 2. Tìm a và b , biết đường thẳng (d : y = ax + b vuông góc với đường thẳng 1 ) ( 1 d : y = −
x và (d đi qua điểm P (1;− ) 1 . 1 ) 2 ) 2 Lời giải  1 
Vì (d ⊥ d nên . a a′ = 1 − ⇔ . a − = 1
− ⇔ a = 3. Ta có: (d : y = 3x + b . 1 ) 1 ) ( 2)    3 
Vì (d đi qua điểm P (1;− ) 1 nên 3.1 + b = 1 − ⇔ b = 4 − . 1 )
Vậy a = 3 và b = 4 − .
Ví dụ 3. Cho ba điểm A(1;2) , B (3;0),C (0; ) 1 . a) Chứng minh rằng ,
A B,C là ba đỉnh của một tam giác.
b) Viết phương trình đường thẳng chứa đường cao AH của ABC ∆ . Lời giải
a) Gọi phương trình đường thẳng đi qua B (3;0) và C (0; )
1 là BC : y = ax + b .
Ta có: B ∈ BC nên 0 = .3
a + b ⇔ 3a + b = 0 (1)
C ∈ BC nên: 1 = .0 a + b ⇔ b = 1 (2) 1 1 Từ ( )
1 và (2) suy ra: 3a +1 = 0 ⇔ a = − ⇒ BC : y = − x +1. 3 3
Vì A ∉ BC nên ba điểm ,
A B,C không thẳng hàng. Vậ ba điểm ,
A B,C là ba đỉnh của một tam giác.
b) Gọi phương trình đường cao AH là (d′) : y = a x ′ + b′.
Vì AH là đường cao của tam giác ABC nên  1 
AH ⊥ BC ⇔ (d′) ⊥ BC ⇔ . a a ' = 1 − ⇔ a '. − = 1 − ⇔ a ' = 3   .  3 
Mặt khác: A(1;2) ∈ (d′) nên 2 = a .1
′ + b′ ⇔ 2 = 3.1+ b′ ⇔ b′ = 1 − .
Vậy phương trình đường cao AH của ABC ∆
là y = 3x −1.
Ví dụ 4. Cho M (0;2), N (1;0), P ( 1 − ;− )
1 lần lượt là trung điểm của các cạnh BC , CA và AB
của tam giác ABC . Viết phương trình đường trung trực của đoạn thẳng AB . Lời giải C M N B P(-1;-1) A Hình 15
Gọi phương trình đường thẳng trung trực đoạn AB là (d ) : y = mx + n .
Gọi phương trình đường thẳng MN là: y = ax + b . Ta có:
N (1;0) ∈ MN ⇒ 0 = .
a 1 + b hay a = b − .
M (0;2) ∈ MN ⇒ 2 = .
a 0 + b hay b = 2 ⇔ a = 2 − .
Do đó phương trình đường thẳng MN là: y = 2 − x + 2.
Vì M , N lần lượt là trugn điểm của CB và CA nên MN là đường trung bình của ABC ∆ ⇒ MN //AB .
Vì (d ) là đường trung trực của đoạn AB nên (d ) ⊥ AB .
⇒ (d ) ⊥ MN ⇒ m (− ) 1 . 2 = 1 − ⇒ m = . 2 ⇒ (d ) 1 : y = x + n . 2 Vì P ( 1 − ;− )
1 là trung điểm của đoạn AB nên đường thẳng (d ) đi qua P ( 1 − ;− ) 1 . 1 ⇒ − = (− ) 1 1 .
1 + n ⇔ n = − . 2 2 1 1
Vậy phương trình đường trung trực của đoạn thẳng AB là: y = x − . 2 2
C. BÀI TẬP TỰ LUYỆN
1. Cho đường thẳng (d ) : y = ax + b . Tìm giá trị của a và b trong mỗi trường hợp sau:
A. (d ) // (d : y = 2x + 3 ;
B. (d ) trùng (d : y = −x +1; 2 ) 1 ) 1 1
C. (d ) cắt (d : y = x ;
D. (d ) ⊥ (d : y = − x . 4 ) 3 ) 2 2
2. Viết phương trình đường thẳng (d′) song song với đường thẳng (d ) : y = 4 − x + 5 và đi qua điểm M (1;− ) 1 .
3. Xác định a và b để đường thẳng (d : y = ax + b vuông góc với đường thẳng 1 ) ( 1 d : y = −
x và đi qua điểm P ( 1 − ;2). 2 ) 2
4. Đường thẳng (d ) : y = −ax + 2011 song song với đường phân giác của góc phần tư ( I ) và
(III ) thì hệ số a của (d) bằng: 1 A. 1 B. 1 − C. 0 D. − 2011 1
5. Cho bốn đường thẳng (d : y = x − 2 ; (d : y = 3
− x ; (d : y = 3 − x + 4 và 3 ) 2 ) 1 ) 3 ( 1 d : y =
x + 2 cắt nhau tại bốn điểm phân biệt M , N , P,Q . 4 ) 3
Khi đó bốn điểm M , N, P,Q là bốn đỉnh: A. Một hình thang
B. Một hình bình hành
C. Một hình chữ nhật
D. Một tứ giác không có gì đặc biệt.
6. Cho tam giác ABC có A(1;5), B ( 3 − ; ) 1 ,C (5;3)
a) Viết phương trình đường trung trực của cạnh BC .
b) Viết phương trình đường trung bình MN của tam giác ABC (MN //BC ) .
7. Cho M (0;4), N (2;0), P ( 1 − ; 2
− ) lần lượt là trung điểm của các cạnh BC,CA và AB của
tam giác ABC . Viết phương trình đường thẳng AB .
8. Cho hai đường thẳng (d : y = mx + m và (d : y = 3x + m + 3 . 2 ) 2 1 )
Chứng minh rằng (d và (d không trùng nhau với mọi giá trị của m . 2 ) 1 )
9. Cho ba điểm không thẳng hàng A( 3
− ;0), B(0;2) và C (1;0). Xác định điểm D trên mặt
phẳng tọa độ sao cho ABCD là hình bình hành.
HƯỚNG DẪN GIẢI – ĐÁP SỐ
1. a) (d ) // (d ⇔ a = 2;b ≠ 3 1 ) b) (d ) ≡ (d ⇔ a = 1 − ;b = 1 2 ) 1
c) (d ) cắt (d ⇔ a ≠ ; b ∈  . 3 ) 2 d) (d ) ⊥ (d ⇔ . a a ' = 1
− ⇔ a = 2; b ∈  4 )
2. Gọi phương trình đường thẳng (d ') là y = ax + b .
Vì (d ') // (d ) : y = 4
− x + 5 nên a = 4
− và b ≠ 5. Mặt khác (d′) đi qua M (1;− ) 1 nên 1 − = .1
a + b ⇔ a + b = 1 − ⇔ 4 − + b = 1 − (vì a = 4
− ) ⇔ b = 3 (thỏa mãn)
Vậy (d ') : y = 4 − x + 3.  1 
3. Vì (d ⊥ d nên . a a ' = 1 − ⇔ . a − = 1
− ⇔ a = 2. Do đó (d : y = 2x + b 1 ) 1 ) ( 2)    2 
Vì (d đi qua điểm P ( 1 − ;2) nên 2.(− )
1 + b = 2 ⇔ b = 4 . 1 ) 4.
(d '): y = x là đường phân giác của góc phần tư (I) và (III).
(d)//(d ') ⇔ −a =1⇔ a = 1 − . Chọn B. 1 1 5.
(d // d vì a = = a';b = 2
− ≠ 2 = b'; tương tự (d // d ; d ⊥ d vì .( 3 − ) = 1 − 2 ) ( 3) ( 2) ( 4) 1 ) ( 4) 3 3 .
Do đó, bốn điểm M , N, P,Q là bốn đỉnh của một hình chữ nhật. Chọn (C).
6. a) Gọi phương trình đường thẳng BC là: y = ax + b . Vì B ( 3 − ; ) 1 ∈ BC nên 1 = 3
− a + b ⇒ b = 1+ 3a ( ) 1 ;
C (5;3) ∈ BC nên 3 = 5a + b (2) . Thay (1) vào (2) ta đượ 1 7 c a = ;b = . Do đó: 1 7 BC : y = x + . 4 4 4 4
Trung trực của BC là đường thẳng (d ) vuông góc với BC tại trung điểm I của BC . x + x y + y
Tọa độ của điểm I là: B C x = = 1; B C y = = 2 hay I (1;2). I 2 I 2
Do đường trung trực (d ) : y = 4
− x + m đi qua I (1;2) nên ta được m = 6 .
Vậy đường thẳng (d ) là: y = 4 − x + 6 .
b) Gọi M , N lần lượt là trung điểm của AB, AC . Khi đó ta có: M ( 1 − ;3) . 1  
Vì MN / / BC nên MN có dạng: y = x + 7 n n ≠   . Do đó M ( 1
− ;3) thuộc MN nên 4  4  13 n = (thỏa mãn). 4
Vậy MN có phương trình: 1 13 y = x + . 4 4
7. Phương trình đường thẳng MN là: y = 2 − x + 4.
Vì AB//MN nên phương trình đường thẳng AB có dạng: y = 2
− x + b'(b' ≠ 2).
Vì đường thẳng AB đi qua P( 1 − ; 2 − ) nên 2 − = 2. − (− )
1 + b′ ⇔ b ' = 4 − .
Vậy phương trình đường thẳng AB là: y = 2 − x + 4. a = a ' m = 3  ( ) 1
8. Cách 1. (d ≡ d ⇔  ⇔  1 ) ( 2) 2 b  = b' m = m + 3  (2)
Thay (1) vào (2) ta được: 0 = 3 (vô lí). Dô đó (d không trùng (d với mọi m. 2 ) 1 ) 1 1 Cách 2. Giả sử: 2 2
b = b ' ⇔ m = m + 3 ⇔ m − m + + 3 − = 0 4 4 2  1   1  ⇔ m − + 3 − = 0    
(vô lí). Do đó điều giả sử là sai.  2   4 
Vậy (d không trùng (d với mọi m . 2 ) 1 )
Chú ý: Chỉ cần a ≠ a ' hoặc b ≠ b ' thì (d : y = ax + b không trùng (d : y = a x ′ + b′ . 2 ) 1 )
9. Đáp số: D ( 2; − 2 − ) .
§5. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG y = ax + b (a ≠ 0)
A. TRỌNG TÂM KIẾN THỨC
1. Hệ số góc của đường thẳng
+ Góc α tạo bởi tia Ax (A là giao điểm của
đường thẳng y = ax + b với trục Ox) và tia AB, y B
trong đó tia AB là phần của đường thẳng
y = ax + b nằm trong nửa mặt phẳng có bờ x’x
và chứa tia Oy được gọi là góc tạo bởi đường
thẳng y = ax + b và trục Ox (hình 16). α A o x
+ Vì có sự liên quan giữa hệ số a với góc tạo bởi y = ax + b
đường thẳng y = ax + b và trục Ox nên người
ta gọi a là hệ số góc của đường thẳng
y = ax + b Hình 16
Khi góc α nhọn thì a = tanα
Khi góc α tù thì a = − ( 0 tan 180 − α )
+ Các đường thẳng có cùng hệ số góc a thì tạo với Ox các góc bằng nhau.
Các đường thẳng song song hoặc trùng nhau thì có hệ số góc bằng nhau
+ Khi a > 0 thì góc α nhọn, hệ số a càng lớn thì α càng lớn.
+ Khi a < 0 thì góc α tù, hệ số a càng lớn thì α càng lớn.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. XÁC ĐỊNH HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG Phương pháp giải
Vận dụng định nghĩa hệ số góc của đường thẳng ; góc giữa
đường thẳng và trục Ox; vận dụng tỉ số lượng giác của góc nhọn.
Ví dụ 1. Đường thẳng y = (m + )
1 x + 5 đi qua điểm F ( 1
− ;3) có hệ số góc bằng bao nhiêu? Giải
Kí hiệu (d ) là đường thẳng y = (m + ) 1 x + 5 . Vì F ( 1
− ;3)∈(d ) nên 3 = (m + ) 1 (− ) 1 + 5 ⇔ m = 1.
Vậy hệ số góc của đường thẳng (d ) là a = m +1 = 1+1 = 2
Ví dụ 2. Tính hệ số góc của đường thẳng (d ) : y = (m − 2) x + 3 biết nó song song với đường
thẳng (d ') : 2x − y −1 = 0 . Vẽ đồ thị (d ) vừa tìm được. Giải + Đường thẳng
(d ') có phương trình
2x − y −1 = 0 ⇔ y = 2x −1. y
Vì (d ) / / (d ') ⇔ a = a ' và b ≠ b ' nên m − 2 = 2 và A 3 3 ≠ 1. −
Do đó hệ số góc của đường thẳng (d ) là 2. B -3 o x
+ Ta có (d ) : y = 2x + 3. Vẽ đường thẳng đi qua hai 2  − điể 3  m A(0;3) và B ;0 
 là đường thẳng (d ) cần  2  vẽ. (h.17) Hình 17
Ví dụ 3. Tính hệ số góc của đường thẳng (d ) : y = (1− m) x +1, biết nó vuông góc với đường
thẳng (d ') : x − 2 y − 4 = 0 . Vẽ đồ thị (d ) vừa tìm được. Giải + Đường thẳng (d ') có phương trình y 1
x − 2 y − 4 = 0 ⇔ y = x − 2 2 1
Vì (d ) ⊥ (d ) 1 ' ⇔ . a a ' = 1 − ⇔ (1− m). = 1 − ⇔ 1− m = 2 − 2 o 1 x
Do đó hệ số góc của đường thẳng (d ) là 2 − 2
+ Ta có (d ) : y − 2x +1. Vẽ đường thẳng đi qua hai điểm  1  Hình 18 A(0; ) 1 và B ;0 
 là đường thẳng (d ) cần vẽ (h.18).  2 
Ví dụ 4. Tính hệ số góc của đường thẳng đi qua hai điểm A( 1 − ; ) 1 và B (2; 3 − ) Giải
Giả sử phương trình đường thẳng đi qua hai điểm A( 1 − ; ) 1 và B (2; 3 − ) là
AB : y = ax + b
Ta có: A ∈ AB nên: 1 = . a (− ) 1 + b ⇔ 1
− + b = 1 ⇔ b = a +1 (1)
B ∈ AB nên: 3 − = .2 a + b ⇔ b = 2 − a − 3 (2) 4 Từ (1) và (2) ta có: 2
− a − 3 = a +1 ⇔ a = − 3 4
Vậy hệ số góc của đường thẳng AB là: a = − . 3
Dạng 2. XÁC ĐỊNH GÓC Phương pháp giải V Vận dụ ận d ng đị ụng định nh nghĩa gnghĩa óc gi g ữ óc giữ a đườ a đư ng thẳờng th ng
ẳng y = ax + b (a ≠ 0 và trụ) và tr c Ox; ục Ox; v vận dụn ận d g tỉ s ụng ố t lượ ỉ số lư ng giác củ ợng giác c a góc nhọ ủa góc nh n; vận dụn ọn; v g ta ận d m gi ụng t ác đồ am g ng dạ iác đồng d ng. ạng.
Ví dụ 1. Tính góc tạo bởi đường thẳng y = 2
− x + 3 và trục Ox. Giải y B 3
Vẽ đường thẳng y = 2 − x + 3. Khi đó 
BAx là góc tạo bởi đường thẳng y = 2
− x + 3 với trục Ox (hình 19) o 1,5 A x Hình 19
Xét tam giác vuông ABO, ta có:  OB 3 = = = ⇔  0 tan OAB 2 OAB ≈ 63 26 ' OA 1,5 ⇒  0 = −  0 BAx 180 OAB ≈ 116 34 '
(Trong đó 2 chính là giá trị tuyệt đối của hệ số góc của đường thẳng y = 2 − x + 3).
Ví dụ 2. Cho đường thẳng (d ) : y = mx + 3 . Tính góc tạo bởi đường thẳng (d ) với trục Ox,
biết (d ) đi qua điểm A( 3 − ;0) . Giải Vì A(− )∈(d ) 1 3;0
: y = mx + 3 ⇒ m = . 3 Khi đó ( 1
d ) có phương trình 1 y = x + 3. y (d):y = x + 3 3 3
Gọi α là góc tạo bởi đường thẳng (d ) với trục Ox. Khi đó ta có: 3 A 1 α 0 tanα = ⇒ α = 30 . -3 o x 3
Vậy góc tạo bởi đường thẳng (d ) với trục Ox Hình 20 là 0 30 . 1
Ví dụ 3. Cho hai đường thẳng (d : y = 2
− x và (d = x . (d ) là đường thẳng song song với 2 ) 1 ) 2
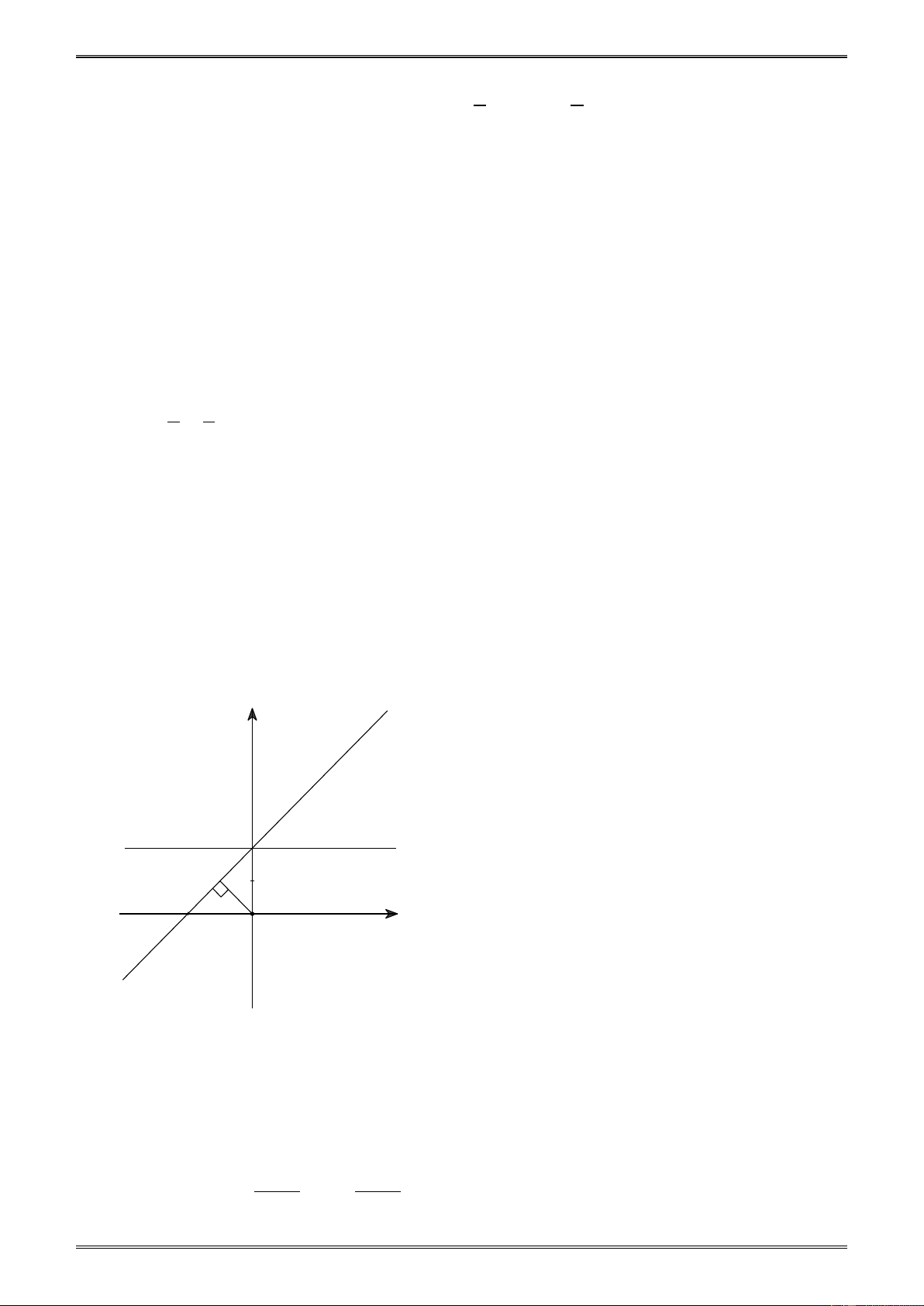
trục Ox và cắt Oy tại điểm có tung độ bằng 3; (d ) cắt (d và (d lần lượt tại A và 2 ) 1 ) B. Chứng minh rằng:  0 AOB = 90 Giải
Vẽ ba đường thẳng , (d ) , (d , (d như hình 21. 2 ) 1 )
Xét hai tam giác AHO và OHB, ta có: y (d ) 1 (d ) 2 ^ ^ HA HO 1 A 3 B 0 AHO = OHB = 90 ; = = . H HO HB 2 Do đó: AHO ∆ ∽ ∆ ⇒  =  OHB AOH OBH . 3 O 6 x - 2 Hình 21 Mà  +  0 = ⇒  0 AOH HOB 90 AOB = 90 1 1
Chú ý: (d : y = 2
− x có hệ số góc a = 2
− ; (d = x có hệ số góc a = . 2 ) 1 ) 1 2 2 2 1
Ta thấy: a .a = 2 − . = 1
− , do đó: (d ⊥ d . 1 ) ( 2) 1 2 ( ) 2
Dạng 3. XÁC ĐỊNH ĐƯỜNG THẲNG Phương pháp giải
• Gọi phương trình đường thẳng cần tìm là
. Ta cần xác định a và b.
• Chú ý rằng: Gọi là góc tạo bởi đường thẳng với trục Ox. Ta có:
Ví dụ 1. Xác định đường thẳng (d ) đi qua điểm A( 2;
− 3) và có hệ số góc bằng 2 − . − Khi góc nhọn thì Giải − Khi góc tù thì .
Gọi phương trình đường thẳng (d ) là: y = ax + b .
Vì (d ) có hệ số góc là 2 − nên a = 2
− ⇒ (d ) : y = 2 − x + b Vì A( 2;
− 3)∈(d ) nên 3 = ( 2 − ).( 2
− ) + b ⇔ b = 1. −
Do đó phương trình đường thẳng (d ) là y = 2 − x −1
Ví dụ 2. Xác định đường thẳng (d ) đi qua điểm A( 1 − ; )
1 và tạo với trục Ox một góc bằng 0 45 . Giải
Đường thẳng (d ) có dạng y = ax + b . Vì A( 1 − ; ) 1 ∈ (d ) nên 1 = a (− )
1 + b ⇔ b = a +1.
Vì (d ) tạo với trục Ox một góc bằng 0 45 nên 0
a = tan 45 = 1 ⇒ b = 2
Do đó phương trình đường thẳng (d ) là y = x + 2
Ví dụ 3. Xác định đường thẳng (d ) đi qua điểm A(0; )
1 và tạo với đường thẳng y = 2 một góc bằng 0 60 . Giải
Đường thẳng (d ) có dạng y = ax + b . Vì A(0; ) 1 ∈ (d ) nên 1 = .0 a + b ⇔ b = 1.
Vì đường thẳng y = 2 song song với trục hoành nên từ đề bài ta có (d ) tạo với trục Ox một góc bằng 0 60 . Ta có: 0
a = tanα = tan 60 = 3 . Vậy (d ) : y = 3x +1.
C. BÀI TẬP TỰ LUYỆN
1. Đường thẳng (d ) đi qua giao điểm của hai đường thẳng y = x +1, y = 2x và song song với
đường thẳng y = 2 x + 2 + 2 là: (A) y = 4x + 2 − 2 ;
(B) y = (2 + 2 ) x +1; (C) y = 2x + 2 − 2 ; (D) y = x + 2 . 1 3
2. Đường thẳng y = x +
vuông góc với đường thẳng nào dưới đây? 2 2 1 3 3 (A) y = − x − ; (B) y = 2x − ; 2 2 2 3 1 3 (C) y = 2 − x + ; (D) y = x − . 2 2 2 1
3. Đường thẳng y = (m + )
1 x − 2 vuông góc với đường thẳng y =
x + 2011 thì m bằng ? 2 (A) 2 − (B) 3 − (C) 1 − (D)1
4. Xác định đường thẳng (d ) biết nó có hệ số góc bằng 2 và đi qua điểm A( 3 − ;2)
5. Tính hệ số góc của đường thẳng đi qua hai điểm A(1;2) và B (3;4)
6. Cho đường thẳng (d ) : mx + 3. Tính góc α tạo bởi đường thẳng (d ) với trục Ox, biết:
a) (d ) đi qua điểm A(− 3;0)
b) (d ) đi qua điểm B (6; 3 − ) .
7. Xác định đường thẳng (d ) đi qua điểm A(0;3) và tạo với đường thẳng y = 2 một góc bằng 0 60 .
HƯỚNG DẪN GIẢI – ĐÁP SỐ 1. (C). 2. (C). 3. (B).
4. y = 2x + 8.
5. AB : y = x +1 ⇒ đường thẳng AB có hệ số góc a = 1. 6. a) 0 α = 60 . b) m = 1 − < 0 nên − ( 0 −α) 0 0 0 tan 180 = 1
− ⇔ 180 −α = 45 ⇔ α = 135 .
7. y = 3x + 3. ÔN TẬP CHƯƠNG II
A. TRỌNG TÂM KIẾN THỨC 1. Hàm số.
+ Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x theo quy tắc f sao cho với mỗi giá
trị x, ta luôn xác định được chỉ một giá trị tương ứng của y mà y = f ( x) thì y được gọi
là hàm số của x và x được gọi là biến số.
+ Cách cho hàm số: Hàm số thường được cho bằng công thức.
Chú ý: Có một số cách khác cho hàm số như: Bảng, sơ đồ Ven, đồ thị.
+ Đồ thị của hàm số: Tập hợp các điểm biểu diễn các cặp giá trị tương ứng ( ;x f (x)) trên
mặt phẳng tọa độ gọi là đồ thị hàm số y = f ( x)
+ Tính đồng biến, nghịch biến của hàm số: Cho hàm số y = f (x) xác định trên tập hợp
D là một khoảng, nửa khoảng hay đoạn, với mọi x , x ∈ D : 1 2
Nếu x < x mà f ( x < f x thì hàm số y = f ( x) đồng biến trên D 1 ) ( 2) 1 2
Nếu x < x mà f ( x > f x thì hàm số y = f ( x) nghịch biến trên D 1 ) ( 2) 1 2
2. Hàm số bậc nhất
+ Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b , trong đó a, b là các số
cho trước và a ≠ 0. + Tập xác định: 
+ Khi a > 0 thì hàm số đồng biến trên  ; Khi a < 0 thì hàm số nghịch biến trên 
+ Đồ thị hàm số là một đường thẳng.
+ Hệ số a(a ≠ 0) được gọi là hệ số góc của đường thẳng y = ax + b
+ Cho hai đường thẳng (d) : y = ax + b (a ≠ 0) và đường thẳng (d ') : y = a'x + b' (a' ≠ 0). Ta có:
(d) / /(d ') ⇔ a = a' và b ≠ b'
(d ) ≡ (d ') ⇔ a = a' và b = b'
(d) cắt (d ') ⇔ a ≠ a'
(d) ⊥ (d ') .aa' = 1 − .
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1. VẼ ĐỒ THỊ CỦA HÀM SỐ BẬC NHẤT. Phương pháp giải
Bước 1. Tìm tập xác định ( TXĐ của hàm số bậc nhất là ).
Bước 2. Vẽ đồ thị
Cách 1. + Xác định hai điểm phân biết bất kì của đồ thị rồi vẽ đường thẳng đi qua hai điểm đó.
Cách 2. + Xác định giao điểm của đồ thị với hai trục tọa độ: • Cho thuộc trục tung. • Cho thuộc trục hoành. Vẽ đ ờ hẳ MN đ đồ hị hà ố
Ví dụ 1. Cho hàm số (d ) : y = x −1 và (d ') : y = −x + 3 .
Vẽ đồ thị (d ) và (d ') trên cùng hệ trục tọa độ. Xác định tọa độ giao điểm của (d ) và (d ') . Giải + TXĐ:  y d d' + Vẽ (d ) : C 3
Cho x = 0 ⇒ y = 0 −1 = 1 − ⇒ A(0;− ) 1 thuộc I 1 B D trục tung. O 1 2 3 x -1 A
Cho y = 0 ⇒ 0 = x −1 ⇒ x = 1 ⇒ B (1;0) thuộc trục hoành. Hình 22
Vẽ đường thẳng AB ta được đồ thị (d ) (hình 22). + Vẽ (d ') :
Cho x = 0 ⇒ y = 0 + 3 = 3 ⇒ C (0;3) thuộc trục tung.
Cho y = 0 ⇒ 0 = −x + 3 ⇒ x = 3 ⇒ D (3;0) thuộc trục hoành.
Vẽ đường thẳng CD ta được đồ thị (d ') .
+ Xác định tọa độ giao điểm I của (d ) và (d ') :
Cách 1. Từ giao điểm I ta vẽ các đường vuông góc với hai trục tọa độ ta xác định được I (2; ) 1 .
Cách 2. Gọi tọa độ giao điểm I là ( x ; y I I )
Vì là giao điểm của (d ) và (d ') nên I vừa thuộc (d ) , vừa thuộc (d ') .
Vì I ( x ; y ) ∈ (d ) : y = x −1 nên y = x −1. I I 1 1
Vì I ( x ; y ) ∈ (d ') : y = −x + 3 nên y = −x + 3. I I 1 1
Suy ra: x −1 = −x + 3 ⇔ 2x = 4 ⇔ x = 2 ⇒ y = −x + 3 = 2 − + 3 = 1 1 1 1 1 1 1
Vậy tọa độ giao điểm I là (2; ) 1 Chú ý.
• Hoành độ giáo điểm I là nghiệm của phương trình x −1 = −x + 3
• Số giao điểm của (d ) : y = f (x) và (d ') : y = g (x) là số nghiệm của phương
trình f ( x) = g ( x) và ngược lại.
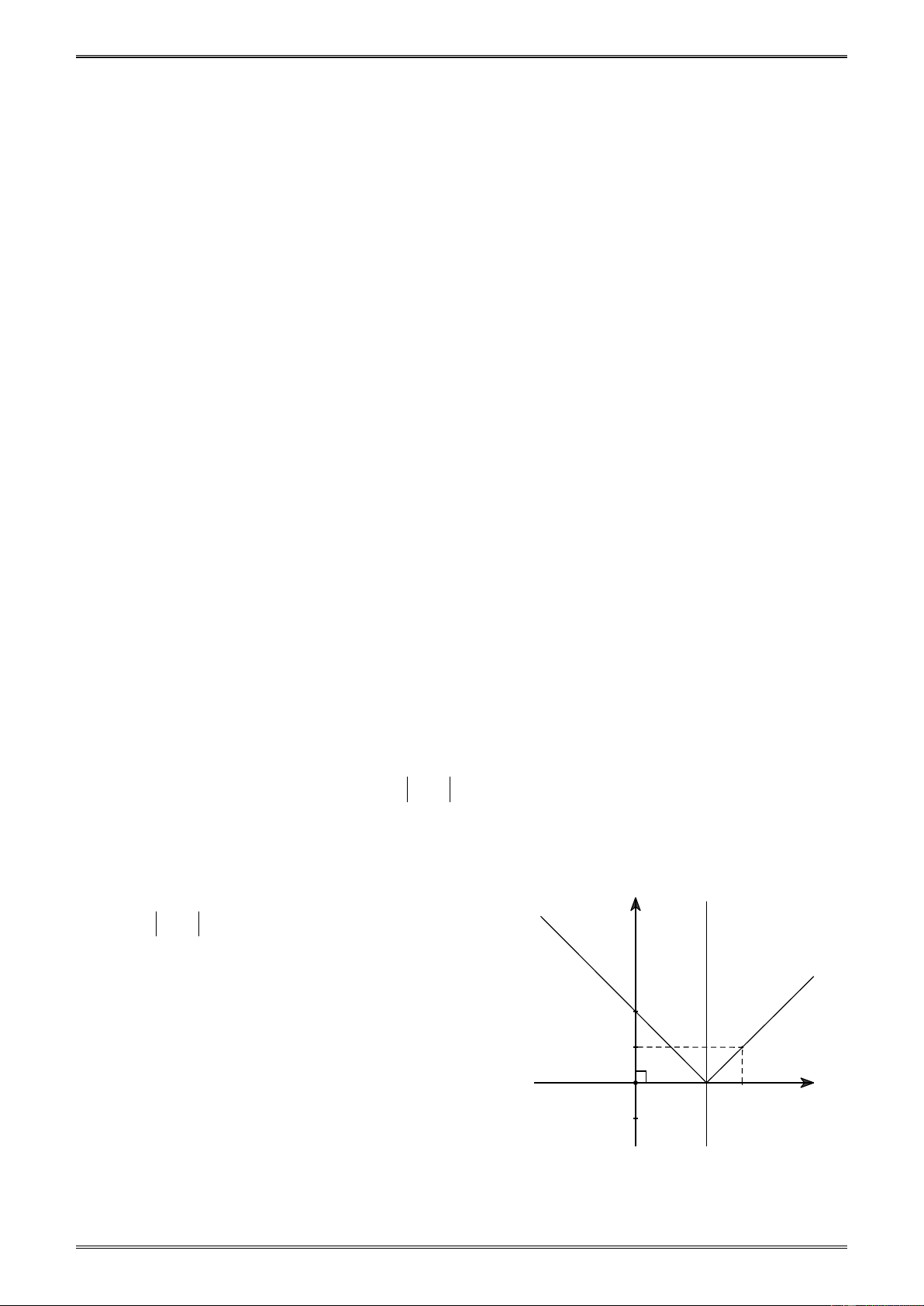
Ví dụ 2. Vẽ đồ thị (G) của hàm số y = x − 2 . Giải Vẽ (  − ≥ y G ) x 2 (x 2) (1)
: y = x − 2 =  (2) −x + 2 (x < 2) (2) (1)
Đồ thị (G) gồm hai nhành (1) và (2). 2
Nhánh (1) của (G) : điều kiện là x ≥ 2 . B 1
Cho x = 2 ⇒ y = 2 − 2 = 0 ⇒ A(2;0) thuộc O A 2 3 x trục hoành x = 2
Cho x = 3 ⇒ y = 3 − 2 = 1 ⇒ B (3; ) 1 . Hình 23
Vẽ tia AB ta được nhánh (1) của đồ thị (G) .
Tương tự, vẽ nhánh (2) ta thu được đồ thị (G) có hình chữ V như hình 23.
Chú ý. Hai nhánh của (G) đối xứng nhau qua đường thẳng x = 2
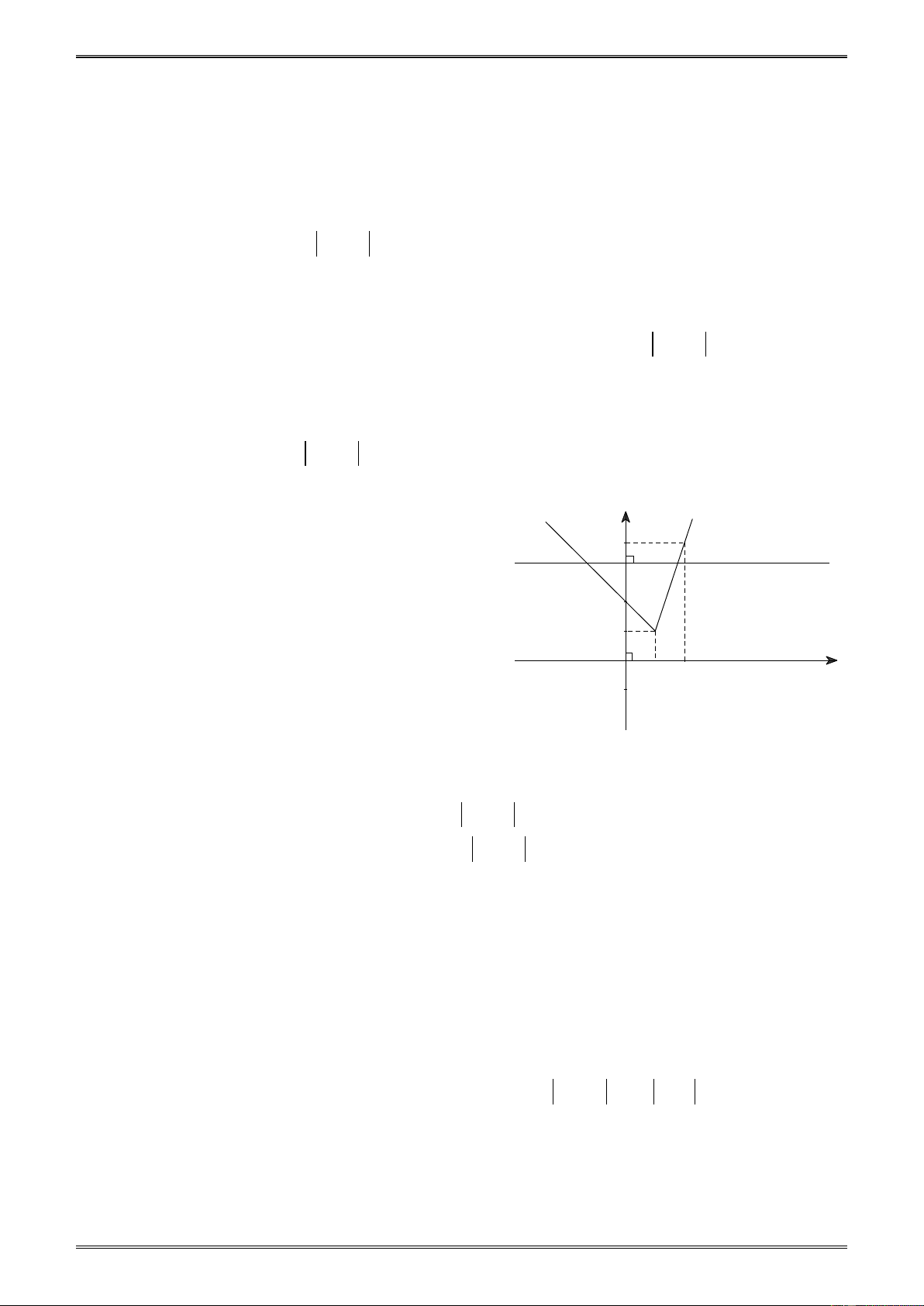
Ví dụ 3. Cho hàm số y = x + 2x − 2
a) Vẽ đồ thị (G) của hàm số trên.
b) Biện luận theo tham số m số nghiệm của phương trình x + 2x − 2 = m . Giải 3  x − 2 (x ≥ 1) (1) 
a) Vẽ (G) : y = x + 2x − 2 = −x + 2  (x < ) 1 (2)
Đồ thị (G) gồm hai nhánh (1) và (2). (2) y 1 ( ) 4 y = m
Nhánh (1) của (G) : điều kiện là x ≥ 1 m 2
Cho x = 1 ⇒ y = 3.1 − 2 = 1 ⇒ A(1; ) 1 1 A
Cho x = 2 ⇒ y = 3.2 − 2 = 4 ⇒ A(2;4) O 1 2 x
Vẽ tia AB ta được nhánh (1) của đồ thị (G) . Hình 24
Tương tự, vẽ nhánh (2) ta thu được đồ thị (G) như hình 24.
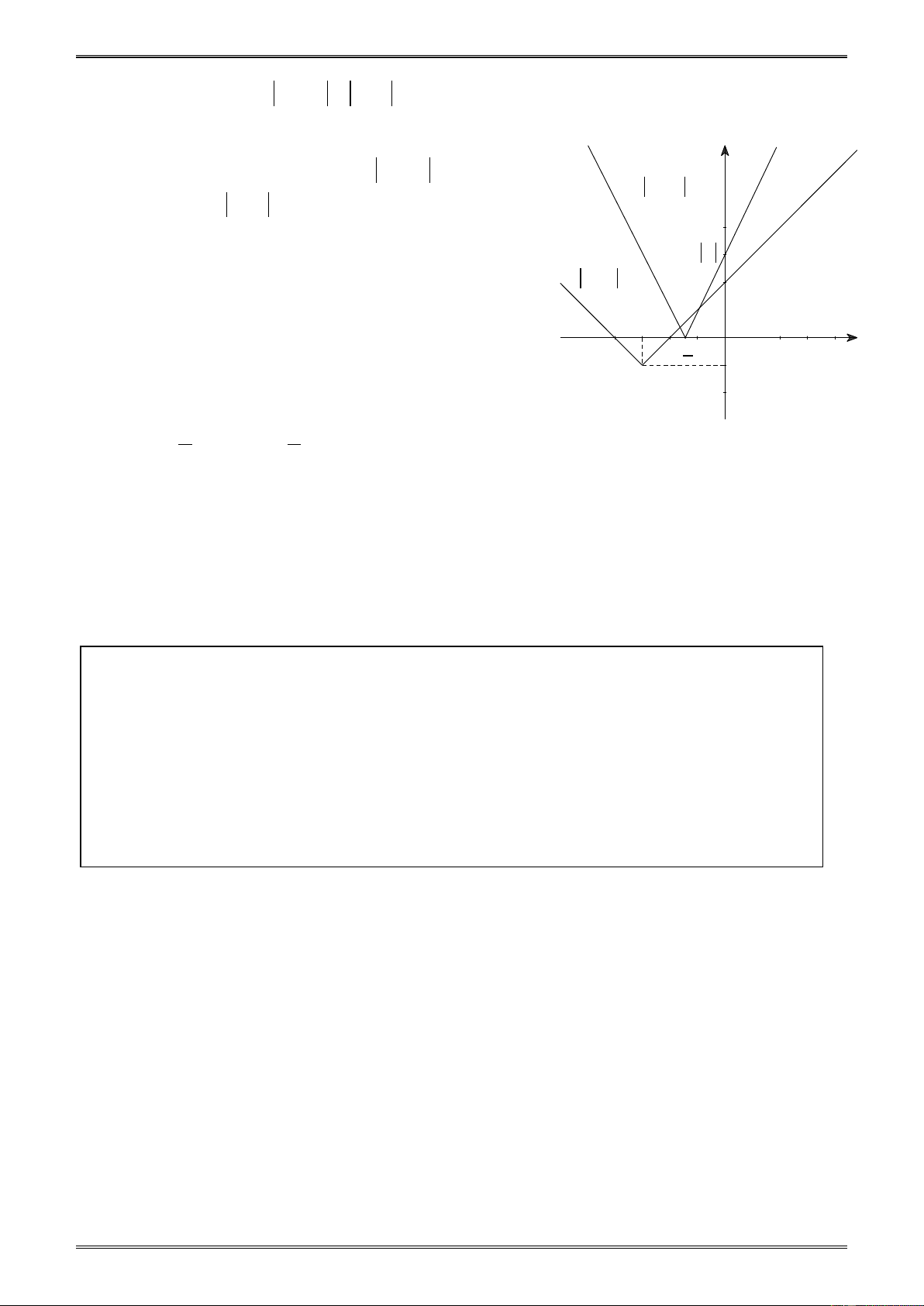
b) Số nghiệm của phương trình x + 2x − 2 = m
(*) là số giao điểm của đường
thẳng (d ) : y = m và đồ thị (G) : y = x + 2x − 2 . Từ đồ thị ta thấy: +
Nếu m < 1 thì phương trình (*) vô nghiệm. +
Nếu m = 1 thì phương trình (*) có một nghiệm. +
Nếu m > 1 thì phương trình (*) hai nghiệm phân biệt.
Ví dụ 4. Với giá trị nào của tham số a thì phương trình 2x − a +1 = x + 3 (*) có nghiệm duy nhất?
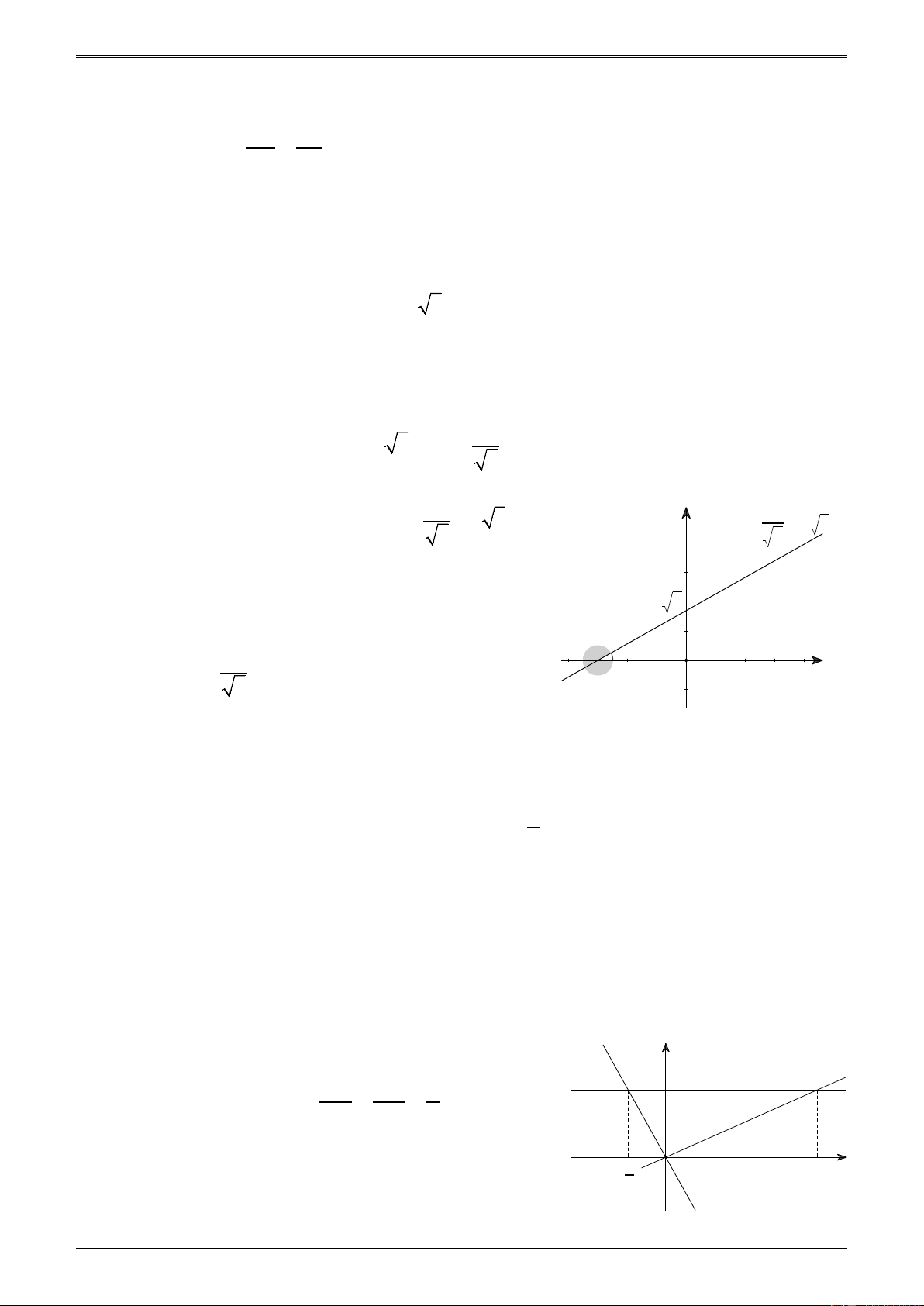
(Thi vào khối PT chuyên Toán – Tin ĐHSPHN năm học 1997-1998) Giải
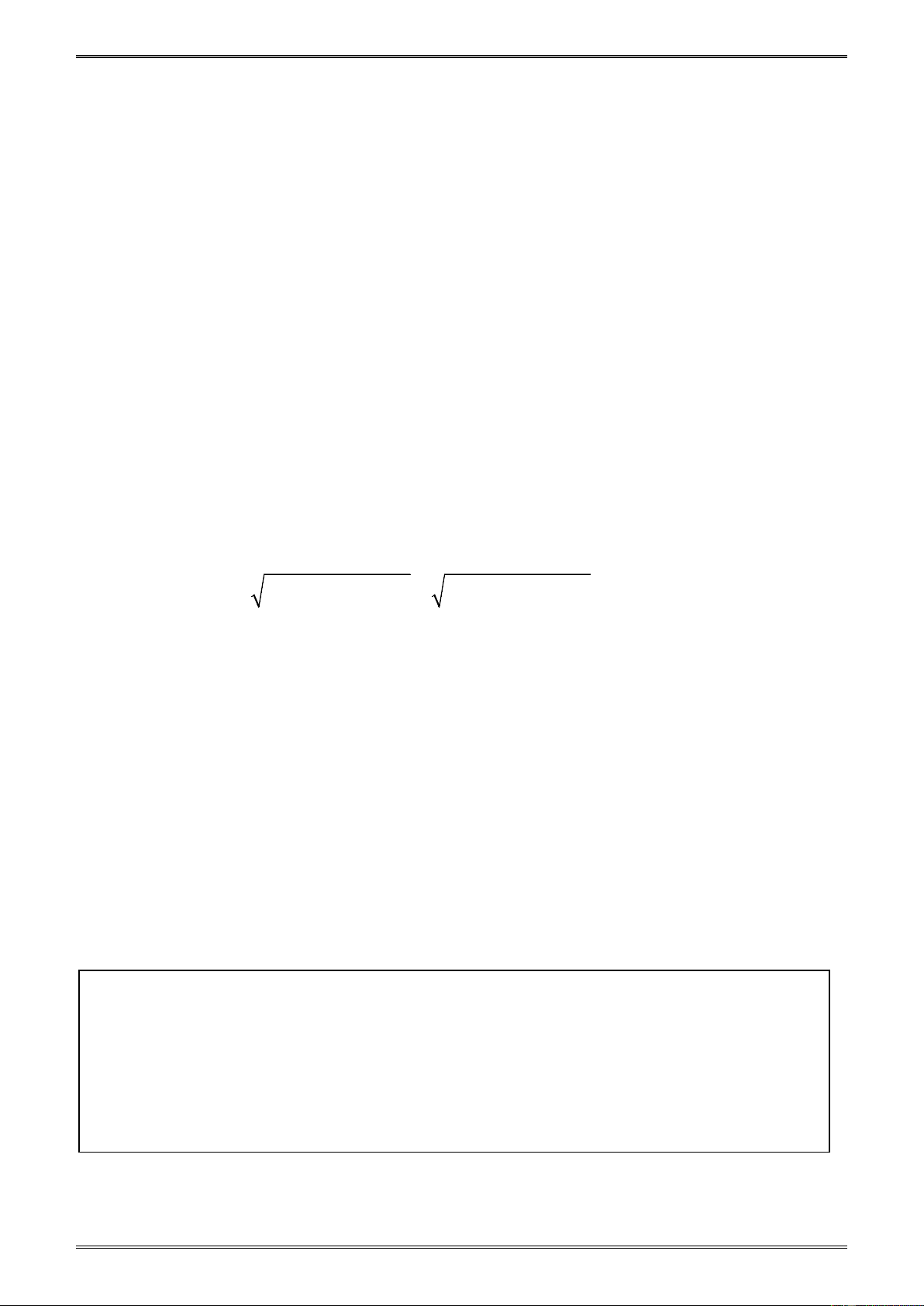
+ Ta có: (*) ⇔ 2x − a = x + 3 −1 (1)
Số nghiệm của phương trình (1) là số giao y điể (G)
m của đồ thị (G) : y = 2x − a và đồ thị (G') ( y = 2x - a
G ') : y = x + 3 −1
Vẽ hai đồ thị (G) và (G ') như hình 25. -a y = x + 3 - 1 2
Phương trình (*) có nghiệm duy nhất ⇔ ( ) 1 có nghiệm duy nhất -3 a -4 -2 O x -1 2
⇔ (G) và (G ') có một điểm chung a ⇔ = a Hình 25 4 − hoặc = 2 − 2 2 ⇔ a = 8 − hoặc a = 4. −
Dạng 2. XÁC ĐỊNH ĐƯỜNG THẲNG Phương pháp giải
1. Viết phương trình đường thẳng đi qua hai điểm cho trước
2. Viết phương trình đường thẳng đi qua một điểm và có hệ số góc cho trước.
3. Viết phương trình đường thẳng đi qua một điểm và song song với một đường cho trước.
4. Viết phương trình đường thẳng đi qua một điểm và vuông góc với một đường thẳng cho trước.
Ví dụ 1. Tìm m và n để đường thẳng (d ) : y = (m − )
1 x + 2 − n đi qua hai điểm A(2;− ) 1 và B ( 3 − ; 6 − ) . Giải
Ta có: A ∈ (d ) nên 1 − = (m − )
1 .2 + 2 − n ⇔ 2m − n = 1
− ⇔ n = 2m +1 (1)
B ∈ (d ) nên 6 − = (m − ) 1 .( 3 − ) + 2 − n ⇔ 3 − m − n = 11 − (2)
Thay (1) vào (2) ta được: 3
− m − (2m + ) 1 = 11 − ⇔ 5 − m = 10 − ⇔ m = 2
⇒ n = 2m +1 = 2.2 +1 = 5
Vậy m = 2 và n = 5 thì (d ) : y = x − 3 đi qua hai điểm A(2;− ) 1 và B ( 3 − ; 6 − ) .
Ví dụ 2. Viết phương trình đường thẳng (d ) cắt (d ') tại điểm có tung độ bằng 1 − biết (d ) có hệ số góc bằng 2. Giải
Gọi A là giao điểm của (d ) và (d ') . Vì A có tung độ bằng 1 − nên hoành độ của điểm A là 1
− = x − 3 hay x = 2 . Do đó : A(2;− ) 1 .
Gọi phương trình đường thằng (d ) là: y = ax + . b
Ta có (d ) có hệ số góc là 2 nên a = 2 ⇒ (d ) : y = 2x + . b Vì A(2;− ) 1 ∈ (d ) nên 1
− = 2.2 + b ⇔ b = 5. −
Do đó phương trình đường thẳng (d ) là y = 2x − 5.
Ví dụ 3. Cho đường thẳng (d ) : y = 3x − 2 và điểm M ( 1 − ; )
1 . Viết phương trình đường thẳng
(d ') đi qua và song song với (d) . Giải
Gọi phương trình đường thẳng (d ') là y = ax + . b
Vì (d ') / / (d ) : y = 3x − 2 nên a = 3 và b ≠ 2. −
Mặt khác (d ') đi qua M ( 1 − ; ) 1 nên: 1 = a (− ) 1 + b ⇔ 3
− + b = 1 ⇔ b = 4 (thỏa mãn)
Vậy phương trình đường thẳng cần tìm là: y = 3x + 4.
Ví dụ 4. Trên mặt phẳng tọa độ Oxy cho M (2;4),
N (0;2) . Tìm các điểm A trên mặt
phẳng tọa độ Oxy sao cho AM = AN. Giải
Cách 1. Tọa độ trung điểm của đoạn MN là: x + x y + y M N x = = 1; M N y = = 3 hay I (1;3). I 2 I 2
Gọi phương trình đường trung trực của MN là (d ) : y = mx + n
Gọi phương trình đường thẳng MN là: y = ax + b . Ta có
M (2;4) ∈ MN ⇒ 4a = .
a 2 + b hay b = 2 − a + 4;
N (0;2) ∈ MN ⇒ 2 = .
a 0 + b hay b = 2 ⇒ a = 1.
Do đó phương trình đường thẳng MN là: y = x + 2.
Vì AM = AN ⇒ A thuộc đường trung trực của đoạn MN hay A∈ (d ) .
Vì (d ) là đường trung trực của MN nên (d ) ⊥ MN ⇔ .1 m = 1 − ⇒ m = 1 −
⇒ (d) : y = −x + n
Vì I (1;3) là trung điểm của đoạn MN nên đường thẳng (d ) đi qua I (1;3) ⇒ 3 = (− )
1 .1 + n ⇒ n = 4.
Vậy tập hợp các điểm A là đường thẳng (d ) : y = −x + 4
Cách 2. Gọi tọa độ A là ( ; x y ) 2 2 2 2
Ta có: AM = AN ⇔ (2 − x) + (4 − y) = (0 − x) + (2 − y)
⇔ (2 − x)2 + (4 − y)2 = (0 − x)2 + (2 − y)2 2 2 2 2
⇔ 4 − 4x + x +16 − 8y + y = x + 4 − 4y + y ⇔16−4x = 4y
⇔ y = −x + 4.
Vậy tập hợp các điểm A trên mặt phẳng Oxy thỏa mãn bài toán là đường thẳng có phương
trình: y = −x + 4 Dạng 3. CỰC TRỊ Phương pháp giải
• Vận dụng bất đẳng thức đại số
• Vận dung quan hệ giữa đường xiên và đường vuông góc
• Vận dụng hệ thức lượng trong tam giác vuông • Vận dụng đồ thị.
Ví dụ 1. Tìm m để khoảng cách từ gốc tọa độ O (0;0) đến đường thẳng (d ) có phương trình 2m − 2 2 y = x + m ≠ − ). m − 2 m −
đạt giá trị lớn nhất ( với 2 2 Giải Vì tung độ 2 gốc b = ≠ 0
d không đi qua gốc tọa độ. m − nên ( ) 2
Trường hợp 1: Xét m =1. Khi đó (d ) : y = 2
− . Do đó khoảng cách từ O(0;0) đến (d) là 2.
Trường hợp 2. Xét m ≠ 1.  − Khi đó ( 1 
d ) cắt trục hoành tại điểm A ;0 
 và cắt trục tung tại điểm  m −1   2  1 2 B 0; ⇒ OA =   và OB = .  m − 2  m −1 m − 2
Kẻ OH vuông góc với (d ) tại H thì độ dài OH là khoảng cách từ O đến (d ) . 1 1 1 Áp dụng hệ thức = +
vào tam giác vuông ABO ta có: 2 2 2 h a b 2 2 1 1 1 OA .OB 4 2 = + ⇒ OH = = 2 2 2 2 2 OH OA OB OA + OB
(m − 2)2 + 4(m − )2 1 2 2 2 ⇒ OH = = ≤ = 5 2 2 5m −12m + 8 4  6  4 5 m − +   5  5  5 6
(dấu “=” xảy ra khi m = ). 5 6
Kết hợp hai trường hợp ta có khi m = thì OH = 5 . 5 max
Ví dụ 2. Trên mặt phẳng tọa độ cho hai điểm A, B đều có hoành độ x và tung độ y thỏa mãn
đẳng thức x −1 + y − 2 = 3
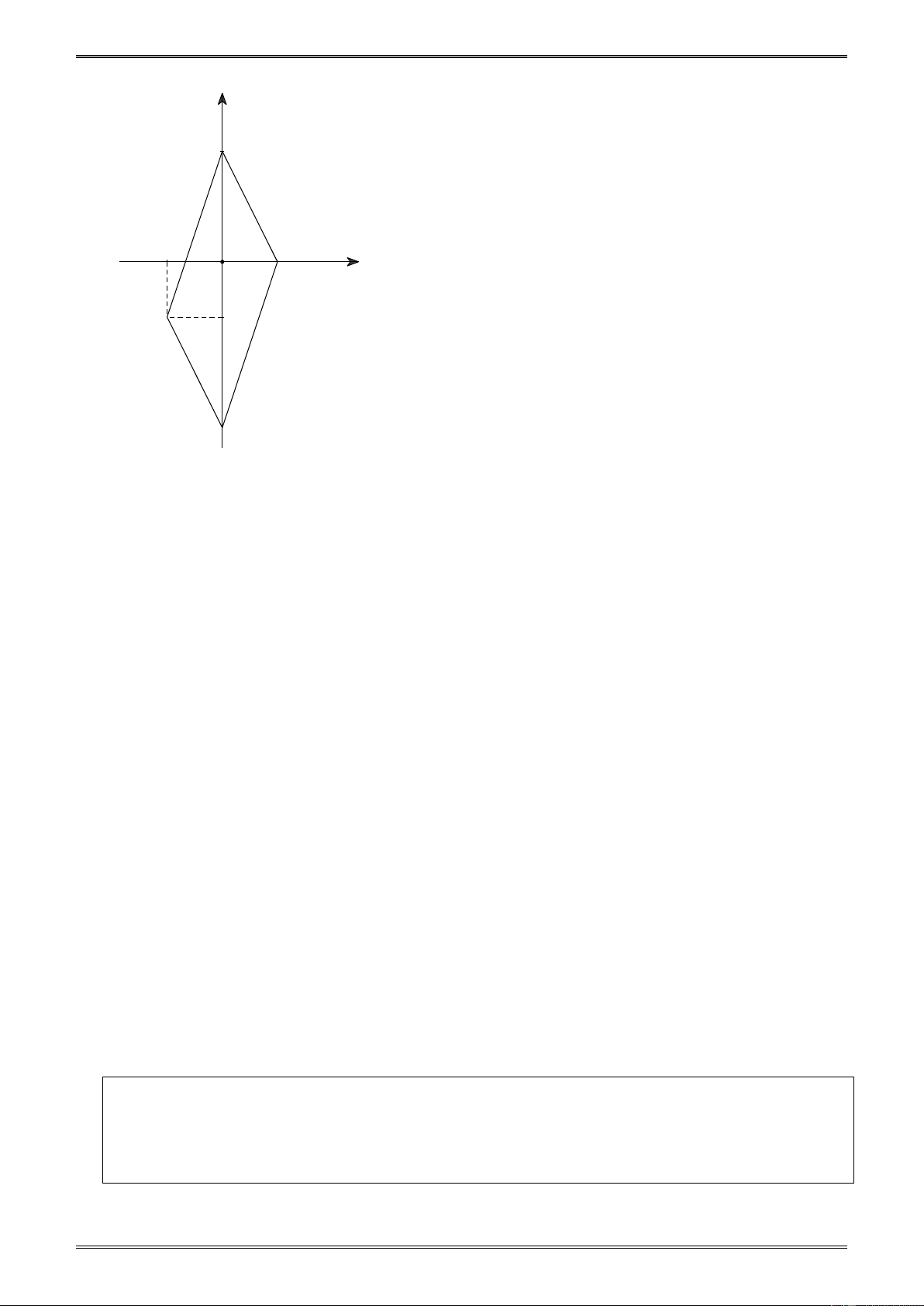
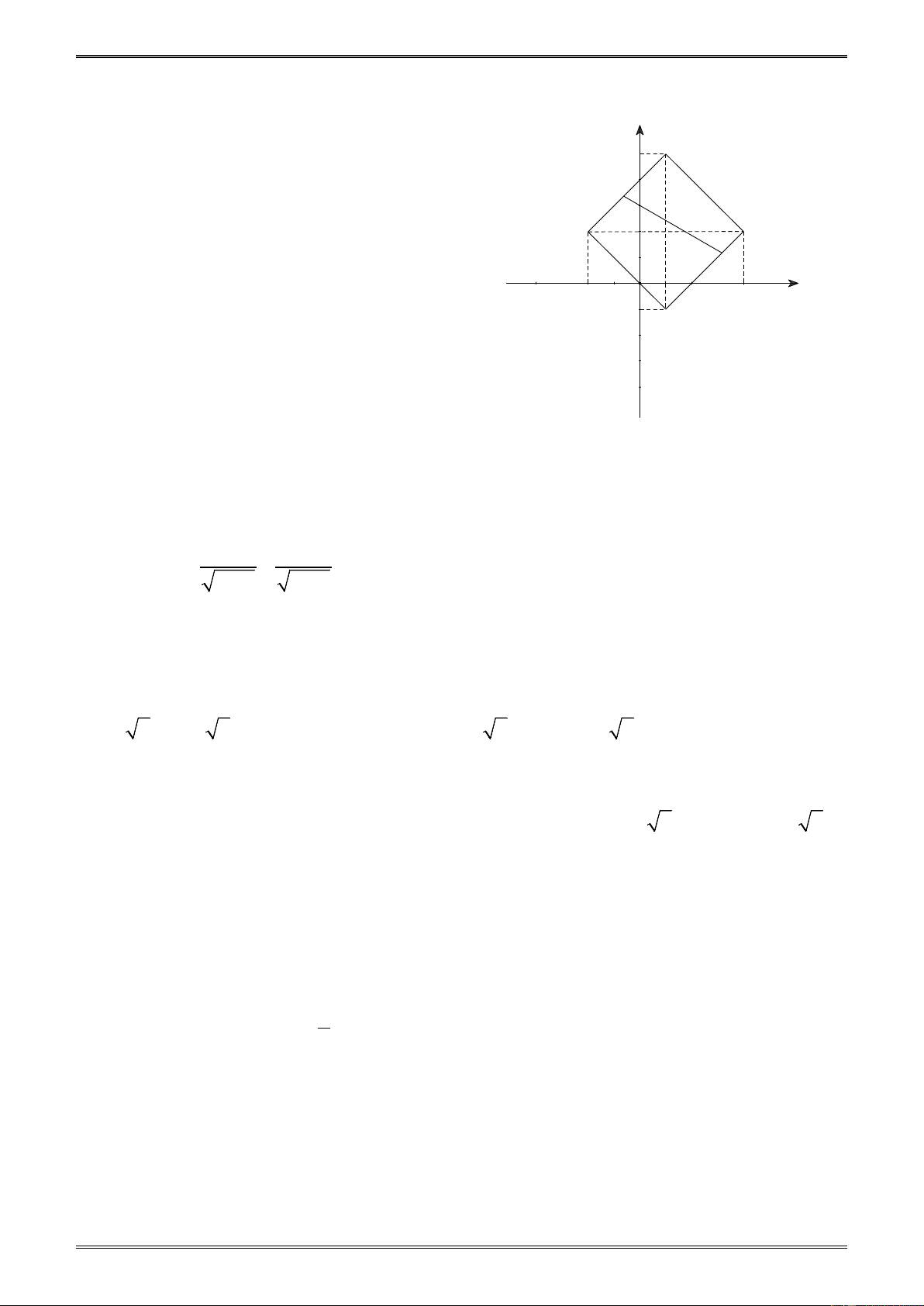
(*) . Chứng minh khoảng cách AB ≤ 6 . Giải x + y = 6
(x ≥1; y ≥ 2) y  5 N x − y = 2
(x ≥1; y ≤ 2) Điều kiện (*) ⇔  − A x + y = 4 
(x ≤1; y ≥ 2) − 2 x − y = 0 
(x ≤1; y ≤ 2) M P B ⇒ 1
Tập hợp các điểm A, B thỏa mãn (*) là hình -2 O 4 x vuông MNPQ hình 26 -1 Q ⇒ Hình 26 AB ≤ MP ≤ 6
Dấu “=” xảy ra khi A, B là hai đỉnh đối nhau của hình vuông MNPQ.
C. BÀI TẬP TỰ LUYỆN 1. Hàm số 1 1 y = +
không xác định với: x − 2 2 − x (A) x = 2 (B) x > 2 (C) x < 2 (D) Với mọi x thuộc 
2. Với giá trị nào của m thì hàm số y = ( 2
m − 2) x +1 là hàm số bậc nhất đồng biến? (A) − 2 < m < 2 ; (B) m >
2 hoặc m < − 2 ; (C) m ≠ 2 ± ;
(D) Với mọi giá trị của m thuộc 
3. Cho hàm số y = f ( x) 5 3
= ax + bx + 2007x +1 với *
a,b ∈  , biết f ( 2 ) = 2 , tính f (− 2 ) .
4. Cho hàm số y = (m − ) 2
3 x + m ( x − ) 1 + 2.
a) Với giá trị nào của m thì hàm số đã cho là hàm số bậc nhất?
b) Với giá trị vừa tìm được của m ở câu a, thì hàm số đã cho đồng biến hay nghịch biến?
5. Cho đường thẳng (d ) 3 : y = x + 3 4
a) Vẽ đường thẳng (d ) .
b) Tính góc tạo bởi đường thẳng (d ) và trục Ox.
c) Tính diện tích tam giác do đường thẳng (d ) tạo với hai trục tọa độ.
6. Xác định hàm số y = ax + b , biết rằng đồ thị của nó song song với đồ thị hàm số y = 2 − x
và đi qua điểm A(1; 3 − ) . 1
7. Cho các đường thẳng (d : y = 2 − x + 3; d : y = x +1; d : y = 2 − x −1. 1 ) ( 2) ( 3) 2
Không vẽ đồ thị của các hàm số đó, hãy cho biết vị trí tương đối giữa các đường thẳng đó đối với nhau như thế nào?
8. Cho các đường thẳng (d ) : y = (2m − ) 2 1 x + m −1; d
: y = m + 3 x − 3 . 1 ( 2) ( )
a) Tìm các giá trị của m để (d / / d . 1 ) ( 2)
b) Tính các giá trị của m để (d đi qua gốc tọa độ. 1 )
9. Tìm điểm trên đường thẳng (d ) : y = 2
− x + 25 sao cho khoảng cách OM nhỏ nhất, với O là gốc tọa độ.
HƯỚNG DẪN GIẢI – ĐÁP SỐ 1. (D) 2. (B)
3. f (− 2 ) = 0 4. a) m = 3. b) Đồng biến. 5. b) 0 36 52 '; c) 6 (đvdt). 6. y = 2 − x −1
7. (d / / d ; d ⊥ d d ⊥ d 1 ) ( 3) ( 1) ( 2) ( 2) ( 3) 8. a) m = 4; b)m = 1 ±
9. Gọi tọa độ điểm M là ( ; a b) . Khoảng cách 2 2 OM = a + b .
Ta có M (a;b) ∈ (d ) : y = 2
− x + 25 nên b = 2
− a + 25 ⇔ 2a + b = 25. 2
Áp dụng bất đẳng thức ( + ) ≤ ( 2 2 + )( 2 2 ax by a b
x + y ) với ( ; x y ) = (2; ) 1 , ta có: = ( a + b)2 2 ≤ ( 2 2 + )( 2 2 a + b ) 2 2 25 2 2 1
⇔ 5 ≤ a + b ⇒ OM ≥ 5. 2a + b = 25   = Do đó a 10 OM = 5 ⇔ a ⇔  ⇒ M 10;5 . min ( ) = b b   = 5 2
Chú ý. Ta có thể giải bài toán như sau : OM
⇔ OM ⊥ d tại . min ( )
Ta xác định tọa độ điểm M bằng cách:
+ Lập phương trình đường thẳng (d ') đi qua O (0;0) và vuông góc với đường thẳng (d ) .
+ M là giao điểm của (d ) và (d ')
Document Outline

  • Chương II. HÀM SỐ BẬC NHẤT
    • §1. NHẮC LẠI VÀ BỔ SUNG CÁC KHÁI NIỆM VỀ HÀM SỐ
    • §2.HÀM SỐ BẬC NHẤT
    • §3. ĐỒ THỊ CỦA HÀM SỐ 𝒚=𝒂𝒙+𝒃(𝒂≠𝟎)
    • §4. ĐƯỜNG THẲNG SONG SONG VÀ ĐƯỜNG THẲNG CẮT NHAU
    • §5. HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG
    • ÔN TẬP CHƯƠNG II