Phương pháp giải hình 9 vị trí tương đối của đường thẳng và đường tròn (có đáp án và lời giải chi tiết)
Tổng hợp Phương pháp giải hình 9 vị trí tương đối của đường thẳng và đường tròn (có đáp án và lời giải chi tiết) rất hay và bổ ích giúp bạn đạt điểm cao. Các bạn tham khảo và ôn tập để chuẩn bị thật tốt cho kỳ thi tốt nghiệp sắp đến nhé. Mời bạn đọc đón xem.
Preview text:
Bài 4. VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN
A. KIẾN THỨC TRỌNG TÂM
1. Vị trí tương đối của đường thẳng và đường tròn
Cho đường tròn (O;R) và một đường thẳng bất kì. Gọi d là khoảng cách từ tâm O của đường
tròn đến đường thẳng đó. Ta có bảng vị trí tương đối của đường thẳng với đường tròn
Vị trí tương đối của đường thẳng và đường tròn Số điểm chung Hệ thức giữa d và R Cắt nhau 2 d R Tiếp xúc nhau 1 d R Không giao nhau 0 d R
2. Vị trí tương đối của đường thẳng và đường tròn
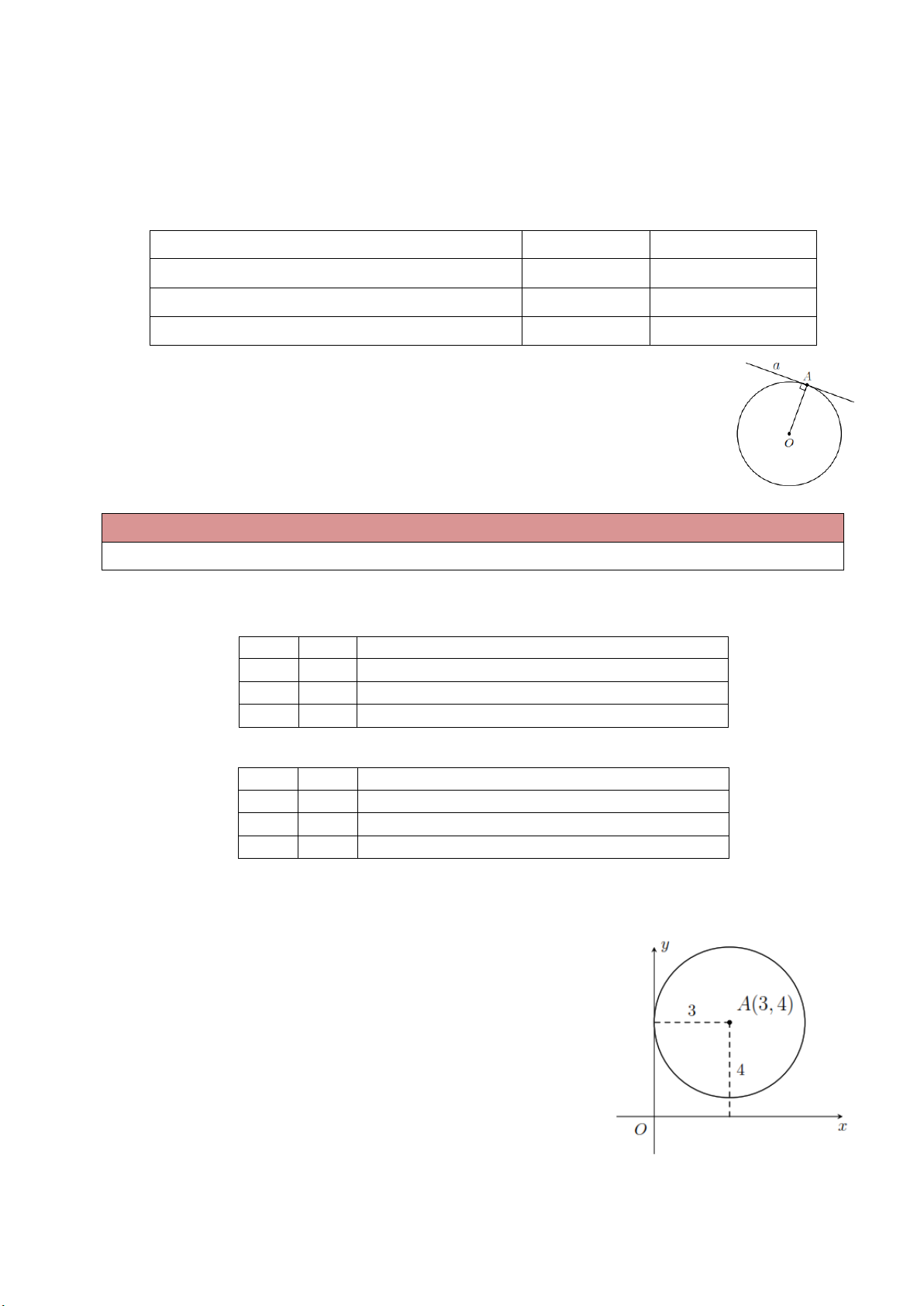
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Xác định vị trí tương đối của đường thẳng và đường tròn
So sánh d và R rồi kết luận dựa vào phần kiến thức trọng tâm.
Ví dụ 1. Điền vào các chỗ trống () trong bảng sau ( R là bán kính của đường tròn, d là khoảng
cách từ tâm đến đường thẳng): R d
Vị trí tương đối của đường thẳng và đường tròn 5 cm 3 cm 6 cm Tiếp xúc nhau 4 cm 8 cm Lời giải R d
Vị trí tương đối của đường thẳng và đường tròn 5 cm 3 cm Cắt nhau 6 cm 6 cm Tiếp xúc nhau 4 cm 8 cm Không giao nhau
Ví dụ 2. Trên mặt phẳng tọa độ Oxy cho điểm (
A 3; 4) . Hãy xác định vị trí tương đối của đường tròn ( ;
A 3) và các trục tọa độ. Lời giải.
Khoảng cách từ A đến Ox là 4 3 R nên ( ; A 3) không giao Ox .
Khoảng cách từ A đến Oy là 3 R nên ( ;
A 3) tiếp xúc với Oy .
Ví dụ 3. Cho điểm A cách đường thẳng là 3 cm. Vẽ đường tròn tâm A , bán kính 3 cm. Chứng
minh đường thẳng tiếp xúc với đường tròn ( ) A . Trang 1 Lời giải
Vì d R 3 cm nên đường thẳng tiếp xúc với đường tròn ( ) A .
Dạng 2: Bài toán liên quan đến tính độ dài
Nối tâm và tiếp điểm để vận dụng định lý về tính chất của tiếp tuyến và định lý Py-ta-go.
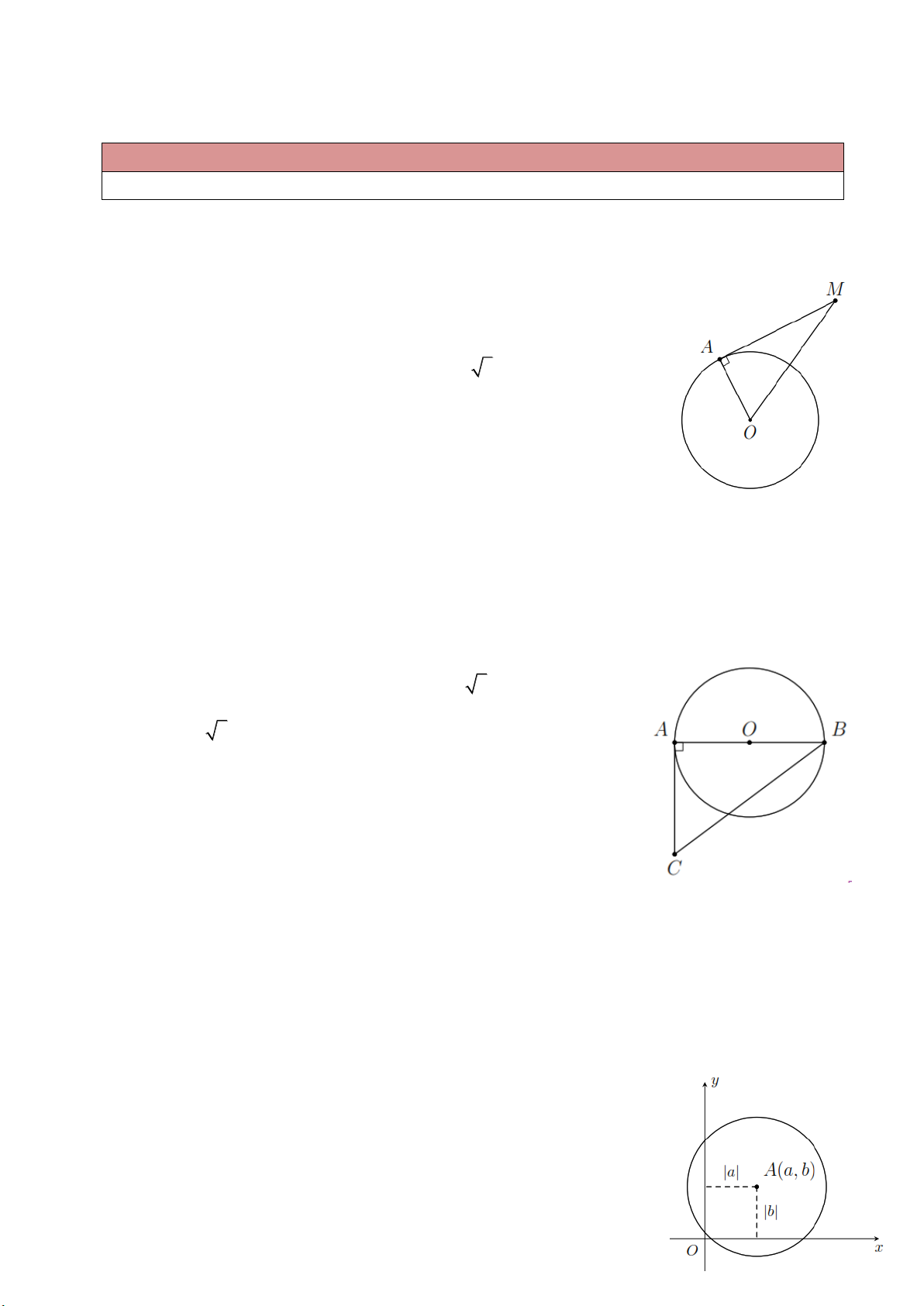
Ví dụ 4. Cho đường tròn ( ;
O R) và điểm M nằm ngoài (O) sao cho MO 2R . Kẻ tiếp tuyến MA
với (O) ( A là tiếp điểm). Tính độ dài đoạn thẳng MA theo R . Lời giải.
Xét tam giác OAM vuông tại A , theo định lý Py-ta-go ta có 2 2 2 2 2 2
MA OM OA 4R R 3R MA R 3.
Ví dụ 5. Cho đường tròn tâm O , đường kính AB 2R . Từ A kẻ tiếp tuyến xy . Trên xy lấy điểm
C sao cho AC R . Tính độ dài đoạn thẳng BC theo R . Lời giải.
Tam giác ABC vuông tại A nên theo định lý Py-ta-go, ta có 2 2 2 2 2 2
BC AB AC 4R R 5R BC R 5.
Vậy BC R 5 .
C. BÀI TẬP VẬN DỤNG
Bài 1. Trên mặt phẳng tọa độ Oxy cho điểm (
A a;b) . Xác định điều kiện của a, b để đường tròn ( ; A 5) thỏa mãn: a) Cắt trục Oy ; b) Cắt trục Ox ;
c) Tiếp xúc với Ox . Lời giải. a) ( , A 5 cm) cắt Oy | a | 5 . b) ( , A 5 cm) cắt Ox | b | 5 . c) ( ,
A 5 cm) tiếp xúc Ox | b | 5 . Trang 2
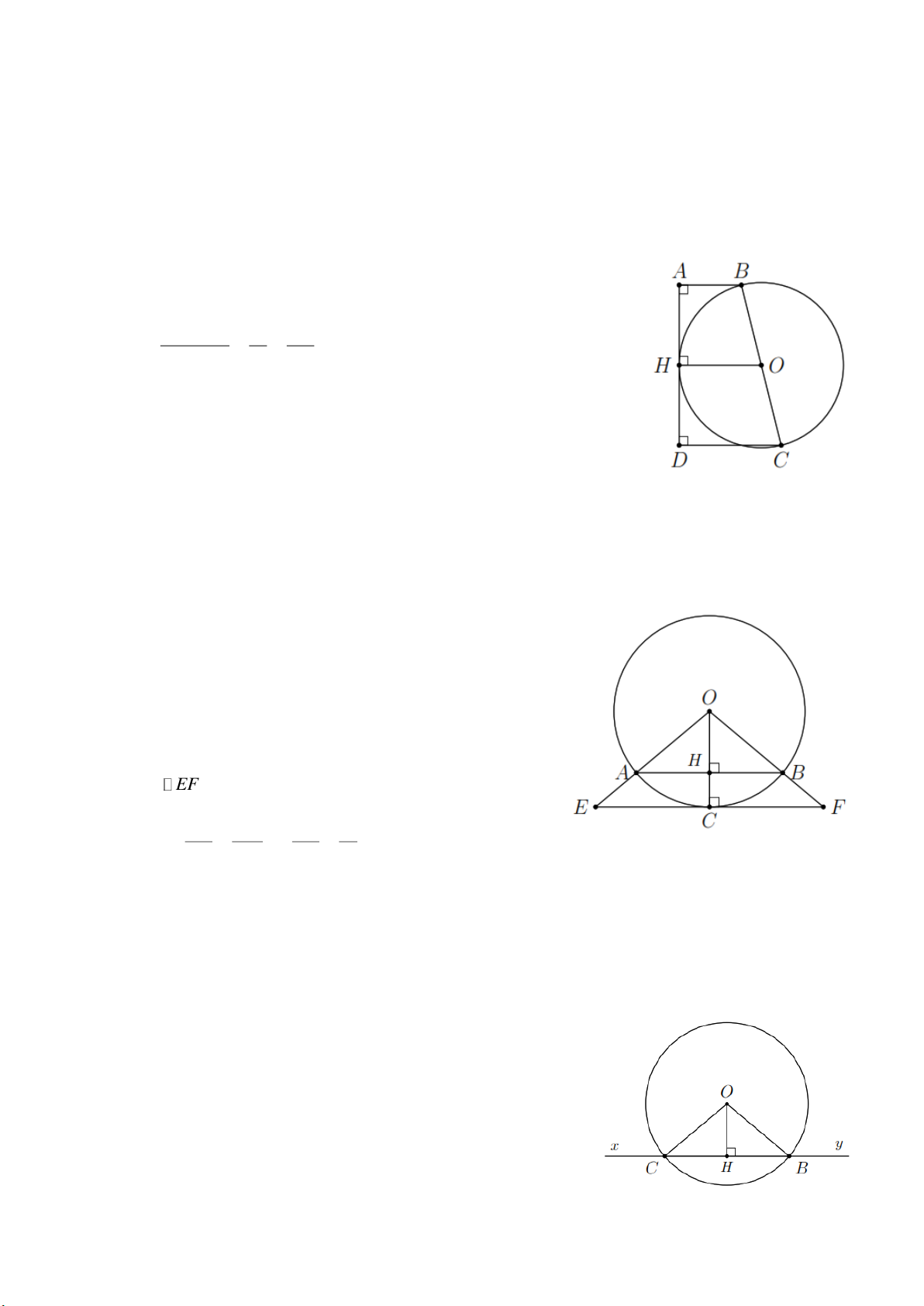
Bài 2. Cho hình thang vuông ABCD ( ˆ ˆ A D 90
). Biết AB 4 cm, BC 13 cm và CD 9 cm.
Vẽ đường tròn tâm O , đường kính BC . Chứng minh AD tiếp xúc với (O) . Lời giải.
Kẻ OH AD(H AD) .
Ta có OH là đường trung bình của hình thang ABCD nên AB CD 13 BC OH . 2 2 2
AD tiếp xúc với (O) .
Bài 3. Cho đường tròn (O;15 cm) có dây AB 24 cm. Gọi H là trung điểm của AB , tia OH cắt
(O) tại C , tiếp tuyến của (O) tại C cắt O ,
A OB lần lượt tại E, F . Tính độ dài OH và EF . Lời giải.
H là trung điểm AB OH AB (quan hệ giữa đường kính và dây cung).
BH 12 cm. Áp dụng định lý Py-ta-go, ta có 2 2 2
OH OB BH 81 OH 9 cm.
Vì AB EF nên theo định lý Ta-lét, ta có AB OH 24 9 EF 10 cm. EF OC EF 15
Bài 4. Cho điểm O cách đường thẳng xy là 5 cm. a) Chứng minh ( ;13 c O
m) cắt đường thẳng xy tại hai điểm phân biệt;
b) Gọi hai giao điểm của (O) với xy là B, C . Tính độ dài đoạn thẳng BC . Lời giải.
a) d 5 13 R nên (O) cắt xy tại hai điểm phân biệt.
Kẻ OH BC . Tam giác OBH vuông tại H nên theo định lý Py-ta-go, ta có 2 2 2
OB OH HB HB 12 cm. Do đó BC 24 cm. Trang 3
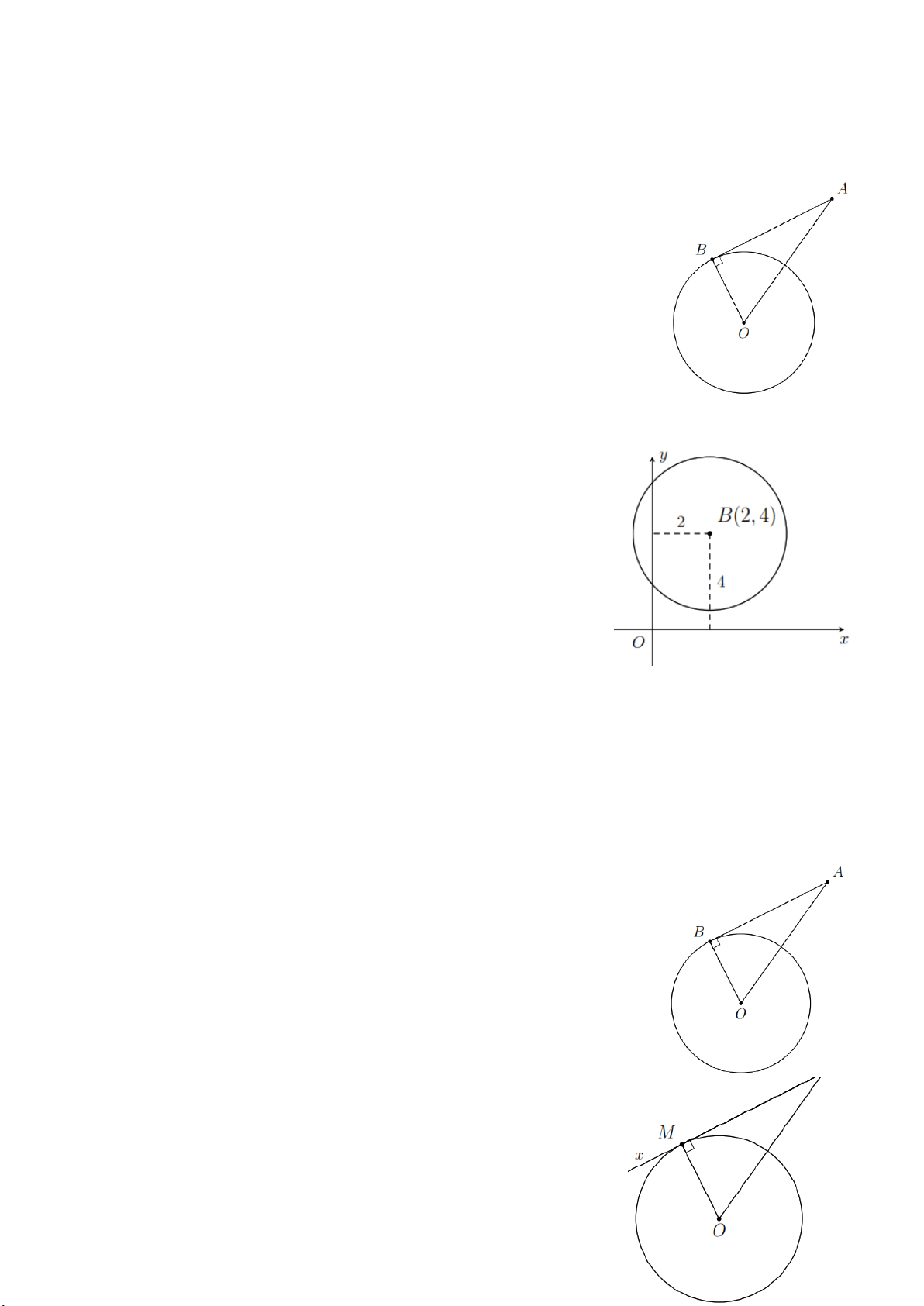
Bài 5. Cho đường tròn tâm O bán kính 6 cm. Điểm A nằm ngoài đường tròn và OA 10 cm. Kẻ
tiếp tuyến AB với (O) trong đó B là tiếp điểm. Tính chu vi tam giác ABO . Lời giải.
Tam giác OAB vuông tại B nên theo định lý Py-ta-to, ta có 2 2 2 2 2
AB OA OB 10 6 64 AB 8 cm.
Vậy chu vi tam giác OAB là OA OB AB 24 cm.
D. BÀI TẬP VỀ NHÀ
Bài 6. Trên mặt phẳng tọa độ Oxy cho điểm B(2; 4) . Hãy xác định vị trí
tương đối của đường tròn (B;3) và các trục tọa độ. Lời giải.
Khoảng cách từ B đến Ox là 4 3 R nên (B;3) không cắt Ox .
Khoảng cách từ B đến Oy là 2 3 R nên (B;3) cắt Oy tại hai điểm phân biệt.
Bài 7. Cho điểm B cách đường thẳng a là 5 cm. Vẽ đường tròn
tâm B , bán kính 7 cm. Chứng minh đường thẳng a cắt đường
tròn (B) tại hai điểm phân biệt. Lời giải
Vì d 5 R 7 nên đường thẳng a cắt đường tròn (B) tại hai điểm phân biệt.
Bài 8. Cho đường tròn (O) bán kính 6 cm và điểm A cách O là 10 cm. Kẻ tiếp tuyến AB với
(O) ( B là tiếp điểm). Tính độ dài đoạn thẳng AB . Lời giải.
Xét tam giác ABO vuông tại B , áp dụng định lý Py-ta-go ta có 2 2 2 2 2
AB OA OB 10 6 64 AB 8 cm. Vậy AB 8 cm.
Bài 9. Cho đường tròn tâm O bán kính 3 cm và điểm M nằm
trên đường tròn đó. Từ M vẽ tiếp tuyến xy . Trên xy lấy điểm P
sao cho MP 4 cm. Tính độ dài đoạn thẳng PO . Lời giải. Trang 4
Xéttam giác OMP vuông tại M , áp dụng định lý Py-ta-go ta có 2 2 2 2 2
OP OM MP 3 4 25 OP 5 cm. Vậy OP 5 cm. --- HẾT --- Trang 5