Phương pháp giải hình học 9 góc có đỉnh ở bên trong, bên ngoài đường tròn (có đáp án và lời giải chi tiết)

Bài 5. GÓC CÓ ĐỈNH Ở BÊN TRONG.
BÊN NGOÀI ĐƯỜNG TRÒN
A. KIẾN THỨC TRỌNG TÂM
1. Góc có đỉnh ở bên trong đường tròn
Là góc có đỉnh nằm bên trong đường tròn, mỗi góc có đỉnh bên
trong đường tròn, một cung nằm bên trong góc và cung kia nằm bên
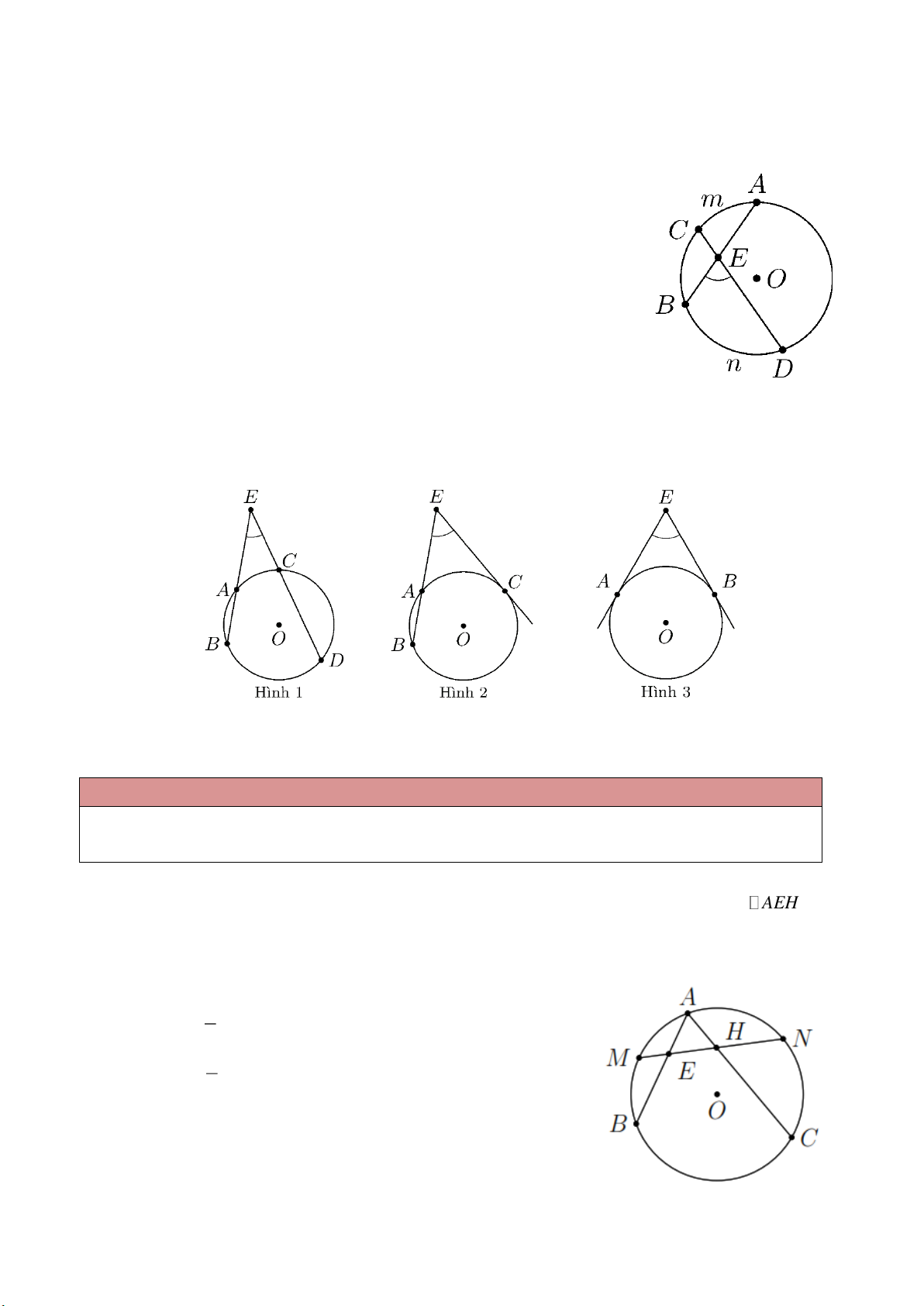
trong góc đối đỉnh của nó. Góc BED là góc có đỉnh ở bên trong đường
tròn chắn cung AmB và BmD .
ĐỊNH LÍ. Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa
tổng số đo hai cung bị chắn.
2. GÓC CÓ ĐỈNH Ở BÊN NGOÀI ĐƯỜNG TRÒN
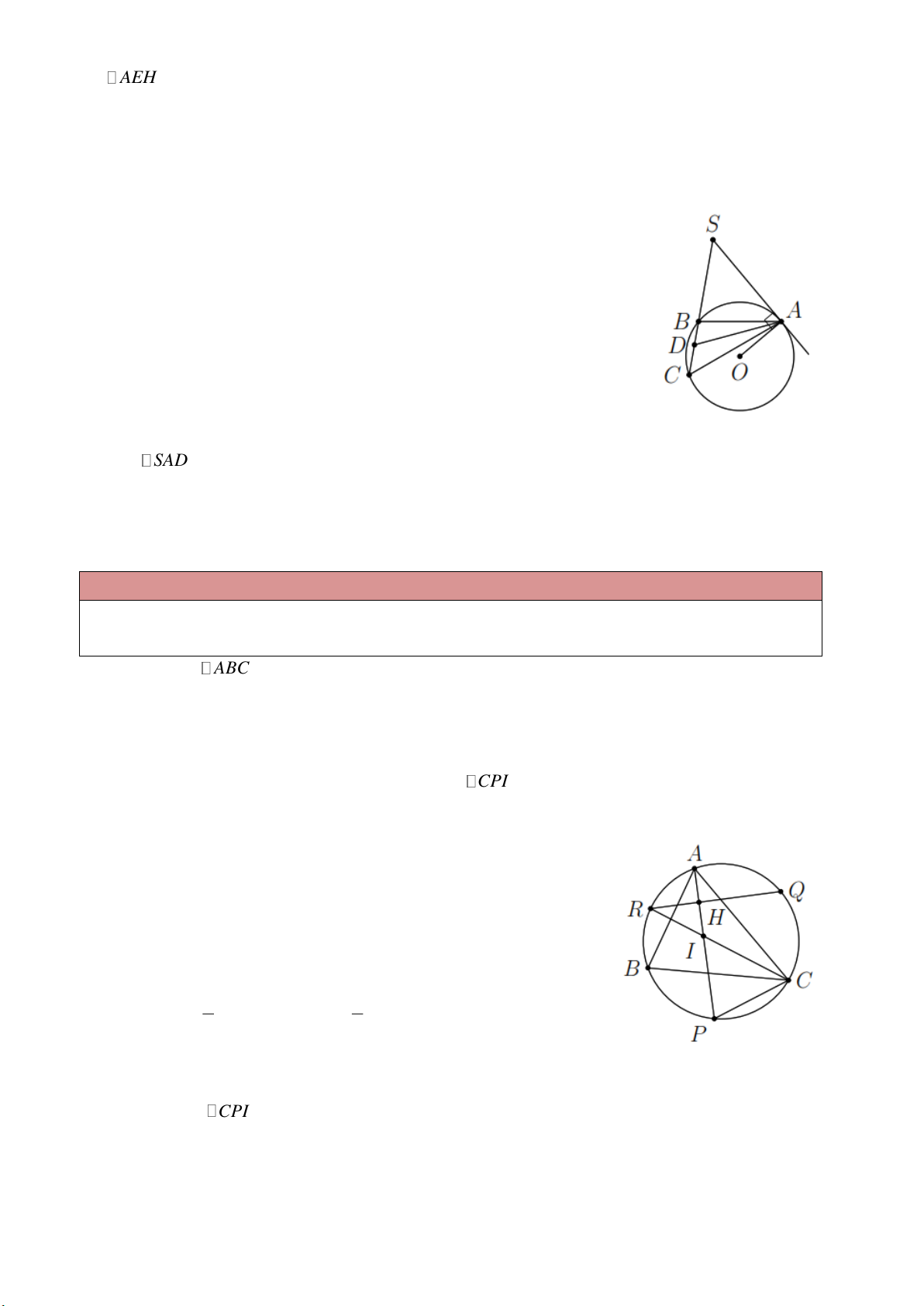
Là góc có đỉnh nằm bên ngoài đường tròn, các cạnh đều có điểm chung với đường tròn. Các góc
có đỉnh E trong hình vẽ là góc có đỉnh ở bên ngoài đường tròn.
ĐỊNH LÍ. Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Chứng minh hai góc hoặc hai đoạn thẳng bằng nhau
 Sử dụng định lý về số đo góc có đỉnh ở bên trong đường tròn và góc có đỉnh ở bên ngoài đường tròn.
Ví dụ 1. Cho đường tròn (O) hai dây AB , AC . Gọi M , N lần lượt là điểm chính giữa của cung
AB , AC . Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H . Chứng minh AEH là tam giác cân. Lời giải  1 AHE  
sñAM sñCN 2  1 AEH  
sñBM sñAN Ta có 2
sñAM sñBM
sñAN sñCN.
 AHE  AEH . Trang 1
 AEH cân tại A .
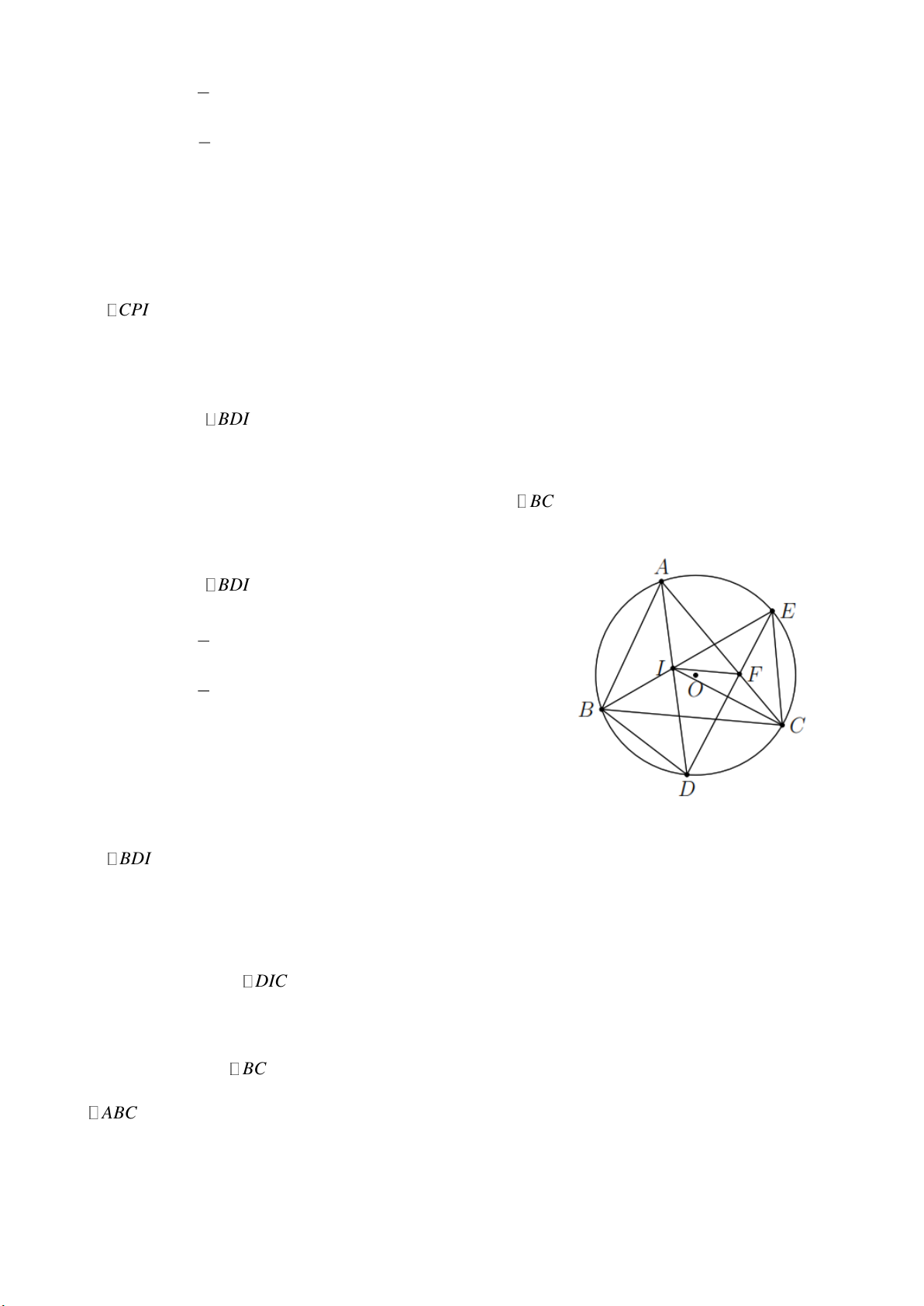
Ví dụ 2. Qua điểm S nằm bên ngoài đường tròn (O) vẽ tiếp tuyến SA và cát tuyến SBC của đường
tròn. Tia phân giác góc BAC cắt dây BC tại D . Chứng minh SA  SD . Lời giải
Ta có SDA  SBA  DAB (góc ngoài của tam giác) (1)
SAD  SAC  DAC (2)
SBA  SAC (góc nội tiếp và góc tạo bởi tiếp tuyến) (3)
DAB  DAC ( AD là phân giác) (4)
Từ (1), (2), (3) và (4) ta có SDA  SAD .
Suy ra SAD cân tại S .
Vậy SA  SD .
Dạng 2: Chứng minh hai đường thẳng song song hoặc vuông góc hoặc các đẳng thức cho trước
 Sử dụng định lý về số đo góc có đỉnh ở bên trong đường tròn và góc có đỉnh ở bên ngoài đường tròn.
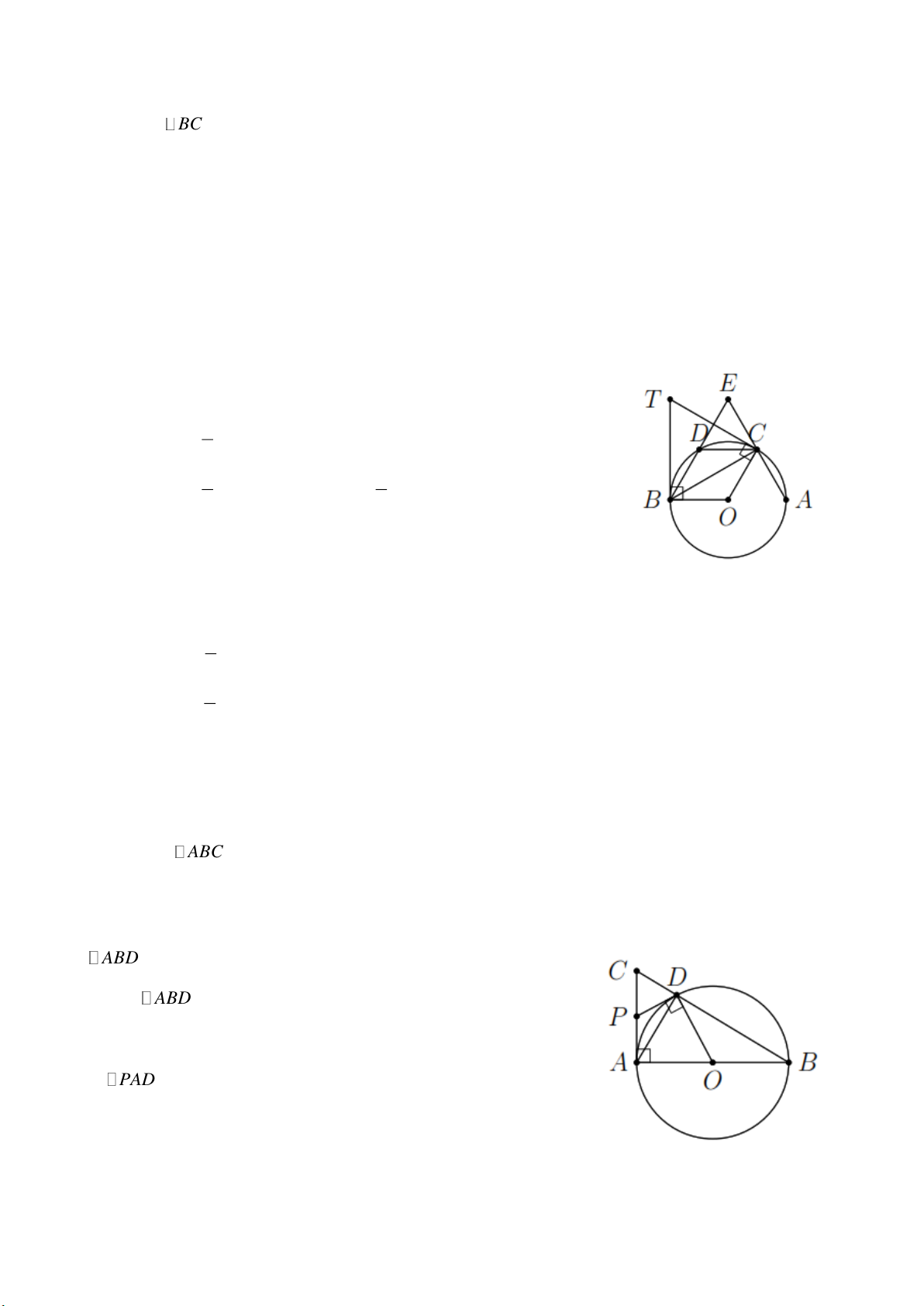
Ví dụ 3. Cho ABC nội tiếp đường tròn. Gọi P , Q , R theo thứ tự là các điểm chính giữa của các
cung bị chắn BC , CA , AB bởi các góc A , B , C .
a) Chứng minh AP  QR .
b) Gọi I là giao điểm của AP , CR . Chứng minh CPI cân. Lời giải
a) Chứng minh AP  QR .
Gọi H là giao điểm của AP và QR .
Ta có AHQ là góc có đỉnh bên trong ( ABC) . 1 1   Suy ra AHQ 
sñAQsñRP 180 90 . 2 2
Vậy AP  QR tại H .
b) Chứng minh CPI cân. Trang 2  1 PIC  
sñARsñCP 2  1 PCI  
sñBRsñBP Ta có 2 sñ  AR  sñBR sñ  CP  sñ . BP
 PIC  PCI .
 CPI cân tại P .
Ví dụ 4. Cho tam giác ABC nội tiếp đường tròn (O) . Các tia phân giác của góc A và góc B cắt nhau
ở I và cắt đường tròn theo thứ tự ở D và E .
a) Chứng minh BDI cân.
b) Chứng minh DE là đường trung trực của IC .
c) Gọi F là giao điểm của AC và DE . Chứng minh IF BC . Lời giải
a) Chứng minh BDI cân.  1 BID  
sñAEsñBD 2  1 IBD  
sñCEsñCD Ta có 2
sñAE sñCE
sñBD sñC .D
 BID  IBD .
 BDI cân tại D .
b) Chứng minh DE là đường trung trực của IC .
Ta có DB  DI và DB  DC .
Suy ra DI  DC và DIC cân tại D .
Mặt khác DE là phân giác (vì sñ AE  sñCE ) nên DE là đường trung trực của IC . c) Chứng minh IF BC .
ABC có AI và BI là phân giác.
 CI là phân giác.
Suy ra ICB  ICA . Trang 3
Mặt khác ICA  FIC ( F thuộc trung trực của IC ) nên ICB  FIC . Suy ra IF BC .
C. BÀI TẬP VẬN DỤNG
Bài 1. Trên một đường tròn lấy ba cung liên tiếp AC , CD , DB sao cho số đo các cung AC , CD ,
DB bằng 60 . Hai đường thẳng AC và BD cắt nhau tại E . Hai tiếp tuyến của đường tròn tại B và
C cắt nhau tại T . Chứng minh
a) AEB  BTC ;
b) CD là tia phân giác của BCT . Lời giải
a) AEB  BTC .  1 AEB  
sñABsñCD  2 Ta có  1 BTC  
 BAC BDC 1 sñ sñ
 sñAB sñDC.  2 2
 AEB  BTC .
CD là tia phân giác của BCT .  1 DCT  CD  30  2 Ta có  1
DCB  BD  30 .  2
 DCT  DCB .
 CD là tia phân giác của BCT .
Bài 2. Cho ABC vuông ở A . Đường tròn đường kính AB cắt BC tại D . Tiếp tuyến ở D cắt AC ở
P . Chứng minh PD  PC . Lời giải
ABD nội tiếp đường tròn đường kính AB .
Suy ra ABD vuông tại D.
Ta có PA  PD (hai tiếp tuyến cắt nhau)
 PAD cân tại P .  PAD  PDA (1) 
Ta có PAD  PCD  90 . (2) 
Ta có PDA  PDC  90 (3) Trang 4
Từ (1), (2) và (3) ta có PDA  PDC .
Suy ra PCD cân tại P . Vậy PD  PC .
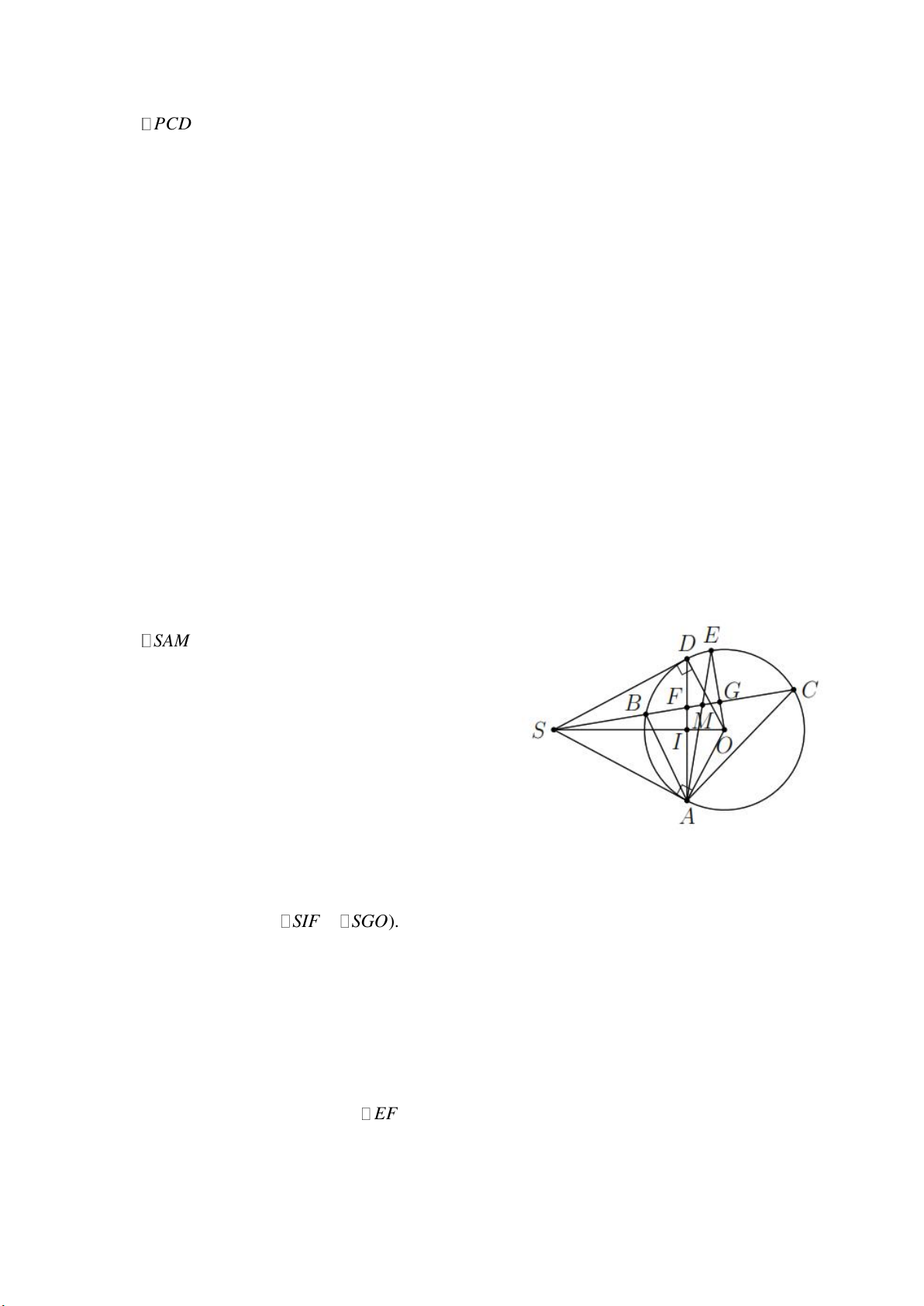
Bài 3. Cho đường tròn (O) và điểm S nằm bên ngoài đường tròn. Từ S kẻ tiếp tuyến SA , SD và cát
tuyến SBC tới đường tròn ( SB  SC ).
a) Phân giác BAC cắt dây cung BC ở M . Chứng minh SA  SM .
b) AM cắt (O) tại E , OE cắt BS tại G , AD cắt BC tại F . Chứng minh 2
SA  SG  SF . Lời giải
a) Chứng minh SA  SM .
Ta có SMA  MAC  MCA (góc ngoài của tam giác); (1)
Ta có SAM  SAB  BAM ; (2)
Ta có MCA  SAB (góc nội tiếp và góc tạo bởi tiếp tuyến); (3)
Ta có MAC  BAM ( AM là phân giác); (4)
Từ (1), (2), (3) và (4) ta có SMA  SAM .
Suy ra SAM cân tại S .
Vậy SA  SM . b) Chứng minh 2
SA  SG  SF .
Gọi I là giao điểm của SO và AD .
Suy ra SO  AD tại I .
Ta có OE là trung trực của BC . 2
SA  SI  SO (heä thöùc löôïng) Ta có 
SI  SO  SG  SF ( SIF ∽ SGO). 2
 SA  SG  SF .
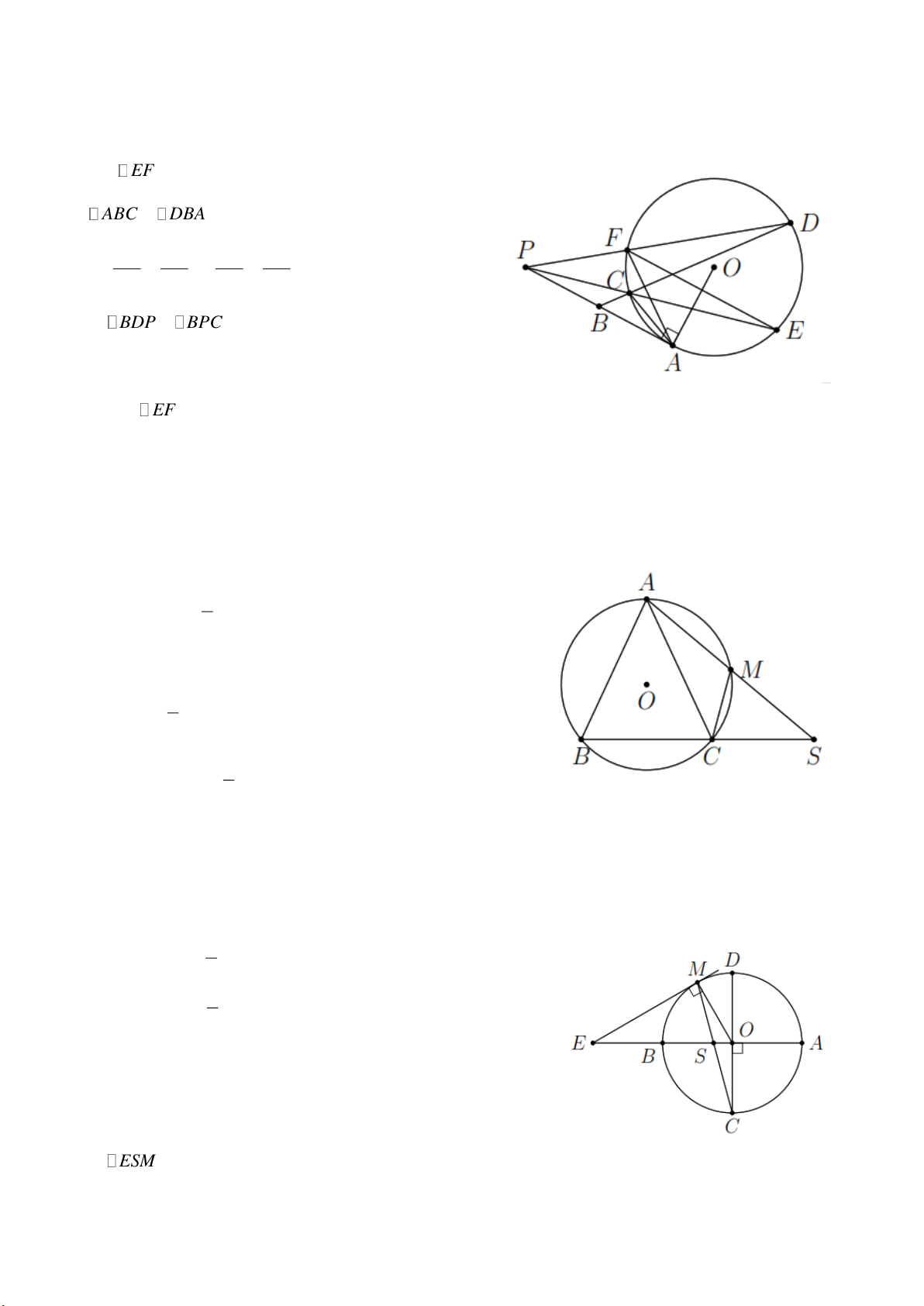
Bài 4. Từ điểm P nằm bên ngoài đường tròn (O) , vẽ tiếp tuyến PA với đường tròn. Qua trung điểm
B của đoạn PA vẽ cát tuyến BCD với đường tròn ( BC  BD ). Các đường thẳng PC và PD lần
lượt cắt đường tròn (O) tại E và F . Chứng minh
a) DCE  DPE  CAF ; b) AP EF . Lời giải
a) DCE  DPE  CAF . Trang 5
Ta có DCE  DPE  CDF (góc ngoài của tam giác).
Mà CDF  CAF (hai góc nội tiếp cùng chắn một cung) nên DCE  DPE  CAF . AP EF .
ABC ∽ DBA (g-g). AB BC BP BC     . DB AB BD BP
 BDP ∽ BPC (c-g-c).
 BPC  BDP  CEF .  AP EF .
D. BÀI TẬP VỀ NHÀ
Bài 5. Cho đường tròn (O) hai dây AB và AC bằng nhau. Trên cung nhỏ AC lấy một điểm M . Gọi
S là giao điểm của AM và BC . Chứng minh ASC  MCA . Lời giải  1 ASC  
sñABsñCM Ta có  2 sñ
 AB  sñ AC. 1
 ASC  sñ AM . 2 1 Mặt khác MCA 
sñ AM nên ASC  MCA . 2
Bài 6. Cho AB và CD là hai đường kính vuông góc của (O) . Trên cung nhỏ BD lấy điểm M . Tiếp
tuyến tại M cắt AB ở E , đoạn thẳng CM cắt AB ở S . Chứng minh ES  EM . Lời giải  1 BSM  
sñACsñBM 2   1
Ta có EMC  sñBC  sñBM  2 
sñAC  sñBC. 
 BSM  EMC .
 ESM cân tại E .  ES  EM . Trang 6
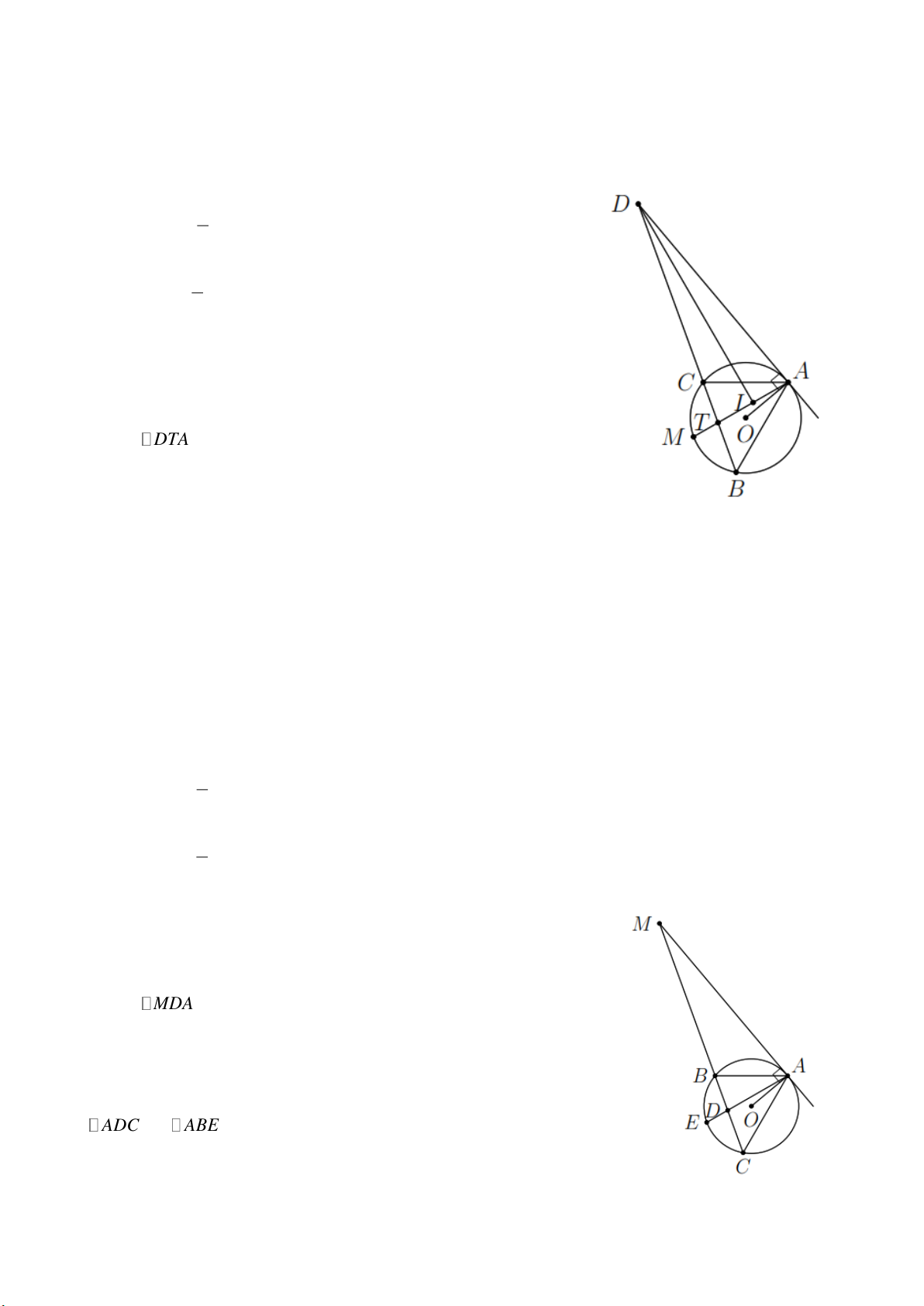
Bài 7. Cho A , B , C là ba điểm thuộc đường tròn (O) sao cho tiếp tuyến tại A cắt tia BC tại D . Tia
phân giác của góc BAC cắt đường tròn ở M , tia phân giác của góc D cắt AM ở I . Chứng minh DI vuông góc AM . Lời giải 1 Ta có MAD 
sñ AM (góc tạo bởi tiếp tuyến, dây cung) (1) 2 1 Ta có DTA 
sñACsñBM (2) 2
Ta có sñCM  sñ BM ( AM là phân giác) (3)
Từ (1), (2) và (3) ta có MAD  DTA .
Suy ra DTA cân tại D .
Mà DI là phân giác nên DI là đường cao.
Vậy DI  AM tại I .
Bài 8. Cho đường tròn (O) và điểm M nằm ngoài đường tròn đó. Từ M kẻ tiếp tuyến MA và cát
tuyến MBC với đường tròn ( MB  MC ). Phân giác góc BAC cắt BC tại D , cắt đường tròn ở E . Chứng minh a) MA  MD ;
b) AD  AE  AC  AB . Lời giải a) MA  MD . 1 Ta có MAD 
sd AE (góc tạo bởi tiếp tuyến, dây cung) (1) 2 1 Ta có MDA 
sdABsdEC (2) 2
Ta có sñCE  sñ BE ( AE là phân giác) (3)
Từ (1), (2) và (3) ta có MAD  MDA .
Suy ra MDA cân tại M .
Vậy MA  MD .
AD  AE  AC  AB .
ADC và ABE có Trang 7
DAC  BAE phan giac 
ACD  AEB (goc noi tiep)
 ADC ∽ ABE (g-g). AD AC  
 AD  AE  AC  AB . AB AE --- HẾT --- Trang 8