Phương pháp lặp đơn giải | Bài giảng môn Phương pháp tính và matlab CTTT | Đại học Bách khoa hà nội
Nếu dãy hội tụ thì giới hạn là nghiệm của phương trình. Tài liệu trắc nghiệm môn Phương pháp tính và matlab CTTT giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!
Môn: Phương pháp tính và matlab CTTT
Trường: Đại học Bách Khoa Hà Nội
Thông tin:
Tác giả:
Tài liệu liên quan:
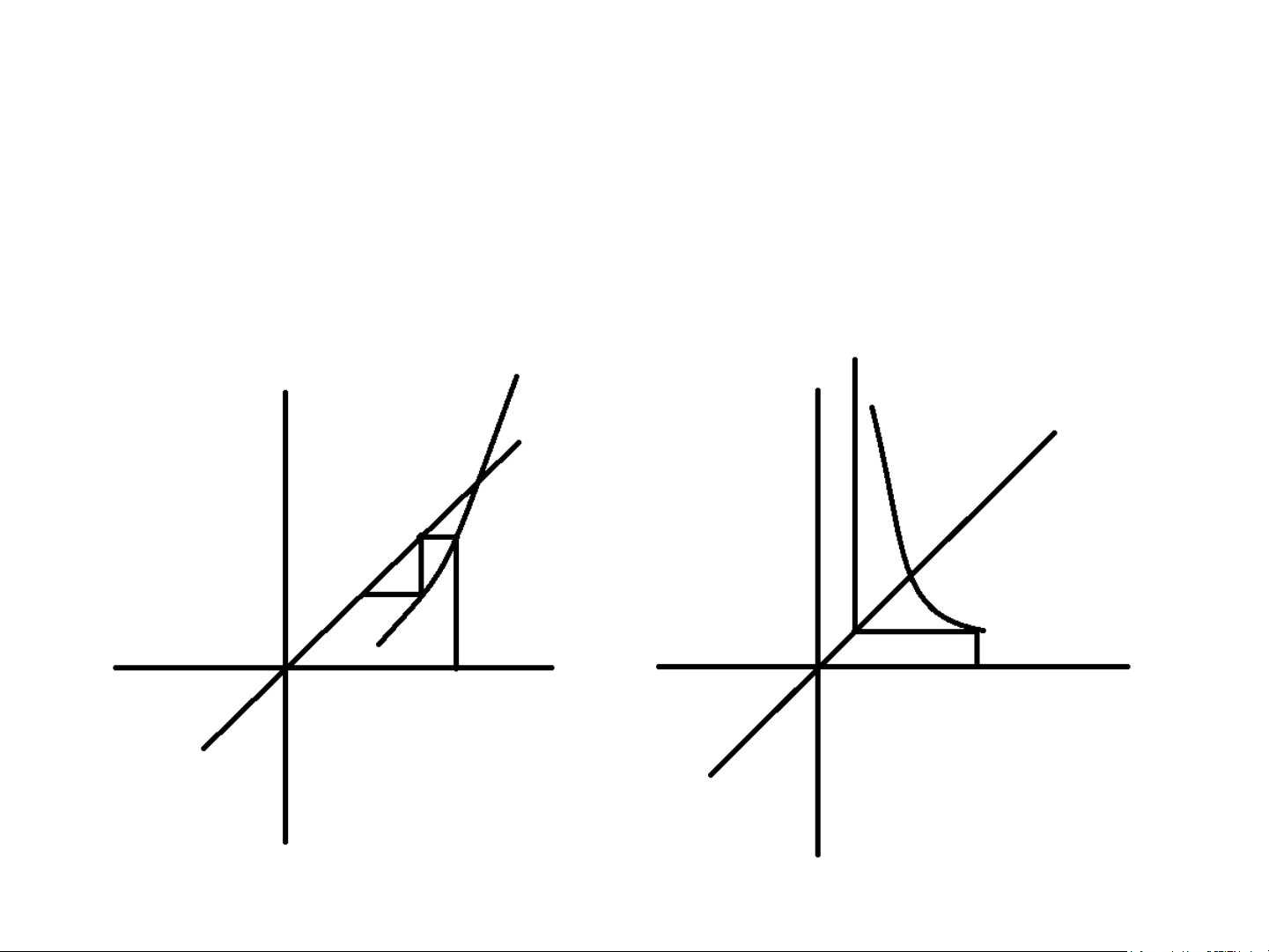
Preview text:
PHƯƠNG PHÁP LẶP ĐƠN GIẢI PT f(x)=0 Ý tưởng phương pháp
- Đưa về phương trình tương đương
f ( x) = 0 x = ( x) - Lập dãy số x = ( x
, x a,b n n 1 − ) 0
- Nếu dãy hội tụ thì giới hạn là nghiệm của phương trình Ý tưởng phương pháp
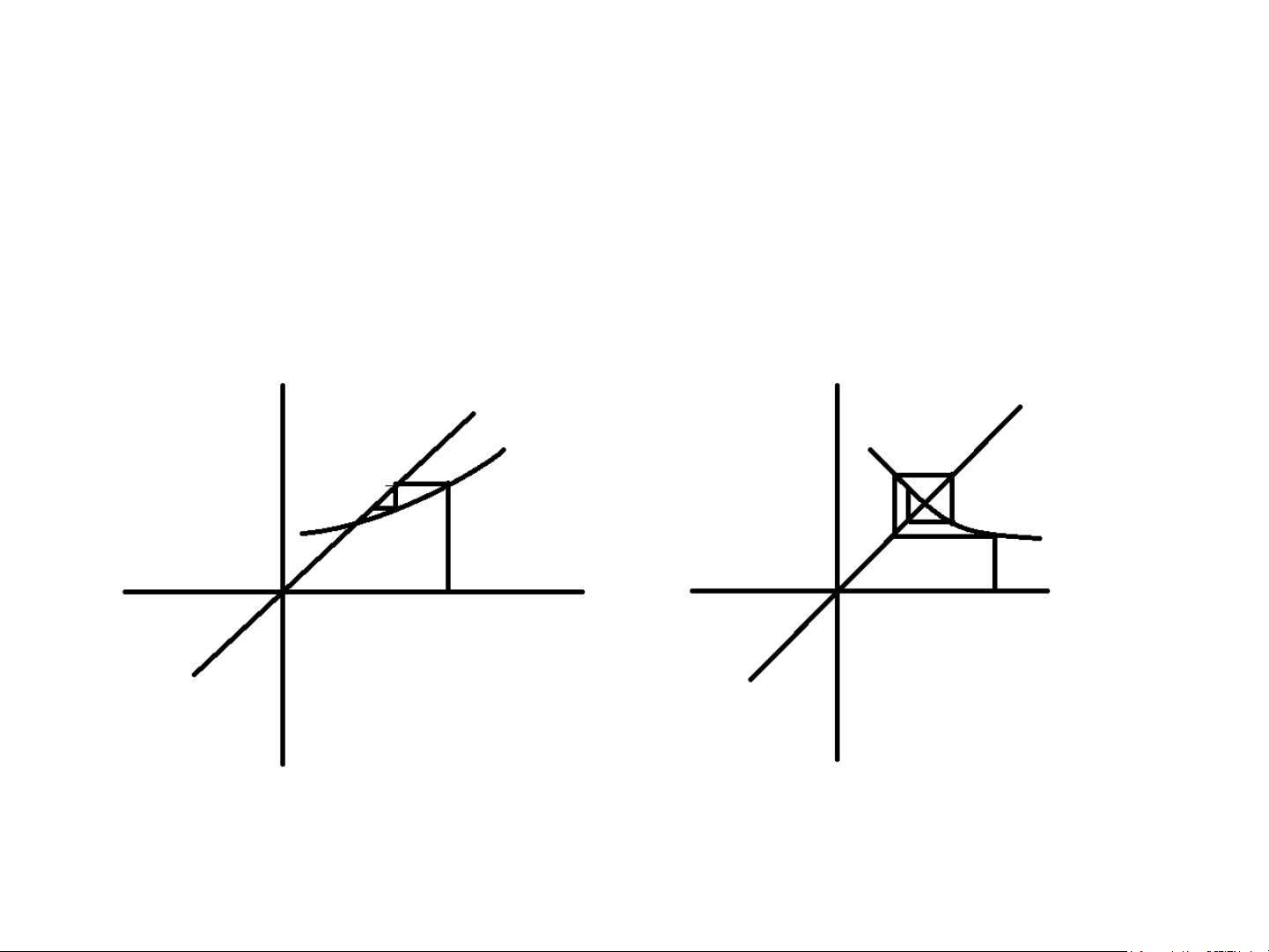
• Trường hợp có xu hướng hội tụ y y (x) ( x) x x x x 0 0 0 0 Ý tưởng phương pháp
• Trường hợp có xu hướng không hội tụ y y x x x x 0 0 Nội dung phương pháp
– Đưa phương trình về dạng x = (x), gọi là hàm lặp.
– Chọn x [a, b] làm xấp xỉ đầu 0
– Tính dãy x theo công thức: n x = (x ), n = 1, 2, 3,... n n – 1
– Nếu dãy x → , n → thì phương pháp n
lặp hội tụ và lấy nghiệm gần đúng x* = xn nào đó. Điều kiện hội tụ
Định lý: Giả sử (a, b) là khoảng phân ly
nghiệm (chứa nghiệm đúng ) của phương
trình f(x) = 0. Xét phương pháp lặp với hàm
lặp : x = (x), và ' liên tục trên [a, b]. Nếu:
1) Mọi x [a, b], (x) [a, b],…
2) Với mọi x [a, b]: |'(x)| q <1,(q= const)
thì phương pháp lặp hội tụ: x → , n → . n Đánh giá sai số
• Công thức sai số theo xấp xỉ ban đầu: n q x − x − x n 1 0 1− q
• Công thức sai số theo hai xấp xỉ liên tiếp q x − x − x n n n 1 − 1− q Nhận xét
• Nếu ’(x) > 0 với mọi x thuộc [a,b], từ x – = ’(c)( x
– ) cho thấy dãy {x } dần n n –1 n
đến từ một phía. Ngược lại, dãy x dần đến n
từ hai phía, giao động xung quanh .
• Phương pháp lặp hội tụ càng nhanh nếu q càng bé.
• Áp dụng công thức sai số theo xấp xỉ ban đầu
có thể xác định được số lần lặp cần thiết để
được nghiệm gần đúng đạt độ chính xác cho trước. Nhận xét
• Ưu điểm của phương pháp lặp:
+ Xấp xỉ đầu không nhất thiết phải rất gần nghiệm
đúng (miễn là các điều kiện của định lý được đảm bảo).
+ Phép lặp có khả năng tự sửa sai: nếu x tính sai k
thì coi như chọn lại xấp xỉ đầu mới.
+ Thuật toán lặp đi lặp lại theo cùng một kiểu, rất
thuận lợi khi dùng máy tính.
• Nhược điểm: Khi q gần bằng 1, phép lặp hội tụ rất chậm. Ví dụ
Cho phương trình x3 + x – 1000 = 0 với
khoảng phân ly nghiệm là (9; 10).
1. Tính đến nghiệm gần đúng x của phương 3
trình theo phương pháp lặp, chọn xấp xỉ ban đầu x = 10. 0
2. Đánh giá sai số của nghiệm gần đúng x3. + f(x) = x3 + x – 1000 + Xác định hàm lặp . Xét 3 khả năng: 1)x = 1000 – x3 2)x = 1000/x2 – 1/x 3)x = (1000 – x)1/3
Chỉ trường hợp 3) cho phương pháp lặp hội tụ.
(x) = (1000 – x)1/3 ; |’(x)| = | 1/3(1000 –x)– 2/3| q
=1/3(1000 – 10)– 2/3 0.0033557<1/300 <1
Phương pháp lặp hội tụ.
Tính theo công thức lặp x = (1000 - x )1/3 , x = 10, n+1 n 0 ta có: x 9.9665549; 1 x 9.9666672; 2 x 9.9666668 . 3
+ Đánh giá sai số của nghiệm gần đúng x theo 3 công thức sai số 3 q x − x − x 3 1 0 1− q 9 x − − 1.2680655*10 3 Bài tập
Cho phương trình x3 + 4x – 3 = 0 và khoảng
phân ly nghiệm (0;1). Tính số lần lặp cần thiết
để thu được nghiệm gần đúng với sai số tuyệt
đối không quá 10 – 3 bằng phương pháp lặp, lấy x = 1. 0
Phương án 1: (x) = (3 – 4x)1/3. Phương pháp lặp không hội tụ
Phương án 2: (x) = (3 – x3)/4. Phương pháp lặp hội tụ với q = ¾
Tính x = 0,5. Lập bất phương trình suy ra n 27. 1
Phương án 3: (x) = 3/(x2 + 4). Phương pháp lặp hội tụ với q = 6/25 <1.
Tính x = 0,6. Lập bất phương trình suy ra n 5. 1