






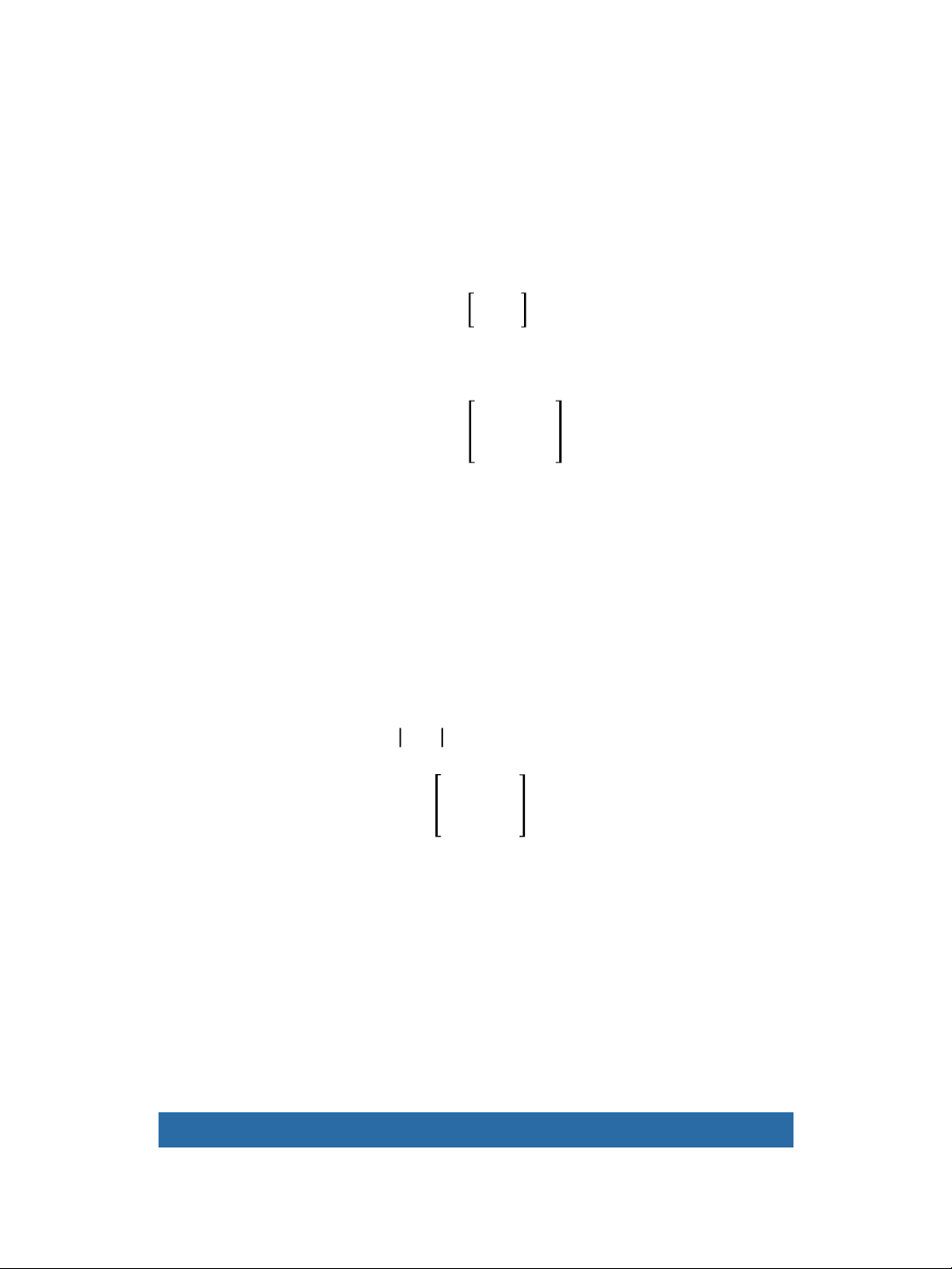




Preview text:
lOMoAR cPSD| 46578282 7/29/2020 CHAPTER 9: MATRIX ALGEBRA
PREPARED BY: FINANCE DEPARTMENT COURSE CODE: B03013 1 lOMoAR cPSD| 46578282 7/29/2020
7/29/2020 B03013 – Chapter 9: Matrix 1 algebra LEARNING OBJECTIVES • Formulate multi-variable economic models in matrix format.
• Add and subtract matrices.
• Multiply matrices by a scalar value and by another matrix.
• Calculate determinants and cofactors. LEARNING OBJECTIVES
• Derive the inverse of a matrix.
• Use the matrix inverse to solve a system of simultaneous equations
• Derive the Hessian matrix of secondorder derivatives 7/29/2020
B03013 – Chapter 9: Matrix algebra 2 2 lOMoAR cPSD| 46578282 7/29/2020
• Derive the bordered Hessian matrix 3 7/29/2020
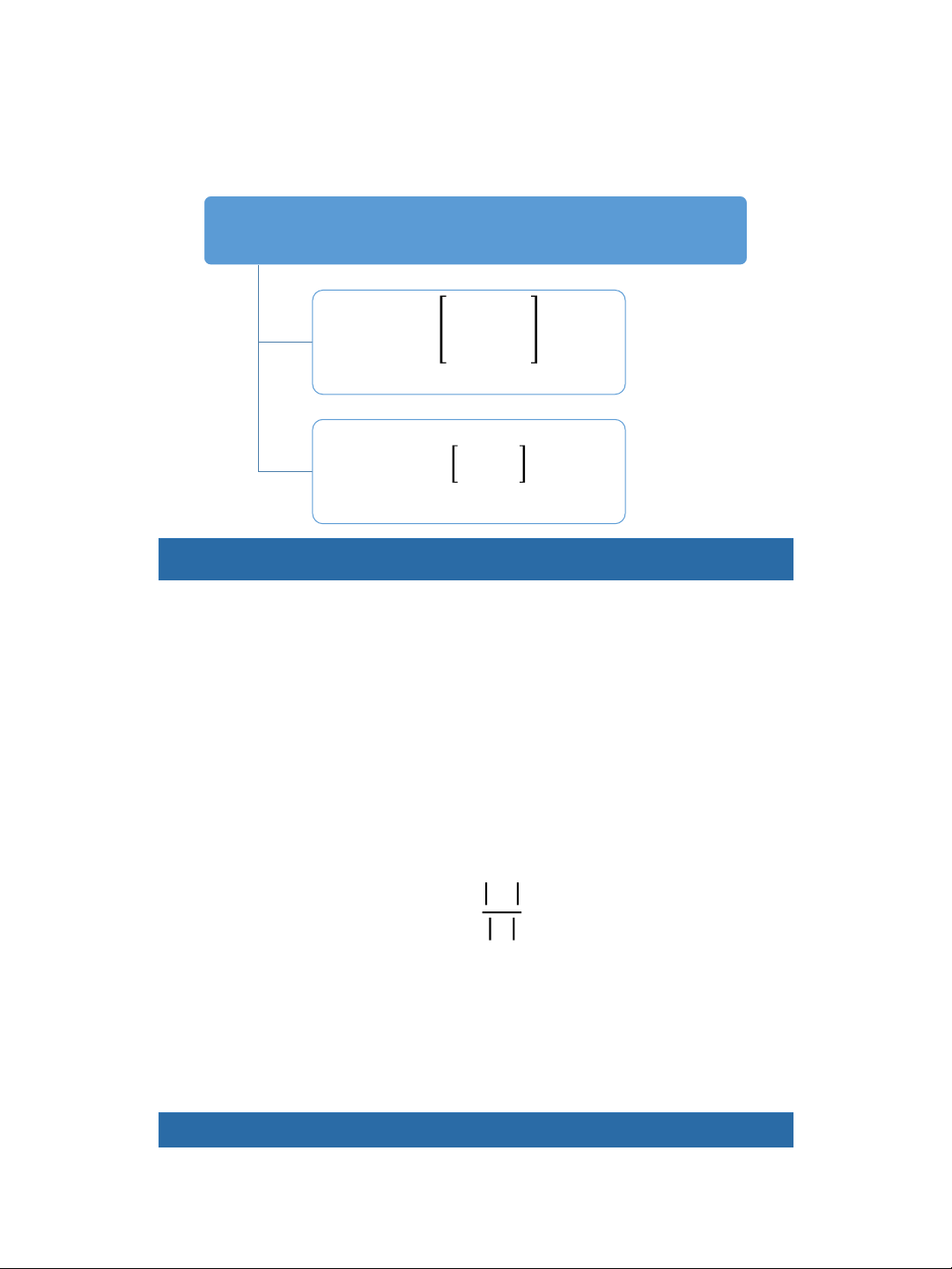
B03013 – Chapter 9: Matrix algebra CONTENT
1 • Introduction matrices and vectors
2 • Basic principles of matrix multiplication
3 • Matrix multiplication – the general case
• Matrix inverse and the solution of 4
simultaneous equations.
5 • Determinants
6 • Minors, cofactors and the Laplace expansion CONTENT •
The transpose matrix, the cofactor
matrix, the 7 adjoint and the matrix inverse formula. •
Application of the matrix inverse to the 8
solution of linear simultaneous equations • Cramer’s rule 9
• Second-order conditions and the Hessian 10 matrix 7/29/2020
B03013 – Chapter 9: Matrix algebra 4 3 lOMoAR cPSD| 46578282 7/29/2020
• Constrained optimization and the bordered 11 Hessian 5 7/29/2020
B03013 – Chapter 9: Matrix algebra
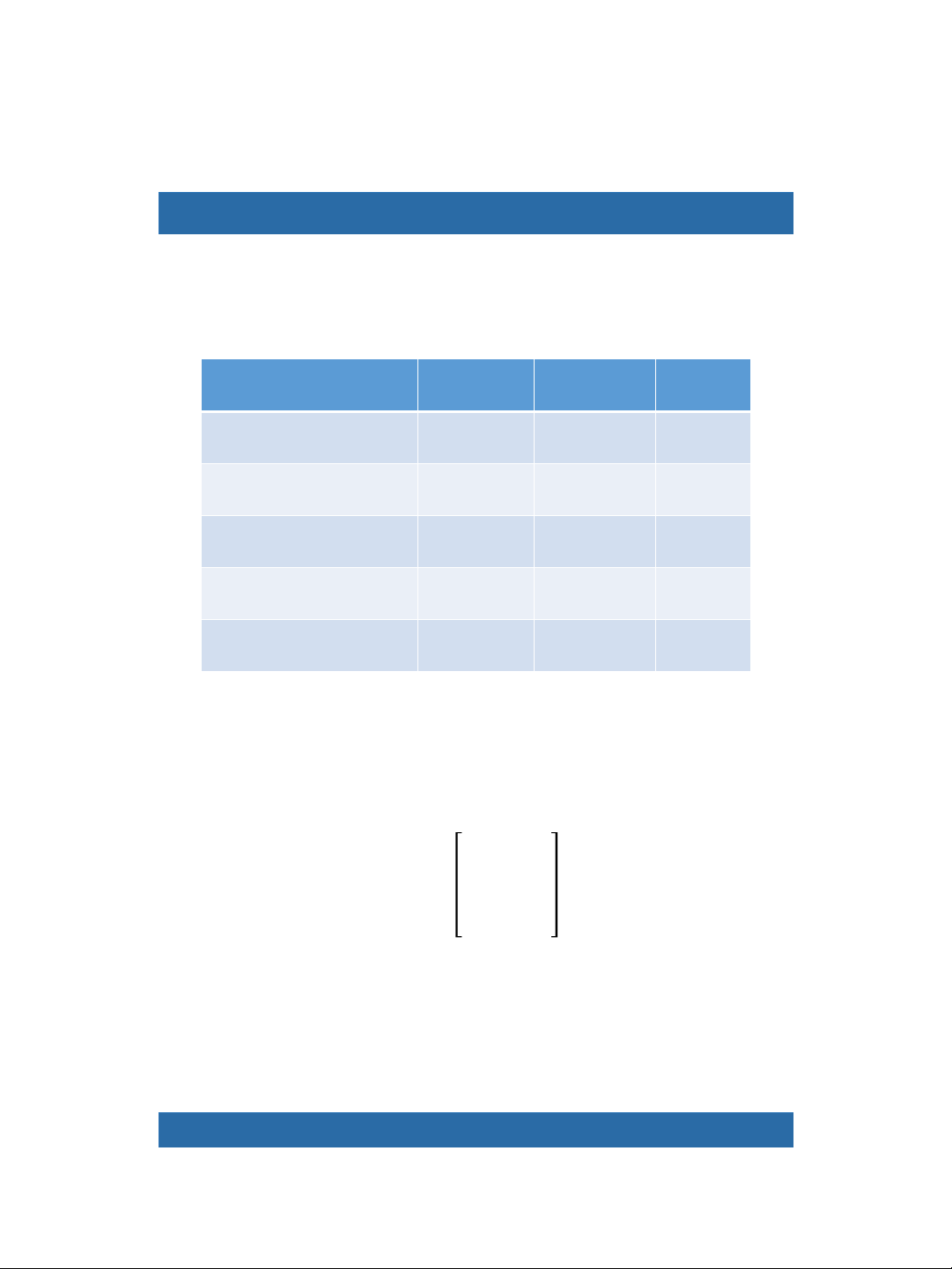
Tabular form - Table 15.1
The car hire requirements for the 3-week period in
this example can be set out as the matrix
Cars required Week 1 Week 2 Week 3 COMPACT 4 7 2 INTERMEDIATE 3 5 5 LARGE 12 9 5 PEOPLE CARRIER 2 1 3 LUXURY LIMOUSINE 1 1 2
Introduction matrices and vectors
• A matrix is defined as an array of numbers (or
algebraic symbols) set out in rows and columns. 4 7 2 3 5 5 𝐴 =12 9 5 2 1 3 1 1 2 7/29/2020
B03013 – Chapter 9: Matrix algebra 6 4 lOMoAR cPSD| 46578282 7/29/2020
Matrices that have the same order can be added
together, or subtracted. The addition, or
subtraction, is performed on each of the corresponding elements. 7/29/2020 7
B03013 – Chapter 9: Matrix algebra
Introduction matrices and vectors
• The size of a matrix is called its ‘order’.
(number of rows) × (number of columns)
• Matrices with only one column or row are known as vectors • Row vector • Column vector 7/29/2020
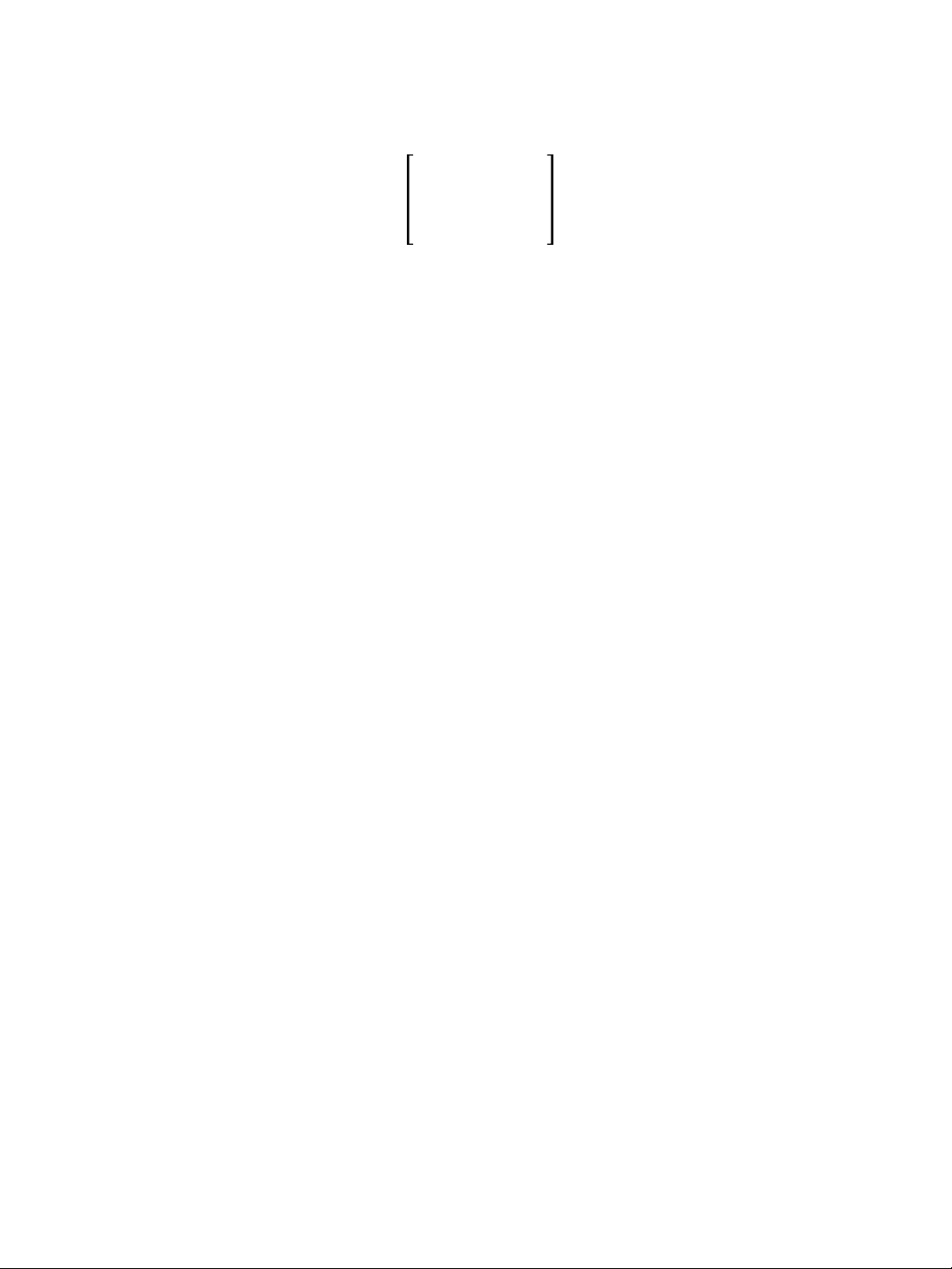
B03013 – Chapter 9: Matrix algebra 8 5 lOMoAR cPSD| 46578282 7/29/2020 • Example 1: • If 𝐴 =12 30 and B =7 35 what is A-B 8 154 8 • Example 2:
• The number of units of a product sold by a retailer for
the last 2 weeks are shown in matrix A below, the
columns represent weeks and the rows correspond to
the two different shop units that sold them. 12 30 𝐴 = 8 15
• If each item sells for £4, derive a matrix for total sales
revenue for this retailer for these two shop units over this two-week period. 7/29/2020
B03013 – Chapter 9: Matrix algebra 9
Basic principles of matrix multiplication
• If one matrix is multiplied by another matrix, the
basic rule is to multiply elements along the rows
of the first matrix by the corresponding elements
down the columns of the second matrix. 6 lOMoAR cPSD| 46578282 7/29/2020 7/29/2020
B03013 – Chapter 9: Matrix algebra 10 Multiply the two matrices 23 •𝐴= 81 752 • B = 481 26 • 34 7 AB = 604817 7/29/2020
B03013 – Chapter 9: Matrix algebra 11
Matrix multiplication – the general case
• The general m × n matrix with any number of rows
m and columns n can be written as 𝑎11 𝑎12 … 𝑎1𝑛 𝐴 =𝑎21 𝑎22 … 𝑎1𝑛 ⋮ ⋮ ⋮ ⋮
𝑎𝑚1 𝑎𝑚2 … 𝑎1𝑛
• a11 = element in row 1, column 1
• a12 = element in row 1, column 2
• a1n = element in row 1, column n
• amn = element in row m, column n 7 lOMoAR cPSD| 46578282 7/29/2020
Find the product C = AB 4 2 12 •𝐴= 6 0 20 1 8 5 10 0.5 • B = 6 3 4 4 2 0 7/29/2020
B03013 – Chapter 9: Matrix algebra 12 1 7 8 2.5 7/29/2020
B03013 – Chapter 9: Matrix algebra 13
Matrix inverse and the solution
of simultaneous equations
• The derivation of the matrix inverse A−1
• Since the number of unknown variables
must equal the number of equations the
matrix of coefficients A must be square
(the number of rows equals the number of columns).
• Identity matrix is any square matrix with
each element along the diagonal being 8 lOMoAR cPSD| 46578282 7/29/2020
equal to 1 and with all other elements being zero. 7/29/2020
B03013 – Chapter 9: Matrix algebra 14 9 lOMoAR cPSD| 46578282 7/29/2020
Matrix inverse and the solution
of simultaneous equations
• To actually find the inverse of a matrix,
we first need to consider some special concepts associated with
square matrices: • The Determinant • Minors • Cofactors 10 lOMoAR cPSD| 46578282 7/29/2020 • The Adjoint Matrix 7/29/2020
B03013 – Chapter 9: Matrix algebra 15 Determinants
• The determinant of the general 2 × 2 matrix A, written as |A|, will 𝒂𝟏𝟏 𝒂𝟏𝟐 𝑨 = 𝒂𝟐𝟏
𝒂𝟐𝟐= 𝒂𝟏𝟏𝒂𝟐𝟐
− 𝒂𝟐𝟏𝒂𝟏𝟐 Determinants • The determinant of a 3rd order matrix
𝒂𝟏𝟏 𝒂𝟏𝟐 𝒂𝟏𝟑
𝑨=𝒂𝟐𝟏 𝒂𝟐𝟐 𝒂𝟐𝟑
𝒂𝟑𝟏 𝒂𝟑𝟐 𝒂𝟑𝟑 𝑨 =
𝒂𝟏𝟏𝒂𝟑𝟐𝟐𝟐 𝒂𝒂𝟑𝟑𝟐𝟑−
𝒂𝟏𝟐𝒂𝒂𝟑𝟏𝟐𝟏
𝒂𝒂𝟑𝟑𝟐𝟑+𝒂𝟏𝟑𝒂𝒂𝟐𝟏𝟑𝟏 𝒂𝒂𝟐𝟐𝟑𝟐 𝒂 7/29/2020
B03013 – Chapter 9: Matrix algebra 17 7/29/2020
B03013 – Chapter 9: Matrix algebra 16 11 lOMoAR cPSD| 46578282 7/29/2020 Examples
• Find the determinant of the matrix 𝑨 = 𝟓 𝟕 𝟒 𝟗
• Derive the determinant of matrix 𝟒 𝟔 𝟏 𝑨 =𝟐 𝟓 𝟐 𝟗 𝟎 𝟒
Minors, cofactors, and the Laplace expansion • Minors
• The minor |Mij | of matrix A is the determinant of the
matrix left when row i and column j have been deleted. • Example • Find the minor 31 𝑀
𝑜𝑓 𝑡ℎ𝑒 𝑚𝑎𝑡𝑟𝑖𝑥 8 2 3 𝐴= 1 9 4 7/29/2020
B03013 – Chapter 9: Matrix algebra 18 12 lOMoAR cPSD| 46578282 7/29/2020 4 3 6 7/29/2020
B03013 – Chapter 9: Matrix algebra 19
Minors, cofactors, and the Laplace expansion • Cofactors
• A cofactor is the same as a minor, except that its
sign is determined by the row and column that it corresponds to.
• 𝐶12 = (−1)3 𝑎𝑎2131 𝑎𝑎2333 =(−1) 𝑎𝑎2131 𝑎𝑎2333 • Examples
• Find the cofactor 𝐶22 of the matrix 8 2 3 𝐴= 1 9 4 4 3 6
Minors, cofactors, and the Laplace expansion
• The Laplace expansion
• For matrices of any order n, using the Laplace
expansion, the determinant can specified as
𝐴 = 𝑖,𝑗=𝑛𝑖,𝑗=1 𝑎𝑖𝑗 𝐶𝑖𝑗 • Example
• Use the Laplace expansion to find the determinant of matrix 7/29/2020
B03013 – Chapter 9: Matrix algebra 20 13 lOMoAR cPSD| 46578282 7/29/2020 8 10 2 3 𝐴 =05 7 10 2 2 1 4 14 lOMoAR cPSD| 46578282 7/29/2020 3 4 4 0 7/29/2020
B03013 – Chapter 9: Matrix algebra 21 The transpose matrix • Transpose of a matrix: AT
• The rows and columns are swapped around
• Row 1 becomes column 1 and column 1
becomes row 1 • For example: 5 20 𝐴 =16 9 12 6 12 𝐴𝑇 =5 16 6 20 9 The cofactor matrix
• If we replace every element in a matrix by its
corresponding cofactor then we get the
cofactor matrix, usually denoted by C. • For example: 2 4 3 25 −15 −12 −14 𝐴= then C 3 5 0 = −2 12 4 2 5 −15 9 −2
𝑐11 = 𝐶11 = −1 1+1 𝑎𝑎3222 𝑎𝑎3323 = −1 2 52 50 = 25 7/29/2020
B03013 – Chapter 9: Matrix algebra 22 15 lOMoAR cPSD| 46578282 7/29/2020 7/29/2020
B03013 – Chapter 9: Matrix algebra 23
The adjoint and the matrix inverse formula • The adjoint matrix • Denoted by AdjA
• The transpose of the cofactor matrix • The inverse matrix
• The formula for A−1, the inverse of matrix A.
• 𝐴−1 = 𝐴𝑑𝑗𝐴 𝐴
• the determinant |A| is non-singular (must not be zero.) 7/29/2020
B03013 – Chapter 9: Matrix algebra 24 16 lOMoAR cPSD| 46578282 7/29/2020 Example Find the inverse matrix A−1 for matrix 243 𝐴= 350 425 205 𝐴= 62 7/29/2020
B03013 – Chapter 9: Matrix algebra 25 Cramer’s rule
• Cramer’s rule says that the value of any one of
the unknown variables xi can be found by
substituting the vector of constant values b for
the i th column of matrix A and then dividing the
determinant of this new matrix by the
determinant of the original A matrix. • Cramer’s rule gives: 𝐴𝑖 𝑥𝑖 = 𝐴 Example
• Find x1 and x2 using Cramer’s rule from the
following set of simultaneous equations 7/29/2020
B03013 – Chapter 9: Matrix algebra 26 17 lOMoAR cPSD| 46578282 7/29/2020 5x1 + 0 .4 x2 = 12 18 lOMoAR cPSD| 46578282 7/29/2020 3x1 + 3x2 = 21 7/29/2020
B03013 – Chapter 9: Matrix algebra 27 The Hessian matrix
• The Hessian will always be a square matrix with
equal numbers of rows and columns.
• For the two variable function f(x,y) the Hessian matrix will be 𝑓𝑥𝑥 𝑓𝑥𝑦 𝐻 = 𝑓𝑦𝑥 𝑓𝑦𝑦 7/29/2020
B03013 – Chapter 9: Matrix algebra 28 19 lOMoAR cPSD| 46578282 7/29/2020
• For any 2 × 2 Hessian there will therefore only be the two principal
minors 𝐻 1 = 𝑓 𝑥𝑥 , 𝐻 2 = 𝑓𝑥𝑥 𝑓𝑥𝑦 𝑓𝑦𝑥 𝑓𝑦𝑦 • SOC for a maximum
• |H1| < 0 and |H2| > 0 • SOC for a minimum 20




