




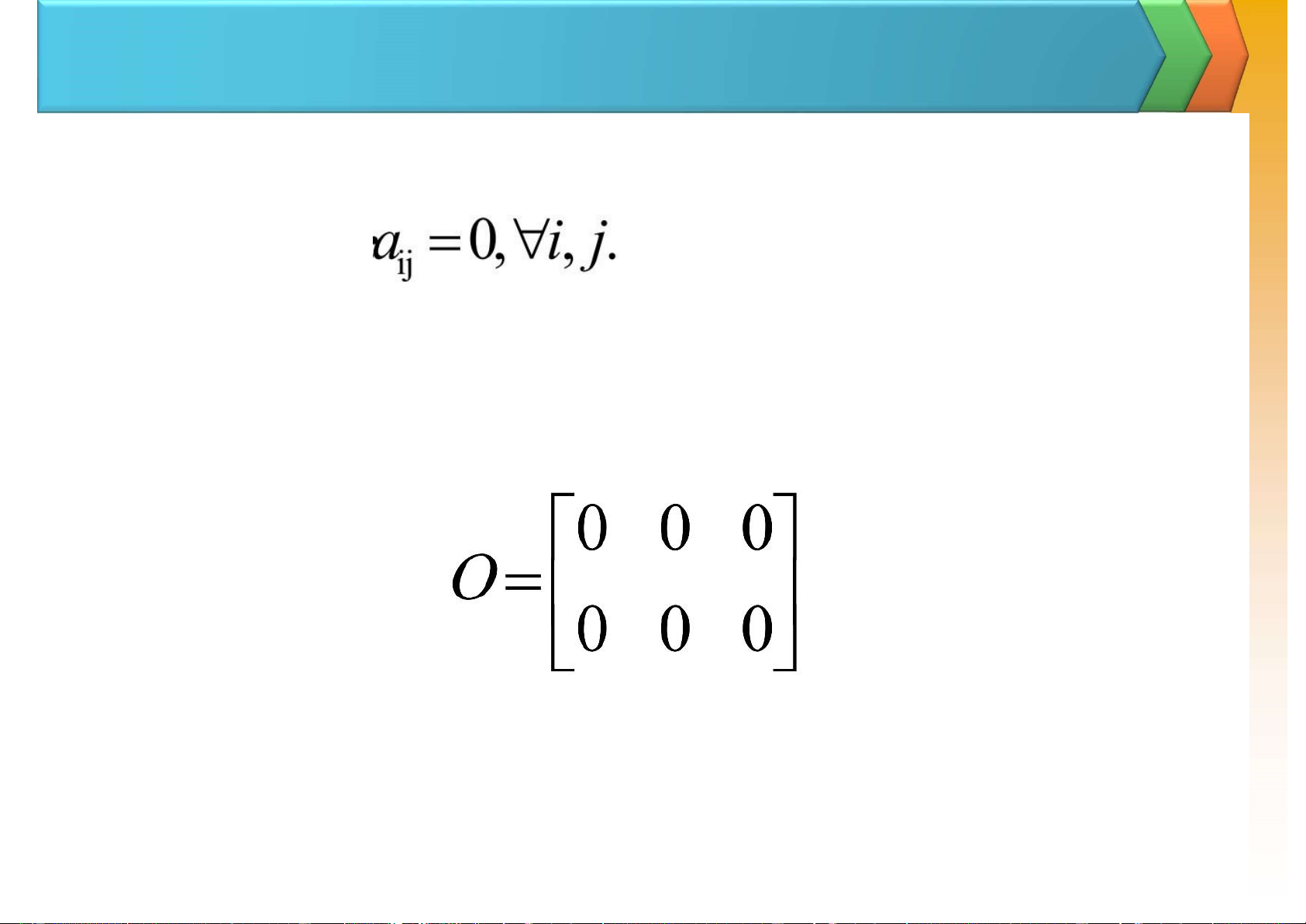










Preview text:
lOMoAR cPSD| 47206071 1 Nội dung môn học: 1. Ma trận lOMoAR cPSD| 47206071 2. Định thức 3. Ma trận nghịch ảo 4. Hạng của ma trận
5. Phương trình tuyến tính 6. Không gian vector 2 lOMoAR cPSD| 47206071 lOMoAR cPSD| 47206071 Tài liệu tham khảo
1. Beezer, R. A. (2015). A first course in linear algebra. Independent.
2. Zill, D. G. (2020). Advanced engineering mathematics. Jones & Bartlett Learning.
3. O'neil, P. V. (1995). Advanced engineering mathematics. PWS-Kent Publishing Company.
4. Đại số tuyến tính. Tác giả: Ngô Việt Trung 4 lOMoAR cPSD| 47206071 5 lOMoAR cPSD| 47206071 I. Ma trận 1.1 Các khái niệm
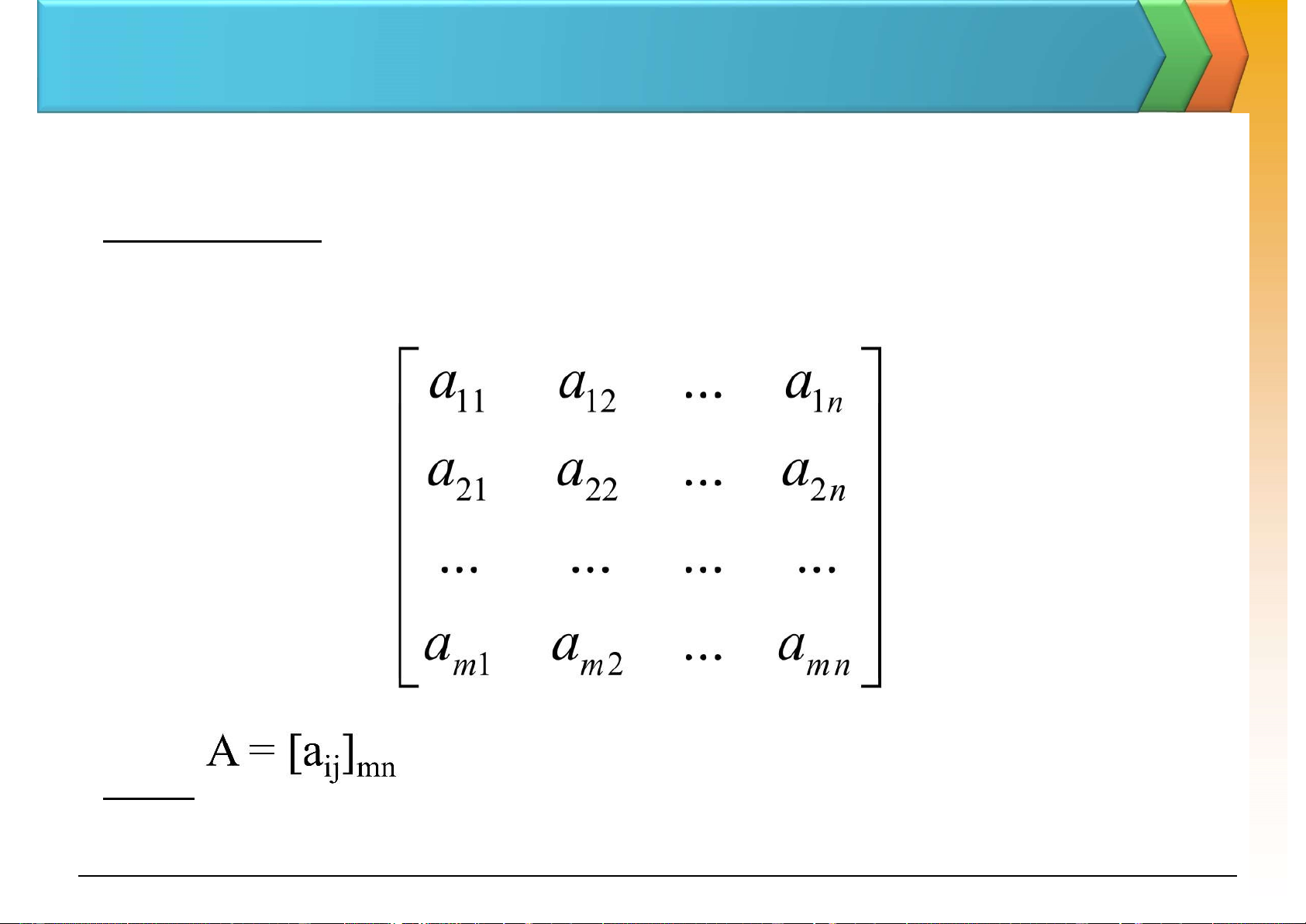
a) Định nghĩa: Ma trận là một bảng gồm m.n số thực (phức) ược viết
thành m hàng và n cột như sau: Ký hiệu: 6 lOMoAR cPSD| 47206071 I. Ma trận 1.1 Concepts Hàng thứ nhất Hàng thứ i mn: gọi là cấp của ma trận Cột thứ 2 Cột thứ j
aij: Phần tử nằm ở hàng i cột j 7 lOMoAR cPSD| 47206071 I. Ma trận Ví dụ: 8 lOMoAR cPSD| 47206071 I. Ma trận b) Các ma trận ặc biệt 1. Ma trận không: (Tất cả các phần tử ều = 0) Ví dụ: 9 lOMoAR cPSD| 47206071 I. Ma trận b) Ma trận vuông
2. Ma trận vuông: m = n (số hàng = số cột)
Def: Ma trận vuông n hàng, n cột
ược gọi là ma trận vuông cấp n. Ví dụ: 10 lOMoAR cPSD| 47206071 I. Ma trận b) Ma trận ặc biệt
Cho ma trận vuông cấp n A=[aij]. Các phân tử aii gọi là các phần tử chéo.
Đường thẳng qua các phần tử chéo gọi là ường chéo chính. Ví dụ: Đường chéo chính 11 lOMoAR cPSD| 47206071 I. Ma trận
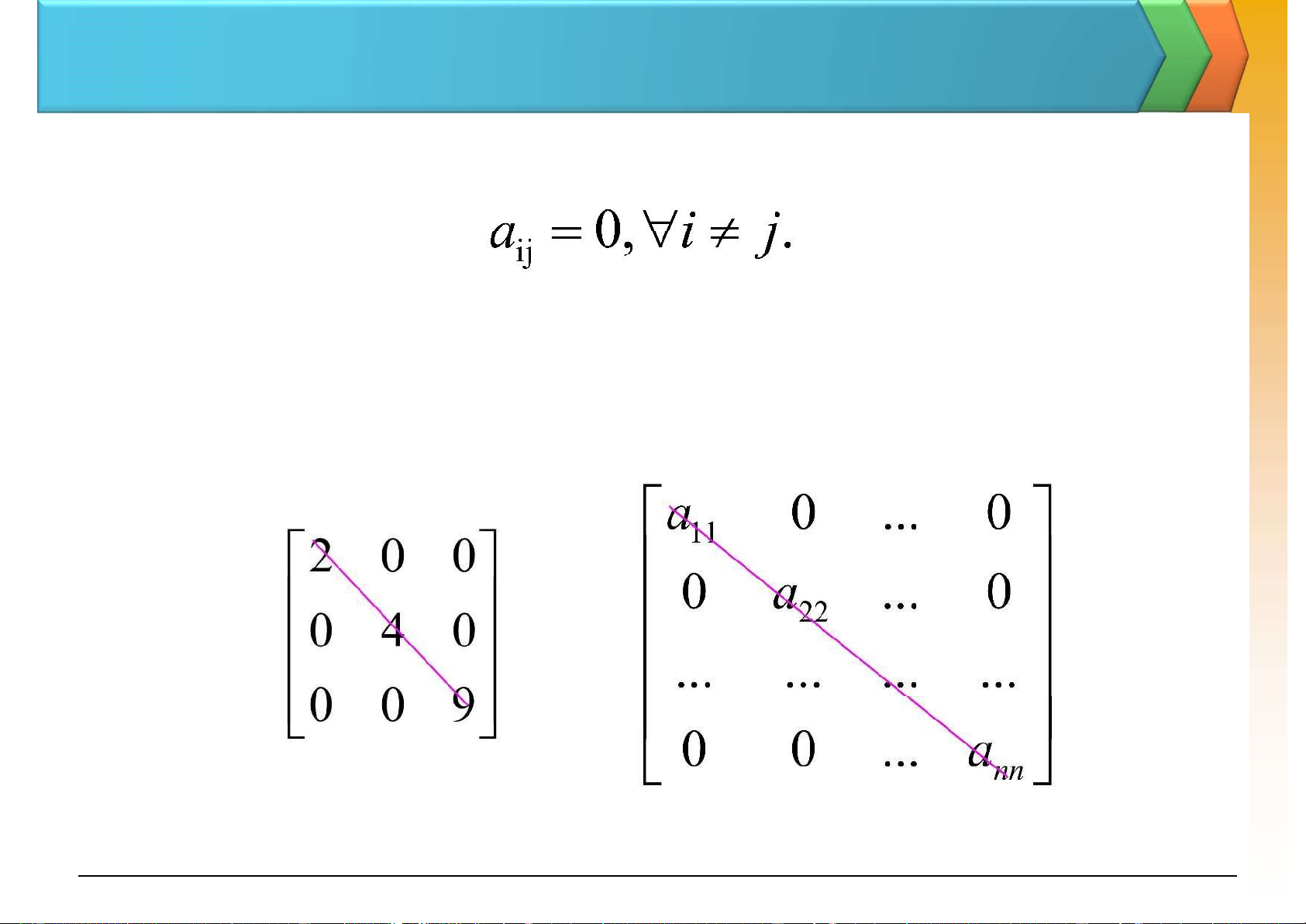
3. Ma trận chéo: là ma trận vuông có:
(các phần tử ngoài ường chéo chính = 0) Ví dụ: 12 lOMoAR cPSD| 47206071 I. Matrices
4. Ma trận n vị: là ma trận chéo có:
Ký hiệu: E, En (hoặc I, In). Ví dụ: 13 lOMoAR cPSD| 47206071 I. Ma trận
5. Ma trận tam giác: là ma trận vuông có: (tam giác trên) (tam giác dưới) Ví dụ: 14 lOMoAR cPSD| 47206071 I. Ma trận (Ma trận tam giác trên) (Ma trận tam giác dưới)
6. Ma trận cột: là ma trận có n=1. 15 lOMoAR cPSD| 47206071 I. Ma trận Ma trận cột có dạng:
7. Ma trận hàng: là ma trận có m=1. Ma trận hàng có dạng:
8. Ma trận chuyển vị: cho ma trận A=[aij]mn, ma trận chuyển vị của ma
trận A ký hiệu: AT và xác ịnh AT=[bij]nm với bij=aji với mọi i,j. 16 lOMoAR cPSD| 47206071 I. Ma trận
(chuyển hàng thành cột, cột thành hàng) Ví dụ: NX: 1.2. Ma trận bằng nhau: 17 lOMoAR cPSD| 47206071 I. Ma trận Ví dụ:
Chú ý: Chỉ xét 2 ma trận bằng nhau nếu chúng cùng cỡ.
1.3. Các phép toán trên ma trận: 18 lOMoAR cPSD| 47206071 I. Ma trận
a. Phép cộng hai ma trận: (cùng cỡ)
(cộng theo từng vị trí tương ứng) Ví dụ: 19 lOMoAR cPSD| 47206071 I. Ma trận Bài tập: 20




