Tài liệu đại số tuyến tính môn toán cao cấp | Trường Đại học Kinh tế Thành phố Hồ Chí Minh

TRUONG DAI HOC KINH TÉ TP. HCM KHOA TOÅN - THÖNG KÉ BO MON TOÅN CO BÄN GIRO TRINH TOÅN CAO cÅp (Dpi sö tuyén tinh) Dånh cho hoc vién chuyén ngånh kinh té Luu hånh nöi bö Ldl NÖI DÄU
Dåy lå giåo trinh s6 tuyén tinh giång trong 30 tiét dånh Cho
Sinh vién 1, hoc Kinh té TP.HCM. Néi dung cuön såch bao göm
cåc kien thi'rc co bån ve Doi so tuyen tinh can thiét cho Sinh vién
cåc khöi ngånh kinh té. Nhung kién thüc nåy cung cåp cho Sinh
vién cåc cong cu tién lei dé trinh biy cåc thöng tin kinh té, giåi cåc
he phuo•ng tinh xuåt hién nhiéu trong nhiéu mö hinh kinh té thuöng gap.
Chüng töi cö gäng sä? xép cåc kien thüc trong såch mot cåch he
thöng, moch loc, nhieu vi du minh hog, de Sinh vién dé dång tv hoc.
Qua 30 näm giång doy toån tai Doi hoc Kinh te TP.HCM vu
toi cåc chucmg trinh hop tåc cüa Dqi hoc Kinh té v6i cåc Dai hoc
ntr&c neoåi, chüng töi thiet nghi Sinh vién kinh té khöng nhåt
thiét phåi hiéu sau vé cåc chirng minh chät ché cho cic dinh If,
cåc két quå toån hoc. Yéu cåu co bån chüng töi nhäm t6i trong
giåo tinh näy lä Sinh vién hiéu rö cåc khåi niém vä st dung thänh
theo cåc cong cu Doi sö tuyen tinh cho cong viéc cüa mét nhå
Kinh té tuong lai. Vi vay tmng quyén såch nåy, chüng töi bö qua
phån tinh båy cåc chirng minh. Quan diém nåy cüng dä thé hién
rö til)ng cåc giåo tinh toån dånh cho cåc khoi ngånh kinh té xuåt
hién nhüng tnrbng dai hoc 16n cüa nu&c ngoåi tmng nhüng näm
gån dåy. Nhüng Sinh vién däc biét thfch thü v6i cic chtng minh
toån hoc chät ché co thé tim doc cåc såch tham khåo.
Thém nüa, trong såch nåy chüng töi co gäng cung cåp nhiéu tng
dung kinh té dé Sinh vién thåy lei ich cüa man Dai sö tuyén tinh döi v6i
cöng viéc tucng lai cüa minh. D6 lå ky thuat st? dung giån dö Venn cho
cåc diéu tra Iciy sö liéu, cåch tinh chi so giå I-nspeyres và chi sb gid
Paasche, nhò phép nhân ma trôn; tinh giü cân bing trong mô hình trao dbi Chuan-g MQnh toån hoc tüp
Leontief, tìm It«mg nguyên liêu dâu vào và scin Itcçmg dàu ra trong mô
hình Input — Output Leontief tbng quüt, nhè kS' thuat tìm ma trin dào, y nghïa câc phàn tt trong
ma trin nghich dào (I — .4)-1 • tlm gid và Ittçmg cân bing trong mô
hình can bàng thi truòng, nhò k}' thuât giài hê phurcmg trinh .
Cuoi cùng, chüng tôi Xin Chân thành câm cm câc ban dông
nghiêp dû ùng quan diem cüa chüng tôi và tao dièu kiên cho ra dèi cùa
giâo tình này. Do trinh dô cé han, quyên Sich này chic Chân không thé
trinh khôi cic sai s6t. Chüng tôi rât mong nhàn câc y kiên dông gép dé
câc lân xuat bin sau durw hoàn thièn hcrn. IP.IICM. nûm 2010 TS . Nguyén vàn N hân 1: då vå hep 1 CHUONG 1 MÉN H DE -roÅN HOC vÅ TÄP HOP {1. MENH DÉ TOÅN HOC. 1.1 Dinh nghia.
Möt menh di toån hec lä möt phåt bieu chi låy möt trong hai giå
tri düng hoäc sai. Tfnh düng sai cüa menh dé toån hoc goi lä chån
tri (giå tri chån l!) cüa menh Mét menh dé toån hoc dugc k! hiéu lä p, q, r... Vidu :
'Mät tr&i moc hu6ng tåy" lä möt menh de toån hoc. "Cöng
ty A kinh doanh rat hiéu quå" khöng phåi lä möt menh dé toån hoc.
"Sån Pham cüa häng B lit durqc tra chuöng" khöng phåi lä mot menh dé toån hoc. "V6i moi a,b IR ta c6 (a + menh dB toån hoc düng. 1.2 Cåc phép toån.
1.2.1 Ménh dwcrng : Hai menh dö p vå q duqc gqi lä turong
ducyng nhau neu chüng c6 cüng chån tri. KY hiéu: Chuan-g MQnh toån hoc tüp
1.2.2 Giao: Giao cüa hai menh dö p vä q, k' hiéu lä p A q (doc lä p vä
q '' ) lä möt menh dé mä chi düng khi p vä q cüng düng. 2 MQnh dd toån hoc top Chuang I: vå hep Vide : (iii)p — A A A (q r) (p q) r (iv) Néu
q Iå mot menh db düng thi : p q p
1.2.3 1-lop : Hop cüa hai menhdé p vä q, kg hiéu lå p V q (doc lä p hay
q"), lä mot menh db måchi sai khi p, q cing sai. Vide :
(iv) Néu q lå mot menh dé toån hoc sai thi : p V q p Vidu : Tinh chåt : Chuan-g MQnh toån dâ hoc tüp vâ hąp Vide •
1.2.4 Mënh suy din: Cho hai menh dë p, q. Mônh dČ ”nĆu p thi
q” hay ” p suy ta q", ky hięu q", lă de chi sai khi p dăng q sai.
V[du : p : măttrôi moc huóng tây q : tôi lă tÔng thong p q : nĆu
măt trôi moc &huóTłg tây thi tôi lă tông thông (m?nh dČ năy dăng vi p sai)
1.2.5 Phti dinh: Phi dinh cua menh dČp, k} hięu lă —p, lă mÔt
menh đČ có chân tri nguqc vói chân tri cua p. Vidu : Ta có: (v) (i)
ChńS' : Căc tinh ch{t & phân tren có thĆ chimg minh băng căch
dăng bâng chân tri. Vfdąl : Chfrng minh Gidi : P q 4 MQnh dd toån hoc top và Đ s Đ s s Đ s s S Đ s s s S 1,3. Dhu ki lumlg.
Mênh dê "moi , cé tfnh chât p" dtrçr ky hiêu là " V Œ, p"
Phù dinh cùa né là "B Œ, doc là "tòn toi mà Œ không cé 1 tinh chât p".
Vidu : Phù dinh cùa menh dè "V a,b, (a + = + b2" là menh
Mênh dê "tôn tai Œ, cé tinh chât p" kj hiêu "B Œ, p" vàphù dinh cùa né là :
"V Œ, —p" dQC là "moi Œ, không cé tinh chât p"
Vidu: Phù dinh cùa menh dè " BT, < O " là menh dè 52. TSP HOP. 2.1. Tâphçp.
Têp hQP là mot khâi nièm nguyên thùy, không c6 dinh nghïa.
hop ky hiêu là A, B,... Neu là phân tùcùa tap hqp A ta Viêt e A.
lai, ta Viét a; g A. Tàp là tap không cé chira phàn tt nào. Ta cé the
biéu dien mot tap hop A bàng câch nêu tfnh chât dac tnrng cùa
câc phân tt cüa A, h04c liêt kê tât Cà câc phân tir cùa A, hoâc dùng giàn do Venn.
A là tâp hqp tât cà cic Sinh viên khéa 35 cüa tnrèng DH Kinh té TP.HCM.
N là tâp hep tâtcâ cüc sô nguyên clitŒng : N = {1, 2, 3, . . Chuan-g I: MQnh toån dd hoc tüp vå hep
Z là tap hep tâtcâ cüc sô nguyên : Z
Q lå tap hop tåtcå cåcso hÜcu ty :
IR lå top hop tåt cå cåc s; thvc.
C = {a + ib / a,b e R,i2 = —1} lå tép hop tåt cå cåc sö phüc. 2.2 Cåc phép toån. 2.2.1 Giao Tac6: (i) A nø=ø
Vide : A lä tap nhüng Sinh vién biét tiéng Anh
B lh tap nhü-ng Sinh vién biét tiéng Phåp
A n B lä tap nhüng Sinh vién biét tiéng Anh vi tiéng Phåp : AuB 2.2.2 v x eB} 6 MQnh dd toån hoc top (iii)A u B -B u A
Vidv : A lå tap hop nhüng déc giå cüa båo Tubi tré 7 Ménh dd toån hoc top hep Chuang 1: vå
B lå tap hop nhüng déc giå cüa båo Thanh nién.
AuB lå tap hop nhüng déc giå cüa båo Tuöi tré hay båo Thanh nién. Tinh chåt :
2.2.3 Tép con : A goi lå tap con cüa B neu moi phan tücüa A déu
lå phån tücüa B. K! hiéu A C B, doc lå A chia troll} B (hoäc B
chia A). Néu A lå tap con cüa B vå c6 it nhåt mét phan til cüa B
khöng lå phån tü cüa A, ta n6i A lå tap con that sv cüa B, k! hiéu AcB. Vidv: Nc Z gQ cR cC
2.2.4 Täp hep bang nhau: Hai tap hop A, B goi lå bång nhau néu moi
phån cüa A cüng lå phån tücüaB vi nguqr lai. K! hiéu A —B. Vide :
2.2.5 Phån bi : Tüy tinh hu6ng dang xét, ta c6 tap U gom tåt cå
cåc phån tü db cap dén trong tinh huöng d6 goi lå tép vü trv. Cho
A C U . Phån bü cüa A, k! hiéu Ac hay , lå tap hep xåc dinh nhu sau Ta : (i) (AC Y = A (ii) (An BY = AC U BC (iii) (A U BY = AC n BC Vide : 8
Ménh æ toån hvc Vå top hep {c/a;2 U &däy lå R. dâ vâ hąp
U : tâp hop tăt că căc sinh viën khóa 35 cua truÔng ĐH
Kinh të TPHCM. A : tâp hgyp tăt că căc sinh viÔn lóp
15 khóa 35; Khi dó AC lă tâp hqp căc sinh viôn khóa 35,
không phâi sinh viën lóp 15.
Qc : tâp hop nhfrng sÓ vô t}. Ta có T2, T, e G Qc
Chń5 : Tit că căc tinh chat cua tâp hop neu phân tîćn dëu có thë
chtng minh nhô căc tinh chât tuo•ng frng cua menh dÔ.
Vidu : Chfrng minh (A n BY = AC CJ BC Ta có : v C c € An B)
2.2.6 Hiëu : Cho 2 tâp hgp A vă B, hiÔu căa A vă B (ky hiÔu lă A
\ B) lă tâp hgp xăc đinh nhu sau :
2.3 SÓ phhn ti•cia mot tâp hęp hău hgn.
Tâp hqp A ducyc goi lă hău hgn nĆu so phân tt trong A lă mÔt sÓ
nguyën không âm. SÓ phân tir trong A duqc k' hiÔu lă n(A) hoăc card(A) . Vidu : Chuang 1: Mënh toón hoc tâp 9
N, Z, Q, IR, C : không phâi lă tâp hău hąn.
Cho A, B, C lă căc tâp hop hiru hąn. Ta có : Chziang I: c Chif •
.NéuAnB=ø thi n(A + n(B) NéuAnB ø, ø, CnB= ø thi Vidv : a.
Ngtr&i ta phåt ra 1000 phiéu thäm dö viéc mua båo ngåy
TP.HCM. Ket quå nhän dtrqc : 800 ngu&i mua båo Tuöi tré, 500
ngu&i mua båo Tuoi tlé Vå båo Ihanh nién, vä moi ngu&i déu mua
båo Tuöi tlé hoäc Ihanh nién. Höi c6 bao nhiéu ngu&i chi mua båo
Tuöi tlé, bao nhiéu ngu&i chi mua båo Ihanh nién? Giåi :
GQi A Iå tap hep nhüng ngu&i mua båo Tubi tré.
B Iå tap hop nhüng ngu&i mua bäo Thanh nién. Düng giån do Venn ta c6 : 10
Ménh æ toån hvc Vå top hep
Väy, so nguöi Chi mua båo Tuöi tré Iå 300 sö
ngu&i Chi mua båo Ihanh nién Iå 200
Ta cüng c6 kétquå tlén bång cåch düng cöng sö phån tir nhusau . Chtmng 1: Mênh toén tap 11 dé hQC và hqp - b.
Trong mot 16p hoc ò tnròng DH Kinh té TP.HCM c6 200
sinh viên. Trong dé c6 150 sinh viên biet tiêng Anh, 70 sinh viên
biet tiêng Phâp, và tht Cà sinh viên biêt tiêng Anh hoâc tiêng Phâp.
Hòi c6 bao nhiêu sinh viên biêt Cà tiêng Anh làn tiêng Phâp, bao
nhiêu sinh viên chi biet tiêng Anh, bao nhiêu sinh viên chi biêt tiêng Phâp ? Giài :
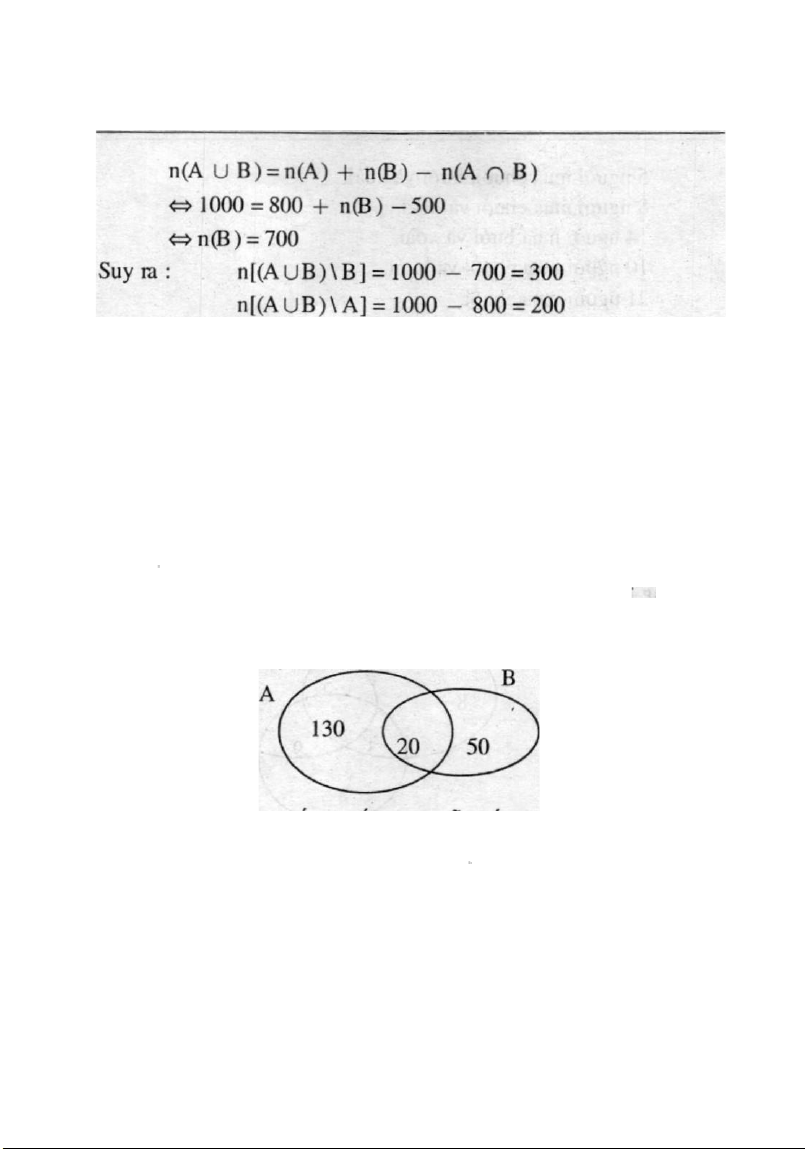
Goi A là tap hop nhùng sinh viên biét tiéng Anh.
Goi B là tap hqp nhüng sinh viên biét tiéng Phâp. Dùng giàn do Venn, ta c6 :
Vây, sosinh viên biêtcà tiêng Anh làn tiéng Phâp là 20
so sinh viên chi biet tiéng Anh là 130 sé sinh viên chi
biét tiéng Phâp là 50 Cich khâc : 12 æ toån hoc Vå top hep Suy ta : c.
Ngtr&i ta thàm dò khâch hàng tai mêtsiêu thi. Kêt quà nhusau : Chztdng 1: MQ nh
5 ngu&i mua chuoi, bu&i vä xoåi, 8 ngubi mua chuoi Vå xoåi,
14 ngtr&i mua bu&i Vå
xoåi, 10 ngu&i mua chuoi vä buöi, 21 ngu&i mua chuoi, 21 ngu&i mua burbi, 21 ngtrbi mua xoåi.
Höi c6 bao nhiéu khåch häng mua ft nhåt I tmng 3 looi trii cåy
n6i tlén, bao nhiéu khåch hing chi mua 1 trong 3 logi tiii cåy nöi
tién, bao nhiéu ngtr&i chi mua chuöi, bao nhiéu ngtrbi chi mua
bu&i, bao nhiéu ngubi chi mua xoåi ? Giåi :
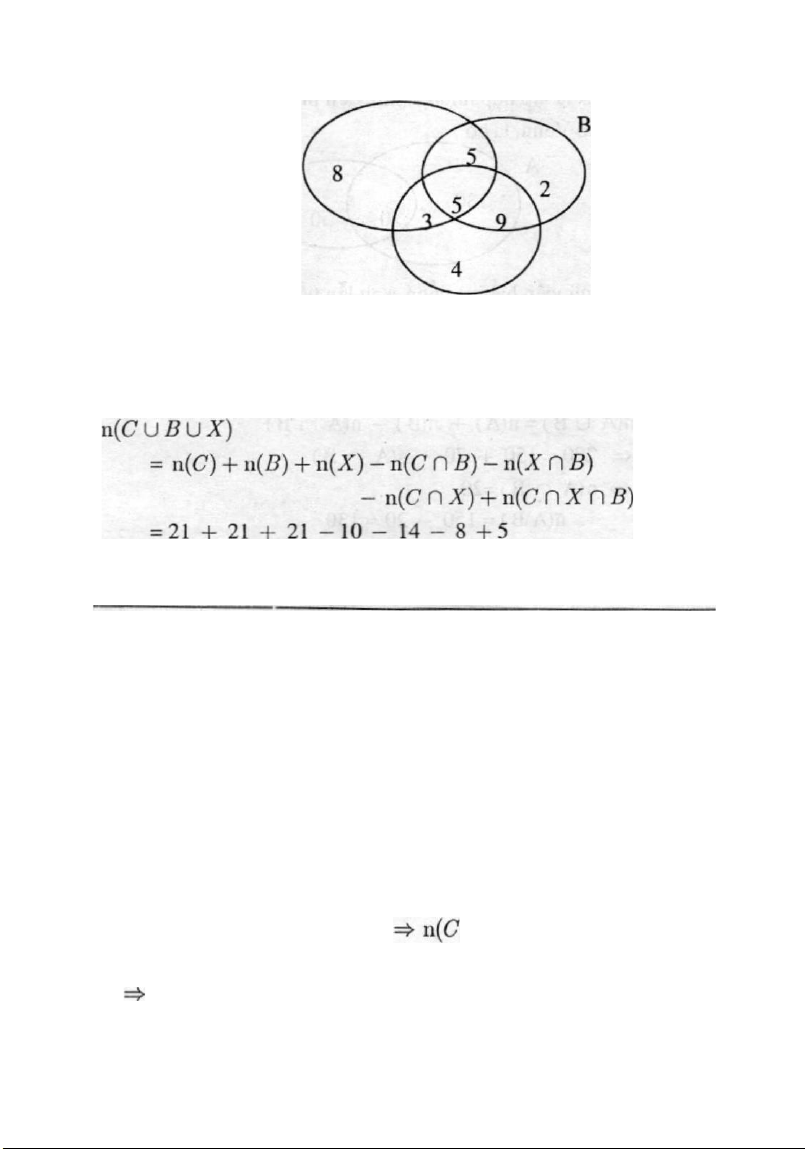
GQi C, B, X Iån lirot Iå tap hvp khåch hing mua chu6i, bur&i, xoåi. Düng gian dö Venn, ta c6 :
ChzWng 1: Mönh toån hoc Vå töp hep 13 c x
Suy ra dåps6 Iän luvt Iå : 36, 14, 8, 2, 4 Cåch khåc, ta c6 : + ¯ = 36 GQi
C' Iå tap hvp khåch hång chi mua chuåi.
B' Iå tap hgp khåch hing chi mua bu&i.
X' Iå tap hop khåch häng chi mua xoäi.
CB Iå täp hq•p khåch häng mua düng hai loqi chu6i Vå bu&i
BX lä täp hop khåch hång mua düng hai loqi buOi Vå xoåi.
XC Iå tap hqp khåch hing mua düng hai loqi xoäi Vå
chuoi. CBX Iå tap hgp khåch hing mua Cå 3 loqi. Taco : (C n B) = (CB) IJ (CBX) n B) = n(CB) + n(CBX) - nl(CB) n (CBX)I 10 n(CB) +5-0— n(CB) = 5 14 æ toån hoc Vå top hep
Tuong tv, ta c6 : n(BX) 9 , n(CX) = 3
C C' U (CB) U (CX) U (CDX) n(C) = n(C') + n(CB) + n(CX) + n(CBX) 21 = n(C') +5+ n(C') = 8
(Luu C', CB, CX, CBX röi nhau nén cåc phån giao c6 sö phån tii bång 0) Ttrong tv :
n(B') = 2 , n(Xt) = 4 Vöy sö
khåch hång chi mua möt loqi lä : n(A' U B' U C') = 14