Tài liệu Toán 9 chủ đề đồ thị của hàm số y = ax + b (a khác 0)

Tài liệu gồm 23 trang, bao gồm kiến thức cần nhớ, các dạng toán và bài tập chủ đề đồ thị của hàm số y = ax + b (a khác 0) trong chương trình môn Toán 9, có đáp án và lời giải chi tiết. Mời bạn đọc đón xem.

29 15 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 2: Hàm số bậc nhất

Môn: Toán 9

Thông tin:

23 trang 6 tháng trước

Tác giả:

Profile Hà Việt Anh
1
ÔN TẬP ĐỒ THỊ HÀM SỐ
( )
0y ax b a=+≠
A. Tóm tắt lý thuyết
1. Đồ thị của hàm số bậc nhất
Hàm số bậc nhất
( )
0y ax b a=+≠
có đồ thị là một đường thẳng, kí hiệu:
(
)
:d y ax b
= +
Trong đó:
a
là hệ số góc của đường thẳng
b
gọi là tung độ gốc của đường thẳng
- Nếu
0b =
thì đường thẳng
y ax=
đi qua gốc tọa độ
- Nếu
0b ≠
thì đường thẳng
y ax b= +
+) Cắt trung tung
tại điểm
( )
0;b
+) Cắt trục hoành
tại điểm
;0
b
a
−



- Đường thẳng
y ax b= +
song song với đường thẳng
y ax=
2. Cách vẽ đồ thị hàm số bậc nhất
(
)
0y ax b a=+≠
Xét đường thẳng
( ) ( )
:0
d y ax b a=+≠
- Nếu
0b =
ta có
y ax=
đi qua gốc tọa độ
( )
0; 0O
và đi qua điểm
( )
1;Aa
- Nếu
0b ≠
ta làm như sau
+) Cách 1: Cho
1
1
x y ab
x y ab
=⇒=+
=−⇒ =−+
+) Cách 2: Cho
0
0
x yb
b
yx
a
=⇒=
−
=⇒=
3. Chú ý:
- Trục hoành là đường thẳng:
0y =
- Trục tung là đường thẳng:
0x =
B. Bài tập và các dạng toán
Dạng 1: Vẽ đồ thị hàm số bậc nhất
Cách giải: Có hai cách cơ bản
Xét đường thẳng
( )
( )
:0
d y ax b a=+≠
2
- Nếu
0b =
ta có
( )
:
d y ax=
đi qua gốc tọa độ
(
)
0; 0O
và đi qua điểm
( )
1;Aa
- Nếu
0b ≠
thì ta làm như sau:
+) Cách 1: Cho
1
1
x y ab
x y ab
=⇒=+
=−⇒ =−+
+) Cách 2: Cho
0
0
x yb
b
yx
a
=⇒=
−
=⇒=
Bài 1: Cho ba đường thẳng
1; 1; 1yxyxy=−+=+=−
a) Vẽ ba đường thẳng trên cùng một hệ trục tọa độ
Oxy
b) Gọi giao điểm của đường thẳng
1yx
=−+
và
1yx= +
là
A
, giao điểm của
1y = −
với hai
đường thẳng
1yx=−+
và
1yx= +
theo thứ tự là
B
và
C
. Tìm tọa độ các điểm
,,ABC
c) Tam giác
,,ABC
là tam giác gì? Tính diện tích
ABC
∆
Lời giải
b) Hai đường thẳng
1yx= +
và
1yx
=−+
cắt nhau tại
A
nên tọa độ
A
nghiệm đúng hai
phương trình:
1yx=−+
và
1yx= +
Ta có:
( )
1 1 0 1 0;1xxx yA+=−+⇔ = ⇒ =⇒
Tương tự ta có:
( ) ( )
2; 1 ; 2; 1BC− −−
c) Gọi
H
là giao điểm của
BC
với
,Oy BC Oy⊥
và
HB HC=
Tam giác
ABC
có
AH
vừa là đường cao, đường trung tuyến vậy
ABC∆
cân tại
A
Ta có:
( )
2
11
. .4.2 4
22
ABC
S BC AH cm= = =
Bài 2:
a) Vẽ trên cùng một hệ trục tọa độ
Oxy
đồ thị các hàm số sau:
( ) ( )
12
: 4; : 2d yx d y x= + =−+
b) Tìm tọa độ giao điểm
của
( )
1
d
và
( )
2
d
c) Gọi giao điểm của
( )
1
d
với
,Ox Oy
theo thứ tự là
A
và
B
. Gọi giao điểm của
( )
2
d
với
Ox
là
C
. Tính diện tích tam giác
BMC
Lời giải
3
b) Xét phương trình hoành độ giao điểm của
( )
1
d
và
( )
2
d
:
( )
4 2 2 2 1 3 1; 3xxx xyM+=−+⇔ =−⇔=−⇒=⇒ −
c) Ta có:
11
.6.4 .6.3 3
22
BMC ABC AMC
S SS
=−= − =
(đvdt)
Bài 3:
a) Vẽ trên cùng một hệ trục tọa độ
Oxy
đồ thị các hàm số sau:
( ) ( )
12
1
: 2; : 1
2
d yx d y x=+ =−+
b) Gọi
A
là giao điểm của
1
d
và
2
d
. Tìm tọa độ điểm
A
c) Gọi
( )
3
d
là đường thẳng đi qua
(
)
0; 0, 25K
song song với trục hoành,
( )
3
d
cắt
( )
1
d
và
(
)
2
d
lần lượt tại
B
và
C
. Tìm tọa độ các điểm
B
và
C
d) Tính
ABC
S
Lời giải
b) Xét phương trình hoành độ giao điểm của
1
d
và
2
d
:
1 3 2 4 24
21 1 ;
2 2 3 3 33
x x x x yA
−−

+ =− +⇔ =−⇔ = ⇒ = ⇒


c) Xét phương trình hoành độ giao điểm của
1
d
và
3
d
:
5 1 15
2;
2 2 22
x xB

+= ⇔= ⇒


Xét phương trình hoành độ giao điểm của
2
d
và
3
d
:
15 5
1 3 3;
22 2
x xC
−

+= ⇔ =−⇒ −


d) Chiều cao
( ) ( )
( )
2
5 4 7 1 7 1 7 49
;3 ; .
2 3 6 2 2 2 6 24
ABC
AH cm BC cm S cm=−= =+= = =
4
Dạng 2: Tìm tọa độ giao điểm của hai đường thẳng
Cách giải: Cho hai đường thẳng
:d y ax b= +
và
': ' 'd y ax b= +
. Để tìm tọa độ giao điểm
của
d
và
'd
, ta làm như sau:
Cách 1: Dùng phương pháp đồ thị (thường sử dụng trong trường hợp
d
và
'd
cắt nhau tại
điểm có tọa độ nguyên)
- Vẽ
d
và
'd
trên cùng một hệ trục tọa độ
- Xác định tọa độ giao điểm trên hình vẽ
- Chứng tỏ tọa độ giao điểm đó cùng thuộc
d
và
'd
Cách 2: Dùng phương pháp đại số
- Xét phương trình hoành độ giao điểm của
d
và
'd
:
''axb axb+= +
- Từ phương trình hoành độ giao điểm, tìm được
x
và thay vào phương trình của
d
(hoặc
'd
)
để tìm
y
- Kết luận tọa độ giao điểm của
d
và
'd
Bài 1:
Cho hai đường thẳng
: 21dy x= +
và
': 3dyx= +
. Bằng phương pháp đồ thị, hãy tìm tọa độ
giao điểm của
d
và
'
d
Lời giải
Từ đồ thị dự đoán được
d
và
'd
tại
( )
2;5I
Thay tọa độ
I
vào
d
và
'
d
thấy thảo mãn. Vậy
I
là tọa độ giao điểm của
d
và
'd
Bài 2:
Tìm tọa độ giao điểm của các đường thẳng
1
:3
2
dy x= −
và
': 2 2dy x=−+
bằng cách vẽ đồ thị
Lời giải
Ta tìm được
( )
2; 2A
−
là tọa độ giao điểm của
d
và
'd
5
Bài 3:
Cho các đường thẳng
: 9 42
dy x= −
và
': 3 2 2 2dyx=−−
không vẽ đồ thị, tìm tọa độ giao
điểm của
d
và
'd
Lời giải
Xét phương trình hoành độ giao điểm của
d
và
'd
:
( ) ( )
221 21 2 2x xx− = − −⇔=−
Thay
2x = −
vào
d
hoặc
'd
tìm được:
( )
42 ' 2;42y dd=−+ ⇒ ∩ =− −+
Bài 4:
Không vẽ đồ thị, hãy tìm tọa độ giao điểm của các đường thẳng
3
:1
4
dy x= +
và
': 2dy x=−+
Lời giải
Xét phương trình hoành độ giao điểm của
d
và
'd
ta được:
3 7 4 10
12 1
4 4 77
xx xx y+=−+ ⇔ =⇔ = ⇒ =
Vậy
4 10
;
77



là tọa độ giao điểm của
d
và
'd
6
Dạng 3: Xét tính đồng quy của ba đường thẳng
Cách giải:
Chú ý: Ba đường thẳng đồng quy là ba đường thẳng phân biệt và cùng đi qua 1 điểm
- Để xét tính đồng quy của ba đường thẳng (phân biệt) cho trước, ta làm như sau:
+) Tìm tọa độ giao điểm của 2 trong 3 đường thẳng đã cho
+) Kiểm tra xem nếu giao điểm vừa tìm được thuộc đường thẳng còn lại thì kết luận ba đường
thẳng đó đồng quy.
Bài 1:
Cho ba đường thẳng
1 23
: 4 3, : 3 1, : 3dy x dy x dyx=− =−=+
. Chứng minh ba đường thẳng trên
đồng quy
Lời giải
Gọi giao điểm của hai đường thẳng
1
d
và
2
d
là
I
Tìm được
( )
2;5I
Thay tạo độ
( )
2;5
I
vào
3
d
thấy thỏa mãn
Vậy ba đường thẳng
123
,,ddd
đồng quy
Bài 2:
Ba đường thẳng
1 23
:3 7 0, : 2 3, :3 2 7 0d xy d y x d x y−−= =− + − −=
có đồng quy hay không
Lời giải
Gọi giao điểm của hai đường thẳng
1
d
và
2
d
là
I
Tìm được
( )
2; 1I −
Thay tạo độ
( )
2;5I
vào
3
d
thấy không thỏa mãn
Vậy ba đường thẳng
123
,,ddd
không đồng quy
Bài 3:
Cho ba đường thẳng
12 3
: 4, : 2 3, : 1d y x d y x d y mx m=− = + = ++
. Tìm m để ba đường thẳng trên
đồng quy
Lời giải
7
Gọi giao điểm của hai đường thẳng
1
d
và
2
d
là
I
Tìm được
( )
7; 11I −−
Thay tạo độ
( )
2;5I
vào
3
d
ta tìm được
32
2 : 23
m dy x d
=⇒ = +≡
Vậy không có giá trị nào của m thỏa mãn bài toán.
Bài 4:
Cho ba đường thẳng
12 3
: 2, : 2 3, :dyx d y x dy x=−=−=−
a) Chứng minh rằng ba đường thẳng trên đồng quy
b) Tìm m sao cho 4 đường thẳng
123
,,ddd
và
:1d y mx= +
đồng quy
Lời giải
a) Gọi
I
là giao điểm của
1
d
và
2
d
suy ra tọa độ
I
là nghiệm của hệ phương trình:
21
(1; 1)
23 1
yx x
I
yx y
=−=

⇔ ⇒−

=+=−

Ta đi chứng minh
I
thuộc vào
3
d
Thật vậy thay tọa độ
( )
1; 1I −
vào
(
)
3
:dy x= −
ta được
11−=−
(đúng)
b) Để 4 đường thẳng đồng quy thì
( )
1; 1I −
phải thuộc vào
( )
1 .1 1 2d mm
⇔− = + ⇔ =−
Bài 5:
Tìm
m
để ba đường thẳng sau đồng quy
a)
22
1 23
: ( 1) ( 5)( 1); : 1; : 3dy m x m m d yx dy x= − + − ≠± = + =− +
b)
12 3
:38;: 23;:3 21dyxdy xdymxm= − =−− = + +
Lời giải
a) Ta có:
2
d
cắt
3
d
tại
( )
1; 2M
Để ba đường thẳng đồng quy thì
( )
1; 2M
thuộc
( )
1
2dm⇒=±
Thử lại với
2m = ±
thì ta được
1
d
không trùng với
23
,dd
Vậy
2m = ±
b) Ta tìm được:
6
5
m
−
=
8
Dạng 4: Tính khoảng cách từ gốc tọa độ O đến một đường thẳng không đi qua O
Cách giải: Để tính khoảng cách từ O đến đường thẳng d (không đi qua O) ta làm như sau:
Bước 1: Tìm
,AB
lần lượt là giao điểm của
d
với
và
Oy
Bước 2: Gọi
H
là hình chiếu vuông góc của
O
trên
d
. Khi đó:
222
1 11
OH OA OB
= +
Bài 1:
Cho hàm số
y ax b
= +
a) Xác định
a
và
b
biết rằng đồ thị hàm số trên đi qua điểm
( )
2;3M
b) Vẽ đồ thị hàm số vừa tìm được ở câu a
c) Tính khoảng cách từ gốc tọa độ đến đường thẳng tìm được ở câu a
Lời giải
a) Ta có
( )
2;3M
thuộc đồ thị hàm số
3 69a yx⇒=⇒= −
b) Gọi
H
là hình chiếu của
O
lên đường thẳng
Xét tam giác
OAB
vuông tại
O
Ta có:
222
22
1 11 . 9
37
OA OB
OH
OH OA OB
OA OB
= + ⇔= =
+
Bài 2:
Trong hệ trục tọa độ
Oxy
cho đường thẳng
( )
: 22dy x= −
và điểm
( )
3; 2I −
. Hãy tính khoảng
cách
a) Từ
O
đến
d
b) Từ
I
đến
d
Lời giải
a) Gọi
,AB
lần lượt là giao điểm của
d
với
và
Ta có:
( ) ( )
1; 0 ; 0; 2 1; 2A B OA OB−⇒ = =
Gọi
H
là hình chiếu vuông góc của
O
trên
( )
d OH
⇒
là khoảng cách từ
O
đến
( )
d
Ta có:
222
1 11
5OH
OH OA OB
= + ⇒=
b) Qua
I
kẻ đường thẳng vuông góc với
,Ox Oy
cắt
( )
d
lần lượt tại
( )
3; 4C
và
( )
0; 2B −
Gọi
K
là hình chiếu vuông góc của
I
trên
( )
d IK⇒
là khoảng cách từ
I
đến
( )
d
9
Sử dụng công thức:
2 22
1 1 1 65
5
IK
IK IC IB
= + ⇒=
Bài 3:
Cho đường thẳng
: 21yx
∆ =−+
và
( )
1; 3M =−−
trên hệ trục tọa độ
Oxy
. Hãy tính khoảng cách
a) Từ
O
đến
∆
b) Từ
M
đến
∆
Lời giải
a) Ta tính được khoảng cách từ
O
đến
∆
là:
5
5
b) Ta tính được khoảng cách từ
M
đến
∆
là:
65
5
10
Dạng 5: Tìm điểm cố định mà hàm số luôn đi qua phụ thuộc vào tham số m
Cách giải:
1. Khái niệm điểm cố định: Điểm
( )
00
;
Mx y
là điểm cố định của
(
)
:d y ax b= +
(
,ab
phụ thuộc vào tham số
,0ma≠
) khi và chỉ khi điểm
M
luôn thuộc
( )
d
với mọi điều kiện
của tham số
m
Hoặc tương đương với điều kiện:
00
y ax b= +
với mội điều kiện của tham số
2. Cách tìm điểm cố định
Gọi
( )
00
;Ix y
là điểm cố định của
( )
00
,d y ax b m⇒ = +∀
- Biến đổi
00
y ax b
= +
về dạng
( ) ( )
00 00
; ;0AxymBxy+=
hoặc
2
0 0 00 00
(; ) (; ) (; ) 0Axym BxymCxy+ +=
+) Ta có:
00
0 0 00
00
(; ) 0
(; ) (; ) 0
(; ) 0
Ax y
AxymBxy m
Bx y
=
+ =∀⇔
=
+)Ta có:
00
2
0 0 00 00 00
00
(; ) 0
(; ) (; ) (; ) 0, (; ) 0
(; ) 0
Ax y
Axym BxymCxy m Bxy
Cx y
=
+ + = ∀⇔ =
=
Từ đó tìm được
00
;xy
rồi kết luận
3. Chú ý: Cách tính khoảng cách từ
( )
11
;Ax y
đến
( )
22
;Bx y
trên hệ trục tọa độ
Oxy
22
12 12
( )( )AB y y x x= − +−
Bài 1:
a) Chứng minh điểm
1
;3
2
I

−


là điểm cố định mà đường thẳng
( )
7
: (1 2 )
2
d y mx m=− +−
luôn
đi qua với mọi giá trị của tham số
m
b) Cho đường thẳng
( )
( )
: 21 2d y m xm= + +−
với
m
là tham số. Tìm điểm cố định mà
( )
d
luôn
đi qua với mọi giá trị của
m
.
Lời giải
a) Thay
1
;3
2
xy= = −
vào
(
)
d
thấy luôn thỏa mãn với mọi m, ta được (đpcm)
b) Gọi
( )
00
;Ix y
là điểm cố định của
( )
d
11
0
0 0 0 00
00
2 10
15
(2 1) 2 (2 1) ( 2) 0 ;
20
22
x
y m xm m x mxy m
xy
+=
−−

⇒ = + + −∀⇒ + + − − =∀⇒ ⇒

− −=

Là điểm cố định mà đường thẳng luôn đi qua.
Bài 2:
a) Cho đường thẳng
( )
: 21 31dy m x m
= + −+
với tham số m. Điểm
31
;
22
K
−



có là điểm mà
( )
d
luôn đi qua với mọi giá trị của
m
hay không?
b) Chứng minh đường thẳng
( )
1
: 2 31dy m x m=− ++
luôn đi qua điểm cố định với mọi giá trị
của tham số m
Lời giải
a) Thay tọa độ điểm
31
;
22
K
−



vào
( )
d
không thỏa mãn. Vậy
K
không là điểm cố định của
(
)
d
b) Tìm được
( )
3; 7−
là điểm cố định đường thẳng luôn đi qua.
Bài 3:
Cho hai đường thẳng
( ) ( )
1
:4 5d y mx m= −+
với
0m ≠
và
( )
( )
22
2
: 31 4d y m xm= + +−
a) Chứng minh rằng
( )
1
d
đi qua điểm
A
cố định,
( )
2
d
đi qua điểm
B
cố định
b) Tính khoảng cách
AB
c) Tìm
m
để
1
d
song song với
2
d
Lời giải
a) Giả sử
1
d
đi qua điểm
( )
00
;Ax y
cố định
( )
00
4 5,y mx m m⇒= −+∀
0
00
0
4 10
1
(4 1) 5 ; 5
50
4
x
x my A
y
−=

⇒ − = +⇒ ⇒ −

+=

Tương tự:
1 13
;
33
B
−−



b) Ta có:
22
1 3 13 113
( ) (5 )
4 4 3 12
AB = + +−+ =
12
c)
2
12
2
' 3 14
1
/ / 1;
'
3
4 ( 5)
aa m m
dd m
bb
mm
= +=

⇔ ⇔ ⇔∈

≠
− ≠− +

Bài 4:
Cho ba đường thẳng
( )
( )
( )
( )
22
1 23
: 1 3; : 5; : 1d y m xm d y x d y x= − − + = + =−+
a) Chứng minh rằng với mọi giá trị của
m
thì
( )
1
d
luôn đi qua 1 điểm cố định
b) Với giá trị nào của
m
thì
( ) ( )
12
//dd
c) Chứng minh rằng nếu
( ) ( )
13
//dd
thì
( )
(
)
12
dd⊥
d) Với giá trị nào của
m
thì ba đường thẳng
( ) ( ) ( )
123
,,
ddd
đồng quy
Lời giải
a) Tìm được
(
)
1
d
luôn đi qua điểm
( )
1; 2I
b)
( ) ( )
12
// 2dd m⇔=±
c) Nếu
( )
( )
13
//dd
thì
( )
( )
1
12
2
:3
0
:5
dy x
m dd
d yx
=−+
=⇒ ⇒⊥
= +
d)
( )
2
d
và
(
)
3
d
cắt nhau tại
(
)
2;3K
−
Để ba đường thẳng đồng quy khi
(
)
1
6
3
Id m
±
∈ ⇒=
13
Dạng 6: Tìm tham số m sao cho khoảng cách từ gốc tọa độ đến đường thẳng cho trước
là lớn nhất
Cách giải
Cho đường thẳng
( )
:d y ax b= +
phụ thuộc tham số
m
. Muốn tìm
m
để khoảng cách từ
O
đến
d
là lớn nhất, ta có thể làm theo một trong hai cách sau
Cách 1: Phương pháp hình học
- Gọi
,AB
lần lượt là giao điểm của
d
với
Ox
và
Oy
;
H
là hình chiếu vuông góc của
O
trên
d
- Ta có khoảng cách từ
O
đến
d
là
OH
và được tính bởi công thức sau:
222
1 11
OH OB OC
= +
- Từ đó tìm điều kiện của
m
để
OH
đạt giá trị lớn nhất
Cách 2: Dùng phương pháp điểm cố định
- Tìm được
I
là điểm cố định mà
d
luôn di qua
- Gọi
H
là hình chiếu vuông góc của
O
trên
d OH OI⇒≤
= hằng số
d
angsoOH OI h⇒ ≤=
- Ta có:
max
OH OI d= ⇔
là đường thẳng qua
I
và vuông
góc với
OI
. Từ đó tìm được tham số
m
Bài 1:
Cho đường thẳng
(
)
: 21
d y mx m=−−
với
m
là tham số. Tìm
m
sao cho khoảng cách từ
O
đến
( )
d
đạt giá trị
a) Lớn nhất b) Nhỏ nhất
Lời giải
a. Khoảng cách từ
O
đến
d
nhỏ nhất bằng 0 khi
O
thuộc vào
( )
d
.
Từ đó tìm được
1
2
m
−
=
b) Cách 1: Xét hai trường hợp
Trường hợp 1: Nếu
( )
0 :1m dy= ⇒ =−⇒
khoảng cách từ
O
đến
( )
d
bằng
1
d
I
H
O
14
Trường hợp 2: Nếu
( )
0md≠⇒
cắt hai trục
,Ox Oy
lần lượt tại
21
;0
m
A
m
+



và
( )
0; 2 1Bm
−−
Gọi
H
là hình chiếu vuông góc của
O
lên
(
)
d
Từ
2
2
222 2
1 1 1 ( 2 1)
1
m
OH
OH OA OB m
+
=+⇒=
+
Lại có:
2
2
2
( 2)
5 0 50
1
m
OH OH m
m
−
−=− ≤⇒ ≤ ∀≠
+
Kết hợp các trường hợp 1 và 2, ta được:
ax
52
m
OH m= ⇔=
Cách 2: Gọi
I
là điểm cố định của
d
. Ta tìm được
(
)
2; 1I
−
Với mỗi m, gọi
H
là hình chiếu vuông góc của
O
trên
d
5,OH OI m⇒ ≤= ∀
ax
52
m
OH d OI m
⇒ = ⇔⊥ ⇒=
Bài 2:
Tìm
m
để khoảng cách từ gốc tọa độ
O
đến đường thẳng
( )
: 12y m xm
∆ = + ++
đạt gía trị
a) Nhỏ nhất b) Lớn nhất
Lời giải
a) Khoảng cách từ
O
đến
d
có giá trị nhỏ nhất bằng 0, đạt được khi
Od∈
. Từ đó tìm được
2m
= −
b) Cách 1: Xét hai trường hợp
Trường hợp 1: Với
( )
1 :1 ; 1m y dO
=− ⇒∆ = ⇒ ∆ =
Trường hợp 2: Với
1m ≠− ⇒∆
cắt
∆
lần lượt tại
( )
2
; 0 ; 0; 2
1
m
A Bm
m
+

−+

+

Gọi
H
là hình chiếu vuông góc của
O
lên
( )
;d O OH∆⇒ ∆ =
Từ
(
)
2
2
222 2
2
1 11
21 2 0
22
max
m
OH m OH m
OH OA OB m m
+
= + ⇒ = ≤ ∀ ≠− ⇒ = ⇔ =
++
Bài 3:
Cho đường thẳng
( )
:2d y mx= +
(m là tham số)
a) Tìm điểm cố định
I
mà
d
luôn đi qua với mọi
m
b) Tìm
m
để khoảng cách từ
O
đến
d
là lớn nhất
15
c) Khi
0m ≠
, tìm
m
để khoảng cách từ
O
đến
d
bằng
25
5
Lời giải
a) Tìm được điểm cố định
(
)
0; 2
I
b) Gọi
H
là hình chiếu của
O
trên
d
,
OH
là khoảng cách
từ
O
đến
d
Ta có:
2, " " (0; 2)OH OI dau H I d Oy
≤ = =⇔ ≡ ⇔⊥
tại
( )
0; 2I
( )
d⇔
có dạng
20ym=⇔=
Vậy khoảng cách từ
O
đến
d
lớn nhất bằng
20m⇔=
c) Gọi
K
là giao điểm của
d
với
2
;0Ox K
m
−

⇒


Xét
OIK∆
vuông tại
O
, có:
2
2
2 22
2; 0OI OK
m mm
−−

= = += =


Ta có:
2
2
2 22
1 115 1
42
444
m
mm
OH OK OI
= + ⇔= +⇔ =⇔ =±
Vậy
2m = ±
2
K
I
H
O
16
BÀI TẬP TRẮC NGHIỆM
Câu 1:
Đường thẳng nào dưới đây là đồ thị hàm số
25yx=−+
A)
( )
1
d
B)
( )
2
d
C)
( )
3
d
D)
( )
4
d
Lời giải
Chọn đáp án C
Giải thích:
Đồ thị của hàm số
25yx=−+
là đường thẳng đi
qua hai điểm
( )
0;5A
và
5
;0
2
B



Câu 2:
Đường thẳng
AB
trong hình vẽ dưới đây là đồ thị hàm số nào
A)
3
3
2
yx
−
= +
B)
2
3
3
yx= +
C)
26yx= +
D)
26yx=−−
Lời giải
Chọn đáp án A
Giải thích:
Đường thẳng
AB
là đồ thị của hàm số
( )
*y ax b= +
d
3
-5
2
5
O
d
4
O
5
2
5
d
1
O
1
2
d
2
O
-2
3
B
A
O
2
3
17
Do đường thẳng
AB
đi qua hai điểm
( )
0;3A
và
( )
2; 0B
nên tọa độ của
A
và
B
nghiệm đúng
y ax b= +
Ta có:
3
3 .0
3
0 .2
2
b
ab
ab
a
=
= +
⇔

−
= +
=
Thay
3
,3
2
ab=−=
vào
( )
*
ta được:
3
3
2
yx
−
= +
Câu 3:
Cho hàm số
42yx
=−+
có đồ thị là
( )
d
. Khẳng định nào sau đây sai
A)
(
)
d
cắt trục hoành tại
1
;0
2
A



B)
(
)
d
cắt trục tung tại
( )
0; 2B
C)
(
)
d
song song với đồ thị hàm số
4yx=
D)
( )
d
đi qua điểm
( )
1; 6
M −
Lời giải
Chọn đáp án C
Giải thích: Ta có :
(
)
( )
: 4 2*
dy x=−+
A) Thay
1
2
A
x =
và
0
A
y
=
vào
( )
*
, ta được:
( )
1
0 4. 2
2
Ad=− +⇒∈
hay
( )
d
cắt trục hoành tại
1
;0
2
A



B) Thay
0
B
x =
và
2
B
y =
vào
( )
*
, ta được:
( )
2 4.0 2 Bd=− +⇒ ∈
hay
( )
d
cắt trục tung tại
(
)
0; 2B
C) Ta đã biết đồ thị của hàm số
( )
0; 0y ax b a b=+ ≠≠
là đường thẳng song song với đường
thẳng
y ax=
Do đó đường thẳng
( )
: 42dy x=−+
song song với đường thẳng
4
yx
= −
D) Thay
1; 6
MM
xy=−=
vào
( )
*
ta được:
( ) ( )
6 4. 1 2 Md
=− −+⇒ ∈
hay
( )
d
đi qua
M
18
Câu 4:
Đồ thị là
( )
d
của hàm số
11
25
yx
−
= +
cắt trục hoành tại
E
và cắt trục tung tại
F
. Tọa độ của
,EF
là:
A)
21
; 0 ; 0;
55
EF



B)
21
0; ; ; 0
55
EF



C)
21
;1 ; ;0
55
EF

−−


D)
12
0; ; ; 0
55
EF
−−



Lời giải
Chọn đáp án A
Giải thích:
Điểm
E
thuộc trục hoành nên có tung độ bằng
(
)
00
E
y =
Thay
0
E
y =
vào
11
25
yx
−
= +
, ta được:
11 2 2
0 5 2 0 ;0
25 5 5
EE
x x xE
−

+ = ⇔− + = ⇔ = ⇒


Điểm
F
thuộc trục tung, nên có hoành độ bằng
( )
00
F
x =
Thay
0
F
x =
vào
11
25
yx
−
= +
, ta được:
11 1 1
.0 0;
25 5 5
FF
y yF

=− +⇔ =⇒


Câu 5:
Giá trị nào của
b
dưới đây thì đồ thị
( )
d
của hàm số
2y xb=−+
đi qua điểm
1
;1
3
P



A)
1
2
b =
B)
1
3
b = −
C)
4
5
b
−
=
D)
0
b =
Lời giải
Chọn đáp án B
Giải thích:
Thay
1
;1
3
PP
xy= = −
vào
2y xb=−+
, ta được:
1 21
1 2. 1
3 33
bb−=− + ⇔ =−+ =−
19
Câu 6:
Giá trị nào của
b
dưới đây thì đồ thị
(
)
d
của hàm số
y ax b= +
đi qua hai điểm
( )
0; 5M −
và
( )
1; 4N −
A)
4; 2ab= =
B)
3; 4ab=−=
C)
1; 5
ab= = −
D)
2; 5ab=−=−
Lời giải
Chọn đáp án B
Giải thích:
Tọa độ của
( )
0; 5M −
và
( )
1; 4N
−
nghiệm đúng
y ax b
= +
, từ đó ta có hệ phương trình:
(
) ( )
5 .0 5
; 1; 5
4 .1 1
ab b
ab
ab a
−= + =−

⇔ ⇒=−

−= + =

Câu 7:
Trên mặt phẳng tọa độ
Oxy
, có các bộ ba điểm. Hỏi có một bộ 3 điểm nào không thẳng hàng
A)
( )
( )
1
2;9 , ; 6 , 0;5
2
AB C
−

−


B)
( ) ( )
1
1;7 , ; 6 , 5;0
2
MN P

−−


C)
(
) ( )
1
1; 7 , ; 4 , 1; 3
2
MEF

−


D)
( ) ( )
3
2;9 , 1;3 , ;2
2
A FK

−


Lời giải
Chọn đáp án B
Giải thích: Ta biểu diễn các bộ ba điểm lên hệ trục tọa độ và thấy rằng ba điểm
,,MNP
thẳng
hàng
Câu 8:
Ba đường thẳng
4; 2 5; 3 10yx yx y x=−+ = − =− +
cùng đi qua một điểm (đồng quy). Điểm đó là
điểm nào
A)
( )
3; 1A −−
B)
( )
3;1B
C)
( )
3;1C −
D)
(
)
3; 1D −
Lời giải
Chọn đáp án B
20
Giải thích:
Thay tọa độ điểm
( )
3;1
B
vào cả ba phương trình đường thẳng, ta có:
1 34
1 2.3 5
1 3.3 10
=−+
= −
=−+
(đúng)
Nên
( )
3;1B
thuộc cả ba đường thẳng.
Câu 9:
Cho hai điểm
( ) ( )
2; 2 , 2;1MN−
. Trong các đường thẳng sau đây, đường thẳng nào đi qua
,MN
A)
13
42
yx= +
B)
31
24
x +
C)
13
42
x
−
D)
31
24
x−+
Lời giải
Chọn đáp án A
Giải thích:
Ta có
( )
13
,:
42
MN d y x∈ = +⇒
đường thẳng đi qua hai điểm
( )
( )
2; 2 , 2;1MN
−
là:
13
42
yx= +
21
BÀI TẬP VỀ NHÀ
Bài 1:
Cho hai đường thẳng
1
: 23
dy x= −
và
2
: 37dy x=−+
a) Vẽ
12
,
dd
trên cùng một hệ trục tọa độ
b) Tìm tọa độ giao điểm của
12
,dd
Lời giải
b) Từ hình vẽ ta thấy
(
)
12
2;1
ddI∩=
Thay tọa độ điểm
I
vào
12
,
dd
thấy thỏa mãn
Bài 2:
Cho hai đường thẳng
: 31dy x=−+
và
': 2dy x=−−
. Tìm tọa độ giao điểm của
,'dd
Lời giải
Xét phương trình hoành độ giao điểm của
d
và
3 7 37
' ';
2 2 22
d x y dd I
− − −−

⇒= ⇒= ⇒∩ =


Bài 3:
Các đường thẳng sau đây có đồng quy hay không:
a)
1 23
1
: 3 1; : ; :
2
d y x d y xd y x=+=−=+
b)
1 23
15
: 1 0; : 3 5; : 0
33
dxy d y x dx y+ −= = + − + =
Lời giải
a) Các đường thẳng đồng quy tại điểm
11
;
44
−



b) Các đường thẳng không đồng quy vì
23
dd≡
Bài 4:
Tìm tham số m để ba đường thẳng sau đồng quy
a)
1 23
4
: 1; : 1; : 3
3
d y x d y x d y mx m= + =− = ++
b)
( )
1 23
1
: 1;:2;:221
4
d y x m d y xd y m x=−+ = = − +
22
Lời giải
a) Tìm được
(
)
12
6; 7
ddI
∩ = −−
Thay tọa độ điểm
I
vào
3
2dm⇒=
b) Tìm được
( )
12
1 ;2 2ddI m m
∩= − −
Thay tọa độ điểm
I
vào
13
2
3
1 23
31
:
44
16 32 15 0
51 1
: , : 2, : 3
44 4
m d d y x loai
d mm
m d y x d y xd y x

= ≡ =+⇒

⇒ − +=⇔ ⇒


= =−= =+


Đôi một phân biệt nên thỏa mãn
Vậy điềm kiện là:
5
4
m =
Bài 5:
Cho đường thẳng
: 43dy x=−+
a) Vẽ đồ thị hàm số đã cho
b) Tìm tọa độ giao điểm
,
AB
của
d
với lần lượt hai trục tọa độ
;
Ox Oy
c) Tính koảng cách từ gốc tọa độ đến
d
d) Tính khoảng cách từ điểm
( )
1; 2I −−
đến
d
e) Tính diện tích tam giác
OAB
Lời giải
b) Tìm được:
(
)
3
; 0 ; 0; 3
4
AB



c) Tính được:
( )
3 3 17
;3 ;
4 17
OA OB d O d OH==⇒==
d) Qua
I
, kẻ các đường thẳng lần lượt song song với
;Ox Oy
cắt
d
lần lượt tại
( )
5
; 2 ; 1; 7
4
MN

−−


Tính được:
( )
9 9 17
;9 ;
4 17
IM IN d I d==⇒=
e) Tìm được:
19
.
28
AOB
S OA OB
= =
23
Bài 6:
Cho đường thẳng
( )
:2
dy m x m=++
(với m là tham số)
a) Tìm điểm cố định mà d luôn đi qua với mọi m
b) Tìm m để d cắt
,Ox Oy
tại
A
và
B
sao cho diện tích tam giác
OAB
bằng
1
2
Lời giải
a) Tìm được
( )
1; 2I −−
là điểm cố định của d
b) Giao điểm của
d
với hai trục
,
Ox Oy
lần lượt là:
( )
2
1
; 0 ; 0;
2 22
AOB
mm
A Bm S
mm
−

⇒=

++

Từ
1
2; 1
2
S mm=⇒= =−
Bài 7:
Cho đường thẳng
(
)
:2 5 1 0d m xy m
− + −+ =
. Tìm m sao cho khoảng cách từ O đến d là:
a) Nhỏ nhất b) Lớn nhất
Lời giải
a) Tìm được
1m
=
b)
10 8
23
max
OH m= ⇔=
| 1/23
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

ÔN TẬP ĐỒ THỊ HÀM SỐ y = ax +b(a ≠ 0) A. Tóm tắt lý thuyết
1. Đồ thị của hàm số bậc nhất
Hàm số bậc nhất y = ax + b(a ≠ 0) có đồ thị là một đường thẳng, kí hiệu: (d ): y = ax + b
Trong đó: a là hệ số góc của đường thẳng
b gọi là tung độ gốc của đường thẳng
- Nếu b = 0 thì đường thẳng y = ax đi qua gốc tọa độ
- Nếu b ≠ 0 thì đường thẳng y = ax + b
+) Cắt trung tung Oy tại điểm (0;b) +) Cắt trục hoành  −
Ox tại điểm b ;0  a   
- Đường thẳng y = ax + b song song với đường thẳng y = ax
2. Cách vẽ đồ thị hàm số bậc nhất y = ax +b(a ≠ 0)
Xét đường thẳng (d ): y = ax + b(a ≠ 0)
- Nếu b = 0 ta có y = ax đi qua gốc tọa độ O(0;0) và đi qua điểm A(1;a)
- Nếu b ≠ 0 ta làm như sau
+) Cách 1: Cho x =1⇒ y = a + b  x = 1
− ⇒ y = −a + b
x = 0 ⇒ y = b +) Cách 2: Cho  − = 0 b y ⇒ x =  a 3. Chú ý:
- Trục hoành là đường thẳng: y = 0
- Trục tung là đường thẳng: x = 0
B. Bài tập và các dạng toán
Dạng 1: Vẽ đồ thị hàm số bậc nhất
Cách giải: Có hai cách cơ bản
Xét đường thẳng (d ): y = ax + b(a ≠ 0) 1
- Nếu b = 0 ta có (d ): y = ax đi qua gốc tọa độ O(0;0) và đi qua điểm A(1;a)
- Nếu b ≠ 0 thì ta làm như sau:
+) Cách 1: Cho x =1⇒ y = a + b  x = 1
− ⇒ y = −a + b
x = 0 ⇒ y = b +) Cách 2: Cho  − = 0 b y ⇒ x =  a
Bài 1: Cho ba đường thẳng y = −x +1; y = x +1; y = 1 −
a) Vẽ ba đường thẳng trên cùng một hệ trục tọa độ Oxy
b) Gọi giao điểm của đường thẳng y = −x +1 và y = x +1 là A , giao điểm của y = 1 − với hai
đường thẳng y = −x +1 và y = x +1 theo thứ tự là B và C . Tìm tọa độ các điểm , A B,C c) Tam giác ,
A B,C là tam giác gì? Tính diện tích A ∆ BC Lời giải
b) Hai đường thẳng y = x +1 và y = −x +1 cắt nhau tại A nên tọa độ A nghiệm đúng hai
phương trình: y = −x +1 và y = x +1
Ta có: x +1= −x +1⇔ x = 0 ⇒ y =1⇒ A(0; ) 1
Tương tự ta có: B(2;− ) 1 ;C ( 2; − − ) 1
c) Gọi H là giao điểm của BC với Oy, BC ⊥ Oy và HB = HC
Tam giác ABC có AH vừa là đường cao, đường trung tuyến vậy A
∆ BC cân tại A Ta có: 1 1 S = BC AH = = cm ABC . .4.2 4( 2 ) 2 2 Bài 2:
a) Vẽ trên cùng một hệ trục tọa độ Oxy đồ thị các hàm số sau: (d : y = x + 4; d : y = −x + 2 1 ) ( 2)
b) Tìm tọa độ giao điểm M của (d d 1 ) và ( 2 )
c) Gọi giao điểm của (d Ox Oy d 1 ) với ,
theo thứ tự là A và B . Gọi giao điểm của ( 2 ) với
Ox là C . Tính diện tích tam giác BMC Lời giải 2
b) Xét phương trình hoành độ giao điểm của (d và (d : 2 ) 1 )
x + 4 = −x + 2 ⇔ 2x = 2 − ⇔ x = 1
− ⇒ y = 3 ⇒ M ( 1; − 3) c) Ta có: 1 1 S = S − S = − = (đvdt) BMC ABC AMC .6.4 .6.3 3 2 2 Bài 3:
a) Vẽ trên cùng một hệ trục tọa độ Oxy đồ thị các hàm số sau: ( 1
d : y = x + 2; d : y = − x +1 1 ) ( 2) 2
b) Gọi A là giao điểm của d và d . Tìm tọa độ điểm A 1 2
c) Gọi (d là đường thẳng đi qua K (0;0,25) song song với trục hoành, (d cắt (d và (d 2 ) 1 ) 3 ) 3 )
lần lượt tại B và C . Tìm tọa độ các điểm B và C d) Tính S ABC Lời giải
b) Xét phương trình hoành độ giao điểm của d và d : 1 2 1 3 2 − 4  2 − 4 x 2 x 1 x 1 x y A ;  + = − + ⇔ = − ⇔ = ⇒ = ⇒ 2 2 3 3 3 3   
c) Xét phương trình hoành độ giao điểm của d và d : 1 3 5 1 1 5 x 2 x B ;  + = ⇔ = ⇒ 2 2 2 2   
Xét phương trình hoành độ giao điểm của d và d : 2 3 1 − 5  5 x 1 x 3 C  3;  + = ⇔ = − ⇒ − 2 2 2    d) Chiều cao 5 4 7 AH = − = (cm) 1 7 BC = + = (cm) 1 7 49 ; 3 ;S = = cm ABC . ( 2) 2 3 6 2 2 2 6 24 3
Dạng 2: Tìm tọa độ giao điểm của hai đường thẳng
Cách giải: Cho hai đường thẳng d : y = ax + b và d ': y = a ' x + b'. Để tìm tọa độ giao điểm
của d và d ', ta làm như sau:
Cách 1: Dùng phương pháp đồ thị (thường sử dụng trong trường hợp d và d ' cắt nhau tại
điểm có tọa độ nguyên)
- Vẽ d và d ' trên cùng một hệ trục tọa độ
- Xác định tọa độ giao điểm trên hình vẽ
- Chứng tỏ tọa độ giao điểm đó cùng thuộc d và d '
Cách 2: Dùng phương pháp đại số
- Xét phương trình hoành độ giao điểm của d và d ': ax + b = a ' x + b'
- Từ phương trình hoành độ giao điểm, tìm được x và thay vào phương trình của d (hoặc d ') để tìm y
- Kết luận tọa độ giao điểm của d và d ' Bài 1:
Cho hai đường thẳng d : y = 2x +1 và d ': y = x + 3. Bằng phương pháp đồ thị, hãy tìm tọa độ
giao điểm của d và d ' Lời giải
Từ đồ thị dự đoán được d và d ' tại I (2;5)
Thay tọa độ I vào d và d ' thấy thảo mãn. Vậy I là tọa độ giao điểm của d và d ' Bài 2:
Tìm tọa độ giao điểm của các đường thẳng 1
d : y = x − 3 và d ': y = 2
− x + 2 bằng cách vẽ đồ thị 2 Lời giải Ta tìm được A(2; 2
− ) là tọa độ giao điểm của d và d ' 4 Bài 3:
Cho các đường thẳng d : y = x 9 − 4 2 và d ': y = x 3− 2 2 − 2 không vẽ đồ thị, tìm tọa độ giao
điểm của d và d ' Lời giải
Xét phương trình hoành độ giao điểm của d và d ': (2 2 − )1x = ( 2 − )1x −2 ⇔ x = − 2
Thay x = − 2 vào d hoặc d ' tìm được: y = 4
− + 2 ⇒ d ∩ d ' = (− 2; 4 − + 2 ) Bài 4:
Không vẽ đồ thị, hãy tìm tọa độ giao điểm của các đường thẳng 3
d : y = x +1 và d ': y = −x + 2 4 Lời giải
Xét phương trình hoành độ giao điểm của d và d ' ta được: 3 7 4 10
x +1 = −x + 2 ⇔ x =1 ⇔ x = ⇒ y = 4 4 7 7 Vậy  4 10 ;  
là tọa độ giao điểm của d và d ' 7 7    5
Dạng 3: Xét tính đồng quy của ba đường thẳng Cách giải:
Chú ý: Ba đường thẳng đồng quy là ba đường thẳng phân biệt và cùng đi qua 1 điểm
- Để xét tính đồng quy của ba đường thẳng (phân biệt) cho trước, ta làm như sau:
+) Tìm tọa độ giao điểm của 2 trong 3 đường thẳng đã cho
+) Kiểm tra xem nếu giao điểm vừa tìm được thuộc đường thẳng còn lại thì kết luận ba đường thẳng đó đồng quy. Bài 1:
Cho ba đường thẳng d : y = 4x −3,d : y = 3x −1,d : y = x + 3. Chứng minh ba đường thẳng trên 1 2 3 đồng quy Lời giải
Gọi giao điểm của hai đường thẳng d và d là I 1 2 Tìm được I (2;5)
Thay tạo độ I (2;5) vào d thấy thỏa mãn 3
Vậy ba đường thẳng d ,d ,d đồng quy 1 2 3 Bài 2:
Ba đường thẳng d :3x − y − 7 = 0,d : y = 2
− x + 3,d :3x − 2y − 7 = 0 có đồng quy hay không 1 2 3 Lời giải
Gọi giao điểm của hai đường thẳng d và d là I 1 2
Tìm được I (2;− ) 1
Thay tạo độ I (2;5) vào d thấy không thỏa mãn 3
Vậy ba đường thẳng d ,d ,d không đồng quy 1 2 3 Bài 3:
Cho ba đường thẳng d : y = x − 4,d : y = 2x + 3,d : y = mx + m +1. Tìm m để ba đường thẳng trên 1 2 3 đồng quy Lời giải 6
Gọi giao điểm của hai đường thẳng d và d là I 1 2 Tìm được I ( 7; − 1 − ) 1
Thay tạo độ I (2;5) vào d ta tìm được m = 2 ⇒ d : y = 2x + 3 ≡ d 3 3 2
Vậy không có giá trị nào của m thỏa mãn bài toán. Bài 4:
Cho ba đường thẳng d : y = x − 2,d : y = 2x −3,d : y = −x 1 2 3
a) Chứng minh rằng ba đường thẳng trên đồng quy
b) Tìm m sao cho 4 đường thẳng d ,d ,d và d : y = mx +1 đồng quy 1 2 3 Lời giải
a) Gọi I là giao điểm của d và d suy ra tọa độ I là nghiệm của hệ phương trình: 1 2 y = x − 2 x =1  ⇔  ⇒ I(1; 1 − ) y = 2x + 3 y = 1 −
Ta đi chứng minh I thuộc vào d 3
Thật vậy thay tọa độ I (1;− )
1 vào (d : y = −x ta được 1 − = 1 − (đúng) 3 )
b) Để 4 đường thẳng đồng quy thì I (1;− )
1 phải thuộc vào (d ) ⇔ 1 − = .1 m +1 ⇔ m = 2 − Bài 5:
Tìm m để ba đường thẳng sau đồng quy a) 2 2
d : y = (m −1)x + (m − 5)(m ≠ 1)
± ;d : y = x +1;d : y = −x + 3 1 2 3
b) d : y = 3x −8;d : y = 2
− x − 3;d : y = 3mx + 2m +1 1 2 3 Lời giải
a) Ta có: d cắt d tại M (1;2) 2 3
Để ba đường thẳng đồng quy thì M (1;2) thuộc (d ⇒ m = 2 ± 1 ) Thử lại với m = 2
± thì ta được d không trùng với d ,d 1 2 3 Vậy m = 2 ± b) Ta tìm được: 6 m − = 5 7
Dạng 4: Tính khoảng cách từ gốc tọa độ O đến một đường thẳng không đi qua O
Cách giải: Để tính khoảng cách từ O đến đường thẳng d (không đi qua O) ta làm như sau: Bước 1: Tìm ,
A B lần lượt là giao điểm của d với Ox và Oy
Bước 2: Gọi H là hình chiếu vuông góc của O trên d . Khi đó: 1 1 1 = + 2 2 2 OH OA OB Bài 1:
Cho hàm số y = ax + b
a) Xác định a và b biết rằng đồ thị hàm số trên đi qua điểm M (2;3)
b) Vẽ đồ thị hàm số vừa tìm được ở câu a
c) Tính khoảng cách từ gốc tọa độ đến đường thẳng tìm được ở câu a Lời giải
a) Ta có M (2;3) thuộc đồ thị hàm số ⇒ a = 3 ⇒ y = 6x −9
b) Gọi H là hình chiếu của O lên đường thẳng
Xét tam giác OAB vuông tại O Ta có: 1 1 1 . OAOB 9 = + ⇔ OH = = 2 2 2 2 2 OH OA OB OA + OB 37 Bài 2:
Trong hệ trục tọa độ Oxy cho đường thẳng (d ): y = 2x − 2 và điểm I (3; 2 − ). Hãy tính khoảng cách
a) Từ O đến d
b) Từ I đến d Lời giải a) Gọi ,
A B lần lượt là giao điểm của d với Ox và Oy
Ta có: A(1;0);B(0; 2
− ) ⇒ OA =1;OB = 2
Gọi H là hình chiếu vuông góc của O trên (d ) ⇒ OH là khoảng cách từ O đến (d ) Ta có: 1 1 1 = + ⇒ OH = 5 2 2 2 OH OA OB
b) Qua I kẻ đường thẳng vuông góc với Ox,Oy cắt (d ) lần lượt tại C (3;4) và B(0; 2 − )
Gọi K là hình chiếu vuông góc của I trên (d ) ⇒ IK là khoảng cách từ I đến (d ) 8 Sử dụng công thức: 1 1 1 6 5 = + ⇒ IK = 2 2 2 IK IC IB 5 Bài 3:
Cho đường thẳng ∆ : y = 2
− x +1 và M = ( 1; − 3
− ) trên hệ trục tọa độ Oxy . Hãy tính khoảng cách a) Từ O đến ∆ b) Từ M đến ∆ Lời giải
a) Ta tính được khoảng cách từ O đến ∆ là: 5 5
b) Ta tính được khoảng cách từ M đến ∆ là: 6 5 5 9
Dạng 5: Tìm điểm cố định mà hàm số luôn đi qua phụ thuộc vào tham số m Cách giải:
1. Khái niệm điểm cố định: Điểm M (x ; y là điểm cố định của (d ): y = ax + b 0 0 )
( a,b phụ thuộc vào tham số ,
m a ≠ 0 ) khi và chỉ khi điểm M luôn thuộc (d ) với mọi điều kiện của tham số m
Hoặc tương đương với điều kiện: y = ax + b với mội điều kiện của tham số 0 0
2. Cách tìm điểm cố định
Gọi I (x ; y là điểm cố định của (d ) ⇒ y = ax + b, m ∀ 0 0 ) 0 0
- Biến đổi y = ax + b về dạng A(x ; y m + B x ; y = 0 hoặc 0 0 ) ( 0 0) 0 0 2 (
A x ; y )m + B(x ; y )m + C(x ; y ) = 0 0 0 0 0 0 0 +) Ta có:  ( A x ; y ) = 0 0 0 (
A x ; y )m + B(x ; y ) = 0 m ∀ ⇔ 0 0 0 0
B(x ; y ) =  0 0 0  ( A x ; y ) = 0 0 0 +)Ta có: 2 (
A x ; y )m
B(x ; y )m C(x ; y ) 0, m  + +
= ∀ ⇔ B(x ; y ) = 0 0 0 0 0 0 0 0 0 C  (x ; y ) =  0 0 0
Từ đó tìm được x ; y rồi kết luận 0 0
3. Chú ý: Cách tính khoảng cách từ A(x ; y đến B(x ; y trên hệ trục tọa độ 2 2 ) 1 1 ) Oxy 2 2
AB = (y − y ) + (x − x ) 1 2 1 2 Bài 1: a) Chứng minh điểm 1 I  ; 3 − 
là điểm cố định mà đường thẳng (d ) 7
: y = (1− 2m)x + m − luôn 2    2
đi qua với mọi giá trị của tham số m
b) Cho đường thẳng (d ): y = (2m + )
1 x + m − 2 với m là tham số. Tìm điểm cố định mà (d ) luôn
đi qua với mọi giá trị của m . Lời giải a) Thay 1 x = ; y = 3
− vào (d ) thấy luôn thỏa mãn với mọi m, ta được (đpcm) 2
b) Gọi I (x ; y là điểm cố định của (d ) 0 0 ) 10 2x +1 = 0 0  1 − 5 y −
(2m 1)x m 2 m
(2x 1)m (x y 2) 0 m   ;  ⇒ = + + − ∀ ⇒ + + − − = ∀ ⇒ ⇒ 0 0 0 0 0 x y 2 0  2 2  − − = 0 0 
Là điểm cố định mà đường thẳng luôn đi qua. Bài 2:
a) Cho đường thẳng d : y = (2m + )
1 x − 3m +1 với tham số m. Điểm  3 1 K − ;  
có là điểm mà (d ) 2 2   
luôn đi qua với mọi giá trị của m hay không?
b) Chứng minh đường thẳng d : y = m − 2 x + 3m +1 luôn đi qua điểm cố định với mọi giá trị 1 ( ) của tham số m Lời giải
a) Thay tọa độ điểm  3 1 K − ;  
vào (d ) không thỏa mãn. Vậy K không là điểm cố định của 2 2    (d) b) Tìm được ( 3
− ;7) là điểm cố định đường thẳng luôn đi qua. Bài 3:
Cho hai đường thẳng (d : y = 4mx − m + 5 với m ≠ 0 và (d : y = 3m +1 x + m − 4 2 ) ( 2 ) 2 1 ) ( )
a) Chứng minh rằng (d đi qua điểm A cố định, (d đi qua điểm B cố định 2 ) 1 )
b) Tính khoảng cách AB
c) Tìm m để d song song với d 1 2 Lời giải
a) Giả sử d đi qua điểm A(x ; y cố định ⇒ y = 4mx − m +5 , m ∀ 0 0 ( ) 0 0 ) 1 4x −1 = 0 0  1 (4x 1)m y 5  A ; 5 ⇒ − = + ⇒ ⇒ − 0 0 y 5 0  4  + = 0  Tương tự:  1 13 B − − ;   3 3    b) Ta có: 1 3 2 13 2 113 AB = ( + ) + ( 5 − + ) = 4 4 3 12 11 2  =  c) a a ' 3  m +1 = 4m  1 d / /d   m 1;  ⇔ ⇔ ⇔ ∈ 1 2   2 b  ≠ b '
m − 4 ≠ −(m + 5)  3 Bài 4:
Cho ba đường thẳng (d ): y = ( 2 m − ) 2
1 x − m + 3; d : y = x + 5; d : y = −x +1 1 ( 2) ( 3)
a) Chứng minh rằng với mọi giá trị của m thì (d luôn đi qua 1 điểm cố định 1 )
b) Với giá trị nào của m thì (d / / d 1 ) ( 2)
c) Chứng minh rằng nếu (d / / d thì (d ⊥ d 1 ) ( 2) 1 ) ( 3)
d) Với giá trị nào của m thì ba đường thẳng (d , d , d đồng quy 1 ) ( 2 ) ( 3 ) Lời giải
a) Tìm được (d luôn đi qua điểm I (1;2) 1 )
b) (d / / d ⇔ m = ± 2 1 ) ( 2) (
d : y = −x +  3 1 )
c) Nếu (d / / d thì m = 0 ⇒  ⇒ d ⊥ d 1 ) ( 3) (  d  ) 1 2 : y = x + 5 2
d) (d và (d cắt nhau tại K ( 2; − 3) 3 ) 2 )
Để ba đường thẳng đồng quy khi I ( 6 d m ± ∈ ⇒ = 1 ) 3 12
Dạng 6: Tìm tham số m sao cho khoảng cách từ gốc tọa độ đến đường thẳng cho trước là lớn nhất Cách giải
Cho đường thẳng (d ): y = ax +b phụ thuộc tham số m . Muốn tìm m để khoảng cách từ O đến
d là lớn nhất, ta có thể làm theo một trong hai cách sau
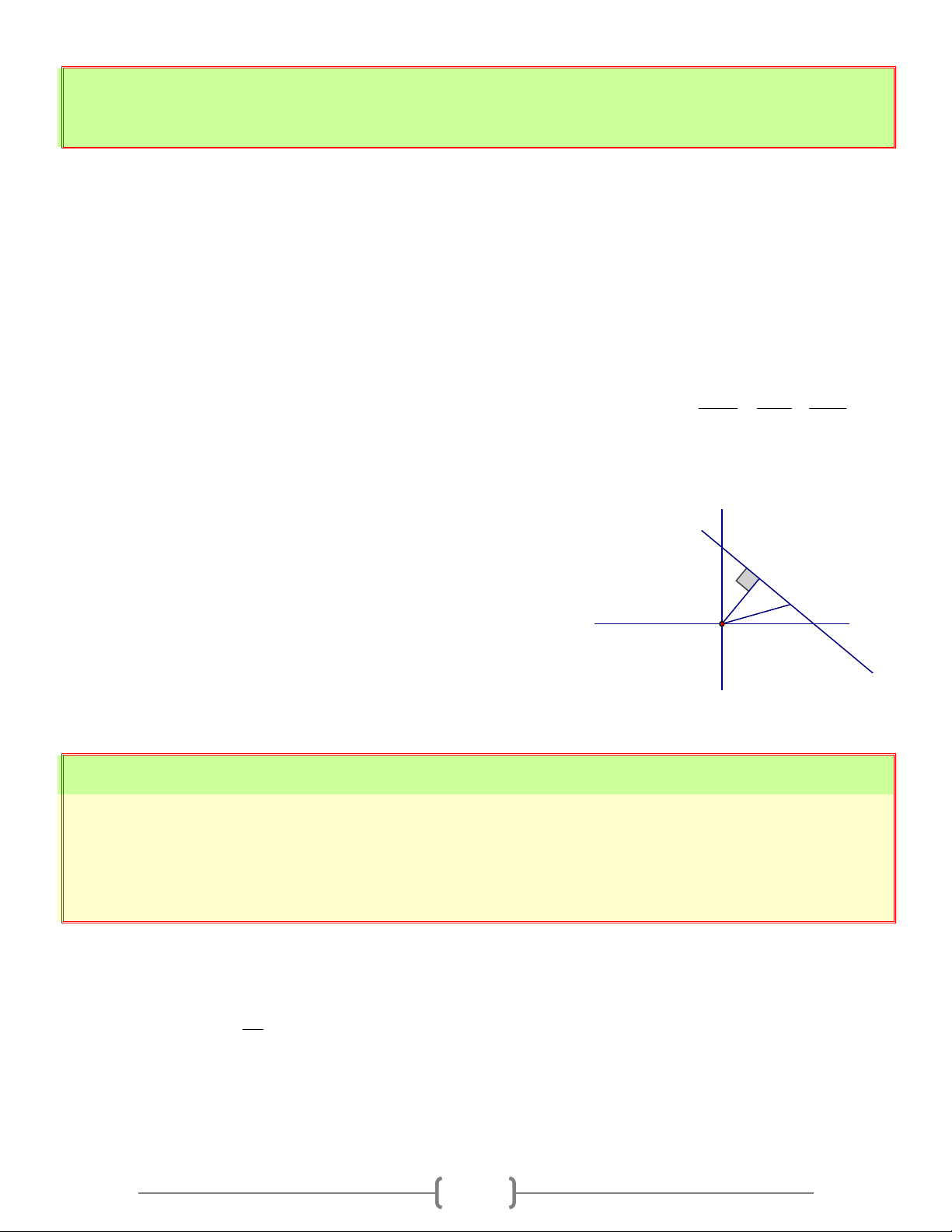
Cách 1: Phương pháp hình học - Gọi ,
A B lần lượt là giao điểm của d với Ox và Oy ; H là hình chiếu vuông góc của O trên d
- Ta có khoảng cách từ O đến d là OH và được tính bởi công thức sau: 1 1 1 = + 2 2 2 OH OB OC
- Từ đó tìm điều kiện của m để OH đạt giá trị lớn nhất
Cách 2: Dùng phương pháp điểm cố định
- Tìm được I là điểm cố định mà d luôn di qua
- Gọi H là hình chiếu vuông góc của O trên H I
d ⇒ OH ≤ OI = hằng số
d ⇒ OH ≤ OI = a h ngso O d
- Ta có: OH = OI ⇔ d là đường thẳng qua max I và vuông
góc với OI . Từ đó tìm được tham số m Bài 1:
Cho đường thẳng (d ): y = mx − 2m −1 với m là tham số. Tìm m sao cho khoảng cách từ O đến (d) đạt giá trị a) Lớn nhất b) Nhỏ nhất Lời giải
a. Khoảng cách từ O đến d nhỏ nhất bằng 0 khi O thuộc vào (d ). Từ đó tìm được 1 m − = 2
b) Cách 1: Xét hai trường hợp
Trường hợp 1: Nếu m = 0 ⇒ (d ): y = 1
− ⇒ khoảng cách từ O đến (d ) bằng 1 13 Trường hợp 2: Nếu  + m m
≠ 0 ⇒ (d ) cắt hai trục Ox,Oy lần lượt tại 2 1 A ;0  và B(0; 2 − m − ) 1 m   
Gọi H là hình chiếu vuông góc của O lên (d ) 2 Từ 1 1 1 2 (2m +1) = + ⇒ OH = 2 2 2 2 OH OA OB m +1 2 Lại có: 2 (m − 2) OH − 5 = −
≤ 0 ⇒ OH ≤ 5 m ∀ ≠ 0 2 m +1
Kết hợp các trường hợp 1 và 2, ta được: OH = ⇔ m = m 5 2 ax
Cách 2: Gọi I là điểm cố định của d . Ta tìm được I (2;− ) 1
Với mỗi m, gọi H là hình chiếu vuông góc của O trên d ⇒ OH ≤ OI = 5, m ∀ ⇒ OH =
⇔ d ⊥ OI ⇒ m = m 5 2 ax Bài 2:
Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng ∆ : y = (m + )
1 x + m + 2 đạt gía trị a) Nhỏ nhất b) Lớn nhất Lời giải
a) Khoảng cách từ O đến d có giá trị nhỏ nhất bằng 0, đạt được khi O∈d . Từ đó tìm được m = 2 −
b) Cách 1: Xét hai trường hợp
Trường hợp 1: Với m = 1
− ⇒ ∆ : y =1⇒ d ( ; O ∆) =1
Trường hợp 2: Với  + m m 2 ≠ 1
− ⇒ ∆ cắt ∆ lần lượt tại A ;0 − ; B(0;m +   2)  m +1 
Gọi H là hình chiếu vuông góc của O lên ∆ ⇒ d ( ; O ∆) = OH Từ 1 1 1 (m + 2)2 2 = + ⇒ OH = ≤ 2 m ∀ ≠ 1 − ⇒ OH = 2 ⇔ m = 0 2 2 2 2 OH OA OB m + 2m + 2 max Bài 3:
Cho đường thẳng (d ): y = mx + 2 (m là tham số)
a) Tìm điểm cố định I mà d luôn đi qua với mọi m
b) Tìm m để khoảng cách từ O đến d là lớn nhất 14
c) Khi m ≠ 0 , tìm m để khoảng cách từ O đến d bằng 2 5 5 Lời giải
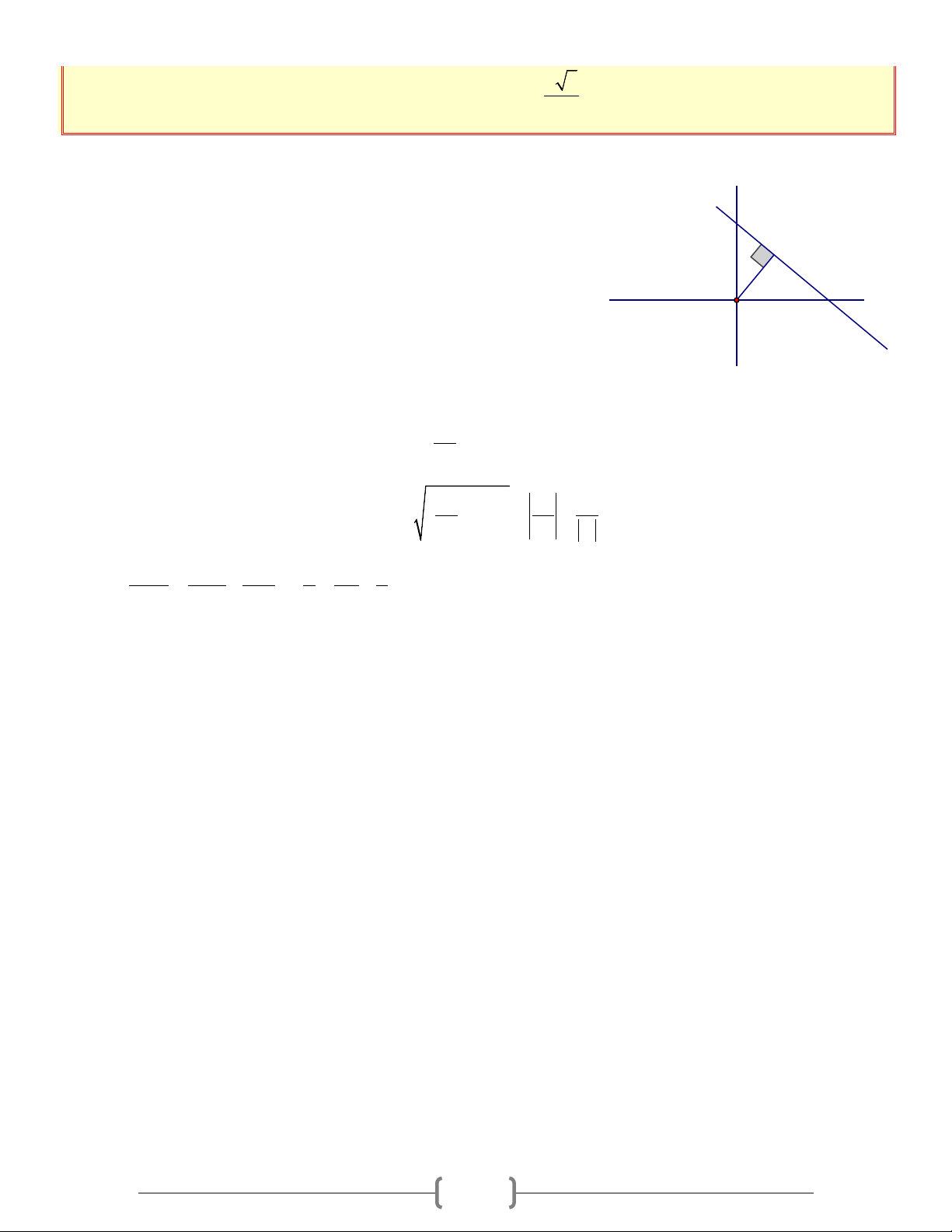
a) Tìm được điểm cố định I (0;2) b) Gọi I
H là hình chiếu của O trên d , OH là khoảng cách 2 H
từ O đến d K
Ta có: OH ≤ OI = 2, dau" = " ⇔ H ≡ I(0;2) ⇔ d ⊥ Oy tại I (0;2) O
⇔ (d ) có dạng y = 2 ⇔ m = 0
Vậy khoảng cách từ O đến d lớn nhất bằng 2 ⇔ m = 0 c) Gọi  −
K là giao điểm của d với 2 Ox K ;0 ⇒  m    2 Xét  −  − O
∆ IK vuông tại O , có: 2 2 2 2 OI = 2;OK = +  0 = =   m m m 2 Ta có: 1 1 1 5 m 1 2 = + ⇔ =
+ ⇔ m = 4 ⇔ m = 2 ± 2 2 2 OH OK OI 4 4 4 Vậy m = 2 ± 15
BÀI TẬP TRẮC NGHIỆM Câu 1:
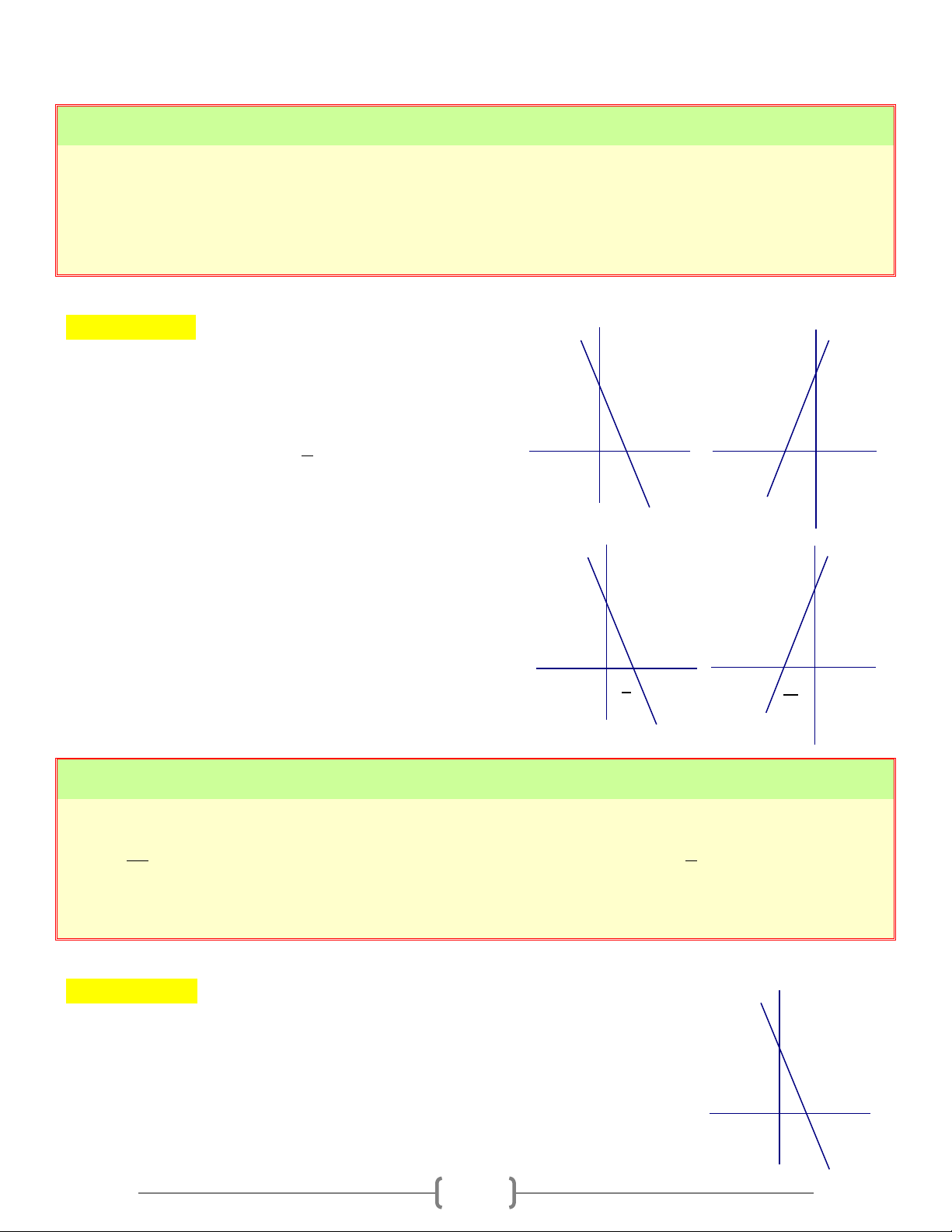
Đường thẳng nào dưới đây là đồ thị hàm số y = 2 − x + 5 A) (d B) (d 2 ) 1 ) C) (d D) (d 4 ) 3 ) Lời giải Chọn đáp án C Giải thích: 3
Đồ thị của hàm số y = 2
− x + 5 là đường thẳng đi 2 qua hai điểm -2 A(0;5) và 5 B ;0  2    O 1 O d d1 2 5 5 O 5 O -5 2 d d4 3 2 Câu 2:
Đường thẳng AB trong hình vẽ dưới đây là đồ thị hàm số nào A) 3 y − = x + 3 B) 2 y = x + 3 2 3 C) y = 2x + 6 D) y = 2 − x − 6 Lời giải Chọn đáp án A Giải thích: A Đường thẳng 3
AB là đồ thị của hàm số y = ax + b (*) B O 2 16
Do đường thẳng AB đi qua hai điểm A(0;3) và B(2;0) nên tọa độ của A và B nghiệm đúng
y = ax + b b  = 3 Ta có: 3  = .0 a + b   ⇔  3 0 .2 a ba − = + =  2 Thay 3 a −
= − ,b = 3 vào (*) ta được: 3 y = x + 3 2 2 Câu 3: Cho hàm số y = 4
− x + 2 có đồ thị là (d ) . Khẳng định nào sau đây sai
A) (d ) cắt trục hoành tại 1 A ;0  2   
B) (d ) cắt trục tung tại B(0;2)
C) (d ) song song với đồ thị hàm số y = 4x
D) (d ) đi qua điểm M ( 1; − 6) Lời giải Chọn đáp án C
Giải thích: Ta có : (d ): y = 4 − x + 2 (*) A) Thay 1
x = và y = vào (*) , ta được: 1 0 = 4. −
+ 2 ⇒ A∈(d ) hay (d ) cắt trục hoành tại A 0 A 2 2 1 A ;0  2   
B) Thay x = và y = vào (*) , ta được: 2 = 4.0 −
+ 2 ⇒ B ∈(d ) hay (d ) cắt trục tung tại B 2 B 0 B(0;2)
C) Ta đã biết đồ thị của hàm số y = ax + b(a ≠ 0;b ≠ 0) là đường thẳng song song với đường thẳng y = ax
Do đó đường thẳng (d ): y = 4
− x + 2 song song với đường thẳng y = 4 − x
D) Thay x = − y = vào (*) ta được: 6 = 4. − (− )
1 + 2 ⇒ M ∈(d ) hay (d ) đi qua M M 1; M 6 17 Câu 4:
Đồ thị là (d ) của hàm số 1 − 1 y =
x + cắt trục hoành tại E và cắt trục tung tại F . Tọa độ của 2 5 E, F là: A)  2   1 E ;0     ; F 0;   B) 2 1
E 0; ;F  ;0 5 5        5   5  C)  2   1 E  −   − ;1  ; F  ;0 − −  D) 1 2
E 0; ;F  ;0 5 5        5   5  Lời giải Chọn đáp án A Giải thích:
Điểm E thuộc trục hoành nên có tung độ bằng 0( y = E 0) Thay − y − = vào 1 1 y = x + , ta được: 1 1 2  2 x x x E  + = ⇔ − + = ⇔ = ⇒ E 0 0 5 E 2 0 E  ;0 2 5 2 5 5 5   
Điểm F thuộc trục tung, nên có hoành độ bằng 0(x = F 0) Thay x − = vào 1 1 y = x + , ta được: 1 1 1 1 y y F   = − + ⇔ = ⇒ F 0 F .0 F  0; 2 5 2 5 5 5    Câu 5:
Giá trị nào của b dưới đây thì đồ thị (d ) của hàm số y = 2
− x + b đi qua điểm 1 P ;1  3    A) 1 b = B) 1 b = − 2 3 C) 4 b − = D) b = 0 5 Lời giải Chọn đáp án B Giải thích: Thay 1 x =
y = − vào y = 2
− x + b , ta được: 1 2 1 1 − = 2. − + b ⇔ b = 1 − + = − P ; P 1 3 3 3 3 18 Câu 6:
Giá trị nào của b dưới đây thì đồ thị (d ) của hàm số y = ax +b đi qua hai điểm M (0; 5 − ) và N (1; 4 − ) A) a = 4;b = 2 B) a = 3 − ;b = 4 C) a =1;b = 5 − D) a = 2; − b = 5 − Lời giải Chọn đáp án B Giải thích:
Tọa độ của M (0; 5 − ) và N (1; 4
− ) nghiệm đúng y = ax + b , từ đó ta có hệ phương trình:  5 − = .0 a + b b  = 5 −  ⇔  ⇒ ( ; a b) = (1; 5 − )  4 − = .1 a + ba = 1 Câu 7:
Trên mặt phẳng tọa độ Oxy , có các bộ ba điểm. Hỏi có một bộ 3 điểm nào không thẳng hàng A) A( )  1 − 2;9 , B ;6 −  1   ,C (0;5) B) M ( 1 − ;7), N ; 6 −  , P (5;0)  2   2  C) M ( )  1 1;7 , E ;4 −   , F (1;3) D) A(− ) F ( ) 3
2;9 , 1;3 , K  ;2  2   2  Lời giải Chọn đáp án B
Giải thích: Ta biểu diễn các bộ ba điểm lên hệ trục tọa độ và thấy rằng ba điểm M, N, P thẳng hàng Câu 8:
Ba đường thẳng y = −x + 4; y = 2x −5; y = 3
− x +10 cùng đi qua một điểm (đồng quy). Điểm đó là điểm nào A) A( 3 − ;− ) 1 B) B(3; ) 1 C) C ( 3 − ; ) 1 D) D(3;− ) 1 Lời giải Chọn đáp án B 19 Giải thích: 1  = 3 − + 4
Thay tọa độ điểm B(3; )
1 vào cả ba phương trình đường thẳng, ta có: 1   = 2.3 − 5 (đúng) 1  = 3.3 − +  10 Nên B(3; )
1 thuộc cả ba đường thẳng. Câu 9:
Cho hai điểm M (2;2), N ( 2; − )
1 . Trong các đường thẳng sau đây, đường thẳng nào đi qua M , N A) 1 3 y = x + B) 3 1 x + 4 2 2 4 C) 1 3 x − D) 3 1 − x + 4 2 2 4 Lời giải Chọn đáp án A Giải thích:
Ta có M N ∈(d ) 1 3 ,
: y = x + ⇒ đường thẳng đi qua hai điểm M (2;2), N ( 2; − ) 1 là: 1 3 y = x + 4 2 4 2 20 BÀI TẬP VỀ NHÀ Bài 1:
Cho hai đường thẳng d : y = 2x −3 và d : y = 3 − x + 7 1 2
a) Vẽ d ,d trên cùng một hệ trục tọa độ 1 2
b) Tìm tọa độ giao điểm của d ,d 1 2 Lời giải
b) Từ hình vẽ ta thấy d ∩ d = I 2;1 1 2 ( )
Thay tọa độ điểm I vào d ,d thấy thỏa mãn 1 2 Bài 2:
Cho hai đường thẳng d : y = 3
− x +1 và d ': y = −x − 2 . Tìm tọa độ giao điểm của d,d ' Lời giải
Xét phương trình hoành độ giao điểm của − −  − − d và 3 7 3 7 d ' x y
d d ' I  ;  ⇒ = ⇒ = ⇒ ∩ = 2 2 2 2    Bài 3:
Các đường thẳng sau đây có đồng quy hay không: a) 1
d : y = 3x +1;d : y = − ;
x d : y = x + 1 2 3 2 b) 1 5
d : x + y −1 = 0;d : y = 3x + 5;d : x − y + = 0 1 2 3 3 3 Lời giải
a) Các đường thẳng đồng quy tại điểm  1 − 1 ;   4 4   
b) Các đường thẳng không đồng quy vì d ≡ d 2 3 Bài 4:
Tìm tham số m để ba đường thẳng sau đồng quy a) 4
d : y = x +1;d : y = x −1;d : y = mx + m + 3 1 2 3 3 b) 1
d : y = x − m +1;d : y = 2 ;
x d : y = 2 2m −1 x + 1 2 3 ( ) 4 21 Lời giải
a) Tìm được d ∩ d = I 6; − 7 − 1 2 ( )
Thay tọa độ điểm I vào d ⇒ m = 2 3
b) Tìm được d ∩ d = I 1− ;2 m − 2m 1 2 ( )
Thay tọa độ điểm I vào  3  1 m =
d ≡ d : y = x + ⇒ loai   1 3 2 4 4
d ⇒16m − 32m +15 = 0 ⇔  ⇒ 3   5  1 1 m =
d : y = x − ,d : y = 2x,d : y = 3x + 1 2 3  4  4 4
Đôi một phân biệt nên thỏa mãn Vậy điềm kiện là: 5 m = 4 Bài 5:
Cho đường thẳng d : y = 4 − x + 3
a) Vẽ đồ thị hàm số đã cho
b) Tìm tọa độ giao điểm ,
A B của d với lần lượt hai trục tọa độ ; Ox Oy
c) Tính koảng cách từ gốc tọa độ đến d
d) Tính khoảng cách từ điểm I ( 1; − 2 − ) đến d
e) Tính diện tích tam giác OAB Lời giải b) Tìm được:  3 A ;0  ; B (0;3)  4  c) Tính được: 3 OA =
OB = ⇒ d (O d ) 3 17 ; 3 ; = OH = 4 17
d) Qua I , kẻ các đường thẳng lần lượt song song với ;
Ox Oy cắt d lần lượt tại  5 M ; 2 − ; N ( 1; −   7)  4  Tính được: 9 IM =
IN = ⇒ d (I d ) 9 17 ; 9 ; = 4 17 e) Tìm được: 1 9 S = OAOB = AOB . 2 8 22 Bài 6:
Cho đường thẳng d : y = (m + 2) x + m (với m là tham số)
a) Tìm điểm cố định mà d luôn đi qua với mọi m
b) Tìm m để d cắt Ox,Oy tại A và B sao cho diện tích tam giác OAB bằng 1 2 Lời giải a) Tìm được I ( 1; − 2
− ) là điểm cố định của d 2 b) Giao điểm của  −
d với hai trục Ox,Oy lần lượt là: m   ( ) 1 ;0 ; 0; m A B m ⇒ S =   m + 2 AOB  2 m + 2 Từ 1
S = ⇒ m = 2;m = 1 − 2 Bài 7:
Cho đường thẳng d :(2m −5) x + y −1+ m = 0 . Tìm m sao cho khoảng cách từ O đến d là: a) Nhỏ nhất b) Lớn nhất Lời giải a) Tìm được m =1 b) 10 8 OH = ⇔ m = max 2 3 23