Tài liệu Ứng dụng của đạo hàm trong phân tích kinh tế | Môn toán cao cấp

lOMoAR cPSD| 49831834
2. Ứng dụng của ạo hàm trong phân tích kinh tế
2.1. Đạo hàm và giá trị cận biên y=f(x), x ầu tư, y lợi nhuận
f x ( 0) = x xlim→ 0 f x( )x−− xf x0( 0) = →limx 0 f x( 0 + xx)− f x( 0) VD. f x 3x2, ’ f 2 ? VD. g x( ) x g, '( )0 ?
y=f(x), y là lợi nhuận, x ầu tư
f x ( 0) = →limx 0 f x( 0 + xx)− f x(
0) f (x0) f x( 0 + xx)− f x( 0) khi x 0
f (x0) f x( 0 +1)− f x( 0) (cho =x1) 1 lOMoAR cPSD| 49831834
Xét hàm số kinh tế y = f(x) biểu diễn ảnh hưởng của biến số kinh tế x ối với biến số kinh
tế y, các nhà kinh tế gọi My(x0)=f (x ) 0 = -2 là giá trị y-cận biên của x tại iểm x0.
Đối với mỗi hàm kinh tế, giá trị cận biên có tên gọi cụ thể như sau:
Ý nghĩa: tại iểm x0, nếu x tăng thêm 1 ơn vị, thì y thay ổi một lượng xấp xỉ bằng f (x ) 0 ơn vị • • •
• Đối với hàm sản xuất Q = f(L) thì f (L) ược gọi là số sản phẩm hiện vật cận biên
của lao ộng tại iểm L, ký hiệu là MPPL: MPPL = f (L) .
Ý nghĩa: Tại iểm L, MPPL cho biết xấp xỉ lượng sản phẩm hiện vật tăng thêm khi sử dụng
thêm một ơn vị lao ộng.
• Đối với hàm doanh thu TR = TR(Q) thì TR (Q) ược gọi là doanh thu cận biên tại iểm Q, ký hiệu là MR: MR = TR (Q).
Ý nghĩa: Tại mức sản lượng Q, MR cho biết xấp xỉ lượng doanh thu tăng thêm khi sản xuất
thêm một ơn vị sản phẩm.
• Đối với hình hàm chi phí TC = TC(Q) thì TC (Q) ược gọi là chi phí cận biên tại iểm Q, ký hiệu là MC: MC = TC (Q) .
Ý nghĩa: Tại mức sản lượng Q, MC cho biết xấp xỉ lượng chi phí tăng thêm khi sản xuất
thêm một ơn vị sản phẩm.
• Đối với hàm tiêu dùng C = C(Y) thì C (Y) ược gọi là xu hướng tiêu dùng cận biên, ký hiệu là MPC: 2 lOMoAR cPSD| 49831834 MPC(Y) = C (Y) .
Ý nghĩa: Tại mức thu nhập Y, MPC là số o xấp xỉ lượng tiêu dùng gia tăng khi người ta có
thêm một ơn vị thu nhập.
Ví dụ 1.74. Cho hàm sản xuất của một doanh nghiệp là Q 5 L=. Ở mức sử dụng 81 ơn vị
lao ộng (chẳng hạn 81 giờ lao ộng một tuần), mức sản lượng tương ứng là Q = 45 ơn vị.
Tính sphvcb của lao ộng tại L=81 và cho biết ý nghĩa. Giải
Sản phẩm hiện vật cận biên của lao ộng tại iểm L = 100 là MPPL = Q (L) = 5 2 L . 5 MPP (100)L == 0,25 2 100
Điều này có nghĩa là khi tăng mức sử dụng lao ộng hàng tuần từ 100 giờ lên 101 giờ thì
sản lượng hàng tuần sẽ tăng thêm khoảng 0,25 ơn vị. VD2 : TR = 200Q −3Q2
Lập hàm doanh thu cận biên, tính doanh thu cận biên tại mức Q bằng 10 và 50 cho biết biết
ý nghĩa; tính hàm cầu ối với sản phẩm, 3 lOMoAR cPSD| 49831834 Giải. MR=TR’(Q)= 200-6Q  MR(10)=200-6.10=140, MR(50)= 200-6.50= -100
TR=pQ=200Q-3Q^2  p=200-3Q (hàm cầu ảo), suy ra có hàm cầu là : Q=(200-p)/3
2. Quy luật lợi ích cận biên giảm dần y=f(x+1)
 My là một hs giảm với x ủ lớn Nuôi cá : 1
tháng thu hoạch : ầu tư 100k  lợi nhuận 10k 2 20k my(1)=10 3 30k My(2)=10 … 1000 +1 My=9 1 triệu My=2
Cho hàm số kinh tế y = f(x). Hàm số y = f(x) ược gọi là tuân theo quy luật lợi ích cận biên
giảm dần nếu giá trị y-cận biên giảm dần với x ủ lớn, tức là My = f (x) là hàm số ơn iệu giảm với x ủ lớn.
Dưới góc ộ toán học, ể hàm số y = f(x) tuân theo quy luật lợi ích cận biên giảm dần thì f (x)
0 với x ủ lớn.
Ví dụ 1.75. Cho hàm sản xuất Q = aL (a > 0,
0, L > 0), hãy tìm iều kiện của tham số
ể hàm sản xuất Q tuân theo quy luật lợi ích cận biên giảm dần.
Giải. Ta có Q = aL −1;Q
= ( −1) aL −2. Để hàm sản xuất Q tuân theo quy luật lợi
ích cận biên giảm dần thì Q 0 − 1 0 1. Do 0 nên 0 1.
Ví dụ 1.76. Cho hàm doanh thu TR(Q) = 1200Q - Q2, (Q > 0). Hàm này có tuân theo quy
luật lợi ích cận biên giảm dần hay không? 4 lOMoAR cPSD| 49831834 Giải. Ta có TR (Q) = 1200 - 2Q , TR (Q) = −2 0, Q 0.
Vậy hàm doanh thu ã cho tuân theo quy luật lợi ích cận biên giảm dần. 3. Hệ số co giãn
Cho hàm số kinh tế y = f(x) và xo là một iểm thuộc tập xác ịnh của hàm số ã cho. Giá trị
x tăng thêm 1 ơn vị thì y tăng xx y x ( )o (% ) y x( )0
x tăng thêm 1 % thì y tăng xx ? (% ) y
x o(x ) = y xy x (( 0o)).xo
ược gọi là hệ số co dãn của y theo x tại xo.
Ý nghĩa: Tại xo, khi ối số x tăng 1% thì giá trị của hàm số y = f(x) thay ổi một lượng xx là y x o (x ) %.
Ví dụ 1.77. Cho hàm cầu của một loại hàng hóa Q = D(p). Tính hệ số co dãn của cầu theo
giá tại mức giá po. Áp dụng với hàm cầu D = 6p – p2 tại mức giá po = 2 và giải thích ý nghĩa
của kết quả nhận ược. Cũng tại mức giá ó, nếu giá tăng 3,2% thì cầu sẽ thay ổi như thế nào? TXĐ: 0

Giải. D’ = 6 – 2p
Hệ số co dãn của cầu theo giá tại mức giá p là Q
p (p) = D (p)D(p) .p = 66p−−2pp2 .p. 5

lOMoAR cPSD| 49831834 ta có Dp (2) = .4 = −1.
Ý nghĩa: Tại mức giá po = 4, nếu giá tăng 1% thì cầu sẽ giảm một lượng xấp xỉ 0,5%.
Còn nếu giá tăng 2% thì cầu sẽ giảm một lượng xấp xỉ 2*1% = 2%.
Còn nếu giá tăng 3,2% thì cầu sẽ giảm một lượng xấp xỉ 3,2*1% = 3,2%.
Ví dụ 1.78. Cho hàm sản xuất Q = a.L (a > 0; 0 < < 1). Tại mức sử dụng lao ộng nào ó,
tính hệ số co dãn của sản lượng theo lao ộng. Giải. Hệ số co giãn của sản lượng theo lao ộng là Q Q'(L) aL −1 L (L) = Q(L) .L = aL L = .
Ý nghĩa: Tại mọi mức sử dụng lao ộng, nếu lao ộng tăng 1% thì sản lượng sẽ tăng một lượng xấp xỉ %.
4. Phân tích mối quan hệ giữa hàm bình quân và hàm cận biên TC=TC(Q) AC=TC/Q =
Cho hàm số kinh tế y = f(x). Hàm số Ay
y (x 0) ược gọi là hàm bình quân. Chúng ta x
sẽ khảo sát khoảng tăng, giảm, cực trị của hàm số này. Ta có − y My − Ay (Ay) = xy
= y .x −x(2x)'.y = y x x = x (x 0) . 6 lOMoAR cPSD| 49831834 Do ó:
• Hàm bình quân tăng My > Ay ( ường cận biên nằm trên ường bình quân).
• Hàm bình quân giảm My < Ay ( ường cận biên nằm dưới ường bình quân).
• Tại iểm hàm bình quân ạt cực trị thì My – Ay = 0 My = Ay ( ường bình quân gặp
ường cận biên tại iểm cực trị của hàm bình quân).
Ví dụ 1.79. Cho hàm chi phí TC = TC(Q) (Q > 0).
a) Hãy phân tích mối quan hệ giữa hàm chi phí bình quân AC(Q) và hàm chi phí cận biên MC(Q).
b) Áp dụng phân tích ối với trường hợp TC(Q) = 3Q2 + 7Q + 27 (Q > 0). Giải. a) Ta có AC(Q) =
TC(Q) → AC (Q) = MC.Q −TC = MC−AC (Q 0) Q Q2 Q . = MC AC− AC(Q) (Q 0) Q Do ó:
Hàm chi phí bình quân tăng MC > AC ( ường chi phí cận biên nằm trên ường chi phí bình quân).
Hàm chi phí bình quân giảm MC < AC ( ường chi phí cận biên nằm dưới ường chi phí bình quân).
Tại iểm hàm chi phí bình quân ạt cực trị thì MC = AC ( ường chi phí bình quân gặp ường
chi phí cận biên tại iểm mà ường chi phí bình quân ặt cực tiểu). b) Ta có 7 lOMoAR cPSD| 49831834 AC(Q) = TC(Q) = 3Q+7+ 27 . Q Q AC (Q) = 3− 27 . Q2
AC (Q) = 0 Q2 = 9 Q = 3 (do Q > 0).
+) Nếu Q < 3 thì hàm chi phí bình quân giảm và MC < AC ( ường chi phí cận biên nằm
dưới ường chi phí bình quân).
+) Nếu Q > 3 thì hàm chi phí bình quân tăng và MC > AC ( ường chi phí cận biên nằm trên
ường chi phí bình quân).
+) Nếu Q = 3 thì hàm chi phí bình quân ạt cực trị và MC = AC ( ường chi phí bình quân
gặp ường chi phí cận biên tại iểm mà ường chi phí bình quân ặt cực tiểu). AC MC
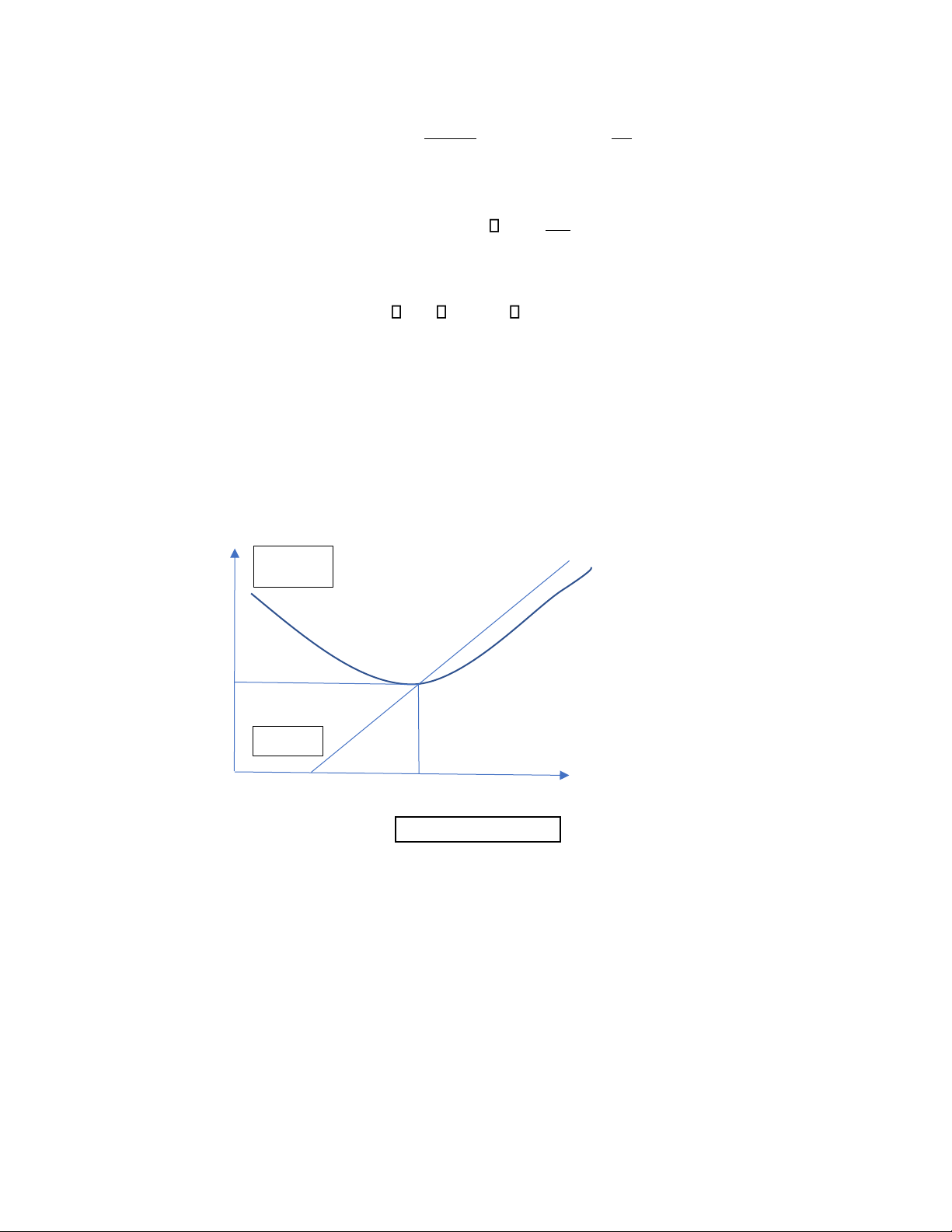
5. Bài toán tối ưu hàm một biến trong kinQ=3 h tế
Bài toán : Tìm GTLN hoặc GTNN của hàm số trên 1 khoảng Nhận xét : -
Trên khoảng (a ;b) có duy nhất 1 iểm cự tiểu x0, không có cực ại thì GTNN của hs
f(x) trên (a ;b) là f(x0) -
Trên khoảng (a ;b) có duy nhất 1 iểm cự ại x0, không có cực tiểu thì GTLN của hs
f(x) trên (a ;b) là f(x0) 8 lOMoAR cPSD| 49831834
a) Chọn mức sản lượng tối ưu
Ví dụ 1.80. Cho hàm tổng chi phí TC = Q3 – 9Q2 + 80Q. Hãy xác ịnh mức sản lượng Q ể
chi phí bình quân nhỏ nhất.
Giải. Hàm chi phí bình quân là AC = TC = Q2 −9Q+80 . Q Ta có AC (Q) = 2Q −9 = 0 Q = . Mặt khác AC = 2 → AC 92 = 2 0.
Suy ra Q=9/2 là iểm cực tiểu.
Trên khoảng (0; dương vô cùng) có duy nhất 1 cực tiểu và không có cực ại nên ta có mức
sản lượng tối ưu là Q = .
Ví dụ 1.81. Cho biết hàm tổng chi phí TC = −Q3 5,5Q2+150Q + 675 và hàm tổng doanh
thu TR = 4350Q - 13Q2 . Hãy xác ịnh mức sản lượng cho lợi nhuận tối a.
Xác ịnh mức sản lượng tối ưu.
Giải. Ta có hàm tổng lợi nhuận là
= TR −TC = (4350Q-13Q2)−(Q3 −5,5Q2 +150Q+675) = −Q3 −7,5Q2 + 4200Q−675 . = − 3Q2 −15Q+ 4200. = 0
QQ == −3540 (lo¹i v× Q > 0). = − 6Q−15
(35) 0. Suy ra Q=35 là iểm cực ại 9 lOMoAR cPSD| 49831834
Do trên khoảng xác ịnh chỉ có 1 cực ại và không có iểm cực tiểu nào nên ta có mức sản
lượng tối ưu là Q = 35.
Ví dụ 1.82. Cho biết hàm chi phí là TC = 2Q3 + 5Q2 + 6Q + 10 và hàm cầu là Q = 4056 -
p. Hãy xác ịnh mức sản lượng cho lợi nhuận tối a. Giải. Hàm tổng doanh thu là
TR = pQ=(4056 - Q)Q = 4056Q - Q2.
Ta có hàm tổng lợi nhuận là
= TR −TC = (4056Q - Q2)−(2Q + 5Q + 6Q + 10 3 2 ) = −2Q3 −6Q2 + 4050Q−10. = − 6Q2 −12Q+ 4050. = 0
QQ == −2527 (lo¹i v× Q > 0). = − 12Q−12 (25) 0.
Do trên khoảng xác ịnh chỉ có 1 cực ại và không có iểm cực tiểu nào nên ta có mức sản
lượng tối ưu là Q = 25.
Ví dụ 1.83. Cho biết hàm tổng chi phí TC =
4860 +15Q+7500000 (Q > 0). Hãy xác ịnh Q
mức sản lượng Q ể chi phí nhỏ nhất Giải. Ta có TC = − 48602 +15. Q TC = 0 Q2 = 324
QQ = −=1818 (lo¹i v× Q > 0) . TC = 97203 TC (18) 0. Q 10 lOMoAR cPSD| 49831834
Do trên khoảng xác ịnh chỉ có 1 cực tiểu và không có iểm cực ại nào nên ta có mức sản lượng tối ưu là Q =18.
Ví dụ 1.84. Cho biết hàm tổng doanh thu TR = −9Q4+
Q -1505Q +1200Q, (Q > 0)3 2 .
Hãy xác ịnh mức sản lượng Q ể cực ại tổng doanh thu. Giải. Ta có
TR = −36Q3 + 4345Q - 30102 Q + 1200. TR = 0 Q =120 . TR
= −108Q2 + 8690Q- 3010 TR (120) = −515410 0.
Do trên khoảng xác ịnh chỉ có 1 cực ại và không có iểm cực tiểu nào nên ta có mức sản
lượng tối ưu là Q =120 .
b) Lựa chọn tối ưu mức sử dụng yếu tố ầu vào
Ví dụ 1.85. Cho hàm sản xuất Q = 120L2 – L3 (L > 0). Hãy xác ịnh mức sử dụng lao ộng ể sản lượng tối a. Giải. Ta có Q = 240L −3L2. Q = 0 L = 80 ( vìL 0). Q = 240−6L Q (80) = 240−6.80 = −240 0.
Vậy, Q ạt giá trị tối a tại L = 80.
Ví dụ 1.86. Cho biết hàm sản xuất ngắn hạn là Q =100.5 L3 (L 0) và giá của sản phẩm là
p = 5USD và giá thuê lao ộng là pL = 3USD. Hãy tìm mức sử dụng lao ộng ể cho lợi nhuận tối a.
Giải. Hàm tổng doanh thu là 11 lOMoAR cPSD| 49831834 TR = p.Q = 500. L5 3 .
Hàm tổng chi phí là TC = p .L = 3L+C0 L
Suy ra hàm tổng lợi nhuận là
= TR −TC = 500. L5 3 −3L-C0 Ta có − 2 = 300L 5 −3 . 2
= 0 L5 =100 L 100000= . Mặt khác −7 −7 = 300 − 52 L5 = −120L5 (100000) 0 .
Vậy, lợi nhuận ạt tối a tại L = 100000. II. Tích phân
1. Tích phân bất ịnh Định nghĩa.
Tập hợp các nguyên hàm của hàm số f(x) ược gọi là tích phân của hàm số f(x).
Cho F(x) là một nguyên hàm của hàm f(x) thì f(x)dx F(x) C= +
2. Tích phân xác ịnh
Bài toán tính diện tích hình thang cong Bài toán 2.1. 12 lOMoAR cPSD| 49831834
Tính diện tích hình phẳng giới hạn bởi trục hoành, ường thẳng ứng x=a, x=b (a
ồ thị của hàm số y=f(x) trên oạn [a; b], trong ó f(x) là hàm số không âm và liên tục trên oạn [a;b].
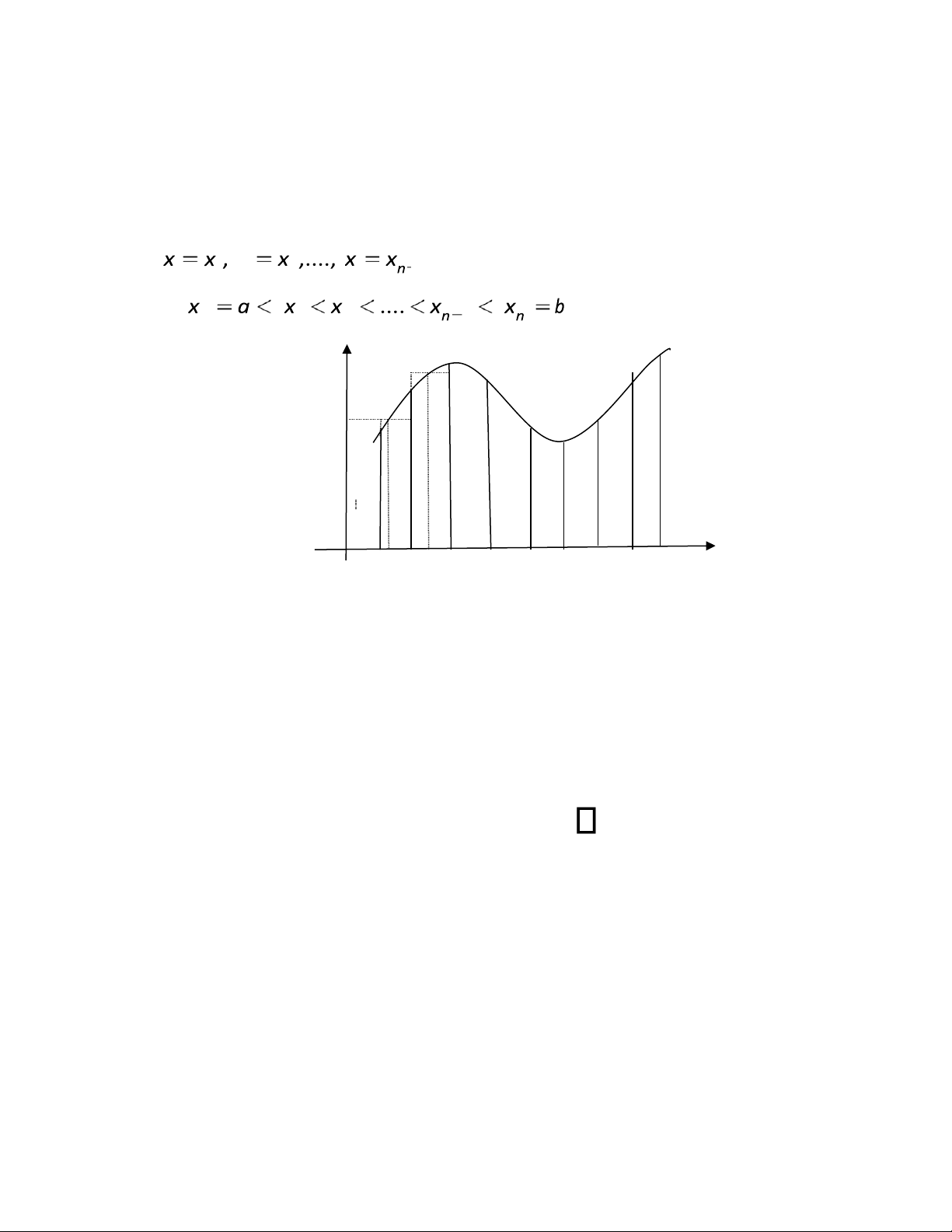
Ta chia hình thang cong cần tính diện tích thành nhiều hình thang cong nhỏ bởi các ường thẳng 1 2 1 (trong ó 0 1 2 ) 1 y y=f(x) f(y 1 ) O
a=x 0 x 1 x 2 x 3 x n-1 x n = b x
Ta tính xấp xỉ diện tích các hình thang cong nhỏ bởi các hình chữ nhật có áy là oạn [xi1; xi]
và chiều cao bằng f(yi) với yi là một iểm bất kỳ trong oạn [xi-1; xi], tức là xấp xỉ của diện
tích hình thang cong thứ i là Si = f(y ).(x -x )i i i-1 n =
Nên xấp xỉ của diện tích hình thang cong ban ầu là: S f(y ).(x -x )i i i-1 i 1=
Ta có cảm nhận rằng diện tích xấp xỉ này càng chính xác nếu n cang lớn và còn hy vọng
rằng nếu n tiến ến vô cực thì ta sẽ ược diện tích úng. Để làm sáng tỏ iều này thì tích phân xác ịnh ra ời. Định nghĩa
Cho hàm số f(x) liên tục trên [a, b]. Chia tuỳ ý oạn [a, b] thành n oạn nhỏ tùy ý bởi các iểm chia: 13 lOMoAR cPSD| 49831834
a = x0 x1 x2
xn –1 xn = b = ma x Ký hiệu Δx − i = xi
xi−1, i = 1, 2, ..., n. d i = n x . i 1,
Trong mỗi oạn [xi-1, xi], (i = 1,n), lấy một iểm yi tùy ý. Lập biểu thức n S = n f y( ).i xi i =1
Sn ược gọi là tổng tích phân của hàm f(x) trên [a, b]
Nếu cho n tiến ến vô cực sao cho d →0 mà tổng Sn tiến ến một giới hạn hữu
hạn I và giới hạn ó không phụ thuộc vào cách chia oạn [a, b] và cách chọn iểm yi thì b =
số I ược gọi là tích phân xác ịnh của hàm f(x) trên [a, b] và ký hiệu là I f(x)dx
a Khi ó, f(x) ược gọi là khả tích trên [a, b]. 1
VD: I = x dx2 theo ịnh nghĩa nói trên 0
III. Ứng dụng trong phân tích kinh tế 1. Xác ịnh quỹ vốn dựa theo mức ầu tư
Giả sử việc ầu tư ược tiến hành liên tục theo thời gian. Ta xem lượng àu tư I và quỹ vốn
K là các biến phụ thuộc vào thời gian t: I = I(t), K = K(t) .
Lượng ầu tư I = I(t) tại thời iểm t chính là lượng bổ sung quỹ vốn tại thời iểm ó.
Nói cách khác, I(t) là tốc ộ tăng của K(t), do ó: I(t) = K (t)
Nếu biết hàm ầu tư I(t) thì ta có thể xác ịnh ược quỹ vốn K(t): 14 lOMoAR cPSD| 49831834 K(t) = I(t)dt
Hằng số C trong tích phân ược xác ịnh nếu biết quỹ vốn ban ầu K = K( ) .
Ví dụ 2.32. Giả sử lượng ầu tư tại thời iểm t ược xác ịnh dưới dạng hàm số: I(t) = Tại thời iểm xuất phát
và quỹ vốn tại thời iểm xuất phát =
. Quỹ vốn tại thời diểm t là : = = + , do ó: = + . K( ) = C =
2. Tìm hàm tổng khi biết hàm cận biên. VD: 21/17
Cho MC=32-18Q+12Q^2 và FC=43 tìm hàm hàm tổng chi phí và chi phí khả biến. TC(Q) = MC(Q).dQ TC(Q) = (32 18Q 12Q ).−+ 2 dQ TC(Q) = 32Q −9Q2 + 4Q3 +C TC(0)=FC 43=32.0-9.0^2+4.0^3+C C=43
TC(Q) = 32Q−9Q2 + 4Q3 + 43
3. Tính thặng dư của người tiêu dùng và nhà sản xuất
Giả sử ta có hàm cầu là Q = d
D(p) . Khi biểu diễn bằng ồ thị giữa giá p và lượng cầu 15 lOMoAR cPSD| 49831834
Q , các nhà kinh tế thường sử dụng trục hoành ể biểu diễn lượng cầu Q và trục tung biểu
diễn giá p.Với cách biểu diẽn như vậy thì ường cầu là ồ thị của hàm cầu ảo p = D (Q )− d
(Hàm ngược của hàm cầu Q = d D(p)).
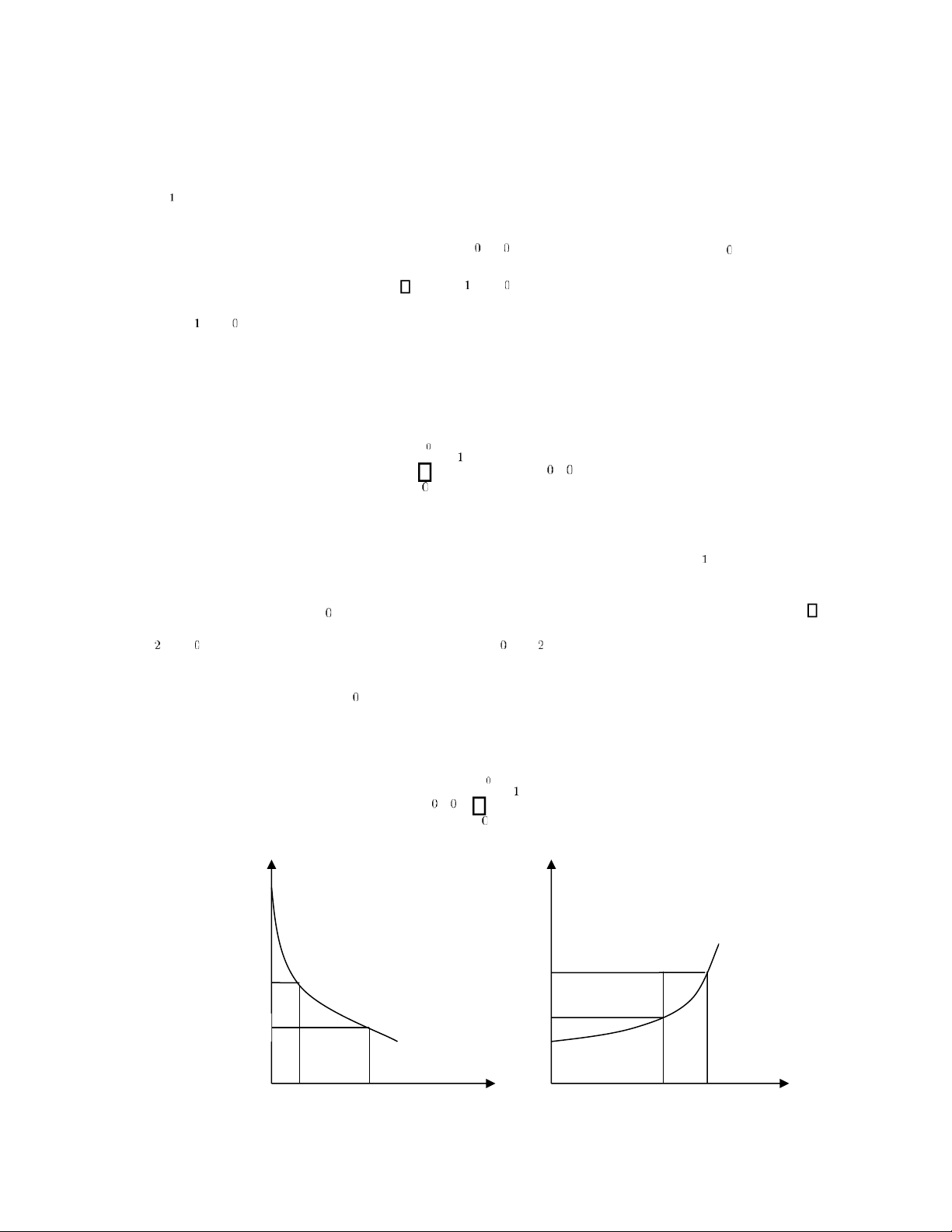
Giả sử iểm cân bằng của thị trường là (p ;Q ) và hàng hoá ược bán với giá p . Khi ó người
mua hàng lẽ ra bằng lòng trả giá p p , ược hưởng một khoản lợi cho mỗi sản phảm là p
p− . Tỏng số hưởng lợi của tất cả những người tiêu dùng bằng diện tích của tam giác cong.
Các nhà kinh tế gọi ó là thặng dư của người tiêu dùng(Consumers’ Surplus). Và ược tính theo công thức: Q
CS = D (Q)dQ− − pQ . Hàm cung Q = s
S(p) của thị trường cho biết lượng hàng hoá mà người bán bằng lòng bán
với mỗi mức giá p. Đường cung là ồ thị của hàm cung ảo p S (Q )= − s . Nếu hàng hoá ược
bán ở mức giá cân bằng p , thì những nhà sản xuất lẽ ra bằng lòng bán ở mức giá p p ,
ược hưởng một khoản lợi bằng: p p− (). Tổng số hưởng lợi của tất cả các nhà sản xuất bằng
diện tích tam giác cong BEp . Các nhà kinh tế gọi ó là thặng dư của nhà sản xuất
(Producers’ Surplus). Và ược tính bằng công thức: Q
PS = pQ − S (Q)dQ− A P 0 E E P B 16 lOMoAR cPSD| 49831834
Ví dụ 2.33. Cho các hàm cung và cầu: QS = p − 2;Qd = 43− p − 2
Hãy tínnh thặng dư của nhà sản xuất và thặng dư của người tiêu dùng.
Giải: Điều kiện: 2 p 43
Các hàm cầu ảo và cung ảo lần lượt là:
D (Q)−1 = 43− (Q + 2)2;S (Q−1) = (Q +1)2 + 2
Sản lượng cân bằng Qo là nghiệm dương của phương trình: D -1(Q) = S-1(Q) Qp o o ==183
Thặng dư sản xuất ược tính theo công thức:
PS=18x3− 3 (Q+1)2 +2 dQ = 27 0
Thặng dư tiêu dùng ược tính theo công thức:
CS = 3 43− +(Q 2)2 dQ−18x3=36 0 17