Thuật Toán DDA Trong Đồ Họa Máy Tính: Hệ Số Gốc và Ví Dụ môn Công nghệ thông tin | Trường Đại Học Nha Trang

lOMoAR cPSD| 58490434 DDA TH2: Hệ số gốc 0
- Xét đoạn thẳng có hệ số góc 0 < m ≤ dx < 0
- Với các đoạn thẳng dạng này, nếu (xi , yi ) là điểm đã xác định ở bước thứ i (điểm màu
đen) thì điểm cần chọn (x
) ở bước thứ (i + 1) là 1 trong 2 trường hợp của hình i + i , yi+1 vẽ sau:
- Với thuật toán DDA việc quyết định chọn yi+1 là yi hay yi+1 được dựa vào phương trình
đường thẳng y = mx + b. Nghĩa là ta sẽ tính: I (xi-1, y) thuộc về đường thẳng thực và y
sẽ là giá trị làm tròn của giá trị tung độ y thực. i+1
- Như vậy o y = mx +b o yI = mxI + b o y = m(xi -1) +b o y = mxi – m +b o y = (mxi + b) – m o ysau = ytrước – m - Lưu đồ thuật toán lOMoAR cPSD| 58490434 BD x1, y1, x2, y2, color dx = x2 - x1 dy = y2 – y1 m = (float) dy/dx x = x1 y = y1
Putpixel(x,int(y +0.5), color) S Đ x > x2 KT x = x - 1 y = y - m
Putpixel(x, int(y +0.5), color) i - xi yi ythực
Ví dụ A(8, 5) và B(4, 3) ta có m =0.5 0 8 5 5 - 1 7 5 4.5
o dx = 4 – 8 = -4 o dy = 3 - 5 = - 2 6 4 4 2 o m = dy / dx = -2/-4 = 0.5 3 5 4 3.5 o 4 4 3 3 xs = xt -1 o ys = yt – m
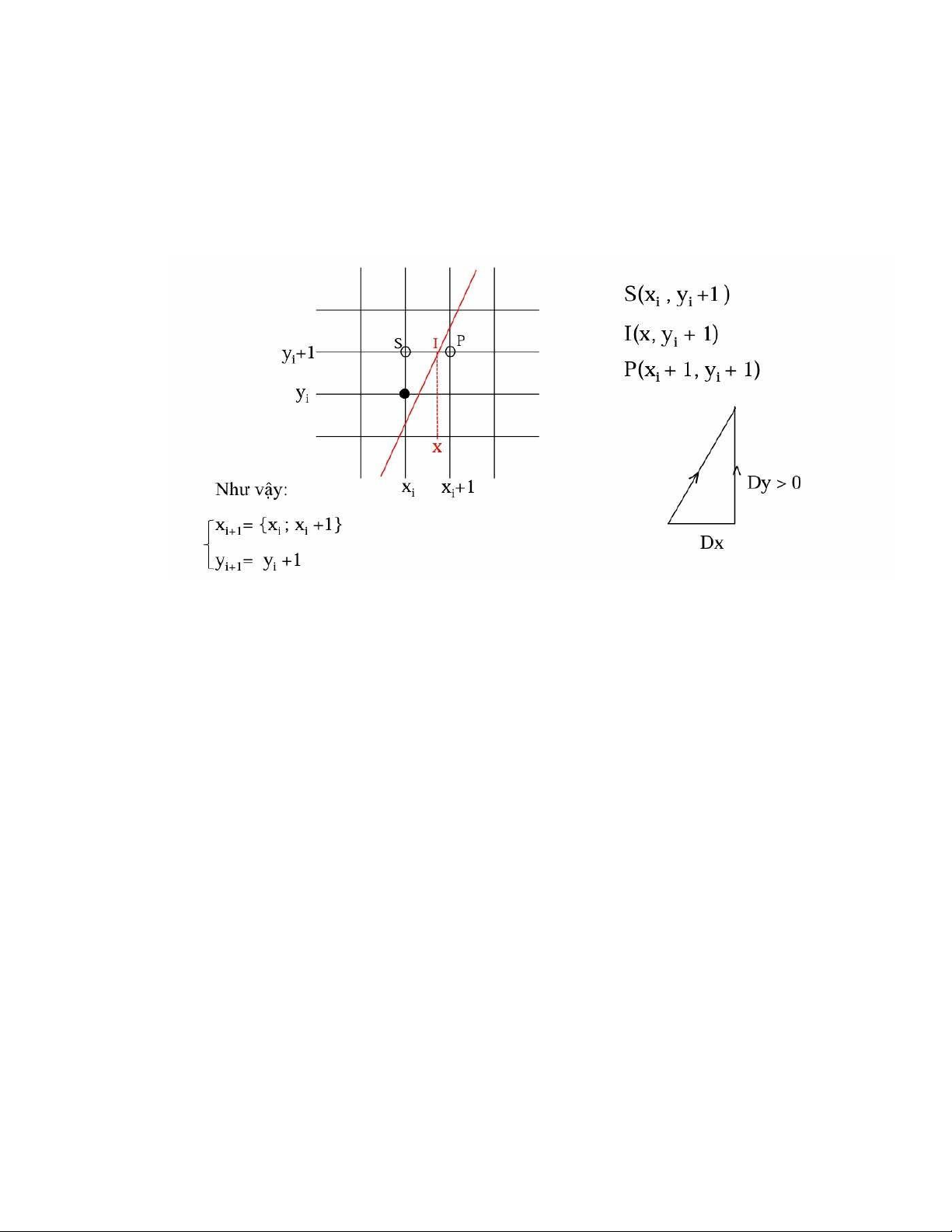
TH3: Hệ số gốc m>1 và dy > 0
- Xét đoạn thẳng có hệ số góc m>1 và dy > 0 lOMoAR cPSD| 58490434
- Với các đoạn thẳng dạng này, nếu (xi , yi ) là điểm đã xác định ở bước thứ i (điểm màu
đen) thì điểm cần chọn (x
) ở bước thứ (i + 1) là 1 trong 2 trường hợp của hình i + i , yi+1 vẽ sau:
- Với thuật toán DDA việc quyết định chọn xi+1 là xi hay xi+1 được dựa vào phương trình
đường thẳng y = mx + b. Nghĩa là ta sẽ tính: I (x, yi +1) thuộc về đường thẳng thực và x
sẽ là giá trị làm tròn của giá trị hoành độ x thực. i+1
- Như vậy o y = mx +b o yI = mxI + b o x –
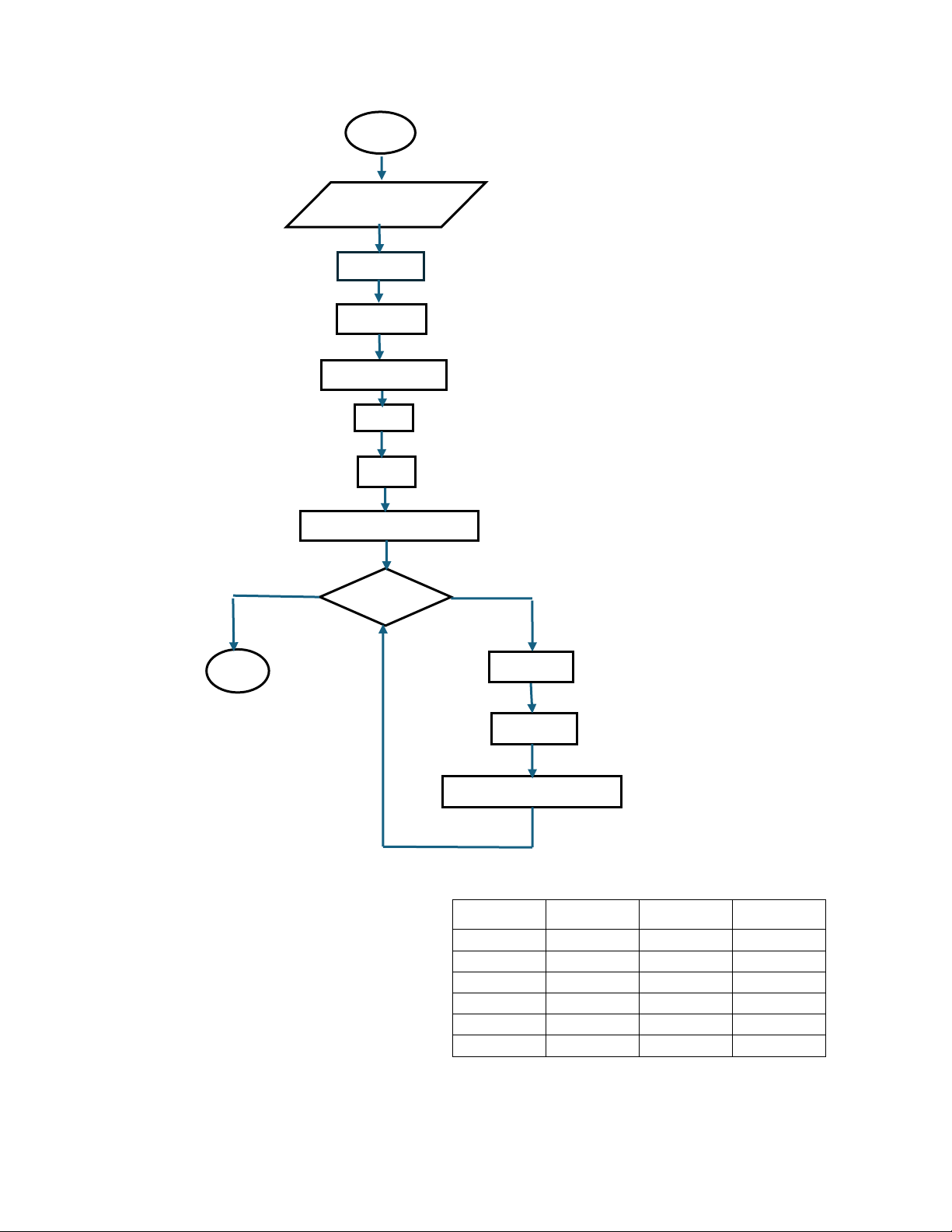
I = (yi b)/m o x = (yi +1 – b) /m o xsau = xtrước + 1/m - Lưu đồ thuật toán lOMoAR cPSD| 58490434 BD x1, y1, x2, y2, color dx = x2 - x1 dy = y2 – y1 m = (float) dy/dx x = x1 y = y1
Putpixel(x,int(y +0.5), color) y < y2 KT y = y +1 x = x + 1/m
Putpixel(x, int(y +0.5), color)
Ví dụ: A(2,5), B(6,10) với m= 1.25 - d i xi yi xthực x = 6 – 2 =4 - 0 2 5 2 dy = 10 -5 = 5 1 3 6 2.8 - m = 5/4 = 1.25 2 4 7 3.6 3 4 8 4.4 - x 4 5 9 5.2 s = xt +1/m 5 6 10 6 - ys = yt + 1
TH4: Hệ số gốc m>1 và dy < 0 lOMoAR cPSD| 58490434
- Xét đoạn thẳng có hệ số góc m>1 và dy < 0
- Với các đoạn thẳng dạng này, nếu (xi , yi ) là điểm đã xác định ở bước thứ i (điểm màu
đen) thì điểm cần chọn (x
) ở bước thứ (i + 1) là 1 trong 2 trường hợp của hình i + i , yi+1 vẽ sau:
- Với thuật toán DDA việc quyết định chọn xi+1 là xi hay xi-1 được dựa vào phương trình
đường thẳng y = mx + b. Nghĩa là ta sẽ tính: I (x, yi - 1) thuộc về đường thẳng thực và x sẽ là giá trị i+1
làm tròn của giá trị hoành độ x thực. - Như vậy o y = mx + b o yi = mxi + b o xI = (yI – b)/m o x = (y – i 1 – b)/m o xsau = xtrước – 1/m - Lưu đồ thuật toán lOMoAR cPSD| 58490434 BD x1, y1, x2, y2, color dx = x2 - x1 dy = y2 – y1 m = (float) dy/dx x = x1 y = y1
Putpixel(x,int(y +0.5), color) y > y2 KT y = y - 1 x = x - 1/m
Putpixel(x, int(y +0.5), color) -
dx = 1 – 5 = -4 dy = 4 – 9 = -5 i xi yi xthực
m = -5/-4 = 1.25 Xs = Xt – 1/m 0 5 9 5 1 4 8 4.2 Ys = Yt - 1 2 3 7 3.4 3 3 6 2.6 4 2 5 1.8 5 1 4 1
TH5: Hệ số gốc -1 0
- Xét đoạn thẳng có hệ số góc -1 0 lOMoAR cPSD| 58490434
- Với các đoạn thẳng dạng này, nếu (xi , yi ) là điểm đã xác định ở bước thứ i (điểm màu
đen) thì điểm cần chọn (x
) ở bước thứ (i + 1) là 1 trong 2 trường hợp của hình vẽ i + i , yi+1 sau:
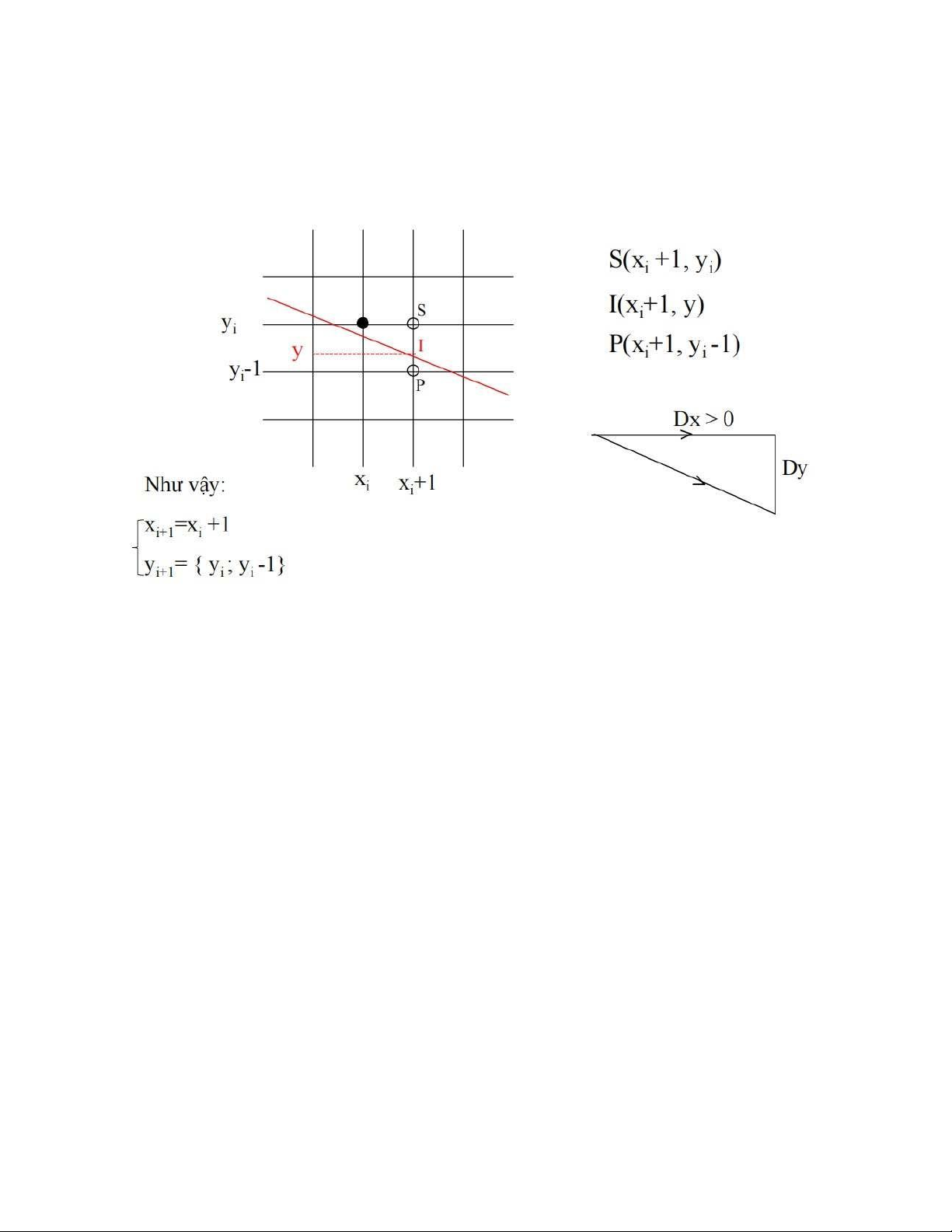
- Với thuật toán DDA việc quyết định chọn yi+1 là yi hay yi-1 được dựa vào phương trình
đường thẳng y = mx + b. Nghĩa là ta sẽ tính: I (xi +1, y) thuộc về đường thẳng thực và yi+1
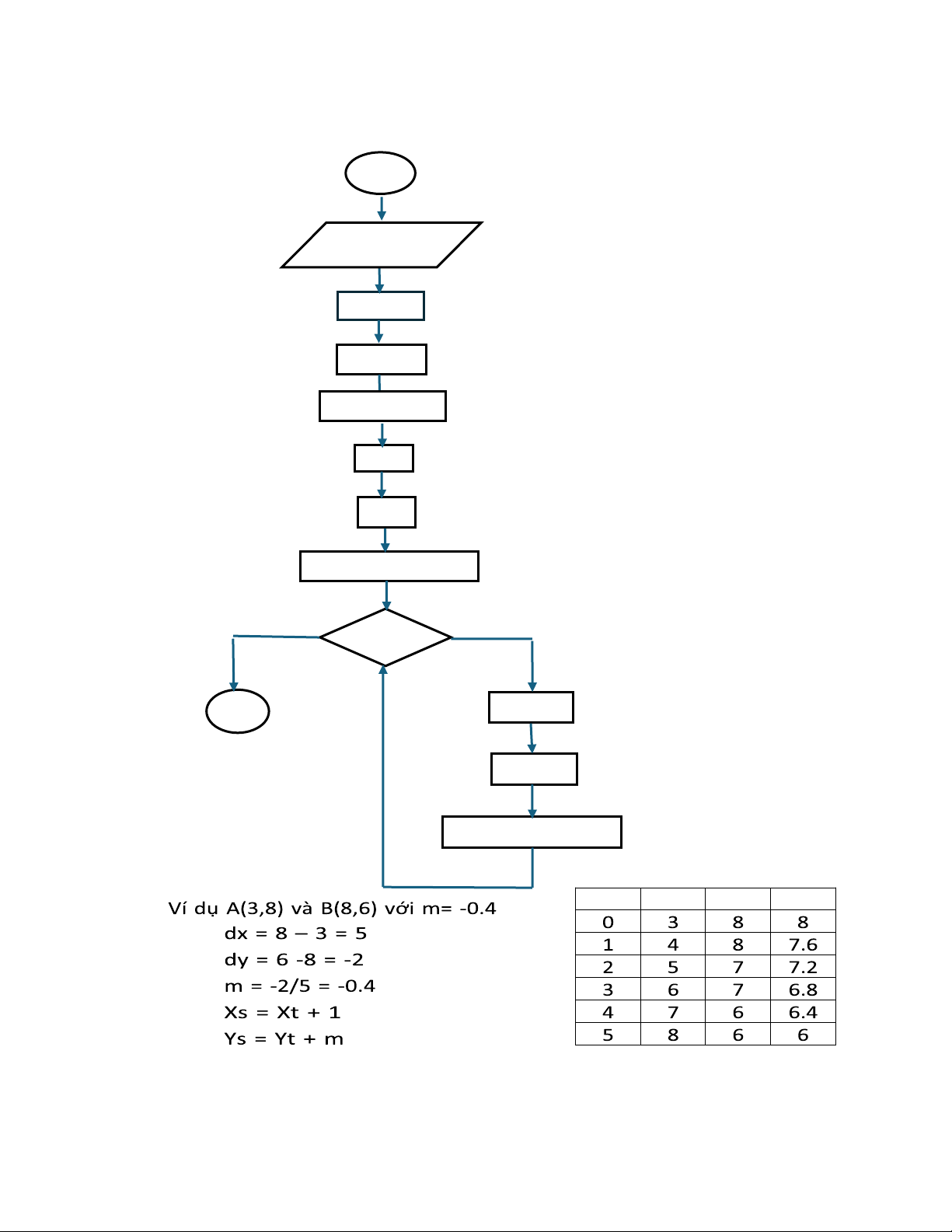
sẽ là giá trị làm tròn của giá trị tung độ y thực. - Như vậy o Y = mx + b o yI = mxI + b o y = m(xi +1 ) + b o y = mxi + m + b o ysau = ytrước + m lOMoAR cPSD| 58490434 - Lưu đồ thuật toán BD x1, y1, x2, y2, color dx = x2 - x1 dy = y2 – y1 m = (float) dy/dx x = x1 y = y1
Putpixel(x,int(y +0.5), color) x < x2 KT x=x + 1 y = y + m
Putpixel(x, int(y +0.5), color) i - x i y i Ythực o o o o o TH6: Hệ số gốc -1
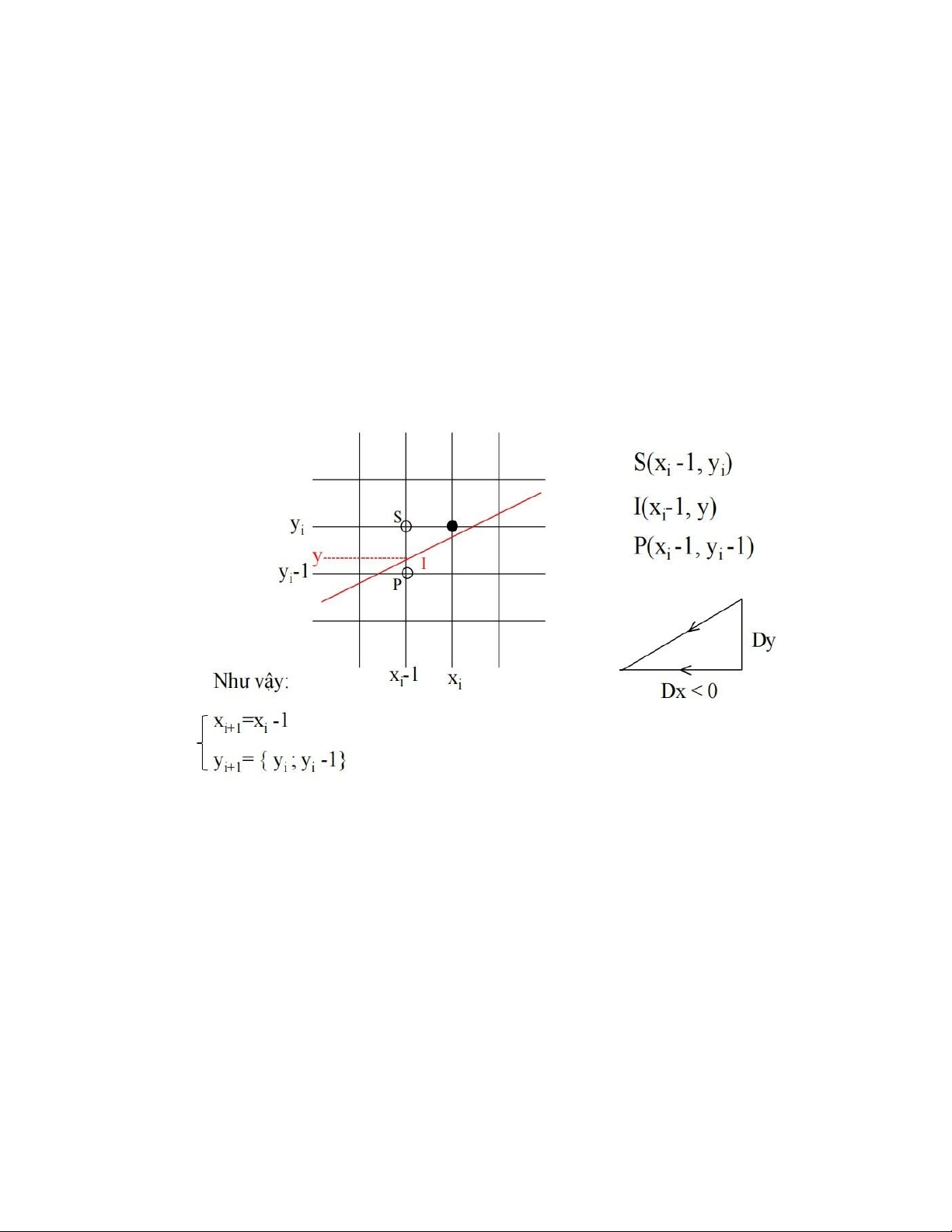
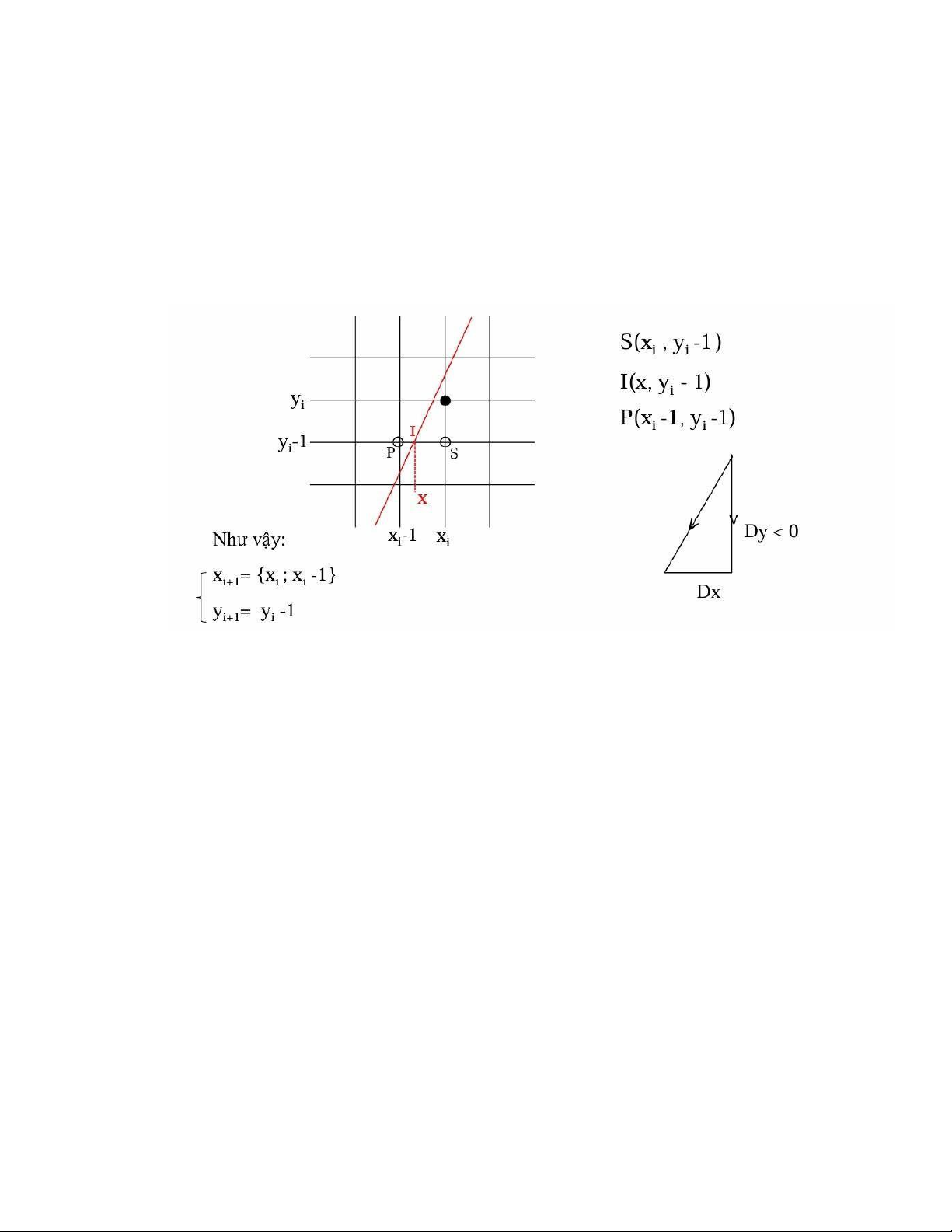
- Xét đoạn thẳng có hệ số góc -1 lOMoAR cPSD| 58490434
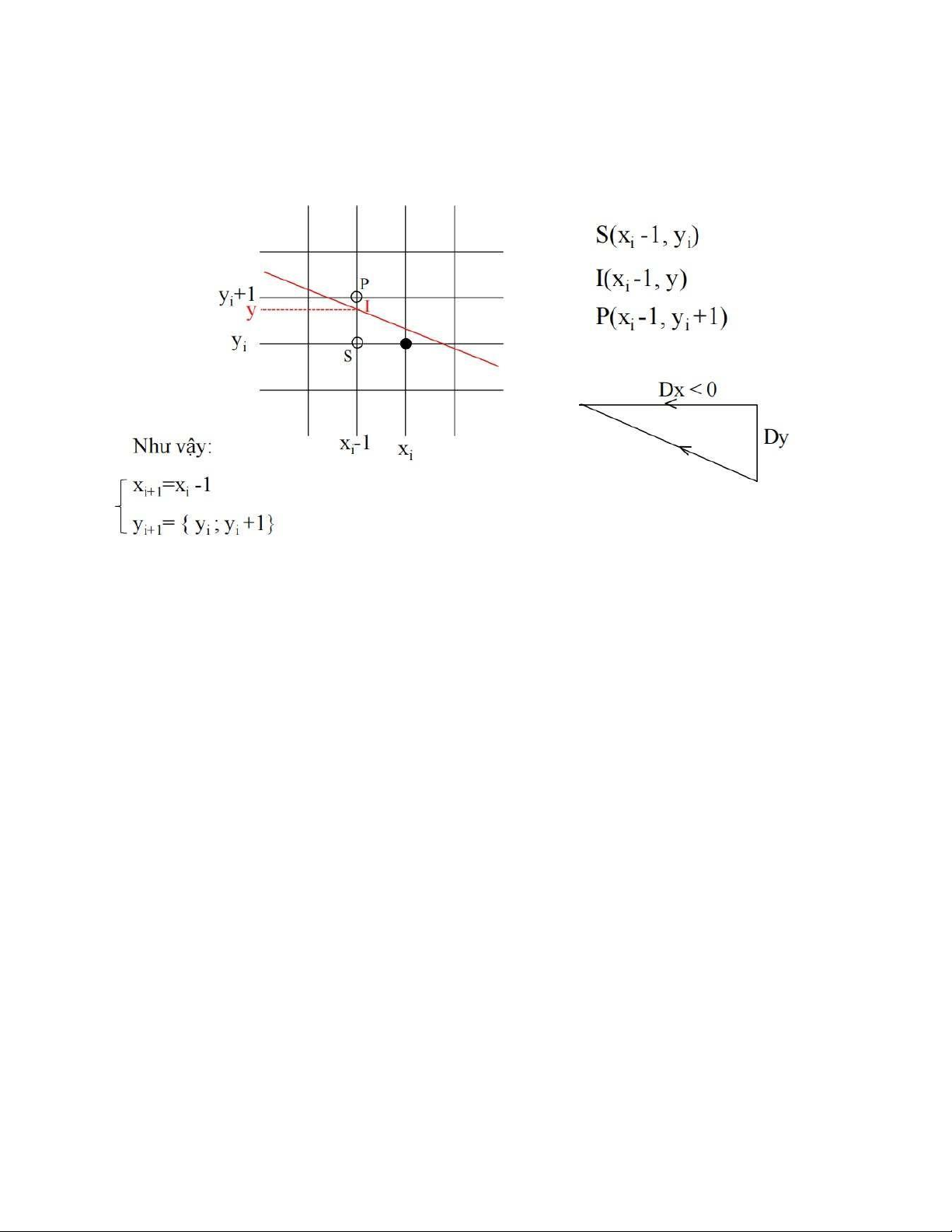
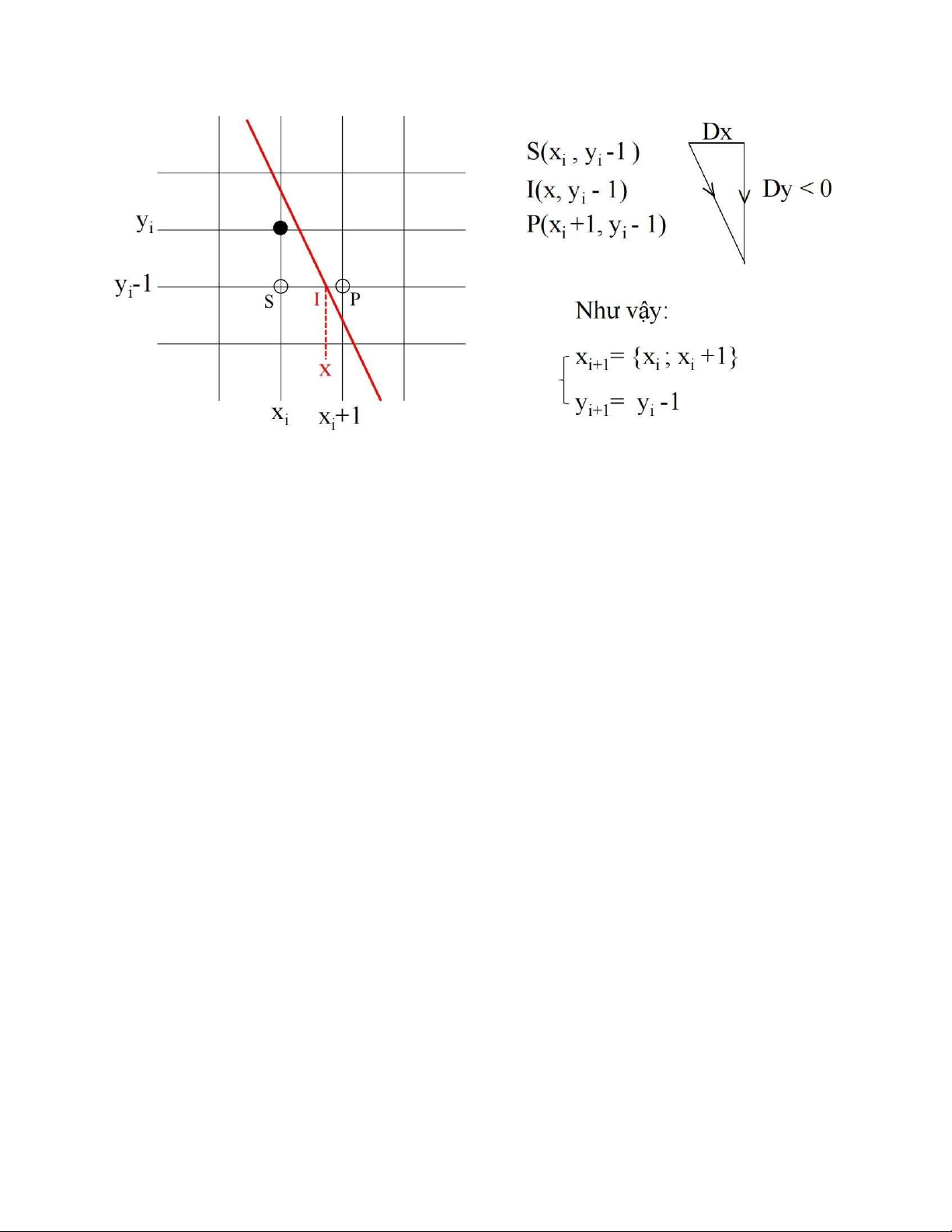
- Với các đoạn thẳng dạng này, nếu (xi , yi ) là điểm đã xác định ở bước thứ i (điểm màu
đen) thì điểm cần chọn (x
) ở bước thứ (i + 1) là 1 trong 2 trường hợp của hình vẽ i + i , yi+1 sau:
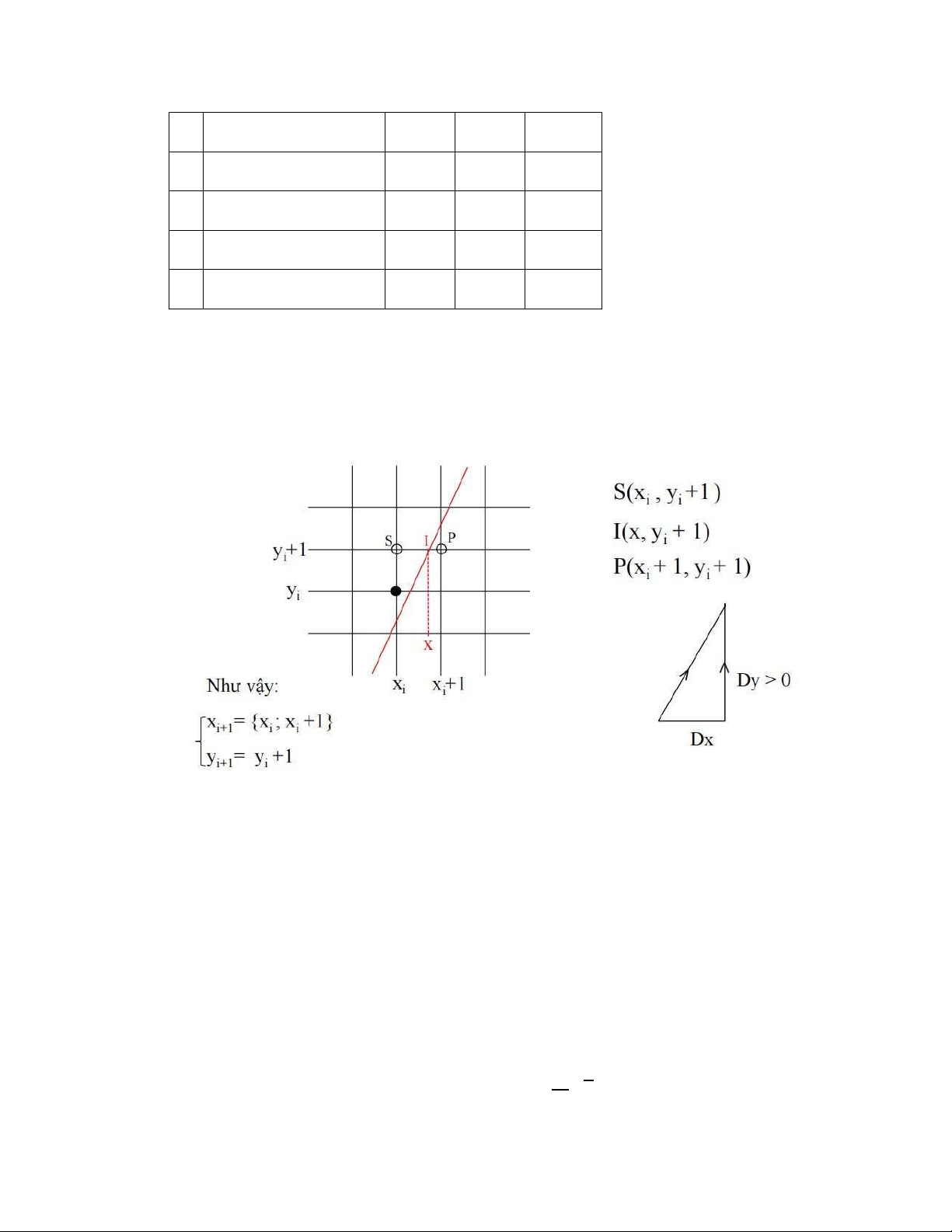
- Với thuật toán DDA việc quyết định chọn yi+1 là yi hay yi+1 được dựa vào phương trình
đường thẳng y = mx + b. Nghĩa là ta sẽ tính: I (xi -1, y) thuộc về đường thẳng thực và yi+1
sẽ là giá trị làm tròn của giá trị tung độ y thực. - Như vậy o y = mx +b
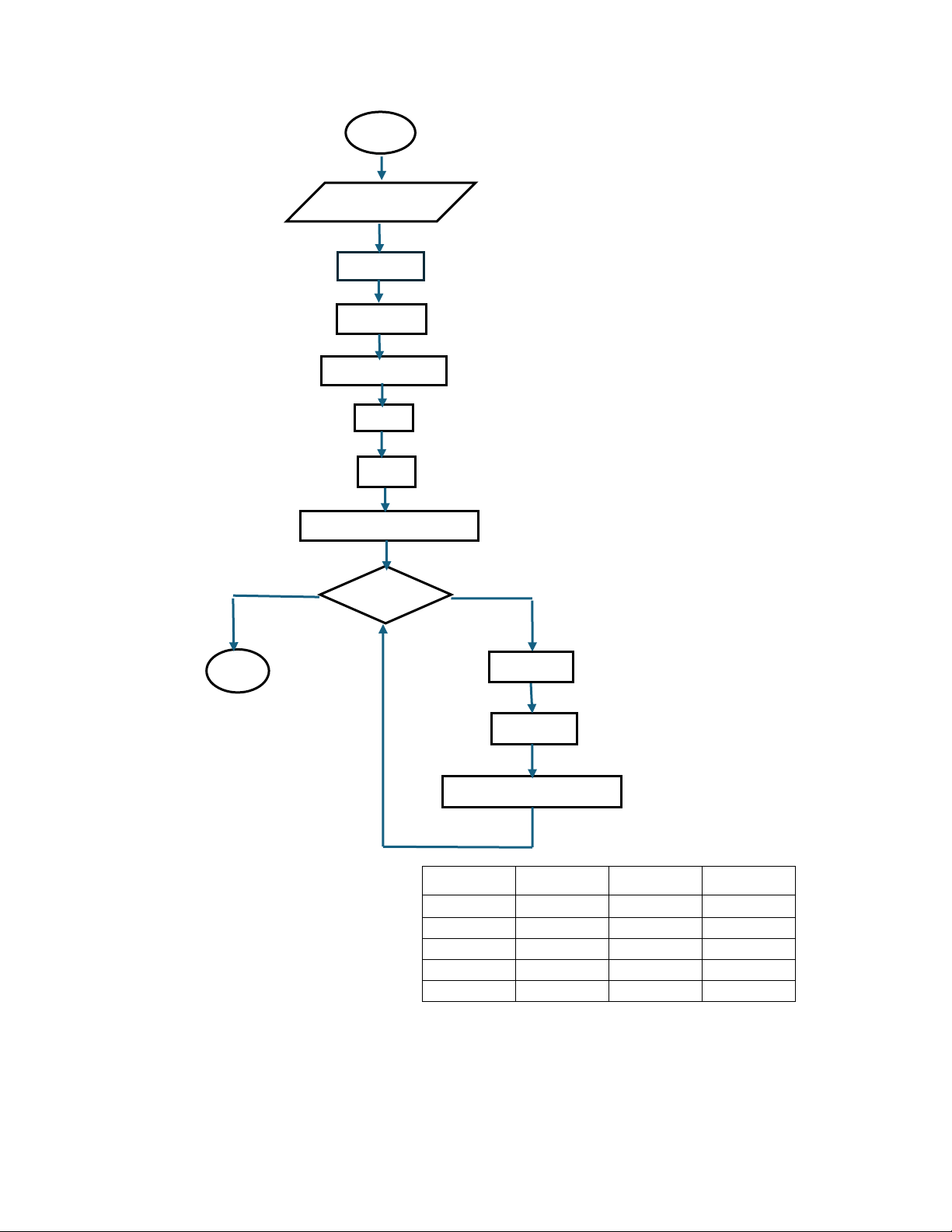
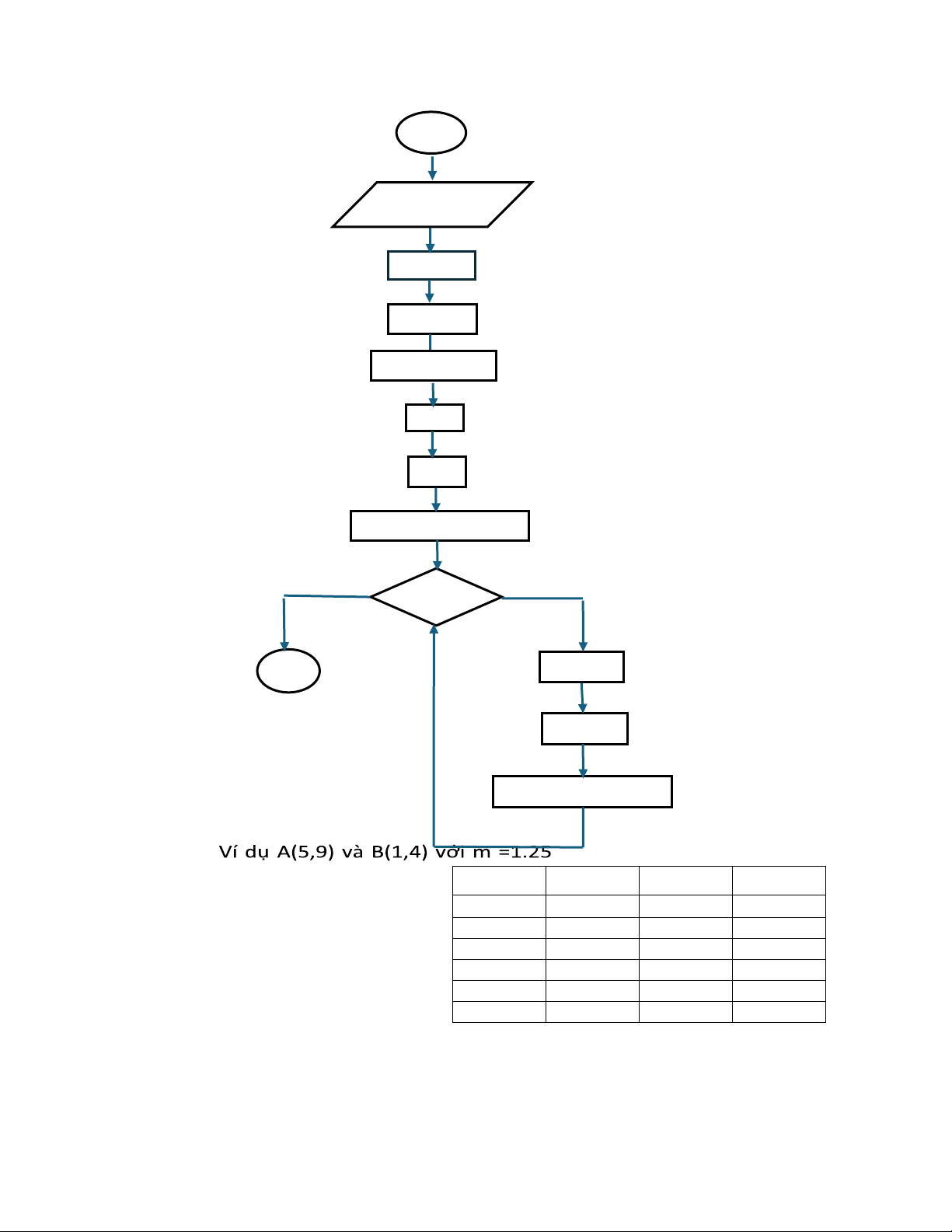
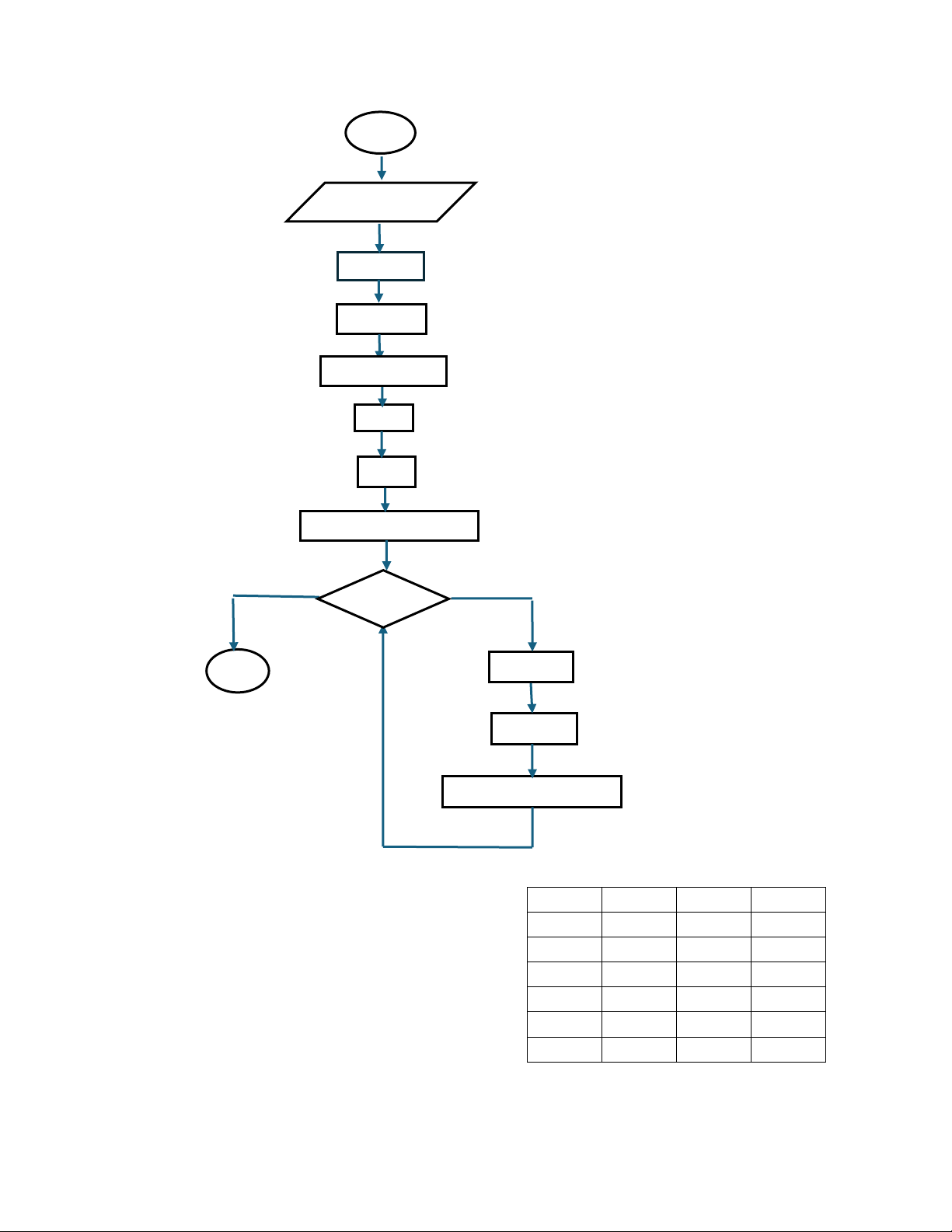
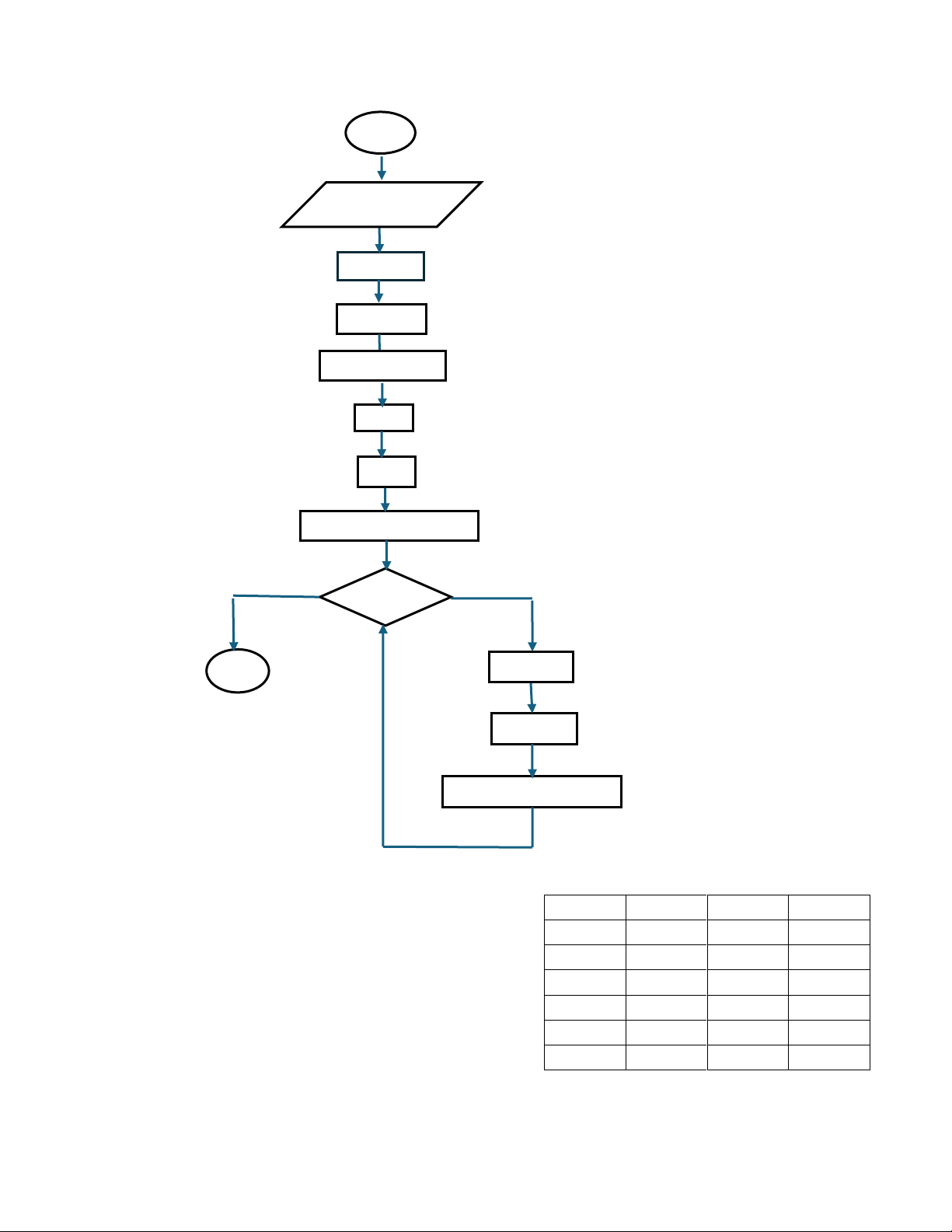
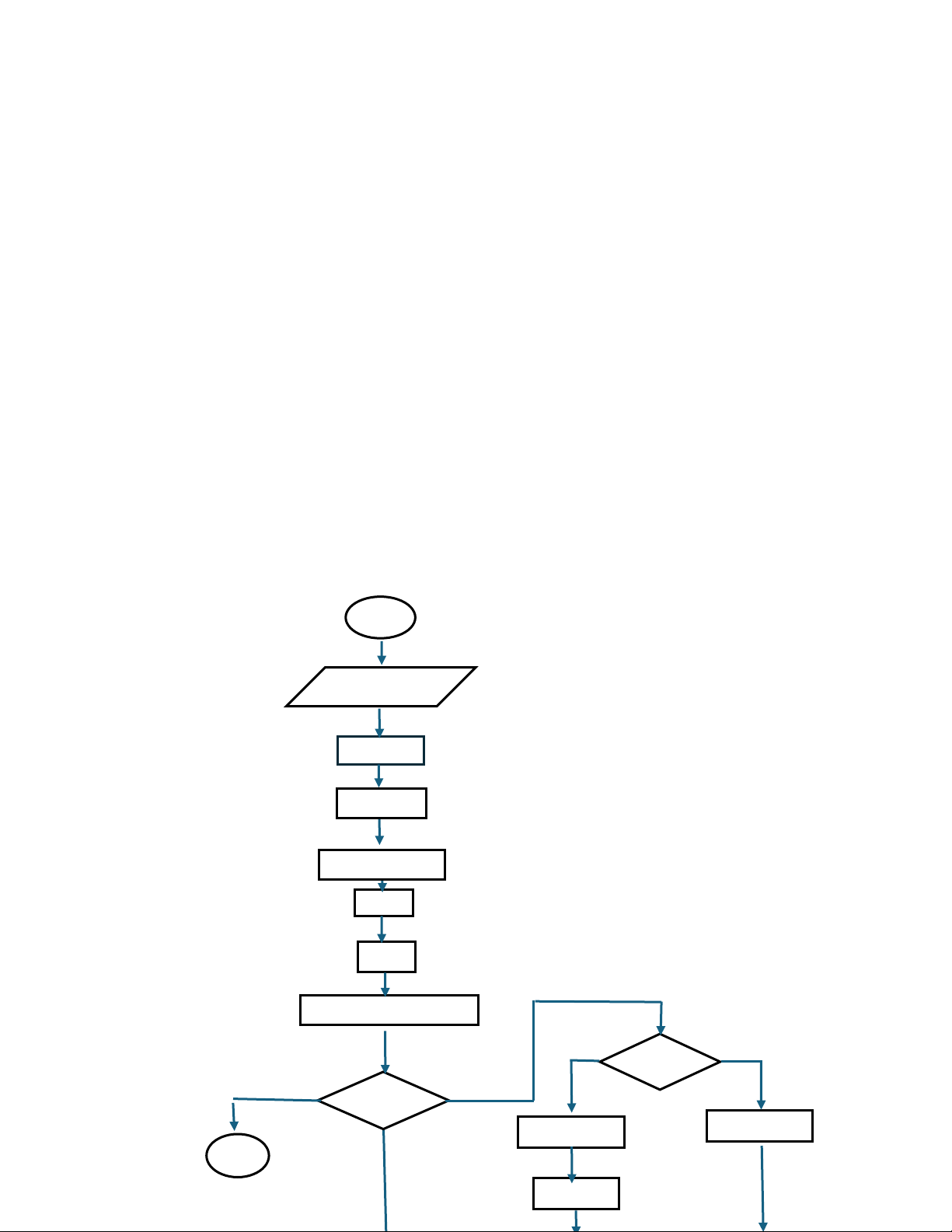
o yI = mxI + b o y = m(xi -1) +b o y = mxi – m +b o ysau = ytrước - m - Lưu đồ thuật toán lOMoAR cPSD| 58490434 BD x1, y1, x2, y2, color dx = x2 - x1 dy = y2 – y1 m = (float) dy/dx x = x1 y = y1
Putpixel(x,int(y +0.5), color) x > x2 KT x = x - 1 y = y - m
Putpixel(x, int(y +0.5), color)
- Ví dụ A(7,6) và B(2,10) với m = -0.8 o dx = 2 i xi yi Ythực
- 7 = -5 o dy = 10 – 6 = 4 o m = dy/dx = 4/-5 0 7 6 6
= -0.8 o Xs = Xt – 1 o Ys = Yt - m 1 6 6 6.8
TH7: Hệ số gốc m < 2 5 7 7.6 -1 và dy > 3 4 8 8.4 0 4 3 9 9.2 5 2 10 10
- Xét đoạn thẳng có hệ số góc m < -1 và dy > 0 lOMoAR cPSD| 58490434
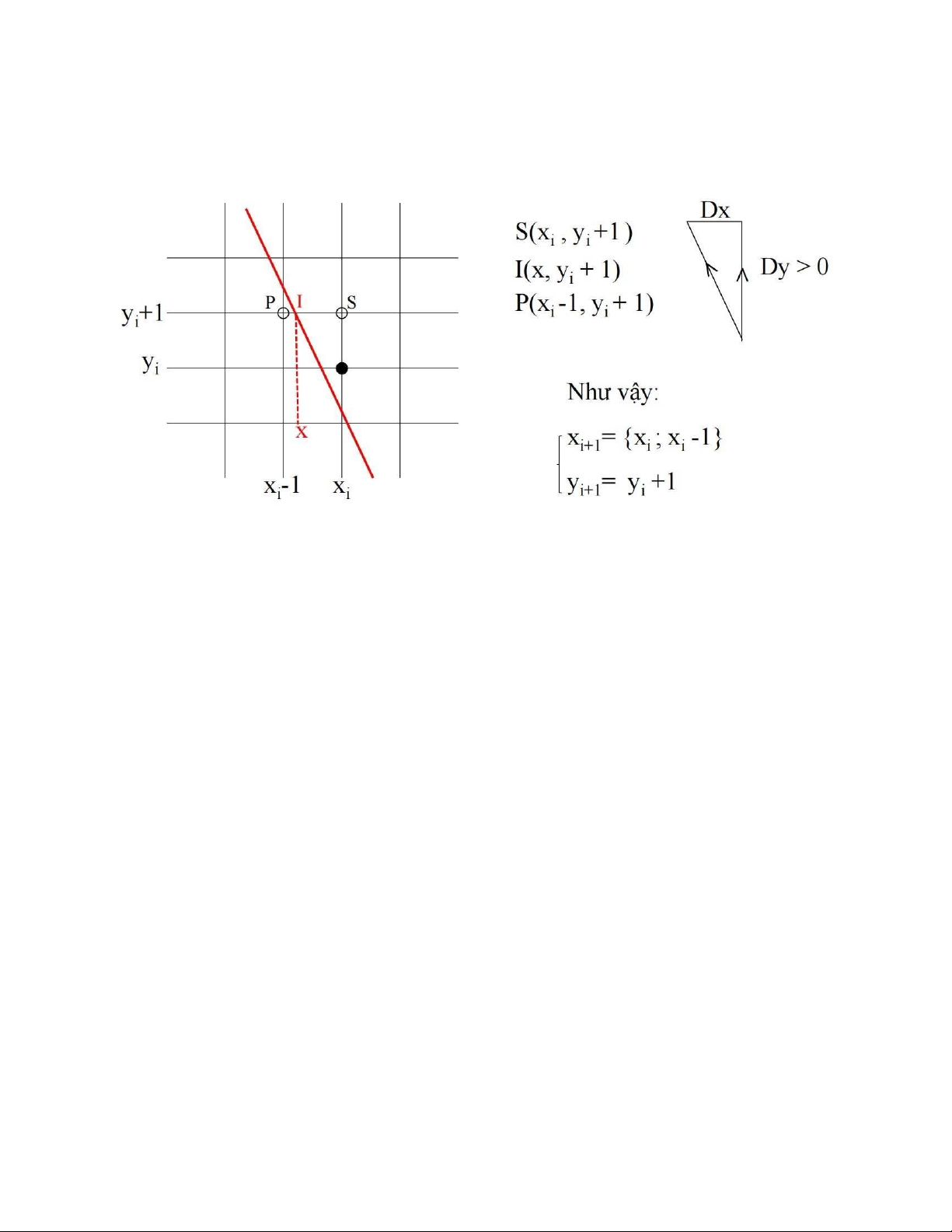
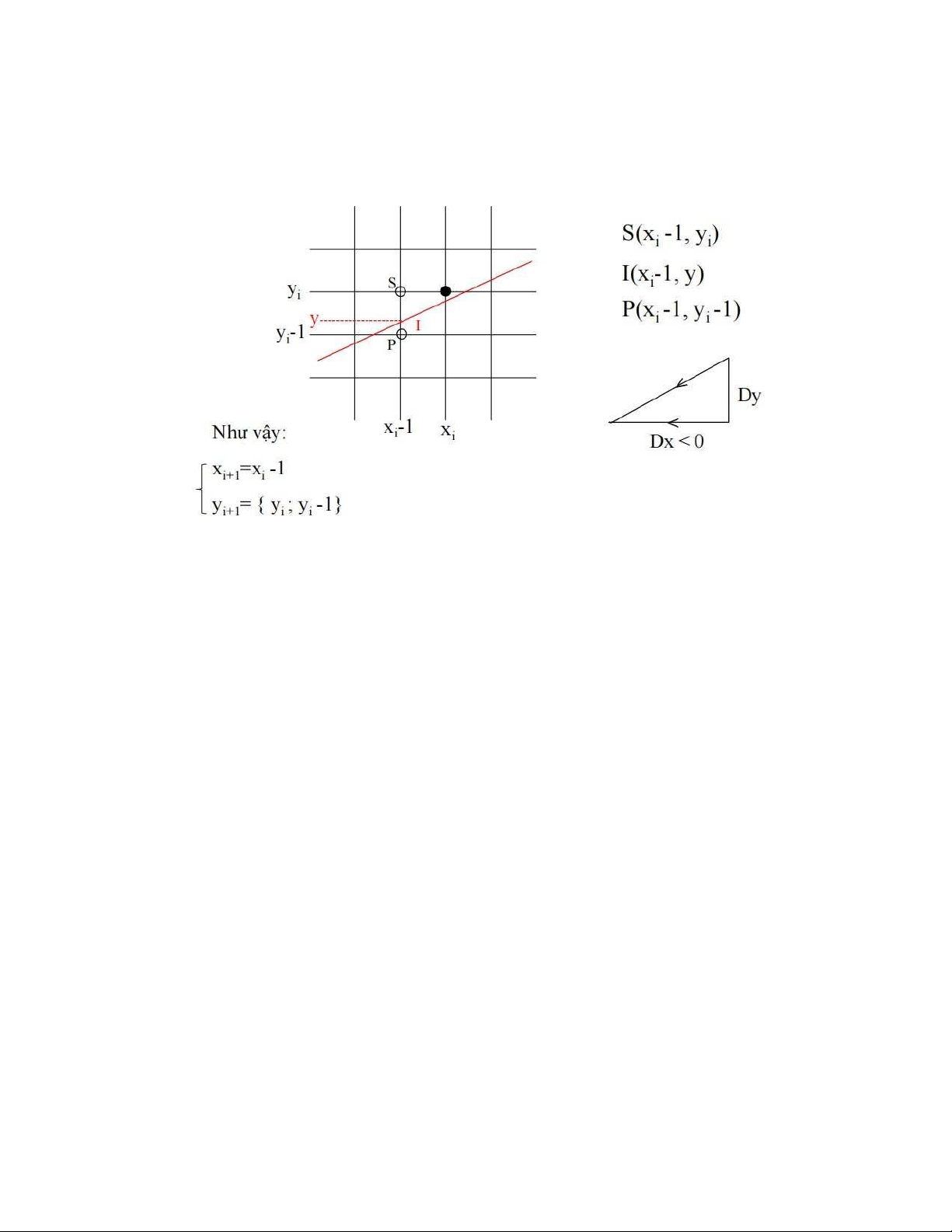
- Với các đoạn thẳng dạng này, nếu (xi , yi ) là điểm đã xác định ở bước thứ i (điểm màu
đen) thì điểm cần chọn (x
) ở bước thứ (i + 1) là 1 trong 2 trường hợp của hình vẽ i + i , yi+1 sau:
- Với thuật toán DDA việc quyết định chọn xi+1 là xi hay xi-1 được dựa vào phương trình
đường thẳng y = mx + b. Nghĩa là ta sẽ tính: I (x, yi +1) thuộc về đường thẳng thực và xi+1
sẽ là giá trị làm tròn của giá trị hoành độ x thực.
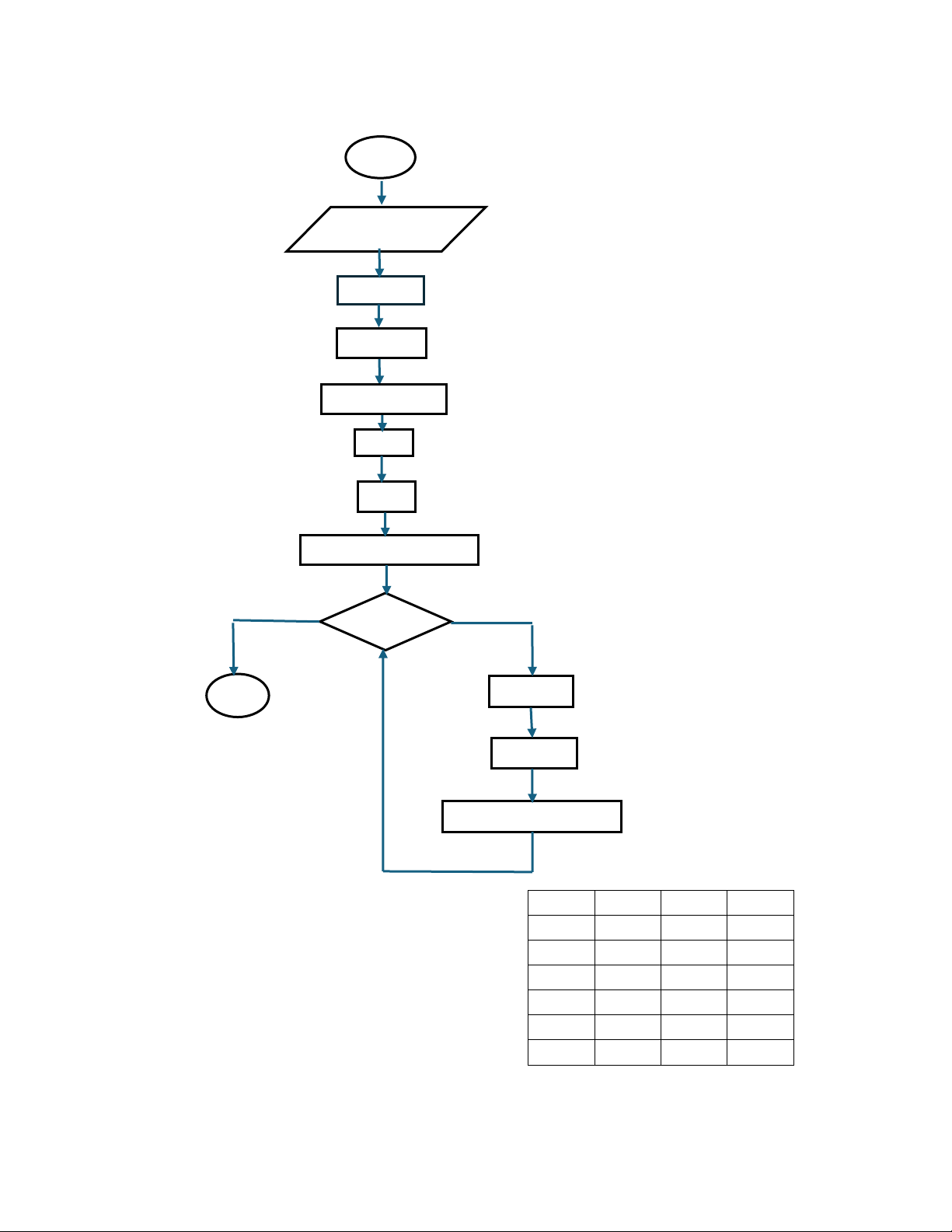
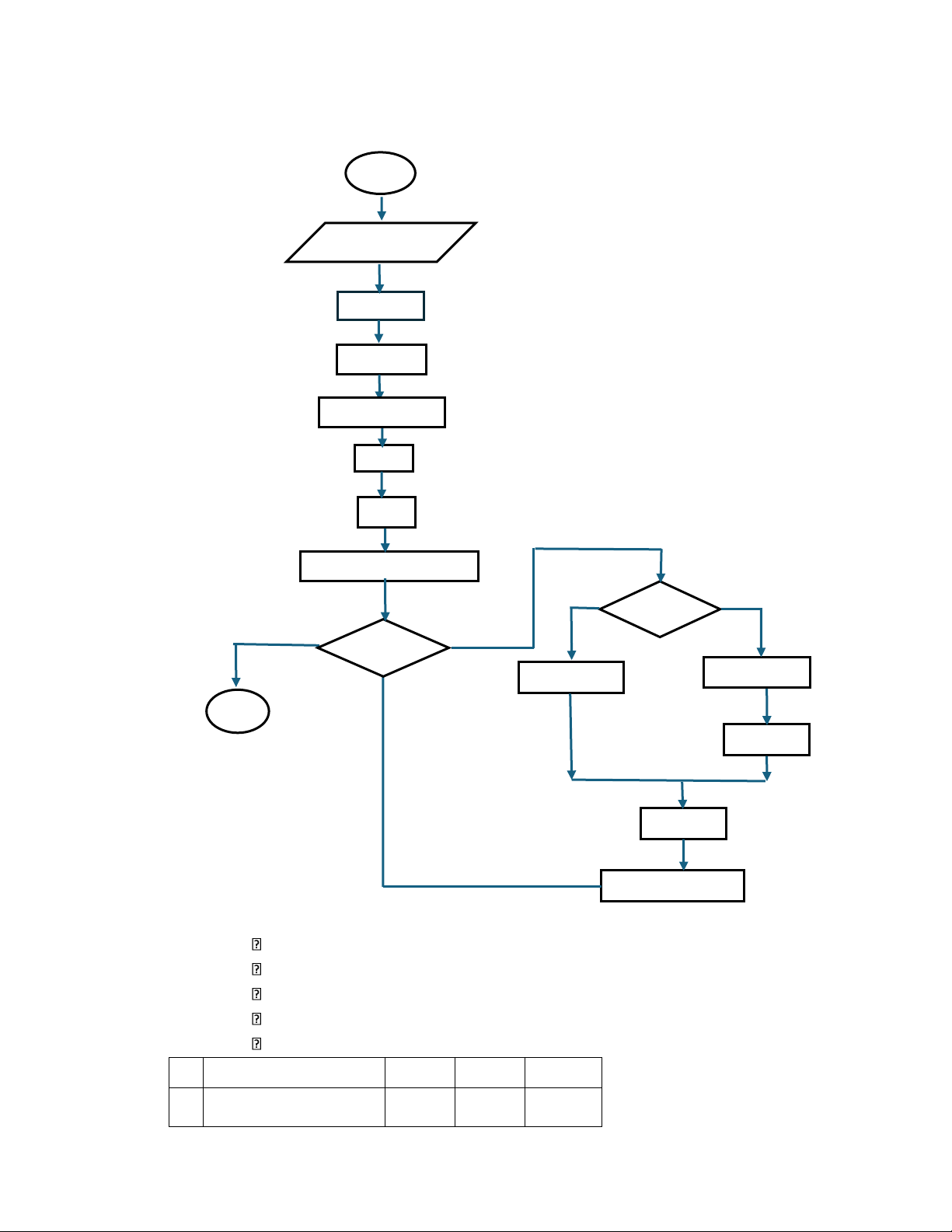
- Như vậy o y = mx + b o yI = mxI + b o x – I = (yI b )/m o x = (yi + 1 - b)/m o x = (yi – b)/m +1/m o xsau = xtrước + 1/m lOMoAR cPSD| 58490434 - Lưu đồ thuật toán BD x1, y1, x2, y2, color dx = x2 - x1 dy = y2 – y1 m = (float) dy/dx x = x1 y = y1
Putpixel(x,int(y +0.5), color) y < y2 KT y = y +1 x = x + 1/m
Putpixel(x, int(y +0.5), color)
- Ví dụ A(5,4) và B(1, 9) với m = -1.25 o dx = 1 i xi yi Xthực – 5 = -4 o dy = 9 – 4 = 5 0 5 4 5
o m = 5/ -4 = -1,25 o Xs = Xt + 1/m o Ys = Yt 1 4 5 4.2 + 1 2 3 6 3.4
TH8: Hệ số gốc m< 3 3 7 2.6 -1 và dy<0 4 2 8 1.8
- Xét đoạn thẳng có hệ số góc m<-1 và dy<0 5 1 9 1
- Với các đoạn thẳng dạng này, nếu (xi , yi ) là điểm đã xác định ở bước thứ i (điểm màu
đen) thì điểm cần chọn (x
) ở bước thứ (i + 1) là 1 trong 2 trường hợp của hình vẽ i + i , yi+1 sau: lOMoAR cPSD| 58490434
- Với thuật toán DDA việc quyết định chọn xi+1 là xi hay xi+1 được dựa vào phương trình
đường thẳng y = mx + b. Nghĩa là ta sẽ tính: I (x, yi -1) thuộc về đường thẳng thực và xi+1
sẽ là giá trị làm tròn của giá trị hoành độ x thực. - Như vậy o y = mx +b o y – –
I = mxI + b o xI = (yI b )/m o x = (yi 1 – b )/ m
o x = (yi – b)/m – 1/m o xsau = Xtrước – 1/m - Lưu đồ thuật toán lOMoAR cPSD| 58490434 BD x1, y1, x2, y2, color dx = x2 - x1 dy = y2 – y1 m = (float) dy/dx x = x1 y = y1
Putpixel(x,int(y +0.5), color) y > y2 KT y = y - 1 x = x - 1/m
Putpixel(x, int(y +0.5), color)
- Ví dụ A(1,9) và B(5,4) với m o dx = 5 – 1 = 4 o dy = 4 – 9 = -5 o m = dy/dx = -5/4 = - 1.25 i xi yi Xthực
o Xs = Xt – 1/m o Ys = Yt - 1 0 1 9 1 1 2 8 1.8 BRESENHAM 2 3 7 2.6 3 3 6 3.4 TH2: Hệ số gốc 0 4 4 5 4.2 dx < 0 5 5 4 5
- Bresenham vẽ đoạn thẳng đi qua 2 điểm (x1 ,y1 ), (x2 ,y2 ) có 0 < m < 1 và dx > 0 lOMoAR cPSD| 58490434
- Với các đoạn thẳng dạng này, nếu (xi, yi) là điểm đã xác định ở bước thứ i (điểm màu
đen) thì điểm cần chọn (xi+1 , yi+1 ) ở bước thứ (i + 1) là 1 trong 2 trường hợp của hình vẽ sau:
- Với thuật toán Bresenham, việc quyết định chọn yi+1 là yi hay yi -1 được dựa vào vị trí
tương đối của điểm I so với điểm S hay điểm P - Đặt o d1 = SI = yi – y o d2 = IP = y – yi + 1
- Việc chọn điểm vẽ (x
) là điểm S hay P được dựa vào việc so sánh d1 và d2 o i+1 , yi+1
Nếu d1 < d2: Chọn S o Nếu d1 ≥ d2: chọn P - Ta có:
o d1 – d2 = yi – y –( y – yi
+ 1) o d1 - d2 = yi – y – y + yi -1 o d1 – d2 = -2y + 2yi -1 - Với y = mx + b
o d1 – d2 = -2(mx + b) + 2yi - 1 o d1 – d2 = -2mx -2b + 2yi - 1
- Ta thấy m là số thực nên việc tính toán chậm. Do đó thay vì xét dấu d1 – d2 ta xét dấu đại
lượng có giá trị nguyên khác có quan hệ với d1 – d2 và khử Dx
- Đặt pi = dx(d1 – d2) o pi = dx(-2y + 2yi -1) - Mà y = mx + b o yI = mxI + b o y = m(xi - 1) +b o y = dy/dx(xi – 1) + b - Suy ra lOMoAR cPSD| 58490434 o pi = dx(-2y + 2yi -1)
o pi = -2dxy + 2dx yi - dx dy
o pi = -2dx(dx(xi -1) +b) + 2dxyi - dx o
pi = -2dyxi + 2dy - 2bdx + 2dxyi - dx o p + C (với C = 2dy i = -2dyxi + 2dxyi
+ 2bdx - dx) I(xi-1, y) - Ta có o pi = -2dyxi + 2dxyi + C (1)
o pi+1 = -2dyxi+1 + 2dxyi+1 + C (2)
- Lấy (2) – (1) ta được
o pi+1 - pi = 2dx(yi+1 - yi ) – 2dy(xi+1 - xi ) o pi+1 - pi = 2dx(yi+1 - yi ) – 2dy(xi -1 - xi ) o
pi+1 = pi + 2dy + 2dx(yi+1 - yi )
- Từ đây ta suy ra được cách tính pi+1 từ pi như sau:
o Nếu pi < 0 thì dx(d1-d2) < 0
d1-d2 > 0 => d1 > d2
=> Chọn P => yi+1 = yi – 1
pi+1 = pi + 2dy - 2dx o Nếu pi ≥ 0 thì dx(d1-d2) ≥ 0
d1 - d2 ≤0 => d1≤ d2
=> Chọn S => yi+1= yi pi+1 = pi +2dy
- Giá trị p0 được tính từ điểm vẽ đầu tiên là (x1, y1)
o pi = -2dyxi + 2dy - 2bdx + 2dxyi - dx o p0 = -2dyx1 + 2dy -
2bdx + 2dxy1 - dx o p0 = -2dyx1 + 2dy - 2bdx + 2dx(mx1+b) -
dx o p0 = -2dyx1 + 2dy - 2bdx + 2dxmx1 + 2bdx -dx
o p0 = -2dyx1 + 2dy - 2bdx + 2dyx1 + 2bdx – dx(với m = dy/dx
=> dy = mdx) o p0 = 2dy -dx lOMoAR cPSD| 58490434 - Lưu đồ thuật toán BD x1, y1, x2, y2, color dx = x2 - x1 dy = y2 – y1 p = 2dy - dx x = x1 y = y1 Putpixel(x,y, color) S Đ p < 0 S Đ x > x2 p += 2dy -2dx p += 2dy KT y = y - 1 x = x- 1 Putpixel(x, y, color) -
Ví dụ vẽ đoạn thẳng AB, A(9,5) và B(4,3) o Ta có dx = 4 -9 = -5 dy = 3 -5 = -2 po = 2dy -dx =2(-2) + 5 =1
const1 = 2dy -2dx = 2(-2) -2(-5) =6 const2 = 2dy = 2*-2 = -4 i pi xi yi (x,y) 0 1 9 5 (9,5) lOMoAR cPSD| 58490434 1 -3 8 5 (8,5) 2 3 7 4 (7,4) 3 -1 6 4 (6,4) 4 5 5 3 (5,3) 5 1 4 3 (4,3)
TH3: Hệ số gốc m>1 và dy > 0 -
Bresenham vẽ đoạn thẳng đi qua 2 điểm (x1 ,y1 ), (x2 ,y2 ) có m>1 và dy > 0 -
Với các đoạn thẳng dạng này, nếu (xi, yi) là điểm đã xác định ở bước thứ i (điểm màu
đen) thì điểm cần chọn (xi+1 , yi+1 ) ở bước thứ (i + 1) là 1 trong 2 trường hợp của hình vẽ sa u: -
Với thuật toán Bresenham, việc quyết định chọn xi+1 là xi hay xi +1 được dựa vào vị trí
tương đối của điểm I so với điểm S hay điểm P - Đặt o d1 = IS = x - x o i d2 = PI = xi + 1 – x - Việc chọn điểm vẽ (x
) là điểm S hay P được dựa vào việc s i+1 , yi+1 o sánh d1 và d2 o
Nếu d1 < d2: Chọn S o Nếu d1 ≥ d2: chọn P - Ta có:
o d1 – d2 = x - xi - (yi + 1 – x) o d1 -
d2 = x - xi - xi -1 + x o d1 – d2 = 2x - 2xi - 1 b -
Với y = mx + b => x = (y – b )/m o d1 – d2 = 2( y−m ) - 2xi - 1 lOMoAR cPSD| 58490434 -
Ta thấy m là số thực nên việc tính toán chậm. Do đó thay vì xét dấu d1 – d2 ta xét dấu
đại lượng có giá trị nguyên khác có quan hệ với d1 – d2 và khử Dy -
Đặt pi = dy(d1 – d2) o pi = dy(2x -2xi - 1) -
Mà y = mx + b => x = (y – b )/m o y –
I = mxI + b o xI = (yI b )/m o x = (yi +1 – b)/m o
x = yi+dy1−bdx - Suy ra
o pi = dy(2x -2xi - 1) o pi = 2dyx – 1−b 2dyx –
i dy o pi = 2dy( yi+dy dx) - 2dyx –
i dy o pi = 2dx(yi +1 – b) - 2dyx –
i dy o pi = 2dxyi + 2dx – 2dbx - 2dyx –
i dy o pi = 2dxyi - 2dyxi + C
(Với C= 2dx – 2dxb - dy ) I(x, yi+1) - Ta có
o pi = 2dxyi - 2dyxi + C (1)
o pi+1 = 2dxyi+1 - 2dyxi +1 + C (2) - Lấy (2) – (1) ta được
o pi+1 - pi = 2dx(yi+1 - yi ) – 2dy(xi +1 - xi
) o pi+1 - pi = 2dx(yi +1 - yi ) –
2dy(xi +1 - xi ) o pi+1 = pi + 2dx - 2dy(xi +1 - xi ) -
Từ đây ta suy ra được cách tính pi+1 từ pi như sau:
o Nếu pi < 0 thì dy(d1-d2) < 0
d1- d2 < 0 => d1 < d2
=> Chọn S => xi +1 = xi
pi+1 = pi + 2dx o Nếu pi ≥ 0 thì dy(d1-d2) ≥ 0
d1 - d2 ≥ 0 => d1≥ d2
=> Chọn P => xi +1 = xi +1
pi+1 = pi +2dx – 2dy -
Giá trị p được tính từ điểm vẽ đầu tiên là (x1, y1) o – o
pi = 2dxyi + 2dx – 2dbx - 2dyxi dy o p – –
o = 2dxy1 + 2dx – 2dbx - 2dyx1 dy o po = 2dx(mx1 + b) + 2dx – 2dbx - 2dyx1 dy o p –
o = 2dyx1 + 2bdx + 2dx – 2dbx - 2dyx1 dy ( với m = dy/dx => dx = dy/m) o po = 2dx – dy lOMoAR cPSD| 58490434 -
Lưu đồ thuật toán BD x1, y1, x2, y2, color dx = x2 - x1 dy = y2 – y1 p = 2dx - dy x = x1 y = y1 Putpixel(x,y, color) S Đ p < 0 S y < y2 Đ p += 2dx p += 2dx -2dy KT x = x + 1