lOMoAR cPSD| 49519085
TRƯỜNG ĐẠI HỌC BÁCH KHOA HÀ NỘI VIỆN CƠ KHÍ -----o0o-----
TIỂU LUẬN MÔN HỌC ROBOTICS
MÃ HỌC PHẦN ME3168
Sinh viên thực hiện: Nguyễn Văn Nghĩa
Lớp: Cơ điện tử 2-K54 SHSV: 20091887 Nhiệm vụ:
Tính toán động học, tĩnh học, động lực học, chọn luật điều khiển thích hợp cho robot 3 bậc tự do RRR. Nội dung:
1. Xây dựng cấu trúc, thiết lập hệ phương trình động học của robot.
2. Giải bài toán động học.
2.1 Giải bài toán động học thuận
2.2 Giải bài toán động học ngược 3. Tính toán tĩnh học.
4. Tính toán động lực học.
5. Điều khiển và mô phỏng Chương 1
XÂY DỰNG CẤU TRÚC THIẾT LẬP HỆ PHƯƠNG TRÌNH ĐỘNG HỌC ROBOT
1.1 XÂY DỰNG CẤU TRÚC ROBOT
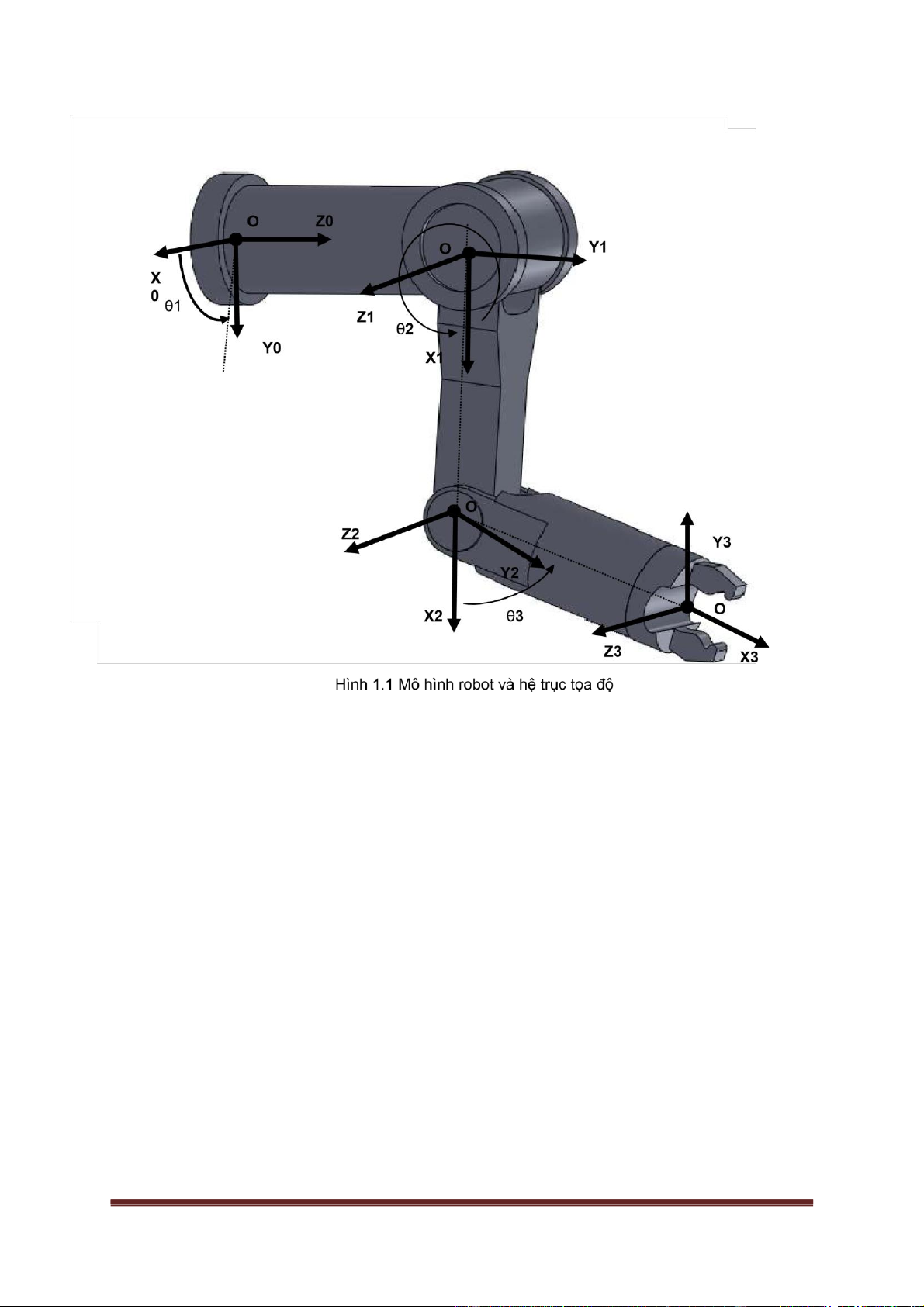
1.1.1 Đặt hệ quy chiếu lOMoAR cPSD| 49519085
• Hệ trục tọa độ OX0Y0Z0 đặt tại khâu đế, trục OZ0 có hướng dọc trục khớp động 1,
trục OX0 hướng thẳng đứng, trục OY0 xác định theo quy tắc bàn tay phải.
• Hệ trục tọa độ OX1Y1Z1 tại khớp động 2, trục OZ1 đặt dọc trục khớp động 2, trục
OX1 vuông góc với OZ0,OZ1 có hướng dọc theo khâu 2, trục OY1 xác định theo quy tắc bàn tay phải.
• Hệ trục tọa độ OX2Y2Z2 đặt tại trục khớp động 3, trục OZ2 đặt dọc trục khớp động 3,
trục OX2 vuông góc với OZ1 và OZ2 hướng từ OZ1 sang OZ2, trục OY2 xác định theo quy tắc bàn tay phải.
• Hệ trục tọa độ OX3Y3Z3 đặt tại khâu thao tác, trục OX3 hướng vào vật trục OZ3 song
song với trục OZ2, trục OY3 xác định theo quy tắc bàn tay phải.
1.1.2 Thiết lập bộ thông số Denavit-Hartenbeg [Type text] Page 2 lOMoAR cPSD| 49519085
1.1.2 Thiết lập bộ thông số Denavit-Hartenbeg
Từ mô hình và hệ trục tọa độ ở trên ta xây dựng được bảng thông số DanavitHartenbeg như sau :
Bảng 1.1: Bộ thông số Denavit-Hartenbeg Khâu θ i d i a i α i 1 θ 1 0 a 1 90 2 θ 2 0 a 2 0 3 θ 3 0 a 3 0 Trong đó :
Các biến khớp là θ1, θ2, θ3, đặt các biến khớp tương ứng là q1,q2,q3.
Dạng tổng quát ma trận Danavit-Hartenbeg :
Thếế b ng thông sôế DH cho môỗi khâu vào ma tr n H t ng quát ả
ậ ổ Ma trận Denavit-Hartenbergcủa khâu 1: lOMoAR cPSD| 49519085 0A1 =
Ma trận Denavit-Hartenbergcủa khâu 2: 0A2 =
Ma trận Denavit-Hartenbergcủa khâu 3: 0A3 =
1.2 THIẾT LẬP PHƯƠNG TRÌNH ĐỘNG HỌC ROBOT
Phương trình động học robot nhận được trong dạng ma trận như sau : (1.4) Trong đó: [Type text] Page 4 lOMoAR cPSD| 49519085 > > > > > > > > (1.6)
Ma trận (1.6) là ma trận cosin chỉ hướng xác định theo một trong các phép quay Roll-PitchYaw, Cardan hoặc Euler.
Phương trình (1.4) chính là phương trình động học dạng ma trận của robot. Nó bao gồm 16
phương trình vô hướng, trong đó có 4 phương trình tầm thường. Các ma trận 31 góc trên bên
phải cho 3 phương trình độc lập, biểu diễn về vị trí của điểm thao tác thuộc khâu thao tác. Các
ma trận 33 ở góc trên bên trái cho 9 phương trình, mô tả về hướng của khâu thao tác. Tuy nhiên
do các điều kiện trực dao nên trong 9 phương trình đó chỉ có 3 phương trình độc lập. Phương
trình (1.4) trên được sử dụng rất nhiều trong các bài toán động học thuận và động học ngược. lOMoAR cPSD| 49519085
Chương 2 BÀI TOÁN ĐỘNG HỌC
2.1 BÀI TOÁN ĐỘNG HỌC THUẬN
Mục tiêu của bài toán động học thuận là tính toán vị trí và hướng của khâu thao tác dưới dạng hàm
của các biến khớp hay chính là cho biết góc quay của các khớp ta tìm hướng và vị trí của khâu thao tác
so với hệ tọa độ cố định.
Xây dựng quy luật chuyển động, vị trí khâu thao tác và ma trận chỉ hướng
Ta chọn quy luật chuyển động bất kì cho robot theo thời gian như sau : (2.1)
Xét phương trình (1.4) thay các giá trị q1,q2,q3 ta có tọa độ của khâu thao tác chính là 3 phần tử đầu tiên của (1.5) :
Thay cá giá tr qị 1 , q2 , q3 vào xe , ye , ze ta có:
Hướng của bàn kẹp có thể được xác định từ các góc Euler, các góc Cardan, các góc Roll – Pitch
– Yaw. Ở trong đồ án này tôi sử dụng các góc Cardan, ký hiệu tương ứng là α, β, γ quay lần lượt
quanh các trục x-y-z. Chi tiết thực hiện phép quay này có thể tham khảo trong giáo trình robot công
nghiệp. Dưới đây chỉ đưa ra công thức chính để thực hiện phép quay này [Type text] Page 6 lOMoAR cPSD| 49519085 A q ( )
để tính được các góc α, β, η ta so sánh ma trận chỉ hướng của 0 3 và ma trận chỉ
hướng của (1.6) giải các hệ phương trình ta có : sin c13 cos 1 sin2 c23 sin cos c33 cos cos c12 sin cos c11 cos cos
Tính vận tốc điểm tác động cuối E, vận tốc góc khâu thao tác
Từ phần trên ta đã xây dựng được quy luật chuyển cũng như tìm được tọa độ của khâu thao
tác cuối, các biến khớp và đạo hàm các cấp theo t đã biết : T
Vận tốc góc của khâu thao tác: A3= (2.3)
Vận tốc của khâu thao tác chính là đạo hàm vị trí khâu thao tác theo thời gian: VE=E= (2.4) lOMoAR cPSD| 49519085
Thay (2.1) vào (2.4) ta tìm được vấn tốc của các khâu thao tác cuối.
Vận tốc góc của khâu thao tác: [Type text] Page 8