Toán 12 Bài 1: Lũy thừa

Toán 12 Bài 1: Lũy thừa
A. Tóm tắt lý thuyết và công thức lũy thừa
1. Lũy thừa với số mũ nguyên a. Nguyên dương n a  . a . a ..
a ..a (n thừa số) n
Trong đó: a là cơ số, n là số mũ b. Nguyên âm và 0 n 1  1 + Với a  0 thì 0 1 1
a  1,a  a,a  ,a  a a + 0
0 ,0n không có nghĩa 2. Căn bậc n
a. Khái niệm:
Cho n là số nguyên dương và số thực a. Nếu n
a  b thì a là căn bậc n của b
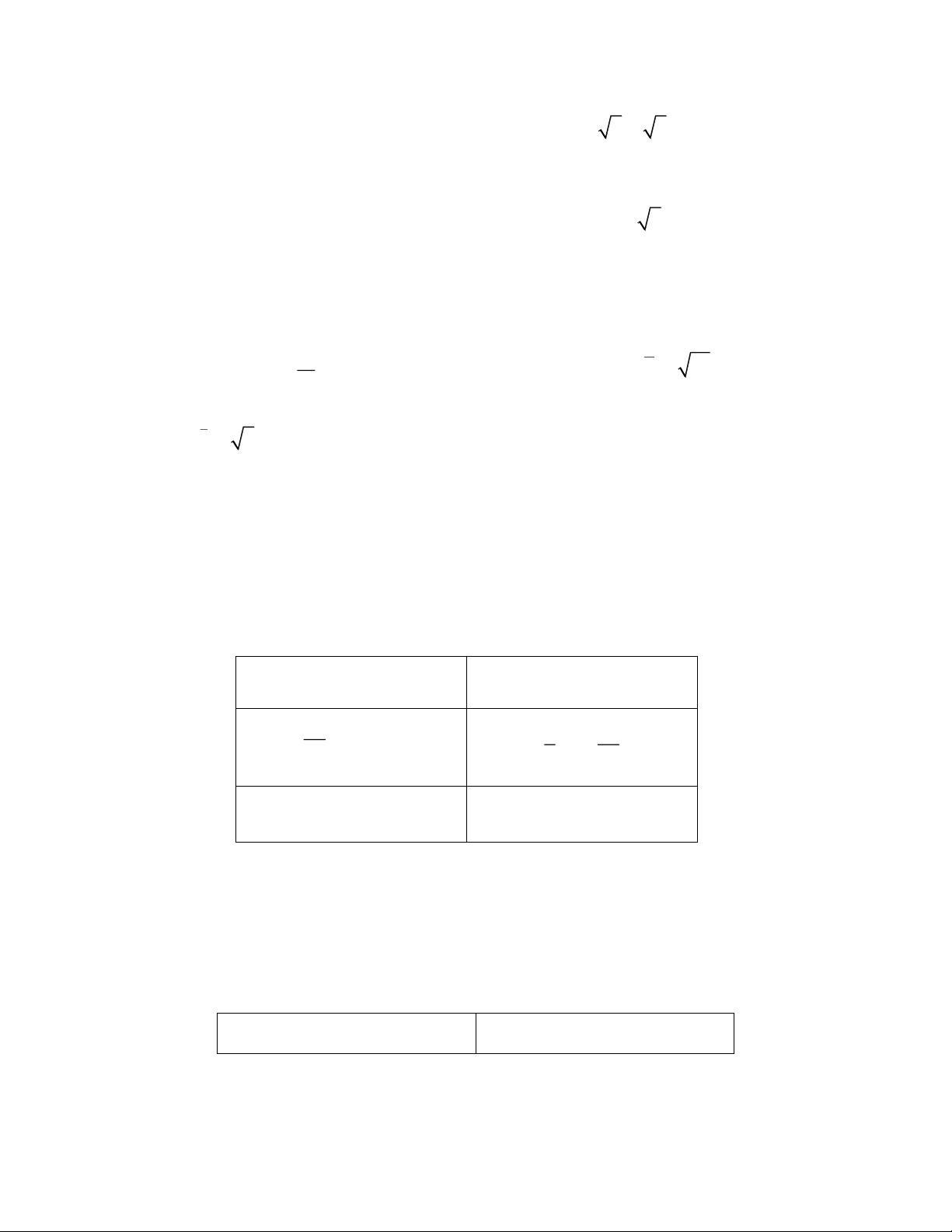
b. Tính chất:  Với * a,b  0; , m n
; p,q  ta có:  n . n  .n a b a b n  a a n  n b b    p n p n a a  m n mn a  a  p q Nếu n p m q 
 a  a ;a  0 n m  Đặc biệt: n mn m a  a
 Nếu n là số nguyên dương lẻ và a < b thì n n a  b
 Nếu n là số nguyên dương chẵn và 0  a  b thì n n a  b Chú ý:
- Khi n lẻ, mỗi số thực a chỉ có một căn thức bậc n. Kí hiệu n a
- Khi n chẵn, mỗi số thực dương a có đúng hai căn bậc n là hai số đối nhau
3. Lũy thừa với số mũ hữu tỉ m m
- Khái niệm: Với r 
(m, n nguyên và m  1). Ta có: r m n n
a  a  a n 1 - Chú ý: n n a  a
4. Lũy thừa với số mũ thực
Cho  là số vô tỉ. Xét dãy số hữu tỉ r mà lim r   ta có: a  lim rn a n n x x
5. Tính chất của lũy thừa
 Với a > 0, b > 0 ta có:
 a .a  a    . a b a .b      a    a  a a  a    b  b      . a a  
 a  1,a  a    
 0  a  1,a  a    
 Với 0  a  b ta có:  m m
a  b  m  0  m m
a  b  m  0 Chú ý:
 Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0
 Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương