lOMoAR cPSD| 49519085
A. TÓM TẮT LÝ THUYẾT: 1. Định nghĩa: .
2. Đạo hàm cơ bản:
3. Đạo hàm của hàm số hợp: lOMoAR cPSD| 49519085
4. Quy tắc đạo hàm:
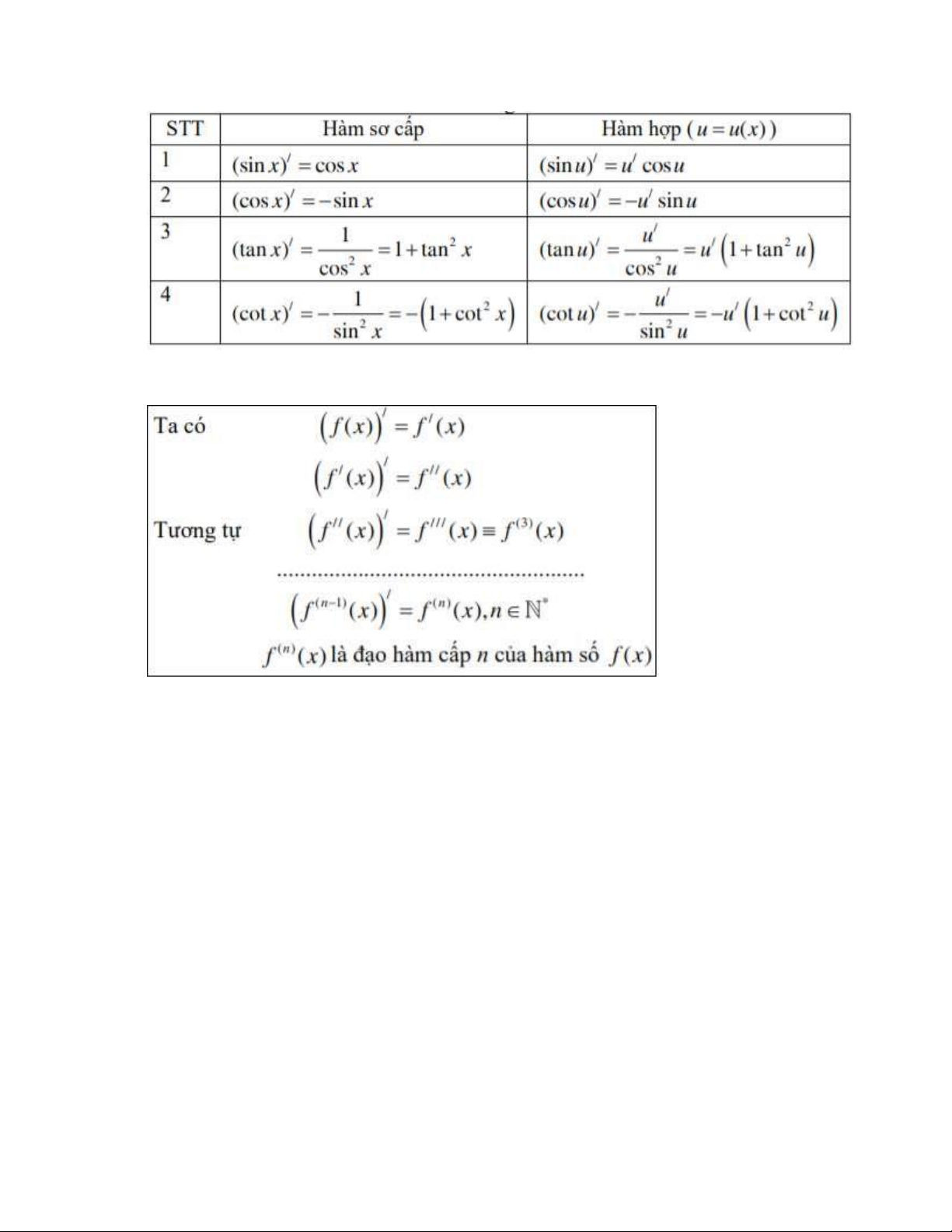
5. Bảng tính đạo hàm của hàm số lượng giác: lOMoAR cPSD| 49519085
6. Đạo hàm cấp 2:
Dựa vào đó, ta suy ra công thức đạo hàm tổng quát bậc n: (f(n-1)(x) )’ = f(n)(x), với n ∈ N*.
7. Bảng công thức đạo hàm đầy đủ: lOMoAR cPSD| 49519085 B. BÀI TẬP:
Dùng định nghĩa tính đạo hàm tại điểm cho trước: a) b) c) d) e) ; f) g) ; h) i) lOMoAR cPSD| 49519085 j)
Phương pháp giải:
B1: Giả sử là số gia của đối số tại . B2: . B3: Tính .
Lưu ý: Câu i, j nên dùng phương pháp tính nhanh.