ứng dụng của đạo hàm riêng trong phân tích kinh tế | Môn toán cao cấp

lOMoAR cPSD| 49519085
3.3. Āng dụng cÿa ạo hàm riêng trong phân tích kinh tế
3.3.1. Đạo hàm riêng và giá trị cận biên
Ý nghĩa của ạo hàm riêng trong kinh tế học
Xét mô hình hàm kinh tế: w =f(x1; x2; ...; xn) trong ó x1; x2; ...; xn; w là các biến số kinh tế.
Đạo hàm riêng của hàm w theo biến xi tại iểm M (x ,x ,...,x ) o o o o 1
2 n ược gọi là giá trị
w – cận biên theo xi tại iểm ó. Nghĩa là w (M )'xi o biểu diễn xap xi lượng thay ổi giá
trị của biến w khi giá trị xi tăng thêm 1 ơn vị trong iều kiện giá trị các biến ộc lập còn lại không thay ổi.
* Hàm sản xuất: Q = f(K, L)
Có các ạo hàm riêng: Q =öQ =öQ ượ K ; QL
c gọi tương ứng là hàm sản phẩm öK öL
hiện vật cận biên của tư bản (MPPK) và hàm sản phẩm hiện vật cận biên của lao
ộng (MPPL) tại iểm (K; L). Ý nghĩa: Q = ' K f (K;L)K
biểu diễn xấp xỉ lượng sản phẩm hiện vật gia tăng khi sử dụng thêm
một ơn vị tư bản và giữ nguyên mức sử dụng lao ộng. Tương tự, Q = ' L
f (K;L)L biểu diễn xấp xỉ lượng sản phẩm gia tăng khi sử dụng thêm
một ơn vị lao ộng và giữ nguyên mức sử dụng tư bản. lOMoAR cPSD| 49519085
Ví dụ 3.21. Giả sử hàm sản xuất của một doanh nghiệp là Q 100K L=4 ; trong ó:
K, L, Q là mức sử dụng tư bản, mức sử dụng lao ộng và sản lượng hàng ngày.
Giả sử doanh nghiệp ó ang sử dụng 16 ơn vị tư bản và 81 ơn vị lao ộng trong
một ngày tức là K = 16; L = 81. Xác ịnh sản lượng cận biên của tư bản và lao
ộng tại iểm ó và giải thích ý nghĩa.
Giải: Hàm sản lượng cận biên của tư bản và của lao ộng lần lượt là: −− 3 3 1 1 4 4 4 Q = ' = = ' = K f (K;L)K 25K L ; QL f (K;L)L 75K L4
Sản lượng cận biên của tư bản và của lao ộng tại K = 16; L = 81 tương ứng là: Q (16;81) = = K f (16;81)K' 25 16 81ö÷ − ö÷= 43 34 25.27 =84,375; ø ø 8 Q (16;81) = = L f (16;81)L' 75 16 81ö÷ ö÷= 14 −41 75.2 = 50. ø ø 3
Nghĩa là, nếu doanh nghiệp tăng mức sử dụng tư bản K từ 16 lên 17 ơn vị và
giữ nguyên lao ộng L = 81 trong 1 ngày thì sản lượng tăng thêm xấp xỉ 84,375 ơn
vị sản phẩm. Tương tự, nếu doanh nghiệp tăng mức sử dụng lao ộng từ 81 lên 82
trong một ngày và giữ nguyên sử dụng tư bản K =16 trong 1 ngày thì sản lượng
tăng thêm xấp xỉ 50 ơn vị sản phẩm.
* Hàm lợi ích: U = U(x1, x2, ..., xn). Trong ó xi là số ơn vị hàng hóa thứ i ( i =1 ,n). öU
Đạo hàm riêng của hàm lợi ích ối với các biến ộc lập là: MU = i (i =1,n) öx i lOMoAR cPSD| 49519085
MUi ược gọi là hàm lợi ích cận biên của hàng hóa thứ i.
Ý nghĩa: Đạo hàm riêng MUi tại iểm M (x ,x ,...,x ) o o o o 1 2 n biểu diễn xấp
xỉ lợi ích tăng thêm khi ngưßi tiêu dùng có thêm một ơn vị hàng hóa thứ i trong
iều kiện số ơn vị các hàng hóa khác không thay ổi.
Ví dụ 3.22. Giả sử hàm tiêu dùng hàng ngày của một ngưßi tiêu dùng ối với hai 2
loại hàng hóa là U = 10x x1 2 .
Trong ó: x1, x2 là mức sử dụng hàng hóa 1 và hàng hóa 2, U là lợi ích của ngưßi tiêu dùng hàng ngày.
Giả sử ngưßi tiêu dùng ang sử dụng 64 ơn vị hàng hóa 1 và 25 ơn vị hàng hóa 2
trong một ngày. Xác ịnh lợi ích cận biên của các hàng hóa tại iểm ó và giải thích ý nghĩa. Giải:
Lợi ích cận biên của hàng hóa 1 và hàng hóa 2 ối với ngưßi tiêu dùng tương ứng là: −− 1 1 1 1 2 2 2 MU = = 2 1 5x x ; MU1 2 2 5x x1 2
Lợi ích cận biên của hàng hóa 1 và hàng hóa 2 ối với ngưßi tiêu dùng tại x1=64; x2=25 tương ứng là: − MU (64,25) = 1 5.64 252 = 5.5 = 3,125; 8 − MU (64,25) = 1 5.64 25 2 = lOMoAR cPSD| 49519085 5.8 =8. 5
Nghĩa là, nếu ngưßi tiêu dùng tăng mức sử dụng hàng hóa 1 thêm một ơn vị x1 =
65 và giữ nguyên mức sử dụng hàng hóa 2 trong một ngày thì lợi ích tăng thêm
khoảng 3,125 ơn vị. Tương tự, nếu giữ nguyên mức sử dụng hàng hóa 1 và tăng
mức sử dụng hàng hóa 2 thêm một ơn vị trong một ngày thì lợi ích tăng thêm khoảng 8 ơn vị.
3.3.2. Đạo hàm riêng cấp hai và quy luật lợi ích cận biên giảm dần
Xét mô hình hàm kinh tế hai biến số: z =f(x; y) xác ịnh trên tập D. z' = x f (x;y) ' = x
là hàm cận biên của mô hình hàm kinh tế trên theo biến x; z 'y
f (x;y) ' y là hàm cận biên của mô hình hàm kinh tế trên theo biến y;
Trong kinh tế học, quy luật lợi ích cận biên giảm dần nói rằng: giá trị z – cận biên
của biến x giảm dần khi x tăng y không ổi. Tương tự, cho giá trị z – cận biên của
biến y giảm dần khi y tăng và x không ổi (Chú ý: chúng ta xét trong iều kiện giá
trị của các biến x, y ủ lớn). Cơ sá toán học: z' = ' x f (x;y)x
là hàm số giảm khi ÿýý′′ = 㕓ýý′′(ý; þ) < 0 với x, y ủ lớn Tượng tự: z ' = ' y
f (x;y)y là hàm số giảm khi ÿþþ′′ = 㕓þþ′′ (ý; þ) < 0 với x, y ủ lớn
Tổng quát x攃Āt hàm kinh tế nhiều biến số w = f(x1, x2, …, xn) xác ịnh trên miền D.
Hàm f tuân theo quy luật lợi ích cận biên giảm dần nếu lOMoAR cPSD| 49519085
∀㕖 = 1, 㕛̅̅̅̅̅̅̅̅: 㕓ý′′㕖2(ý1, ý2, … , ý㕛) < 0; với x1, x2,…, xn ủ lớn
Ví dụ 3.23. Hàm sản xuất của một doanh nghiệp có dạng Cobb- Douglas như sau: Q = aK L (a, ,ñ ò ñòþ 0)
Tìm iều kiện của ñò, ể hàm số trên tuân theo quy luật lợi ích cận biên giảm dần. Giải:
Hàm sản phẩm cận biên của tư bản: Q' = K a Kñ ñ− ò1L Hàm
sản phẩm cận biên của lao ộng: Q' = L
a K Lò ñ ò−1 Biểu hiện
của quy luật lợi ích cận biên giảm dần: üÿþÿýQQ = KLòò22
añ ñ( −1)K Lñ− ò2 ü 0 ýüò üñ ü11 òò
= aò ò( −1)K Lñ ò− ü 2 0 þ ü0 üñü1
Vậy iều kiện là ýþ0 üòü1 .
Áp dụng cho bài toán cụ thể với hàm sản xuất Q 100K L=4 . Trong ó K, L, Q là
mức sử dụng tư bản, mức sử dụng lao ộng và sản lượng hàng ngày. Hàm này
thỏa mãn quy luật lợi ích cận biên giảm dần.
Ví dụ 3.24. Cho hàm lợi ích U = 3xy – 2x2 – y2 (x, y >0). Hàm số U có tuân theo
quy luật lợi ích cận biên giảm dần hay không?
Giải: Ta có U '' =− =− xx 4 ü 0;U ''yy
2 ü 0moi x, y duong nên hàm tuân theo quy luật
lợi ích cận biên giảm dần. lOMoAR cPSD| 49519085
3.3.3. Hệ số co giãn
Cho hàm kinh tế: w = f(x1,x2, ..., xn)
Định nghĩa 3.10. Hệ số co giãn của w theo biến xk tại iểm M (x ,x ,...,x ) o o o o 1 2 n là xx
lượng thay ổi tính bằng phần trăm của w khi xk tăng thêm 1% trong iều kiện giá
trị của các biến ộc lập khác không ổi, ược ký hiệu và xác ịnh như sau:
f k (Mo ) =öf(x ,x ,...,x )1o o2 on . o xook o õ ö x xk f(x ,x ,...,x )12 n õ f (M ) =
fxòk (M0).xo x o k k f M( ) 0
Ví dụ 3.25. Giả sử hàm cầu của hàng hóa 1 trên thị trưßng hai hàng hóa có liên quan có dạng: Q = 2 − ; trong ó p 1d 6300−2p1 3p22
1, p2 tương ứng là giá của hàng hóa 1, 2.
Xác ịnh hệ số co giãn của cầu hàng hóa 1 ối với giá của hàng hóa ó tại (p1; p2)
Và hệ số co giãn của cầu hàng hóa 1 ối với giá của hàng hóa thứ hai p2 tại (p1; p2).
Xác ịnh hệ số co giãn của cầu theo giá p1, p2 và cho biết ý nghĩa tại iểm (p1, p2) =(20, 30) Giải:
* Hệ số co giãn của cầu hàng hóa 1 ối với giá của hàng hóa ó tại (p1; p2): õ = − = − Qp11d 4p1 p1 2
− 4p12 2 6300 2p 3p2 6300 2p 3p2 − − − lOMoAR cPSD| 49519085
* Hệ số co giãn của cầu hàng hóa 1 ối với giá của hàng hóa thứ hai p2 tại (p1; p2): õ =− = − Qp21d − 6p2 p2 2 6p22 2 − − − 6300 2p 3p2 6300 2p 3p2
Tại iểm (20; 30) ta có: õ =−p 0,57143;õ =− 1,92857 . 1 p2
Điều ó có nghĩa khi hàng hóa 1 ang á mức giá 20 và hàng hóa 2 á mức giá 30
nếu tăng giá hàng hóa 1 thêm 1% còn giá hàng hóa 2 không ổi thì cầu ối với
hàng hóa 1 sẽ giảm xx 0,57%. Tương tự nếu giá của hàng hóa 1 không ổi nhưng
giá của hàng hóa hai tăng thêm 1% thì cầu ối với hàng hóa 1 cũng giảm khoảng 1,9%.
Ví dụ 3.26. Giả sử hàm sản xuất của doanh nghiệp có dạng: 1 2 Q 120K L=4 3
Xác ịnh hệ số co giãn của sản lượng theo vốn, lao ộng tại thßi iểm (K; L). Giải:
Hệ số co giãn của sản lượng theo vốn tại thßi iểm (K, L) là −43 23 K 30 õ = = = K 30K L 1 2 = 0,25 % 120K L3 3 120
Và hệ số co giãn của sản lượng theo lao ộng tại thßi iểm (K, L) là õ = = L 80K L13 −31 L1 2 80 ==0,67% 3 120 120K L3 lOMoAR cPSD| 49519085
Nhận xét: Nếu mô hình hàm số kinh tế có dạng mô hình hàm Cobb- Douglass thì
hệ số co giãn của w theo xk úng bằng lũy thừa của xk trong công thức xác ịnh w.
Ví dụ 3.27. Ngưßi ta ước lượng hàm sản xuất hàng ngày của một doanh nghiệp như sau: Q = 803 K L
a) Với K =64; L = 25 hãy cho biết mức sản xuất hàng ngày của doanh nghiệp.
b) Bằng các ạo hàm riêng của Q, cho biết nếu doanh nghiệp: *
Sử dụng thêm một ơn vị lao ộng mỗi ngày và giữ nguyên mức K =64 thì sản
lượng sẽ thay ổi là bao nhiêu. *
Ngược lại, nếu sử dụng thêm một ơn vị vốn mỗi ngày và giữ nguyên mức L
= 25 thì sản lượng sẽ thay ổi bằng bao nhiêu. Giải:
a) Mức sản xuất hàng hóa của doanh nghiệp khi K =64; L = 25 là Q(64;25)
=80 64 253=80.4.5=1600 ( ơn vị sản phẩm)
b) Các ạo hàm riêng của hàm sản xuất: = = ;Q K ' = L 80. K.3 1 = 40 3 2 L L = . 8,3333;Q' K (25;64) = 40. = = 32
Vậy, nếu giữ nguyên mức sử dụng vốn K = 64 và sử dụng thêm một ơn vị lao
ộng mỗi ngày thì sản lượng tăng một lượng xấp xỉ là 8,333 ơn vị. Ngược lại, nếu
giữa nguyên mức sử dụng lao ộng L = 25 thì sản lượng thay ổi một lượng xấp xỉ 32 ơn vị.
3.3.4. Hàm thuần nhất và vấn ề hiệu quả theo quy mô
3.3.4.1. Khái niệm hàm thuần nhất lOMoAR cPSD| 49519085
Định nghĩa 3.11. Hàm số f(x1, x2, …,xn) ược gọi là hàm thuần nhất cấp k ( k 0 )
nếu với þt 0, chúng ta có: f(t.x1, t.x2, …, t.xn ) = tk.f(x1, x2, …, xn).
Ví dụ 3.28. Hàm Q aK L= ñ òlà hàm thuần nhất cấp (ñ+ò)vì þt 0 ta có
Q(tK, tL) = a(tK)ñ (tL)ò = tñ+ò (aKñ òL ) = tñ+òQ(K,L)
Ví dụ 3.29. Hàm Q K L(, ) = 1 K + 4 K L0,5 0,5 + 4 L là hàm thuần nhất cấp 1 9 9 9
Q(tK, tL)= 1/9. t.K + 4/9. (t.K)^0,5. (t.L)^0,5 +4/9. t.L
= t ( 1/9.K+ 4/9. (K)^0,5. (L)^0,5 +4/9 L) =t. Q(K, L) Ví dụ 3.30. Hàm 2xy z= 2
2 là hàm thuần nhất cấp 0. x −y F=x+2xy
F(tx, ty)=tx+2(tx)(ty)=tx+t^2.xy hamf ko thuan nhaats Ccc tính chất
Tknh chất 1. DL Euler: Hàm w=f(x1, x2, …, xn) có các ạo hàm riêng liên tục:
f là thuần nhất bậc k x .f + + + = 1 x' 1 x .f2x' 2 ... x .fn x' n k.f
Q = aKñ òL là hàm thuần nhất bậc (ñ+ò)
QKò = a K L Q a K L.ñ ñ− ò1 ; Lò = .ò ñ ò−1 lOMoAR cPSD| 49519085 KQ. ò + ò = K
LQ a K L a K L. L
.ñ ñ ò + .ò ñ ò = (ñ+ò)aK Lñ ò
Tknh chất 2. Nếu f là hàm thuần nhất bậc k và g là hàm thuần nhất bậc m thì f.g
là hàm thuần nhất bậc k+m; fn là hàm thuần nhất bậc kn, f là hàm thuần nhất g bậc k –m (nếu k m).
3.3.4.2. Vấn ề hiệu quả theo quy mô
Xét hàm sản xuất Q = f(K, L); trong ó K, L là yếu tố ầu vào; Q là yếu tố ầu ra.
Bài toán ặt ra là. Nếu các yếu tố ầu vào K, L tăng gấp m lần (m > 1) thì ầu ra Q có
tăng gấp m lần hay không? Giải:
+) Nếu Q(mK, mL) > m.Q(K, L) thì chúng ta nói hàm sản xuất cos hiệu quả tăng theo quy mô.
+) Nếu Q(mK, mL) < m.Q(K, L) thì chúng ta nói hàm sản xuất cos hiệu quả giảm theo quy mô.
+) Nếu Q(mK, mL) = mQ(K, L) thì chúng ta nói hàm sản xuất biểu thị hiệu quả không ổi theo quy mô.
* Liên hệ hiệu quả của quy mô với bậc thuần nhất
Giả sử hàm sản xuất Q = f(K, L) là hàm thuần nhất bậc k.
- Nếu k > 1 thì hàm sản xuất có hiệu quả tăng theo quy mô; - Nếu k < 1 thì
hàm sản xuất có hiệu quả giảm theo quy mô;
- Nếu k = 1 thì hàm sản xuất có hiệu quả không ổi theo quy mô. Ví dụ 3.31. Hàm sản xuất Q= K + K L0,5 0,5 + L
có cấp thuần nhất bằng 1, nên nó có hiệu
quả không ổi theo quy mô.
Ví dụ 3.32. Hàm sản xuất: Q aK L= ñ ò có cấp thuần nhất ñ+ò nên lOMoAR cPSD| 49519085
- Nếu ñ+ò> 1 thì hàm sản xuất biểu thị hiệu quả tăng theo quy mô;
- Nếu ñ+ò< 1 thì hàm sản xuất biểu thị hiệu quả giảm theo quy mô;
- Nếu ñ+ò= 1 thì hàm sản xuất biểu thị hiệu quả không ổi theo quy mô.
3.3.5. Hàm ẩn và ạo hàm của nó
3.3.5.1. Hàm ẩn m ⌀t biến
a) Khái niệm hàm ẩn
Giả sử các giá trị của 2 biến x và y quan hệ với nhau bái phương trình F(x, y) = 0 (3.1)
à ây coi F(x, y) như một hàm 2 biến xác ịnh trên miền D R2.
Nếu với mọi x X, tồn tại y = f(x) thỏa mãn hệ thức (5.1) thì ta nói hệ thức này xác
ịnh hàm ẩn y = f(x) trên tập X.
Ví dụ 3.33. Xét hệ thức F(x, y) = x2 + y2 – 4 (3.2) Tìm y ể F(x, y) = 0 Giải:
Với mọi x − 2;2 = D ta có: y(x) = 4−x 2 .
Vậy các hàm y(x) = 4−x 2 xác ịnh trên D là các hàm ẩn xác ịnh bái (3.2). b) Sư뀣
t n tại hàm ẩn à ây chúng ta chỉ x攃Āt sự tồn tại ạo hàm của hàm ẩn ối với phương trình (3.1).
Trên trục số ta gọi khoảng V = (x −ô −ô o
;xo ) là lân cận của iển xo bán kính ô (ô>0).
Ngưßi ta chứng minh ược ịnh lý sau: lOMoAR cPSD| 49519085
Định l{ 3.3. Giả sử F(x, y) xác ịnh, liên tục, có các ạo hàm riêng liên tục trong một
lân cận của iểm Mo(xo, yo) và tại iểm Mo(xo, yo) thỏa m愃̀n các iều kiện: F(x o, yo) = 0; F (x ,y ) ' y o o 0 Khi ó
* Phương trình (3.1) xác ịnh một hàm số y = f(x) trong một lân cận V của iểm xo;
* Tại iểm xo hàm y = f(x) nhận giá trị yo: f(xo) = yo;
* Hàm số y = f(x) có ạo hàm liên tục trong lân cận V của iểm xo.
c) Đạo hàm của hàm ẩn *
X攃Āt phương trình (3.1).
Định lý 3.3 khẳng ịnh sự tồn tại hàm ẩn y = y(x) xác ịnh bái phương trình (3.1),
ồng thßi khẳng ịnh sự tồn tại ạo hàm của hàm ẩn (khi 愃̀ biết ạo hàm tồn tại) có
thể thực hiện tương ối ơn giản. Với hàm y = f(x) xác ịnh bái (3.1): F(x,y(x)) = 0 F (x,y(x)) ' + ' ' = x F (x,y(x)).yy x 0 (3.3)
Từ (3.3), với iều kiện F 0 ' y , ta tìm ược − ' ' F (x,y)x = yx ' (3.4) F (x,y)y
Ví dụ 3.34. Cho hàm cầu D = D(p, Yo) với p là giá, Yo là mức thu nhập và hàm S =
S(p) với giả thiết D' ü þ p
0;D'Yo 0,S'þ 0. Chứng minh rằng khi thu nhập Yo tăng thì giá
tại iểm cân bằng tăng. lOMoAR cPSD| 49519085 Giải:
Giả sử giá cân bằng p phụ thuộc vào mức thu nhập Yo là hàm ẩn biểu diễn bái hệ
thức: F(p; Yo) = D(p; Yo) – S(p) = 0. ' FY' Khi ó o D'Yo D'Yo p Yo =− =− = þ ' ' ' 0. F − p D p S' S'−D p
Điều ó nói lên rằng khi thu nhập Yo tăng thì sẽ kéo theo giá tại iểm cân bằng tăng.
3.3.5.2. Hàm ẩn nhiều biến số
Giả sử mối liên hệ giữa biến số y và các biến số x1, x2, …, xn ược biểu diễn dưới dạng phương trình: F(x1, x2, …, xn, y) = 0 (3.5)
Trong ó F là một hàm số của n + 1 biến số x1, x2, …, xn, y.
Nếu với mỗi iểm M(x1, x2, …, xn) thuộc miền D R n tồn tại một và chỉ một giá trị
của biến y sao cho (x1, x2, …, xn,y) thỏa m愃̀n phương trình (3.5) thì phương trình
(3.5) xác ịnh một hàm số y = y(x1, x2, …, xn).
Hàm số y = y(x1, x2, …, xn) xác ịnh một cách gián tiếp thông qua phương trình
(3.5) ược gọi là hàm ẩn. Ta nói phương trình (3.5) xác ịnh hàm ẩn y = y(x1, x2, …,
xn) trong miền D R n khi và chỉ khi:
F(x ,x ,...,x ,y(x ,x ,...,x ))1 2 n 1 2 = n 0; M(x ,x ,...,x )1 2 n D.
Định lý về sự tồn tại hàm ẩn trong trưßng hợp này ược phát biểu như sau:
Định l{ 3.4. Giả sử hàm số F(x1, x2, …, xn) xác ịnh, liên tục, có ạo hàm riêng lOMoAR cPSD| 49519085
liên tục trong một lân cận của iểm M (x ,x ,...,x ,y)o 1 2 nvà tại iểm M (x ,x ,...,x ,y)o 1 2 n
thỏa m愃̀n các iều kiện: F(x ,x ,...,x ,y) = ' 1 2 n 0, F (x ,x ,...,x ,y)y 1 2 n 0. Khi ó:
* Phương trình (3.5) xác ịnh hàm ẩn y = y(x1, x2, …, xn) trong một lân cận V của iểm M (x ,x ,...,x )o 1 2 n ;
* Hàm số y = y(x1, x2, …, xn) nhận giá trị y tại iểm M = Mo: y(x ,x ,...,x ) = 1 2 n y ;
* Hàm ẩn y = y(x1, x2, …, xn) liên tục và có các ạo hàm riêng liên tục trong
lân cận V của iểm M (x ,x ,...,x )o 1 2 n .
Việc tính các ạo hàm riêng của hàm ẩn nhiều biến số ược thực hiện tương tự như
việc tính ạo hàm của hàm ẩn một biến số.
Chẳng hạn tính ạo hàm riêng của hàm ẩn y theo biến xk, lấy ạo hàm riêng của (3.5) theo biến xk ta có öF öF öy + . = 0. öx ö k y öx k öF
Với giả thiết 0, từ ây ta tìm ược: öy lOMoAR cPSD| 49519085 öF =− k (3.6) öx ö k F öy
Vk dụ 3.35. X攃Āt hàm ẩn z = z(x,y) xác ịnh bái phương trình x 2 y2 z2 + + = 2 2 2 1 a b c (3.7) ö ö F x
Tính ạo hàm riêng của z theo x và y. Giải x 2 y2 z2 ' 2x ' 2y ' 2z = = = Đặt F(x,y,z) = + +2 2 2 , ta có Fx 2 ;Fy 2 ;Fz 2 . a b c a b c
Với iều kiện z 0, theo công thức (3.7) ta tìm ược: z =− =− =− =− 'x Fx'' c x22 ;z'y Fy'' c y22 . (3.8) Fz a z Fz b z
Vk dụ 3.36. Cho hàm ẩn z = z(x, y) xác ịnh bái phương trình:
x2 + 2y2 + 3z2 + 2x + 4y - 6z = 0
Tính các ạo hàm riêng của z theo x và y. Giải lOMoAR cPSD| 49519085
Đặt F(x, y, z) = x2 + 2y2 + 3z2 + 2x + 4y - 6z, ta có F ' = + ' = + ' = − x 2x 2;Fy 4y 4;Fz 6z 6.
Với iều kiện z 1 , ta có z =− ' = =− ' = 'x Fx ' x +1 ;z'y Fy ' 2(y+1) . Fz 3(1−z) Fz 3(1−z)
3.3.6. Hệ số thay thế hay bổ sung
Cho hàm số kinh tế w = f(x1, x2, …, xn) và iểm M (x ;x ;....,x ) o o o . o 1 2 n Khi ó
wo = f(Mo). Bài toán ặt ra khi hai biến xi và xj thay ổi còn các biến khác giữ nguyên
sao cho w không ổi (tức là w = wo), thì sự thay ổi của hai biến này phải tuân theo
tỷ lệ nào? Tùy vào thực tiễn của hai biến, tỷ lệ này có thể gọi là tỷ lệ (hệ số) thay
thế (ví dụ: thay thế giữa vốn và lao ộng), tỷ lệ bổ sung (ví dụ: bổ sung giữa hai
mặt hàng), tỷ lệ chuyển ổi (ví dụ: chuyển ổi giữa tiêu dùng hiện tại và tiêu dùng
tương lai). Ta có thể tính hệ số này như sau: Theo công thức vi phân toàn phần, ta có ö dw = öf dx + öf + + f 1 dx 2 ... dx n öx ö ö 1 x 2 x n
Do các biến xi và xj thay ổi còn các biến khác không ổi nên: lOMoAR cPSD| 49519085 f = x 0 = ò + ò dxj = − i j ò ( )ò i f dxx i
f dxx j dxi fxòi xj xi dx j dx Nếu
ü 0 thì ta nói xj có thể thay thế (chuyển ổi) cho xi tại Mo với tỷ lệ j dx i dx i . dx j dx j Nếu
þ 0 thì ta nói xj bổ sung cho xi tại Mo với tỷ lệ . dx i dx i dx j Nếu
= 0 thì ta nói xi, xj không thể thay thế hoặc bổ sung cho nhau tại Mo. dx i
3.3.7. Phương trình ường ng lượng, ường bàng quan
3.3.7.1. Phương trình ường ng lượng
Cho hàm sản xuất Q = f(K,L). Giả sử K=K =
o, L=Lo; sản lượng khi ó là Qo f(K ,L ) . Phương trình o o Q = Qo f(K,L) = Qo (3.9)
ược gọi là phương trình ưßng ồng lượng tại iểm (Ko, Lo).
Phương trình (3.9) xác ịnh hàm ẩn K = K(L). Dọc theo ưßng ồng lượng, các yếu
tố sản xuất có thể thay thế cho nhau ể cho cùng một mức sản lượng Qo. Tỷ số −dK f ' L MPPL = = = KL ' lOMoAR cPSD| 49519085 dL fK MPPK
ược gọi là tỷ lệ thay thế k礃̀ thuật cận biên (marginal rate of technical
substition). Tỷ lệ này cho biết xấp xỉ lượng vốn phải tăng thêm khi lượng lao ộng
giảm 1 ơn vị ể giữ nguyên mức sản lượng.
Tương tự như lý thuyết ngưßi tiêu dùng, khi phân tích sản xuất ngưßi ta thừa nhận các tiên ề sau:
" Sản lượng ầu ra Q biến thiên cùng chiều với lượng sử dụng một yếu tố sản
xuất (với các yếu tố khác giữ nguyên);
" Tỷ lệ thay thế k礃̀ thuật cận biên giảm dần, tức là khi lượng sử dụng lao
ộng càng lớn thì lượng vốn phải tăng thêm ể thay thế cho 1 ơn vị lao ộng bớt i
(mà giữ nguyên mức sản lượng) càng nhỏ.
Với các tiên ề nói trên, ta có: dK MPPK > 0, MPPL >0, k攃Āo theo ü 0; dL ö ( KL ) d K2 d K2 = − ü 2 0, k攃Āo theo þ 2 0. öL dL dL
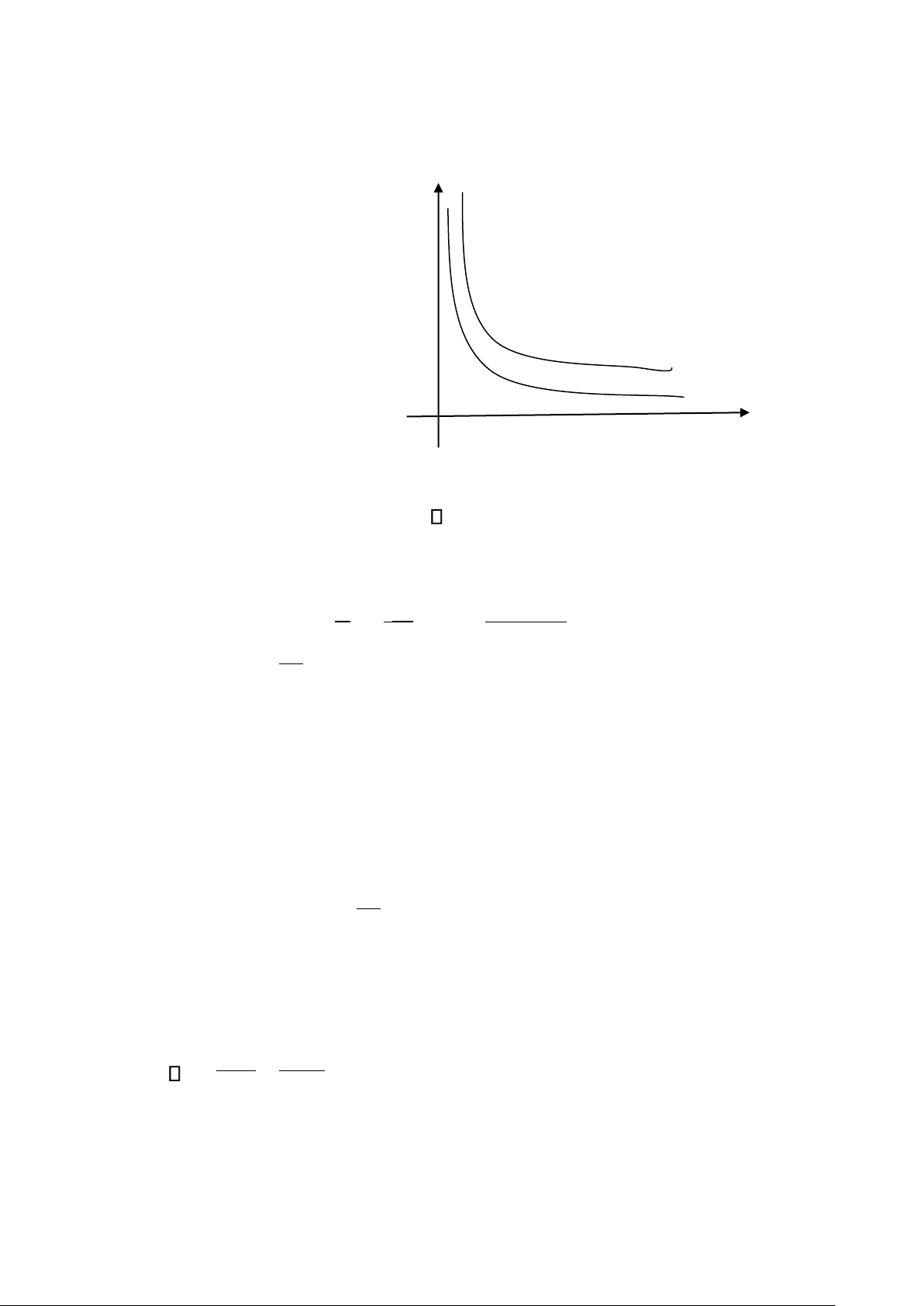
Đưßng ồng lượng có ồ thị dốc xuống và quay bề lom lên trên. VD.
Cho ham san xuat: Q=100.K^0,5. L^0,5
Viet phuong trinh duong dong luong tai diem M0(81; 16). lOMoAR cPSD| 49519085
Q0=Q(M0)=100.sqrt(81).sqrt(16)=100.9.4=3600
Phuong trinh duong dong luong: 100.K^0,5. L^0,5=36 Tuong duong K^0,5. L^0,5=36 Tuong duong K.L=1296 Tuong duong K=1296/L
3.3.7.2. Phương trình ường bàng quan
Cho hàm lợi ích U = U(x,y). Giả sử x = xo, y = yo; sản lượng khi ó là U = . Phương trình ượ o U(x ,y )o o U = Uo U(x,y) = Uo
c gọi là phương trình ưßng
bàng quan tại iểm (xo, yo). Hệ số góc (hoặc ộ dốc) của ưßng ó tại dy −MU − iể 1 U (x ;y )'x o o m (xo, yo) bằng: (x ;yo o ) = = ' . dx MU 2 U (x ;y )y o o
Lý thuyết ngưßi tieu dùng trong Kinh tế học thừa nhận tiên ề về tính không bảo
hòa, hay (ngưßi tiêu dùng ưa thích hơn) khi có thêm một loại hàng hóa trong cơ cấu tiêu
dùng mà không bớt i các hàng hóa khác. Về mặt toán học iều ó có nghĩa là MU = 1 dy U' þ = þ ü x 0, MU U' 0, do ó
0, tức là y = y(x) là hàm nghịch dx 1 2 x2
biến. Như vậy, các hàng hóa có thể thay thế nhau ể duy trì một mức lợi ích nhất
ịnh. Theo ý nghĩa của ạo hàm thì −dy MU1 = = 21 dx MU 2 lOMoAR cPSD| 49519085
xấp xỉ bằng lượng tăng hàng hóa B ể bù cho 1 ơn vị hàng hóa A bị bớt i mà v n
giữ nguyên lợi ích ngưßi tiêu dùng. Các nhà kinh tế gọi tỷ số 21 là tỷ lệ thay thế
cận biên (marginal rate of substitution) của hàng hóa B cho hàng hóa A. Một tiên
ề khác ược thừa nhận trong kinh tế học là là 21 giảm khi x tăng và y không ổi. Dạng toán học là: ö ( 12 ) −d y2 d y2 = ó 2 0 2 0. öx dx dx
Như vậy, ưßng bàng quan có ồ thị dáng dốc xuống và quay bề lom lên trên.
Ví dụ 3.37. Một hộ gia ình có hàm lợi ích tiêu dùng với 2 loại hàng hóa như
sau: U(x, y ) = 5x y0,4 0,4
(x là số ơn vị hàng hóa 1, y là số ơn vị hàng hóa 2; xþ 0; yþ 0).
a) Hai hàng hóa này là thay thế hay bổ sung cho nhau.
b) Tại iểm (xo, yo) = (32; 32); viết phương trình ưßng bàng quan, xác ịnh hệ số
góc của ưßng ó và nêu ý nghĩa. Giải: a) Ta có dxdy=−UU = − =− 'y'x 22x yx y0,−40,6−0,06,4 xyü0 với mọi x > 0; y > 0. Vậy hai
hàng hóa trên là thay thế cho nhau.
b) Tại iểm (xo, yo) = (32; 32): Uo = 5.320,4.320,4 = 80. Phương trình ưßng bàng
quan tại iểm (xo, yo): U = Uo x y0,4 0,4 − =16 0.
Hệ số góc của ưßng bàng quan: y' = dy =− U 'x =− y x ' . dx U y x