Vậy hệ có nghiệm duy nhất hay đa thức nội suy tồn tại và duy nhất | Bài giảng môn Phương pháp tính và matlab CTTT | Đại học Bách khoa hà nội

Vậy hệ có nghiệm duy nhất hay đa thức nội suy tồn tại và duy nhất. Tài liệu trắc nghiệm môn Phương pháp tính và matlab CTTT giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem! khoa hà nội

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Phương pháp tính và matlab CTTT

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

13 trang 1 tháng trước

Tác giả:

Profile Lê Na
XẤP XỈ HÀM SỐ BẰNG
ĐA THỨC NỘI SUY
Hà Thị Ngọc Yến
Hà nội, 9/2020
ĐA THỨC NỘI SUY
- Cho bộ điểm
- Đa thức bậc không quá n, đi qua bộ
điểm trên được gọi là đa thức nội suy với các
mốc nội suy
- Khi đó
( )
0,
, , , [ , ]
i i i i j i
in
x y f x x x i j x a b
=
=
( )
n
Px
( ) ( )
n
f x P x
0,
i
in
x
=
ĐA THỨC NỘI SUY
• Định lý:
Với bộ điểm cho
trước, đa thức nội suy tồn tại và duy nhất
0,
, , ,
i i i j
in
x y x x i j
=
ĐA THỨC NỘI SUY
( )
( )
2
0 1 2
2
1 0 2 0 0 0
2
1 1 2 1 1 1
2
12
0,
n
nn
n
on
n
on
n i i
n
o n n n n n
P x a a x a x a x
a a x a x a x y
a a x a x a x y
P x y i n
a a x a x a x y
= + + + +
+ + + =
+ + + =
= =
+ + + =
ĐA THỨC NỘI SUY
• Định thức
• Vậy hệ có nghiệm duy nhất hay đa thức nội suy tồn
tại và duy nhất
( )
00
11
1
1
0.
1
n
n
ij
ij
n
nn
xx
xx
xx
xx
= −
SAI SỐ CỦA ĐA THỨC NỘI SUY
• Đặt
• Chọn k sao cho
• F(t) có ít nhất n+2 nghiệm phân biệt nên F’(x) có ít
nhất n+1 nghiệm phân biệt, …..
( ) ( ) ( )
1nn
F t R t kw t
+
=−
SAI SỐ CỦA ĐA THỨC NỘI SUY
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( 1)
1
1
1
[ , ], 0
1!
w
1!
n
n
n
n
n
a b F
f
k
n
f
R x x
n

+
+
+
+
=
=
+
=
+
Ví dụ
• Xấp xỉ hàm
• Với 5 mốc nội suy
( )
2
1
25 1
fx
x
=
+
Ví dụ
• Với 10 và 17 mốc nội suy
Tối ưu hóa mốc nội suy
• Bài toán: Chọn mốc nội suy sao cho sai số xấp
xỉ hàm đạt được nhỏ nhất
( )
( )
( )
( )
( )
,
1
1
1
sup
1!
min min
nn
ab
n
n
nn
f P R x
M
R x w x
n
f P w x
+
+
+
−=
+
− → →
Tối ưu mốc nội suy
• Xét khoảng nội suy [-1,1]
• Xét họ các hàm đa thức Chebysev:
( ) ( )
( ) ( ) ( )
( ) ( )
( ) ( )
11
01
21
2
cos .arccos
2
1,
2 1, 2
n
n n n
nn
n
T x n x
T x xT x T x
T x T x x
T x x T x x
+−
−
=
=−
==
= − = +
Tối ưu mốc nội suy
• Định lý: trong các đa thức bậc n có hệ số cả
bằng 1, đa thức là đa thức có độ
lệch so với 0 nhỏ nhất, tức là
( )
1
1
2
n
n
Tx
−
( )
( )
( )
1
10
1
1,1 1,1
max max
2
nn
n
n
n
p x x a x a
Tx
px
−
−
−
−−
= + + +
Tối ưu mốc nội suy
• Chọn mốc nội suy là n+1 các nghiệm của
• Trường hợp khoảng nội suy đặt ẩn:
( )
n
Tx
cos , 0, .
i
i
x i n
n
==
,ab
( )
2x b a
t
ba
−+
=
−
| 1/13
| | Tải xuống

Có thể bạn quan tâm:

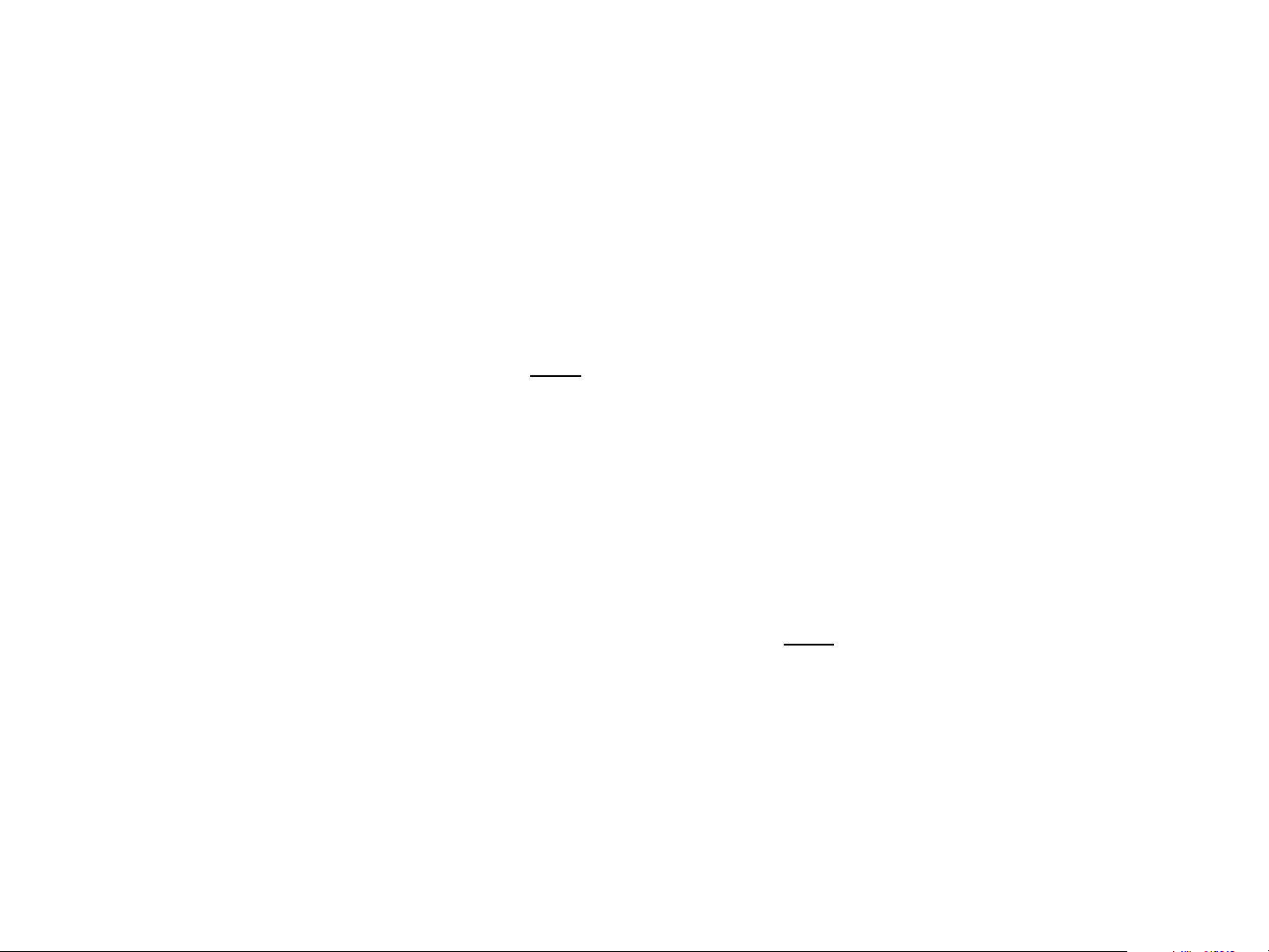
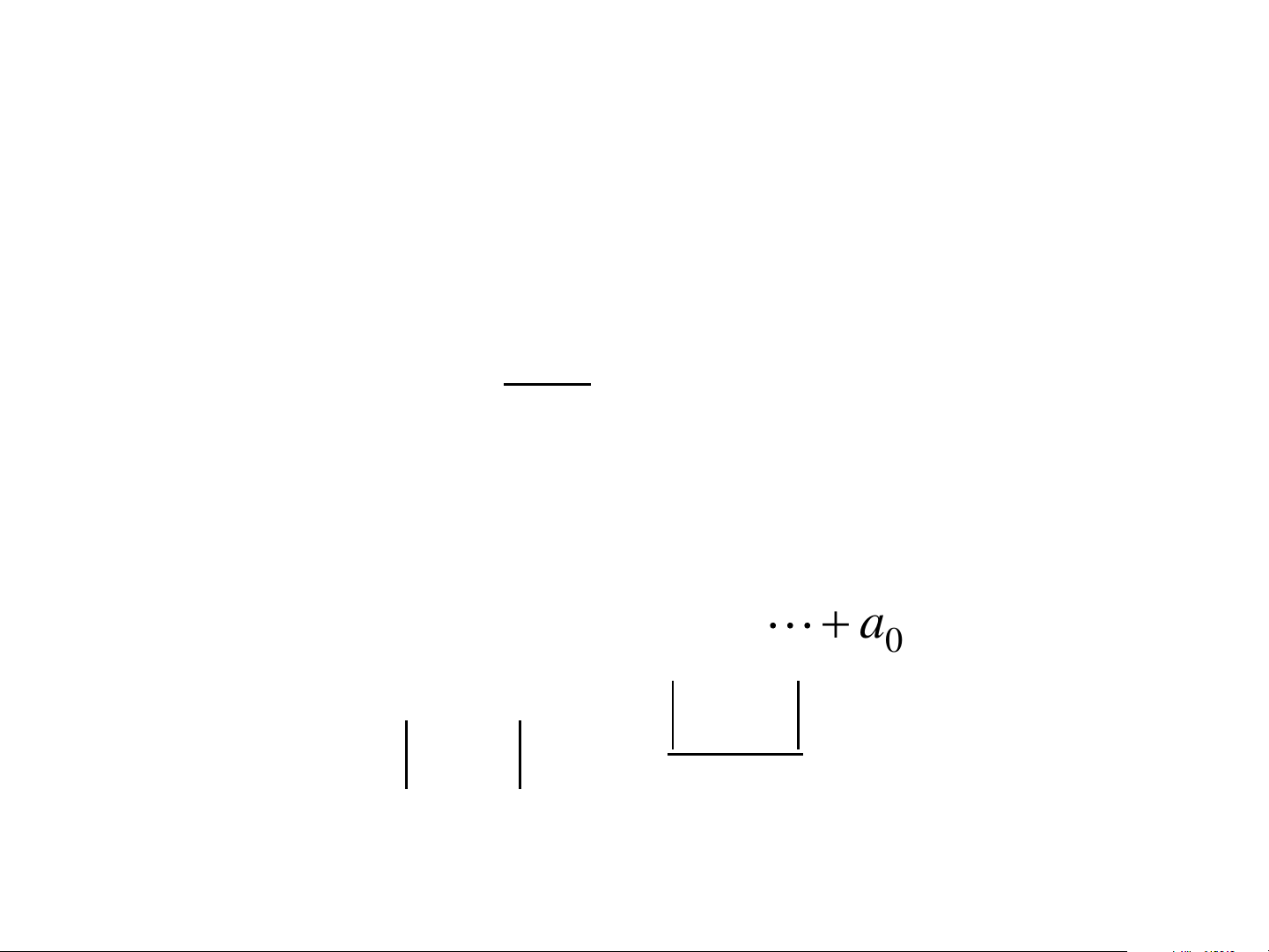
Preview text:

XẤP XỈ HÀM SỐ BẰNG ĐA THỨC NỘI SUY Hà Thị Ngọc Yến Hà nội, 9/2020 ĐA THỨC NỘI SUY - Cho bộ điểm
x , y = f (x ) , x x i
  j, x [a,b] i i i =0, i j i i n
- Đa thức bậc không quá n, P x n ( ) đi qua bộ
điểm trên được gọi là đa thức nội suy với các mốc nội suy
xii=0,n - Khi đó
f ( x)  P x n ( ) ĐA THỨC NỘI SUY • Định lý:
Với bộ điểm x , y x x i   j i i  , , cho =0, i j i n
trước, đa thức nội suy tồn tại và duy nhất ĐA THỨC NỘI SUY P ( x) 2 n
= a + a x + a x + + a x n 0 1 2 n 2 n
a + a x + a x + a x = y o 1 0 2 0 n 0 0 
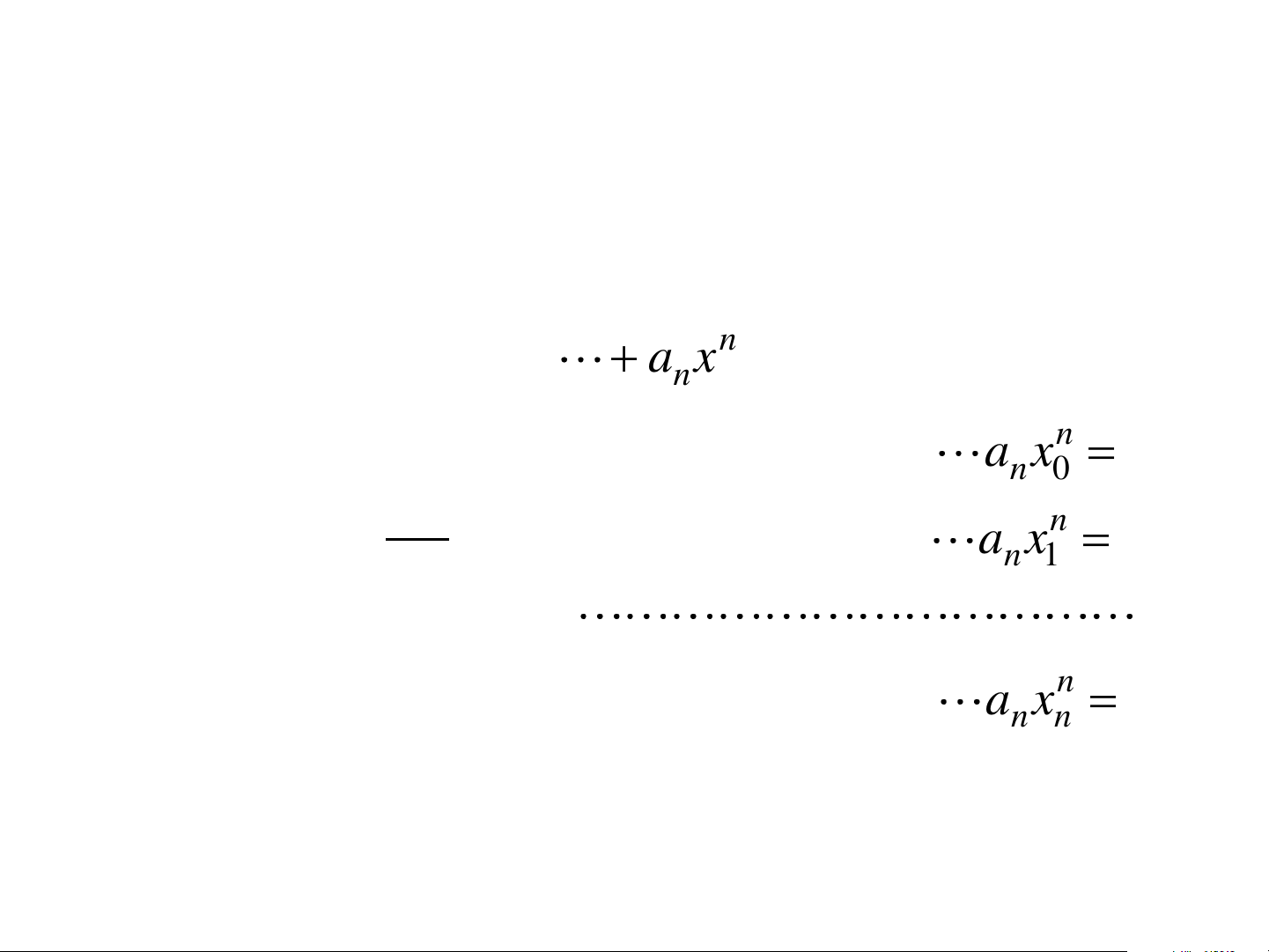
a + a x + a x + a x = y P x = y i  = n   n ( i ) 2 n o 1 1 2 1 n 1 1 0, i   2 n
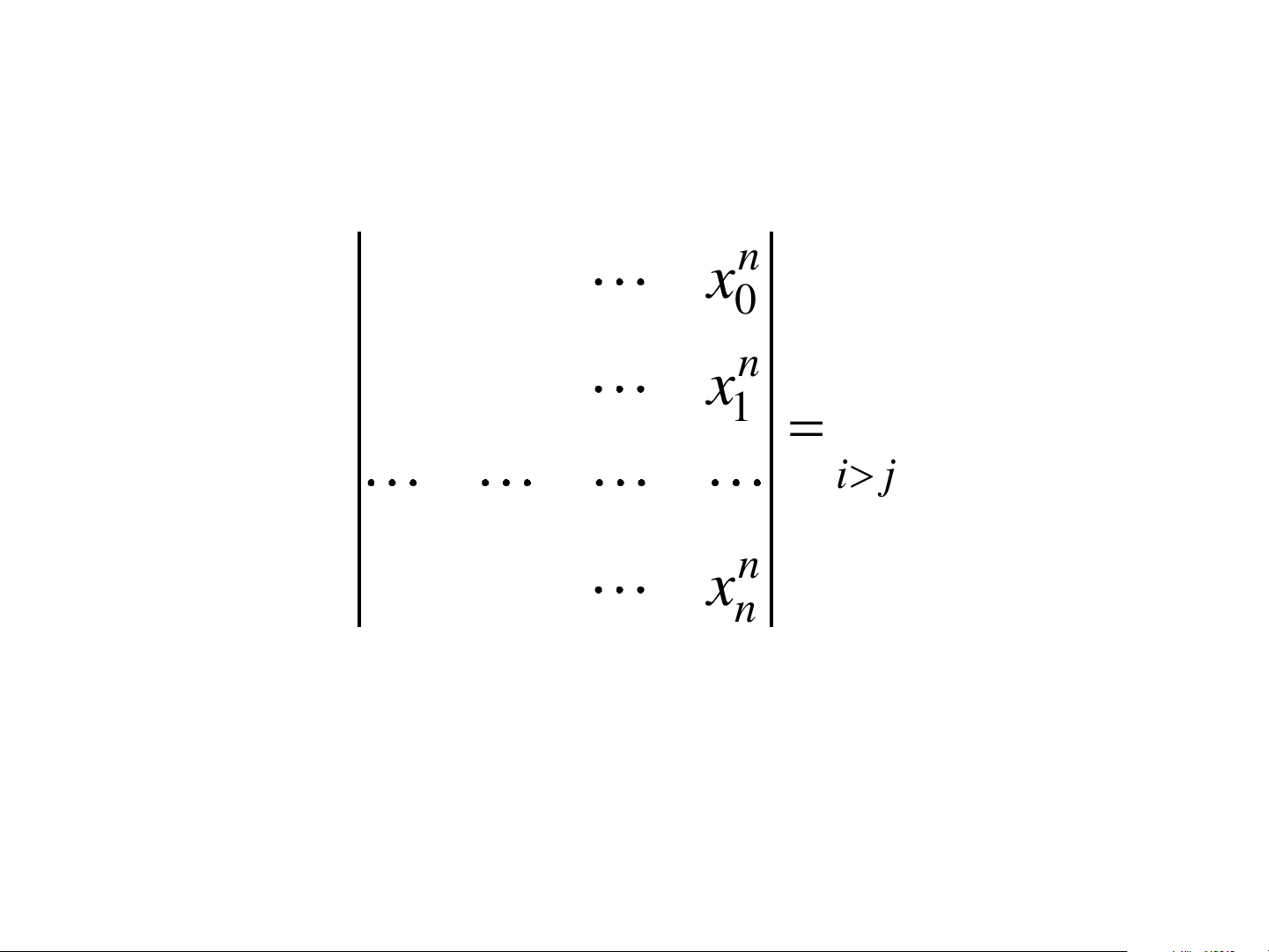
a + a x + a x + a x = yo 1 n 2 n n n n ĐA THỨC NỘI SUY • Định thức 1 n x x 0 0 1 n x x 1
1 =  (x − x i j ) 0. ij 1 n x x n n
• Vậy hệ có nghiệm duy nhất hay đa thức nội suy tồn tại và duy nhất
SAI SỐ CỦA ĐA THỨC NỘI SUY • Đặt
F (t ) = R t − kw t n ( ) n 1 + ( ) • Chọn k sao cho
F ( x) := f ( x) − P ( x) − kw x = 0 n n 1 + ( )
• F(t) có ít nhất n+2 nghiệm phân biệt nên F’(x) có ít
nhất n+1 nghiệm phân biệt, …..
SAI SỐ CỦA ĐA THỨC NỘI SUY (n 1 + ) 
 [a,b], F ( ) = 0 (n+ )1 f ( )  k = (n+ )1! (n+ )1 f   R x = x n ( ) ( ) ( + n + ) w(n ) 1 ( ) 1 ! Ví dụ
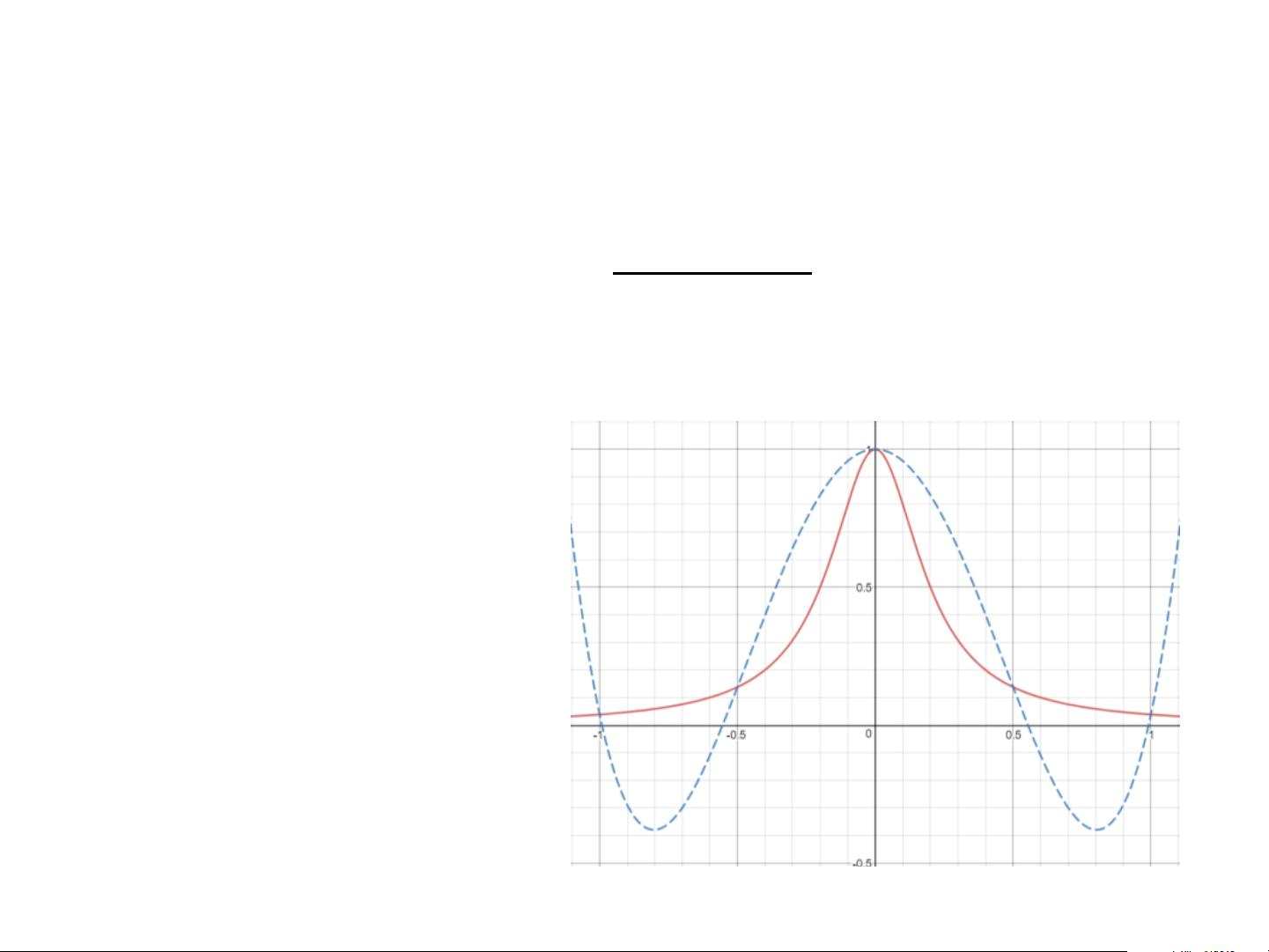
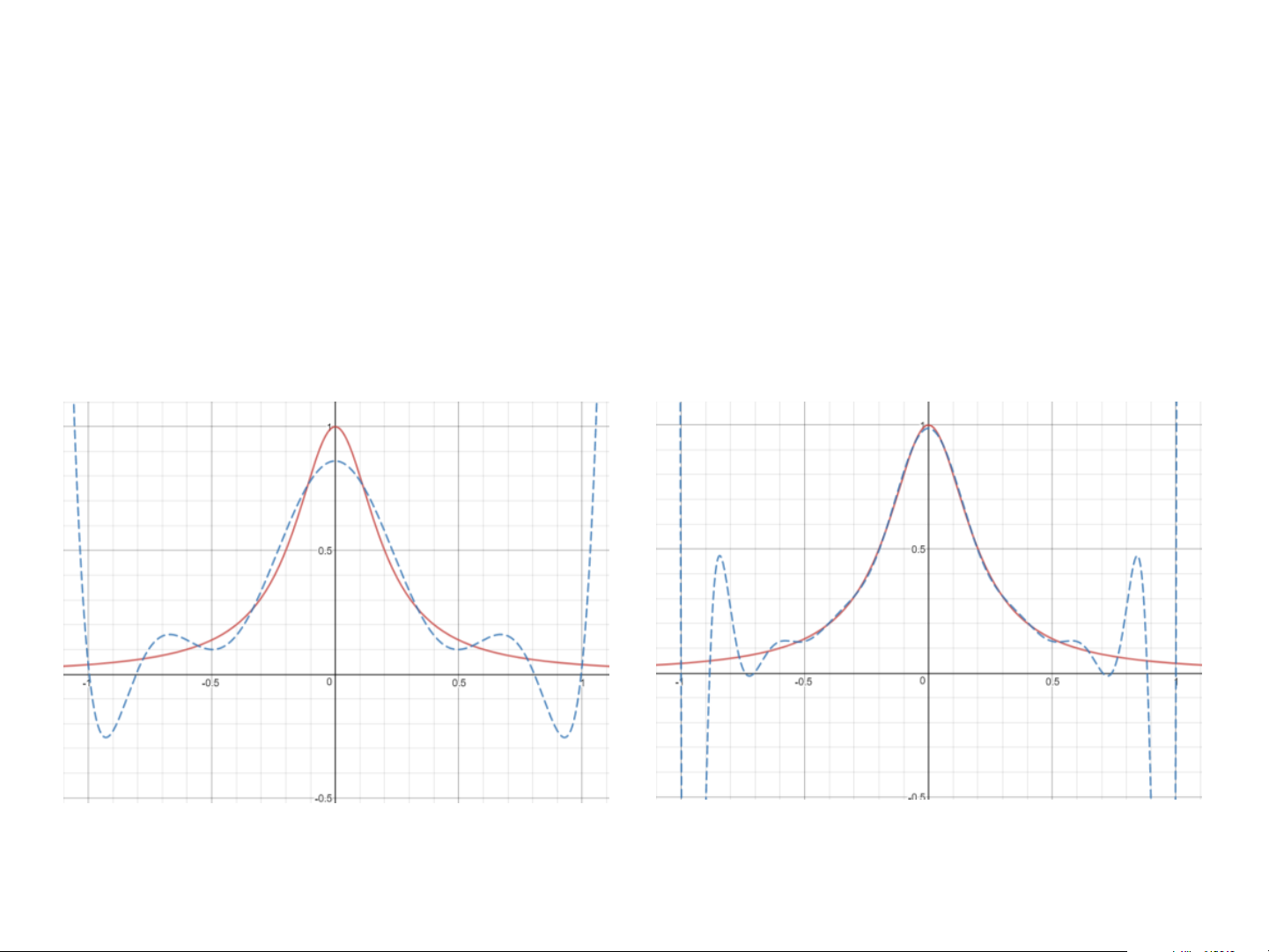
• Xấp xỉ hàm f (x) 1 = 2 25x + 1 • Với 5 mốc nội suy Ví dụ
• Với 10 và 17 mốc nội suy Tối ưu hóa mốc nội suy
• Bài toán: Chọn mốc nội suy sao cho sai số xấp
xỉ hàm đạt được nhỏ nhất
f − P = sup R x n n ( ) a,bR ( x) M n 1 +  ( + n + ) w x n 1 ( ) 1 !
f − P → min  w x → min n n 1 + ( ) Tối ưu mốc nội suy
• Xét khoảng nội suy [-1,1]
• Xét họ các hàm đa thức Chebysev: T x = n x n ( ) cos( .arccos ) T x = 2xT x − T x n 1 + ( ) n ( ) n 1−( )
T x = 1, T x = x 0 ( ) 1 ( ) − T ( x) 2 = 2x −1, T x = x + n ( ) n 1 2 n 2 Tối ưu mốc nội suy
• Định lý: trong các đa thức bậc n có hệ số cả 1 bằng 1, đa thức T x − n ( ) là đa thức có độ n 1 2
lệch so với 0 nhỏ nhất, tức là − p ( x) n n 1 = x + a x + + a n 1 − 0 T x max p ( x) n ( )  max −  −  n 1 − 1,1 1,1 2 Tối ưu mốc nội suy
• Chọn mốc nội suy là n+1 các nghiệm của T x n ( ) ix = cos , i = 0, . n i n
• Trường hợp khoảng nội suy đặt a,b ẩn:
2x − (b + a) t = b − a