Xấp xỉ hàm số bằng đa thức nội suy LAGRANGE | Bài giảng môn Phương pháp tính và matlab CTTT | Đại học Bách khoa hà nội

Hãy xác định đa thức nội suy Lagrange đi qua các điểm trên. Tài liệu trắc nghiệm môn Phương pháp tính và matlab CTTT giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

9 5 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Phương pháp tính và matlab CTTT

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

11 trang 1 tháng trước

Tác giả:

Profile Lê Na
XẤP XỈ HÀM SỐ BẰNG
ĐA THỨC NỘI SUY LAGRANGE
ĐA THỨC NỘI SUY
- Cho bộ điểm
- Đa thức bậc không quá n, đi qua bộ
điểm trên được gọi là đa thức nội suy với các
mốc nội suy
- Khi đó
( )
0,
, , , [ , ]
i i i i j i
in
x y f x x x i j x a b
=
=
( )
n
Px
( ) ( )
n
f x P x
0,
i
in
x
=
ĐA THỨC NỘI SUY
ĐỊNH LÝ:
Với bộ điểm cho
trước, đa thức nội suy tồn tại và duy nhất.
0,
,,
i i i j
in
x y x x i j
=
ĐA THỨC NỘI SUY LAGRANGE
• Đa thức Lagrange cơ bản
• Đa thức nội suy Lagrange
( )
( )
( )
( )( ) ( )
( )( ) ( )( ) ( )
( )
0 1 1 1
0 1 1 1
.
1
deg
0
i i n
i
i i i i i i i n
i j i
x x x x x x x x x x
Lx
x x x x x x x x x x
ij
L x L n
ij
−+
−+
− − − − −
=
− − − − −
=
=
( ) ( )
0
n
n i i
i
P x y L x
=
=
Đánh giá sai số
VÍ DỤ
Xét hàm số
1. Hãy xác định đa thức nội suy Lagrange đi qua
các điểm trên? Tính giá trị gần đúng của hàm
số tại điểm x = 0.1
2. Hãy đánh giá sai số tại x = 0.1
x -1 0 1
y 1/3 1 3
3
x
y =
( )
( )
( )( )
( )
( )( )
( )( )
( )
( )
( )( )
( ) ( ) ( ) ( )
2
0
2
1
2
2
2
0 1 2
1
11
1 0 1 1 2 2
11
1
0 1 0 1
1
11
1 1 1 0 2 2
1 2 4
31
3 3 3
xx
L x x x
xx
L x x
xx
L x x x
P x L x L x L x x x
−
= = −
− − − −
+−
= = − +
+−
+
= = +
+−
= + + = + +
10
(3) 3
(3)
3
[ 1,1]
3
11
3 1.14
10 10
( ) 3 (ln(3))
sup | (x)| 3.9779069
| R(x)| |( 1) ( 1)|
3!
| R(0.1)| 0.0656355
x
x
fP
fx
Mf
M
x x x
−
= =
=
→ =
+ −
→
Ví dụ
• Xấp xỉ hàm
• Với 5 mốc nội suy
( )
2
1
25 1
fx
x
=
+
Ví dụ
• Với 10 và 17 mốc nội suy
Sơ đồ Horner tính giá trị đa thức
| 1/11
| | Tải xuống

Có thể bạn quan tâm:

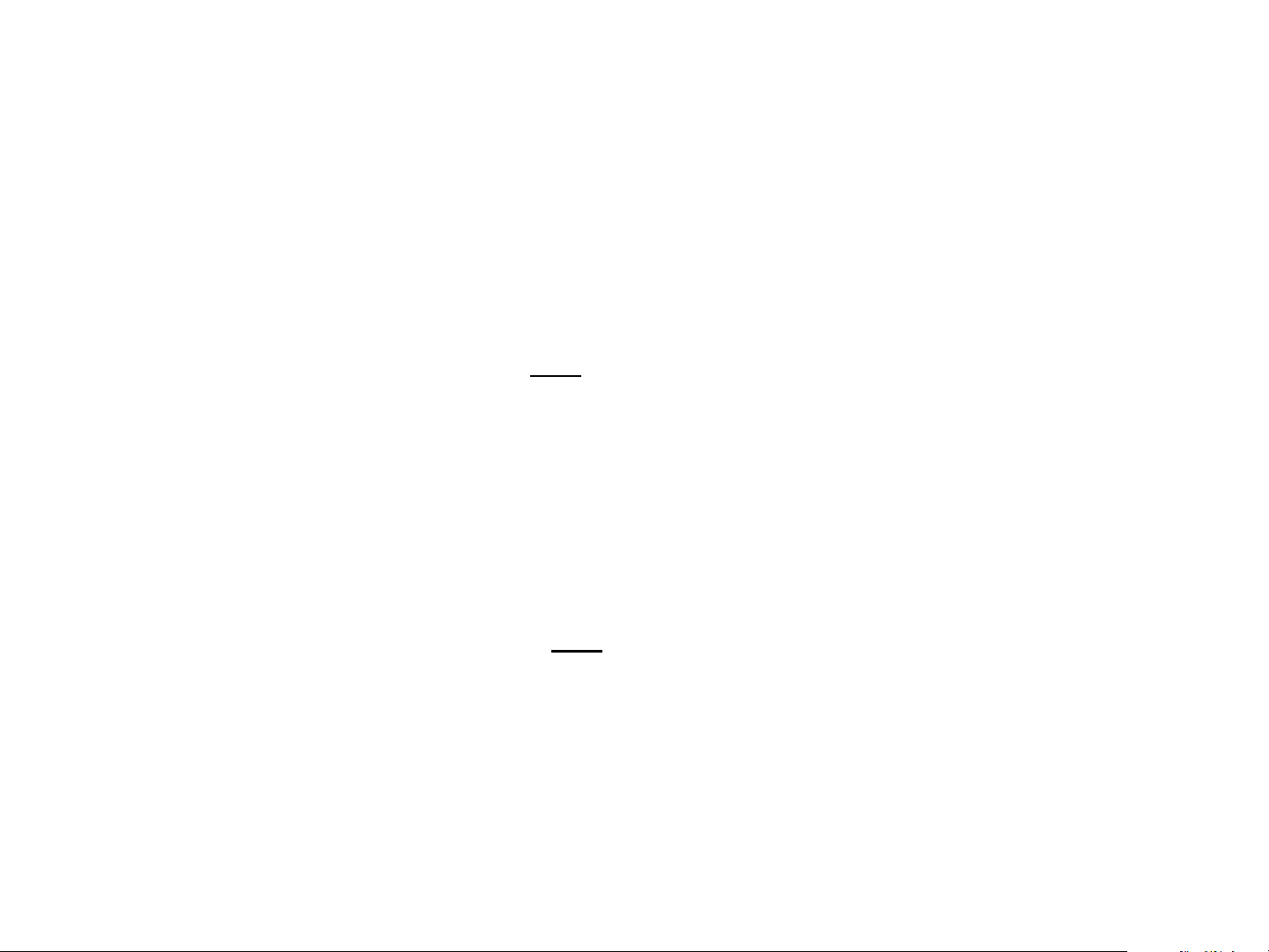
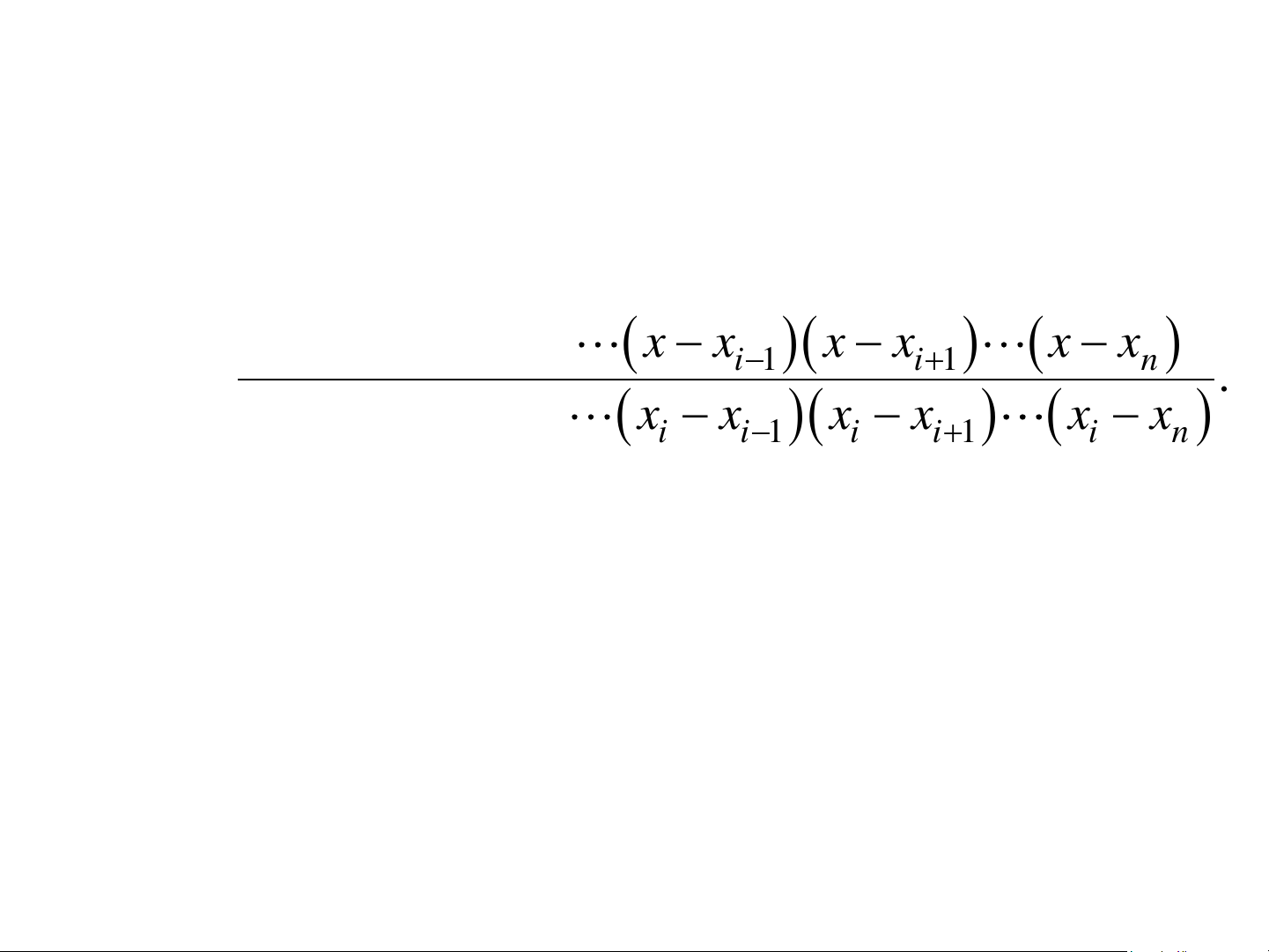
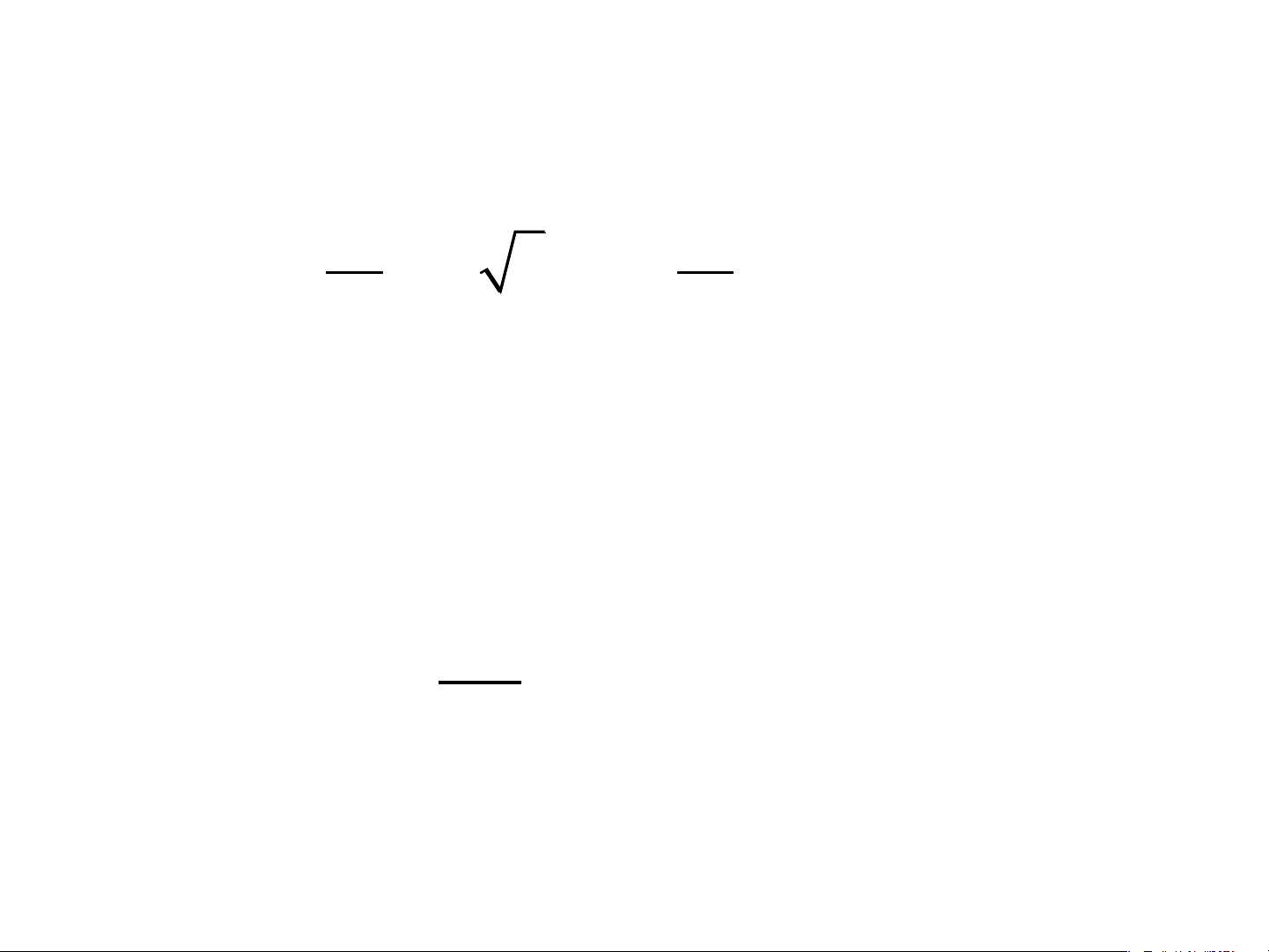
Preview text:

XẤP XỈ HÀM SỐ BẰNG
ĐA THỨC NỘI SUY LAGRANGE ĐA THỨC NỘI SUY - Cho bộ điểm
x , y = f (x ) , x x i
  j, x [a,b] i i i =0, i j i i n
- Đa thức bậc không quá n, P x n ( ) đi qua bộ
điểm trên được gọi là đa thức nội suy với các
mốc nội suy xii=0,n - Khi đó
f ( x)  P x n ( ) ĐA THỨC NỘI SUY ĐỊNH LÝ:
Với bộ điểm x , y  , x x i   j i i = i j cho i 0,n
trước, đa thức nội suy tồn tại và duy nhất. ĐA THỨC NỘI SUY LAGRANGE
• Đa thức Lagrange cơ bản x − x x − x x − x x − x x − x − + L x = i ( ) ( 0 ) ( 1 ) ( i 1 ) ( i 1 ) ( n ) ( . x − x x − x x − x x − x x − x i 0 ) ( i 1 )
( i i 1−)( i i 1+) ( i n)  i = j L x =  L n i ( j ) 1 deg 0 i i j
• Đa thức nội suy Lagrange P ( x) n =  y L x n i i ( ) i=0 Đánh giá sai số
f (x) = P x + R x n ( ) n ( ) M R x +  x n ( ) n 1 ( + n + ) wn 1( ) 1 ! n + w
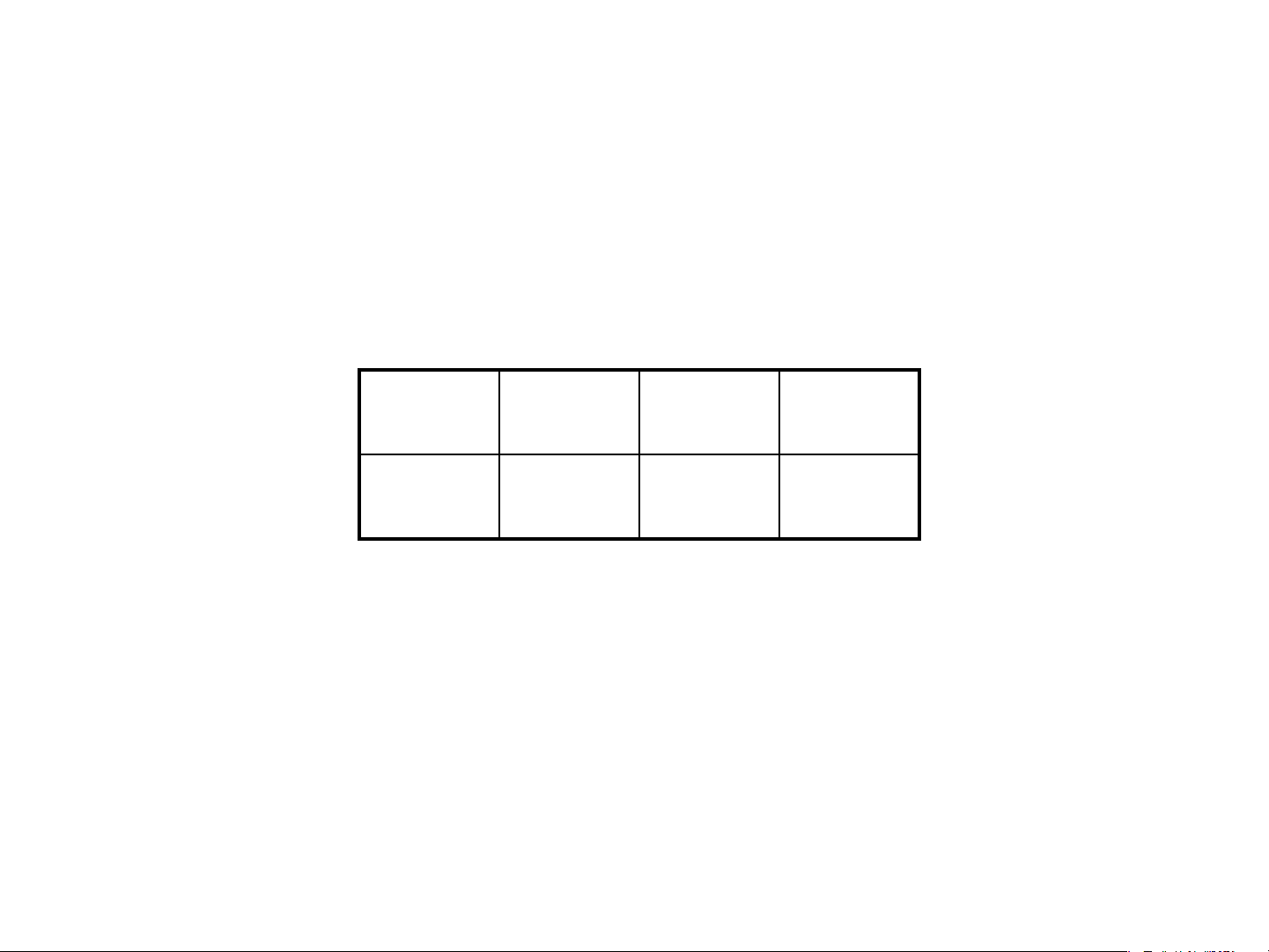
x =  x − x M = f x n+ ( ) ( i) (n )1 , sup | | 1 n 1 + ( ) i=0 x [  a,b] VÍ DỤ Xét hàm số 3x y = x -1 0 1 y 1/3 1 3
1. Hãy xác định đa thức nội suy Lagrange đi qua
các điểm trên? Tính giá trị gần đúng của hàm số tại điểm x = 0.1
2. Hãy đánh giá sai số tại x = 0.1 − L ( x) x ( x )1 1 2 1 = = x − x 0 ( 1 − − 0)( 1 − − ) 1 2 2 + −
L ( x) ( x ) 1 ( x ) 1 2 = = −x +1 1 (0 + ) 1 (0 − ) 1 + L ( x) (x ) 1 x 1 2 1 = = x + x 2 (1+ ) 1 (1− 0) 2 2 P ( x) 1
= L (x) + L (x) + L (x) 2 2 4 3 = x + x +1 0 1 2 3 3 3  1    10 1 f = 3  P =1.14     10  10  (3) x 3 f (x) = 3 (ln(3)) (3)
→ M = sup | f (x) | 3.9779069 3 x [  1 − ,1] M3 | R(x) |
| (x + 1)x(x −1) | 3! | → R(0.1) | 0.0656355 Ví dụ
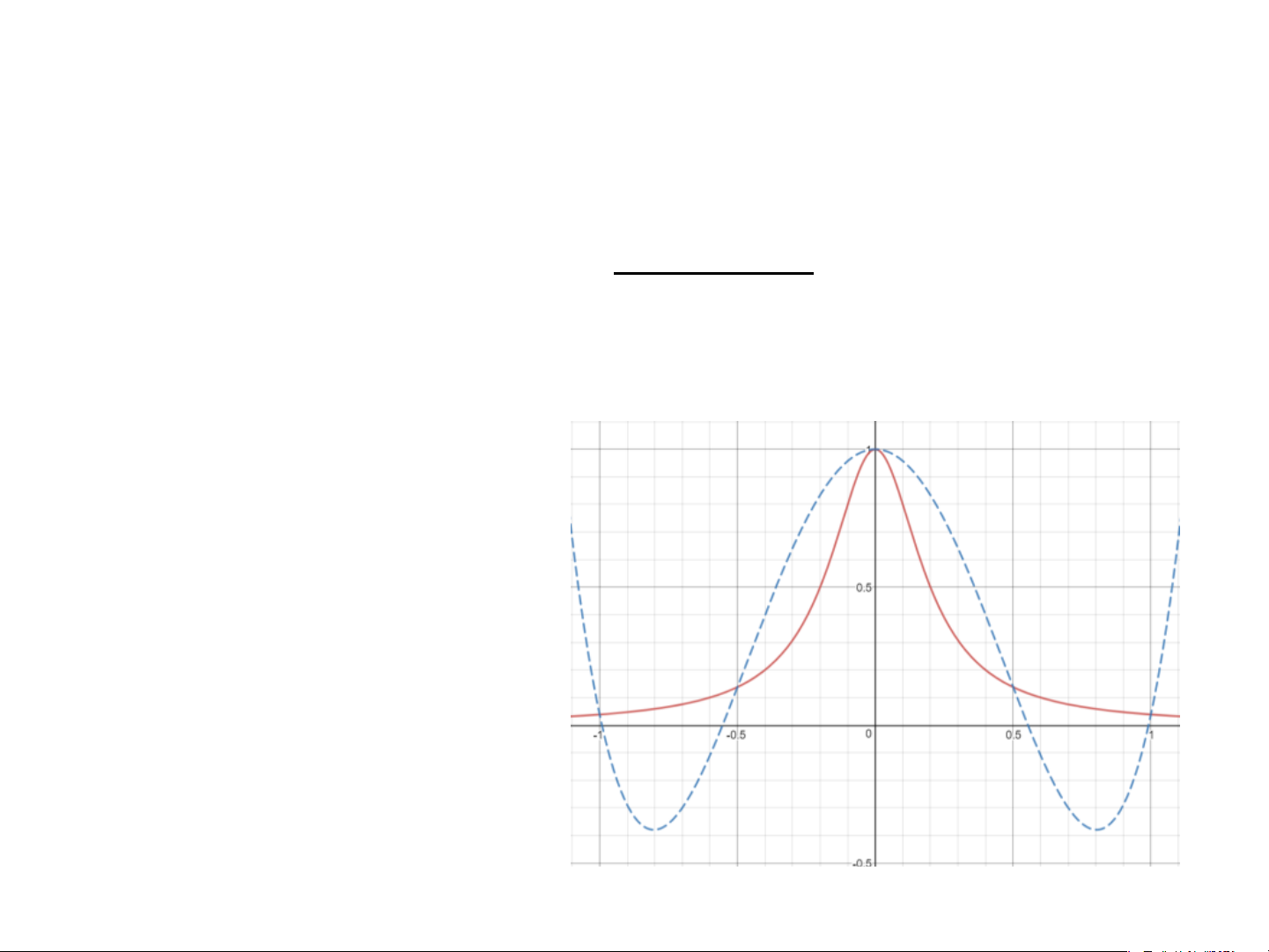
• Xấp xỉ hàm f ( x) 1 = 2 25x + 1 • Với 5 mốc nội suy Ví dụ
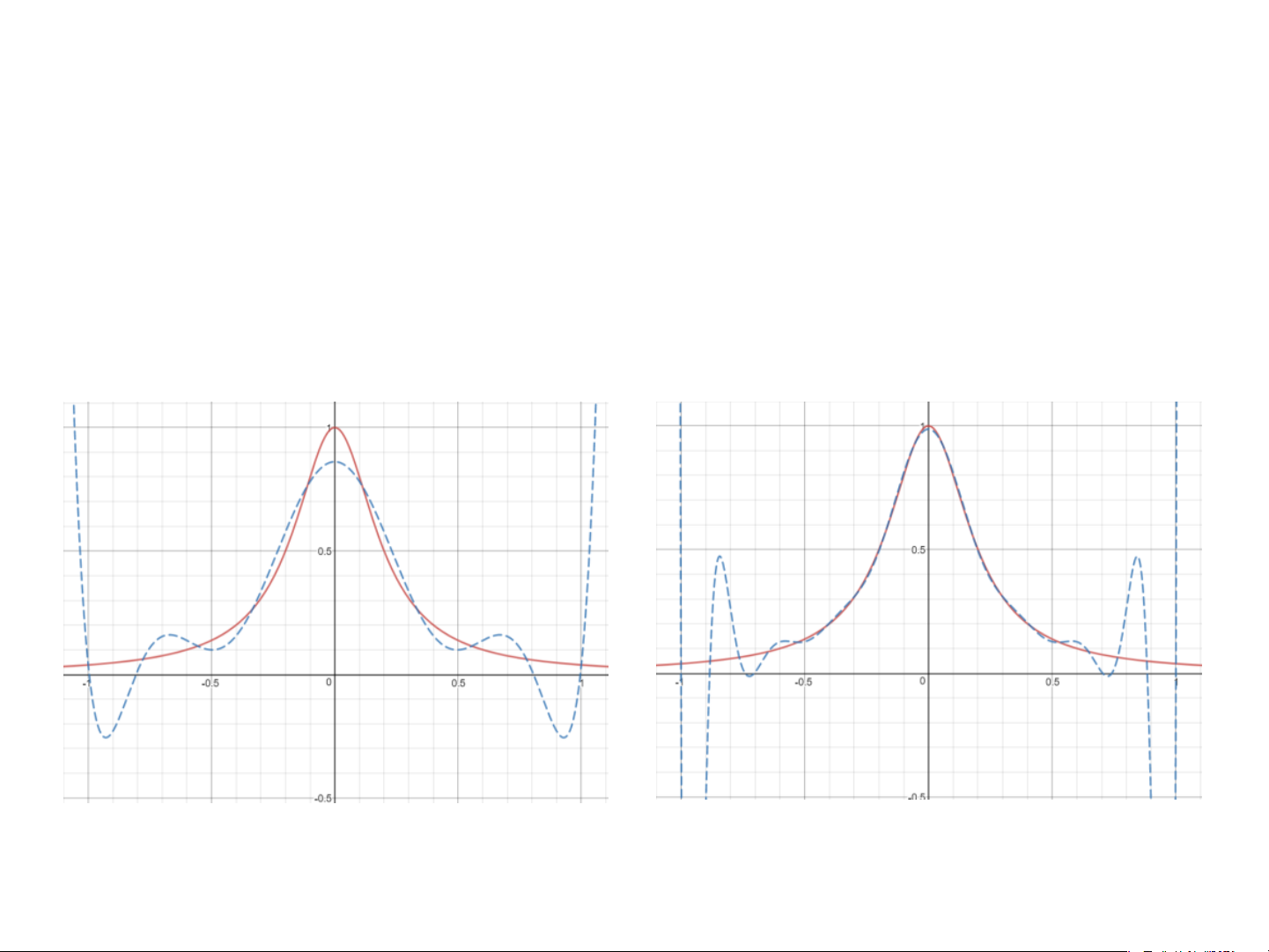
• Với 10 và 17 mốc nội suy
Sơ đồ Horner tính giá trị đa thức