Xấp xỉ hàm số bằng đa thức nội suy newton | Bài giảng môn Phương pháp tính và matlab CTTT | Đại học Bách khoa hà nội

Tìm đa thức nội suy theo cách xây dựng khai triển Taylor của hàm số. Tài liệu trắc nghiệm môn Phương pháp tính và matlab CTTT giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem!

9 5 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Môn: Phương pháp tính và matlab CTTT

Trường: Đại học Bách Khoa Hà Nội

Thông tin:

9 trang 1 tháng trước

Tác giả:

Profile Lê Na
XẤP XỈ HÀM SỐ BẰNG
ĐA THỨC NỘI SUY NEWTON
KHAI TRIỂN TAYLOR
( )
( ) ( )
( )
( )
( )
( )
( )
( )
( )
2
0 1 0 2 0
00
01
0
0 2 2
0
0
'
''
'' 2!
2!
!
!
n
n
nn
f x a a x x a x x
f x a
f x a
fx
f x a a
fx
f x n a a
n
= + − + − +
=
=
= =
= =
ĐA THỨC NỘI SUY NEWTON
• Ý tưởng: Tìm đa thức nội suy theo cách
xây dựng khai triển Taylor của hàm số
( )
( ) ( )
( )
( )
( )
( ) ( )
0 1 0 2 0 1
0 0 0 0
10
1 0 1 1 0 1 1 0
10
'
f x a a x x a x x x x
f x a a y
yy
f x a a x x y a f x
xx
= + − + − − +
= =
−
= + − = =
−
ĐA THỨC NỘI SUY NEWTON
• Tỷ hiệu
( )
( )
10
01
10
1 2 0 1
0 1 2
20
1 0 1
01
0
,:
,,
, , :
,..., ,...,
, ,..., :
kk
k
k
f x f x
f x x
xx
f x x f x x
f x x x
xx
f x x f x x
f x x x
xx
−
−
=
−
−
=
−
−
=
−
NỘI SUY NEWTON TIẾN
• Xây dựng đa thức nội suy Newton theo
quy nạp các mốc theo thứ tự tăng dần
( )
( )
( )
( )
( )
( )
( )
( )
0
0
0
0 0 0
0 0 1
01
1
0 0 1 0 1 1
0 0 1 0 0 1 0 1
,
,
,,
,,
, , , ,
, , ,
f x y
f x x
xx
f x y f x x x x
f x x f x x
f x x x
xx
f x x f x x f x x x x x
f x y f x x x x f x x x x x x x
−
=
−
= + −
−
=
−
= + −
= + − + − −
NỘI SUY NEWTON LÙI
• Xây dựng đa thức nội suy Newton theo
quy nạp các mốc theo thứ tự giảm dần
( )
( )
( )
( )
( )
( )
( )( )
1
1
1
1 1 1
1 1 1
,
,
,,
,,
, , , ,
, , ,
n
n
n
n n n
n n n
nn
n
n n n n n n
n n n n n n n n
f x y
f x x
xx
f x y f x x x x
f x x f x x
f x x x
xx
f x x f x x f x x x x x
f x y f x x x x f x x x x x x x
−
−
−
− − −
− − −
−
=
−
= + −
−
=
−
= + −
= + − + − −
ĐTNS NEWTON MỐC CÁCH ĐỀU
• Sai phân
( )
( )
0
11
1
1
0
0
,...,
!!
k
k k k k
ll
kk
ll
kk
kk
k
k
kk
x x kh
y y y y
yy
yy
yy
f x x
k h k h
++
−
−
=+
= − =
=
=

==
ĐTNS NEWTON MỐC CÁCH ĐỀU
( )
( )
( ) ( ) ( )
( )
( ) ( ) ( )
0
2
0 0 0
0
2
1 1 1
1! 2! !
1 1 1
1! 2! !
nn
n
nn
n
n n n
n
P x P x th
y y y
y t t t t t t n
n
P x th
y y y
y t t t t t t n
n
=+
= + + − + + − − +
=+
= + + + + + + + −
ĐÁNH GIÁ SAI SỐ
( ) ( ) ( )
( )
( )
( )
( )
( )
( )
( )
1
1
1
11
0
[ ,b]
w
1!
w , sup | |
nn
n
nn
n
n
n i n
i
xa
f x P x R x
M
R x x
n
x x x M f x
+
+
+
++
=
=+
+
= − =
| 1/9
| | Tải xuống

Có thể bạn quan tâm:

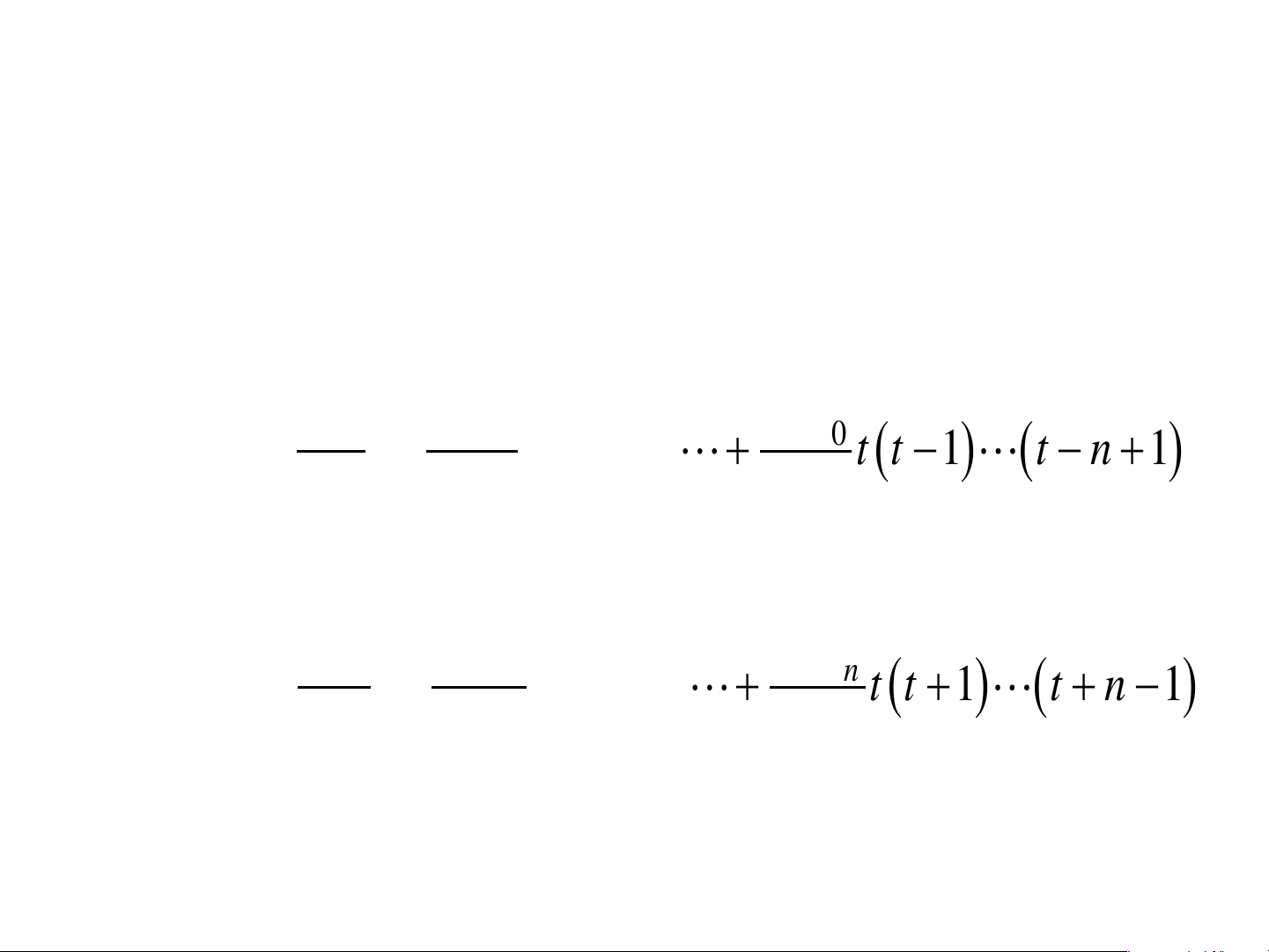
Preview text:

XẤP XỈ HÀM SỐ BẰNG
ĐA THỨC NỘI SUY NEWTON KHAI TRIỂN TAYLOR
f ( x) = a + a ( x − x ) + a ( x − x )2 + 0 1 0 2 0 f ( x = a 0 ) 0
f '( x = a 0 ) 1 ( f '' x f ' x = 2!a a = 0 ) ( 0) 2 2 2! ( ) n n ( f x f x
= n!a a = 0 ) ( 0) n n n! ĐA THỨC NỘI SUY NEWTON
• Ý tưởng: Tìm đa thức nội suy theo cách
xây dựng khai triển Taylor của hàm số
f ( x) = a + a x − x + a x − x x − x + 0 1 ( 0 ) 2 ( 0 ) ( 1 )
f ( x = a a = y 0 ) 0 0 0 −
f ( x ) = a + a ( x − x ) y y 1 0 = y a =  f ' x 1 0 1 1 0 1 1 ( 0) x − x 1 0 ĐA THỨC NỘI SUY NEWTON • Tỷ hiệu  f x − f x f x , x := 0 1 ( 1) ( 0) x − x 1 0  f x , x − f x , x
f x , x , x := 0 1 2   1 2  0 1 x − x 2 0  f x ,..., x
− f x ,..., x −
f x , x ,..., x : k k = 0 1 k   1   0 1 x − x k 0 NỘI SUY NEWTON TIẾN
• Xây dựng đa thức nội suy Newton theo
quy nạp các mốc theo thứ tự tăng dần  f x − y f x, x  ( ) 0 = 0 x − x0
f (x) = y + f x, x x − x 0  0( 0 )  f x, x − f x , x
f x, x , x = 0 1  0  0 1 x − x1
f x, x = f x , x + f x, x , x x − x 0   0 1  0 1( 1 )
f (x) = y + f x , x x − x + f x, x , x x − x x − x 0  0 1( 0 )  0 1( 0 ) ( 1 ) NỘI SUY NEWTON LÙI
• Xây dựng đa thức nội suy Newton theo
quy nạp các mốc theo thứ tự giảm dần  f x − y f x, x  ( ) n = n x − xn
f (x) = y + f x x x − x n  , n( n ) 
f x, x − f x , x − f x, x , n n n x = n n 1 −     1 x − xn 1 −
f x,x = f x x + f x x x x − x n   , , , n n 1 −   n n 1−( n 1 − )
f (x) = y + f x x x − x + f x x x x − x x − x n  , , , n n 1 − ( n )  n n 1−( n )( n 1 − )
ĐTNS NEWTON MỐC CÁCH ĐỀU
• Sai phân x = x + kh k 0 y  = y − y = y k k 1 + k k 1 + l −
y =   y k ( l 1 k ) l −
y =   y k ( l 1 k )  k kyy f x ,..., x = = k  0 k 0 k ! k h k ! k h
ĐTNS NEWTON MỐC CÁCH ĐỀU
P x = P x + th n ( ) n ( 0 ) 2 n y   yy 0 0 = y + t + t (t − ) 0 1 + + t t −1 t − n +1 0 ( ) ( ) 1! 2! n! = P x + th n ( n ) 2 yy  = y + t + t (t + ) n y n n 1 n + + t t + t + n − n ( )1 ( )1 1! 2! n! ĐÁNH GIÁ SAI SỐ
f (x) = P x + R x n ( ) n ( ) M R x +  x n ( ) n 1 ( + n + ) wn 1( ) 1 ! n + w
x =  x − x M = f x n+ ( ) ( i) (n )1 , sup | | 1 n 1 + ( ) i=0 x [  a,b]