Bài tập toán 9 tuần 17 (có đáp án và lời giải chi tiết)

BÀI TẬP TOÁN 9 TUẦN 17
I. ĐẠI SỐ: ÔN TẬP VỀ GIẢI HỆ PHƯƠNG TRÌNH Bài 1. Giải hệ phương trình:
2x  3y  5 
x  4y  6
2x  y  3 a)  b)  c)   3
 x  4y  2
4x  3y  5
5  y  4x 2 5   2   x  y  1 2x  4  0  x x  y d)  e)  f)  x  y  5
4x  2y  3 3 1   1,7 x x  y Bài 2.
Xác định a và b để đồ thị hàm số y  ax  b đi qua điểm A và B trong mỗi trường hợp sau: a) A 3  ;3và B 1  ;2 b) A4;   1 và B  4  ;  1
c) A 5; 2  và B 0; 2 
Bài 3. Viết phương trình đường thẳng thỏa mãn một trong các điều kiện sau:  1 7  a) Đi qua điểm A ; 
 và song song với đường thẳng y  2x  3 .  2 4 
b) Cắt trục tung Oy tại điểm có tung độ bằng 3 và đi qua điểm B 2;  1 .
c) Căt trục hoành Ox tại điểm có hoành độ bằng 2 và đi qua điểm C 1;2 .
d) Cắt trục tung tại điểm có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng 2 . 3
e) Đi qua hai điểm M 1;2 và N 3;6 .
II. HÌNH H ỌC: ÔN TẬP CHƯƠNG 2 Bài 1.
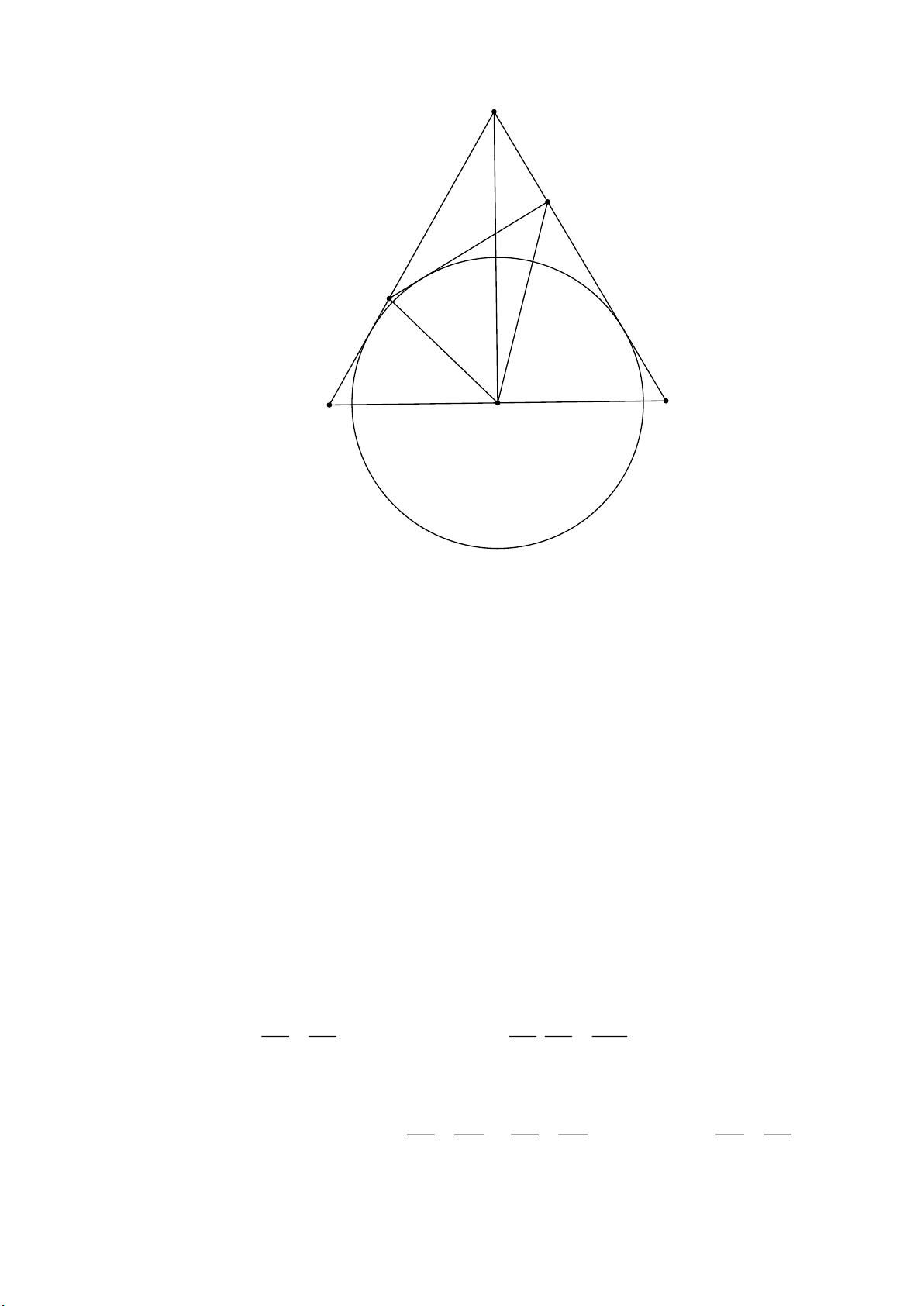
Cho tam giác đều ABC , O là trung điểm của BC . Trên các cạnh AB, AC lần lượt lấy các điểm
di động D, E sao cho 0 DOE  60
a) Chứng minh rằng tích B . D CE không đổi. b) Chứng minh B
 OD đồng dạng với O  ED
c) Vẽ đường tròn tâm O tiếp xúc với AB . Chứng minh rằng đường tròn này luôn tiếp xúc với DE . Bài 2.
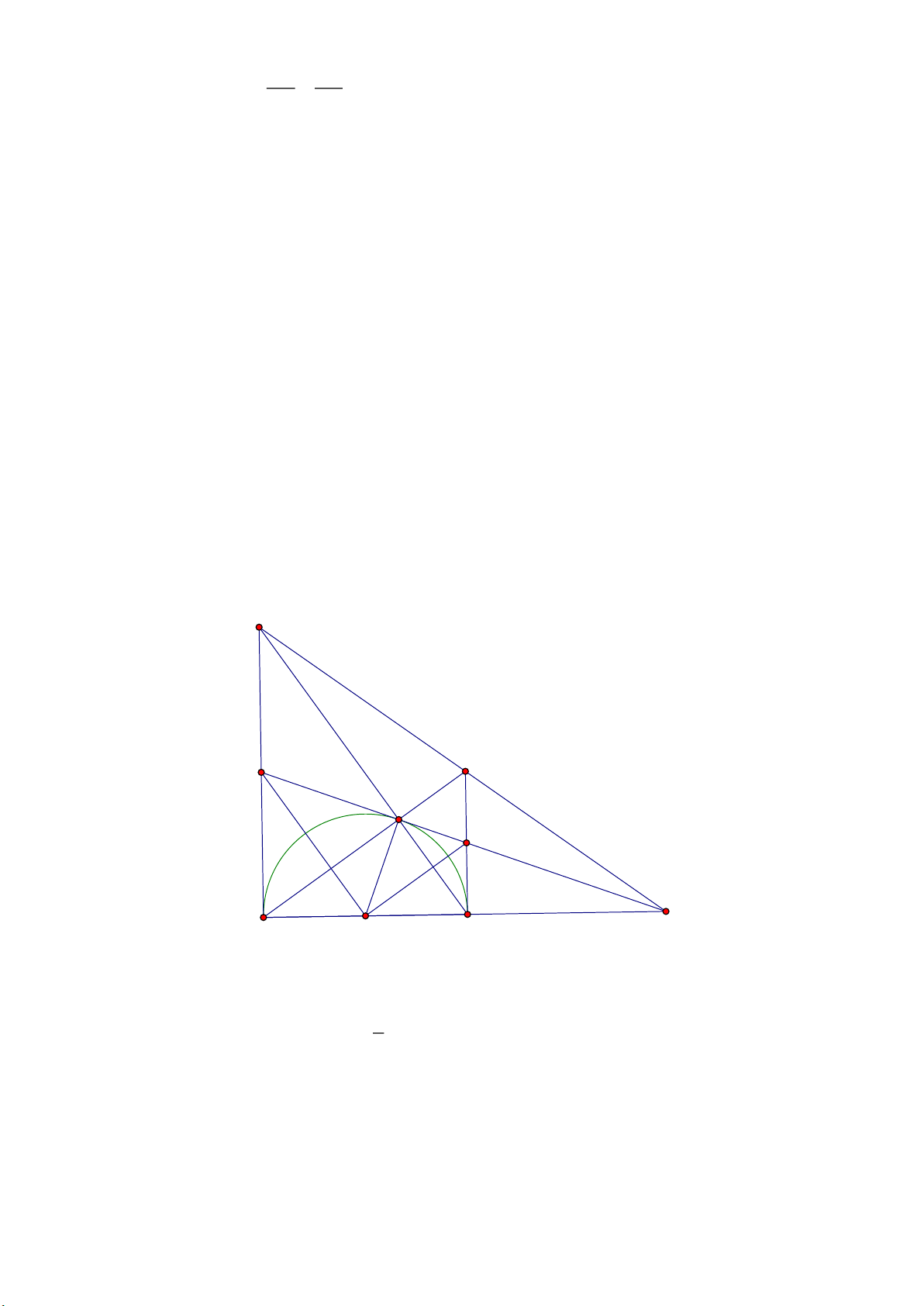
Cho nửa đường tròn  ;
O R đường kính AB và một điểm E di động trên nửa đường tròn ( E
không trùng với A và B ). Vẽ các tiếp tuyến Ax và By với nửa đường tròn. Tia AE cắt By tại
C , tia BE cắt Ax tại D .
a) Chứng minh rằng tích A . D BC không đổi.
b) Tiếp tuyến tại E của nửa đường tròn cắt Ax và By theo thứ tự tại M và N . Chứng minh rằng ba
đường thẳng MN, AB và CD đồng quy hoặc song song với nhau.
c) Xác định vị trí của điểm E trên nửa đường tròn để diện tích tứ giác ABCD nhỏ nhất. Tính diện tích nhỏ nhất đó. Trang 1
HƯỚNG DẪN GIẢI CHI TIẾT
I. ĐẠI SỐ: ÔN TẬP VỀ GIẢI HỆ PHƯƠNG TRÌNH Bài 1. Giải hệ phương trình
2x  3y  5 
6x  9y  15  y  11   y  11 x  14 a)           3
 x  4y  2  6
 x  8y  4
6x  9y  15  6x  9.11  15   y  11
Vậy nghiệm của hệ phương trình là  ; x y  14;1  1
x  4y  6  4
 x 16y  24   1  9y  19  y  1 x  2 b)         
4x  3y  5
4x  3y  5
4x  3y  5 4x  3.1  5  y  1
Vậy nghiệm của hệ phương trình là  , x y  2;  1
2x  y  3
2x  y  3 2x  2 x  1 x 1 c)         
5  y  4x
4x  y  5
4x  y  5 4.1 y  5 y  1 
Vậy nghiệm của hệ phương trình là  , x y  1;  1 x  y 1 x  y  1 x  3 x  3 d)        x  y  5
2x  y  6 2.3  y  6  y  2
Vậy nghiệm của hệ phương trình là  , x y  3;2     x 2 2x  4  0  2x  4   x  2   e)        5 
4x  2y  3 
4x  2y  3  4.   2    2y  3  y   2   
Vậy nghiệm của hệ phương trình là  x y 5 ,  2;    2  2 5   2 x x  y f)  I  3 1   1,7 x x  y Đặ 1 1 t u  và v 
; ĐK : x  0; x   y x x  y  1   u 2u  5v  2  2
Hệ phương trình  I  trở thành   
3u  v  1,7 1 v   5 1 1  x 2    x 2    1 1    y  3  x  y 5
Vậy nghiệm của hệ phương trình là  , x y  2;3 Bài 2.
Xác định a và b để đồ thị hàm số y  ax  b đi qua điểm A và B trong mỗi trường hợp sau: a) A 3  ;3và B 1  ;2 Vì A 3
 ;3thuộc đồ thị hàm số y  ax  b 3  3  a b Trang 2 B  1
 ;2 thuộc đồ thị hàm số y  ax  b 2  a  b  1   a 3a  b  3  2
Suy ra ta có hệ phương trình :   
a  b  2 3 b   2 1  3 Vậy a  và b  . 2 2 b) A4;   1 và B  4  ;  1 Vì A4;  
1 thuộc đồ thị hàm số y  ax  b  1
  4a b B  4  ; 
1 thuộc đồ thị hàm số y  ax  b 1  4  a b    1 4a  b  1  a 
Ta có hệ phương trình :    4  4
 a  b  1 b   0 1  Vậy a  và b  0. 4
c) A 5; 2  và B 0; 2 
Vì A 5; 2  thuộc đồ thị hàm số y  ax  b  2   5a  b
B 0; 2  thuộc đồ thị hàm số y  ax  b  2  b
 5a b  2 a  0 
Ta có hệ phương trình :    b   2 b   2
Vậy a  0 và b  2 .
Bài 3. Viết phương trình đường thẳng thỏa mãn một trong các điều kiện sau:  1 7  a) Đi qua điểm A ; 
 và song song với đường thẳng y  2x  3 .  2 4 
b) Cắt trục tung Oy tại điểm có tung độ bằng 3 và đi qua điểm B 2;  1 .
c) Căt trục hoành Ox tại điểm có hoành độ bằng 2 và đi qua điểm C 1;2 . 2
d) Cắt trục tung tại điểm có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng . 3
e) Đi qua hai điểm M 1;2 và N 3;6 . Lời giải
a) Gọi phương trình đường thẳng cần tìm là d  : y  ax  ba  0 . 1 7 7 1 Mà ( A
; )  (d ) nên ta có:  .a  b .(1) 2 4 4 2
Vì (d) song song với đường thẳng y=2x  3 nên a  2 . Trang 3 7 1 3
Thay a  2 vào (1) ta có: 
.2  b  b  4 2 4 3
Vậy phương trình đường thẳng d  : y  2x  4
b) Gọi phương trình đường thẳng cần tìm là d  : y  ax  ba  0
Vì d  cắt trục tung tại điểm có tung độ bằng 3 nên b  3.
Mà B(2;1)  (d )  1  2.a  b mà b  3 nên: 1
 2.a  3  2a  2   a  1  .
Vậy phương trình đường thẳng d  : y  - x  3 .
c) Gọi phương trình đường thẳng cần tìm là d  : y  ax  ba  0
Vì đường thẳng d  cắt trục hoành Ox tại điểm có hoành độ bằng 2 tức là điểm có x  2; y  0 hay
M 2;0(d)  0  2.a  b  2a  b  0 (1 )
Và có điểm C(1;2) (d)  2  1.a  b  a  b  2 ( 2 )
Từ ( 1 ) và ( 2 ) có a  2  ;b  4 .
Vậy phương trình đường thẳng d  : y  - 2x  4
d) Gọi phương trình đường thẳng cần tìm là d  : y  ax  b
(d) cắt trục tung tại điểm có tung độ bằng 3 suy ra (
A 0;3)  (d )  3  0.a  b  b  3  2  2 
d  cắt trục hoành Ox tại điểm có hoành độ bằng  N ; 0  (d )   3  3  2
 0  .a  b  2a 3b  0 3 9
mà có b = 3 nên: 2a  3.3  0  a   2 9
Vậy phương trình đường thẳng (d ) : y  - x  3. 2
e) Gọi phương trình đường thẳng cần tìm là d  : y  ax  ba  0 .
Do d  đi qua điểm M 1;2 nên ta có: 2  a  b  b  2  a .
Do d  đi qua điểm N 3;6 nên ta có: 6  3a  b , thay b  2  a vào ta được
6  3a  2  a  2a  4  a  2 .
Với a  2  b  0 .
Phương trình đường thẳng cần tìm là d  là y  2x .
II. HÌNH H ỌC: ÔN TẬP CHƯƠNG 2 Bài 1.
Cho tam giác đều ABC , O là trung điểm của BC . Trên các cạnh AB, AC lần lượt lấy các điểm
di động D, E sao cho 0 DOE  60
a) Chứng minh rằng tích B . D CE không đổi. b) Chứng minh B
 OD đồng dạng với O  ED
c) Vẽ đường tròn tâm O tiếp xúc với AB . Chứng minh rằng đường tròn này luôn tiếp xúc với DE . Trang 4 Lời giải A E D O C B a) Ta có : BOC 180
BODDOEEOC 180
DOE  60 (gt) 
 BOD  EOC 120   1 Xét B  OD có: 0
BOD  OBD  BDO 180 (t / c)  0
OBD  60 (gt) 0
 BOD  ODB 120 (2)
+ Từ (1) và (2) suy ra BDO  COE
BDO  COE(cmt) + Xét BOD  , C  EO có  0
DBO  OCE  60 (gt)  BO  D# C  O
E (g  g) 2 BD BO BC BC BC + Vì  D BO ∽ CE  O    B . D CE  B . O CO  .  CO CE 2 2 4
Mà BC không đổi nên tích B .
D CE cũng không đổi BD DO BD DO BD BO
b) + Từ chứng minh trên B  OD ∽ CE  O     ( vì OC=OB)   CO OE BO OE OD OE Trang 5  BD BO   + Xét B  OD, O
 ED có OD OE
 BOD ∽ OE 
D(c  g  c)  0
DBO  DOE  60 (gt) + Từ B  OD ∽ O
 ED  BDO  O E
D suy ra DO là phân giác góc BDE (3) c) + Vì ABC 
đều, có O là trung điểm của BC nên AO là tia phân giác của góc BAC (4)
+ Từ (3) và (4) kết hợp đường tròn tâm O tiếp xúc với AB (gt) suy ra O là tâm đường tròn bàng tiếp góc
A của tam giác ADE . Từ đó suy ra đường tròn này cũng tiếp xúc với DE (đpcm) Bài 2.
Cho nửa đường tròn  ;
O R đường kính AB và một điểm E di động trên nửa đường tròn ( E
không trùng với A và B ). Vẽ các tiếp tuyến Ax và By với nửa đường tròn. Tia AE cắt By tại
C , tia BE cắt Ax tại D .
d) Chứng minh rằng tích A . D BC không đổi.
e) Tiếp tuyến tại E của nửa đường tròn cắt Ax và By theo thứ tự tại M và N . Chứng minh rằng ba
đường thẳng MN, AB và CD đồng quy hoặc song song với nhau.
f) Xác định vị trí của điểm E trên nửa đường tròn để diện tích tứ giác ABCD nhỏ nhất. Tính diện tích nhỏ nhất đó. Lời giải D C M E N N' S A O B
a) Vì Ax, By là các tiếp tuyến của O  Ax    90o    90o AB DAB ADB ABD . 1
Xét tam giác AEQ có EO  AO  BO 
AB  AEB vuông tại E    90o EAB EBA 2
Suy ra ADB  EAB . Xét ABD  và B  CA có:   90o DAB ABC
, ADB  EAB (Chứng minh trên)  A  DB ∽ B
 AC g  g. Trang 6 AD AB 2    A .
D BC  AB mà AB là bán kính, không đổi nên A .
D BC không đổi. (đpcm). AB BC
b) Xét O có tiếp tuyến tại A và tiếp tuyến tại E cắt nhau tại M suy ra MA  ME  M
 AE cân tại M
 MAE  MEA . Mà   90o,   90o MAE MDE MEA MED
 MDE  MED  M
 DE cân tại M suy ra ME  MD 
MA  MD (1). Chứng minh tương tự ta có N là trung điểm của BC .
*TH1: Nếu AB / /CD  AB / /CD / /MN .
*TH2: Nếu AB cắt CD . Gọi S là giao điểm của AB và CD , SM cắt BC tại N ' . BN ' CN '  SN ' 
Vì AD / /BC (cùng vuông góc với AB ), áp dụng định lý Ta- lét ta có:    2 AM DM  SM 
Từ (1) và (2) suy ra BN '  CN '  N ' là trung điểm của BC  N  N '  MN đi qua S hay
AB, CD, MN đồng quy tại S (đpcm).
c) Vì AD / /BC nên tứ giác ABCD là hình thang vuông
AB  AD  BC   S 
 R AD  BC  R AD BC  R AB  R R  R ABCD   2 2 2 . 2 2 .2 4 2
Dấu bằng xảy ra khi AD  BC  MN / / AB  E là điểm chính giữa của nửa đường tròn.
Vậy khi E là điểm chính giữa của nửa đường tròn thì tứ giác ABCD có diện tích nhỏ nhất và min 2 S  4R . ABCD HẾT Trang 7