Chùm bài toán về Cát tuyến - Tiếp tuyến | Ôn tập Hình học 9

CHÙM BÀI TOÁN VỀ HAI TIẾP TUYẾN CẮT NHAU VÀ CÁT TUYẾN
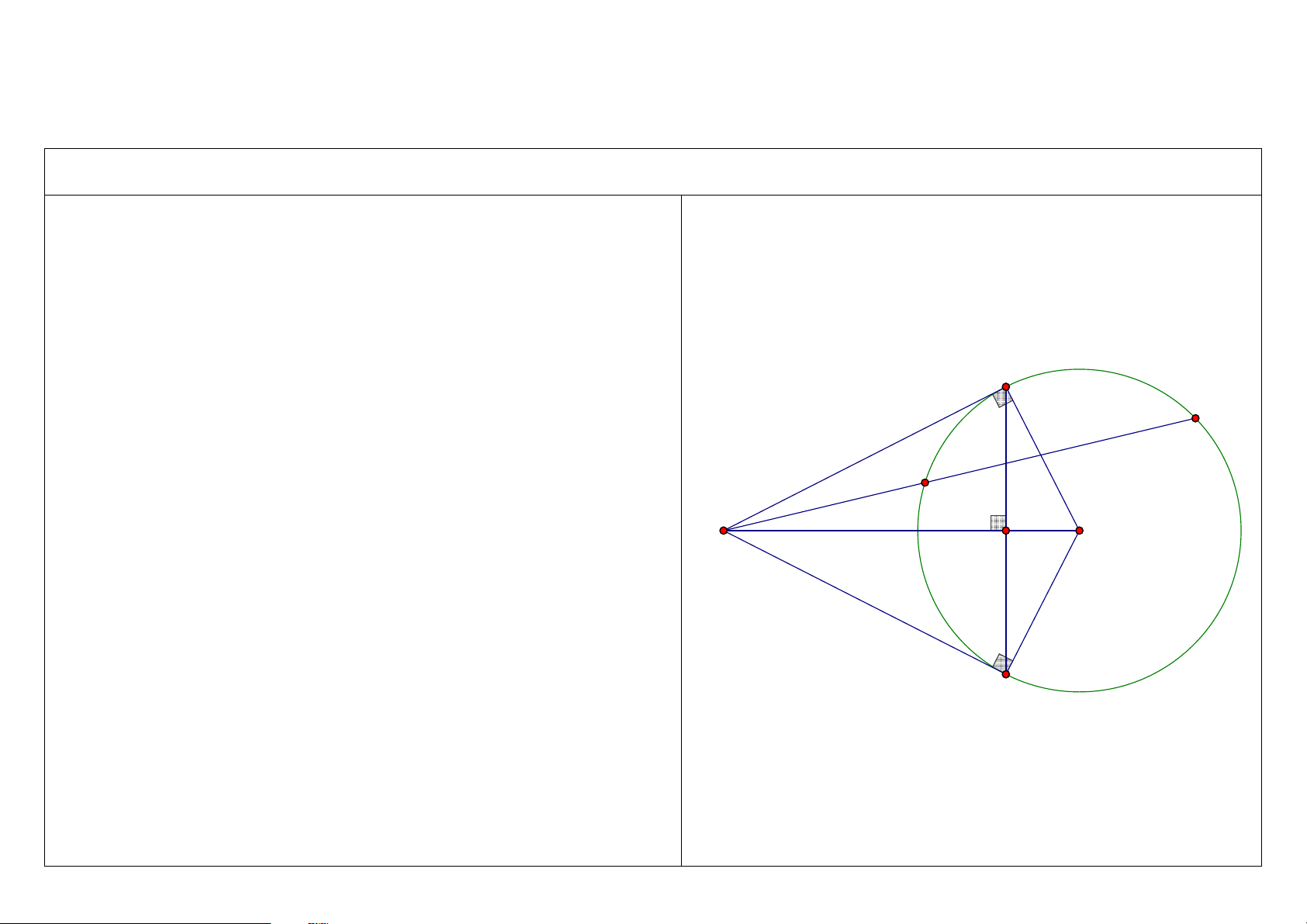
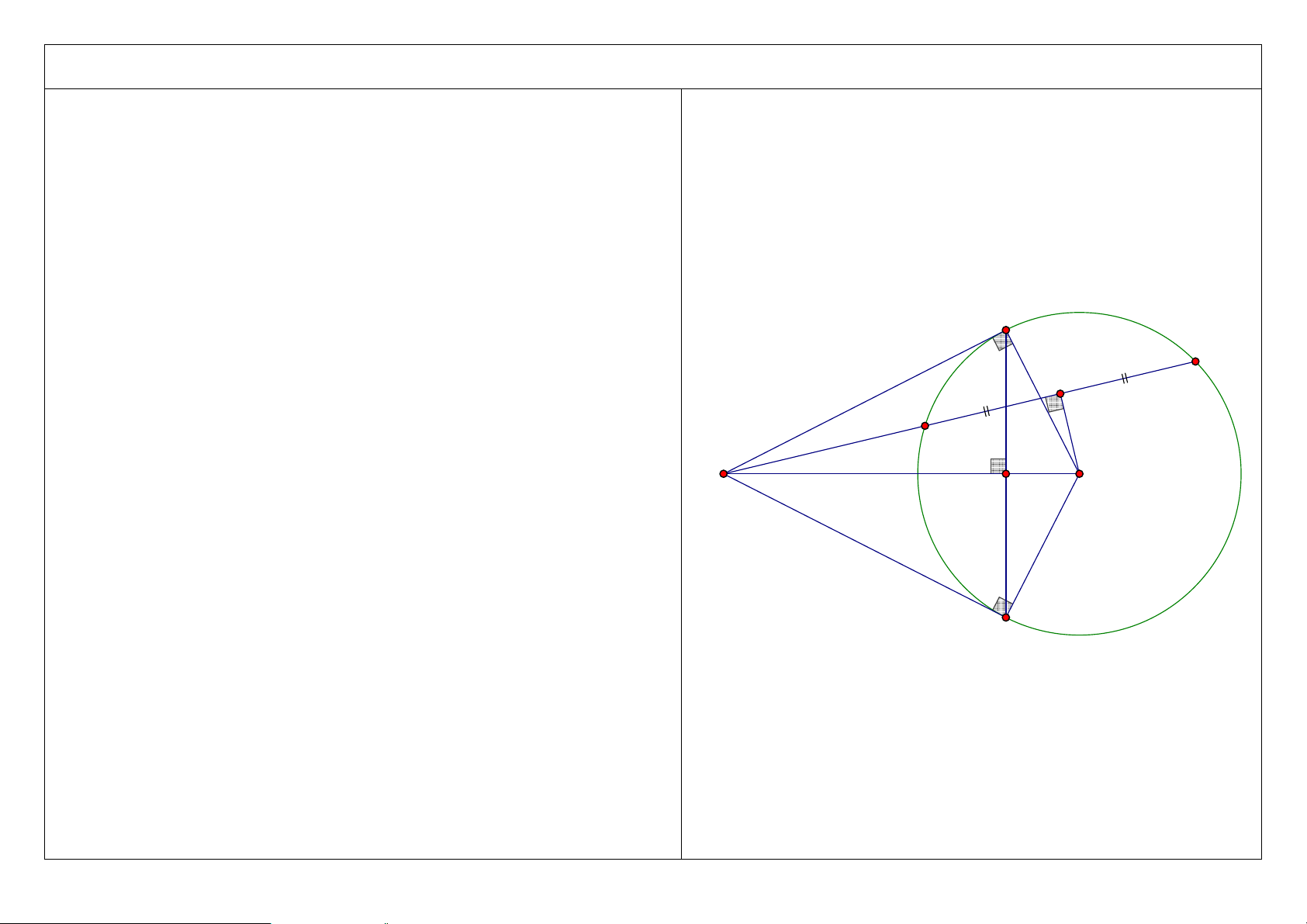
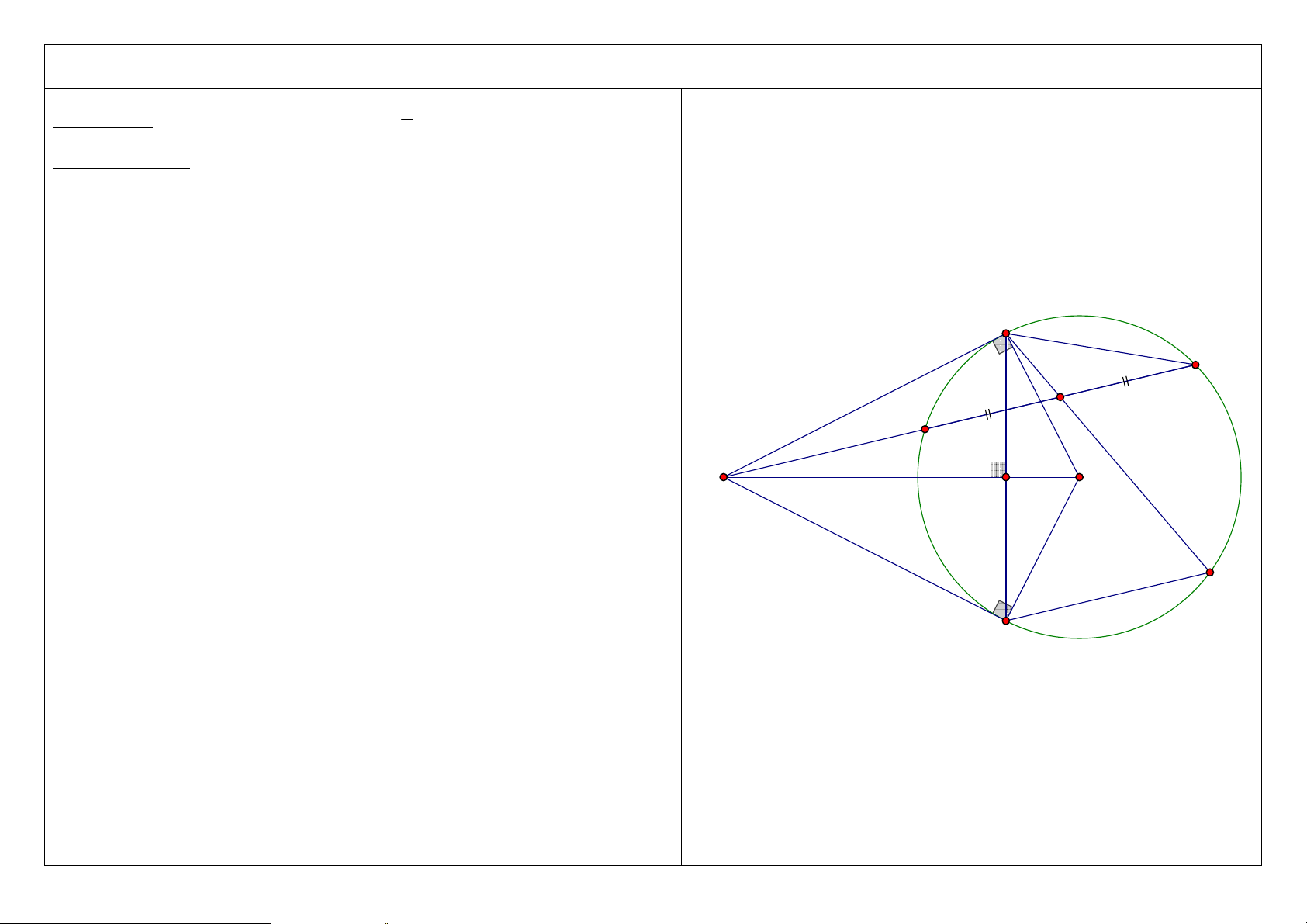
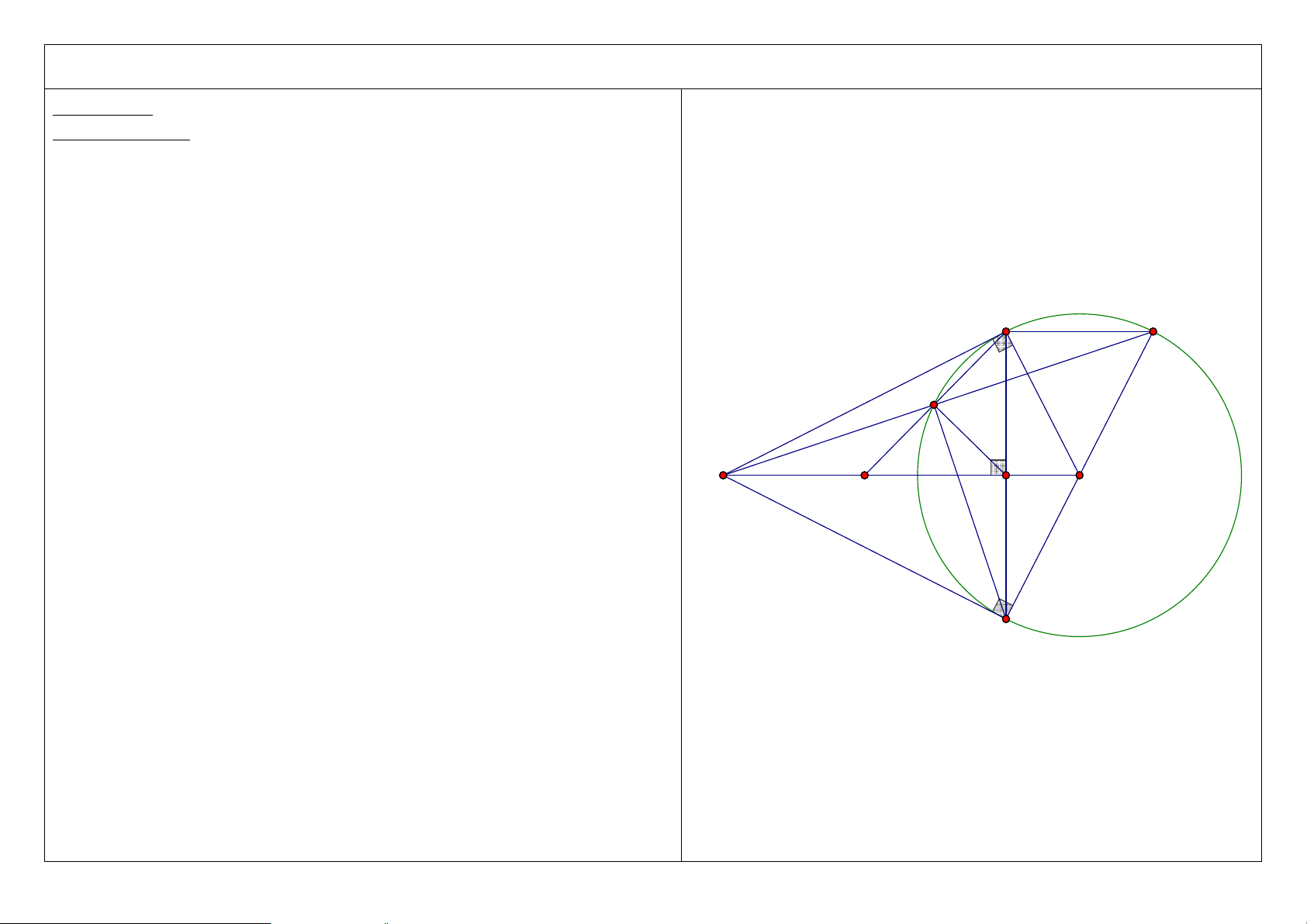
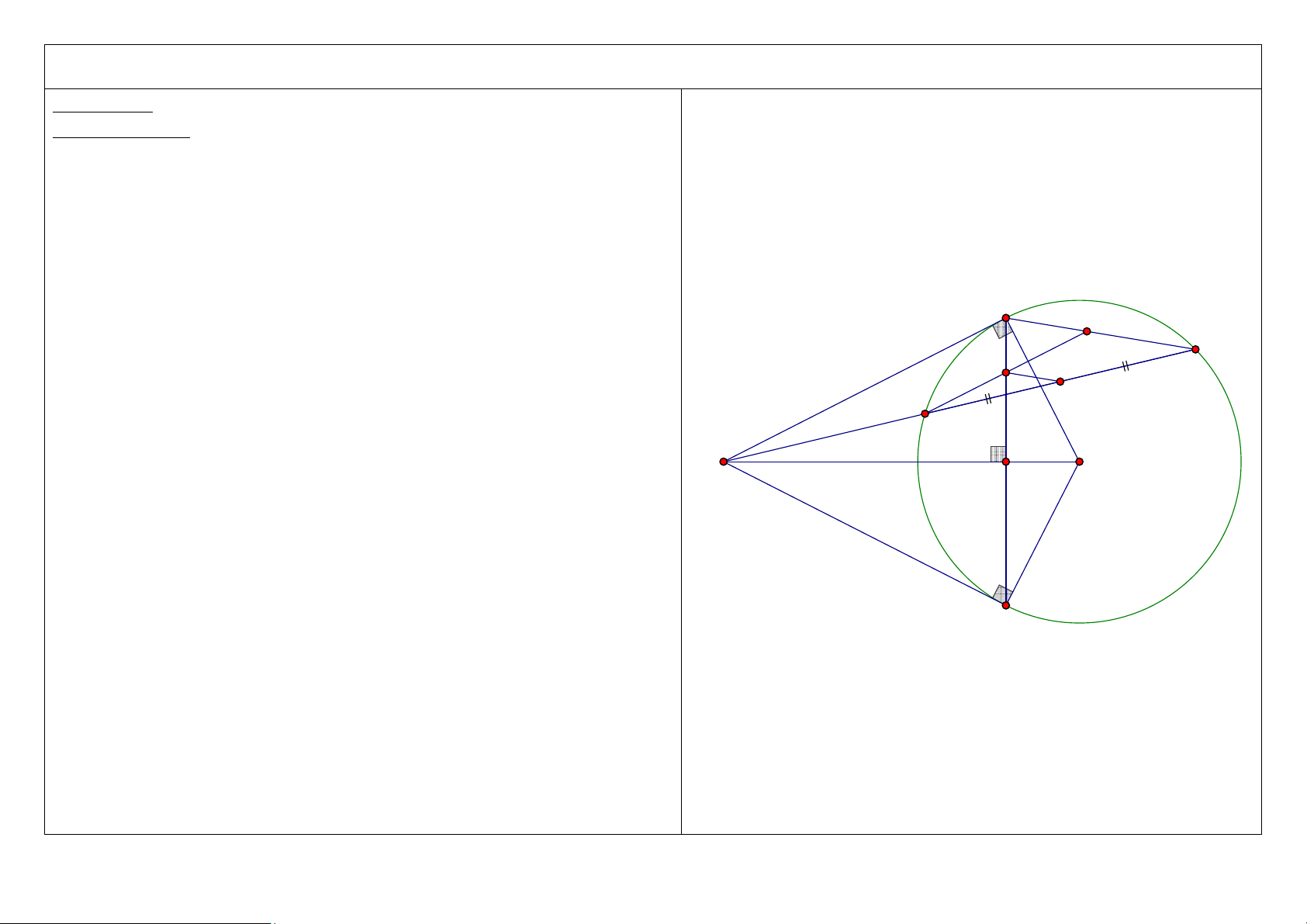
Đề bài: Từ điểm M nằm bên ngoài đường tròn (O; R), vẽ các tiếp tuyến MA, MB (A, B là các tiếp điểm) với đường tròn (O). Vẽ cát tuyến MCD
không đi qua tâm O (C nằm giữa M và D; tia MD nằm giữa hai tia MA và MO). Gọi H là giao điểm của AB và MO. 1. Chứng minh: 2 2
MC .MD = MH .MO = MA = MB = M . A MB . A D C M O H B 1 2. Chứng minh: 2
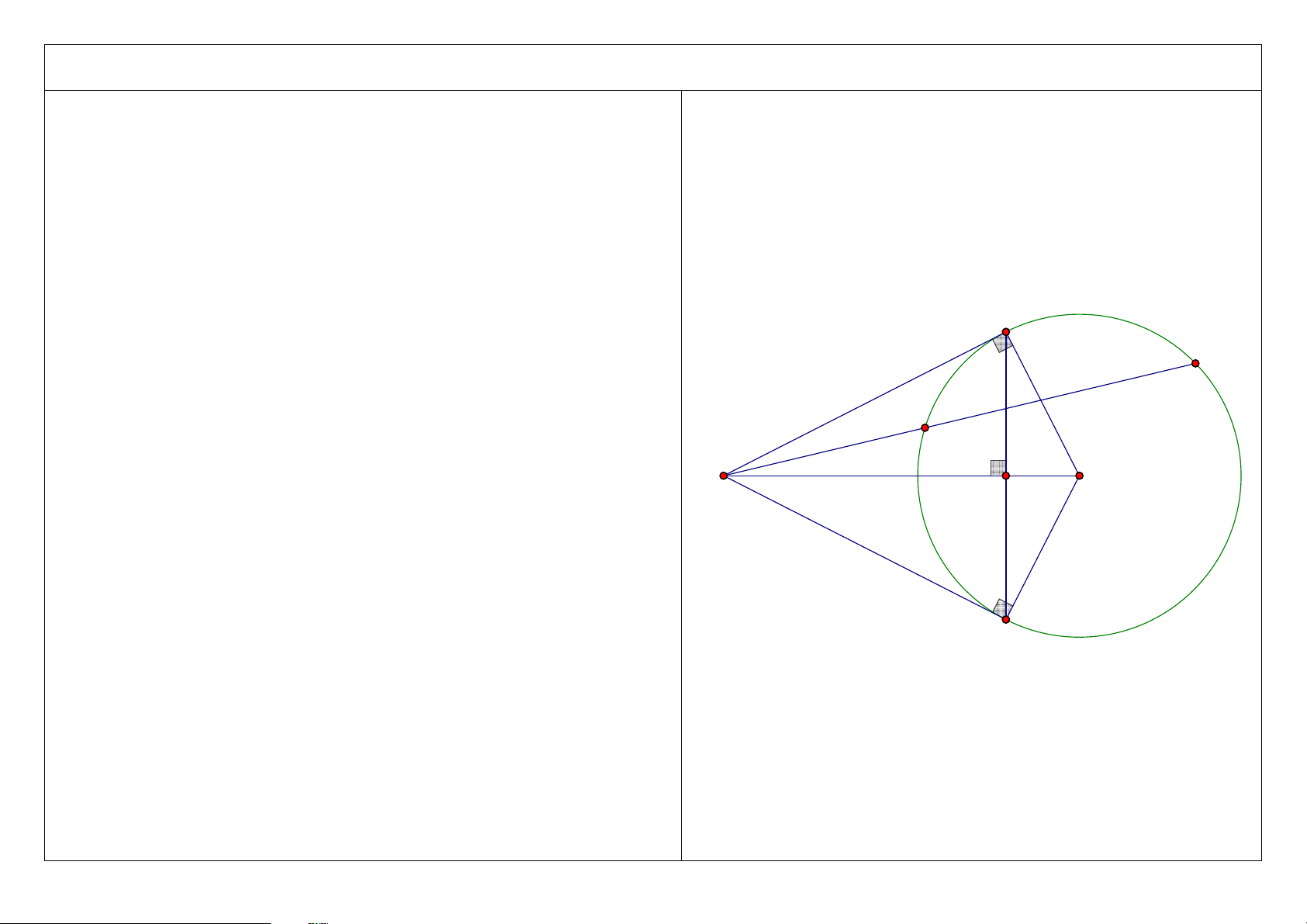
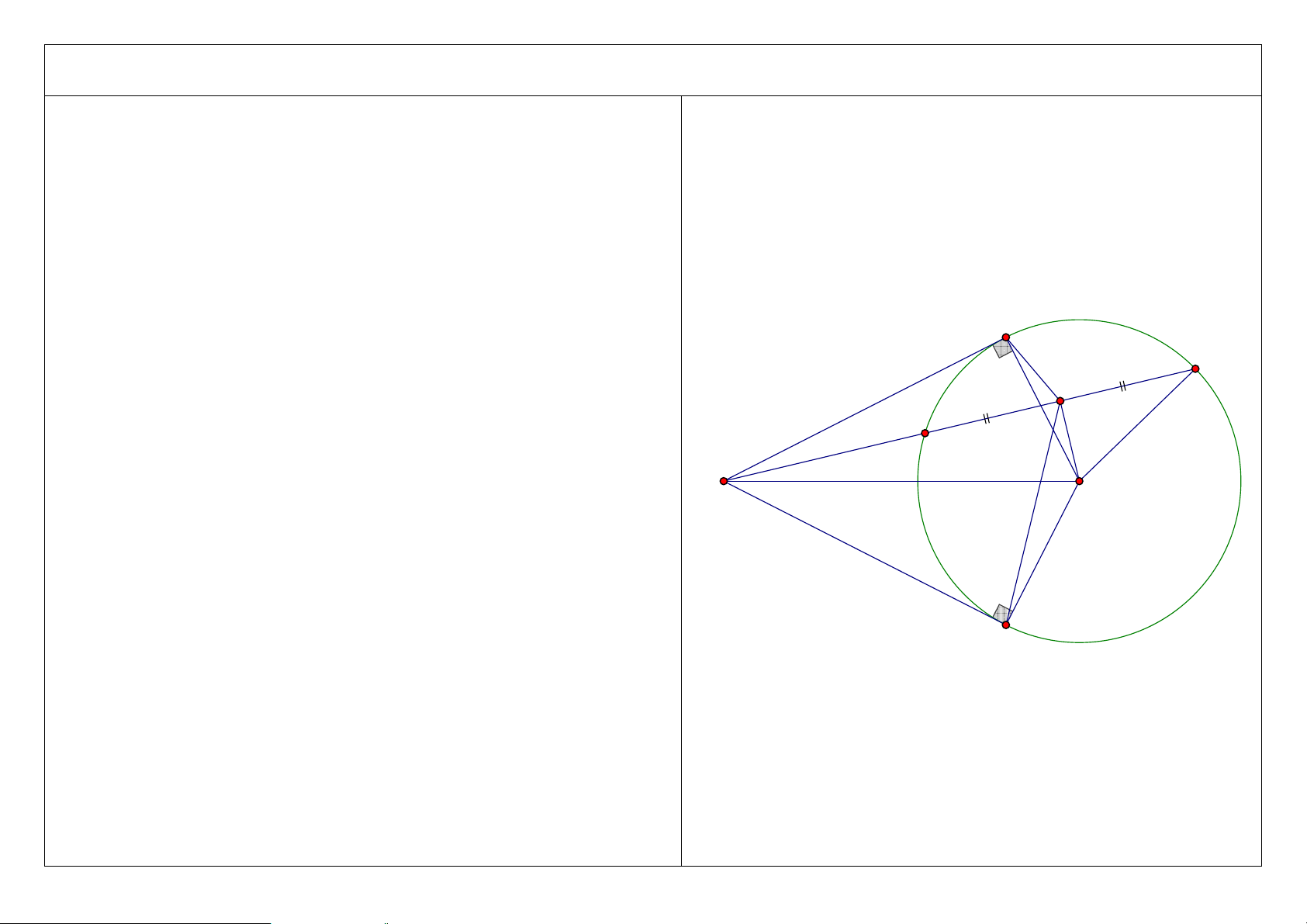
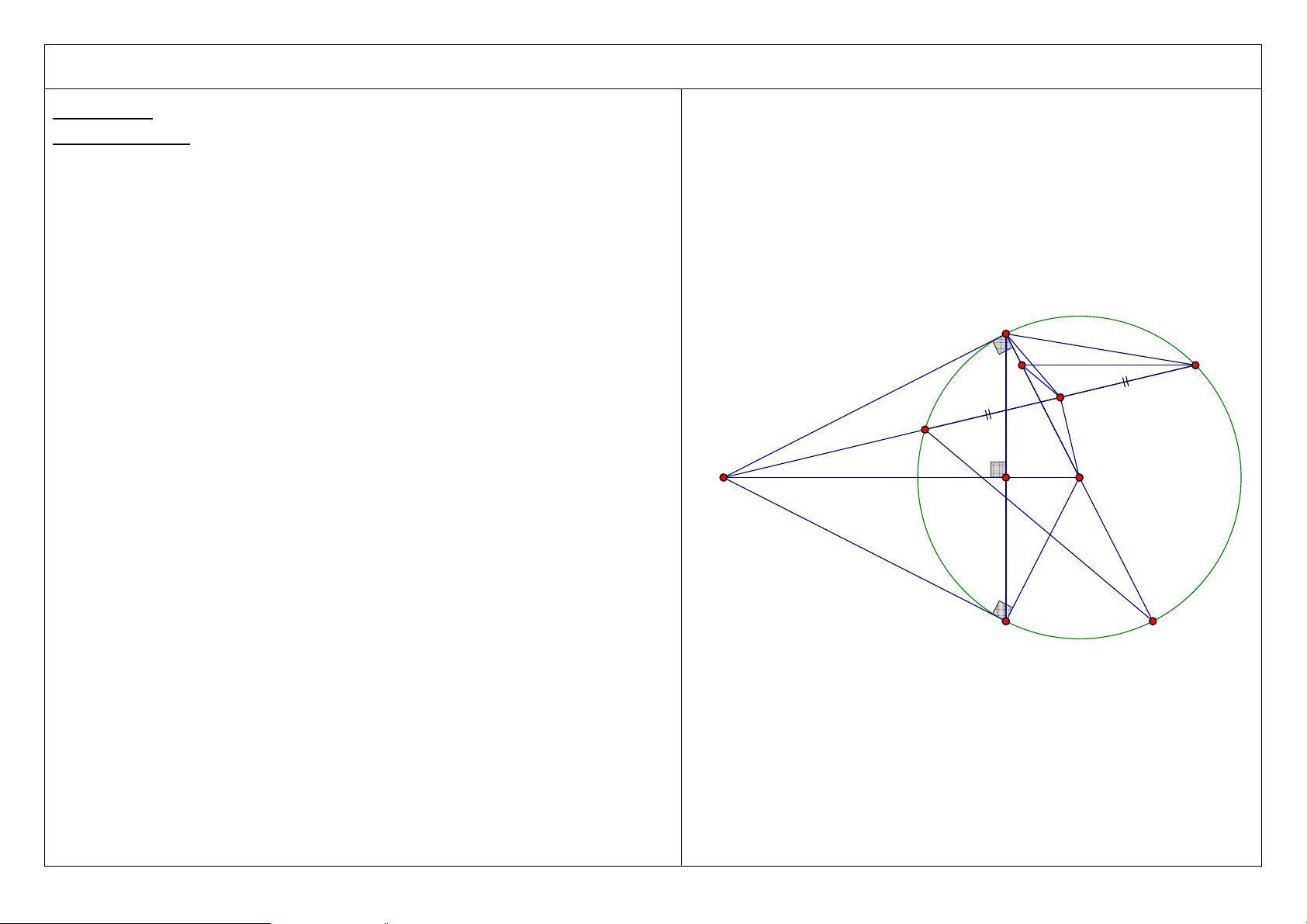
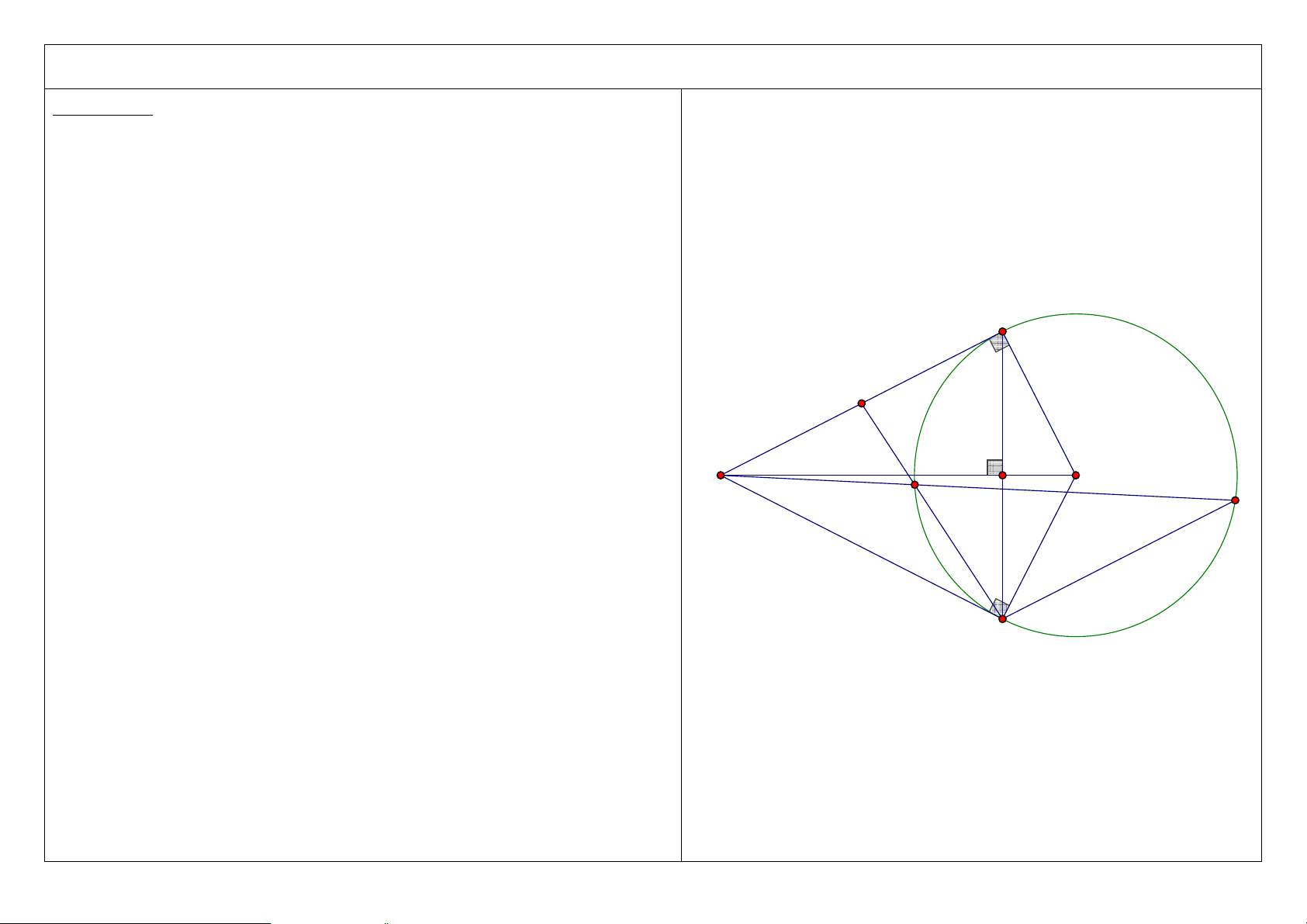
OH .OM + MC .MD = MO . A D C M O H B 2 3. Chứng minh M ∆
CH đồng dạng M ∆
OD , suy ra tứ giác OHCD nội tiếp và HA là tia phân giác của góc CHD . A D C M H O B 3
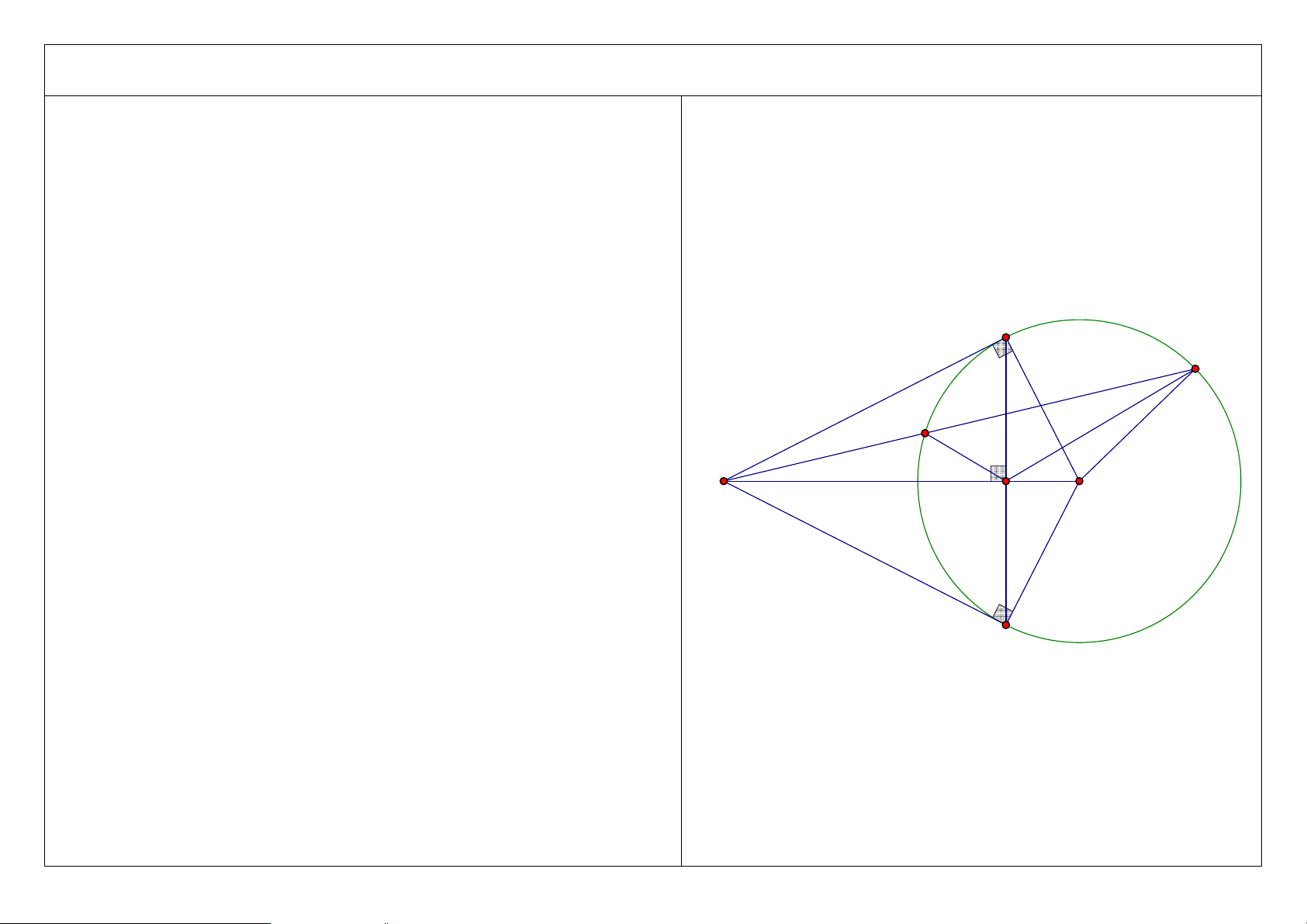
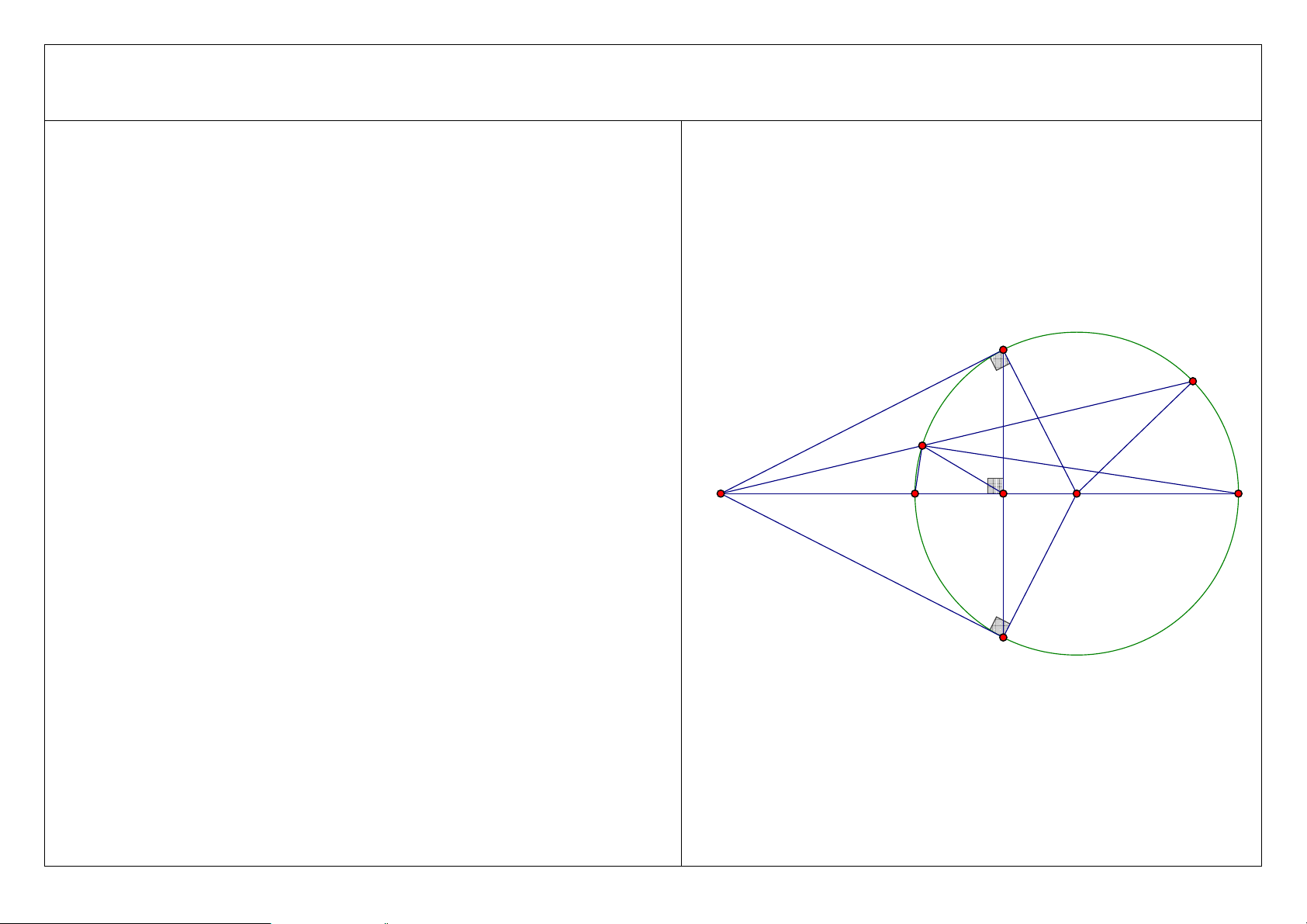
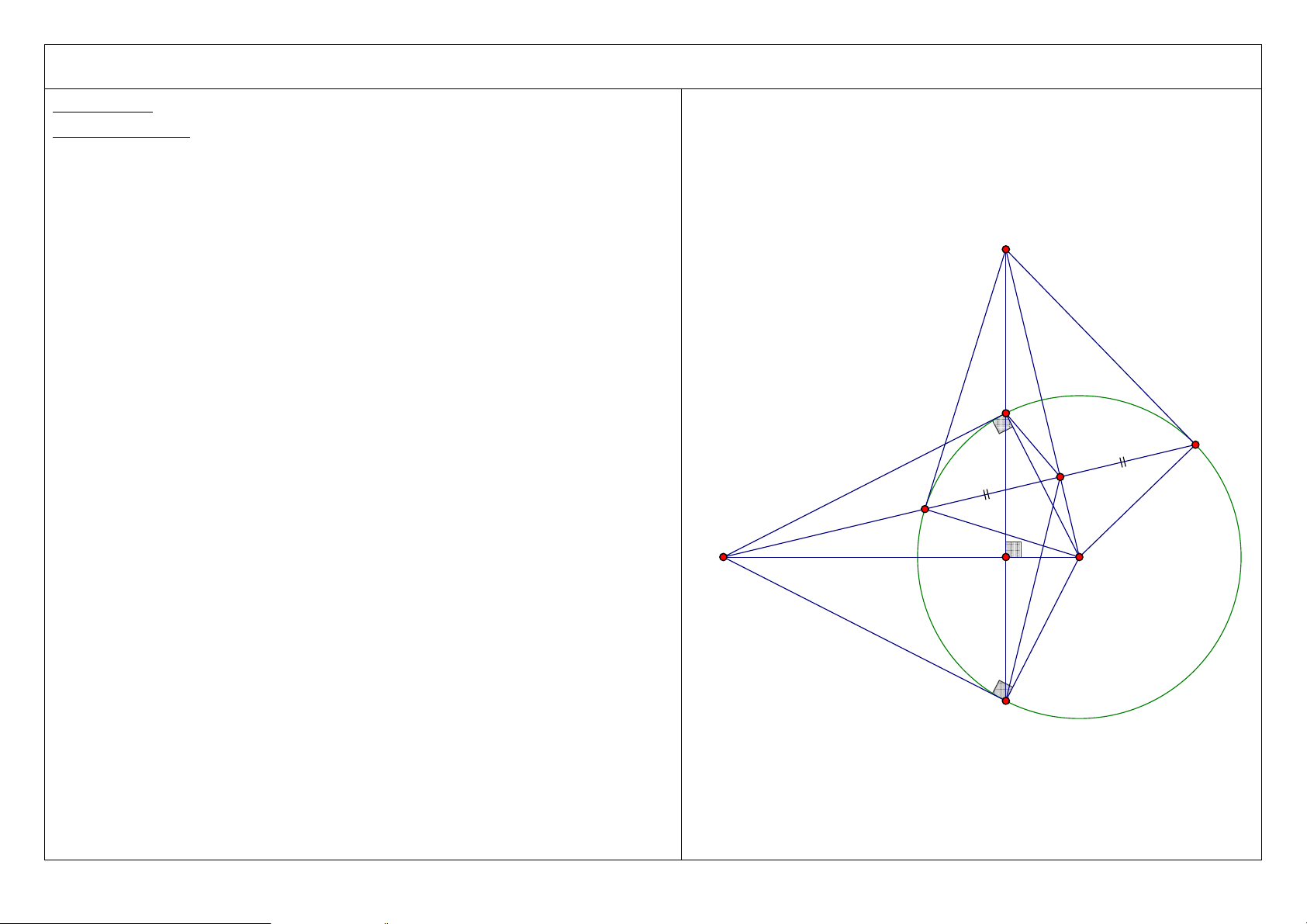
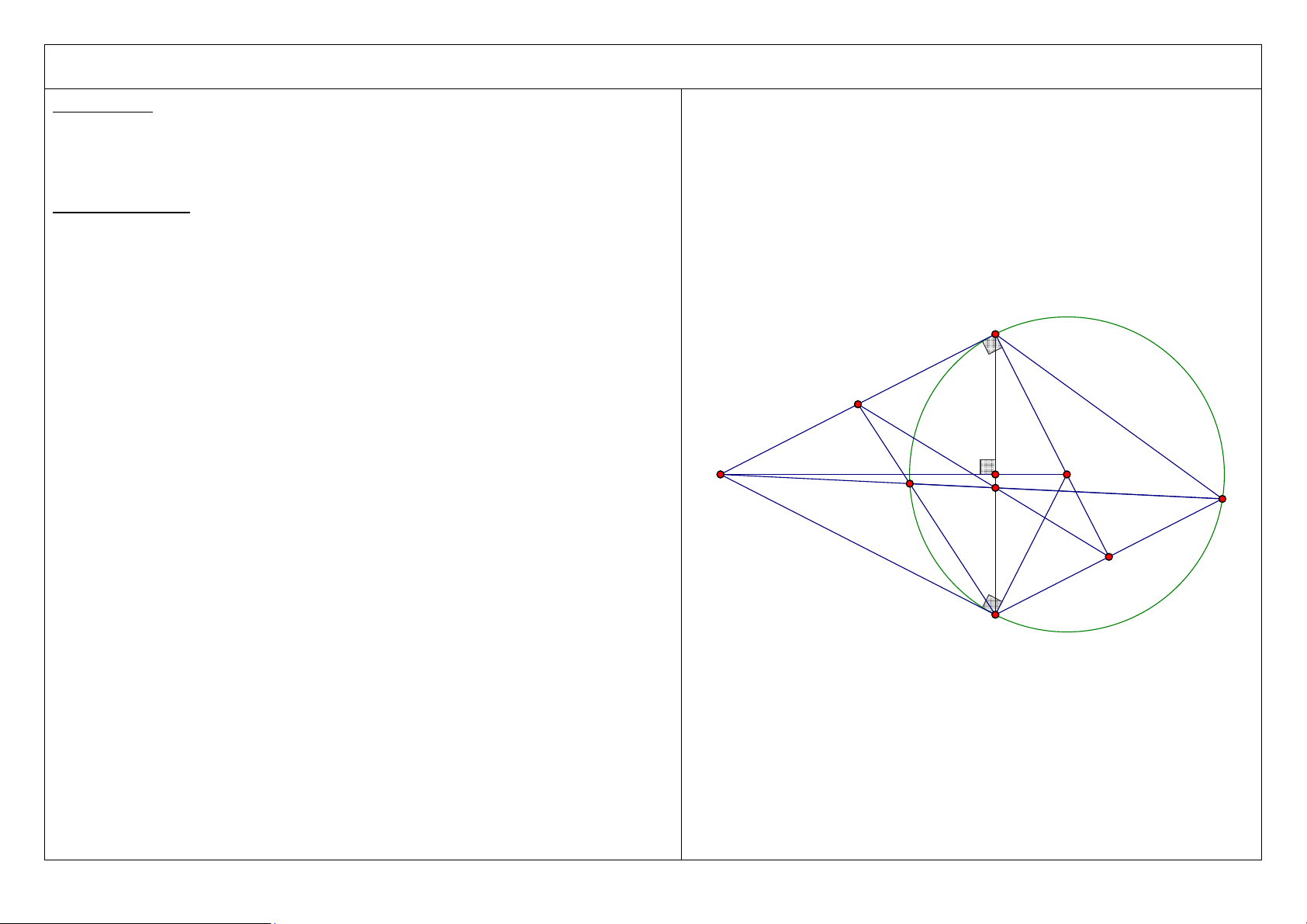
4. Gọi F là điểm đối xứng của C qua MO. Chứng minh ba điểm D, H, E thẳng hàng.
Hướng dẫn: Chứng minh MHE = DHO . Tóm tắt lời giải: A D C M H O E B 4
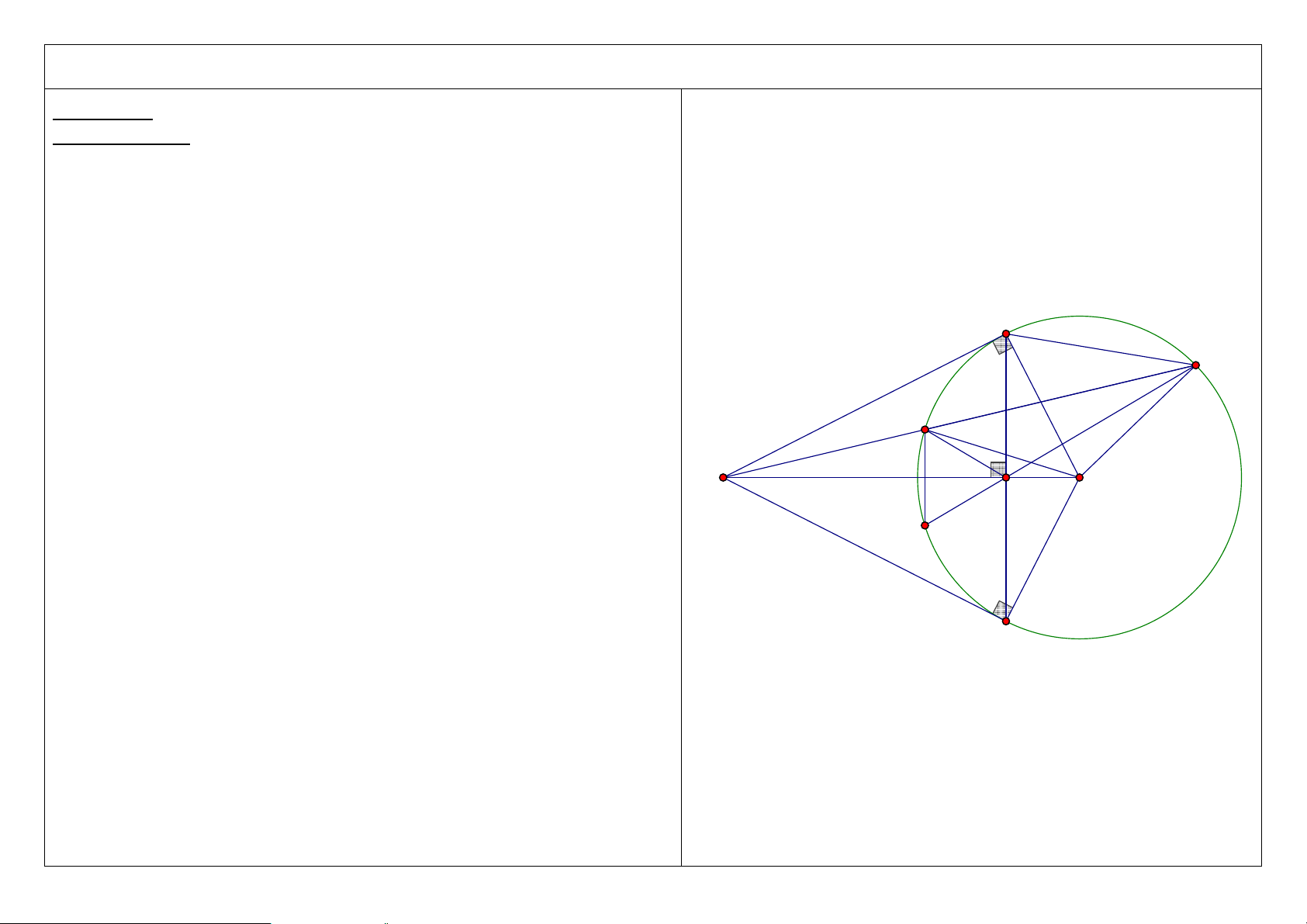
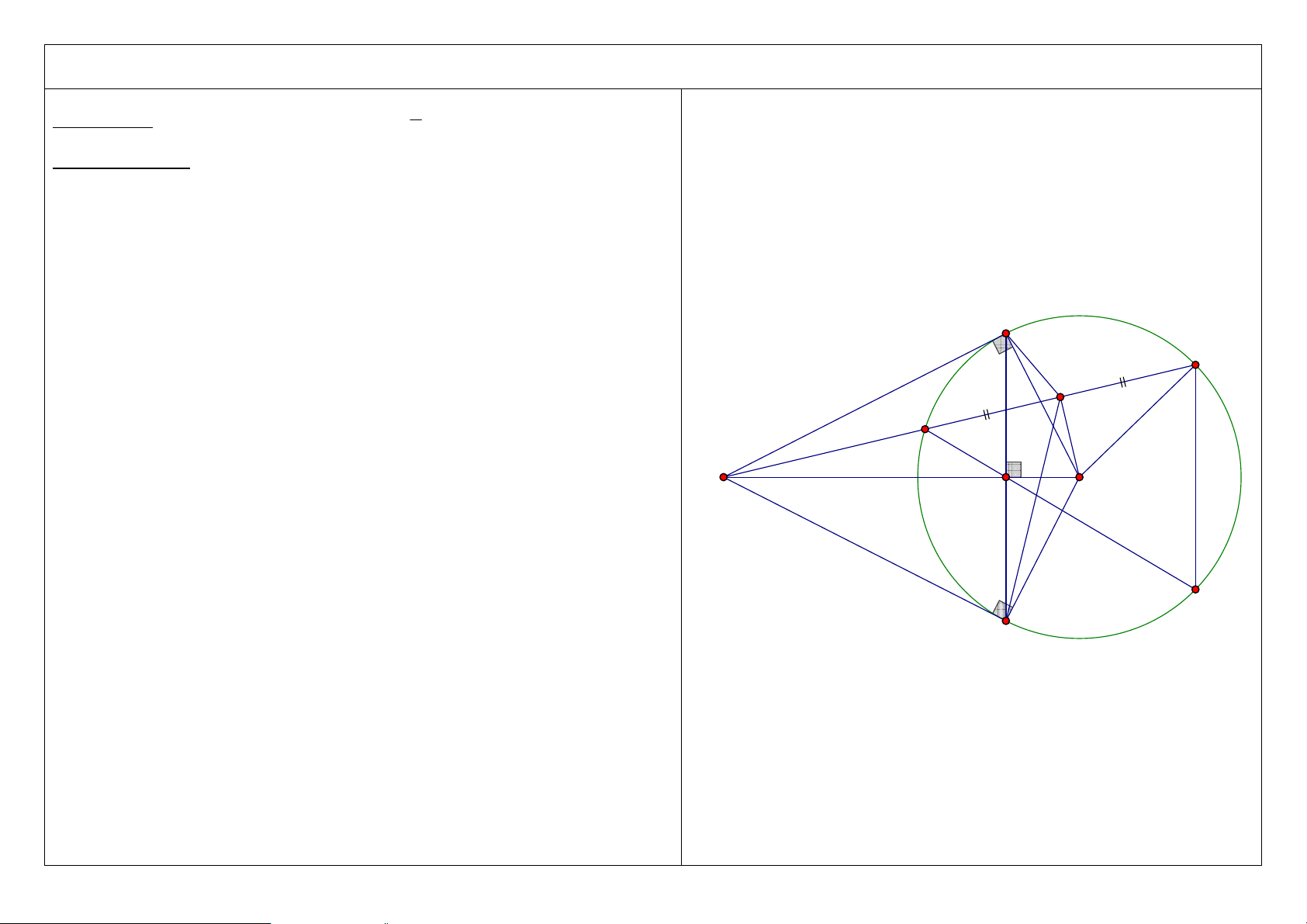
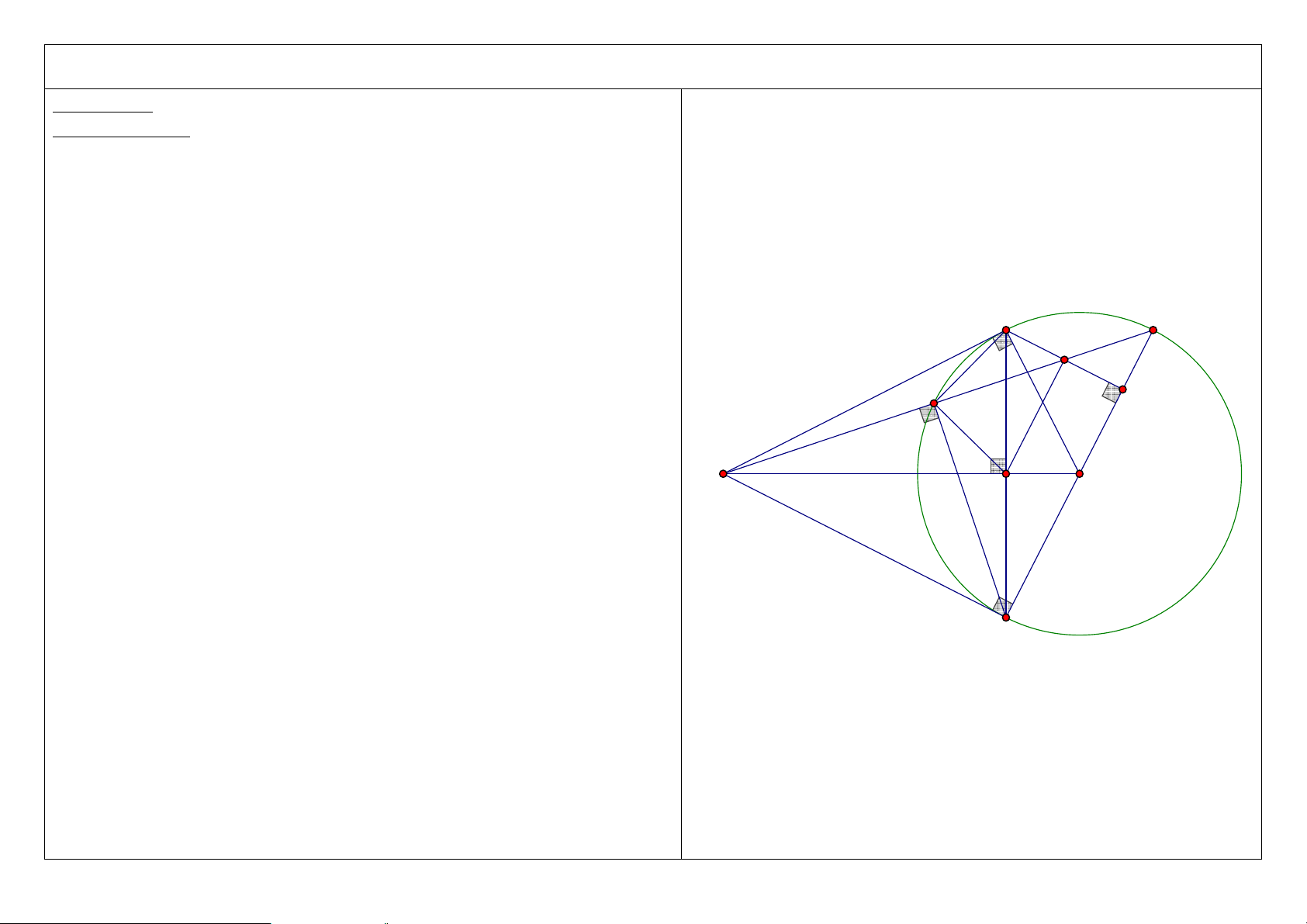
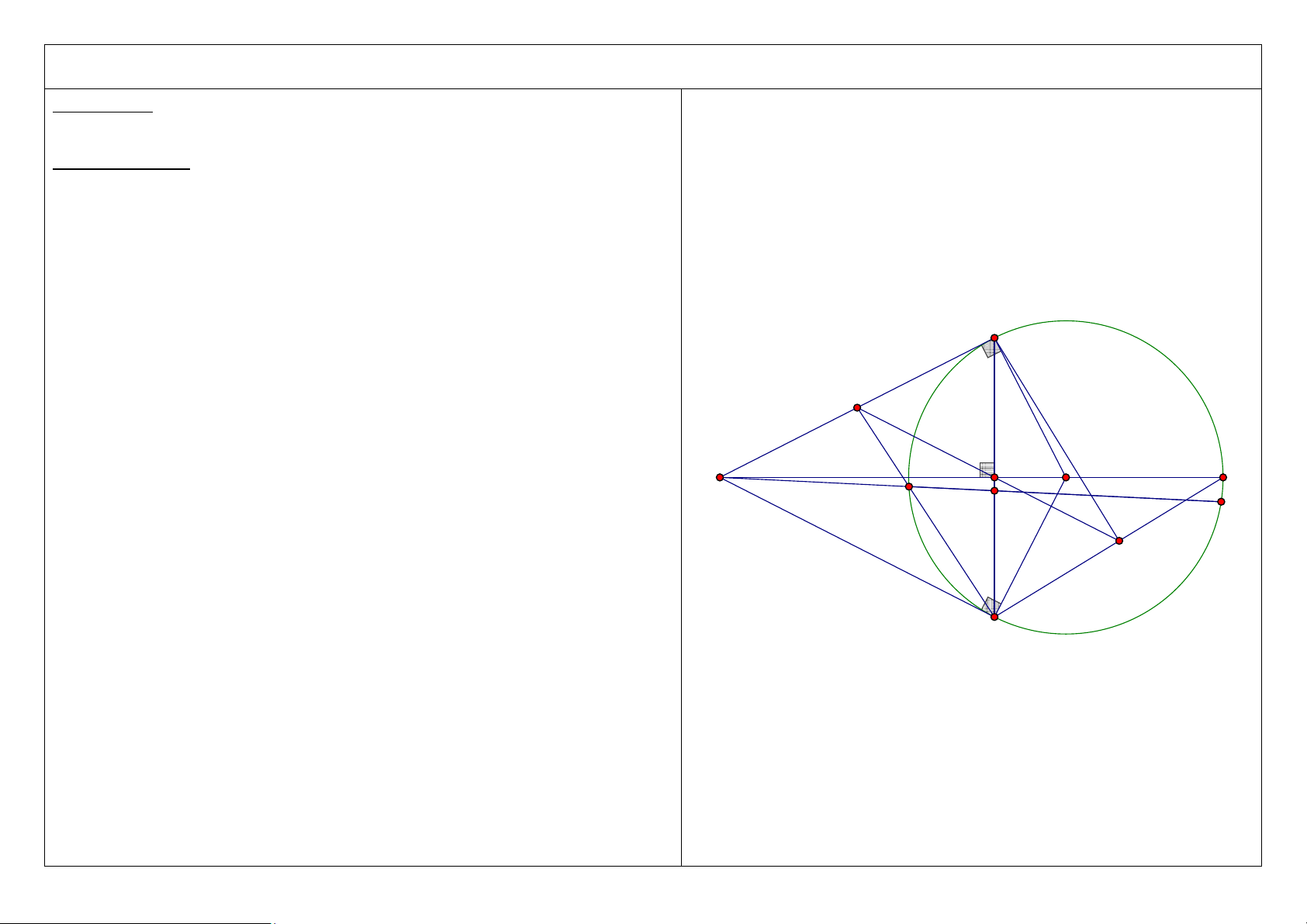
5. Gọi I là trung điểm của CD. Chứng minh 5 điểm M, A, O, I, B cùng nằm trên một đường tròn. A D I C M O H B 5
6. Chứng minh IM là tia phân giác của AIB A D I C M O B 6
7. Đường thẳng MO cắt đường tròn tại I, K (I nằm giữa M và K). Chứng minh CK là tia phân giác của DCH và CI là tia phân giác của MCH và IC.DH = DC.IH. A D C M K I H O B 7
8. Tia CH cắt đường tròn (O) tại điểm thứ hai E. Chứng minh DE // AB. 1
Hướng dẫn: Chứng minh AHC = DEC = sđCD . 2 Tóm tắt lời giải: A D I C M H O E B 8
9. Đường thẳng AI cắt (O) tại E. Chứng minh BE // AC. 1
Hướng dẫn: Chứng minh AIC = AEB = sđ AB. 2 Tóm tắt lời giải: A D I C H O M E B 9
10. Kẻ đường kính AE, đường thẳng d đi qua điểm D song song OM, cắt AE tại F. Chứng minh IF // CE.
Hướng dẫn: Chứng minh FIC = ICE ⇒ Chứng minh AFID nội tiếp. Tóm tắt lời giải: A D F I C H O M B E 10
11. Tiếp tuyến tại C và D của (O) cắt nhau tại K. Chứng minh ba điểm A, B, K thẳng hàng. Hướng dẫn: Chứng minh K ∆ OH đồng dạng M ∆ IO (c.g.c) ⇒ KH ⊥ OM Tóm tắt lời giải: K A D I C M H O B 11
12. BO cắt (O) tại điểm D, đường thẳng MD cắt (O) tại C. Kẻ AE vuông góc BD. MD cắt AE tại F, chứng minh F là trung điểm của AE.
Hướng dẫn: Chứng minh FH // BE. Tóm tắt lời giải: A D F C E M H O B 12
13. BO cắt (O) tại điểm D, đường thẳng MD cắt (O) tại E. Tia AE cắt MH tại F. Chứng minh F là trung điểm của MH. Hướng dẫn: Chứng minh 2 2 FM = FH = FC.FA Tóm tắt lời giải: A D C M H O F B 13
14. Kẻ dây BE // AM, ME cắt (O) tại D, AD cắt MB tại S. Chứng minh S là trung điểm của AM. Hướng dẫn: Chứng minh 2 2 SM = SA = SD.SB A S H M O D E B 14
15. Kẻ dây BE // AM, ME cắt (O) tại D, AD cắt MB tại S, AB cắt DE tại N và SN cắt BE tại P. Chứng minh ba điểm A, O, P thẳng hàng. Hướng dẫn:
- Chứng minh SM = SA ⇒ PB = PE (Đ/L Talet) - Chứng minh A ∆ BE cân suy ra AP ⊥ BE .
- Có OP ⊥ BE ⇒ A, O, P thẳng hàng. Tóm tắt lời giải: A S O H M D E P B 15
16. Gọi K là giao điểm của MO với (O) (O nằm giữa M và K). SH cắt BK tại I. Chứng minh AI vuông góc với BK. Hướng dẫn:
- Chứng minh tứ giác AHIK nội tiếp, suy ra: 0 AHK = AIK = 90 . Tóm tắt lời giải: A S H O M K D E I B 16
17. Đường thẳng qua C song song với AM cắt AB, AD lần lượt tại P và Q. Chứng minh QD = 2PI.
Hướng dẫn: Chứng minh IP // QD⇒ Chứng minh CPIB nội tiếp. Tóm tắt lời giải: A Q D P I C H O M B 17