Chuyên đề một số hệ thức về cạnh và góc trong tam giác vuông

Tài liệu gồm 52 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề một số hệ thức về cạnh và góc trong tam giác vuông. Mời bạn đọc đón xem.

76 38 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hệ thức lượng trong tam giác vuông

Môn: Toán 9

Thông tin:

21 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
A. KIẾN THỨC CẦN NHỚ
I. Định lí
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
• Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
• Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề
Trong hình bên thì:
sin cos ; sin cos
tan cot ; tan cot
ba Ba Cca Ca B
bc Bc Ccb Cb B


II. Giải tam giác vuông
Là tìm tất cả các cạnh và góc của tam giác vuông B khi
biết hai yếu tố của nó (trong đó ít nhất có một yếu tố về độ
dài).
B. MỘT SỐ DẠNG BÀI CƠ BẢN VÀ NÂNG CAO
Ví dụ 1. Cho tam giác ABC vuông tại A, đường cao AH,
B
. Tính giá trị của để BH = 3CH.
Giải
Đặt AH = h.
Xét ABH vuông tại H ta có:
BH = AH.cot B = h.cot .
Xét ACH vuông tại H ta có:
CH = AH.cot C = AH.tan B = h.tan .
2
1
3 .cot 3 .tan 3tan
tan
13
tan tan tan30 30
33
BH CH h h




Nhận xét: Trong bài giải ta đã biểu diễn BH và CH theo AH và theo một tỉ số lượng giác của góc . Từ
mối quan hệ giữa BH và CH ta tìm được giá trị của .
Ví dụ 2. Giải tam giác ABC biết
35 , 50BC
và đường cao AH = 5,0cm.
Giải
Ta phải tìm
A
, AB, AC và BC.


180 95ABC
• Xét ABH vuông tại H ta có:

5, 0
.sinB 8,7
sinB sin 35
AH
AH AB AB cm

.cotB 5,0.cot 35 7,1BH AH cm
2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
• Xét ACH vuông tại H ta có:

5,0
.sin 6,5
sin sin 50
AH
AH AC C AC cm
C


.cot 5,0.cot 50 4,2CH AH C cm
Do đó

7,1 4,2 11,3BC BH CH cm
Vậy
95 ; 8,7 ; 6,5 ; 11,3AABcmACcmBCcm
Lưu ý: Sau khi tính được AB và AC, có thể tính BH và CH theo AB và AC:
.cos ; .cosBH AB B CH AC C
Tuy nhiên, ta nên tính BH và CH theo các số đo đã cho trong đề bài để kết quả được chính xác hơn.
Ví dụ 3. Cho tam giác ABC, cạnh BC cố định. Biết BC = 4cm, AB + AC = 8cm. Tính giá trị lớn nhất của
góc A.
Giải
Vẽ đường phân giác AD. Vẽ BH AD và CK AD.
Xét ABH vuông tại H, ACK vuông tại K, ta có:
.sin ; sin
22
AA
BH AB CK AC
Vậy

sin 8sin
22
AA
BH CK AB AC
Mặt khác ,

4BH CK BD CD BC cm
nên
1
8sin 4 sin sin 30
222
AA

Do đó
30 60
2
A
A
vậy
max 60A  khi D, H, K trùng nhau ABC đểu.
Nhận xét: Nhờ có việc vẽ đường phân giác AD và các đường thẳng BH, CK cùng vuông góc với AD mà
ta tìm được sự liên hệ giữa AB, AC với BH, CK; sự liên hệ giữa BH, CK với BC. Do đó giữa AB, AC và
BC có sự liên hệ với nhau, từ đó tìm được số đo của góc A.
Ví dụ 4. Chứng minh định lí côsin: Trong một tam giác nhọn, bình phương của một cạnh bằng tổng các
bình phương của hai cạnh kia trừ
đi hai lần tích của hai cạnh ấy với côsin của góc xen giữa của chúng.
Giải
3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vẽ đường cao BH. Xét HBC vuông tại H ta có:



2
2222
22 2
22 2
22
2.
2.
2. 1
BC HB HC HB AC AH
HB AC AC AH AH
HB AH AC AC AH
AB AC AC AH




Xét ABH vuông tại H ta có : AH = AB. cosA
Thay vào (1) ta được
222
2..cosABC AB AC AC AB
Nhận xét: Trong một tam giác nhọn, nếu biết hai cạnh và góc xen giữa thì nhờ định lí côsin ta có thế tính
được cạnh thứ ba.
C. BÀI TẬP TỰ LUYỆN
• Vận dụng hệ thức về cạnh và góc trong tam giác vuông để chứng minh hoặc tính toán
Bài 1. Cho tam giác nhọn ABC. Vẽ các đường cao AD, BE, CF. Chứng minh rằng:
a) AD.BE.CF = AB.BC.CA.sin A.sin B.sin C; b) AE.BF.CD = AB.BC.CA.cos A.cos B.cos C.
Bài 2. Cho tam giác nhọn ABC. Vẽ các đường cao AA', BB', CC’. Chứng minh rằng:
'. '. ' ' . ' . ' . . .cos .cos .cosAB BC CA A B B C C A AB BC CA A B C
Bài 3. Cho đường thẳng xy và điểm A cố định cách xy là 2cm. Gọi M là một điểm di động trên xy. Vẽ
tam giác ABM vuông tại M sao cho

090ABM


. Tính độ dài ngắn nhất của AB.
Bài 4. Cho tam giác ABC, cạnh BC cố định và 33BC cm . Điểm A di động sao cho AB + AC = 6cm.
Tính giá trị lớn nhất của góc A.
Bài 5. Cho tam giác ABC, AB = 14cm, AC = 11cm và
40B . Tính độ dài BC.
Bài 6. Cho tam giác ABC, AB = 3,2cm; AC = 5,0cm và
70B . Tính độ dài BC.
Bài 7. Cho tam giác ABC cân tại A, góc ở đáy bằng < 90°. Vẽ các đường cao AH và BK. Biết BK = h,
tính AH.
Bài 8. Cho tam giác ABC,
40 , 65BC
a) Tính số đo của góc tạo thành bởi đường cao AH và đường trung tuyến AM (làm tròn đến độ);
b) Cho biết BC = 45cm, tính độ dài AH (làm tròn đến centimet).
Bài 9. Tam giác ABC là tam giác nhọn hay tam giác tù nếu có:
a)
50A , AB = 2,4cm, AC = 6,2cm; b)
55A , AB = 3,5cm, AC = 4,5cm.
Bài 10. Cho tam giác ABC vuông tại A,
64A , AB = c, AC = 4,5cm. Xác định giá trị của c để tam giác
ABC là tam giác tù.
Bài 11. Cho tam giác nhọn ABC, AB = 4cm, BC = 6cm. Một hình chữ nhật DEFG nội tiếp tam giác
đó với
,;F,GBCDABEAC
. Chứng minh rằng diện tích hình chữ nhật DEFG nhỏ hơn 6cm
2
.
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài 12. Cho tam giác ABC, AB = 5cm,
39BC cm và CA = 7cm. Tính số đo góc A.
Bài 13. Giải tam giác ABC, biết:
)6,8;62;53 )6,8;40;35aBC cmB C bBC cmB C 
Bài 14. Giải tam giác ABC, biết: AB = 5cm, BC = 7cm, CA = 6cm (các số đo góc làm tròn đến độ).
Bài 15. Giải tam giác ABC, biết:
68A , AB = 5,0cm, AC = 5,7cm (làm tròn các độ dài đến chữ số thập
phân thứ nhất, làm tròn các số đo góc đến độ).
Bài 16. Giải tam giác ABC, biết:
50A , AB = 4,6cm, BC = 3,7cm (làm tròn số đo góc đến độ, làm tròn
độ dài đến hàng phần mười).
HƯỚNG DẪN
• Vận dụng hệ thức về cạnh và góc trong tam giác vuông để chứng minh hoặc tính toán
Bài 1. Cho tam giác nhọn ABC. Vẽ các đường cao AD, BE, CF. Chứng minh rằng:
a) AD.BE.CF = AB.BC.CA.sin A.sin B.sin C;
b) AE.BF.CD = AB.BC.CA.cos A.cos B.cos C.
Giải
a) ACD vuông tại D, có AD = ACsin C.
ABE vuông tại E, có BE = ABsin A.
BCF vuông tại F, có CF = BCsin B.
Suy ra AD.BE.CF = AB.BC.CA.sin A.sin B.sin C.
b) ABE vuông tại E, có AE = ABcos A.
BCF vuông tại F, có BF = BCcos B.
ACD vuông tại D, có CD = ACcos C.
Suy ra AE.BF.CD = AB.BC.CA.cos A.cos B.cos C.
Bài 2. Cho tam giác nhọn ABC. Vẽ các đường cao AA', BB', CC’. Chứng minh rằng:
'. '. ' ' . ' . ' . . .cos .cos .cosAB BC CA A B B C C A AB BC CA A B C
Giải
ABB' vuông tại B', có AB' = ABcos A.
BCC’ vuông tại C', có BC' = BCcos B.
CAA' vuông tại A', có CA' = ACcos C.
Suy ra AB'.BC'.CA' = AB.BC.CA.cos A.cos B.cos C.
Chứng minh tương tự ta được:
A'B.B'C.C'A = AB.BC.CA.cos A.cos B.cos C.
Do đó AB’.BC’.CA' = A'B.B'C.C'A
5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
= AB.BC.CA.cos A.cos B.cos C.
Nhận xét: Vì ba đường cao tam giác cùng đi qua một điểm nên nếu đề bài chỉ yêu cầu chứng minh
AB'.BC’.CA' = A'B.B'C.C’A thì theo định lí Xê-va ta có
'''
.. 1
'''B
AB BC C A
AC B A C
từ đó suy ra ngay đpcm.
Bài 3. Cho đường thẳng xy và điểm A cố định cách xy là 2cm. Gọi M là một điểm di động trên xy. Vẽ
tam giác ABM vuông tại M sao cho

090ABM


. Tính độ dài ngắn nhất của AB.
Giải
ABM vuông tại M, có
.sin
sin
AM
AM AB AB

Do đó AB ngắn nhất AM ngắn nhất
2M H AM cm
Vậy
2
min
sin
AB
khi
MH
Bài 4. Cho tam giác ABC, cạnh BC cố định và
33BC cm . Điểm A di động sao cho AB + AC = 6cm.
Tính giá trị lớn nhất của góc A.
Giải
Vẽ đường phân giác AD. Vẽ BH AD,
CK AD. Ta có
,BH BD CK CD
Suy ra
BH CK BD CD BC
ABH vuông tại H, có:
.sin
2
A
BH AB
ACK vuông tại K, có:
.sin
2
A
CK AC
Do đó

.sin 6sin
22
AA
BH CK AB AC
mà 33BH CK BC cm nên
6sin 3 3
2
A
Do đó
33 3
sin sin 60
26 2
A

. Suy ra
60 120
2
A
A
Vậy
max 120A  khi
HKD
ABC vuông cân tại A.
Bài 5. Cho tam giác ABC, AB = 14cm, AC = 11cm và
40B . Tính độ dài BC.
Giải
* Tìm cách giải
6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vẽ đường cao AH để vận dụng các hệ thức về cạnh và góc trong tam giác vuông. Tính HB và HC từ đó
tính được BC.
* Trình bày lời giải
Vẽ đường cao AH. Xét ABH vuông tại H có:


.sin 14sin 40 9.0
.cos 14.cos40 10,7
AH AB B cm
BH AB B cm


Xét AHC vuông tại H có:

22 22
11 9 6,3HC AC AH cm
• Nếu H nằm giữa B và C thì

10,7 6,3 17BC BH HC cm
• Nếu C’ nằm giữa B và H thì

''10,76,34,4BC BH HC cm
Bài 6. Cho tam giác ABC, AB = 3,2cm; AC = 5,0cm và
70B . Tính độ dài BC.
Giải
Vẽ đường cao AH. Xét ABH vuông tại H có:


.sin 3, 2sin 70 3,0
.cos 3,2.cos70 1,1
AH AB B cm
BH AB B cm


Xét AHC vuông tại H có:

22 22
5,0 3,0 4,0HC AC AH cm
Điểm C không thể nằm giữa H và B vì trên tia HB có HC > HB.
Chỉ còn trường hợp điểm H nằm giữa B và C.
Ta có

1,1 4, 0 5,1BC BH HC cm
Bài 7. Cho tam giác ABC cân tại A, góc ở đáy bằng < 90°. Vẽ các đường cao AH và BK. Biết BK = h,
tính AH.
Giải
Xét KBC vuông tại K, có:
.sin
sin sin
BK h
BK BC BC


Vì ABC cân tại A nên
2sin
h
HB HC

Xét AHC vuông tại H có:
sin
.tan .
2sin cos 2cos
hh
AH HC


Bài 8. Cho tam giác ABC,
40 , 65BC
a) Tính số đo của góc tạo thành bởi đường cao AH và đường trung tuyến AM (làm tròn đến độ);
7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
b) Cho biết BC = 45cm, tính độ dài AH (làm tròn đến centimet).
Giải
Đặt
MAH
a) Xét ABH và AHC vuông tại H ta có:
cot ; cot ; tanBH AH B CH AH C MH AH

Ta có

2BH CH BM MH CM MH MH
Do đó
cot cot 2 tanAH B AH C AH

Suy ra
cot cot 2 tanBC

Hay
cot cot cot 40 cot 65
tan 0,3627
22
BC


tan tan19 56' 20


b) Ta có BH + CH = BC hay

cot cot 45 cot cot 45AH B AH C AH B C
Suy ra

45 45
27
cot cot cot 40 cot 65
AH cm
BC


Bài 9. Tam giác ABC là tam giác nhọn hay tam giác tù nếu có:
a)
50A , AB = 2,4cm, AC = 6,2cm;
b)
55A , AB = 3,5cm, AC = 4,5cm.
Giải
a) Vẽ CH AB. Xét ACH vuông tại H, ta có:

.cos 6,2.cos50 4,0AH AC A cm
Trên tia AB có AB < AH nên điểm B nằm giữa A và H.
Suy ra
90ABC H
Vậy ABC là tam giác tù.
b) Vẽ CH AB, BK AC. Xét ACH vuông tại H, ta có:

.cos 4,5.cos55 2,6AH AC A cm
Xét ABK vuông tại K, ta có:

.cos 3,5.cos55 2,0AK AB A cm
• Trên tia AB có AH < AB nên điểm H nằm giữa A và B.
Xét HBC có
90H nên
HBC nhọn.
• Trên tia AC có AK < AC nên điểm K nằm giữa A và C.
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Xét KBC có
90K  nên
ACB nhọn.
Tam giác ABC có ba góc nhọn nên là tam giác nhọn.
Bài 10. Cho tam giác ABC vuông tại A,
64A , AB = c, AC = 4,5cm. Xác định giá trị của c để tam giác
ABC là tam giác tù.
Giải
Vẽ CH AB, BK AC. AHC vuông tại H, ta có:

.cos 4,5.cos64 2,0AH AC A cm
AKB vuông tại K, ta có:
.cos .cos64AK AB A c
ABC tù
B
tù hoặc
C tù.
• Xét trường hợp
B
tù.
Ta có
90 2 2B AH AB c hay c
và
0c
• Xét trường hợp
C tù.
Ta có :
4,5
90 .cos64 4,5 10,3.
cos64
o
o
CAKABc c
Tóm lại, ABC tù khi
02ccm
hoặc
10,3ccm
Bài 11. Cho tam giác nhọn ABC, AB = 4cm, BC = 6cm. Một hình chữ nhật DEFG nội tiếp tam giác
đó với
,;F,GBCDABEAC
. Chứng minh rằng diện tích hình chữ nhật DEFG nhỏ hơn 6cm
2
.
Giải
Ta đặt
;BADx

thì
4DB x
Ta có
//DE BC
suy ra
DE AD
BC AB
(hệ quả định lí Ta-lét)
Do đó
..63
42
AD BC x x
DE
AB

Xét DBG vuông tại G, ta có

.sin 4 sinDG DB x


Diện tích hình chữ nhật DEFG là

3
.4sin
2
SDEDG x x

Vận dụng bất đẳng thức Cô-si đối với hai số không âm
2
2
ab
ab



ta được

2
4
44
2
xx
xx





(dấu “=” xảy ra khi x = 4-x x = 2).
9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Do đó
3
.4sin 6sin
2
S


Vì
0sin 1

nên

2
6Scm
khi D là trung điểm của AB.
Bài 12. Cho tam giác ABC, AB = 5cm,
39BC cm và CA = 7cm. Tính số đo góc A.
Giải
Xét ABC có CA là cạnh lớn nhất nên góc B là góc lớn nhất.
Ta thấy
222
AC BA BC
(vì

2
22
75 39 ) nên góc B là góc nhọn (xem bài 1.18).
Do đó ABC là tam giác nhọn. Theo định lí cô-sin ta có:

2
222 22
2 . .cosA 39 5 7 2.5.7.cosBC AB AC AB AC A
Suy ra
1
cos ,
2
A
do đó
60A 
Bài 13. Giải tam giác ABC, biết:
)6,8;62;53
)6,8;40;35
aBC cmB C
bBC cmB C


Giải
a) Ta có

180 65ABC
Vì ABC nhọn nên theo định lí sin ta có:
sin sin sin
abc
ABC

Do đó
6,8
sin 65 sin 62 sin 53
bc


Suy ra
 
6,8.sin 62 6,8.sin 53
6,6 ; 6,0
sin 65 sin 65
bcmccm



Nhận xét: Để giải tam giác trường hợp (g.c.g) ta dùng định lí sin.
b) Ta có

180 105ABC
Vậy ABC là tam giác tù, không vận dụng được đính lí sin.
Vẽ đường cao AH. Vì các góc B và C nhọn nên điểm H nằm giữa B và C.
Ta có
cot ,CH AHcotCBH AH B
Mà
BH CH BC
nên

cot cot 6,8AH B C
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com

6,8
2,6
cot 40 cot 35
AH cm

ABH vuông tại H, có
.sinAH AB B
Suy ra

2,6
4,0
sin sin 40
AH
AB cm
B

ACH vuông tại H, có
.sinAH AC C
Suy ra

2,6
4,5
sin sin 35
AH
AC cm
C

Bài 14. Giải tam giác ABC, biết: AB = 5cm, BC = 7cm, CA = 6cm (các số đo góc làm tròn đến độ).
Giải
Xét ABC, cạnh BC là cạnh lớn nhất nên góc A là góc lớn nhất.
Ta có
222
BC AB AC
(vì
222
756) nên góc A là góc nhọn (xem bài 1.18).
Vậy ABC là tam giác nhọn. Theo định lí cô-sin, ta có:
•
222
2..cosBC AB AC AB AC A
Do đó
222
7 5 6 2.5.6.cos A
Suy ra
1
cos ,
5
A
do đó
78A 
•
222
2..cosBAC AB BC AB BC
Do đó
222
6 5 7 2.5.7.cos B
Suy ra
19
cos ,
35
B
do đó
57B 
•

180 78 57 45C 
Nhận xét: Để giải tam giác khi biết ba cạnh ta thường sử dụng định lí cô-sin.
Bài 15. Giải tam giác ABC, biết:
68A , AB = 5,0cm, AC = 5,7cm (làm tròn các độ dài đến chữ số thập
phân thứ nhất, làm tròn các số đo góc đến độ).
Giải
Vẽ CH AB. Xét ACH vuông tại H, ta có:

.sin 5,7.sin68 5,3CH AC A cm

.cos 5,7.cos68 2,1AH AC A cm
Trên tia AB có AH < AB (2,1 < 5,0) nên điểm H nằm giữa A và B. Do
đó BH = 5,0 - 2,1 = 2,9 (cm).
11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Xét HBC vuông tại H, ta có:

22 22
5,3 2, 9 6, 0BC CH BH cm
Xét ABC có BC là cạnh lớn nhất nên góc A là góc lớn nhất.
Ta có
222
BC AB AC
(vì
22 2
655,7) nên góc A là góc nhọn, suy ra ABC nhọn. Do đó
222
5,7 5,0 6,0 2.5,0.6,0.cosB
Suy ra
cos 0,4752 62BB
Từ đó

180 68 62 50C 
Bài 16. Giải tam giác ABC, biết:
50A , AB = 4,6cm, BC = 3,7cm (làm tròn số đo góc đến độ, làm tròn
độ dài đến hàng phần mười).
Giải
Vẽ BH AC. ABH vuông tại H, ta có:


.cos 4,6.cos50 3,0
.sin 4,6.sin50 3,5
AH AB A cm
BH AB A cm


HBC vuông tại H, ta có:

22 22
3, 7 3, 5 1, 2HC BC BH cm
• Nếu H nằm giữa A và C thì

3, 0 1, 2 4, 2AC AH HC cm
Khi đó
90C  và
3, 5
sin sin 71
3, 7
BH
C
BC

Suy ra
71C  và

180 50 71 59B 
• Nếu C’ nằm giữa H và A thì

''3,01,21,8AC AH HC cm
Khi đó
'90AC B 
Ta có
' 71 ' 180 71 109BC C C AC B  và

' 180 50 109 21AB C 
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
Câu 1: Cho tam giác
MNP
vuông tại
N
. Hệ thức nào sau đây là đúng?
A.
.sinMN MP P=
. B.
.cosMN MP P=
. C.
.tanMN MP P=
. D.
.cotMN MP P=
.
Câu 2: Cho tam giác
MNP
vuông tại
N
. Hệ thức nào sau đây là đúng?
12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
.cosNP MP P=
. B.
.cosNP MN P=
. B.
.tanNP MN P=
. D.
.cotNP MP P=
.
Câu 3: Cho tam giác
ABC
vuông tại
A
có
,,BC a AC b AB c===
. Chọn khẳng định sai?
A.
.sin .cosba Ba C==
. B.
. tan .cotac Bc C==
. C.
222
abc=+
. D.
.sin .cosca C a B==
.
Câu 4: Cho tam giác
ABC
vuông tại
A
có
,,, 50BC a AC b AB c ABC=== =
. Chọn khẳng định
đúng?
A.
.sin50bc=
. B.
.tan50ba=
. C.
.cot 50bc=
. D.
.cot50cb=
.
Câu 5: Cho tam giác
ABC
vuông tại
A
có
10 , 30AC cm C==
. Tính
;AB BC
.
A.
53 203
;
33
AB BC==
. B.
10 3 14 3
;
33
AB BC==
.
C.
10 3
;203
3
AB BC==
. D.
10 3 20 3
;
33
AB BC==
.
Câu 6: Cho tam giác
ABC
vuông tại
A
có
20 , 60AC cm C==
. Tính
;AB BC
.
A.
20 3; 40AB BC==
.B.
20 3; 40 3AB BC==
.C.
20; 40AB BC==
.D.
20; 20 3AB BC==
.
Câu 7: Cho tam giác
ABC
vuông tại
A
có
12 ; 40BC cm B==
. Tính
;AC C
(làm tròn đến chữ số thập
phân thứ hai)
A.
7, 71 ; 40AC C»=
. B.
7, 72; 50AC C»=
. C.
7, 71 ; 50AC C»=
. D.
7, 73; 50AC C»=
.
Câu 8: Cho tam giác
ABC
vuông tại
A
có
15 , 55BC cm B==
. Tính
;AC C
(làm tròn đến chữ số thập
phân thứ hai).
A.
12,29; 45AC C»=
. B.
12, 29; 35AC C»=
. C.
12, 2; 35AC C»=
. D.
12,92; 40AC C»=
.
Câu 9: Cho tam giác
ABC
vuông tại
A
có
15 , 12BC cm AB cm==
. Tính
;AC B
.
A.
8( ); 36 52AC cm B
¢
=»
. B.
9( ); 36 52AC cm B
¢
=»
.
C.
9( ); 37 52AC cm B
¢
=»
. D.
9( ); 36 55AC cm B
¢
=»
.
Câu 10: Cho tam giác
ABC
vuông tại
A
có
26 , 10BC cm AB cm==
. Tính
;AC B
(làm tròn đến độ).
P
N
M
13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
22; 67AC C=»
. B.
24; 66AC C=»
. C.
24; 67AC C=»
. D.
24; 68AC C=»
.
Câu 10: Cho tam giác
ABC
vuông tại
A
có
7, 5AC cm AB cm==
. Tính
;BC C
.
A.
74( ); 35 32BC cm C
¢
=»
. B.
74( ); 36 32BC cm C
¢
=»
.
C.
74( ); 35 33BC cm C
¢
=»
. D.
75( ); 35 32BC cm C
¢
=»
.
Câu 11: Cho tam giác
ABC
có
16, 14AB AB==
và
60B =
. Tính
BC
.
A.
10BC =
. B.
11BC =
. C.
9BC =
. D.
12BC =
.
Câu 12: Cho tam giác
ABC
có
12, 15AB AC==
và
60B =
. Tính
BC
.
A.
33 6BC =+
. B.
313 6BC =+
. C.
9BC =
. D.
6BC =
.
Câu 13: Cho tam giác
ABC
có

60 , 50 , 3, 5BC CAcm== =
. Diện tích tam giác
ABC
gần nhất với
giá trị nào dưới đây?
A.
4
. B.
5
. C.
7
. D.
8
.
Câu 14: Cho tứ giác
ABCD
có
90 , 40 , 4 , 3AD C AB cmAD cm=== = =
. Tính diện tích tứ giác
ABCD
. (làm tròn đến chữ số thập phân thứ hai).
A.
2
17, 34cm
. B.
2
17, 4cm
. C.
2
17, 54cm
. D.
2
17, 54cm
.
Câu 15: Cho tứ giác
ABCD
có
90 , 45 , 6 , 8AD C AB cmAD cm=== = =
. Tính diện tích tứ giác
ABCD
.
A.
2
60cm
. B.
2
80cm
. C.
2
40cm
. D.
2
160cm
.
Cho tam giác
ABC
có
11 , 40BC cm ABC==
và
30ACB =
. Gọi
N
là chân đường vuông góc hạ từ
A
xuống cạnh
BC
.
Câu 16: Độ dài
AN
gần nhất với giá trị nào dưới đây?
A.
5
. B.
4
. C.
6
. D.
7
.
Câu 17: Độ dài
AC
gần nhất với giá trị nào dưới đây?
A.
7
. B.
6
. C.
5
. D.
4
.
Câu 18: Diện tích tam giác
ABC
gần nhất với giá trị nào dưới đây?
N
B
C
A
14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
N
B
C
A
A.
27
. B.
23
. C.
22
. D.
21
.
Cho tam giác
ABC
có
9, 50BC cm ABC==
và
35ACB =
. Gọi
N
là chân đường vuông góc hạ từ
A
xuống cạnh
BC
.
Câu 19: Độ dài
AN
gần nhất với giá trị nào dưới đây?
A.
5
. B.
4
. C.
2
. D.
3
.
Câu 20: Độ dài
AC
gần nhất với giá trị nào dưới đây?
A.
7
. B.
6
. C.
5
. D.
4
.
Câu 21: Diện tích tam giác
ABC
gần nhất với giá trị nào dưới đây?
A.
13
. B.
15
. C.
16
. D.
25
.
HƯỚNG DẪN
1. Lời giải:
Ta có
sin .sin
MN
PMNMPP
MP
==
.
Đáp án cần chọn là A.
2. Lời giải:
Ta có
cot . cot
NP
PNPMNP
MN
==
Đáp án cần chọn là B.
3. Lời giải:
Cho tam giác
ABC
vuông tại
A
có
,,BC a AC b AB c===
. Ta có:
+ Theo định lý Pytago ta có
222
abc=+
nên C đúng.
+ Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
P
N
M
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
. .cos ; .sin .cos ; .tan .cot ; .tan .cotbacinBa Cca C a Bbc Bc Ccb C b B== = = = = = =
.
Nên A, D đúng.
Đáp án cần chọn là B.
4. Lời giải:
Cho tam giác
ABC
vuông tại
A
có
,,BC a AC b AB c===
.
+ Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
.sin . sin 50 ; . cos cos 50 ; . tan 50 ; . cot 50ba Ba ca Ba bc cb=== == =
.
Nên D đúng.
Đáp án cần chọn là D.
5. Lời giải:
Xét tam giác
ABC
vuông tại
A
có:
10 3
tan . tan 10. tan 30
3
AB
CABACC
AC
== = =
;
10 20 3
cos
cos 3
3
2
AC AC
CBC
BC C
== ==
. Vậy
10 3 20 3
;
33
AB BC==
.
Đáp án cần chọn là D.
6. Lời giải:
B
A
C
C
B
A
C
B
A
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Xét tam giác
ABC
vuông tại
A
có:
tan .tan 20. tan 30 20 3
AB
CABACC
AC
== = =
;
20
cos 40
cos 1
2
AC AC
CBC
BC C
== ==
. Vậy
20 3; 40AB BC==
.
Đáp án cần chọn là A.
7. Lời giải:
Xét tam giác
ABC
vuông tại
A
có
+
sin .sin 1 2.sin 40 7, 71
AC
BACBCB
BC
== = »
.
+

180 180 40 90 50ABC C+ + = = - - =
.
Vậy
7, 71 ; 50AC C»=
.
Đáp án cần chọn là C.
8. Lời giải:
Xét tam giác
ABC
vuông tại
A
có
+
sin . sin 15. sin 55 12, 29
AC
BACBCB
BC
== = »
.
+

180 180 55 90 35ABC C++= = --=
.
Vậy
12,29; 35AC C»=
.
Đáp án cần chọn là B.
9. Lời giải:
Xét tam giác
ABC
vuông tại
A
có:
B
A
C
B
A
C
17.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
+
222 22 22
15 12 9( )BC AB AC AC BC AB cm=+= -=-=
.
+
93
sin
15 5
AC
B
BC
===
36 52B
¢
»
.
Vậy
9( ); 36 52AC c m B
¢
=»
.
Đáp án cần chọn là B.
10. Lời giải:
Xét tam giác
ABC
vuông tại
A
có:
+
222 22 22
26 10 24( )BC AB AC AC BC AB cm=+= -= -=
.
+
24 12
sin 67
26 13
AC
BB
BC
===»
.
Vậy
24; 67AC C=»
.
Đáp án cần chọn là C.
10. Lời giải:
Xét tam giác
ABC
vuông tại
A
có:
+
22222
5 7 74 74( )BC AB AC BC cm=+=+==
.
+
5
tan 35 32
7
AB
CC
AC
¢
==»
Vậy
74( ); 35 32BC cm C
¢
=»
.
Đáp án cần chọn là A.
11. Lời giải:
Kẻ đường cao
AH
.
Xét tam giác vuông
ABH
, ta có:
1
.cos .cos60 16. 8
2
BH A B B AB====
3
.sin .sin60 16. 8 3
2
AH AB B AB====
.
60°
H
A
C
B
18.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Áp dụng định lý Pytago vào tam giác vuông
AHC
ta có:
2222 2
14 (8 3) 196 192 4HC AC AH=-=- =-=
.
Suy ra
2HC =
.
Vậy
2810BC C H HB=+=+=
.
Đáp án cần chọn là A.
12. Lời giải:
Kẻ đường cao
AH
.
Xét tam giác vuông
ABH
, ta có:
1
.cos .cos60 12. 6
2
BH A B B AB====
3
.sin .sin60 12. 6 3
2
AH AB B AB====
.
Áp dụng định lý Pytago vào tam giác vuông
AHC
ta có:
2222 2
15 (6 3) 117HC AC AH=-=- =
.
Suy ra
313HC =
.
Vậy
313 6BC CH HB=+= +
.
Đáp án cần chọn là B.
13. Lời giải:
Kẻ đường cao
AD
.
Xét tam giác vuông
ACD
, ta có:
.sin 3,5.sin50 2,68AD AC C cm==»
.cos 3, 5.cos 50 2,25CD AC C cm==»
.
60°
H
A
C
B
D
B
C
A
19.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Xét tam giác
ABD
, có
.cot 2, 68. cot 60 1, 55BD AD B cm=» »
.
Suy ra
3, 8BC BD CD=+=
.
Do đó
2
.
5, 09
2
ABC
AD BC
Scm=»
.
Đáp án cần chọn là B.
14. Lời giải:
Vì
90AD ADBC==
hay
ABCD
là hình thang vuông tại
,AD
.
Kẻ
BE DC^
tại
E
.
Tứ giác
ABED
có ba góc vuông
90ADE===
nên
ABED
là hình chữ nhật.
Suy ra
4; 3DE AB cm BE AD cm== ==
.
Xét tam giác
BEC
vuông tại
E
có
.cot 40 3,56( )EC BE cm=» 7, 56 ( )DC DE EC cm=+»
.
Do đó
2
().
17, 34
2
ABCD
AB CD AD
Scm
+
=»
.
Đáp án cần chọn là A.
15. Lời giải:
Vì
90AD ADBC==
hay
ABCD
là hình thang vuông tại
,AD
.
Kẻ
BE DC^
tại
E
.
Tứ giác
ABED
có ba góc vuông
90ADE===
nên
ABED
là hình chữ nhật.
Suy ra
6; 8DE AB cm BE AD cm== ==
.
Xét tam giác
BEC
vuông tại
E
có
45BCE =
nên
BEC
vuông cân tại
E
.
86814
EC BE cm DC DE EC cm== =+=+=
.
Do đó
2
().(614).8
80
22
ABCD
AB CD AD
Scm
++
===
.
Đáp án cần chọn là B.
A
C
D
B
20.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
16. Lời giải:
Đặt
(0 11) 11
BN x x N C x=<< =-
.
Xét tam giác
ABN
vuông tại
N
có
. tan . tan 40
AN BN B x==
Xét tam giác
ACN
vuông tại
N
có
. tan (11 ). tan 30AN CN C x==-
Nên
tan 40 (11 ). tan 30 4, 48xxx= -  »
(thoả mãn).
Khi đó
.tan 4,48.tan40 3,76( )
AN BN B cm== »
.
Đáp án cần chọn là B.
17. Lời giải:
Theo câu trước ta có
3, 76AN »
Xét tam giác
ACN
vuông tại
N
có
sin 7, 52
sin
AN AN
CAC
AC C
== =
Đáp án cần chọn là A.
18. Lời giải:
Theo kết quả các câu trước ta có
3, 76AN »
nên
2
.
20,68
2
ABC
AN BC
Scm==
.
Đáp án cần chọn là D.
19. Lời giải:
Đặt
(0 9) 9
BN x x NC x=<< =-
.
Xét tam giác
ABN
vuông tại
N
có
. tan . tan 50
AN BN B x==
Xét tam giác
ACN
vuông tại
N
có
.tan (9 ).tan35AN CN C x==-
Nên
tan 50 (9 ). tan 35 3, 33xxx= -  »
(thoả mãn).
Khi đó
. tan 3, 33. tan 35 2,79AN BN B== »
.
Đáp án cần chọn là D.
20. Lời giải:
Theo câu trước ta có
2, 79AN »
Xét tam giác
ACN
vuông tại
N
có
sin 4, 87
sin
AN AN
CAC
AC C
== »
Đáp án cần chọn là C.
21. Lời giải:
21.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Theo kết quả các câu trước ta có
2, 79AN »
nên
2
.
12,555
2
ABC
AN BC
Scm==
.
Đáp án cần chọn là A.
‐‐‐‐‐‐‐‐‐‐ToánHọcSơĐồ‐‐‐‐‐‐‐‐‐
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

CHUYÊN ĐỀ MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
A. KIẾN THỨC CẦN NHỚ I. Định lí
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:
• Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề;
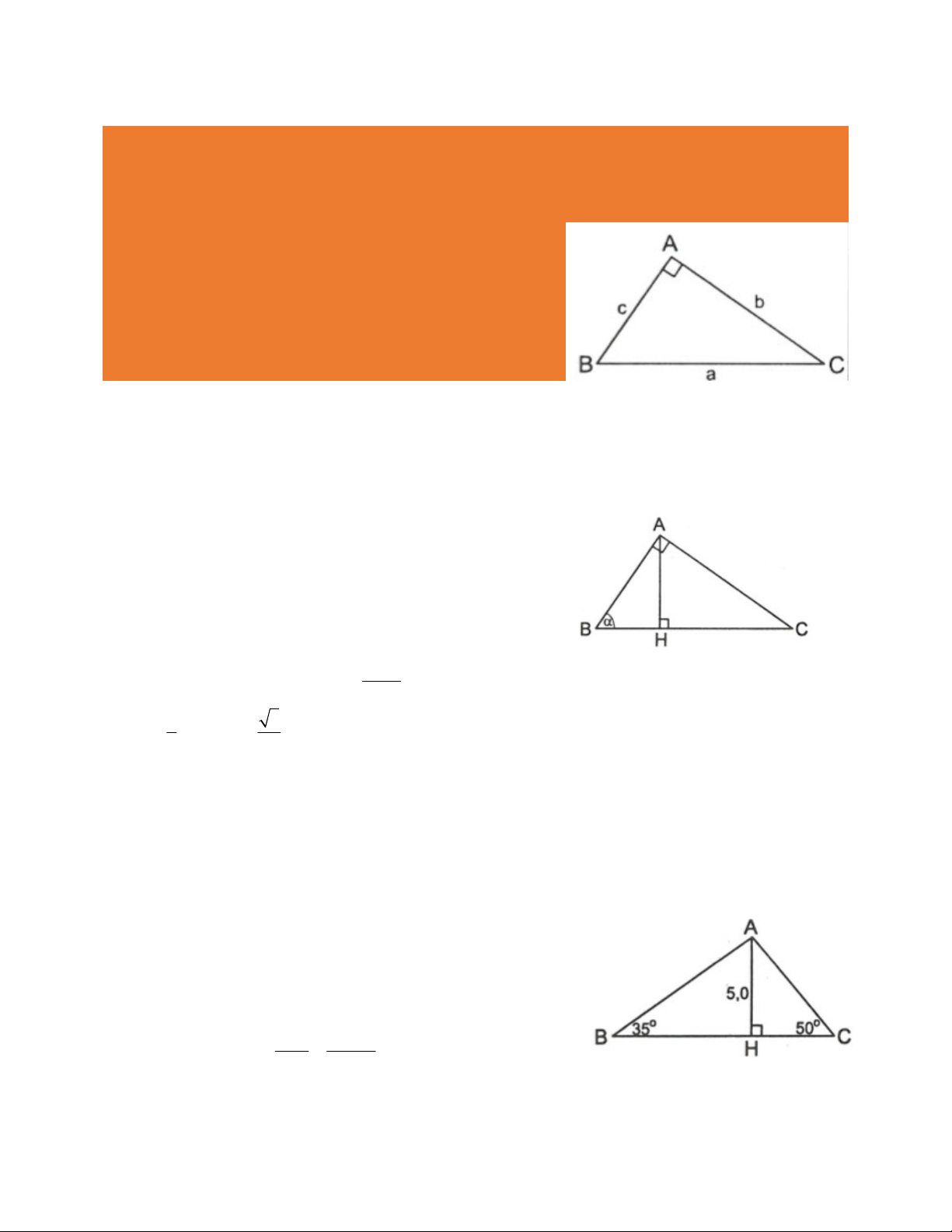
• Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề Trong hình bên thì:
b a sin B a cos C;c a sin C a cos B
b c tan B c cot C;c b tan C b cot B
II. Giải tam giác vuông
Là tìm tất cả các cạnh và góc của tam giác vuông B khi
biết hai yếu tố của nó (trong đó ít nhất có một yếu tố về độ dài).
B. MỘT SỐ DẠNG BÀI CƠ BẢN VÀ NÂNG CAO
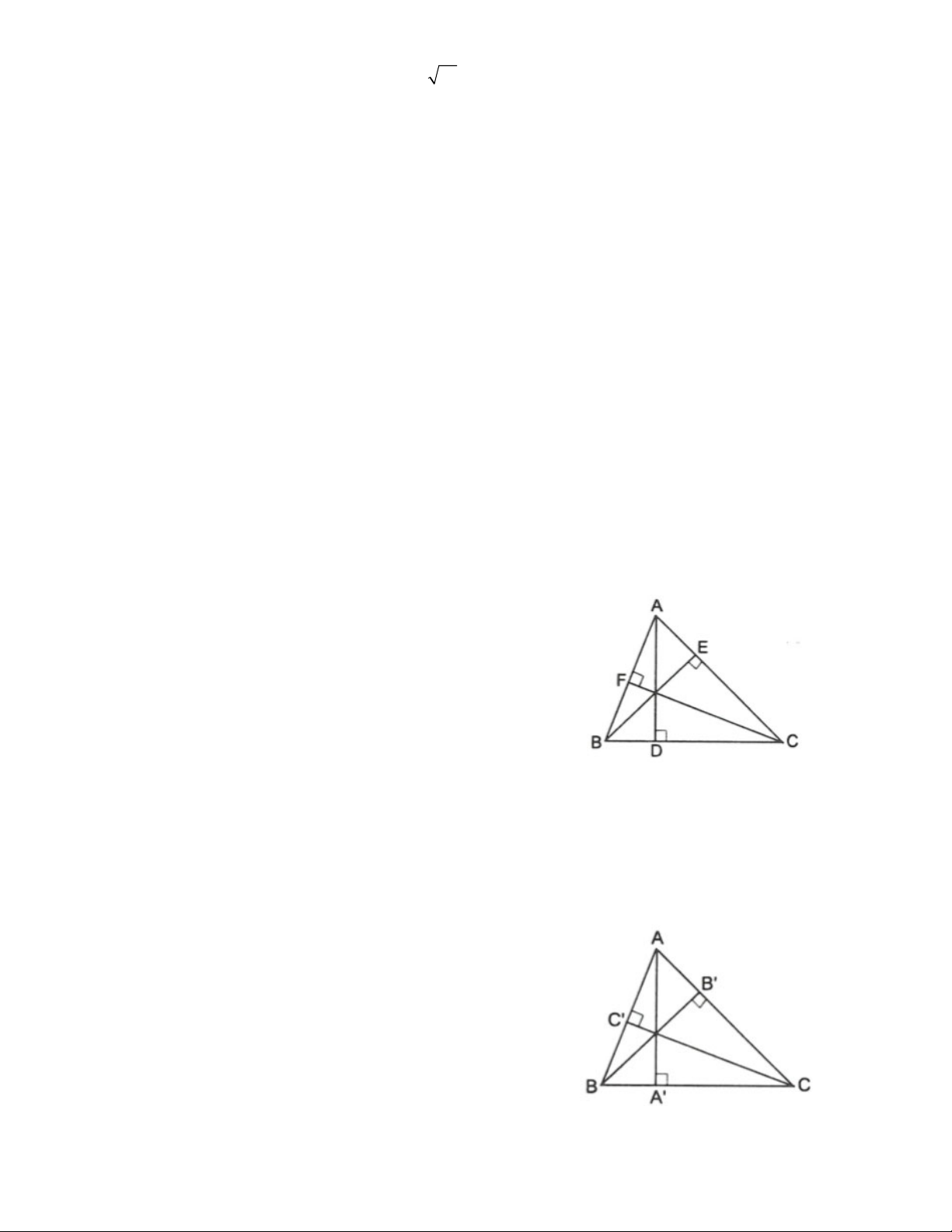
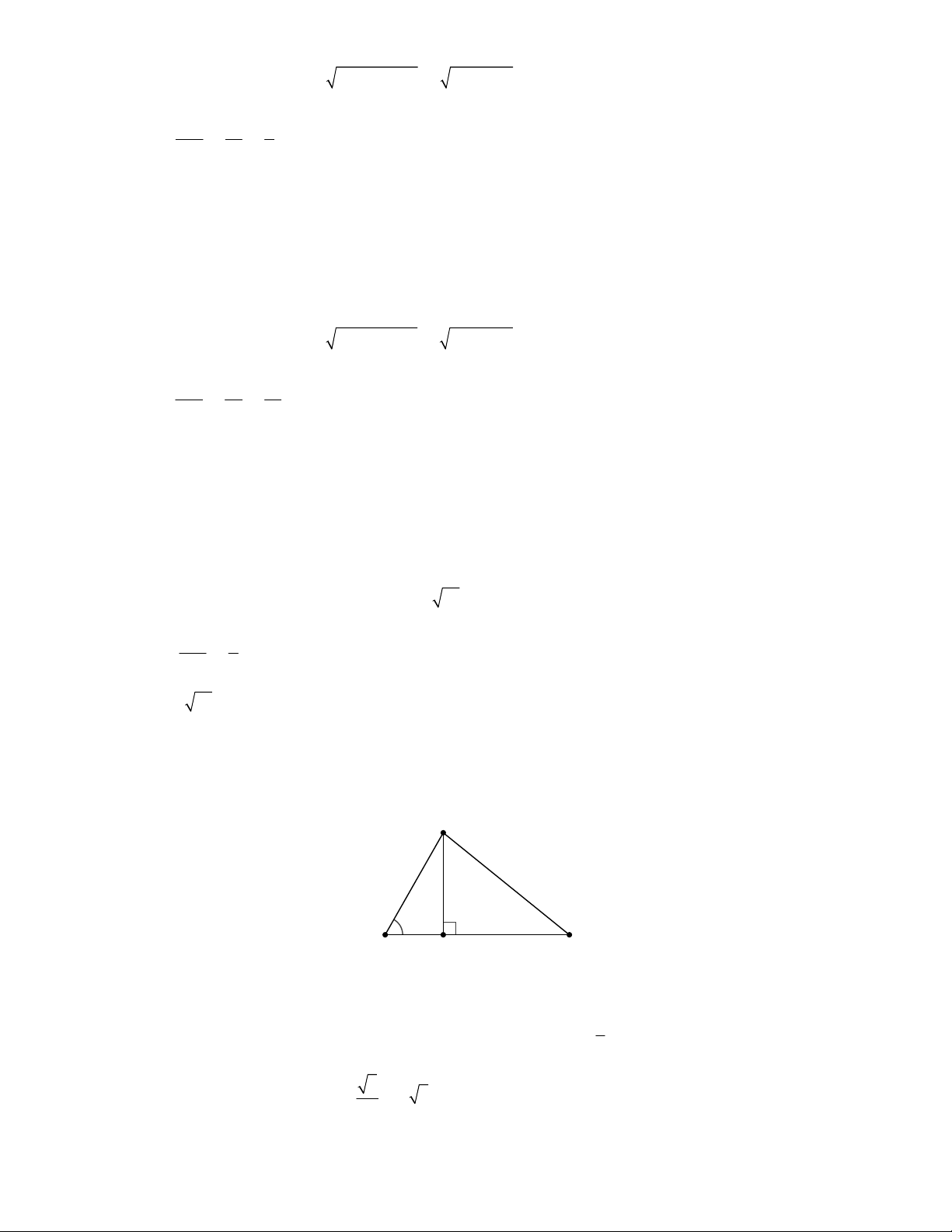
Ví dụ 1. Cho tam giác ABC vuông tại A, đường cao AH, B   . Tính giá trị của  để BH = 3CH. Giải Đặt AH = h.
Xét ABH vuông tại H ta có: BH = AH.cot B = h.cot .
Xét ACH vuông tại H ta có:
CH = AH.cot C = AH.tan B = h.tan . 1 BH  3CH  . h cot  3 . h tan   3tan tan 1 3 2 tan    tan 
 tan 30    30 3 3
Nhận xét: Trong bài giải ta đã biểu diễn BH và CH theo AH và theo một tỉ số lượng giác của góc . Từ
mối quan hệ giữa BH và CH ta tìm được giá trị của .
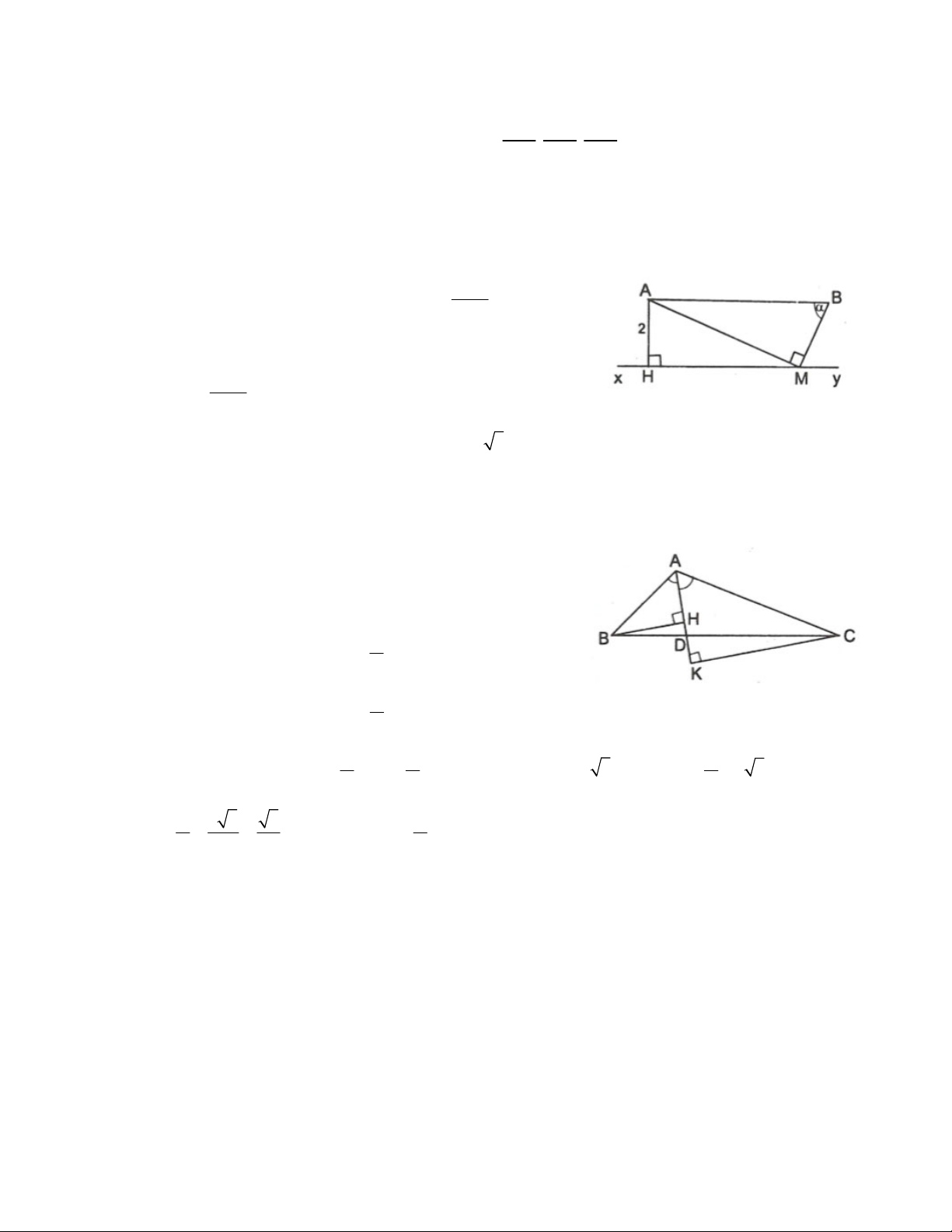
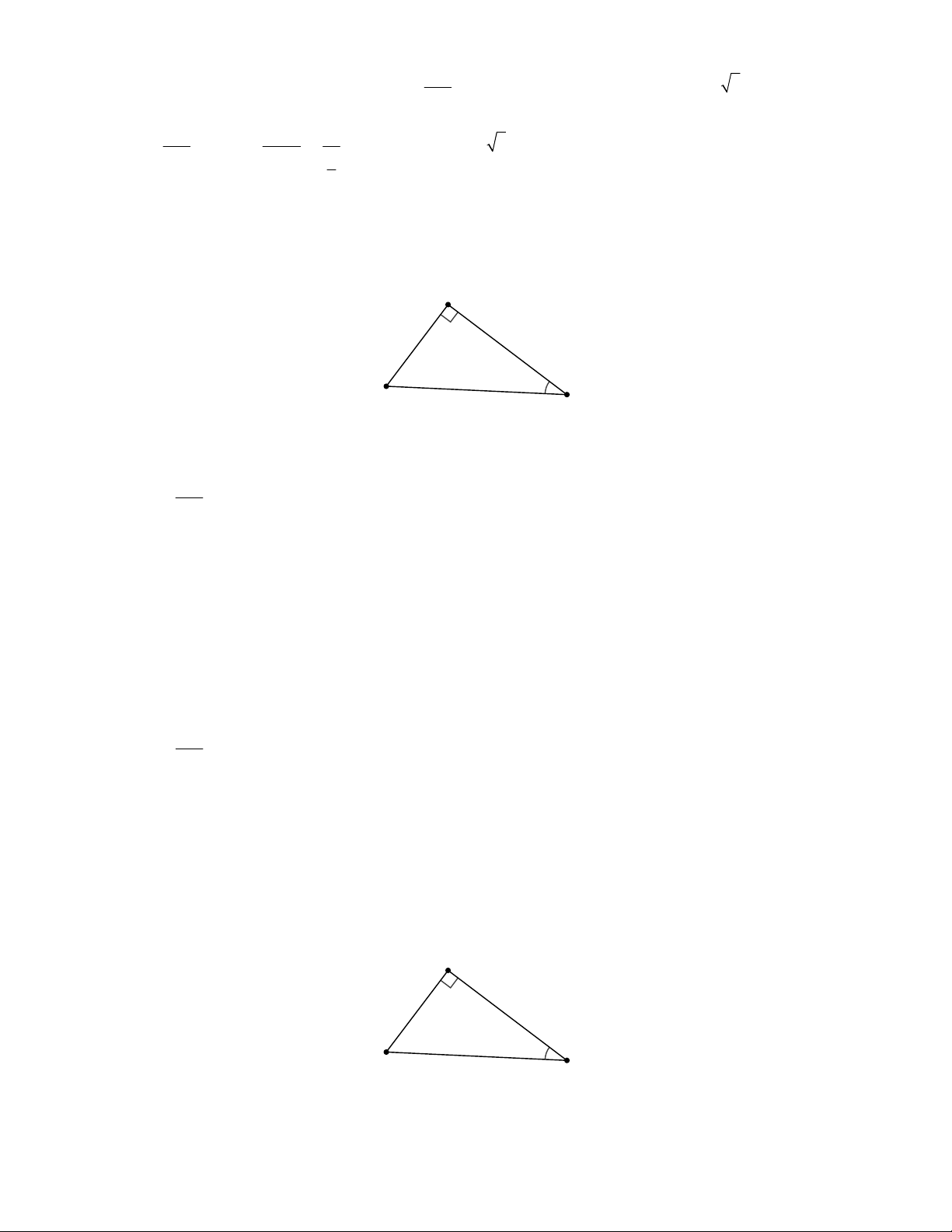
Ví dụ 2. Giải tam giác ABC biết   B  35 ,
C  50 và đường cao AH = 5,0cm. Giải
Ta phải tìm A , AB, AC và BC.   
A  180  B C  95
• Xét ABH vuông tại H ta có: AH 5,0 AH A .s B inB  AB    8,7cm sinB sin 35
BH AH.cotB  5,0.cot 35  7,1cm
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
• Xét ACH vuông tại H ta có: AH 5,0
AH AC.sin C AC    6,5cm sin C sin 50
CH AH.cot C  5,0.cot 50  4, 2cm
Do đó BC BH CH  7,1 4, 2  11,3cm Vậy A  95 ;
AB  8,7c ; m AC  6,5c ;
m BC  11,3cm
Lưu ý: Sau khi tính được AB và AC, có thể tính BH và CH theo AB và AC: BH  .c
AB os B;CH AC.cos C
Tuy nhiên, ta nên tính BH và CH theo các số đo đã cho trong đề bài để kết quả được chính xác hơn.
Ví dụ 3. Cho tam giác ABC, cạnh BC cố định. Biết BC = 4cm, AB + AC = 8cm. Tính giá trị lớn nhất của góc A. Giải
Vẽ đường phân giác AD. Vẽ BH  AD và CK  AD. A A
Xét ABH vuông tại H, ACK vuông tại K, ta có: BH  .
AB sin ;CK AC sin 2 2 A A
Vậy BH CK   AB ACsin  8sin 2 2 Mặt khác ,
BH CK BD CD BC  4cmA A 1 nên 8sin
 4  sin   sin 30 2 2 2 A Do đó 
 30  A  60 2 vậy 
max A  60 khi D, H, K trùng nhau  ABC đểu.
Nhận xét: Nhờ có việc vẽ đường phân giác AD và các đường thẳng BH, CK cùng vuông góc với AD mà
ta tìm được sự liên hệ giữa AB, AC với BH, CK; sự liên hệ giữa BH, CK với BC. Do đó giữa AB, AC và
BC có sự liên hệ với nhau, từ đó tìm được số đo của góc A.
Ví dụ 4. Chứng minh định lí côsin: Trong một tam giác nhọn, bình phương của một cạnh bằng tổng các
bình phương của hai cạnh kia trừ đi hai lần tích của hai cạnh ấy với côsin của góc xen giữa của chúng. Giải
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Vẽ đường cao BH. Xét HBC vuông tại H ta có:
BC HB HC HB   AC AH 2 2 2 2 2 2 2 2
HB AC  2AC.AH AH   2 2 HB AH  2
AC  2AC.AH 2 2
AB AC  2AC.AH   1
Xét ABH vuông tại H ta có : AH = AB. cosA Thay vào (1) ta được 2 2 2
BC AB AC  2AC. . AB cosA
Nhận xét: Trong một tam giác nhọn, nếu biết hai cạnh và góc xen giữa thì nhờ định lí côsin ta có thế tính được cạnh thứ ba.
C. BÀI TẬP TỰ LUYỆN
• Vận dụng hệ thức về cạnh và góc trong tam giác vuông để chứng minh hoặc tính toán
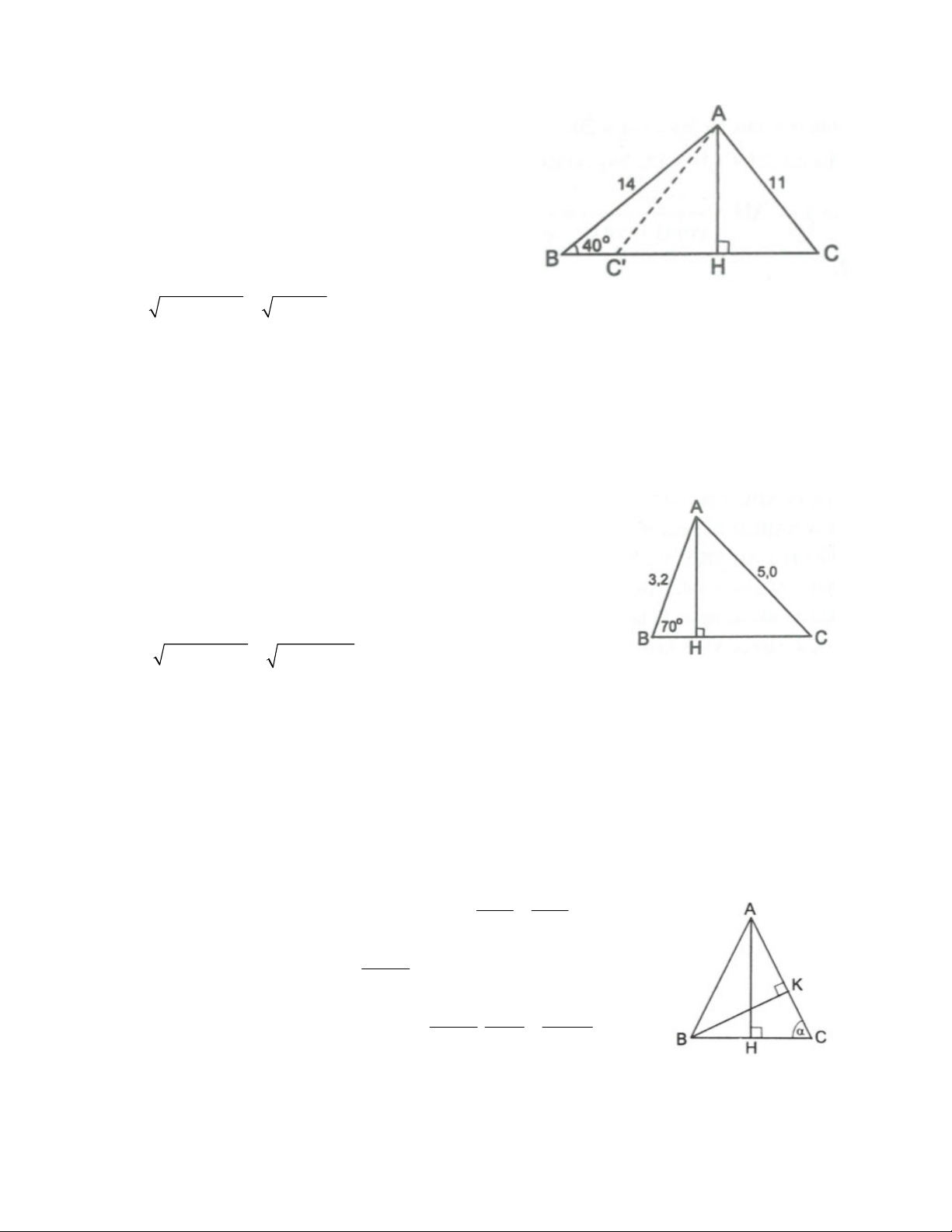
Bài 1. Cho tam giác nhọn ABC. Vẽ các đường cao AD, BE, CF. Chứng minh rằng:
a) AD.BE.CF = AB.BC.CA.sin A.sin B.sin C;
b) AE.BF.CD = AB.BC.CA.cos A.cos B.cos C.
Bài 2. Cho tam giác nhọn ABC. Vẽ các đường cao AA', BB', CC’. Chứng minh rằng:
AB '.BC '.CA'  A' .
B B 'C.C ' A  . AB BC. .c CA os .c A os .c B osC
Bài 3. Cho đường thẳng xy và điểm A cố định cách xy là 2cm. Gọi M là một điểm di động trên xy. Vẽ
tam giác ABM vuông tại M sao cho 
ABM   0    90 . Tính độ dài ngắn nhất của AB.
Bài 4. Cho tam giác ABC, cạnh BC cố định và BC  3 3cm . Điểm A di động sao cho AB + AC = 6cm.
Tính giá trị lớn nhất của góc A.
Bài 5. Cho tam giác ABC, AB = 14cm, AC = 11cm và B  40. Tính độ dài BC.
Bài 6. Cho tam giác ABC, AB = 3,2cm; AC = 5,0cm và B  70 . Tính độ dài BC.
Bài 7. Cho tam giác ABC cân tại A, góc ở đáy bằng  < 90°. Vẽ các đường cao AH và BK. Biết BK = h, tính AH.
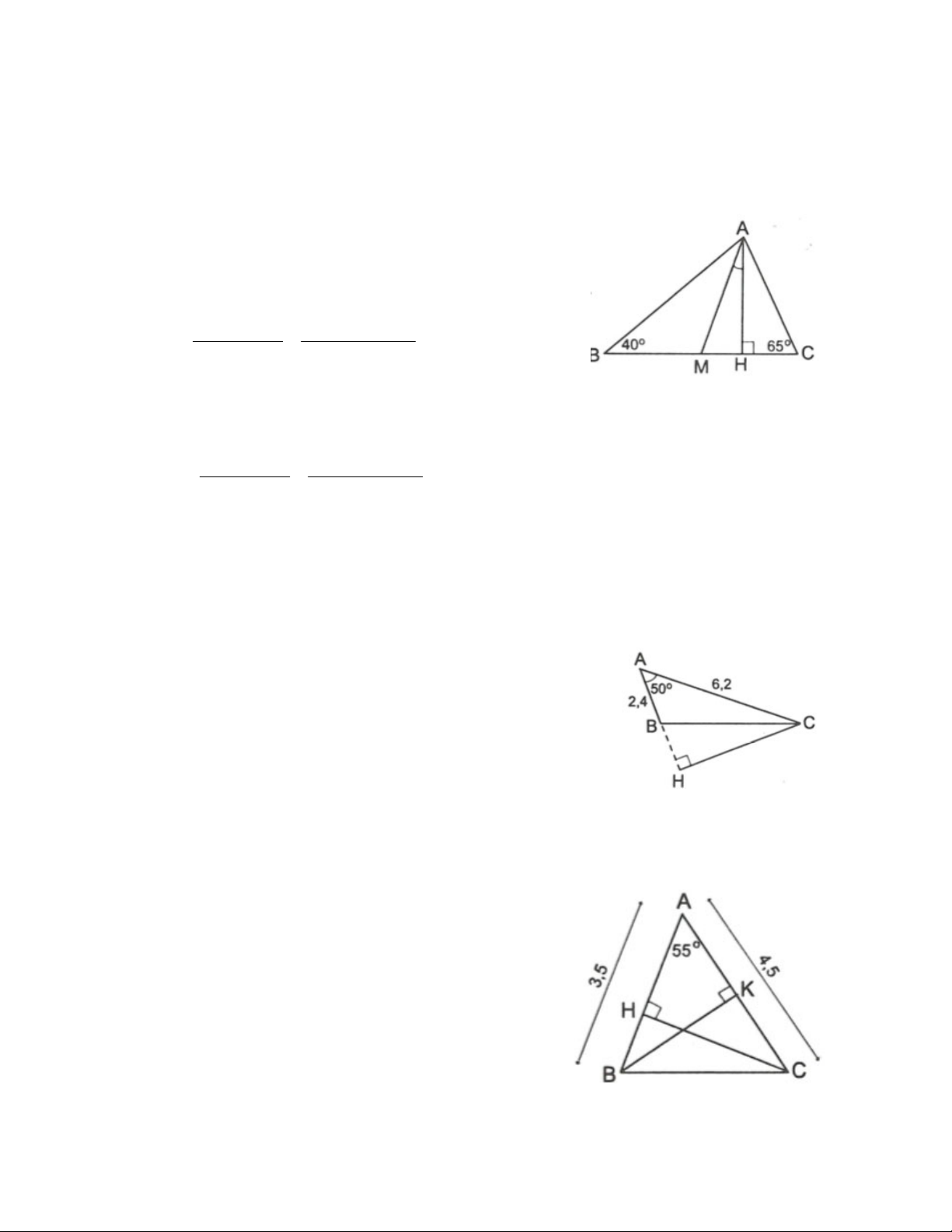
Bài 8. Cho tam giác ABC,   B  40 ,  C  65
a) Tính số đo của góc tạo thành bởi đường cao AH và đường trung tuyến AM (làm tròn đến độ);
b) Cho biết BC = 45cm, tính độ dài AH (làm tròn đến centimet).
Bài 9. Tam giác ABC là tam giác nhọn hay tam giác tù nếu có:
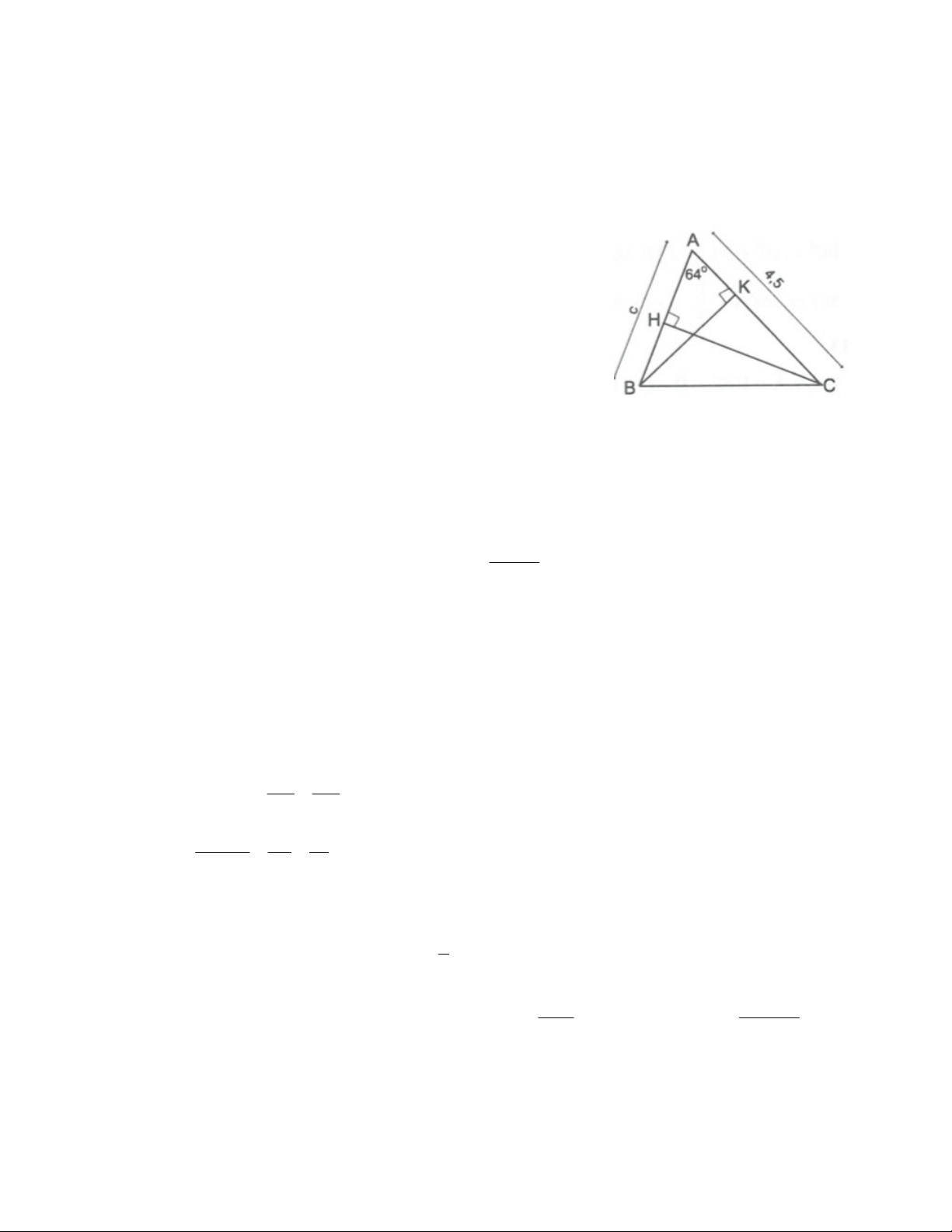
a) A  50 , AB = 2,4cm, AC = 6,2cm;
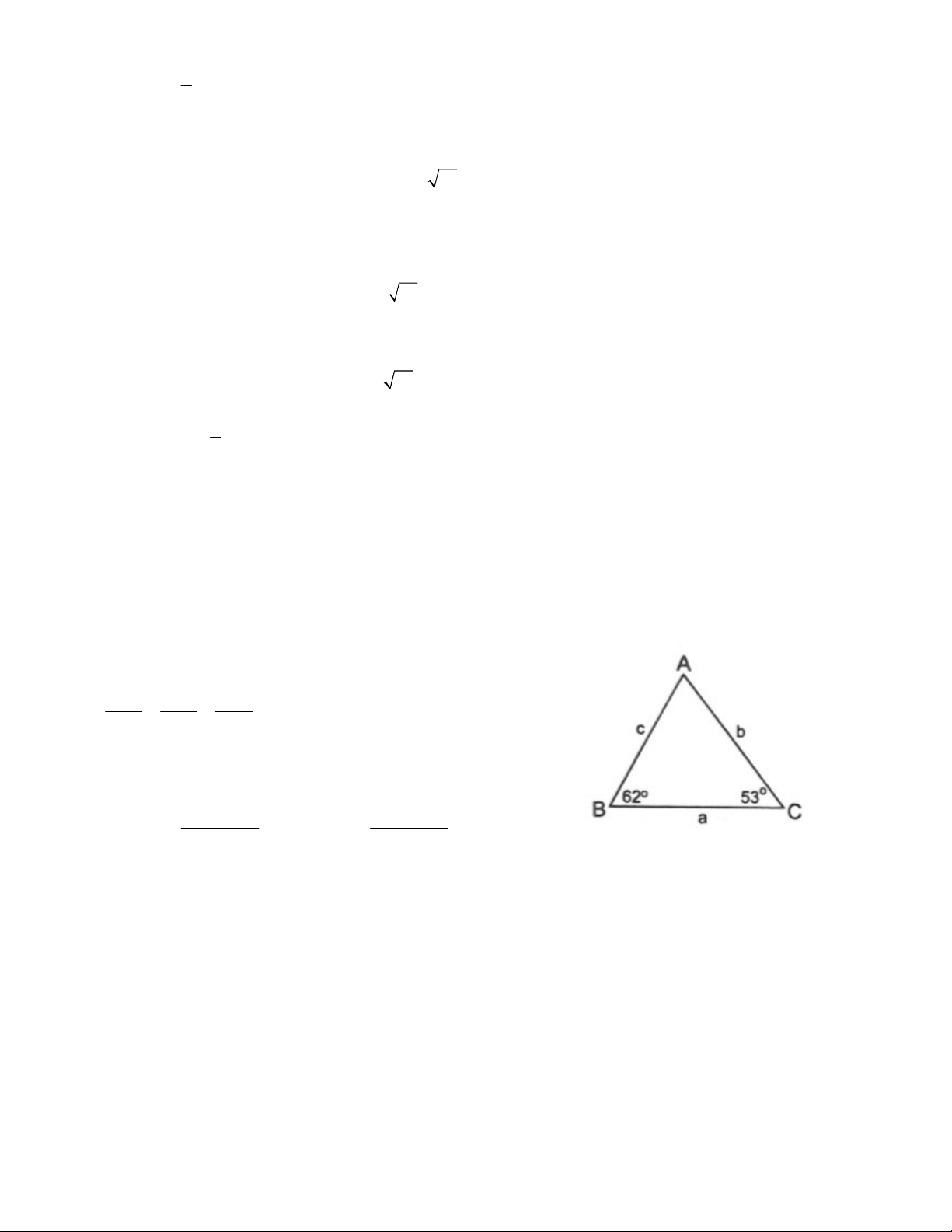
b) A  55 , AB = 3,5cm, AC = 4,5cm.
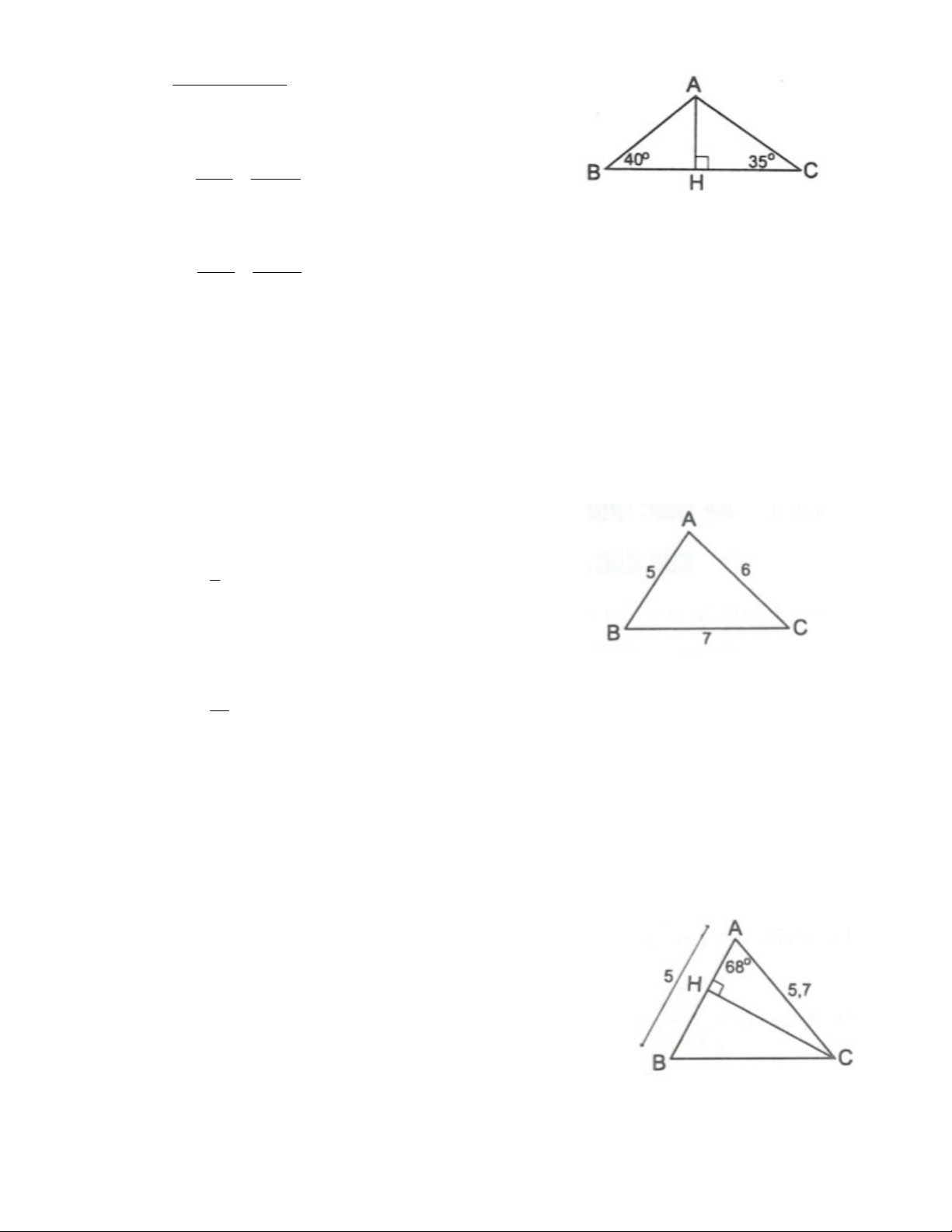
Bài 10. Cho tam giác ABC vuông tại A, A  64 , AB = c, AC = 4,5cm. Xác định giá trị của c để tam giác ABC là tam giác tù.
Bài 11. Cho tam giác nhọn ABC, AB =
4cm, BC = 6cm. Một hình chữ nhật DEFG nội tiếp tam giác
đó với D AB, E AC; F,G  BC . Chứng minh rằng diện tích hình chữ nhật DEFG nhỏ hơn 6cm2.
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Bài 12. Cho tam giác ABC, AB = 5cm, BC  39cm và CA = 7cm. Tính số đo góc A.
Bài 13. Giải tam giác ABC, biết:    
a)BC  6,8c ; m B  62 ;  C  53
b)BC  6,8c ; m B  40 ;  C  35
Bài 14. Giải tam giác ABC, biết: AB = 5cm, BC = 7cm, CA = 6cm (các số đo góc làm tròn đến độ).
Bài 15. Giải tam giác ABC, biết: A  68 , AB = 5,0cm, AC = 5,7cm (làm tròn các độ dài đến chữ số thập
phân thứ nhất, làm tròn các số đo góc đến độ).
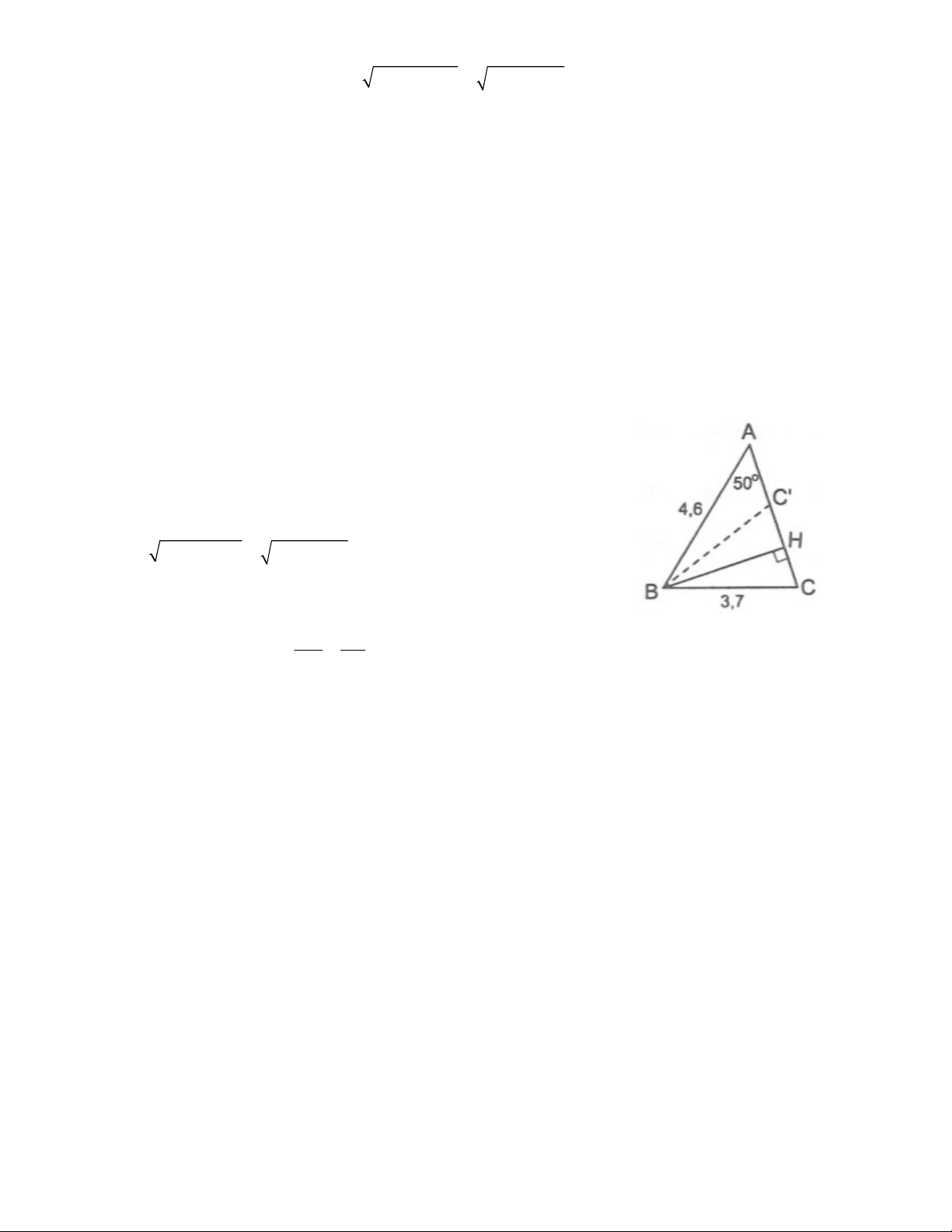
Bài 16. Giải tam giác ABC, biết: A  50 , AB = 4,6cm, BC = 3,7cm (làm tròn số đo góc đến độ, làm tròn
độ dài đến hàng phần mười). HƯỚNG DẪN
• Vận dụng hệ thức về cạnh và góc trong tam giác vuông để chứng minh hoặc tính toán
Bài 1. Cho tam giác nhọn ABC. Vẽ các đường cao AD, BE, CF. Chứng minh rằng:
a) AD.BE.CF = AB.BC.CA.sin A.sin B.sin C;
b) AE.BF.CD = AB.BC.CA.cos A.cos B.cos C. Giải
a) ACD vuông tại D, có AD = ACsin C.
ABE vuông tại E, có BE = ABsin A.
BCF vuông tại F, có CF = BCsin B.
Suy ra AD.BE.CF = AB.BC.CA.sin A.sin B.sin C.
b) ABE vuông tại E, có AE = ABcos A.
BCF vuông tại F, có BF = BCcos B.
ACD vuông tại D, có CD = ACcos C.
Suy ra AE.BF.CD = AB.BC.CA.cos A.cos B.cos C.
Bài 2. Cho tam giác nhọn ABC. Vẽ các đường cao AA', BB', CC’. Chứng minh rằng:
AB '.BC '.CA'  A' .
B B 'C.C ' A  . AB BC. .c CA os .c A os .c B osC Giải
ABB' vuông tại B', có AB' = ABcos A.
BCC’ vuông tại C', có BC' = BCcos B.
CAA' vuông tại A', có CA' = ACcos C.
Suy ra AB'.BC'.CA' = AB.BC.CA.cos A.cos B.cos C.
Chứng minh tương tự ta được:
A'B.B'C.C'A = AB.BC.CA.cos A.cos B.cos C.
Do đó AB’.BC’.CA' = A'B.B'C.C'A
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com = AB.BC.CA.cos A.cos B.cos C.
Nhận xét: Vì ba đường cao tam giác cùng đi qua một điểm nên nếu đề bài chỉ yêu cầu chứng minh
A' B B 'C C ' A
AB'.BC’.CA' = A'B.B'C.C’A thì theo định lí Xê-va ta có . .
 1 từ đó suy ra ngay đpcm.
A'C B ' A C 'B
Bài 3. Cho đường thẳng xy và điểm A cố định cách xy là 2cm. Gọi M là một điểm di động trên xy. Vẽ
tam giác ABM vuông tại M sao cho 
ABM   0    90 . Tính độ dài ngắn nhất của AB. Giải AM
ABM vuông tại M, có AM  .s
AB in  AB  sin
Do đó AB ngắn nhất  AM ngắn nhất  M H AM  2cm 2 Vậy min AB  khi M H sin
Bài 4. Cho tam giác ABC, cạnh BC cố định và BC  3 3cm . Điểm A di động sao cho AB + AC = 6cm.
Tính giá trị lớn nhất của góc A. Giải
Vẽ đường phân giác AD. Vẽ BH  AD,
CK  AD. Ta có BH BD,CK CD
Suy ra BH CK BD CD BC A
ABH vuông tại H, có: BH A .s B in 2  A
ACK vuông tại K, có: CK AC.sin 2 A A A
Do đó BH CK   AB AC .sin  6sin mà BH CK BC  3 3cm nên 6sin  3 3 2 2 2 A 3 3 3 A Do đó sin    sin 60 . Suy ra 
 60  A  120 2 6 2 2 Vậy 
max A  120 khi H K D  ABC vuông cân tại A.
Bài 5. Cho tam giác ABC, AB = 14cm, AC = 11cm và B  40. Tính độ dài BC. Giải * Tìm cách giải
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Vẽ đường cao AH để vận dụng các hệ thức về cạnh và góc trong tam giác vuông. Tính HB và HC từ đó tính được BC. * Trình bày lời giải
Vẽ đường cao AH. Xét ABH vuông tại H có: AH A .
B sin B  14sin 40  9.0cmBH  .
AB cos B  14.cos 40  10, 7 cm
Xét AHC vuông tại H có: 2 2 2 2
HC AC AH  11  9  6,3cm
• Nếu H nằm giữa B và C thì BC BH HC  10,7  6,3  17cm
• Nếu C’ nằm giữa B và H thì BC '  BH HC '  10,7  6,3  4, 4cm
Bài 6. Cho tam giác ABC, AB = 3,2cm; AC = 5,0cm và B  70 . Tính độ dài BC. Giải
Vẽ đường cao AH. Xét ABH vuông tại H có: AH  .
AB sin B  3, 2sin 70  3, 0cmBH  .
AB cos B  3, 2.cos 70  1,1cm
Xét AHC vuông tại H có: 2 2 2 2
HC AC AH  5,0  3,0  4,0cm
Điểm C không thể nằm giữa H và B vì trên tia HB có HC > HB.
Chỉ còn trường hợp điểm H nằm giữa B và C.
Ta có BC BH HC  1,1 4,0  5,1cm
Bài 7. Cho tam giác ABC cân tại A, góc ở đáy bằng  < 90°. Vẽ các đường cao AH và BK. Biết BK = h, tính AH. Giải BK h
Xét KBC vuông tại K, có: BK BC.sin  BC   sin sin h
Vì ABC cân tại A nên HB HC  2sin h sin h
Xét AHC vuông tại H có: AH HC.tan  .  2sin cos 2 cos
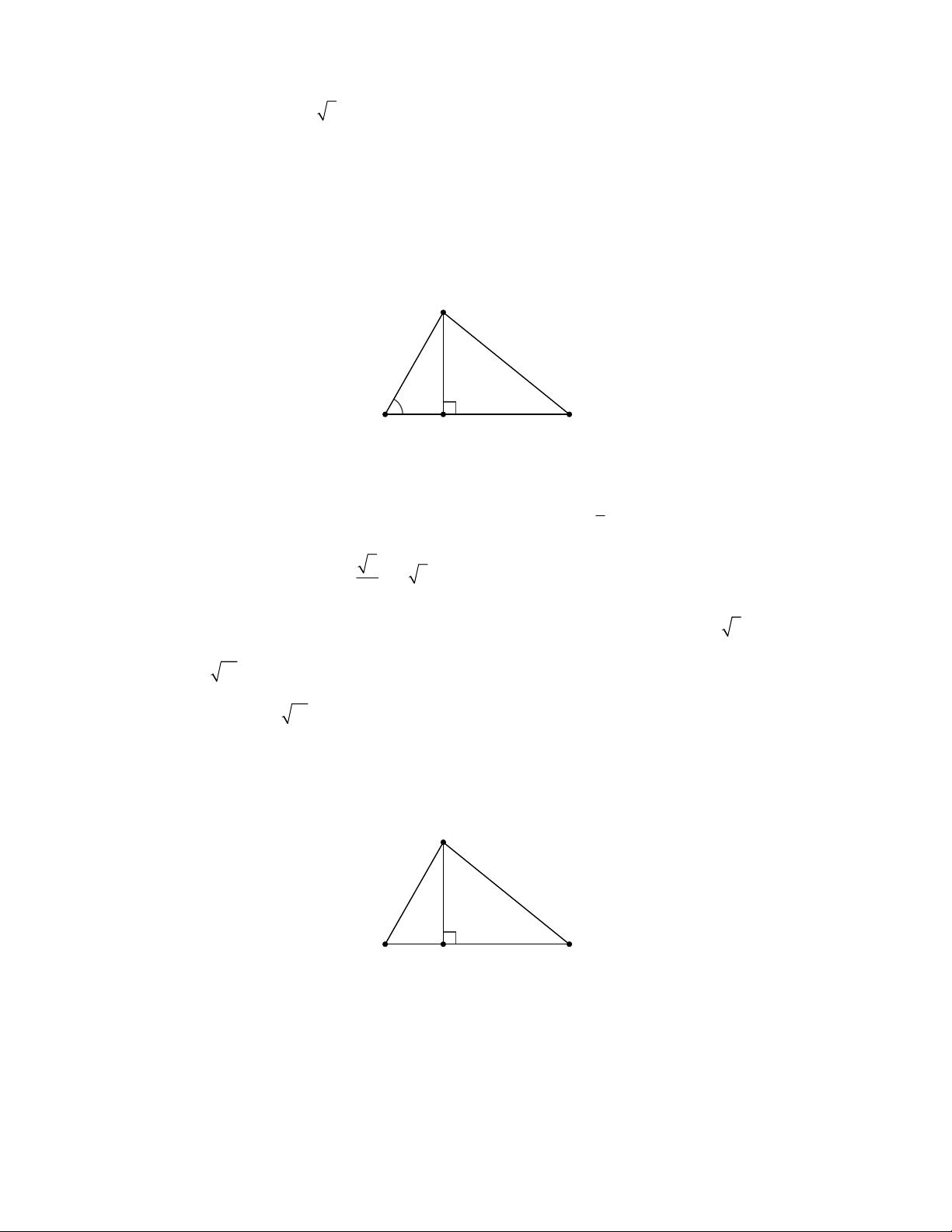
Bài 8. Cho tam giác ABC,   B  40 ,  C  65
a) Tính số đo của góc tạo thành bởi đường cao AH và đường trung tuyến AM (làm tròn đến độ);
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
b) Cho biết BC = 45cm, tính độ dài AH (làm tròn đến centimet). Giải Đặt  MAH  
a) Xét ABH và AHC vuông tại H ta có: BH AH cot B;CH AH cot C; MH AH tan
Ta có BH CH  BM MH   CM MH   2MH
Do đó AH cot B AH cot C  2AH tan
Suy ra cot B  cot C  2 tan cot B cot C cot 40 cot 65 Hay tan        0,3627 2 2 tan  tan19 56  '    20
b) Ta có BH + CH = BC hay AH cot B AH cot C  45  AH cot B  cot C  45 45 45 Suy ra AH    27cm cot B  cot C cot 40  cot 65
Bài 9. Tam giác ABC là tam giác nhọn hay tam giác tù nếu có:
a) A  50 , AB = 2,4cm, AC = 6,2cm;
b) A  55 , AB = 3,5cm, AC = 4,5cm. Giải
a) Vẽ CH  AB. Xét ACH vuông tại H, ta có:
AH AC.cos A  6, 2.cos50  4,0cm
Trên tia AB có AB < AH nên điểm B nằm giữa A và H. Suy ra  
ABC H  90
Vậy ABC là tam giác tù.
b) Vẽ CH  AB, BK  AC. Xét ACH vuông tại H, ta có:
AH AC.cos A  4,5.cos55  2,6cm
Xét ABK vuông tại K, ta có: AK  .
AB cos A  3,5.cos55  2,0cm
• Trên tia AB có AH < AB nên điểm H nằm giữa A và B. Xét HBC có  H  90 nên  HBC nhọn.
• Trên tia AC có AK < AC nên điểm K nằm giữa A và C.
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Xét KBC có  K  90 nên  ACB nhọn.
Tam giác ABC có ba góc nhọn nên là tam giác nhọn.
Bài 10. Cho tam giác ABC vuông tại A, A  64 , AB = c, AC = 4,5cm. Xác định giá trị của c để tam giác ABC là tam giác tù. Giải
Vẽ CH  AB, BK  AC. AHC vuông tại H, ta có:
AH AC.cos A  4,5.cos 64  2,0cm
AKB vuông tại K, ta có: AK  .c AB os A  .c c os 64
ABC tù  B tù hoặc  C tù.
• Xét trường hợp B tù.
Ta có B  90  AH AB  2  c hay c  2 và c  0 • Xét trường hợp  C tù. Ta có :  o 4,5
C  90  AK AB  .
c c os64  4,5  c   10,3. cos64o
Tóm lại, ABC tù khi 0  c  2cm hoặc c  10,3cm
Bài 11. Cho tam giác nhọn ABC, AB =
4cm, BC = 6cm. Một hình chữ nhật DEFG nội tiếp tam giác
đó với D AB, E AC; F,G  BC . Chứng minh rằng diện tích hình chữ nhật DEFG nhỏ hơn 6cm2. Giải
Ta đặt B  ; AD x thì DB  4  x DE AD
Ta có DE / /BC suy ra 
(hệ quả định lí Ta-lét) BC AB . AD BC . x 6 3x Do đó DE    AB 4 2
Xét DBG vuông tại G, ta có DG D .
B sin  4  xsin 3
Diện tích hình chữ nhật DEFG là S DE.DG x 4  xsin 2 2  a b  2
x  4  x
Vận dụng bất đẳng thức Cô-si đối với hai số không âm ab  
 ta được x 4  x   4    2   2 
(dấu “=” xảy ra khi x = 4-x  x = 2).
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 3
Do đó S  .4sin  6sin 2
Vì 0  sin 1 nên S   2
6 cm  khi D là trung điểm của AB.
Bài 12. Cho tam giác ABC, AB = 5cm, BC  39cm và CA = 7cm. Tính số đo góc A. Giải
Xét ABC có CA là cạnh lớn nhất nên góc B là góc lớn nhất. Ta thấy 2 2 2
AC BA BC (vì    2 2 2 7 5
39 ) nên góc B là góc nhọn (xem bài 1.18).
Do đó ABC là tam giác nhọn. Theo định lí cô-sin ta có:
BC AB AC AB AC   2 2 2 2 2 2 2 . .cosA 39
 5  7  2.5.7.cos A 1
Suy ra cos A  , do đó A  60 2
Bài 13. Giải tam giác ABC, biết:  
a)BC  6,8c ; m B  62 ;  C  53  
b)BC  6,8c ; m B  40 ;  C  35 Giải a) Ta có   
A  180  B C  65
Vì ABC nhọn nên theo định lí sin ta có: a b c   sin A sin B sin C 6,8 b c Do đó   sin 65 sin 62 sin 53 6,8.sin 62 6,8.sin 53 Suy ra b
 6,6cm;c   6,0cm sin 65 sin 65
Nhận xét: Để giải tam giác trường hợp (g.c.g) ta dùng định lí sin. b) Ta có   
A  180  B C  105
Vậy ABC là tam giác tù, không vận dụng được đính lí sin.
Vẽ đường cao AH. Vì các góc B và C nhọn nên điểm H nằm giữa B và C.
Ta có BH AH cot B, CH  AHcotC
Mà BH CH BC nên AH cot B  cot C  6,8
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 6,8  AH   2,6cm cot 40  cot 35
ABH vuông tại H, có AH  .s AB in B AH 2, 6 Suy ra AB    4,0cm sin B sin 40
ACH vuông tại H, có AH AC.sin C AH 2, 6 Suy ra AC    4,5cm sin C sin 35
Bài 14. Giải tam giác ABC, biết: AB = 5cm, BC = 7cm, CA = 6cm (các số đo góc làm tròn đến độ). Giải
Xét ABC, cạnh BC là cạnh lớn nhất nên góc A là góc lớn nhất. Ta có 2 2 2
BC AB AC (vì 2 2 2
7  5  6 ) nên góc A là góc nhọn (xem bài 1.18).
Vậy ABC là tam giác nhọn. Theo định lí cô-sin, ta có: • 2 2 2
BC AB AC  2 . AB AC.cos A Do đó 2 2 2
7  5  6  2.5.6.cos A 1
Suy ra cos A  , do đó A  78 5 • 2 2 2
AC AB BC  2 . AB BC.cosB Do đó 2 2 2
6  5  7  2.5.7.cos B 19 Suy ra cos B
, do đó B  57 35 • 
C  180  78  57  45
Nhận xét: Để giải tam giác khi biết ba cạnh ta thường sử dụng định lí cô-sin.
Bài 15. Giải tam giác ABC, biết: A  68 , AB = 5,0cm, AC = 5,7cm (làm tròn các độ dài đến chữ số thập
phân thứ nhất, làm tròn các số đo góc đến độ). Giải
Vẽ CH  AB. Xét ACH vuông tại H, ta có:
CH AC.sin A  5,7.sin 68  5,3cm
AH AC.cos A  5,7.cos 68  2,1cm
Trên tia AB có AH < AB (2,1 < 5,0) nên điểm H nằm giữa A và B. Do
đó BH = 5,0 - 2,1 = 2,9 (cm).
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Xét HBC vuông tại H, ta có: 2 2 2 2
BC CH BH  5,3  2,9  6,0cm
Xét ABC có BC là cạnh lớn nhất nên góc A là góc lớn nhất. Ta có 2 2 2
BC AB AC (vì 2 2 2
6  5  5, 7 ) nên góc A là góc nhọn, suy ra ABC nhọn. Do đó 2 2 2
5,7  5, 0  6, 0  2.5, 0.6, 0.cos B Suy ra 
cos B  0, 4752  B  62 Từ đó 
C  180  68  62  50
Bài 16. Giải tam giác ABC, biết: A  50 , AB = 4,6cm, BC = 3,7cm (làm tròn số đo góc đến độ, làm tròn
độ dài đến hàng phần mười). Giải
Vẽ BH  AC. ABH vuông tại H, ta có: AH A .
B cos A  4, 6.cos 50  3, 0cmBH  .s
AB in A  4,6.sin 50  3,5cm
HBC vuông tại H, ta có: 2 2 2 2
HC BC BH  3,7  3,5  1, 2cm
• Nếu H nằm giữa A và C thì AC AH HC  3,0 1, 2  4, 2cmBH 3,5 Khi đó 
C  90 và sin C    sin 71 BC 3,7 Suy ra 
C  71 và B  180  50  71  59
• Nếu C’ nằm giữa H và A thì AC '  AH HC '  3,0 1, 2  1,8cm Khi đó 
AC ' B  90 Ta có   
BC 'C C  71  AC ' B  180  71  109 và 
AB 'C  180  50 109  21
C.TRẮC NGHIỆM RÈN LUYỆN PHẢN XẠ
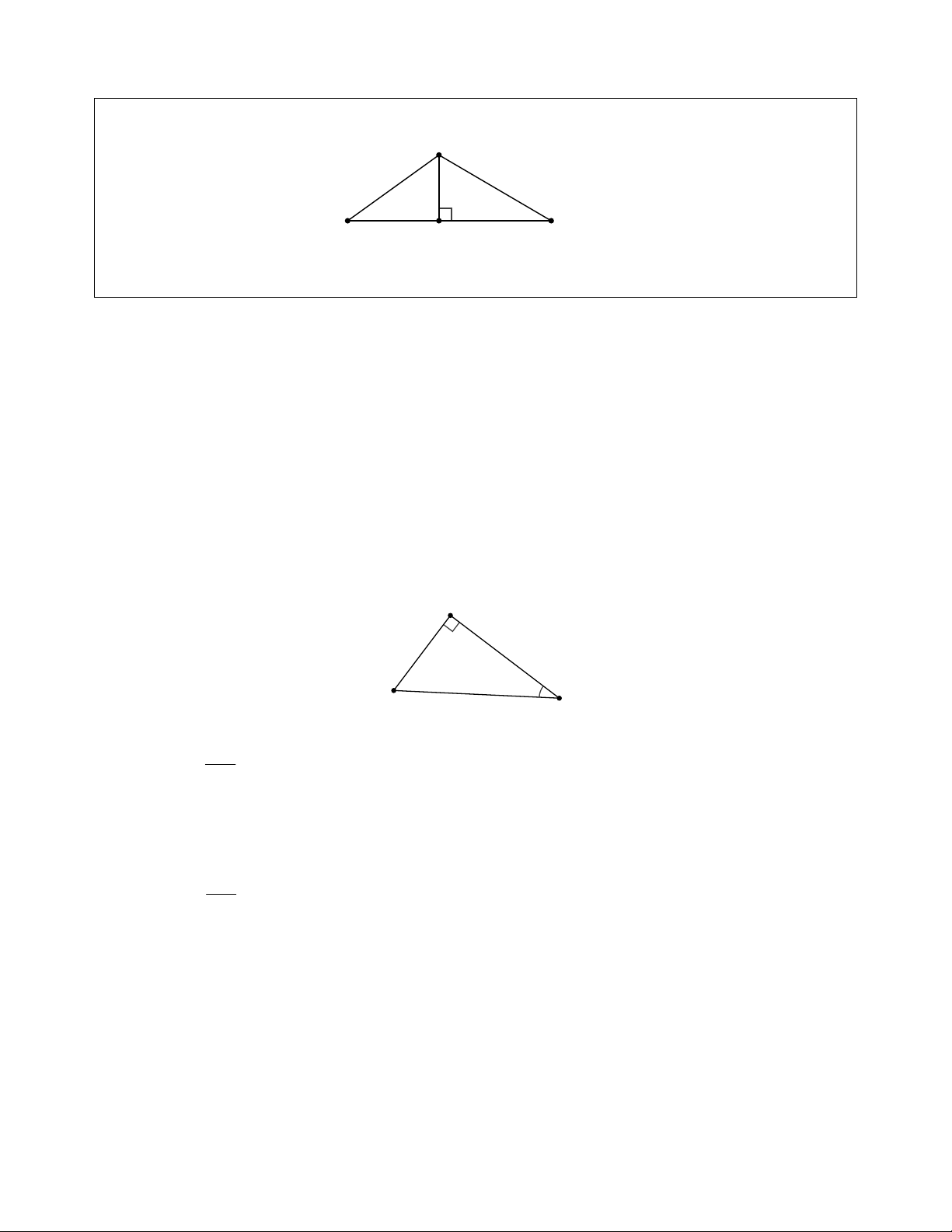
Câu 1: Cho tam giác MNP vuông tại N . Hệ thức nào sau đây là đúng?
A. MN = MP. sin P . B. MN = MP. cos P . C. MN = MP. tan P . D. MN = MP. cot P .
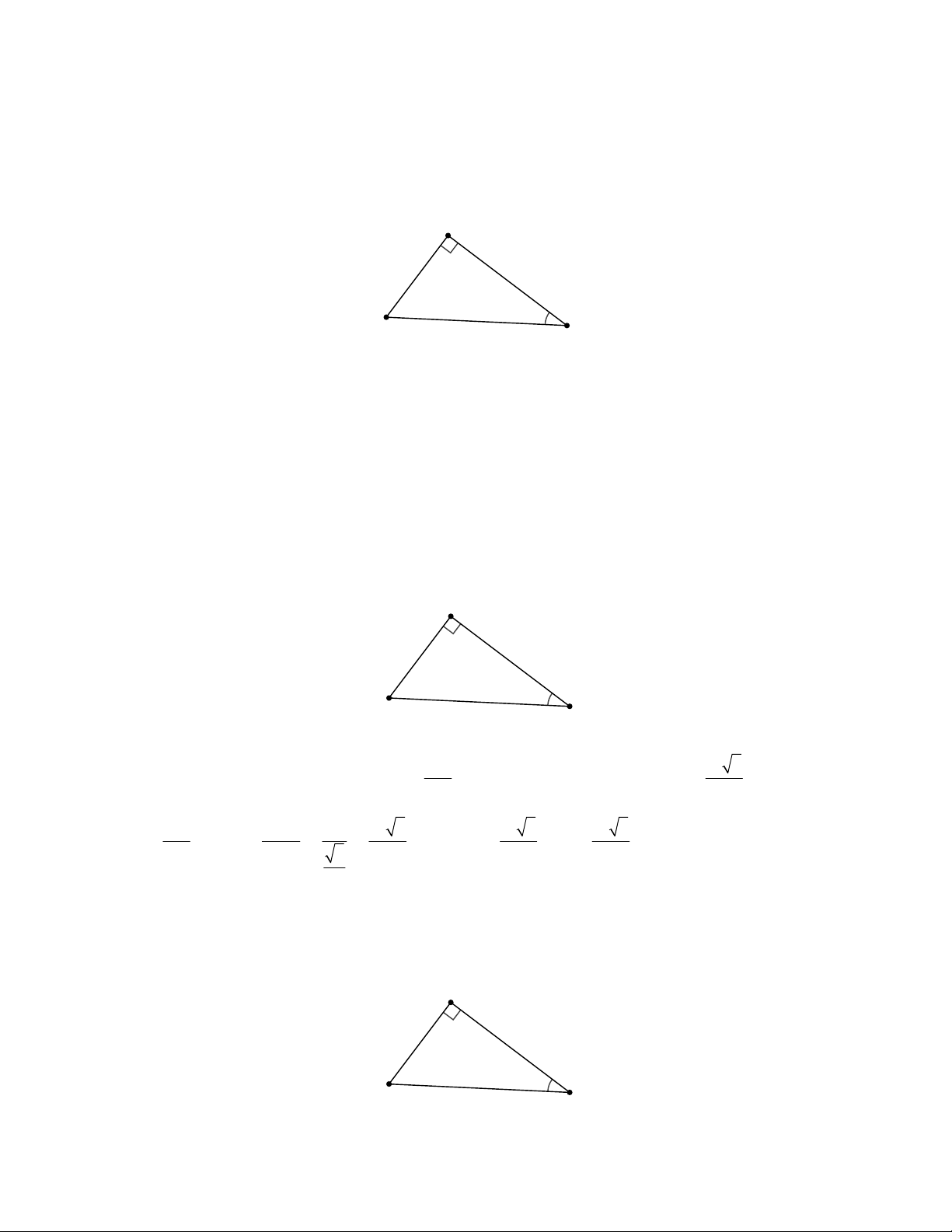
Câu 2: Cho tam giác MNP vuông tại N . Hệ thức nào sau đây là đúng?
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com M N P
A. NP = MP. cos P . B. NP = MN . cos P . B. NP = MN . tan P . D. NP = MP. cot P .
Câu 3: Cho tam giác ABC vuông tại A có BC = a,AC = ,
b AB = c . Chọn khẳng định sai?
A. b = a. sin B = a. cosC .
B. a = c. tan B = c. cotC . C. 2 2 2
a = b + c . D. c = a. sinC = a. cos B .
Câu 4: Cho tam giác ABC vuông tại A có  BC = , a AC = , b AB = ,
c ABC = 50 . Chọn khẳng định đúng?
A. b = c. sin 50 .
B. b = a. tan 50 .
C. b = c. cot 50 .
D. c = b. cot 50 .
Câu 5: Cho tam giác ABC vuông tại A có  AC = 10c ,
m C = 30 . Tính AB;BC . 5 3 20 3 10 3 14 3 A. AB = ;BC = . B. AB = ;BC = . 3 3 3 3 10 3 10 3 20 3 C. AB = ;BC = 20 3 . D. AB = ;BC = . 3 3 3
Câu 6: Cho tam giác ABC vuông tại A có  AC = 20c ,
m C = 60 . Tính AB;BC .
A. AB = 20 3;BC = 40 .B. AB = 20 3;BC = 40 3 .C. AB = 20;BC = 40 .D. AB = 20;BC = 20 3 .
Câu 7: Cho tam giác ABC vuông tại A có  BC = 12 ; cm B = 40 . Tính 
AC;C (làm tròn đến chữ số thập phân thứ hai) A.
AC » 7, 71;C = 40 . B.
AC » 7, 72;C = 50 . C.
AC » 7, 71;C = 50 . D.
AC » 7, 73;C = 50 .
Câu 8: Cho tam giác ABC vuông tại A có  BC = 15 , cm B = 55 . Tính 
AC;C (làm tròn đến chữ số thập phân thứ hai). A.
AC » 12, 29;C = 45 . B.
AC » 12, 29;C = 35 . C.
AC » 12, 2;C = 35 . D.
AC » 12, 92;C = 40 .
Câu 9: Cho tam giác ABC vuông tại A có BC = 15 ,
cm AB = 12cm . Tính  AC;B . A.
AC = 8(cm);B » 3652¢ . B.
AC = 9(cm);B » 3652¢ . C.
AC = 9(cm);B » 37 52  ¢ . D.
AC = 9(cm);B » 36 55  ¢ .
Câu 10: Cho tam giác ABC vuông tại A có BC = 26 ,
cm AB = 10cm . Tính 
AC;B (làm tròn đến độ).
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com A.
AC = 22;C » 67 . B.
AC = 24;C » 66 . C.
AC = 24;C » 67 . D.
AC = 24;C » 68 .
Câu 10: Cho tam giác ABC vuông tại A có AC = 7c ,
m AB = 5cm . Tính  BC;C . A.
BC = 74(cm);C » 3532¢ . B.
BC = 74(cm);C » 3632¢ . C.
BC = 74(cm);C » 3533¢ . D.
BC = 75(cm);C » 3532¢ .
Câu 11: Cho tam giác ABC có AB = 16,AB = 14 và 
B = 60 . Tính BC . A. BC = 10 . B. BC = 11 . C. BC = 9 . D. BC = 12 .
Câu 12: Cho tam giác ABC có AB = 12,AC = 15 và 
B = 60 . Tính BC .
A. BC = 3 3 + 6 .
B. BC = 3 13 + 6 . C. BC = 9 . D. BC = 6 .
Câu 13: Cho tam giác ABC có   B = 60 ,  C = 50 ,
CA = 3, 5cm . Diện tích tam giác ABC gần nhất với
giá trị nào dưới đây? A. 4 . B. 5 . C. 7 . D. 8 .
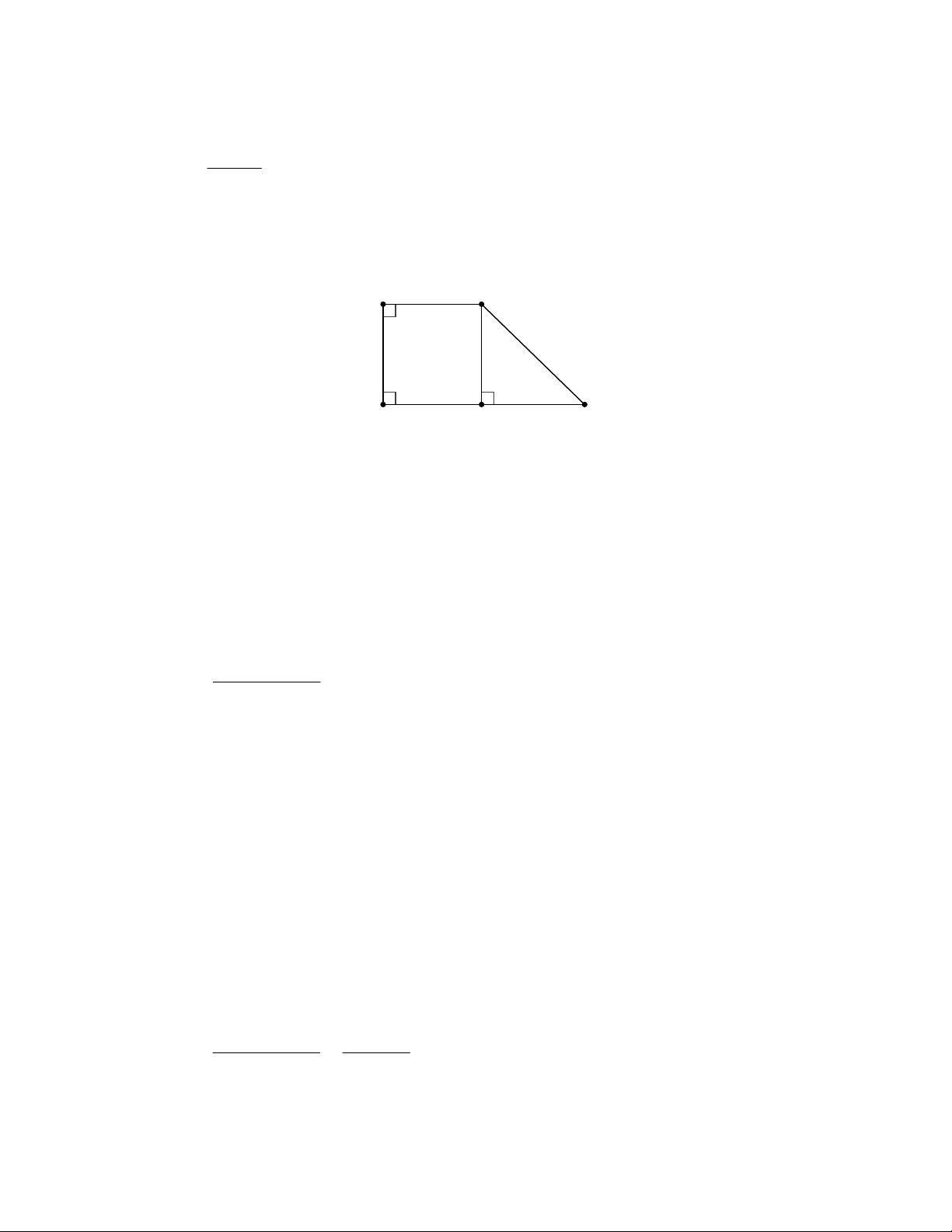
Câu 14: Cho tứ giác ABCD có    A = D = 90 ,  C = 40 ,  AB = 4c ,
m AD = 3cm . Tính diện tích tứ giác
ABCD . (làm tròn đến chữ số thập phân thứ hai). A. 2 17, 34cm . B. 2 17, 4cm . C. 2 17, 54cm . D. 2 17, 54cm .
Câu 15: Cho tứ giác ABCD có    A = D = 90 ,  C = 45 ,  AB = 6c ,
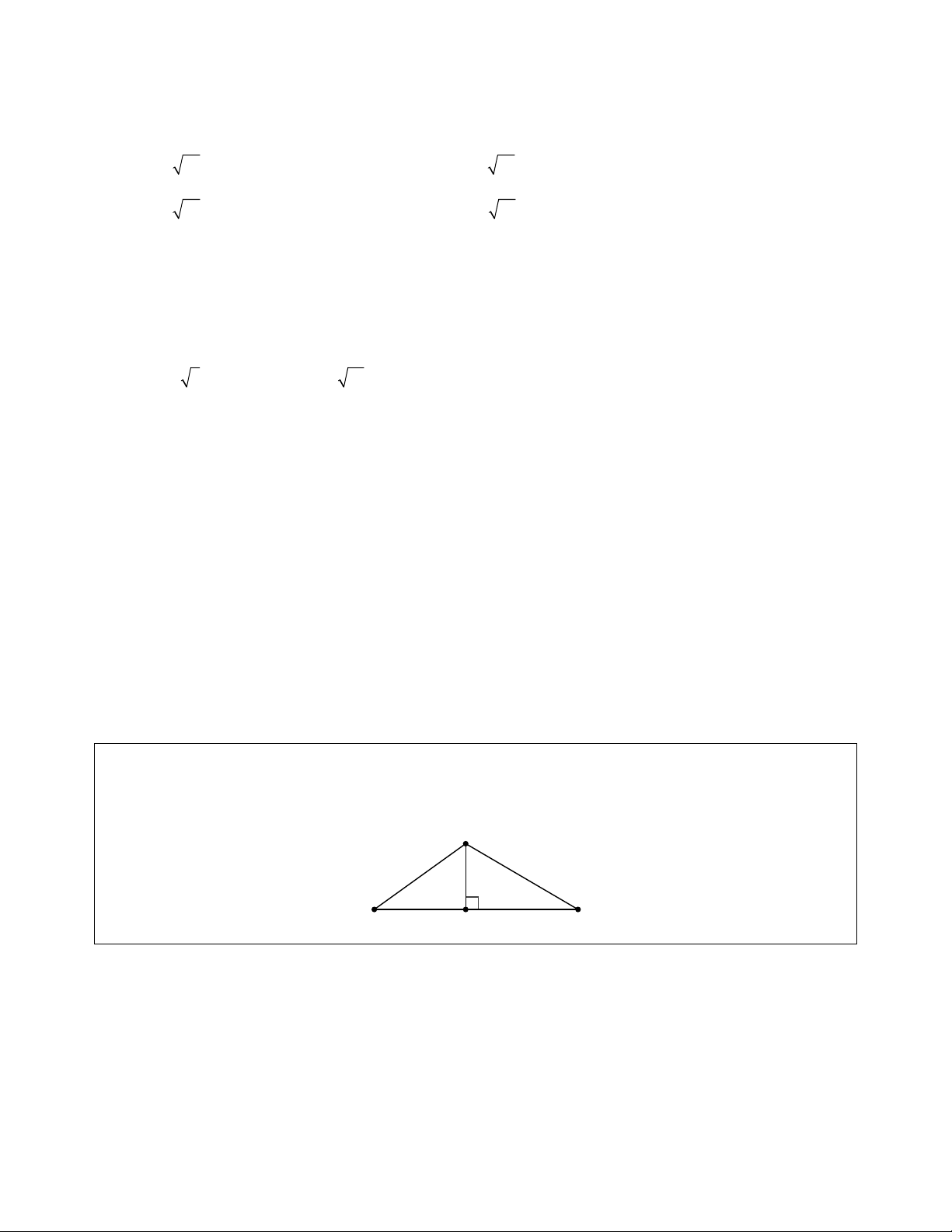
m AD = 8cm . Tính diện tích tứ giác ABCD . A. 2 60cm . B. 2 80cm . C. 2 40cm . D. 2 160cm . Cho tam giác ABC có  BC = 11 , cm ABC = 40 và 
ACB = 30 . Gọi N là chân đường vuông góc hạ từ
A xuống cạnh BC . A B N C
Câu 16: Độ dài AN gần nhất với giá trị nào dưới đây? A. 5 . B. 4 . C. 6 . D. 7 .
Câu 17: Độ dài AC gần nhất với giá trị nào dưới đây? A. 7 . B. 6 . C. 5 . D. 4 .
Câu 18: Diện tích tam giác ABC gần nhất với giá trị nào dưới đây?
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com A. 27 . B. 23 . C. 22 . D. 21 . Cho tam giác ABC có  BC = 9 , cm ABC = 50 và 
ACB = 35 . Gọi N là chân đường vuông góc hạ từ A xuống cạnh BC . A B N C
Câu 19: Độ dài AN gần nhất với giá trị nào dưới đây? A. 5 . B. 4 . C. 2 . D. 3 .
Câu 20: Độ dài AC gần nhất với giá trị nào dưới đây? A. 7 . B. 6 . C. 5 . D. 4 .
Câu 21: Diện tích tam giác ABC gần nhất với giá trị nào dưới đây? A. 13 . B. 15 . C. 16 . D. 25 . HƯỚNG DẪN
1. Lời giải: M N P MN Ta có sin P =
MN = MP. sin P . MP Đáp án cần chọn là A. 2. Lời giải: NP Ta có cotP =
NP = MN. cot P MN Đáp án cần chọn là B. 3. Lời giải:
Cho tam giác ABC vuông tại A có BC = a,AC = ,
b AB = c . Ta có:
+ Theo định lý Pytago ta có 2 2 2
a = b + c nên C đúng.
+ Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
b = a.cinB = a. cosC;c = a. sinC = a. cos B;b = . c tan B = .
c cotC;c = . b tanC = . b cot B . Nên A, D đúng. Đáp án cần chọn là B. 4. Lời giải: A C B
Cho tam giác ABC vuông tại A có BC = a,AC = , b AB = c .
+ Theo hệ thức về cạnh và góc trong tam giác vuông ta có:
b = a.sin B = a.sin 50 ;
c = a.cos B = a cos 50 ;  b = . c tan 50 ;  c = . b cot 50 . Nên D đúng. Đáp án cần chọn là D. 5. Lời giải: A B C AB 10 3
Xét tam giác ABC vuông tại A có: tanC =
AB = AC. tanC = 10. tan 30 = ; AC 3 AC AC 10 20 3 10 3 20 3 cosC =  BC = = = . Vậy AB = ;BC = . BC cosC 3 3 3 3 2 Đáp án cần chọn là D. 6. Lời giải: A B C
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Xét tam giác AB
ABC vuông tại A có: tanC =
AB = AC. tanC = 20. tan 30 = 20 3 ; AC AC AC 20 cosC =  BC = =
= 40 . Vậy AB = 20 3;BC = 40 . BC cosC 1 2 Đáp án cần chọn là A. 7. Lời giải: A C B
Xét tam giác ABC vuông tại A có AC + sin B =
AC = BC. sin B = 12. sin 40 » 7, 71. BC +    
A + B +C = 180  C = 180 - 40 - 90 = 50 . Vậy 
AC » 7, 71;C = 50 . Đáp án cần chọn là C. 8. Lời giải:
Xét tam giác ABC vuông tại A có + AC sin B =
AC = BC. sin B = 15. sin 55 » 12, 29 . BC +    
A + B +C = 180  C = 180 - 55 - 90 = 35 . Vậy 
AC » 12, 29;C = 35 . Đáp án cần chọn là B. 9. Lời giải: A C B
Xét tam giác ABC vuông tại A có:
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com + 2 2 2 2 2 2 2
BC = AB + AC AC = BC -AB = 15 -12 = 9( ) cm . AC + 9 3 sin B = = =   B » 36 5  2¢ . BC 15 5 Vậy 
AC = 9(cm);B » 36 5  2¢ . Đáp án cần chọn là B. 10. Lời giải:
Xét tam giác ABC vuông tại A có: + 2 2 2 2 2 2 2
BC = AB + AC AC = BC -AB = 26 -10 = 24( ) cm . + AC 24 12  sin B = = =  B » 67 . BC 26 13 Vậy 
AC = 24;C » 67 . Đáp án cần chọn là C. 10. Lời giải:
Xét tam giác ABC vuông tại A có: + 2 2 2 2 2
BC = AB + AC = 5 + 7 = 74  BC = 74(cm). + AB 5  tanC = =  C » 3532¢ AC 7 Vậy 
BC = 74(cm);C » 3532¢ . Đáp án cần chọn là A. 11. Lời giải: A 60° B H C
Kẻ đường cao AH .
Xét tam giác vuông ABH , ta có: 1
BH = AB. cos B = AB. cos 60 = 16. = 8 2 3
AH = AB. sin B = AB. sin 60 = 16. = 8 3 . 2
17. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Áp dụng định lý Pytago vào tam giác vuông AHC ta có: 2 2 2 2 2
HC = AC - AH = 14 - (8 3) = 196 - 192 = 4 . Suy ra HC = 2 .
Vậy BC = CH + HB = 2 + 8 = 10 . Đáp án cần chọn là A. 12. Lời giải: A 60° B H C
Kẻ đường cao AH .
Xét tam giác vuông ABH , ta có: 1
BH = AB. cos B = AB. cos 60 = 12. = 6 2 3
AH = AB. sin B = AB. sin 60 = 12. = 6 3 . 2
Áp dụng định lý Pytago vào tam giác vuông AHC ta có: 2 2 2 2 2
HC = AC - AH = 15 - (6 3) = 117 . Suy ra HC = 3 13 .
Vậy BC = CH + HB = 3 13 + 6 . Đáp án cần chọn là B. 13. Lời giải: A B D C
Kẻ đường cao AD .
Xét tam giác vuông ACD , ta có: AD = AC.sinC = 3, 5.sin 50 » 2, 68cm
CD = AC.cosC = 3, 5. cos 50 » 2,25cm .
18. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Xét tam giác ABD , có BD = AD.cotB » 2, 68.cot 60 » 1, 55cm .
Suy ra BC = BD +CD = 3, 8 . Do đó AD.BC 2 S = » 5, 09cm . ABC 2 Đáp án cần chọn là B. 14. Lời giải: A B D E C Vì  
A = D = 90  AD BC hay ABCD là hình thang vuông tại , A D .
Kẻ BE ^ DC tại E .
Tứ giác ABED có ba góc vuông   
A = D = E = 90 nên ABED là hình chữ nhật.
Suy ra DE = AB = 4 ;
cm BE = AD = 3cm .
Xét tam giác BEC vuông tại E có EC = BE. cot 40 » 3, 56(cm)  DC = DE + EC » 7, 56(cm) .
(AB +CD).AD Do đó 2 S = » 17, 34cm . ABCD 2 Đáp án cần chọn là A. 15. Lời giải: Vì  
A = D = 90  AD BC hay ABCD là hình thang vuông tại , A D .
Kẻ BE ^ DC tại E .
Tứ giác ABED có ba góc vuông   
A = D = E = 90 nên ABED là hình chữ nhật.
Suy ra DE = AB = 6 ;
cm BE = AD = 8cm .
Xét tam giác BEC vuông tại E có 
BCE = 45 nên BEC vuông cân tại E .
EC = BE = 8cm DC = DE + EC = 6 + 8 = 14cm .
(AB +CD).AD (6 + 14).8 Do đó 2 S = = = 80cm . ABCD 2 2 Đáp án cần chọn là B.
19. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 16. Lời giải:
Đặt BN = x (0 < x < 11)  NC = 11 - x .
Xét tam giác ABN vuông tại N có AN = BN. tan B = x. tan 40
Xét tam giác ACN vuông tại N có AN = CN. tanC = (11 - x). tan 30
Nên x tan 40 = (11- x). tan 30  x » 4, 48 (thoả mãn).
Khi đó AN = BN. tan B = 4, 48. tan 40 » 3, 76(cm) . Đáp án cần chọn là B. 17. Lời giải:
Theo câu trước ta có AN » 3, 76 Xét tam giác AN AN
ACN vuông tại N có sinC =  AC = = 7, 52 AC sinC Đáp án cần chọn là A. 18. Lời giải:
Theo kết quả các câu trước ta có AN.BC AN » 3, 76 nên 2 S = = 20, 68cm . ABC 2 Đáp án cần chọn là D. 19. Lời giải:
Đặt BN = x (0 < x < 9)  NC = 9 - x .
Xét tam giác ABN vuông tại N có AN = BN. tan B = x. tan 50
Xét tam giác ACN vuông tại N có AN = CN.tanC = (9 - x). tan 35
Nên x tan 50 = (9 - x). tan 35  x » 3, 33 (thoả mãn).
Khi đó AN = BN. tan B = 3, 33. tan 35 » 2, 79 . Đáp án cần chọn là D. 20. Lời giải:
Theo câu trước ta có AN » 2, 79 AN AN
Xét tam giác ACN vuông tại N có sinC =  AC = » 4, 87 AC sinC Đáp án cần chọn là C. 21. Lời giải:
20. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Theo kết quả các câu trước ta có AN.BC AN » 2, 79 nên 2 S = = 12, 555cm . ABC 2 Đáp án cần chọn là A.
‐‐‐‐‐‐‐‐‐‐Toán Học Sơ Đồ‐‐‐‐‐‐‐‐‐
21. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com