Chuyên đề tỉ số lượng giác của góc nhọn, hệ thức về cạnh và góc trong tam giác vuông

Tài liệu gồm 30 trang, được biên soạn bởi tác giả Toán Học Sơ Đồ, tổng hợp kiến thức trọng tâm, phân dạng và hướng dẫn giải các dạng bài tập tự luận & trắc nghiệm chuyên đề tỉ số lượng giác của góc nhọn, hệ thức về cạnh và góc trong tam giác vuông. Mời bạn đọc đón xem.

267 134 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hệ thức lượng trong tam giác vuông

Môn: Toán 9

Thông tin:

30 trang 8 tháng trước

Tác giả:

Profile Hà Việt Anh
1.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
CHUYÊN ĐỀ TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN, HỆ THỨC VỀ CẠNH VÀ GÓC
TRONG TAM GIÁC VUÔNG
A.KIẾN THỨC CẦN NHỚ
Một số tính chất của các
tỉ số lượng giác
Cho hai góc
,

phụ nhau. Khi đó:
sin cos ; cos sin ;


tan cot ; cot tan .


Cho góc nhọn
. Ta có:
0sin 1;0cos 1;


22
sin cos 1; tan . cot 1;


sin cos
tan ; cot .
cos sin




B.CÁC DẠNG BÀI TẬP CƠ BẢN VÀ NÂNG CAO
Dạng 1: Các bài toán tính toán
Phương pháp giải
Bước 1: Đặt độ dài cạnh, góc bằng ẩn.
Bước 2: Thông qua giả thiết và các hệ thức lượng lập phương trình chứa ẩn.
Bước 3: Giải phương trình, tìm ẩn số. Từ đó tính độ dài đoạn thẳng hoặc góc cần tìm.
Bài tập minh họa
Câu 1: Tam giác ABC có
60 ; 28 ; 35AABcmACcm
. Tính độ dài BC.
Lời giải
2.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Kẻ
BH AC
(
HAC
)
Xét tam giác vuông AHB vuông tại H có:

1
. 28. 60 28. 14
2
AH AB cos A cos cm

3
.sin 28.sin 60 28. 14 3
2
BH AB A cm

35 14 21HC AC AH cm
222
588 441 1029BC BH HC
721BC
Vậy

721BC cm
Chú ý
Bằng cách tính tương tự như trên có: tam giác ABC có
60 ; ;AABaACb
thì
222
BC a b ab
;
3
4
ABC
Sab
.
Câu 2: Cho hình vẽ sau biết
45 ; 120 ; 8 ; 5QPT PTQ QT cm TR cm
.
a) Tính PT.
b) Tính diện tích tam giác PQR.
Lời giải
Kẻ
QM PR
(M thuộc tia đối tia TP).
3.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Có

180 180 180 120 60PTQ QTM QTM PTQ
Xét tam giác vuông QTM có:

3
.sin 8.sin60 8. 4 3
2
QM QT QTM cm

1
.cos 8.cos 60 8. 4
2
TM QT QTM cm
TM TR
M nằm giữa T và R.
Xét tam giác vuông QPM có:

43 43
43
tan 45 1
tan
QM
PM cm
QPM



43 4 4 3 1PT PM TM cm


4315431PR PT TR cm


2
11
. 43.43 1 6 23
22
PQR
SQMPR cm
Vậy

43 1PR cm ;

2
623
PQR
Scm
.
Câu 3: Cho
ABC
có
60 ; 80BC
. Tính số đo góc tạo bởi đường cao AH và trung tuyến AM.
Lời giải
Gọi góc tạo bởi đường cao AH và trung tuyến AM là
.
Xét tam giác AMH vuông tại H có
tan tan .
MH
MH AH
AH


Lại có:

2
2
BH HC
BH HC BM MH MC MH MH MH

Mà
tan
AH
BH
B
(hệ thức lượng trong tam giác vuông AHB)
tan
AH
CH
C
(hệ thức lượng trong tam giác vuông AHC).
4.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
11 11
..
11 1
tan tan
tan tan
tan 11 20
222
tan
tan
AH AH
CC
BB
MH
AH
C
B

 

 

 



Vậy số đo góc tạo bởi đường cao AH và trung tuyến AM xấp xỉ bằng
11 20
.
Câu 4: Tính chu vi và diện tích hình thang cân ABCD biết hai cạnh đáy
12 , 18 , 75AB cm CD cm ADC
.
Lời giải
Diện tích hình thang được tính bởi công thức

1
2
ShABCD
(Trong đó h là chiều cao của hình thang).
Đối với bài tập này, chúng ta đã biết độ dài hai cạnh đáy. Do vậy, ta cần tìm chiều cao.
Kẻ
,AH CD BK CD
.
Do ABCD là hình thang cân nên
12 , 3
2
CD AB
HK AB cm DH KC cm

.
Trong tam giác AHD vuông tại H ta có:
tan tan 75 11,196
3
AH AH
DAHcm
DH

Từ đó,
 
2
11
. .11,196. 12 18 167,94
22
ABCD
SAHABCD cm
.
Để tính chu vi hình thang, ta cần tính AD.
Áp dụng định lý Py-ta-go cho tam giác vuông ADH ta có:
222
134,35AD AH HD cm
. Suy ra
11,59AD cm
.
Ngoài ra, ta cũng có thể sử dụng công thức tỉ số lượng giác của góc trong tam giác vuông ADH để tính
AD.
Do đó, chu vi hình thang cân ABCD là
12 11,59 18 11,59 53,18AB BC CD DA cm
.
Dạng 2: Chứng minh đẳng thức, mệnh đề
Phương pháp giải
Đưa mệnh đề về dạng đẳng thức, sử dụng hệ thức lượng và một số kiến thức đã học biến đổi các vế trong
biểu thức, từ đó chứng minh các vế bằng nhau.
5.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Bài tập minh họa
Câu 1: Cho
ABC
có
60A . Kẻ
BH AC
;
CK AB
.
a) Chứng minh
.KH BC cosA .
b) Trung điểm của BC là M. Chứng minh
MKH
là tam giác đều.
Lời giải
a) Xét
AHB
và
AKC
vuông tại H, K có: chung góc
BAC
Suy ra

.
AB AH
AHB AKC g g
AC AK
 ∼
Xét
AHK
và
ABC
chung góc
BAC và
AB AH
AC AK
Suy ra
AH KH
AHK ABC
AB BC
∼
..
AH
HK BC BC cosA
AB

.
b) Theo câu a) có
11
..
22
HK BC cosBAC BC BC
(1).
Mặt khác xét tam giác HBC vuông tại H có: HM là trung tuyến ứng với cạnh huyền BC
1
2
HM BC
(2).
Tương tự có
1
2
KM BC
(3).
Từ (1), (2) và (3) có
HM HK KM
suy ra
HKM
là tam giác đều.
Câu 2: Cho tam giác ABC vuông tại B. Lấy điểm M trên cạnh AC. Kẻ
,
AH BM CK BM
a) Chứng minh:
.tanCK BH BAC
b) Chứng minh:
2
.tanMC BH BAC
MA BK
Lời giải
6.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
a) Xét
AHB
và
BKC
vuông tại H và K có:
HBA BCK (cùng phụ với
CBH ).

...tan
CK BC BC
AHB BKC g g CK BH BH BAC
BH AB AB
 ∼
b) Theo câu a) ta có:
.tanCK BH BAC
Mà
MC CK
MA AH
(vì
//CK AH
)
.tanMC BH BAC
MA AH

(1)
Mặt khác
1tan
.
BK BC BC BAC
AHB BKC
AH AB AH AB BK BK

∼
(2)
Từ (1) và (2) suy ra
2
.tanMC BH BAC
MA BK
Câu 3: Cho hình thoi ABCD có
120BAD , tia Ax tạo với tia AB góc
15BAx , cắt BC, CD lần
lượt tại M, N. Chứng minh:
22 2
11 4
3AM AN AB

Lời giải
Từ A dựng đường thẳng vuông góc với AN cắt CD tại P, hạ
AH CD

HCD
.
Có

120 15 90 120 15 90 15BAD BAM MAP PAD PAD PAD    
Xét
ABM
và
ADP
có:
MAB PAD
(theo trên)
BA AD
(tính chất hình thoi)
MBA PDA
(tính chất hình thoi)

..ABM ADP g c g AM AP 
Áp dụng hệ thức lượng vào tam giác vuông NAP vuông tại A đường cao AH, ta có:
22 2 22 2
11 1 1 1 1
AP AN AH AM AN AH
 
Mà
33
sin . sin 60 . .
22
AH ADH AD AD AD AB
7.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Từ (1) và (2) ta có:
2
22 22 2
11 1 11 4
3
3
2
AM AN AM AN AB
AB
 



Vậy
22 2
11 4
3AM AN AB

.
8.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
C.TRẮC NGHỆM RÈN LUYỆN PHẢN XẠ
Câu 1: Cho tam giác
MNP
vuông tại
M
. Khi đó
cos MNP
bằng
A.
MN
NP
. B.
MP
NP
. C.
MN
MP
. D.
MP
MN
.
Câu 2:
Cho tam giác
MNP
vuông tại
M
. Khi đó
tan MNP
bằng:
A.
MN
NP
. B.
MP
NP
. C.
MN
MP
. D.
MP
MN
.
Câu 3: Cho
a
là góc ngọn bất kỳ. Chọn khẳng định đúng.
A.
sin cos 1aa+=
. B.
22
sin cos 1aa+=
.C.
33
sin c os 1aa+=
.D.
sin cos 1aa-=
.
Câu 4: Cho
a
là góc nhọn bất kỳ. Chọn khẳng định sai.
A.
sin
tan
cos
a
a
a
=
. B.
cos
cot
sin
a
a
a
=
. C.
tan .cot 1aa=
. D.
22
tan 1 cosaa-=
.
Câu 5: Cho
a
và
b
là hai góc nhọn bất kỳ thoả mãn
90ab+=
. Khẳng định nào sau đây là đúng?
A.
tan sinab=
. B.
tan cotab=
. C.
tan cosab=
. D.
tan tanab=
.
Câu 6: Khẳng định nào sau đây là đúng? Cho hai góc phụ nhau thì
A.
sin
góc nọ bằng cosin góc kia. B. sin hai góc bằng nhau.
C. tan góc nọ bằng cotan góc kia. D. Cả A, C đều đúng.
Câu 7: Cho tam giác
ABC
vuông tại
C
có
1, 2AC cm BC cm==
. Tính các tỉ số lượng giác
sin ; cosBB
.
A.
123
sin ; cos
3
3
BB==
. B.
525
sin ;cos
55
BB==
.
C.
12
sin ;cos
2
5
BB==
. D.
25 5
sin ; cos
55
BB==
.
P
M
N
P
M
N
9.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Câu 8: Cho tam giác
ABC
vuông tại
C
có
1, 2 , 0, 9BC cm AC cm==
. Tính các tỉ số lượng giác
sin ; cosBB
.
A.
sin 0, 6; cos 0, 8BB==
. B.
sin 0, 8; cos 0, 6BB==
.
C.
sin 0, 4;cos 0, 8BB==
. D.
sin 0,6;cos 0,4BB==
.
Câu 9: Cho tam giác
ABC
vuông tại
A
có
8, 6BC cm AC cm==
. Tính tỉ số lượng giác
tanC
(làm
tròn đến chữ số thập phân thứ 2).
A.
tan 0, 87C »
. B.
tan 0, 86C »
. C.
tan 0, 88C »
. D.
tan 0, 89C »
.
Câu 10: Cho tam giác
ABC
vuông tại
A
có
9, 5BC cm AC cm==
. Tính tỉ số lượng giác
tanC
(làm
tròn đến chữ số thập phân thứ 1)
A.
tan 0, 67C »
. B.
tan 0,5C »
. C.
tan 1, 4C »
. D.
tan 1, 5C »
.
Câu 11: Cho tam giác
ABC
vuông tại
A
, đường cao
AH
có
13 , 0, 5AB cm BH dm==
. Tính tỉ số lượng
giác
sinC
(làm tròn đến chữ số thập phân thứ 2)
A.
sin 0, 35C »
. B.
sin 0, 37C »
. C.
sin 0, 39C »
. D.
sin 0, 38C »
.
Câu 12: Cho tam giác
ABC
vuông tại
A
, đường cao
AH
có
15 , 6AC cm CH cm==
. Tính tỉ số lượng
giác
cos B
.
A.
5
sin
21
C =
. B.
21
sin
5
C =
. C.
2
sin
5
C =
. D.
3
sin
5
C =
.
Câu 13: Cho tam giác
ABC
vuông tại
A
, đường cao
AH
có
4, 3CH cm BH cm==
. Tính tỉ số lượng
giác
cosC
(làm tròn đến chữ số thập phân thứ 2).
A.
cos 0, 76C »
. B.
cos 0, 77C »
. C.
cos 0, 75C »
. D.
cos 0, 78C »
.
Câu 14: Cho tam giác
ABC
vuông tại
A
, đường cao
AH
có
11 , 12CH cm BH cm==
. Tính tỉ số lượng
giác
cosC
(làm tròn đến chữ số thập phân thứ 2).
A.
cos 0, 79C »
. B.
cos 0, 69C »
. C.
cos 0, 96C »
. D.
cos 0, 66C »
.
Câu 15: Cho tam giác
ABC
vuông tại
A
. Hãy tính
tanC
biết rằng
tan 4B =
.
A.
1
tan
4
C =
. B.
tan 4C =
. C.
tan 2C =
. D.
1
tan
2
C =
.
Câu 16: Cho tam giác
ABC
vuông tại
A
. Hãy tính
tanC
biết rằng
cot 2B =
.
A.
1
tan
4
C =
. B.
tan 4C =
. C.
tan 2C =
. D.
1
tan
2
C =
.
Câu 17: Cho tam giác
ABC
vuông tại
A
có
7
5,cot
8
AB cm C==
. Tính độ dài các đoạn thẳng
AC
và
BC
(làm tròn đến chữ số thập phân thứ 2)
A.
4, 39 ( ); 6, 66 ( )AC cm BC cm»»
. B.
4, 38( ); 6, 65 ( )AC cm BC cm»»
.
10.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
C.
4, 38 ( ); 6, 64 ( )AC cm BC cm»»
. D.
4, 37 ( ); 6, 67 ( )AC cm BC cm»»
.
Câu 18: Cho tam giác
ABC
vuông tại
A
có
5
9,tan
4
AB cm C==
. Tính độ dài các đoạn thẳng
AC
và
BC
. (làm tròn đến chữ số thập phân thứ 2).
A.
11, 53; 7, 2AC BC==
. B.
7; 11, 53AC BC=»
.
C.
5, 2; 11AC BC=»
. D.
7, 2; 11, 53AC BC=»
.
Câu 19: Cho
a
là góc nhọn. Tính
sin , cotaa
biết
2
cos
5
a =
.
A.
21 3 21
sin ; cot
25 21
aa==
. B.
21 5
sin ; cot
5
21
aa==
.
C.
21 3
sin ; cot
3
21
aa==
. D.
21 2
sin ; cot
5
21
aa==
.
Câu 20: Tính
sin , tanaa
biết
3
cos
4
a
=
.
A.
43
sin ; tan
4
7
aa==
. B.
73
sin ; tan
4
7
aa==
.
C.
77
sin ; tan
43
aa==
. D.
77
sin ; tan
34
aa==
.
Câu 21: Không dùng bảng số và máy tính, hãy so sánh
cot 50
và
cot 46
.
A.
cot 46 cot 50=
. B.
cot 46 cot 50>
. C.
cot 4 6 cot 50<
. D.
cot 46 cot 50³
.
Câu 22: Không dùng bảng số và máy tính, hãy so sánh
sin 20
và
sin 70
.
A.
sin 20 sin 70<
. B.
sin 20 sin 70>
. C.
sin 20 sin 7 0=
. D.
sin 20 sin 70³
.
Câu 23: Sắp xếp các tỉ số lượng giác
sin 40 , cos 67 , sin 35 , cos 44 35 , sin 28 10
¢¢

theo thứ tự tăng dần.
A.
cos 67 sin 35 sin 28 10 sin 40 cos 45 25
¢¢
< < < <
.
B.
cos 67 cos 45 25 sin 40 sin 28 10 sin 35
¢¢
< < < <
.
C.
cos67sin2810sin35sin40cos4525
¢¢
> > > >
.
D.
cos 67 sin 28 10 sin 3 5 sin 40 cos 45 25
¢¢
< < < <
.
Câu 24: Sắp xếp các tỉ số lượng giác
tan 43 , cot 71 , tan 38 , cot 69 15 , tan 28
¢
 
theo thứ tự tăng dần.
A.
cot 71 cot 60 15 tan 28 tan 38 tan 43
¢
< < < <
.
B.
cot 60 15 cot 71 tan 28 tan 38 tan 43
¢
< < < <
.
C.
tan 28 tan 38 tan 43 cot 60 15 cot71
¢
< < < <
.
D.
cot 60 15 tan 28 tan 38 tan 43 cot 71
¢
< < < <
.
Câu 25: Tính giá trị biểu thức
22 222
sin 1 sin 2 ... sin 88 sin 89 sin 90A = + + + + +
11.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
A.
46A =
. B.
93
2
A =
. C.
91
2
A =
. D.
45A =
.
Câu 26: Tính giá trị biểu thức
22 22
sin 10 sin 20 ... sin 70 sin 80+ + + +
A.
0
. B.
8
. C.
5
. D.
4
.
Câu 27: Cho
a
là góc nhọn bất kỳ. Khi đó
66 22
sin cos 3 sin cosaa aa++
bằng
A.
22
13sin.cosC aa=-
. B.
1
. C.
22
sin .cosC aa=
. D.
22
3sin .cos 1C aa=-
.
Câu 28: Cho
a
là góc nhọn bất kỳ. Khi đó
44
sin cosC aa=+
bằng:
A.
22
12sin .cosC aa=-
. B.
1C =
.
C.
22
sin . cosC aa=
. D.
22
12sin.cosC aa=+
.
Câu 29: Cho
a
là góc nhọn bất kỳ. Rút gọn
22 2
(1 sin ).cot 1 cotP aa a=- +-
ta được:
A.
2
sinP a=
. B.
2
cosP a=
. C.
2
tanP a=
. D.
2
2sinP a=
.
Câu 30: Cho
a
là góc nhọn bất kỳ. Cho
22 22
(1 sin ). tan (1 cos ). cotP
aa aa
=- +-
, chọn kết luận đúng.
A.
1P >
. B.
1P <
. C.
1P =
. D.
2
2sinP a=
.
Câu 31: Cho
a
là góc nhọn bất kỳ. Biểu thức
22
cos sin
cos .sin
Q
aa
aa
-
=
bằng:
A.
cot tanQ aa=-
. B.
cot tanQ aa=+
. C.
tan cotQ aa=-
. D.
2tanQ a=
.
Câu 32: Chọn
a
là góc nhọn bất kỳ. Biểu thức
2
2
1sin
1sin
Q
a
a
+
=
-
.
A.
2
1tanQ
a
=+
. B.
2
12tanQ
a
=+
. C.
2
12tanQ
a
=-
. D.
2
2tanQ
a
=
.
Câu 33: Cho
tan 2a =
. Tính giá trị của biểu thức
2sin cos
cos 3 si n
G
aa
aa
+
=
-
.
A.
1G =
. B.
4
5
G =-
. C.
6
5
G =-
. D.
1G =-
.
Câu 34: Cho tam giác nhọn
ABC
hai đường cao
AD
và
BE
cắt nhau tại
H
. Biết
:3:2HD HA =
. Khi
đó
tan . tanABC ACB
bằng:
A.
3
. B.
5
. C.
3
5
. D.
5
3
.
Câu 35: Cho tam giác nhọn
ABC
hai đường cao
AD
và
BE
cắt nhau tại
H
. Biết
:1:2HD HA =
. Khi
đó
tan . tanABC ACB
bằng:
A.
2
. B.
3
. C.
1
. D.
4
.
Câu 36: Tính các giá trị lượng giác còn lại của góc
a
, biết
3
sin
5
a
=
.
A.
334
cos , tan , cot
445
aaa===
. B.
434
cos , tan , cot
543
aaa===
.
12.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
C.
434
cos , tan , cot
545
aaa
===
. D.
344
cos , tan , cot
453
aaa
===
.
Câu 37: Cho
a
là góc nhọn bất kỳ. Tính
cot a
biết
5
sin
13
a =
.
A.
12
cot
5
a
=
. B.
11
cot
5
a
=
. C.
5
cot
12
a
=
. D.
13
cot
5
a
=
.
Câu 38: Tính giá trị biểu thức
tan 10 . tan 20 . tan 30 ..... t an 80B =
.
A.
44B =
. B.
1B =
. C.
45B =
. D.
2B =
.
Câu 39: Tính giá trị biểu thức
tan 1 . tan 2 . tan 3 ..... tan 88 . tan 89B =
A.
44B =
. B.
1B =
. C.
45B =
. D.
2B =
.
Câu 40: Cho kết luận đúng về giá trị biểu thức
22
2
cos 3 sin
3sin
B
aa
a
-
=
-
biết
tan 3a =
.
A.
0
B
>
. B.
0
B
<
. C.
01
B
<<
. D.
1B =
.
HƯỚNG DẪN
1. Lời giải:
Ta có
cos
MN
MNP
NP
=
Đáp án cần chọn là A.
2. Lời giải:
Ta có
tan
MP
MNP
MN
=
.
Đáp án cần chọn là D.
3. Lời giải:
Chọn
a
là góc bất kỳ, khi đó
22
sin cos 1aa+=
Đáp án cần chọn là B.
4. Lời giải:
Chọn
a
là góc nhọn bất kỳ, khi đó:
22
sin cos 1aa+=
;
tan .cot 1aa=
sin cos
tan ; cot
cos sin
aa
aa
aa
==
;
2
2
1
1tan
cos
a
a
+=
;
2
2
1
1cot
sin
a
a
+=
.
Đáp án cần chọn là D.
13.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
5. Lời giải:
Với hai góc
,ab
mà
90ab+=
Ta có:
sin cos ; cos sin ; tan cot ; cot tanabababa b====
.
Đáp án cần chọn là B.
6. Lời giải:
Với hai góc phụ nhau thì sin góc nọ bằng sin góc kia và tan góc nọ bằng cotan góc kia.
Đáp án cần chọn là D.
7. Lời giải:
Theo định lý Pytago ta có:
222 22
12 5AB AC BC AB=+=+=
.
Xét tam giác
ABC
vuông tại
C
có
15
sin
5
5
AC
B
AB
===
;
225
cos
5
5
BC
B
AB
===
.
Đáp án cần chọn là B.
8. Lời giải:
Theo định lý Pytago ta có:
222 22
0, 9 1, 2 1 , 5AB AC BC AB=+= +=
Xét tam giác
ABC
vuông tại
C
có
0, 9 3
sin 0, 6
1, 5 5
AC
B
AB
====
và
1, 2 4
cos 0, 8
1, 5 5
BC
B
AB
====
.
Đáp án cần chọn là A.
9. Lời giải:
1
2
B
C
A
0,9
1,2
B
A
C
6
8
B
C
A
14.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Theo định lý Pytago ta có:
222 22
86 5,29BC AC AB AB=+=-»
.
Xét tam giác
ABC
vuông tại
C
có
5, 29
tan 0, 88
6
AB
C
AC
=» »
.
Đáp án cần chọn là C.
10. Lời giải:
Theo định lý Pytago ta có:
222 22
95 214BC AC AB AB=+=-=
.
Xét tam giác
ABC
vuông tại
C
có
214
tan 1, 5
5
AB
C
AC
== »
.
Đáp án cần chọn là D.
11. Lời giải:
Đổi
0, 5 5dm cm=
Xét tam giác
ABC
vuông tại
A
, theo hệ thức lượng
trong tam giác vuông ta có:
22
2
13
.33,8
5
AB
AB BH BC BC cm
BH
====
13
sin 0, 38
33, 8
AB
C
BC
==»
Đáp án cần chọn là D.
12. Lời giải:
Xét tam giác
AHC
vuông tại
H
, theo định lý Pytago ta có:
22222
15 6 189 3 21AH AC CH AH=-=-==
321 21
sin
15 5
AH
C
AC
== =
Mà tam giác
ABC
vuông tại
A
nên

,BC
là hai góc phụ nhau. Do đó
21
cos sin
5
BC==
.
Đáp án cần chọn là B.
13. Lời giải:
H
B
A
C
15.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Xét tam giác
ABC
vuông tại
A
có
7
BC BH CH cm
=+=
Theo hệ thức lượng trong tam giác vuông ta có
22
.4.75,29AC CH BC AC AC cm==»
5, 29
cos 0, 76
7
AC
C
BC
==»
.
Đáp án cần chọn là A.
14. Lời giải:
Xét tam giác
ABC
vuông tại
A
có
11 12 23BC BH C H cm=+=+=
.
Theo hệ thức lượng trong tam giác vuông ta có:
22
. 11.23 253 253AC CH BC AC AC cm====
253
cos 0, 69
23
AC
C
BC
== »
.
Đáp án cần chọn là B.
15. Lời giải:
Vì tam giác
ABC
vuông tại
A
nên

90 cot tan 4BC C B+= = =
Mà
1
cot .tan 1 tan
4
CC C= =
.
Đáp án cần chọn là A.
16. Lời giải:
Vì tam giác
ABC
vuông tại
A
nên

90 tan cot 2BC C B+= = =
.
Đáp án cần chọn là C.
17. Lời giải:
Vì tam giác
ABC
vuông tại
A
nên
735
cot .cot 5 . 4, 38
88
AC
CACABC cm
AB
== ==»
.
Theo định lý Pytago ta có
2222 2
54,38 6,65BC AB AC BC=+=+ »
.
H
B
A
C
B
C
A
16.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy
4, 38( ); 6, 65 ( )AC cm BC cm»»
.
Đáp án cần chọn là B.
18. Lời giải:
Vì tam giác
ABC
vuông tại
A
nên
5
tan : tan 9 : 7,2
4
AB
CACABC cm
AC
== = =
Theo định lý Pytago ta có
22222
941
9 7,2 132, 84 11, 53
5
BC AB AC BC=+=+= = »
.
Vậy
7, 2; 11, 53AC BC=»
.
Đáp án cần chọn là D.
19. Lời giải:
Ta có
22 2 2
421
sin cos 1 sin 1 cos 1
25 25
aa a a
+==-=-=
21
sin
5
a=
.
Lại có
2
cos 2
5
cot
sin
21 21
5
a
a
a
===
.
Vậy
21 2
sin ; cot
5
21
aa
==
.
Đáp án cần chọn là D.
20. Lời giải:
Ta có
22 2 2
97
sin cos 1 sin 1 cos 1
16 16
aa a a+==-=-=
7
sin
4
a=
.
Lại có
7
sin 7
4
tan
cos 3 3
4
a
a
a
===
.
Vậy
77
sin ; tan
43
aa==
.
Đáp án cần chọn là C.
21. Lời giải:
Vì
46 50 cot 46 cot 50< >
.
Đáp án cần chọn là B.
22. Lời giải:
Vì
20 70 sin 20 sin 70< <
.
Đáp án cần chọn là A.
23. Lời giải:
17.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Ta có
cos 67 sin 2 3=
vì
67 23 90+ =
;
cos 44 35 sin 45 25
¢¢
=
vì
44 35 45 25 90
¢¢
+=
Mà
23 28 10 35 40 45 25
¢¢
< < < <
nên
sin 23 sin 28 10 sin 35 sin 40 sin 45 25
¢¢
< < < <
cos 67 sin 28 10 sin 35 sin 40 cos 45 25
¢¢
<<<<
.
Đáp án cần chọn là D.
24. Lời giải:
Ta có
cot 7 1 tan 19=
vì
71 19 90 ; cot 69 15 tan 20 45
¢¢
+ = =
vì
69 15 20 45 90
¢¢
+=
Mà
19 20 45 28 38 43
¢
< < < <
nên
tan19 tan 20 45 tan 28 tan 38 tan 43
¢
< < < <
cot71 cot60 15 tan 28 tan 38 tan 43
¢
<<<<
.
Đáp án cần chọn là A.
25. Lời giải:
Ta có
222222
sin 89 cos 1 ; sin 88 cos 2 ;...; sin 46 cos 44= = =
và
22
sin cos 1aa+=
Nên
22 22 22 22
(sin 1 sin 89 ) (sin 2 sin 88 ) ... (sin 44 sin 4 6 ) sin 45 sin 90A =+ ++ ++ + + +
22 22 2 2 2 2
(sin 1 cos 1 ) (sin 2 cos 2 ) ... (sin 44 cos 44 ) sin 45 sin 90=+++++ + + +
44 1
1391
11...1 1 44.1
222
so
=++ ++ += + =

.
Vậy
91
2
A =
.
Đáp án cần chọn là C.
26. Lời giải:
Ta có
22222222
sin 80 cos 10 ; sin 70 cos 20 ; sin 60 cos 30 ; sin 50 cos 40= = = =
và
22
sin cos 1aa+=
Nên
22222222
sin 10 sin 20 sin 30 sin 40 sin 50 sin 60 sin 70 sin 80+ + + + + + +
2222 2 2 2 2
sin 10 sin 20 sin 30 sin 40 cos 40 cos 30 cos 20 cos 10=+++++++
22 22 22 22
(sin 10 cos 10 ) (sin 20 cos 20 ) (sin 30 cos 30 ) (sin 40 cos 40 )=+++++++
1111 4=+++=
.
Vậy giá trị cần tìm là
4
.
Đáp án cần chọn là D.
27. Lời giải:
Ta có
66 2266 22
sin cos 3 sin . cos sin cos 3 sin . cos .1aa aaaa aa++ =++
66 2222
sin cos 3 sin . cos .(sin cos )
aa aaaa
=++ +
(vì
22
sin cos 1aa+=
)
23 22 2 2 22 23
(sin ) 3(sin ) .cos 3 sin .(cos ) (cos )
aaaaaa
=+ + +
223
(sin cos ) 1
aa
=+ =
(vì
22
sin cos 1aa+=
)
Đáp án cần chọn là B.
18.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
28. Lời giải:
Ta có
4444 22 22
sin cos sin cos 2 sin .cos 2 sin .cosC aaaa aa aa=+=++ -
22222 22
(s in cos ) 2 sin .cos 1 sin .cos
a a aa aa
=+ - =-
(vì
22
sin cos 1aa+=
)
Vậy
22
12sin .cosC aa=-
.
Đáp án cần chọn là A.
29. Lời giải:
Với
22
cos
cot ; sin cos 1
sin
a
aaa
a
=+=
22 2 2 22 2
(1 sin ).cot 1 cot cot sin .cot 1 cotA
aa a a aa a
=- +- = - +-
2
222
2
cos
1sin. 1cos sin
sin
a
aaa
a
=- =- =
.
Vậy
2
sinP a=
.
Đáp án cần chọn là A.
30. Lời giải:
Với
22
sin cos
tan ; cot ; sin cos 1
cos sin
aa
aa aa
aa
== +=
2222
sin 1 cos , cos 1 sin
aaaa
=- =-
.
22 22
(1 sin ). tan (1 cos ). cotP
aa aa
=- +-
22
22 22
22
sin cos
cos . sin . sin cos 1
cos sin
aa
aaaa
aa
=+=+=
.
Đáp án cần chọn là C.
31. Lời giải:
Với
sin cos
tan ; cot
cos sin
aa
aa
aa
==
ta có:
22 2 2
cos sin cos sin cos sin
cot tan
cos .sin sin .cos sin .cos sin cos
Q
aa a a aa
aa
aa aa a a a a
-
==-=-=-
.
Vậy
cot tanQ aa=-
.
Đáp án cần chọn là A.
32. Lời giải:
Với
22
sin
tan ; cos 1 sin
cos
a
aaa
a
==-
2
22222
2
2222
1 sin 1 sin 2 sin 1 sin 2 sin sin
12. 12tan
cos
1sin 1sin 1sin cos
Q
aaaaa a
a
a
aaaa
æö
+-+ -
÷
ç
÷
= = = + =+ =+
ç
÷
ç
÷
ç
---
èø
.
Vậy
2
12tanQ
a
=+
.
Đáp án cần chọn là B.
33. Lời giải:
Vì
tan 2a =
nên
cos 0a ¹
19.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Ta có
sin cos
2
2sin cos 2.tan 1
cos cos
cos 3 sin cos sin 1 3 tan
3.
cos cos
G
aa
aa a
aa
aaa a a
aa
+
++
== =
--
-
Thay
tan 2a =
ta được
2.2 1 5
1
13.2 5
G
+
==-=-
-
.
Vậy
1G =-
.
Đáp án cần chọn là D.
34. Lời giải:
Xét tam giác vuông
ABD
và
ADC
, ta có
tan ; tan
AD AD
BC
BD CD
==
.
Suy ra
2
tan . t an
.
AD
BC
BD CD
=
(1)
Lại có
HBD CAD=
(cùng phụ với
ACB
) và
90HDB ADC==
.
Do đó
BDH ADCDD
(g.g) suy ra
DH BD
DC AD
=
, do đó
..BD DC DH A D=
(2).
Từ (1) và (2) suy ra
2
tan . tan
.
AD AD
BC
DH A D DH
==
(3).
Theo giả thiết
3
2
HD
AH
=
suy ra
3
23
HD
AH HD
=
++
hay
3
5
HD
AD
=
, suy ra
5
3
AD HD=
.
Thay vào (3) ta được:
5
5
3
tan . tan
3
HD
BC
DH
==
.
Đáp án cần chọn là D.
35. Lời giải:
Xét tam giác vuông
ABD
và
ADC
, ta có
tan ; tan
AD AD
BC
BD CD
==
.
Suy ra
2
tan . t an
.
AD
BC
BD CD
=
(1)
Lại có
HBD CAD=
(cùng phụ với
ACB
) và
90HDB ADC==
.
Do đó
BDH ADCDD
(g.g) suy ra
DH BD
DC AD
=
, do đó
..BD DC DH A D=
(2).
E
D
B
C
A
20.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Từ (1) và (2) suy ra
2
tan . tan
.
AD AD
BC
DH A D DH
==
(3).
Theo giả thiết
1
2
HD
AH
=
suy ra
1
21
HD
AH HD
=
++
hay
1
3
HD
AD
=
, suy ra
3AD HD=
.
Thay vào (3) ta được:
3
tan . tan 3
HD
BC
DH
==
.
Đáp án cần chọn là B.
36. Lời giải:
Ta có
3
sin
5
a
=
, suy ra
2
9
sin
25
a
=
, mà
22
sin cos 1aa+=
, do đó:
22
916
cos 1 sin 1
25 25
aa=- =- =
suy ra
4
cos
5
a =
.
Do đó
sin 3 4 3 5 3
tan : .
cos 5 5 5 4 4
a
a
a
====
.
cos 4 3 4 5 4
cot : .
sin 5 5 5 3 3
a
a
a
====
.
Vậy
434
cos , tan , cot
543
aaa
===
.
Đáp án cần chọn là B.
37. Lời giải:
Ta có
5
sin
13
a =
suy ra
2
25
sin
169
a =
mà
22
sin cos 1aa+=
do đó
22
25 144
cos 1 sin 1
169 169
aa=- =- =
Suy ra
12
cos
13
a
=
.
Do đó
cos 12 5 12 13 12
cot : .
sin 1313 135 5
a
a
a
== = =
.
Đáp án cần chọn là A.
38. Lời giải:
Ta có
tan 80 cot10 ; tan 70 cot 20 ; tan 50 cot 40 ; cot 60 cot 30= = = =
và
tan .cot 1aa=
Nên
tan 10 . tan 20 . tan 30 . tan 40 . ta n 50 . tan 60 . tan 70 . tan 80B =
tan10.tan20.tan30.tan40.cot40.cot30.cot20.cot10= 
(tan10 .cot10 ).(tan 20 .cot20 ).(tan 30 . cot 30 ).(tan 40 .cot 40 )=
1.1.1.1 1==
.
Vậy
1B =
.
Đáp án cần chọn là B.
39. Lời giải:
Ta có
tan 89 cot1 ; tan 88 cot 2 ;...; tan 46 cot 44= = =
và
tan .co t 1aa=
21.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Nên
(tan1 . tan 89 ).(tan 2 . tan 88 ).....(tan 46 . tan 44 ). tan 45B =
(tan1 . cot1 ).(tan 2 . cot2 ).(tan 3 .cot 3 )....(tan 44 .cot 44 ). tan 45=
1.1.1 ...1.1 1==
Vậy
1B =
.
Đáp án cần chọn là B.
40. Lời giải:
Vì
tan 3 0 cos 0aa=¹ ¹
. Chia cả tử và mẫu của
B
cho
2
cos a
ta được:
22
22
22
222
2
2
22
cos sin
3
13tan 13tan
cos cos
1
3 sin 3(1 tan ) tan
3. tan
cos
cos cos
B
aa
aa
aa
aaa
a
a
aa
-
--
== =
+-
-
-
2
2
13tan 13.9 26
32.9 21
32tan
a
a
--
===-
+
+
.
Hay
26
0
21
B =- <
.
Đáp án cần chọn là B.
22.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
C
B
A
α
CB
A
D.BÀI TẬP TỰ LUYỆN
I.PHIẾU LUYỆN CƠ BẢN
Bài 1: Cho tam giác
ABC
vuông tại
A
. Chứng minh rằng:
Sin
Sin
AB C
AC B
=
Bài 2: Với góc nhọn
a
tùy ý. Chứng minh rằng:
a)
sin 1, cos <1aa<
b)
sin
tg
cos
a
a
a
=
a)
tg .cotg 1aa=
d)
22
sin cos 1aa+=
Bài 3: Cho biết
4
sin
5
a
=
. Tìm
cos , tgaa
.
Bài 4: Tính:
a)
0
0
sin 46
cos 44
b)
00
cotg28 tg62-
Bài 5: Tính
20 20 20 20
sin 10 sin 20 ... sin 70 sin 80++++
Bài 6: Cho tam giác
ABC
có ba góc nhọn,
,,BC a AC b AB c===
.
Chứng minh rằng:
sin sin sin
abc
ABC
==
Bài 7: Chứng minh rằng diện tích của tam giác bằng một nửa tích của hai cạnh nhân với sin của góc
nhọn tạo bởi các đường thẳng chứa hai cạnh ấy.
Bài 8: Cho tam giác
ABC
nhọn, có
,,BC a AC b AB c===
.
Chứng minh rằng:
222
2cos
abc bcA
=+-
.
Bài 9: Cho hai góc
,ab
sao cho
0
90ab+<
Chứng minh rằng
( ) sin cos sin cosab a b b a+= +
.
Bài 10: Cho góc nhon
xAy
. Các điểm
,BC
lần lượt di động trên các tia
,AB AC
sao cho:
6
AB AC cm
+=
. Xác định vị trí
,BC
để diện tích tam giác
ABC
lớn nhất.
Hướng dẫn giải
Bài 1:
sin , sin
AB AC
CB
BC BC
==
Do đó:
Sin
:
Sin
CABACAB
BBCBC AC
==
Bài 2:
Xét
ABCD
vuông tại
,AC a=
a) Ta có
,AB BC AC BC<<
23.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Do đó:
sin sin 1
AB
C
BC
a
==<
;
cos = cos 1
AC
c
BC
a =<
b)
tg =t gC= ; cotg cotg
AB AC
C
AC AB
aa
==
Do đó:
tg .cotg = . 1
AB AC
AC AB
aa =
c)
sin , cos
AB AC
BC BC
aa
==
Do đó:
sin
:tg
cos
AB AC AB
BC BC AC
a
a
a
===
d)
ABCD
vuông tại
A
theo định lí Py-ta-go có:
22 2
AB AC BC
+=
Do đó:
22
22
sin cos
AB AC
BC BC
aa
æöæö
÷÷
çç
÷÷
+= +
çç
÷÷
çç
÷÷
çç
èøèø
2222
22 2
1
AB AC AB AC
BC BC BC
+
=+= =
Bài 3:
Ta có:
22
sin cos 1aa+=
và
4
sin
5
a
=
(gt)
2
16 9
cos 1
25 25
a =- =
3
cos
5
a
=
4
sin 4
5
tg
cos 3 3
5
a
a
a
===
Bài 4:
a)
00 0
46 44 90+=
nên
00
sin46 =cos44
Do đó:
0
0
sin 46
1
cos44
=
b)
00 0
28 62 90+=
nên
00
cotg28 tg62=
Do đó:
00
cotg28 tg62 0-=
Bài 5:
Ta có
sin10 cos 80=

(hai góc phụ nhau thì sin góc này bằng côsin góc kia)
22
sin 10 cos 80=

.
24.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
α
c
b
a
H
A
B
C
C
B
A
H
α
c
b
a
H
A
B
C
Do đó:
2222
sin10sin20sin30sin40+++

2222
sin 50 sin 60 sin 70 sin 80++++
2222
sin 10 sin 20 sin 30 sin 40=+++

2222
cos 40 cos 30 cos 20 cos 10++++

22 22
(sin 10 cos 10 ) (sin 20 cos 20 )=+++

22 22
(sin 30 cos 30 ) (sin 40 cos 40 )++ + +
 
1111 4=+++=
.
Bài 6:
Vẽ
,AH BC H BC^Î
Xét
HABD
có
0
90H =
, nên
sin
AH
B
AB
=
Xét
HACD
có
0
90H =
, nên
sin
AH
C
AC
=
Do đó:
sin
sin sin sin
BACb b c
CABc B C
== =
Chứng minh tương tự, ta có:
sin sin
ab
AB
=
Vậy
sin sin sin
abc
ABC
==
.
Bài 7:
Giả sử có tam giác
ABC
cos
,AB c BC a==
Góc nhọn tạo bởi hai đường thẳng
,AB BC
là
a
.
Vẽ đường cao
AH
của tam giác
ABC
HABD
có
0
90H =
nên
sin sin
AH
BAHABB
AB
==
Do đó:
11 1
. .sin . . . sin
22 2
ABC
SAHBCABBBCcaa== =
Bài 8:
Vẽ đường cao
CH
của tam giác
ABC
.
HACD
vuông tại
H
, nên
cos cos
AH
AAHACA
AC
==
25.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
H
C
B
A
K
H
C
B
A
y
xA
B
C
H
HACD
vuông tại
H
theo định lý Py-ta-go, ta có:
22 2
AH HC AC
+=
HBCD
vuông tại
H
theo định lý Py-ta-go, ta có:
222
BC HB HC
=+
22
()AB AH HC=- +
222
2.
AB AB AH AH HC
=- ++
22
2. cos
AB AB AC A AC
=- +
22
2.cos
AC AB AC AB A
=+-
Vậy
222
2cos
abc bcA
=+-
.
Bài 9:
Xét
ABCD
có
,BCab==
, vì
0
90ab+<
nên
BAC
là góc tù.
Vẽ các đường cao
,AH BK
của
ABCD
Ta có:

1
(BAK B C BAK=+
là góc ngoài của
ABCD
)
ABKD
có
0
90K =
nên
sinBK AB BAK=
Do đó:
11
..sin()
22
ABC
SBKACABAC
ab
== +
Mặt khác:
HABD
có
0
90H =
Nên
sin sin , cos co s
AH BH
ABH ABH
AB AB
aa
== ==
Và
HACD
có
0
90H =
Nên
sin sin , cos cos
AH HC
ACH ACH
AC AC
bb
== ==
Do đó:
sin cos sin cos . .
AH HC AH BH
AB AC AC AB
ab ba+=+
()
.
AH
HC BH
AB AC
=+
2
.
..
ABC
S
AH BC
AB AC AB AC
==
..sin( )
sin( )
.
AB AC
AB AC
ab
ab
+
==+
Vậy
sin( ) sin cos sin cosab a b b a+= +
.
Bài 10:
Vẽ
CH
là đường cao của tam giác
ABC
.
Xét
AHCD
vuông tại
H
, theo tỉ lệ số lượng giác
của góc nhọn, ta có:
26.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
sin
CH
HAC
AC
=
.sinCH AC BAC=
Mặt khác, ta có:
222
11
.( )( )9()
44
AB AC AB AC AB AC cm=+--=
Do đó:
11 9
...sinsin
22 2
ABC
SCHABABACBAC BAC== £
9
sin
2
BAC
không đổi.
Dấu “=” xảy ra
3
AB AC cm
==
Vậy khi
,BC
lần lượt trên các tia
,AB AC
sao cho
3AB AC cm==
thì diện tích
ABCD
lớn nhất.
II.PHIẾU LUYỆN NÂNG CAO PHÁT TRIỂN TƯ DUY
Câu 1: Cho
ABC
có độ dài các cạnh BC, CA, AB lần lượt là a, b, c.Chứng minh rằng:
sin
2
Aa
bc
Câu 2: Cho tam giác ABC vuông tại A. Từ trung điểm E của cạnh AC kẻ
EF BC
. Nối AF và BE.
a) Chứng minh rằng
.AF BE cosC .
b) Biết
10BC cm
,
sin 0,6ACB
. Tính diện tích tứ giácABFE.
c) AFvà BE cắt nhau tại O. Tính
sin AOB .
Câu 3: Cho tam giác ABC có

20 , 30 , 60ABABcm 
. Đường cao hạ từ C đến AB cắt BA tại P.
Hãy tính AP, BP, CP.
Câu 4: Tam giác đều ABC có cạnh 60 cm. Trên cạnh BC lấy điểm D sao
cho
20BD cm
. Đường trung trực của AD cắt các cạnh AB, AC theo
thứ tự ở E, F. Tính độ dài các cạnh của tam giác DEF.
Câu 5: Cho hai hình chữ nhật có hai kích cỡ 3 và 5; 4 và 6 được đặt sao
cho các cạnh hình chữ nhật song song với nhau (như hình vẽ). Tính diện
tích tứ giác ANCQ.
Câu 6: Tứ giác ABCD có các đường chéo cắt nhau tại O và không
vuông góc với nhau. Gọi H và K lần lượt là trực tâm của các tam giác
AOB và COD. Gọi G và I lần lượt là trọng tâm của các tam giác BOC và
AOD.
a) Gọi E là trọng tâm của tam giác AOB, F là giao điể
m của AH và DK.
Chứng minh rằng các tam giác IEG và HFK đồng dạng.
b) Chứng minh rằng IG vuông góc với HK.
Hướng dẫn
Câu 1:
27.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Định hướng
- Tạo ra góc
2
A
bằng cách dựng tia phân giác AD của góc
A
.
Hạ
BK AD

KAD
để chứng minh
sin
2
ABK
AB
.
Lời giải
Kẻ đường phân giác AD của
A

DBC
.
Hạ
BK AD

KAD
.
Trong
ABK
vuông tại K có
sin
BK
KAB
BA
. Hay
sin
2
ABK
AB
(1).
Trong
BDK
vuông tại K có cạnh huyền BD:
BK BD
(2).
Từ (1) và (2) suy ra
sin
2
ABD
AB
(3).
Do AD là tia phân giác của
A
nên ta có:
DB AB
DC AC
BD AB BD BC a
BC AB AC AB AB AC b c
 

(4)
Từ (3) và (4) ta có:
sin
2
Aa
bc

đpcm.
Câu 2:
a) Xét
FEC
và
ABC
vuông tai F và A có
C chung
FC AC
FEC ABC
EC BC

∼


..
FA AC FA
CFA CEB c g c cos ACB FA BEcos ACB
BE BC BE

∼
b) Xét tam giác ABC vuông tại A có:
 
.sin 0,6.10 6 8AB BC ACB cm AC cm

4AE EC cm
28.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Mặt khác
 
.sin 0,6.4 2,4 3,2FE EC ECF cm FC cm


2
1
..20,16
2
ABFE ABC CFE
SSS ABACFEFC cm
c) Hạ
;
AH BE FK BE

,HK BE
Ta có:


11
. . .sin .sin
22
ABFE ABE BFE
SSS AHBEFKBEBEAOAOBFOFOE

11
.sin . .sin
22
BE AOB AO FO BE FA AOB
Lại có:
52BE
(định lý Py-ta-go) (2).
Theo câu a) có:
8
..52
10
AC
FA BE
BC

Từ (1), (2) và (3) có:
22.20,1663
sin
.65
52.0,8. 52
ABFE
S
AOB
BE FC

.
Câu 3:
Kẻ
AH BC
. Tam giác AHB vuông tại H suy ra
.sin 60.sin 30 30AH AB B
Tam giác AHC vuông tại H có
30
39,162
40
AH
AC
cos
cosHAC

Tam giác APC vuông tại P có
. 39,162.cos 20 36,8AP AC cosPAC
60 36,8 23, 2
PB AB AP
Tam giác APC vuông tại P có
.sin 39,162.sin 20 13,394CP AC PAC
.
Câu 4:
29.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Đặt
DE AE x
,
DF FA y
. Kẻ
DI AB
,
DK AC
Ta có:
. 20.cos60 10BI BD cosIBD,
.sin 20.sin 60 10 3DI BD IBD
Do đó áp dụng định lý Py-ta-go vào tam giác vuông EDI vuông tại I có:


2
2
22
50 10 3 28xDE IE ID x x
Tương tự có:
35
y
Như vậy
28, 35, 60AE FA EAF
. Ta tính được
721FE
.
Câu 5:
Gọi giao của AC và NQ là O; giao của NQ và CD là L
Kẻ
;
CK NQ AH NQ

,KH NQ
Theo giả thiết có:
3
tan 30 57
5
MQN MQN

4
tan 33 41
6
ACD ACD

Ta có:

1
..
2
ANCQ ANQ CNQ
SSS AHNQCKNQ

.
1
...
2
ANCQ
AH AO cosOAH
CK OC cosOCK S cosOAH NQ AO OC
OCK OAH

1
..A
2
cosOAH NQ C
Ta chứng minh số đo
OAH không đổi.
Thật vậy:

90 90OAH AOH OCD OLC 
mà

90 90 90OLC MQN OAH OCD MQN MQN ACD 
(cố định).
30.
TOÁNHỌCSƠĐỒ‐THCS.TOANMATH.com
Vậy


2
11
.. .AC.NQ21
22
ANCQ
S cosOAH AC NQ cos MQN ACD cm
Câu 6:
a) Gọi
90COD
 Ta chứng minh được
,IEG DOC HFK DOC IEG HFK
(1 ).
Lại có áp dụng Ta-lét dễ thấy:
11
,
33
EG AC
EG AC EI BD
EI BD

Gọi M là giao điểm của FK và AC, ta có:
.cotg .cotg .cotg
FK FM MK AM MC AC


Tương tự có:
.cotg
FK AC
FK BD
FH BD

(3).
Từ (1), (2), (3) suy ra
IGE HKF∼
(c.g.c).
b) Theo câu a) có
IGE HKF EIG KHF∼
Gọi giao của EI và AF là N; giao của IG và HK là P.
Vì
// ; 90EI BD BD HF EI HF HNI
Vì

180 360 90EIG KHF NHP AIP HPI NHP AIP HNP IG HK  
.
----------Toán Học Sơ Đồ---------
| 1/30
| | Tải xuống

Có thể bạn quan tâm:

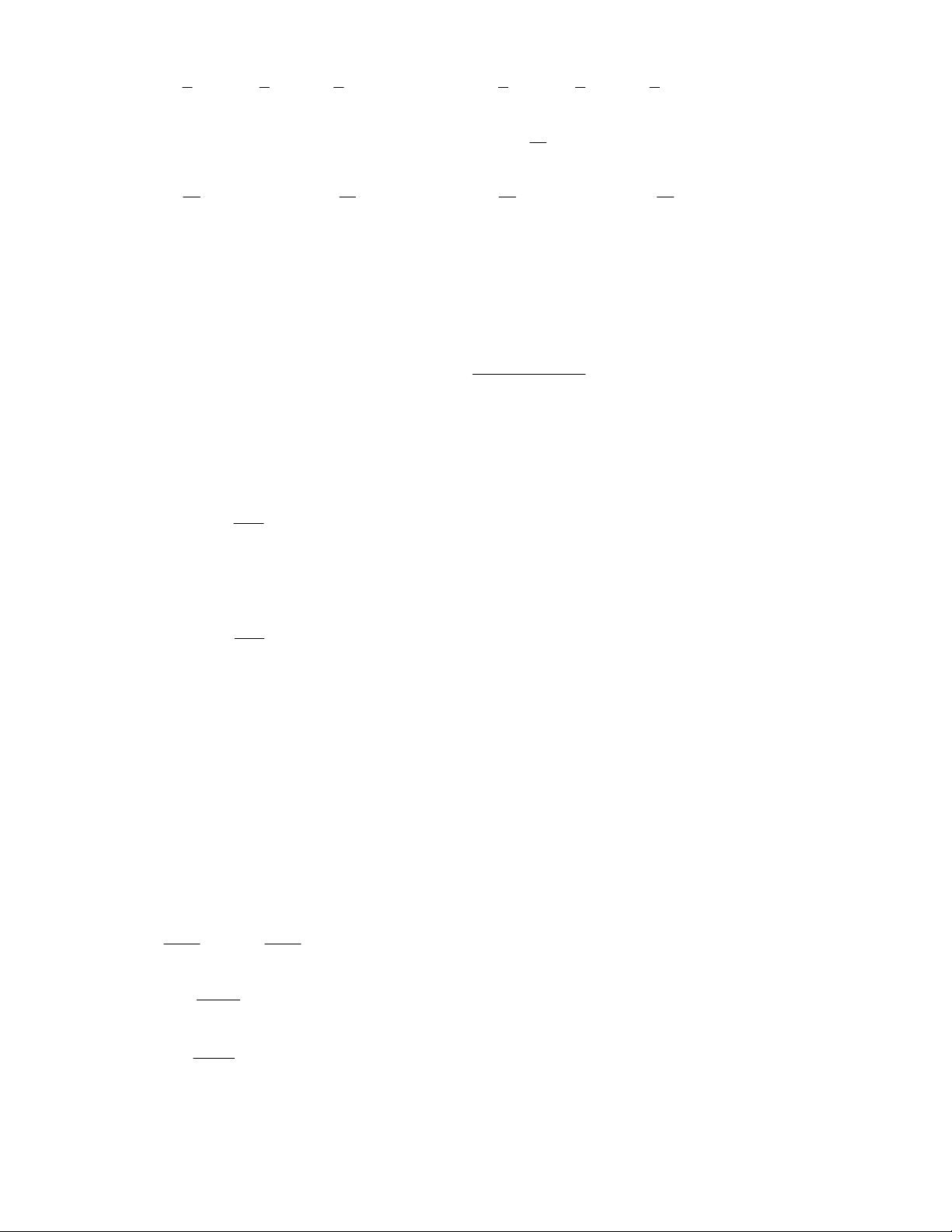
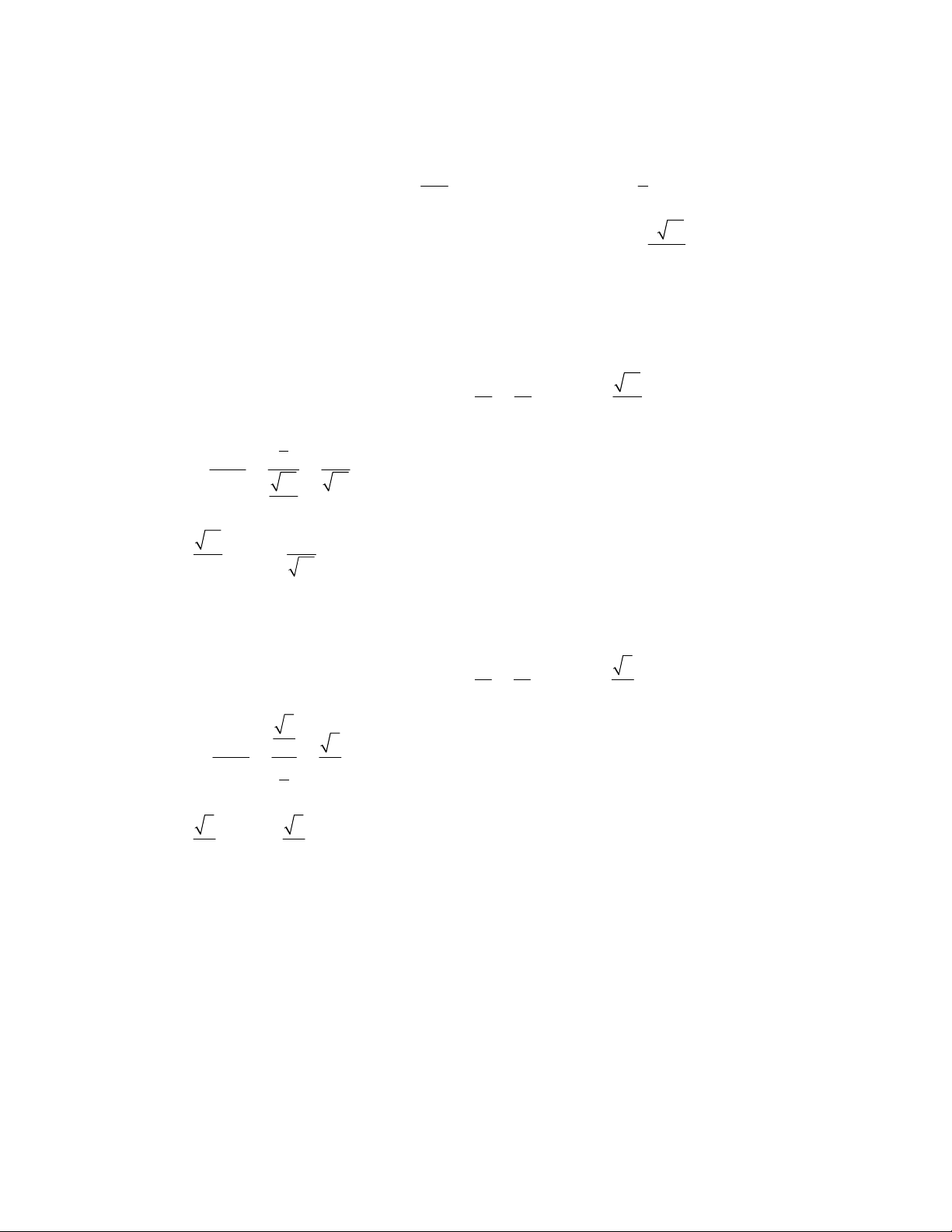
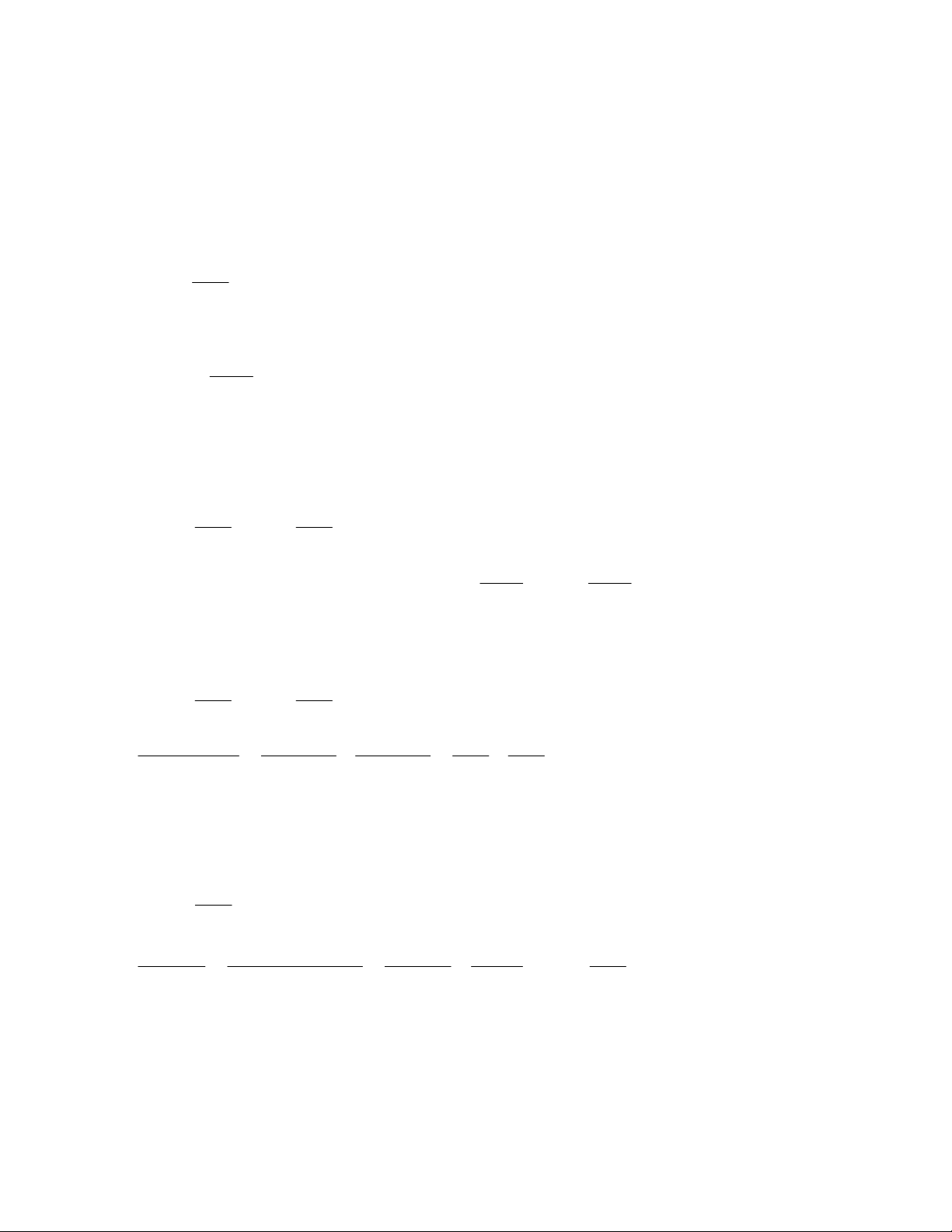
Preview text:


CHUYÊN ĐỀ TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN, HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
A.KIẾN THỨC CẦN NHỚ
Một số tính chất của các tỉ số lượng giác
Cho hai góc ,  phụ nhau. Khi đó:
sin  cos  ; cos  sin  ;
tan  cot  ; cot  tan  .
Cho góc nhọn . Ta có:
0  sin  1; 0  cos  1; 2 2
sin   cos   1; tan. cot   1;   sin cos tan  ; cot   . cos sin
B.CÁC DẠNG BÀI TẬP CƠ BẢN VÀ NÂNG CAO
Dạng 1: Các bài toán tính toán
Phương pháp giải
Bước 1: Đặt độ dài cạnh, góc bằng ẩn.
Bước 2: Thông qua giả thiết và các hệ thức lượng lập phương trình chứa ẩn.
Bước 3: Giải phương trình, tìm ẩn số. Từ đó tính độ dài đoạn thẳng hoặc góc cần tìm. Bài tập minh họa
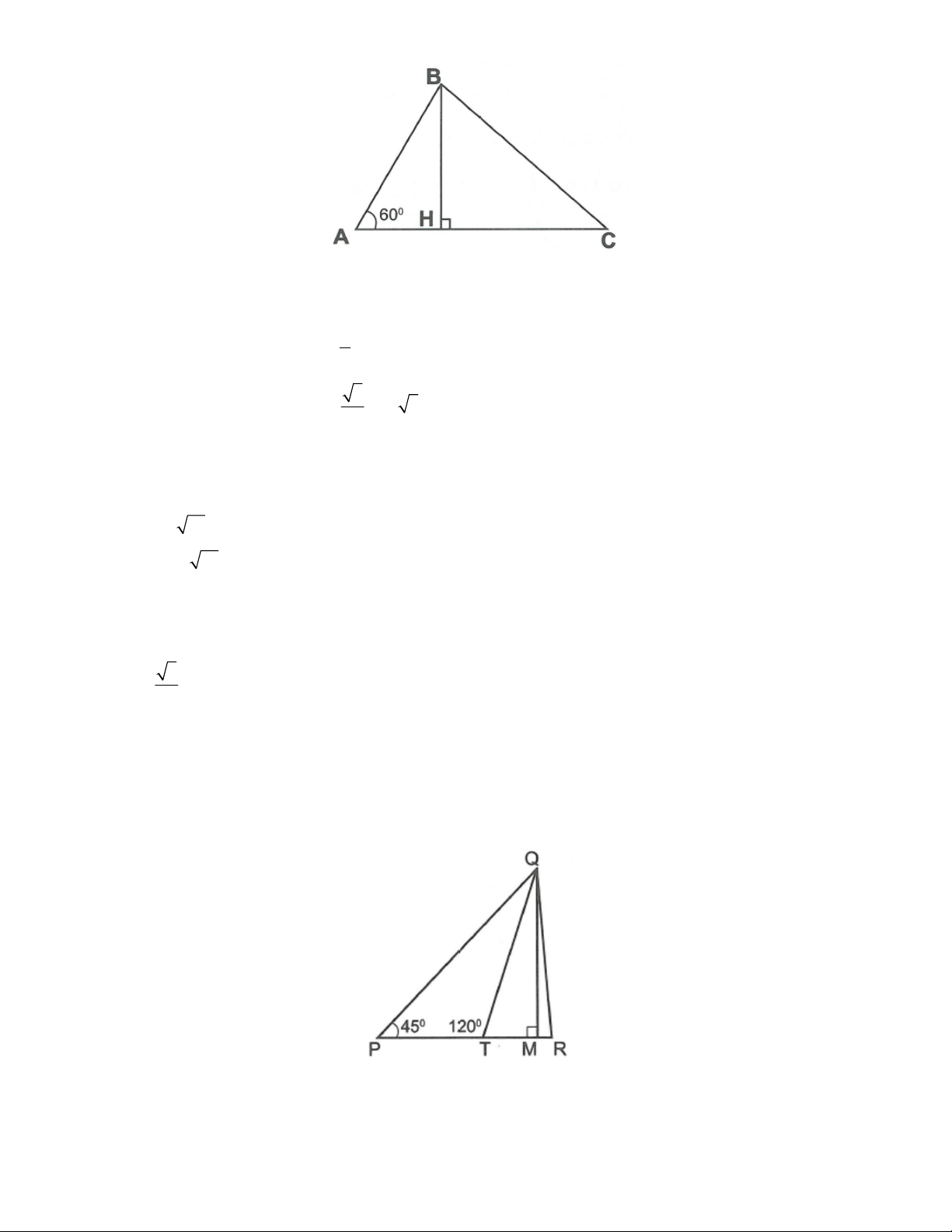
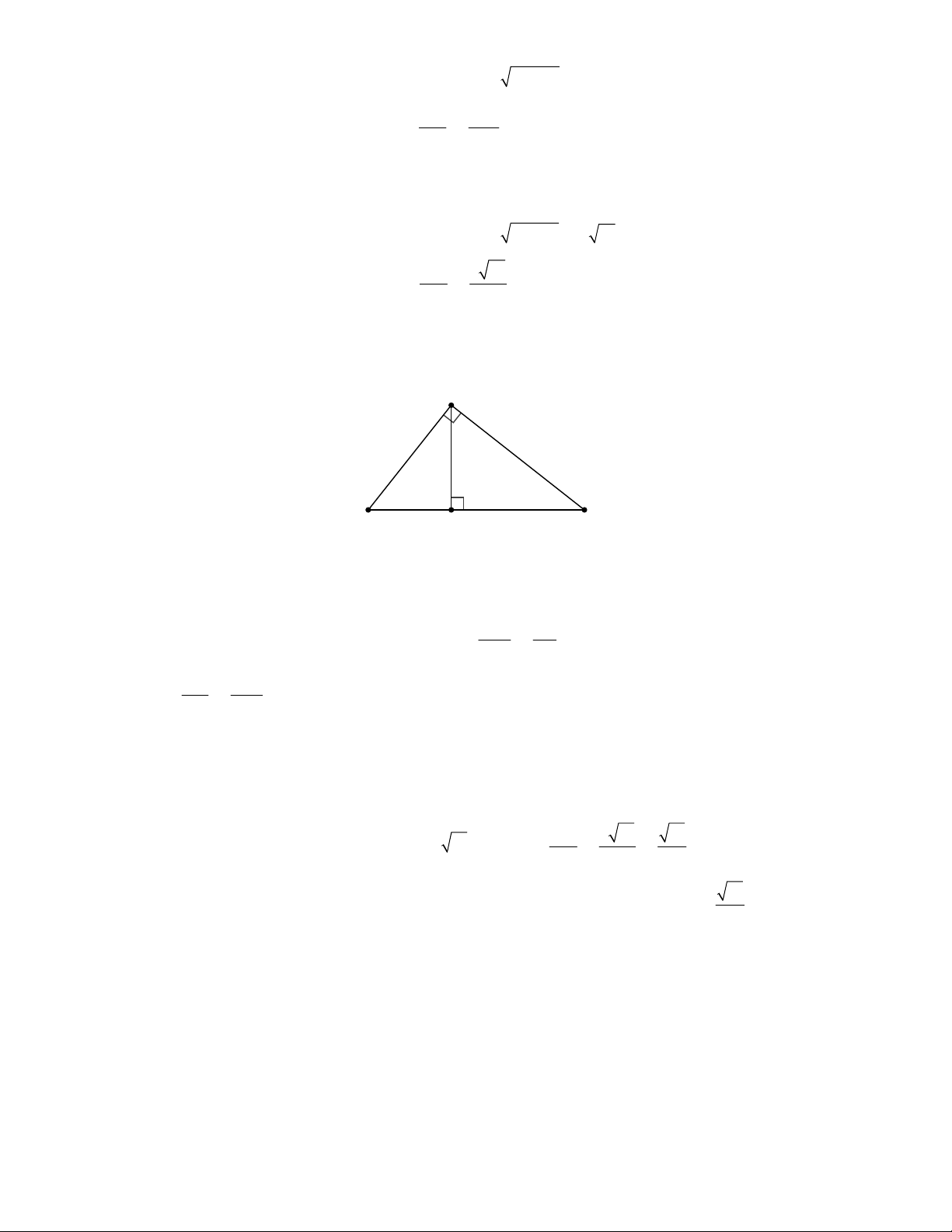
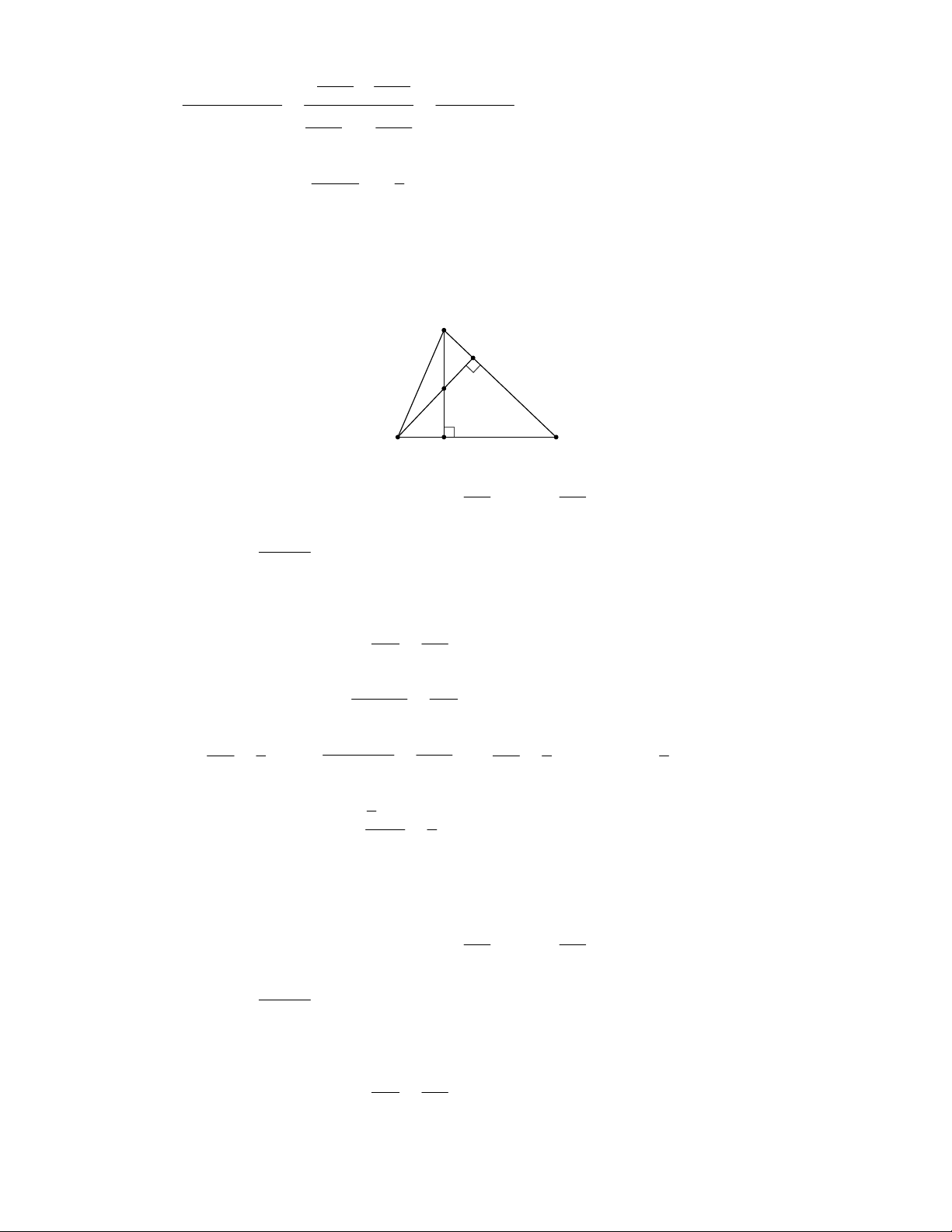
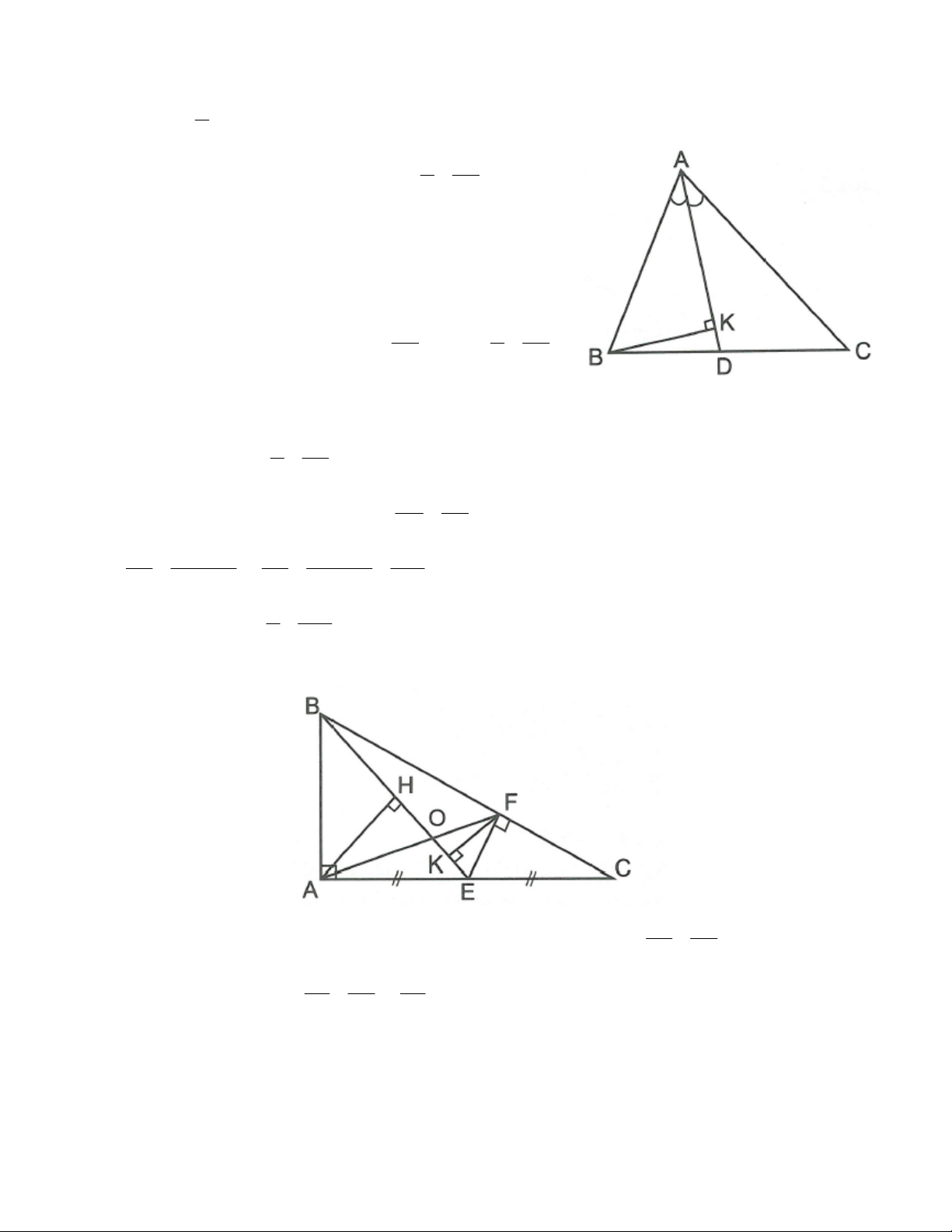
Câu 1: Tam giác ABC có A  60 ;  AB  28c ;
m AC  35cm . Tính độ dài BC. Lời giải
1. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Kẻ BH AC ( H AC )
Xét tam giác vuông AHB vuông tại H có:  1 AH  .
AB cos A  28.cos60  28.  14cm 2  3 BH  .
AB sin A  28.sin 60  28.  14 3 cm 2
HC AC AH  35 14  21cm 2 2 2
BC BH HC  588  441  1029  BC  7 21
Vậy BC  7 21cmChú ý
Bằng cách tính tương tự như trên có: tam giác ABC có A  60 ;  AB  ;
a AC b thì 2 2 2
BC a b ab ; 3 Sab . ABC 4
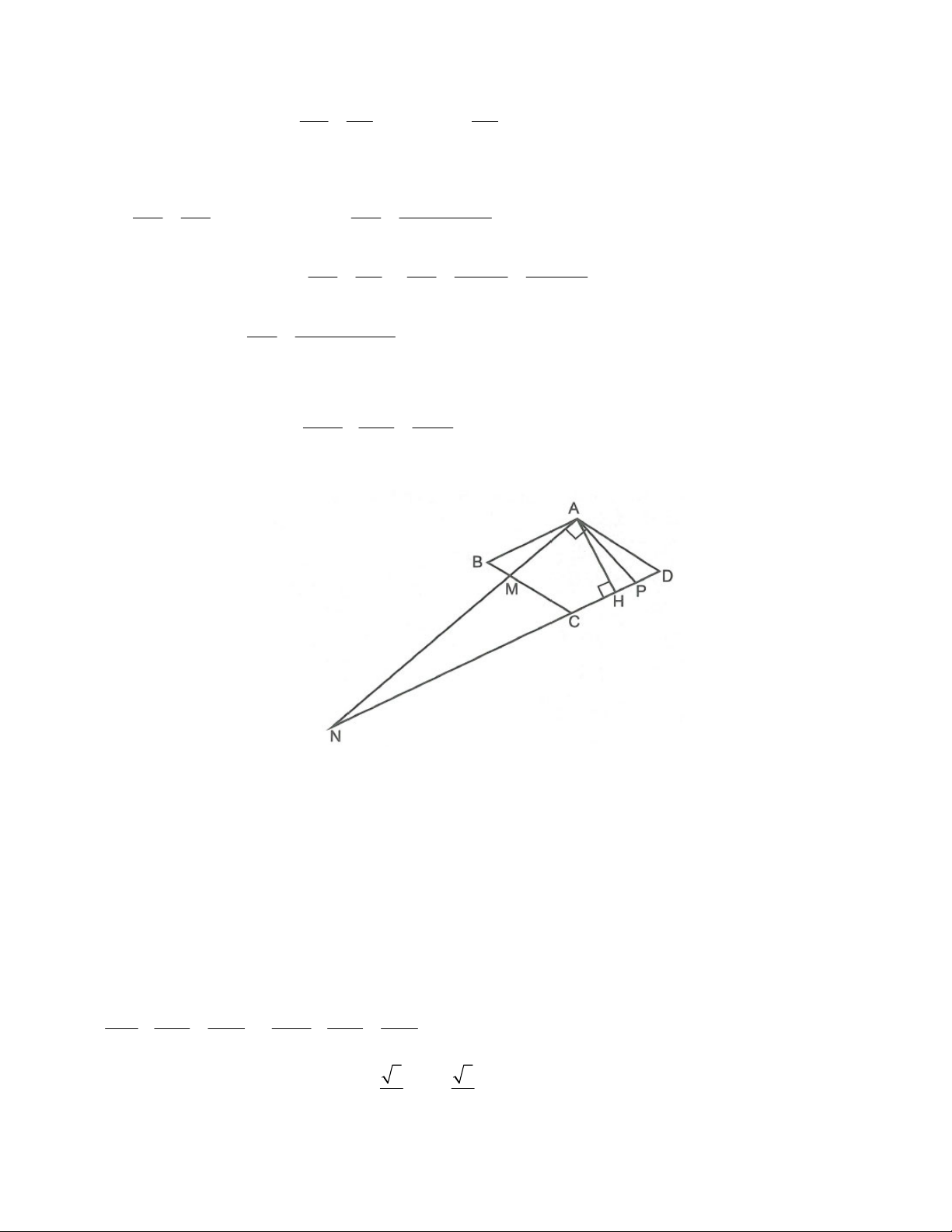
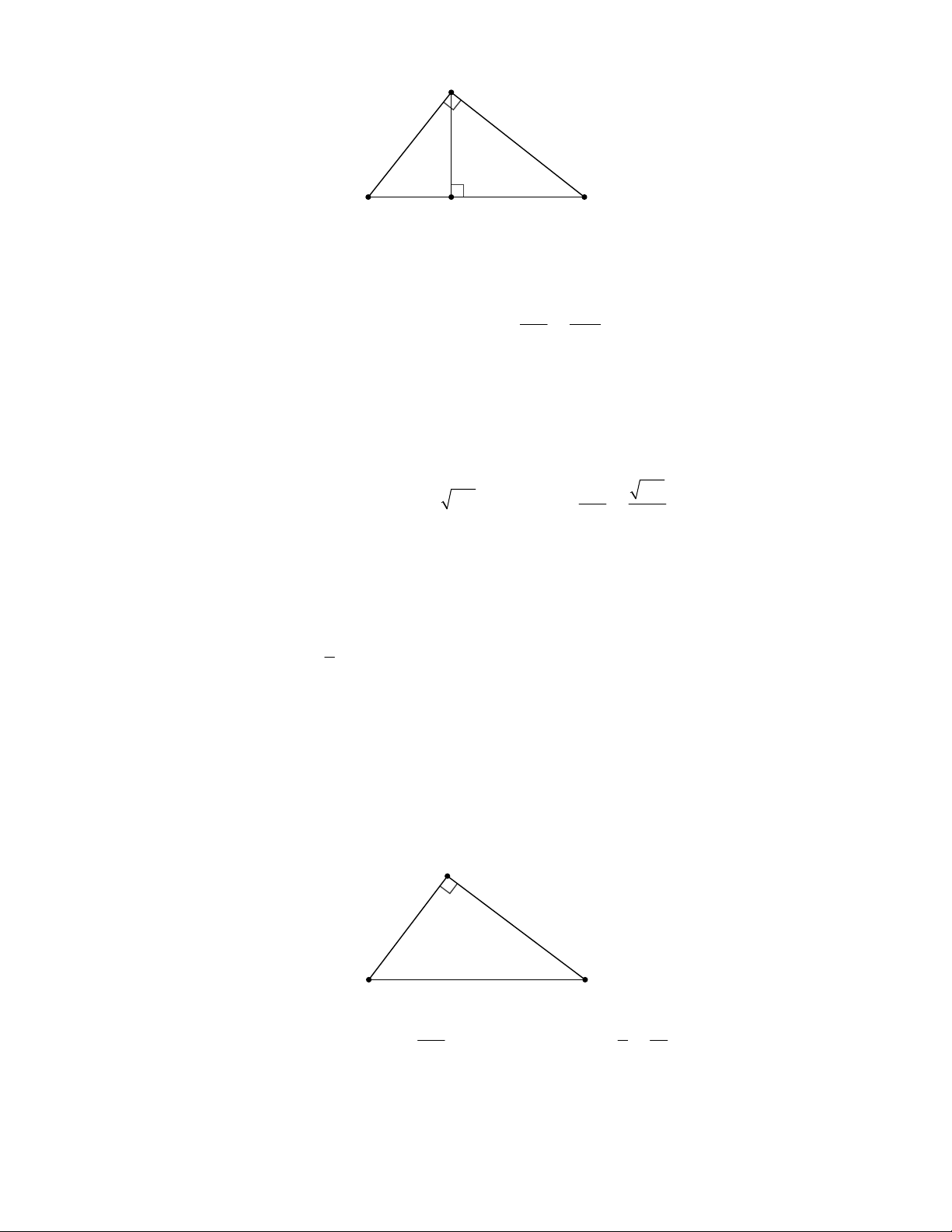
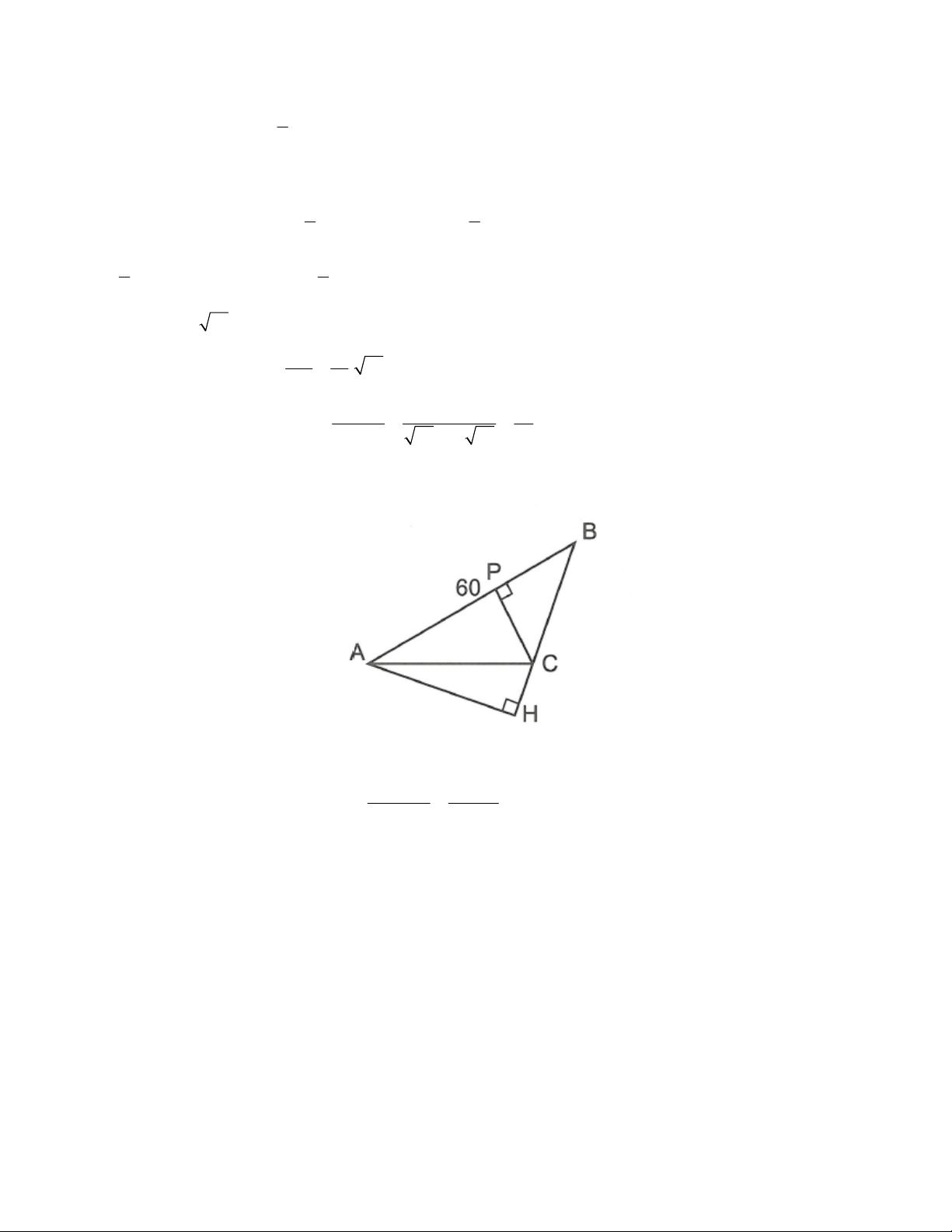
Câu 2: Cho hình vẽ sau biết   QPT  45 ;  PTQ 120 ;  QT  8 ; cm TR  5cm . a) Tính PT.
b) Tính diện tích tam giác PQR. Lời giải
Kẻ QM PR (M thuộc tia đối tia TP).
2. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Có    
PTQ QTM  180  QTM  180  PTQ  180 120  60 3
Xét tam giác vuông QTM có: 
QM QT.sin QTM  8.sin 60  8.  4 3 cm 2  1
TM QT.cos QTM  8.cos 60  8.  4cm 2
TM TR  M nằm giữa T và R. QM 4 3 4 3
Xét tam giác vuông QPM có: PM     4 3 cm  tan QPM tan 45 1
PT PM TM  4 3  4  4 3   1 cm
PR PT TR  4 3  
1  5  4 3 1cm 1 1  S
QM .PR  4 3.    cm PQR 4 3 1 6 2 3 2 2 2
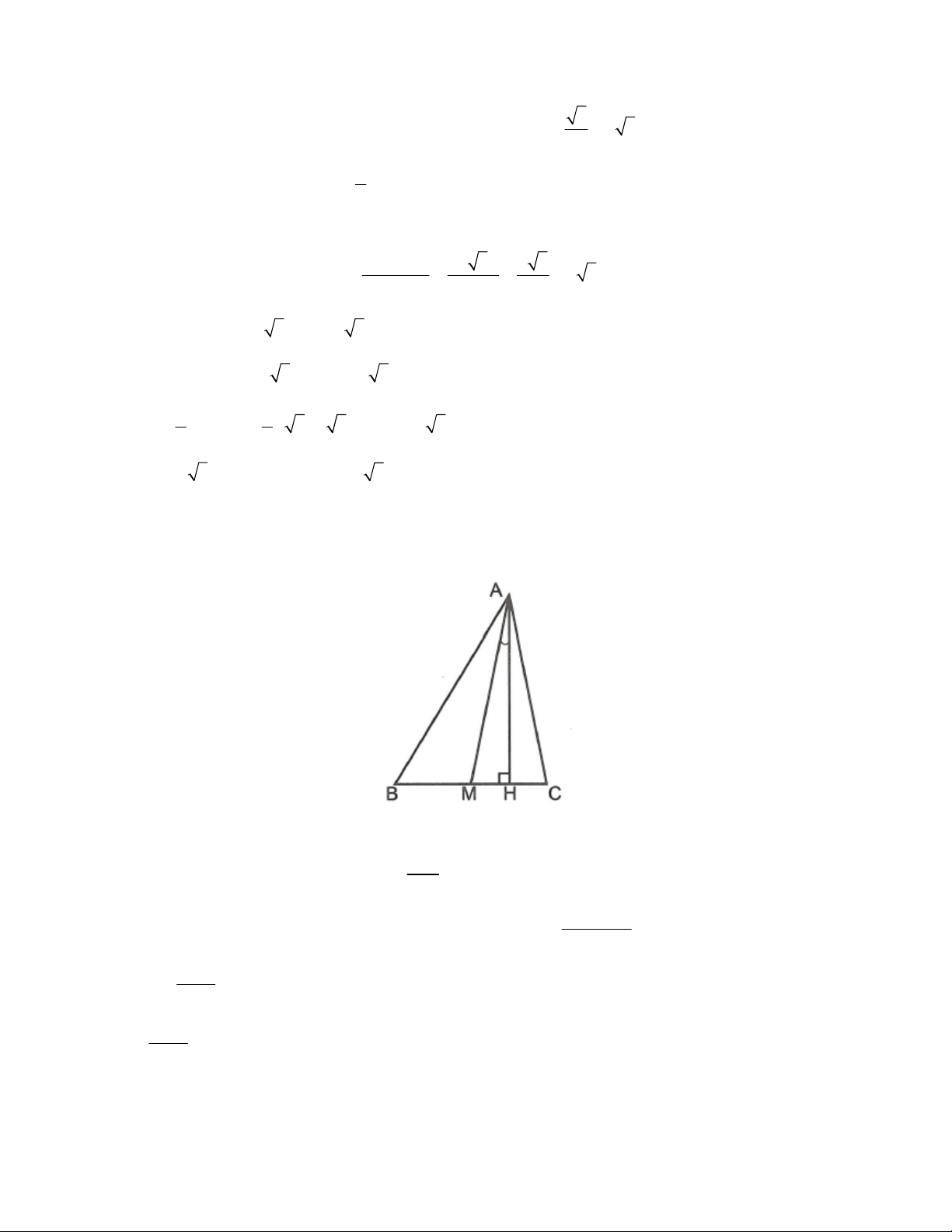
Vậy PR  4 3 1cm ; S    2 6 2 3 cm . PQRCâu 3: Cho ABC  có   B  60 ;
C  80 . Tính số đo góc tạo bởi đường cao AH và trung tuyến AM. Lời giải
Gọi góc tạo bởi đường cao AH và trung tuyến AM là  . MH
Xét tam giác AMH vuông tại H có tan 
MH  tan.AH AH BH HC
Lại có: BH HC  BM MH   MC MH   2MH MH  2 AH Mà BH
(hệ thức lượng trong tam giác vuông AHB)  tan B AH CH
 (hệ thức lượng trong tam giác vuông AHC). tan C
3. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com  1 1   1 1  AH.      AH.     
 tan B tan C
 tan B tan C  1  1 1   MH   tan      11 2  0    2 2AH 2 
 tan B tan C
Vậy số đo góc tạo bởi đường cao AH và trung tuyến AM xấp xỉ bằng 11 20   .
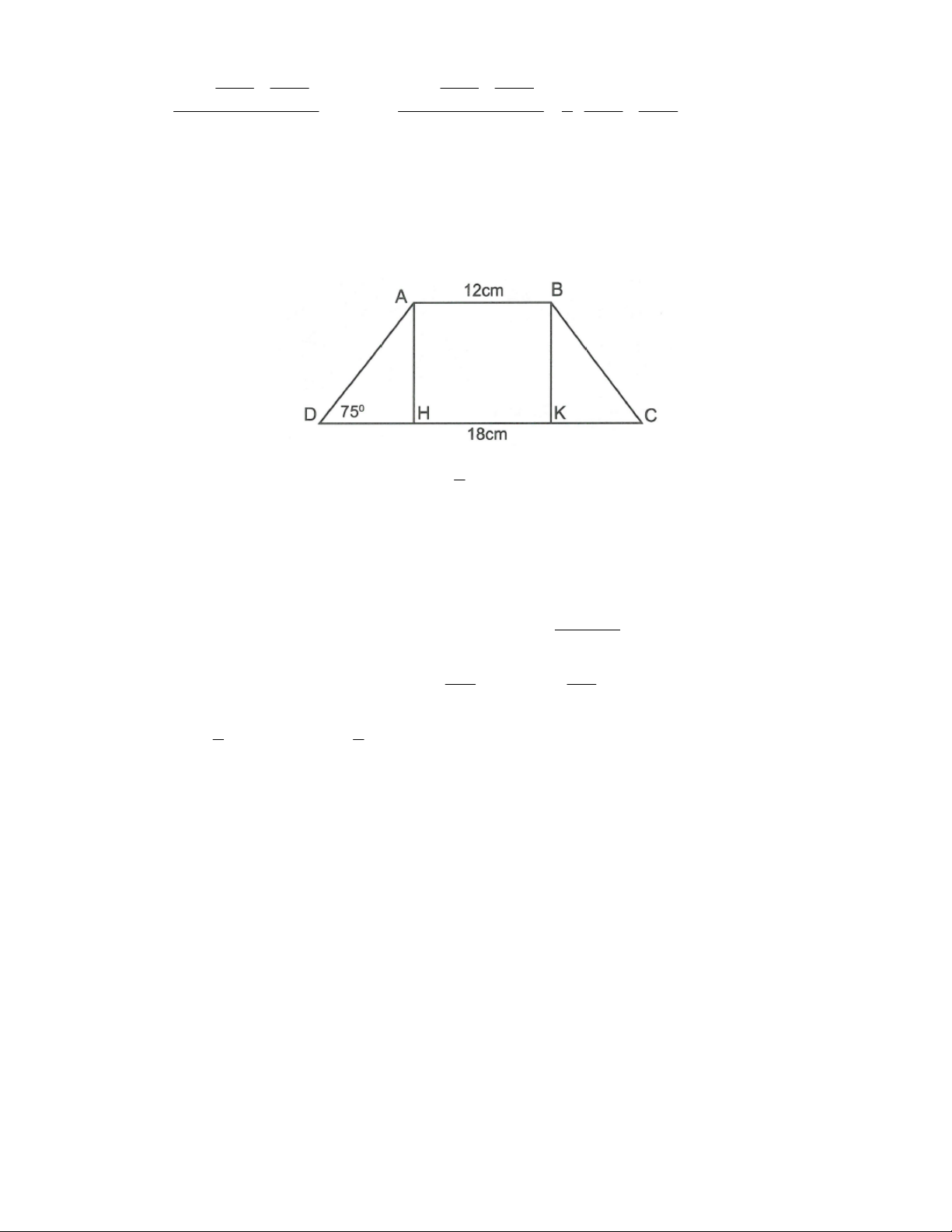
Câu 4: Tính chu vi và diện tích hình thang cân ABCD biết hai cạnh đáy  AB  12 , cm CD  18 ,
cm ADC  75. Lời giải 1
Diện tích hình thang được tính bởi công thức S h AB CD 2
(Trong đó h là chiều cao của hình thang).
Đối với bài tập này, chúng ta đã biết độ dài hai cạnh đáy. Do vậy, ta cần tìm chiều cao.
Kẻ AH CD, BK CD . CD AB
Do ABCD là hình thang cân nên HK AB  12cm, DH KC   3cm . 2 AH AH
Trong tam giác AHD vuông tại H ta có:  tan D   tan 75 
AH  11,196cm DH 3 1 1 Từ đó, S
AH. AB CD    cm . ABCD   .11,196.12 18 2 167,94 2 2
Để tính chu vi hình thang, ta cần tính AD.
Áp dụng định lý Py-ta-go cho tam giác vuông ADH ta có: 2 2 2
AD AH HD  134,35cm . Suy ra
AD  11,59cm .
Ngoài ra, ta cũng có thể sử dụng công thức tỉ số lượng giác của góc trong tam giác vuông ADH để tính AD.
Do đó, chu vi hình thang cân ABCD là
AB BC CD DA  12 11,59 18 11,59  53,18cm .
Dạng 2: Chứng minh đẳng thức, mệnh đề
Phương pháp giải
Đưa mệnh đề về dạng đẳng thức, sử dụng hệ thức lượng và một số kiến thức đã học biến đổi các vế trong
biểu thức, từ đó chứng minh các vế bằng nhau.
4. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Bài tập minh họa Câu 1: Cho ABC
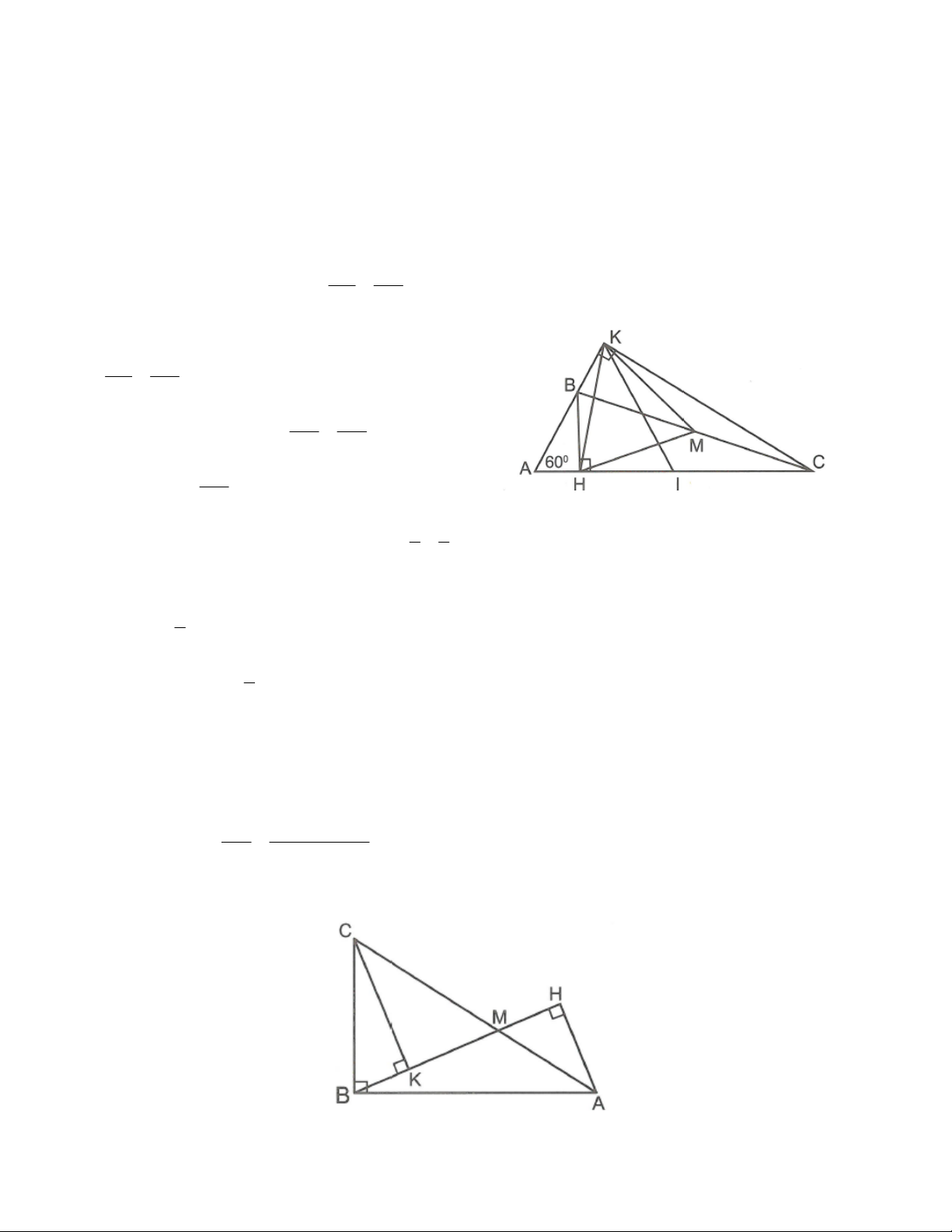
có A  60 . Kẻ BH AC ; CK AB . a) Chứng minh 
KH BC.cos A .
b) Trung điểm của BC là M. Chứng minh MKH là tam giác đều. Lời giải
a) Xét AHB và AK
C vuông tại H, K có: chung góc  BAC AB AH
Suy ra AHB ∼ AKC g.g    AC AK
Xét AHK và ABC  chung góc  BAC và AB AHAC AK AH KH
Suy ra AHK ∼ ABC   AB BC AH   HK BC.  BC.cos A . AB b) Theo câu a) có  1 1
HK BC.cosBAC BC.  BC (1). 2 2
Mặt khác xét tam giác HBC vuông tại H có: HM là trung tuyến ứng với cạnh huyền BC 1
HM BC (2). 2 1
Tương tự có KM BC (3). 2
Từ (1), (2) và (3) có HM HK KM suy ra HKM là tam giác đều.
Câu 2: Cho tam giác ABC vuông tại B. Lấy điểm M trên cạnh AC. Kẻ AH BM ,CK BM a) Chứng minh: 
CK BH.tan BAC 2  MC BH.tan BAC b) Chứng minh:  MA BK Lời giải
5. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
a) Xét AHB và BK
C vuông tại H và K có:  
HBA BCK (cùng phụ với  CBH ).
 AHB ∼ BKC g g CK BC BC  .    CK BH.  BH.tan BAC BH AB AB b) Theo câu a) ta có: 
CK BH.tan BAC MC CKMC BH.tan BAC Mà 
(vì CK / / AH )   (1) MA AH MA AHBK BC 1 BC tan BAC
Mặt khác AHB ∼ BKC      (2) AH AB AH . AB BK BK 2  MC BH.tan BAC Từ (1) và (2) suy ra  MA BK
Câu 3: Cho hình thoi ABCD có 
BAD  120 , tia Ax tạo với tia AB góc 
BAx  15 , cắt BC, CD lần 1 1 4
lượt tại M, N. Chứng minh:   2 2 2 AM AN 3AB Lời giải
Từ A dựng đường thẳng vuông góc với AN cắt CD tại P, hạ AH CD H CD . Có      
BAD BAM MAP PAD  120  15  90  PAD PAD  120 15  90  15
Xét ABM và ADP có:  
MAB PAD (theo trên)
BA AD (tính chất hình thoi)  
MBA PDA (tính chất hình thoi)  ABM   A
DPg. .cg  AM AP
Áp dụng hệ thức lượng vào tam giác vuông NAP vuông tại A đường cao AH, ta có: 1 1 1 1 1 1      2 2 2 2 2 2 AP AN AH AM AN AH Mà  3 3
AH  sin ADH.AD  sin 60 .  AD  .AD AB 2 2
6. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 1 1 1 1 4 Từ (1) và (2) ta có:      2 2 2 2 2 2 AM AN   AM AN 3 3 ABAB  2   1 1 4 Vậy   . 2 2 2 AM AN 3AB
7. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
C.TRẮC NGHỆM RÈN LUYỆN PHẢN XẠ
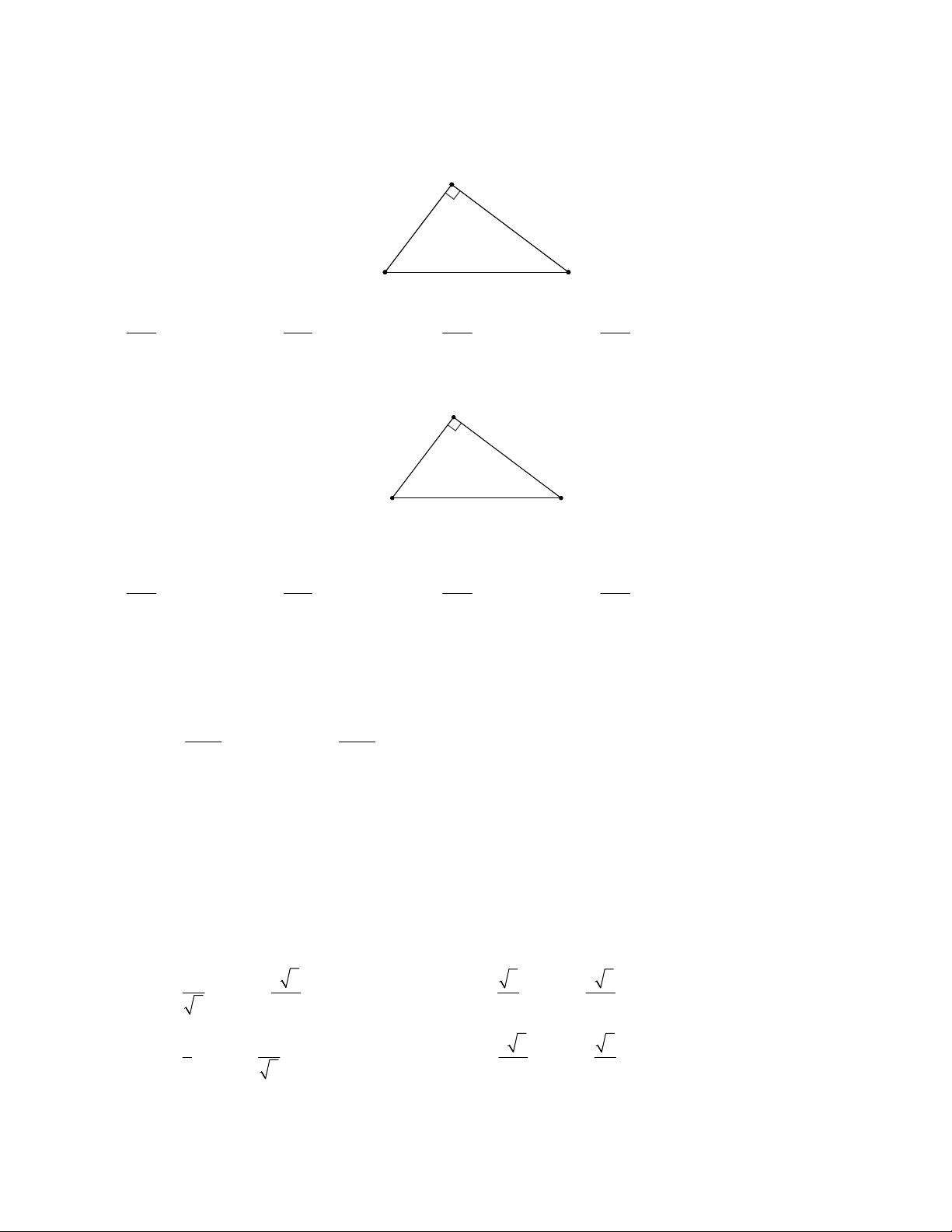
Câu 1: Cho tam giác MNP vuông tại M . Khi đó  cos MNP bằng M N P
A. MN . B. MP . C. MN . D. MP . NP NP MP MN Câu 2: M N P
Cho tam giác MNP vuông tại M . Khi đó 
tan MNP bằng: MN MP MN MP A. . B. . C. . D. . NP NP MP MN
Câu 3: Cho a là góc ngọn bất kỳ. Chọn khẳng định đúng.
A. sin a + cos a = 1. B. 2 2
sin a + cos a = 1.C. 3 3
sin a + cos a = 1 .D. sin a - cos a = 1 .
Câu 4: Cho a là góc nhọn bất kỳ. Chọn khẳng định sai. a a A. sin tan a = . B. cos cot a = .
C. tan a. cot a = 1 . D. 2 2
tan a - 1 = cos a . cos a sin a
Câu 5: Cho a và b là hai góc nhọn bất kỳ thoả mãn a + b = 90 . Khẳng định nào sau đây là đúng?
A. tan a = sin b .
B. tan a = cot b .
C. tan a = cos b .
D. tan a = tan b .
Câu 6: Khẳng định nào sau đây là đúng? Cho hai góc phụ nhau thì
A. sin góc nọ bằng cosin góc kia.
B. sin hai góc bằng nhau.
C. tan góc nọ bằng cotan góc kia.
D. Cả A, C đều đúng.
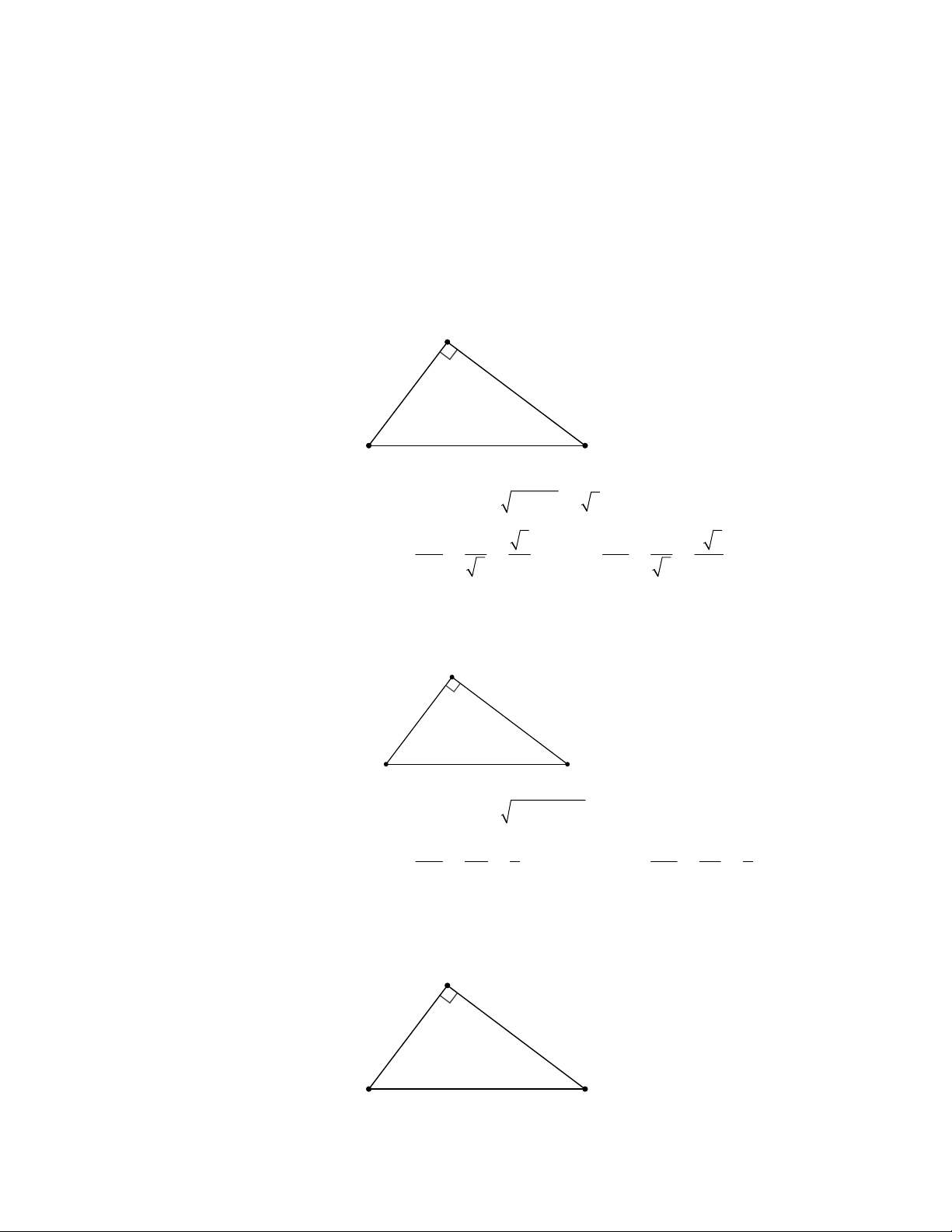
Câu 7: Cho tam giác ABC vuông tại C có AC = 1 ,
cm BC = 2cm . Tính các tỉ số lượng giác sin B; cos B . 1 2 3 5 2 5 A. sin B = ; cos B = . B. sin B = ; cos B = . 3 3 5 5 1 2 2 5 5
C. sin B = ; cos B = . D. sin B = ; cos B = . 2 5 5 5
8. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Câu 8: Cho tam giác ABC vuông tại C có BC = 1,2 ,
cm AC = 0, 9cm . Tính các tỉ số lượng giác sin B; cos B .
A. sin B = 0, 6; cos B = 0, 8 .
B. sin B = 0, 8; cos B = 0, 6 .
C. sin B = 0, 4; cos B = 0, 8 .
D. sin B = 0, 6; cos B = 0, 4 .
Câu 9: Cho tam giác ABC vuông tại A có BC = 8 ,
cm AC = 6cm . Tính tỉ số lượng giác tanC (làm
tròn đến chữ số thập phân thứ 2).
A. tanC » 0, 87 .
B. tanC » 0, 86 .
C. tanC » 0, 88 .
D. tanC » 0, 89 .
Câu 10: Cho tam giác ABC vuông tại A có BC = 9cm,AC = 5cm . Tính tỉ số lượng giác tanC (làm
tròn đến chữ số thập phân thứ 1)
A. tanC » 0, 67 .
B. tanC » 0, 5 .
C. tanC » 1, 4 .
D. tanC » 1, 5 .
Câu 11: Cho tam giác ABC vuông tại A , đường cao AH có AB = 13c ,
m BH = 0, 5dm . Tính tỉ số lượng
giác sinC (làm tròn đến chữ số thập phân thứ 2)
A. sinC » 0, 35 .
B. sinC » 0, 37 .
C. sinC » 0, 39 .
D. sinC » 0, 38 .
Câu 12: Cho tam giác ABC vuông tại A , đường cao AH có AC = 15cm,CH = 6cm . Tính tỉ số lượng giác cos B . 5 21 A. sinC = . B. sinC = . C. 2 sinC = . D. 3 sinC = . 21 5 5 5
Câu 13: Cho tam giác ABC vuông tại A , đường cao AH có CH = 4cm,BH = 3cm . Tính tỉ số lượng
giác cosC (làm tròn đến chữ số thập phân thứ 2).
A. cosC » 0, 76 .
B. cosC » 0, 77 .
C. cosC » 0, 75 .
D. cosC » 0, 78 .
Câu 14: Cho tam giác ABC vuông tại A , đường cao AH có CH = 11c ,
m BH = 12cm . Tính tỉ số lượng
giác cosC (làm tròn đến chữ số thập phân thứ 2).
A. cosC » 0, 79 .
B. cosC » 0, 69 .
C. cosC » 0, 96 .
D. cosC » 0, 66 .
Câu 15: Cho tam giác ABC vuông tại A . Hãy tính tanC biết rằng tan B = 4 . A. 1 tanC = . B. tanC = 4 . C. tanC = 2 . D. 1 tanC = . 4 2
Câu 16: Cho tam giác ABC vuông tại A . Hãy tính tanC biết rằng cot B = 2 . A. 1 tanC = . B. tanC = 4 . C. tanC = 2 . D. 1 tanC = . 4 2
Câu 17: Cho tam giác ABC vuông tại A có 7
AB = 5cm, cotC =
. Tính độ dài các đoạn thẳng AC và 8
BC (làm tròn đến chữ số thập phân thứ 2)
A. AC » 4, 39(cm);BC » 6, 66(cm).
B. AC » 4, 38(cm);BC » 6, 65(cm) .
9. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
C. AC » 4, 38(cm);BC » 6, 64 (cm) .
D. AC » 4, 37 (cm);BC » 6, 67 (cm) .
Câu 18: Cho tam giác ABC vuông tại A có 5
AB = 9cm, tanC =
. Tính độ dài các đoạn thẳng AC và 4
BC . (làm tròn đến chữ số thập phân thứ 2).
A. AC = 11, 53;BC = 7, 2 .
B. AC = 7;BC » 11, 53 .
C. AC = 5, 2;BC » 11. D. AC = 7,2;BC » 11, 53 .
Câu 19: Cho a là góc nhọn. Tính sin , a cot a biết 2 cos a = . 5 21 3 21 21 5 A. sin a = ; cot a = . B. sin a = ; cot a = . 25 21 5 21 21 3 21 2 C. sin a = ; cot a = . D. sin a = ; cot a = . 3 21 5 21 Câu 20: Tính sin , a tan a biết 3 cos a = . 4 4 3 7 3 A. sin a = ; tan a = . B. sin a = ; tan a = . 7 4 4 7 7 7 7 7 C. sin a = ; tan a = . D. sin a = ; tan a = . 4 3 3 4
Câu 21: Không dùng bảng số và máy tính, hãy so sánh cot 50 và cot 46 .
A. cot 46 = cot 50 . B. cot 46 > cot 50 . C. cot 46 < cot 50 . D. cot 46 ³ cot 50 .
Câu 22: Không dùng bảng số và máy tính, hãy so sánh sin 20 và sin 70 .
A. sin 20 < sin 70 . B. sin 20 > sin 70 . C. sin 20 = sin 70 . D. sin 20 ³ sin 70 .
Câu 23: Sắp xếp các tỉ số lượng giác sin 40 , cos 67 , sin 35 , cos 4435 ,¢ sin 2810¢ theo thứ tự tăng dần.
A. cos 67 < sin 35 < sin 2810¢ < sin 40 < cos 4525¢ .
B. cos 67 < cos 4525¢ < sin 40 < sin 2810¢ < sin 35 .
C. cos 67 > sin 2810¢ > sin 35 > sin 40 > cos 4525¢ .
D. cos 67 < sin 2810¢ < sin 35 < sin 40 < cos 4525¢ .
Câu 24: Sắp xếp các tỉ số lượng giác tan 43 , cot 71 , tan 38 , cot 6915 ,¢ tan 28 theo thứ tự tăng dần.
A. cot 71 < cot 6015¢ < tan 28 < tan 38 < tan 43 .
B. cot 6015¢ < cot 71 < tan 28 < tan 38 < tan 43 .
C. tan 28 < tan 38 < tan 43 < cot 6015¢ < cot 71 .
D. cot 6015¢ < tan 28 < tan 38 < tan 43 < cot 71 .
Câu 25: Tính giá trị biểu thức 2 2 2 2 2
A = sin 1 + sin 2 + ... + sin 88 + sin 89 + sin 90
10. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com A. A = 46 . B. 93 A = . C. 91 A = . D. A = 45 . 2 2
Câu 26: Tính giá trị biểu thức 2 2 2 2
sin 10 + sin 20 + ... + sin 70 + sin 80 A. 0 . B. 8 . C. 5 . D. 4 .
Câu 27: Cho a là góc nhọn bất kỳ. Khi đó 6 6 2 2
sin a + cos a + 3 sin a cos a bằng A. 2 2 C = 1 - 3 sin . a cos a . B. 1 . C. 2 2 C = sin .
a cos a . D. 2 2 C = 3 sin . a cos a - 1 .
Câu 28: Cho a là góc nhọn bất kỳ. Khi đó 4 4
C = sin a + cos a bằng: A. 2 2 C = 1 - 2 sin . a cos a . B. C = 1 . C. 2 2 C = sin . a cos a . D. 2 2 C = 1 + 2 sin . a cos a .
Câu 29: Cho a là góc nhọn bất kỳ. Rút gọn 2 2 2 P = (1 - sin )
a .cot a + 1- cot a ta được: A. 2 P = sin a . B. 2 P = cos a . C. 2 P = tan a . D. 2 P = 2 sin a .
Câu 30: Cho a là góc nhọn bất kỳ. Cho 2 2 2 2 P = (1 - sin )
a . tan a + (1- cos )
a .cot a , chọn kết luận đúng.
A. P > 1 . B. P < 1. C. P = 1 . D. 2 P = 2 sin a . 2 2 a - a Câu 31: Cho cos sin
a là góc nhọn bất kỳ. Biểu thức Q = bằng: cos . a sin a
A. Q = cot a - tan a . B. Q = cot a + tan a . C. Q = tan a - cot a . D. Q = 2 tan a . 2 1 + sin a
Câu 32: Chọn a là góc nhọn bất kỳ. Biểu thức Q = . 2 1 - sin a A. 2
Q = 1 + tan a . B. 2
Q = 1 + 2 tan a . C. 2
Q = 1 - 2 tan a . D. 2 Q = 2 tan a . a + a
Câu 33: Cho tan a = 2 . Tính giá trị của biểu thức 2 sin cos G = . cos a - 3 sin a
A. G = 1 . B. 4 G = - . C. 6 G = - . D. G = -1 . 5 5
Câu 34: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H . Biết HD : HA = 3 : 2 . Khi đó  
tan ABC. tan ACB bằng: A. 3 . B. 5 . C. 3 . D. 5 . 5 3
Câu 35: Cho tam giác nhọn ABC hai đường cao AD và BE cắt nhau tại H . Biết HD : HA = 1 : 2 . Khi đó  
tan ABC. tan ACB bằng: A. 2 . B. 3 . C. 1 . D. 4 .
Câu 36: Tính các giá trị lượng giác còn lại của góc a , biết 3 sin a = . 5 A. 3 3 4
cos a = , tan a = , cot a = . B. 4 3 4
cos a = , tan a = , cot a = . 4 4 5 5 4 3
11. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com C. 4 3 4
cos a = , tan a = , cot a = . D. 3 4 4
cos a = , tan a = , cot a = . 5 4 5 4 5 3
Câu 37: Cho a là góc nhọn bất kỳ. Tính cot a biết 5 sin a = . 13 A. 12 cot a = . B. 11 cot a = . C. 5 cot a = . D. 13 cot a = . 5 5 12 5
Câu 38: Tính giá trị biểu thức B = tan 10. tan 20. tan 30..... tan 80 . A. B = 44 .
B. B = 1 . C. B = 45 . D. B = 2 .
Câu 39: Tính giá trị biểu thức B = tan 1. tan 2. tan 3..... tan 88. tan 89 A. B = 44 .
B. B = 1 . C. B = 45 . D. B = 2 . 2 2 cos a - 3 sin a
Câu 40: Cho kết luận đúng về giá trị biểu thức B = biết tan a = 3 . 2 3 - sin a
A. B > 0 . B. B < 0 . C. 0 < B < 1 . D. B = 1 . HƯỚNG DẪN 1. Lời giải: MN Ta có  cos MNP = NP Đáp án cần chọn là A. 2. Lời giải: MP Ta có  tan MNP = . MN Đáp án cần chọn là D. 3. Lời giải:
Chọn a là góc bất kỳ, khi đó 2 2
sin a + cos a = 1 Đáp án cần chọn là B. 4. Lời giải:
Chọn a là góc nhọn bất kỳ, khi đó: 2 2
sin a + cos a = 1;
tan a. cot a = 1 sin a cos a tan a = ; cot a = ; cos a sin a 1 2 1 + tan a = ; 2 cos a 1 2 1 + cot a = . 2 sin a Đáp án cần chọn là D.
12. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 5. Lời giải: Với hai góc ,
a b mà a + b = 90
Ta có: sin a = cos b; cos a = sin b; tan a = cot b; cot a = tan b . Đáp án cần chọn là B. 6. Lời giải:
Với hai góc phụ nhau thì sin góc nọ bằng sin góc kia và tan góc nọ bằng cotan góc kia. Đáp án cần chọn là D. 7. Lời giải: C 1 2 A B
Theo định lý Pytago ta có: 2 2 2 2 2
AB = AC + BC AB = 1 + 2 = 5 . AC 1 5 BC 2 2 5
Xét tam giác ABC vuông tại C có sin B = = = ; cos B = = = . AB 5 5 AB 5 5 Đáp án cần chọn là B. 8. Lời giải: C 0,9 1,2 A B
Theo định lý Pytago ta có: 2 2 2 2 2
AB = AC + BC AB = 0, 9 + 1, 2 = 1, 5 AC 0, 9 3 BC 1, 2 4
Xét tam giác ABC vuông tại C có sin B = = = = 0, 6 và cos B = = = = 0, 8 . AB 1, 5 5 AB 1, 5 5 Đáp án cần chọn là A. 9. Lời giải: A 6 C 8 B
13. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Theo định lý Pytago ta có: 2 2 2 2 2
BC = AC + AB AB = 8 - 6 » 5, 29 . Xét tam giác AB
ABC vuông tại C có 5, 29 tanC = » » 0, 88 . AC 6 Đáp án cần chọn là C. 10. Lời giải:
Theo định lý Pytago ta có: 2 2 2 2 2
BC = AC + AB AB = 9 - 5 = 2 14 . AB 2 14
Xét tam giác ABC vuông tại C có tanC = = » 1, 5 . AC 5 Đáp án cần chọn là D. 11. Lời giải: A C H B
Đổi 0, 5dm = 5cm
Xét tam giác ABC vuông tại A , theo hệ thức lượng 2 2
trong tam giác vuông ta có: AB 13 2
AB = BH .BC BC = = = 33, 8cm BH 5 AB 13  sinC = = » 0, 38 BC 33, 8 Đáp án cần chọn là D. 12. Lời giải:
Xét tam giác AHC vuông tại H , theo định lý Pytago ta có: 2 2 2 2 2 AH
AH = AC -CH = 15 - 6 = 189  AH = 3 21 21 3 21  sinC = = = AC 15 5 21
Mà tam giác ABC vuông tại A nên  
B,C là hai góc phụ nhau. Do đó cos B = sinC = . 5 Đáp án cần chọn là B. 13. Lời giải:
14. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com A C H B
Xét tam giác ABC vuông tại A có BC = BH +CH = 7cm
Theo hệ thức lượng trong tam giác vuông ta có 2 2 AC
AC = CH.BC AC = 4.7  AC » 5,29cm 5, 29  cosC = = » 0, 76 . BC 7 Đáp án cần chọn là A. 14. Lời giải:
Xét tam giác ABC vuông tại A có BC = BH +CH = 11 + 12 = 23cm .
Theo hệ thức lượng trong tam giác vuông ta có: 2 2 AC
AC = CH.BC AC = 11.23 = 253  AC = 253 253cm  cosC = = » 0, 69 . BC 23 Đáp án cần chọn là B. 15. Lời giải:
Vì tam giác ABC vuông tại A nên  
B +C = 90  cotC = tan B = 4 Mà 1
cotC. tanC = 1  tanC = . 4 Đáp án cần chọn là A. 16. Lời giải:
Vì tam giác ABC vuông tại A nên  
B +C = 90  tanC = cotB = 2 . Đáp án cần chọn là C. 17. Lời giải: A C B AC
Vì tam giác ABC vuông tại A nên 7 35 cotC =
AC = AB. cotC = 5. = » 4, 38cm . AB 8 8
Theo định lý Pytago ta có 2 2 2 2 2
BC = AB + AC = 5 + 4, 38  BC » 6, 65 .
15. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Vậy AC » 4, 38(cm);BC » 6, 65(cm) .
Đáp án cần chọn là B. 18. Lời giải: Vì tam giác AB
ABC vuông tại A nên 5 tanC =
AC = AB : tanC = 9 : = 7, 2cm AC 4 9 41
Theo định lý Pytago ta có 2 2 2 2 2
BC = AB + AC = 9 + 7, 2 = 132, 84  BC = » 11, 53 . 5
Vậy AC = 7,2;BC » 11, 53 . Đáp án cần chọn là D. 19. Lời giải: 21 Ta có 4 21 2 2 2 2
sin a + cos a = 1  sin a = 1 - cos a = 1 - =  sin a = . 25 25 5 2 cos a 2 Lại có 5 cot a = = = . sin a 21 21 5 21 2 Vậy sin a = ; cot a = . 5 21 Đáp án cần chọn là D. 20. Lời giải: 7 Ta có 9 7 2 2 2 2
sin a + cos a = 1  sin a = 1 - cos a = 1 - =  sin a = . 16 16 4 7 sin a 7 Lại có 4 tan a = = = . cos a 3 3 4 7 7 Vậy sin a = ; tan a = . 4 3 Đáp án cần chọn là C. 21. Lời giải:
Vì 46 < 50  cot 46 > cot 50 . Đáp án cần chọn là B. 22. Lời giải:
Vì 20 < 70  sin 20 < sin 70 . Đáp án cần chọn là A. 23. Lời giải:
16. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Ta có cos 67 = sin 23 vì 67 + 23 = 90 ; cos 4435¢ = sin 4525¢ vì 4435¢ + 4525¢ = 90
Mà 23 < 2810¢ < 35 < 40 < 4525¢ nên sin 23 < sin 2810¢ < sin 35 < sin 40 < sin 4525¢
 cos 67 < sin 2810¢ < sin 35 < sin 40 < cos 4525¢ . Đáp án cần chọn là D. 24. Lời giải:
Ta có cot 71 = tan 19 vì 71 +19 = 90 ;  cot69 1  5¢ = tan20 4
 5¢ vì 6915¢ + 2045¢ = 90
Mà 19 < 2045¢ < 28 < 38 < 43 nên tan 19 < tan 2045¢ < tan 28 < tan 38 < tan 43
 cot 71 < cot 6015¢ < tan 28 < tan 38 < tan 43 . Đáp án cần chọn là A. 25. Lời giải: Ta có 2 2 2 2 2 2 sin 89 = cos 1 ;  sin 88 = cos 2 ;
 ...;sin 46 = cos 44 và 2 2
sin a + cos a = 1 Nên 2 2 2 2 2 2 2 2
A = (sin 1 + sin 89 )  + (sin 2 + sin 88 )
 + ... + (sin 44 + sin 46 )  + sin 45 + sin 90 2 2 2 2 2 2 2 2 = (sin 1 + cos 1 )  + (sin 2 + cos 2 )
 + ... +(sin 44 + cos 44 )  + sin 45 + sin 90 1 3 91
= 1 + 1 + ... + 1 + + 1 = 44.1 + =
 . 2 2 2 44so 1 Vậy 91 A = . 2 Đáp án cần chọn là C. 26. Lời giải: Ta có 2 2 2 2 2 2 2 2 sin 80 = cos 10 ;  sin 70 = cos 20 ;  sin 60 = cos 30 ;  sin 50 = cos 40 và 2 2
sin a + cos a = 1 Nên 2 2 2 2 2 2 2 2
sin 10 + sin 20 + sin 30 + sin 40 + sin 50 + sin 60 + sin 70 + sin 80 2 2 2 2 2 2 2 2
= sin 10 + sin 20 + sin 30 + sin 40 + cos 40 + cos 30 + cos 20 + cos 10 2 2 2 2 2 2 2 2 = (sin 10 + cos 10 )  + (sin 20 + cos 20 )  + (sin 30 + cos 30 )  + (sin 40 + cos 40 )  = 1 + 1 + 1 + 1 = 4 .
Vậy giá trị cần tìm là 4 . Đáp án cần chọn là D. 27. Lời giải: Ta có 6 6 2 2 6 6 2 2
sin a + cos a + 3 sin .
a cos a = sin a + cos a + 3 sin . a cos . a 1 6 6 2 2 2 2
= sin a + cos a + 3 sin . a cos .(s a in a + cos ) a (vì 2 2
sin a + cos a = 1) 2 3 2 2 2 2 2 2 2 3 = (sin ) a + 3(sin )
a .cos a + 3 sin . a (cos ) a +(cos ) a 2 2 3 = (sin a + cos ) a = 1 (vì 2 2
sin a + cos a = 1) Đáp án cần chọn là B.
17. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 28. Lời giải: Ta có 4 4 4 4 2 2 2 2
C = sin a + cos a = sin a + cos a + 2 sin .
a cos a - 2 sin . a cos a 2 2 2 2 2 2 2 = (sin a + cos ) a -2 sin .
a cos a = 1- sin . a cos a (vì 2 2
sin a + cos a = 1) Vậy 2 2 C = 1 - 2 sin . a cos a . Đáp án cần chọn là A. 29. Lời giải: a Với cos 2 2 cot a =
; sin a + cos a = 1 sin a 2 2 2 2 2 2 2 A = (1 - sin )
a .cot a + 1- cot a = cot a - sin .c
a ot a + 1- cot a 2 cos a 2 2 2 = 1 - sin . a
= 1 - cos a = sin a . 2 sin a Vậy 2 P = sin a . Đáp án cần chọn là A. 30. Lời giải: a a Với sin cos 2 2 tan a = ; cot a =
; sin a + cos a = 1 2 2 2 2  sin a = 1- cos ,
a cos a = 1- sin a . cos a sin a 2 2 sin a cos a 2 2 2 2 P = (1 - sin )
a . tan a + (1- cos ) a .cot a 2 2 2 2 = cos . a + sin . a
= sin a + cos a = 1. 2 2 cos a sin a Đáp án cần chọn là C. 31. Lời giải: a a Với sin cos tan a = ; cot a = ta có: cos a sin a 2 2 2 2 cos a - sin a cos a sin a cos a sin a Q = = - = -
= cot a - tan a . cos . a sin a sin . a cos a sin . a cos a sin a cos a
Vậy Q = cot a - tan a . Đáp án cần chọn là A. 32. Lời giải: a Với sin 2 2 tan a =
; cos a = 1 - sin a cos a 2 2 2 2 2 2 1 sin a 1 sin a 2 sin a 1 sin a 2 sin a æ sin a ö + - + - ç ÷ 2 Q = = = + = 1 + 2.ç ÷ = 1 + 2 tan a . 2 2 2 2 ç ÷ 1 - sin a 1 - sin a 1 - sin a cos a çècos a÷ø Vậy 2
Q = 1 + 2 tan a . Đáp án cần chọn là B. 33. Lời giải:
Vì tan a = 2 nên cos a ¹ 0
18. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com sin a cos a 2 + 2 sin a + cos a 2. tan a + 1 Ta có cos a cos G a = = = cos a - 3 sin a cos a sin a 1 - 3 tan a - 3. cos a cos a +
Thay tan a = 2 ta được 2.2 1 5 G = = - = -1 . 1 - 3.2 5 Vậy G = -1 . Đáp án cần chọn là D. 34. Lời giải: A E H B D C AD AD
Xét tam giác vuông ABD và ADC , ta có tan B = ; tanC = . BD CD 2 Suy ra AD tan B. tanC = (1) BD.CD Lại có  
HBD =CAD (cùng phụ với  ACB ) và  
HDB = ADC = 90.
Do đó DBDH  DADC (g.g) suy ra DH BD =
, do đó BD.DC = DH .AD (2). DC AD 2 Từ (1) và (2) suy ra AD AD tan B. tanC = = (3). DH .AD DH HD HD 3 HD Theo giả thiết 3 = suy ra = hay 3 = , suy ra 5 AD = HD . AH 2 AH + HD 2 + 3 AD 5 3 5 HD Thay vào (3) ta được: 5 3 tan B. tanC = = . DH 3 Đáp án cần chọn là D. 35. Lời giải: Xét tam giác vuông AD AD
ABD và ADC , ta có tan B = ; tanC = . BD CD 2 Suy ra AD tan B. tanC = (1) BD.CD Lại có  
HBD =CAD (cùng phụ với  ACB ) và  
HDB = ADC = 90. DH BD
Do đó DBDH  DADC (g.g) suy ra =
, do đó BD.DC = DH .AD (2). DC AD
19. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 2 Từ (1) và (2) suy ra AD AD tan B. tanC = = (3). DH .AD DH HD HD 1 HD Theo giả thiết 1 = suy ra = hay 1
= , suy ra AD = 3HD . AH 2 AH + HD 2 + 1 AD 3 HD Thay vào (3) ta được: 3 tan B. tanC = = 3 . DH Đáp án cần chọn là B. 36. Lời giải: Ta có 3 9 sin a = , suy ra 2 sin a = , mà 2 2
sin a + cos a = 1, do đó: 5 25 9 16 2 2
cos a = 1 - sin a = 1 - = suy ra 4 cos a = . 25 25 5 a Do đó sin 3 4 3 5 3 tan a = = : = . = . cos a 5 5 5 4 4 cos a 4 3 4 5 4 cot a = = : = . = . sin a 5 5 5 3 3 Vậy 4 3 4
cos a = , tan a = , cot a = . 5 4 3 Đáp án cần chọn là B. 37. Lời giải: Ta có 5 25 25 144 sin a = suy ra 2 sin a = mà 2 2
sin a + cos a = 1 do đó 2 2
cos a = 1 - sin a = 1 - = 13 169 169 169 Suy ra 12 cos a = . 13 a Do đó cos 12 5 12 13 12 cot a = = : = . = . sin a 13 13 13 5 5 Đáp án cần chọn là A. 38. Lời giải: Ta có tan 80 = cot10 ;  tan 70 = cot20 ;  tan 50 = cot 40 ;
 cot 60 = cot 30 và tan a. cot a = 1
Nên B = tan 10. tan 20. tan 30. tan 40. tan 50. tan 60. tan 70. tan 80
= tan 10. tan 20. tan 30. tan 40. cot 40. cot 30. cot 20. cot10 = (tan10 .  cot10 )  .(tan 20.cot20 )  .(tan 30.cot 30 )  .(tan 40 .  cot 40 )  = 1.1.1.1 = 1 . Vậy B = 1 . Đáp án cần chọn là B. 39. Lời giải: Ta có tan 89 = cot1 ;  tan 88 = cot2 ;
 ...; tan 46 = cot 44 và tan a. cot a = 1
20. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Nên B = (tan1 .  tan 89 ).(  tan 2 .  tan 88 )  .....(tan 46 .  tan 44 )  . tan 45 = (tan1 .  cot1 ).  (tan 2 .  cot2 )  .(tan 3 .  cot 3 )  ....(tan 44 .  cot 44 )
 . tan 45 = 1.1.1...1.1 = 1 Vậy B = 1 . Đáp án cần chọn là B. 40. Lời giải:
Vì tan a = 3 ¹ 0  cos a ¹ 0 . Chia cả tử và mẫu của B cho 2 cos a ta được: 2 2 cos a sin a - 3 2 2 2 2 1 - 3 tan a 1 - 3 tan cos a cos a 2 1 - 3 tan a 1 - 3.9 26 B a = = = = = = - . 2 2 2 3 sin a 1 2 + + 2
3(1 + tan a) - tan a 3 2 tan a 3 2.9 21 - 3. - tan a 2 2 2 cos a cos a cos a Hay 26 B = - < 0 . 21 Đáp án cần chọn là B.
21. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
D.BÀI TẬP TỰ LUYỆN
I.PHIẾU LUYỆN CƠ BẢN Bài 1: Cho tam giác AB C
ABC vuông tại A . Chứng minh rằng: Sin = AC Sin B
Bài 2: Với góc nhọn a tùy ý. Chứng minh rằng: a
a) sin a < 1, cos < a 1 b) sin tga = cos a a) tg . a cotga = 1 d) 2 2
sin a + cos a = 1 Bài 3: Cho biết 4 sin a = . Tìm cos , a tga . 5 Bài 4: Tính: 0 sin 46 a) b) 0 0 cotg28 - tg62 0 cos 44 Bài 5: Tính 2 0 2 0 2 0 2 0
sin 10 + sin 20 + ... + sin 70 + sin 80
Bài 6: Cho tam giác ABC có ba góc nhọn, BC = a,AC = , b AB = c . a b c Chứng minh rằng: = = sin A sin B sinC
Bài 7: Chứng minh rằng diện tích của tam giác bằng một nửa tích của hai cạnh nhân với sin của góc
nhọn tạo bởi các đường thẳng chứa hai cạnh ấy.
Bài 8: Cho tam giác ABC nhọn, có BC = a,AC = , b AB = c . Chứng minh rằng: 2 2 2
a = b + c - 2bc cos A . Bài 9: Cho hai góc , a b sao cho 0 a + b < 90
Chứng minh rằng (a + b) = sin acosb + sin b cos a .
Bài 10: Cho góc nhon xAy . Các điểm B,C lần lượt di động trên các tia AB, AC sao cho:
AB + AC = 6cm . Xác định vị trí B,C để diện tích tam giác ABC lớn nhất. B Hướng dẫn giải Bài 1: AB AC sinC = , sin B = BC BC C AB AC AB C A Do đó: Sin = : = Sin B BC BC AC Bài 2:
Xét DABC vuông tại , A C = a
a) Ta có AB < BC,AC < BC A
22. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com α B C Do đó: AB sin a = sinC = < 1; BC AC cosa= cosc = < 1 BC b) AB AC tga=tgC=
; cotga = cotgC = AC AB AB AC Do đó: tg . a cotga= . = 1 AC AB c) AB AC sin a = , cosa = BC BC a Do đó: sin AB AC AB = : = = tga cosa BC BC AC
d) DABC vuông tại A theo định lí Py-ta-go có: 2 2 2
AB + AC = BC 2 2 æAB ö æ ç ÷ AC ö Do đó: 2 2 sin a + cos a ç ÷ = ç ÷ + ç ÷ ç çèBC ÷÷ ç ø èBC ÷÷ø 2 2 2 2 AB AC AB + AC = + = = 1 2 2 2 BC BC BC Bài 3: Ta có: 2 2
sin a + cos a = 1 và 4 sin a = (gt) 5 16 9 2 cos a = 1 - = 25 25 3 cosa = 5 4 sin a 4 5 tga = = = cosa 3 3 5 Bài 4: a) 0 0 0 46 + 44 = 90 nên 0 0 sin46 =cos44 0 sin 46 Do đó: = 1 0 cos44 b) 0 0 0 28 + 62 = 90 nên 0 0 cotg28 = tg62 Do đó: 0 0 cotg28 - tg62 = 0 Bài 5:
Ta có sin 10 = cos 80 (hai góc phụ nhau thì sin góc này bằng côsin góc kia) 2  2  sin 10 = cos 80 .
23. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Do đó: 2  2  2  2
sin 10 + sin 20 + sin 30 + sin 40 2  2  2  2
+ sin 50 + sin 60 + sin 70 + sin 80 2  2  2  2
= sin 10 + sin 20 + sin 30 + sin 40 2  2  2  2
+ cos 40 + cos 30 + cos 20 + cos 10 2  2  2  2
= (sin 10 + cos 10 ) + (sin 20 + cos 20) 2  2  2  2 (sin +
30 + cos 30 ) + (sin 40 + cos 40) = 1 + 1 + 1 + 1 = 4 . Bài 6:
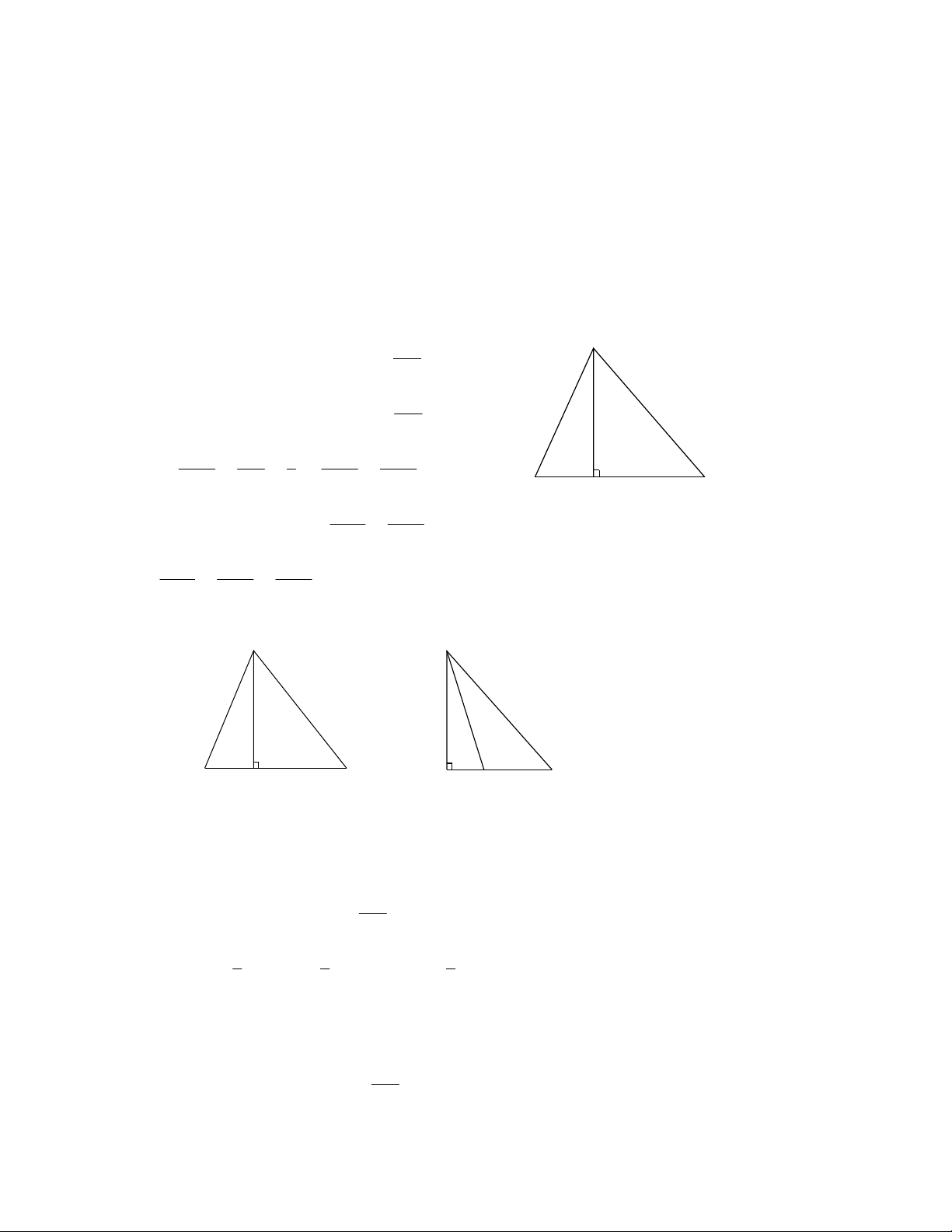
Vẽ AH ^ BC,H Î BC A AH Xét DHAB có  0
H = 90 , nên sin B = AB AH Xét HAC D có  0
H = 90 , nên sinC = AC Do đó: sin B AC b b c = =  = sinC AB c sin B sinC B C H
Chứng minh tương tự, ta có: a b = sin A sin B a b c Vậy = = . sin A sin B sinC Bài 7: A A b c b c α B α a C H C H B a
Giả sử có tam giác ABC cos AB = , c BC = a
Góc nhọn tạo bởi hai đường thẳng AB,BC là a .
Vẽ đường cao AH của tam giác ABC AH DHAB có  0
H = 90 nên sin B =
AH = AB sin B AB Do đó: 1 1 1 S
= AH.BC = AB. sin B.BC = . c a. sin a ABC 2 2 2 Bài 8:
Vẽ đường cao CH của tam giác ABC . AH HA D
C vuông tại H , nên cos A =
AH = ACcosA AC
24. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com HA D
C vuông tại H theo định lý Py-ta-go, ta có: 2 2 2
AH + HC = AC
DHBC vuông tại H theo định lý Py-ta-go, ta có: A 2 2 2
BC = HB + HC H 2 2
= (AB - AH ) + HC 2 2 2
= AB - 2AB.AH + AH + HC 2 2
= AB - 2AB.AC cos A + AC B C 2 2
= AC + AB - 2AC.AB cos A Vậy 2 2 2
a = b + c - 2bc cos A . Bài 9:
Xét DABC có B = , a C = b , vì 0
a + b < 90 nên  BAC là góc tù.
Vẽ các đường cao AH,BK của AB D C Ta có:  
BAK = B +C(BAK là góc ngoài của AB D C ) 1 DABK có  0 K = 90 nên 
BK = AB sin BAK Do đó: 1 1 S
= BK.AC = AB.AC sin(a + b) ABC 2 2 Mặt khác: HA D B có  0 H = 90 Nên  AHBH
sin a = sin ABH =
, cosa = cosABH = AB AB Và HA D C có  0 H = 90 Nên  AHHC
sin b = sin ACH =
, cosb = cosACH = AC AC AH HC AH BH
Do đó: sin a cos b + sin b cos a = . + . AB AC AC AB AH = (HC + BH ) K AB.AC A AH.BC 2SABC = = AB.AC AB.AC B C
AB.AC. sin(a + b) H = = sin(a + b) AB.AC
Vậy sin(a + b) = sin a cos b + sin b cos a . Bài 10: y
Vẽ CH là đường cao của tam giác ABC . C Xét AHC D
vuông tại H , theo tỉ lệ số lượng giác của góc nhọn, ta có:
25. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com A H B x CH sin HAC = AC
CH = AC. sin BAC Mặt khác, ta có: 1 1 2 2 2
AB.AC = (AB + AC ) - (AB - AC ) = 9(cm ) 4 4 Do đó: 1 1 9 S
= CH.AB = AB.AC. sin BAC £ sin BAC ABC 2 2 2 9 
sin BAC không đổi. 2
Dấu “=” xảy ra  AB = AC = 3cm Vậy khi ,
B C lần lượt trên các tia AB, AC sao cho AB = AC = 3cm thì diện tích DABC lớn nhất.
II.PHIẾU LUYỆN NÂNG CAO PHÁT TRIỂN TƯ DUY A a Câu 1: Cho ABC
có độ dài các cạnh BC, CA, AB lần lượt là a, b, c.Chứng minh rằng: sin  2 b c
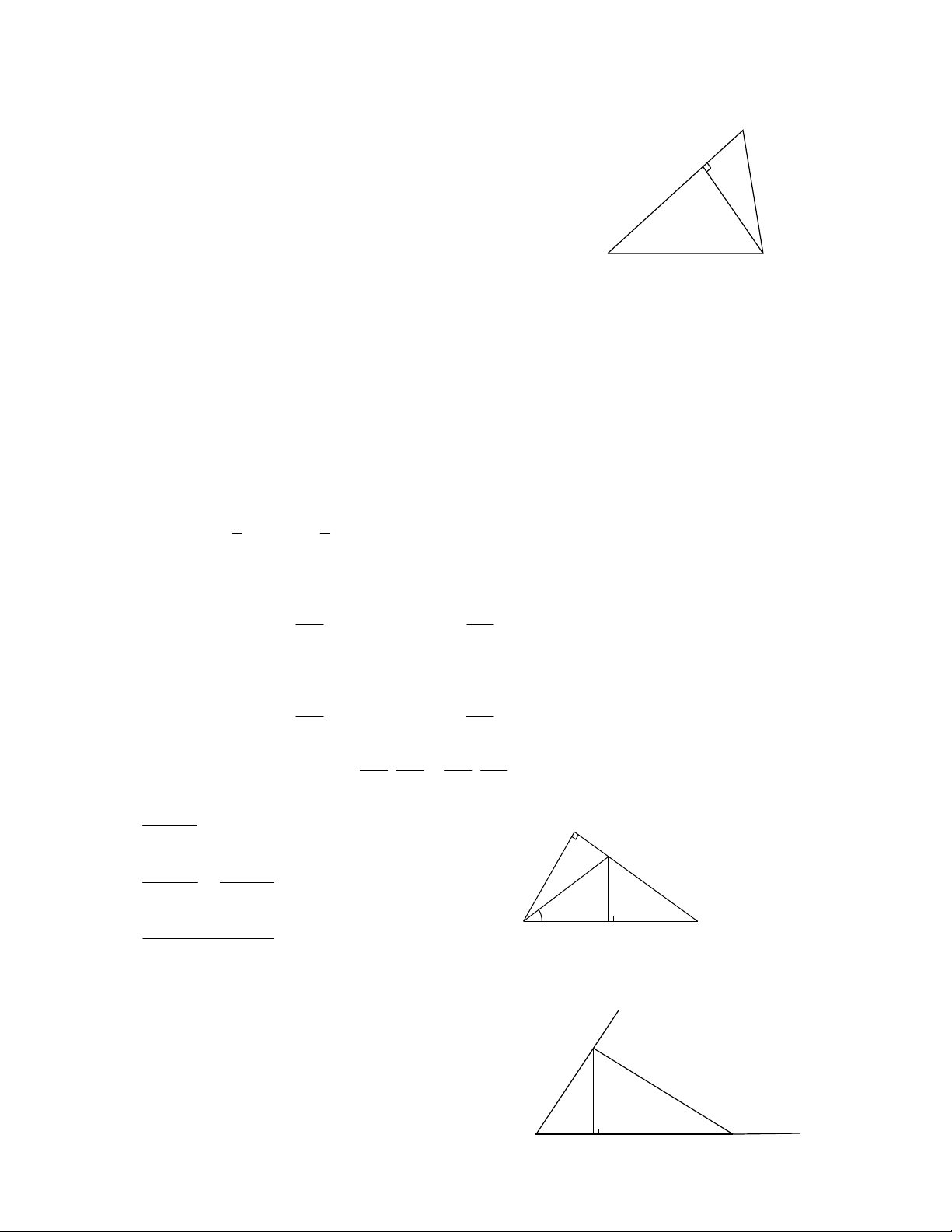
Câu 2: Cho tam giác ABC vuông tại A. Từ trung điểm E của cạnh AC kẻ EF BC . Nối AF và BE. a) Chứng minh rằng 
AF BE.cosC .
b) Biết BC 10cm , 
sin ACB  0,6 . Tính diện tích tứ giácABFE.
c) AFvà BE cắt nhau tại O. Tính  sin AOB .
Câu 3: Cho tam giác ABC có   A  20 ,  B  30 ,
AB  60cm . Đường cao hạ từ C đến AB cắt BA tại P. Hãy tính AP, BP, CP.
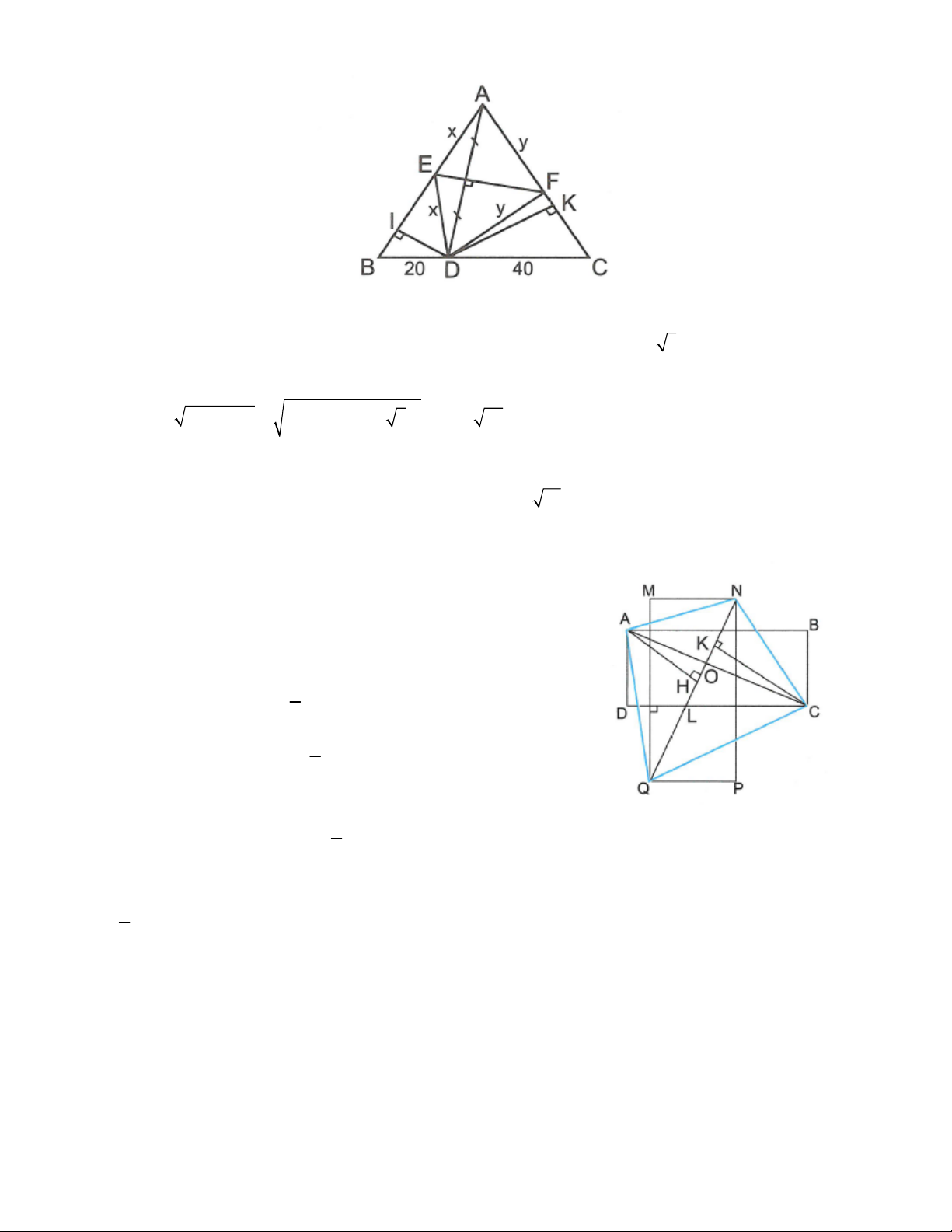
Câu 4: Tam giác đều ABC có cạnh 60 cm. Trên cạnh BC lấy điểm D sao
cho BD  20cm . Đường trung trực của AD cắt các cạnh AB, AC theo
thứ tự ở E, F. Tính độ dài các cạnh của tam giác DEF.
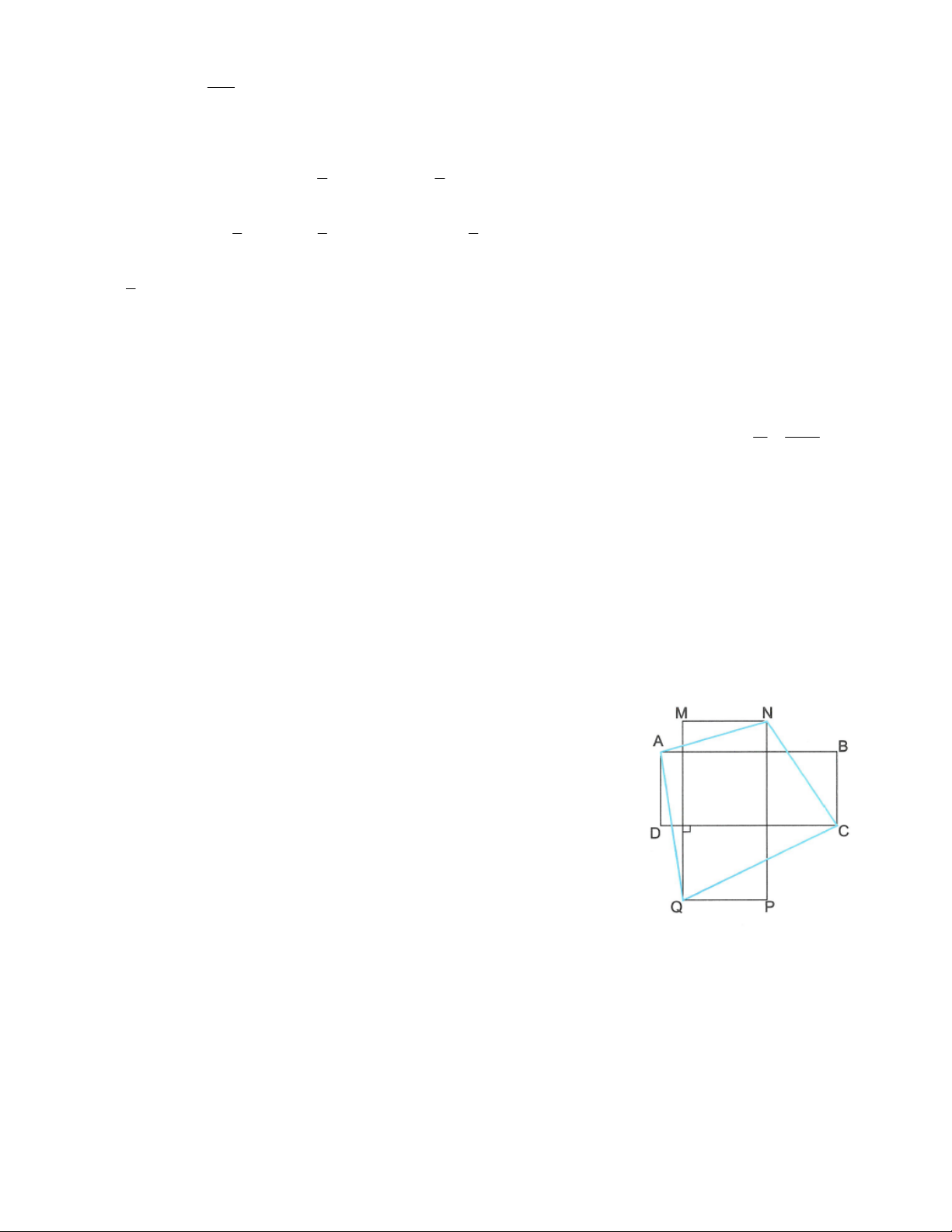
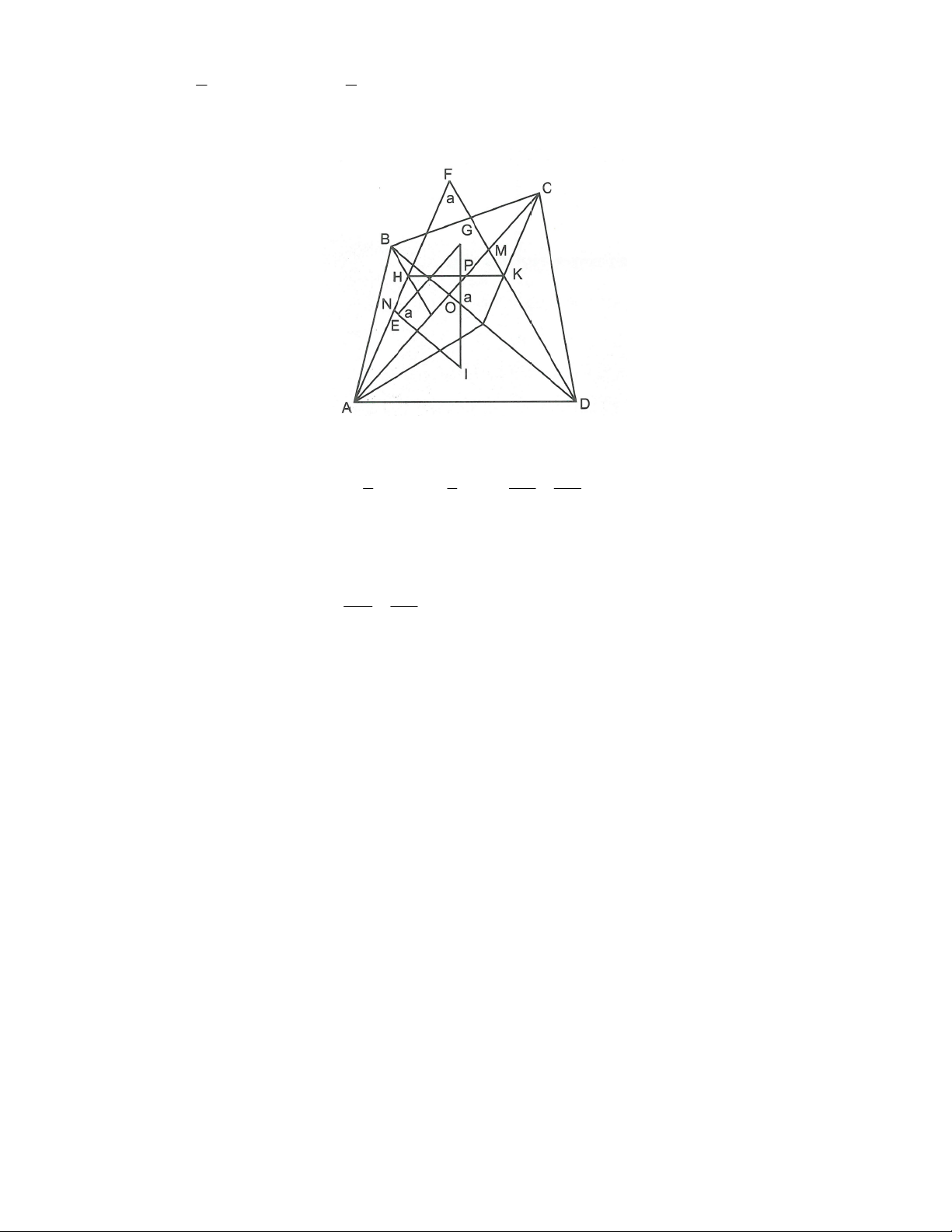
Câu 5: Cho hai hình chữ nhật có hai kích cỡ 3 và 5; 4 và 6 được đặt sao
cho các cạnh hình chữ nhật song song với nhau (như hình vẽ). Tính diện tích tứ giác ANCQ.
Câu 6: Tứ giác ABCD có các đường chéo cắt nhau tại O và không
vuông góc với nhau. Gọi H và K lần lượt là trực tâm của các tam giác
AOB và COD. Gọi G và I lần lượt là trọng tâm của các tam giác BOC và AOD.
a) Gọi E là trọng tâm của tam giác AOB, F là giao điểm của AH và DK.
Chứng minh rằng các tam giác IEG và HFK đồng dạng.
b) Chứng minh rằng IG vuông góc với HK. Hướng dẫn Câu 1:
26. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Định hướng A - Tạo ra góc
bằng cách dựng tia phân giác AD của góc A . 2 A BK
Hạ BK AD K AD để chứng minh sin  . 2 AB Lời giải
Kẻ đường phân giác AD của A D BC .
Hạ BK AD K AD . BK A BK
Trong ABK vuông tại K có  sin KAB  . Hay sin  BA 2 AB (1).
Trong BDK vuông tại K có cạnh huyền BD: BK BD (2). A BD Từ (1) và (2) suy ra sin  (3). 2 AB DB AB
Do AD là tia phân giác của A nên ta có:  DC AC BD AB BD BC a      (4) BC AB AC AB AB AC b c A a Từ (3) và (4) ta có: sin   đpcm. 2 b c Câu 2: FC AC a) Xét FEC  và AB
C vuông tai F và A có 
C chung  FEC ∼ ABC   EC BC
 CFA∼ CEB c g cFA AC FA   . .   
cos ACB FA BEcos ACB BE BC BE
b) Xét tam giác ABC vuông tại A có: 
AB BC.sin ACB  0,6.10  6cm  AC  8cm
AE EC  4cm
27. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com Mặt khác 
FE EC.sin ECF  0, 6.4  2, 4cm  FC  3, 2cm 1  SSS
AB AC FE FC cm ABFE ABC CFE  . .  20,16 2  2
c) Hạ AH BE; FK BE H, K BE 1 1 Ta có: SSS
AH BE FK BE BE AO AOB FO FOE ABFE ABE BFE  . .     .sin .sin  2 2 1 
BE.sin AOB AO FO 1   BE.F . A sin AOB 2 2
Lại có: BE  52 (định lý Py-ta-go) (2). AC 8
Theo câu a) có: FA BE.  . 52 BC 10 S Từ (1), (2) và (3) có:  2 2.20,16 63 sin ABFE AOB    . BE.FC 52.0,8. 52 65 Câu 3:
Kẻ AH BC . Tam giác AHB vuông tại H suy ra  AH  .
AB sin B  60.sin 30  30 AH 30
Tam giác AHC vuông tại H có AC    39,162  cosHAC cos40
Tam giác APC vuông tại P có 
AP AC.cosPAC  39,162.cos 20  36,8
PB AB AP  60  36,8  23, 2
Tam giác APC vuông tại P có 
CP AC.sin PAC  39,162.sin 20  13,394 . Câu 4:
28. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com
Đặt DE AE x , DF FA y . Kẻ DI AB , DK AC Ta có:  BI  .
BD cosIBD  20.cos 60  10 ,  DI  .
BD sin IBD  20.sin 60  10 3
Do đó áp dụng định lý Py-ta-go vào tam giác vuông EDI vuông tại I có:
x DE IE ID    x   2 2 2 2 50 10 3  x  28
Tương tự có: y  35 Như vậy 
AE  28, FA  35, EAF  60 . Ta tính được FE  7 21 . Câu 5:
Gọi giao của AC và NQ là O; giao của NQ và CD là L
Kẻ CK NQ; AH NQ K, H NQ 3 Theo giả thiết có:  
tan MQN   MQN  30 5  7 5 4  
tan ACD   ACD  33 4  1 6 1 Ta có: SSS
AH NQ CK NQ ANCQ ANQ CNQ  . .  2   AH  . AO cosOAH   1  CK
OC.cosOCK ScosOAH.N . Q AO OC ANCQ   2   OCK OAH  1   cosOAH.N . Q A C 2 Ta chứng minh số đo  OAH không đổi. Thật vậy:    
OAH  90  AOH  90  OCD OLC mà      OLC
  MQN OAH    OCD   MQN   90 90 90
MQN ACD (cố định).
29. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com 1 1 Vậy    S
cosOAH.AC.NQ cos MQN ACDcm ANCQ  .AC.NQ 21 2 2 2 Câu 6: a) Gọi 
COD    90 Ta chứng minh được      
IEG DOC, HFK DOC IEG HFK (1 ). 1 1 EG AC
Lại có áp dụng Ta-lét dễ thấy: EG AC, EI BD   3 3 EI BD
Gọi M là giao điểm của FK và AC, ta có:
FK FM MK AM .cot g  MC.cot g  AC.cot g FK AC
Tương tự có: FK  .c BD ot g   (3). FH BD
Từ (1), (2), (3) suy ra IGE ∼ HKF (c.g.c). b) Theo câu a) có   IGE ∼ H
KF EIG KHF
Gọi giao của EI và AF là N; giao của IG và HK là P. Vì  EI / /B ;
D BD HF EI HF HNI  90 Vì        
EIG KHF NHP AIP  180  HPI  360  NHP AIP HNP  90  IG HK .
----------Toán Học Sơ Đồ---------
30. TOÁN HỌC SƠ ĐỒ ‐ THCS.TOANMATH.com