Phương pháp giải hình 9 vị trí tương đối của hai đường tròn tiếp theo (có đáp án và lời giải chi tiết)

Bài 8. VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN (TT)
A. KIẾN THỨC TRỌNG TÂM
Vị trí tương đối của hai đường tròn Số điểm
Hệ thức giữa OO ' với Số tiếp tuyến  ;
O R và O ';rR  r chung
R và r chung
Hai đường tròn cắt nhau. 2
R  r  OO'  R  r 2
Hai đường tròn tiếp xúc nhau 1  Tiếp xúc ngoài.
OO'  R  r 1  Tiếp xúc trong.
OO'  R  r
Hai đường tròn không giao nhau. 0  Ngoài nhau.
OO'  R  r 4  Đựng nhau.
OO'  R  r 0  Đồng tâm. OO'  0 0
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Xác định vị trí tương đối của hai đường tròn
 Vận dụng lý thuyết về vị trí tương đối của hai đường tròn ở phần kiến thức trọng tâm.
Ví dụ 1. Điền vào ô trống trong bảng, biết rằng hai đường tròn ( ; O R) và (O ;
 r) có OO  d,R  r .
Vị trí tương đối của hai Số điểm chung
Hệ thức liên hệ giữa Số tiếp tuyến chung đường tròn
d , R, r Đựng nhau
d  R  r Tiếp xúc trong Ngoài nhau Cắt nhau Lời giải
Vị trí tương đối của hai Số điểm chung
Hệ thức liên hệ giữa Số tiếp tuyến chung đường tròn
d , R, r Đựng nhau 0
d  R  r 0 Tiếp xúc ngoài 1
d  R  r 3 Tiếp xúc trong 1
d  R  r 1 Ngoài nhau 0
d  R  r 4 Cắt nhau 2
R  r  d  R  r 2
Ví dụ 2. Điền các từ thích hợp vào chỗ trống (…):
a) Tâm của đường tròn có bán kính bằng 2 cm tiếp xúc ngoài với đường tròn ( O; 3 cm) nằm trên ...
................................................................................................................................................................
b) Tâm của đường tròn có bán kính bằng 5 cm tiếp xúc trong với đường tròn ( O;8 cm) nằm trên …
................................................................................................................................................................ Lời giải Trang 1
a) Tâm của đường tròn có bán kính bằng 2 cm tiếp xúc ngoài với đường tròn ( O; 3 cm) nằm trên
đường tròn ( O;5 cm).
b) Tâm của đường tròn có bán kính bằng 5 cm tiếp xúc trong với đường tròn ( O;8 cm) nằm trên
đường tròn ( O;3 cm).
Dạng 2: Các bài toán liên quan đến hai đường tròn tiếp xúc nhau
 Vận dụng tính chất đường nối tâm, tính chất hai tiếp tuyến cắt nhau; tính chất tiếp tuyến
chung của hai đường tròn; hệ thực lượng trong tam giác vuông…
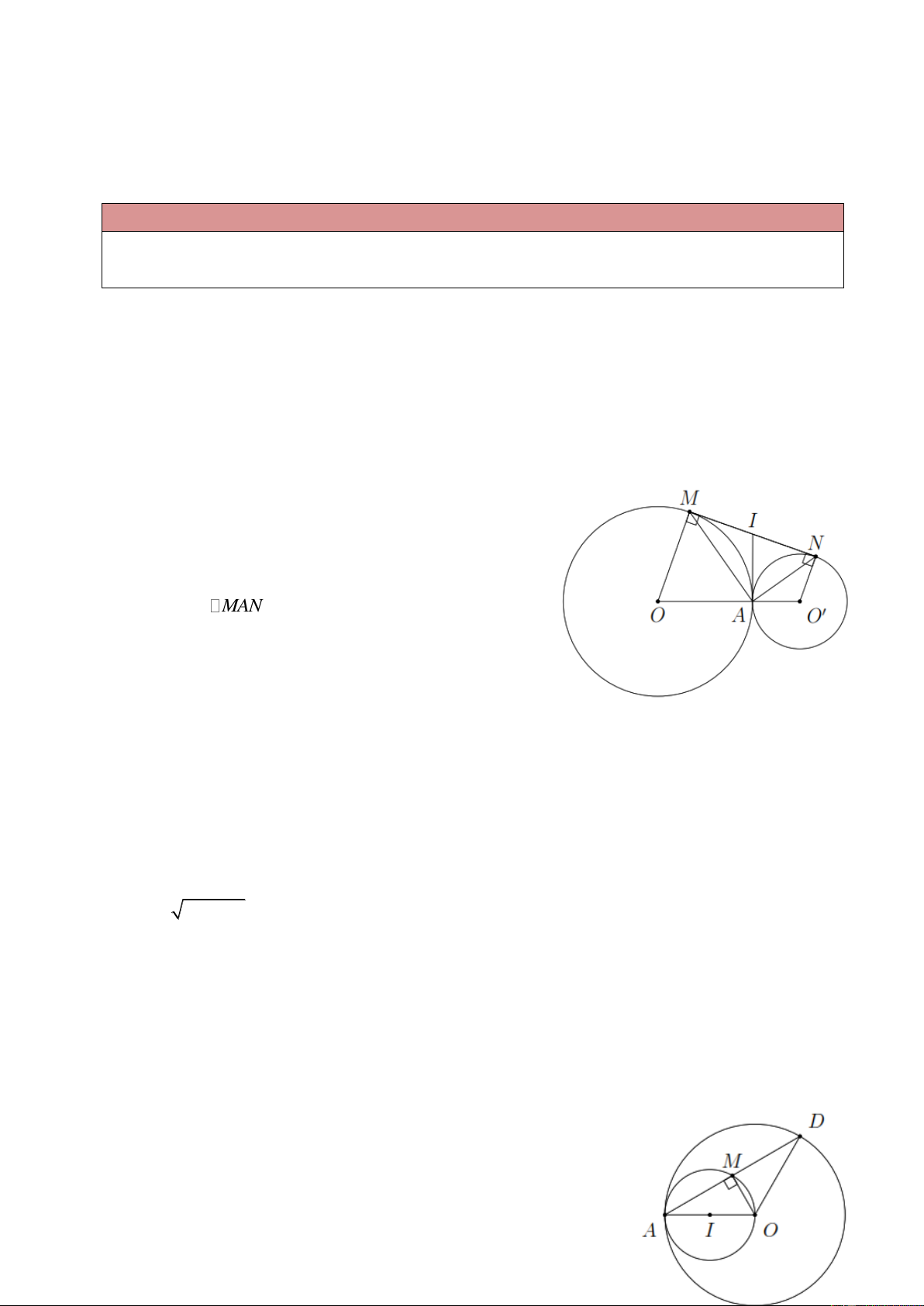
Ví dụ 3. Cho hai đường tròn (O) và (O )
 tiếp xúc ngoài tại A . Gọi MN là tiếp tuyến chung ngoài
của hai đường tròn với M  (O) và N  (O )  .
a) Tính số đo MAN .
b) Tính độ dài MN biết OA  9 cm; O A   4 cm. Lời giải
a) Từ A kẻ tiếp tuyến chung của hai đường tròn cắt MN tại I .
Theo tính chất của hai tiếp tuyến cắt nhau IM  IA  IN .
Từ đó suy ra MAN vuông tại A MAN 90   .
b) Theo tính chất hai tiếp tuyến cắt nhau ta có
IOlà phân giác AIM 
IOlà phân giác AIN.
Mà AIM kề bù AIN
 IO  IO
 IA  OAO A   6 cm
 MN  2IA 12 cm.
Ví dụ 4. Cho đường tròn ( ; O )
OA và đường tròn tâm I có đường kính . OA
a) Xác định vị trí tương đối của hai đường tròn.
b) Dây AD của đường tròn lớn cắt đường tròn nhỏ ở M . Chứng minh AM  M . D Lời giải
a) OI  OA IA nên hai đường tròn tiếp xúc trong. Trang 2 b) Ta có 
AMO có AO là đường kính của đường tròn ( I ) nên AMO  90 AMO 90    OM  AD .
Mà AOD cân tại O nên OM là đường trung tuyến.
C. BÀI TẬP VẬN DỤNG
Bài 1. Cho đường tròn ( O; 9 cm) và ( O ;3
 cm) tiếp xúc ngoài tại .
A Vẽ hai bán kính OB và O C 
song song với nhau và thuộc cùng một nửa mặt phẳng bờ OO .
a) Tính số đo của BAC.
b) Gọi I là giao điểm của BC và OO . Tính độ dài OI . Lời giải a) Ta có  OB O C
  AOB  AO C  180 . Ta lại có 180  AOB 180  AO C  BAO  CAO   2 2
360  ( AOB  AO C  )  2  90 . BAC 90   .
b) Áp dụng định lí Ta-lét ta có IO O C  1 IO 1   
  IO  6cm  IO  IOO O     cm. IO OB 3 IO  6 12 18 12 3
Bài 2. Cho đường tròn ( O; R ) và điểm M nằm bên ngoài đường tròn (R  OM  3R) . Vẽ đường
tròn (M ; 2R) .
a) Hai đường tròn (O) và (M ) có vị trí tướng đối như thế nào với nhau?
b) Gọi K là một giao điểm của hai đường tròn trên. Vẽ đường kính KOH của đường tròn (O) .
Chứng minh NH  NM. Lời giải
a) Ta có R  OM  3R nên ( O ) và ( M ) cắt nhau.
b) Vì MK  HK  2R  MHK cân tại K . Mà KNH 90 
( KH là đường kính).  KN  MN Trang 3
 KN là đường trung tuyến của MKH  NH  NM .
Bài 3. Cho ABC vuông tại A , đường cao AH . Gọi D là hình chiếu của H trên AB, E là hình chiếu của H trên .
AC Gọi ( O ) là tâm đường tròn kính HB , ( O ) là tâm đường tròn đường kính . HC Chứng mình:
a) Điểm D thuộc đường tròn (O), điểm E thuộc đường tròn (O )  ;
b) Hai đường tròn (O) và (O )  tiếp xúc ngoài;
c) AH là tiếp tuyến chung của hai đường tròn đó; d) AH  DE ;
e) DE là tiếp tuyến chung của hai đường tròn (O) và (O )  ;
f) Diện tích của tứ giác DEOO bằng nửa diện tích của tam giác . ABC Lời giải a) BDH 90 
nên D thuộc đường tròn đường kính BH .
b) Tương tự, E thuộc đường tròn đường kính CH .
c) OO  OH  O H
 nên ( O ) và (O ) tiếp xúc ngoài.
d) AH  OO nên AH là tiếp tuyến chung của (
O ) và ( O ).
e) ADHE là hình chữ nhật nên AH  DE .
Ta có OH  OD do đó ODH cân tại O .
 ODH  OHD .
Ta lại có ADHE là hình chữ nhật nên IDH  IHD . Mà IHD DHO 90 IDH ODH 90     
 OD  DE tại D .
Từ đó ta có DE là tiếp tuyến của đường tròn ( O ).
Chứng minh tương tự ta cũng có DE là tiếp tuyến của đường tròn ( O ).
Vậy DE là tiếp tuyến chung của hai đường tròn ( O ) và ( O ). 1 1  BH CH  1 1 1 f) S             (OD O E) DE AH AH BC S . DEO O   2 2  2 2  2 2 2 ABC
D. BÀI TẬP VỀ NHÀ Trang 4
Bài 4. Cho hai đường tròn (O) và (O )
 tiếp xúc ngoài tại A . Kẻ các đường kính AOB, AO . C  Gọi
DE là tiếp tuyến chung của hai đường tròn, D  (O) và E  (O )
 . Gọi M là giao điểm của BD và . CE
a) Tính số đo của DAE.
b) Tứ giác ADME là hình gì? Vì sao?
c) Chứng minh MA là tiếp tuyến chung của hai đường tròn. Lời giải
a) Từ A kẻ tiếp tuyến chung của hai đường tròn cắt DE tại I .
Theo tính chất của hai tiếp tuyến cắt nhau IE I A ID .
Từ đó suy ra DAE vuông tại A DAE 90   . b) Ta có
 BDA  90 (AB là đường kính của đường tròn (O));
 CEA  90 (AC là đường kính của đường tròn (O’)).
Do đó tứ giác ADME là hình chữ nhật vì có 3 góc vuông.
c) Ta có tứ giác ADME là hình chữ nhật nên ba điểm M , I , A thẳng hàng, suy ra AM là tiếp
tuyến chung của hai đường tròn.
Bài 5. Cho hai đường tròn đồng tâm O . Dây AB của đường tròn lớn cắt đường tròn nhỏ ở C và D
. Chứng minh AC  BD. Lời giải
Kẻ OM  AB . Theo quan hệ vuông góc giữa đường kính và dây cung ta có MA  MB 
  AC  BD . MC  MD --- HẾT --- Trang 5