

















Preview text:
Tài liệu học tập 4 2 - Kết Nối Tri Thức - - Chân Trời Sáng Tạo - - Cánh Diều - 20 LƯU HÀNH NỘI BỘ 5 2 20 Giá bán: 248.000 VNĐ
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025 MỤC LỤC
Phần SỐ VÀ ĐẠI SỐ .................................................................................................................................................. 5
Chương 1. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH ....................................................................................... 5
Bài 1 & 2. Phương trình bậc nhất hai ẩn – Hệ phương trình bậc nhất hai ẩn – Giải hệ phương trình
bậc nhất hai ẩn .................................................................................................................................................... 5
A. KIẾN THỨC CẦN NHỚ ......................................................................................................................................................... 5
B. BÀI TẬP MẪU ........................................................................................................................................................................... 6
Dạng 1. Nhận dạng và xác định hệ số a, b, c của phương trình bậc nhất hai ẩn ........................................................... 6
Dạng 2. Kiểm tra điểm M(xo;yo) có phải là nghiệm của phương trình bậc nhất hai ẩn .............................................. 6
Dạng 3. Biểu diễn nghiệm của phương trình bậc nhất hai ẩn trên mặt phẳng Oxy ..................................................... 6
Dạng 4. Nhận dạng hệ phương trình bậc nhất hai ẩn ............................................................................................................ 6
Dạng 5. Kiểm tra điểm M(xo;yo) có phải là nghiệm của hệ phương trình bậc nhất hai ẩn ........................................ 6
Dạng 6. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp đồ thị ....................................................................... 7
Dạng 7. Giải hệ phương trình bằng phương pháp thế ........................................................................................................... 7
Dạng 8. Giải hệ phương trình bằng phương pháp cộng đại số ........................................................................................... 7
Dạng 9. Toán thực tế (Giải toán bằng cách lập hệ phương trình) ..................................................................... 7
C. BÀI TẬP TỰ LUẬN .............................................................................................................................................................. 13
Dạng 1. Kiểm tra điểm M(xo;yo) có phải là nghiệm của phương trình bậc nhất hai ẩn ........................................... 13
Dạng 2. Biểu diễn nghiệm của phương trình bậc nhất hai ẩn trên mặt phẳng Oxy .................................................. 13
Dạng 3. Kiểm tra điểm M(xo;yo) có phải là nghiệm của hệ phương trình bậc nhất hai ẩn ..................................... 14
Dạng 4. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp đồ thị .................................................................... 14
Dạng 5. Giải hệ phương trình bằng phương pháp thế - phương pháp cộng ................................................................ 15
Dạng 6. Toán thực tế (Giải toán bằng cách lập hệ phương trình) .................................................................. 18
Một số bài toán nâng cao .......................................................................................................................................................... 28
Bài tập trắc nghiệm cuối chương ................................................................................................................... 28
Dạng 3. Phương trình bậc nhất hai ẩn ................................................................................................................................. 28
Dạng 4. Hệ hai phương trình bậc nhất hai ẩn ................................................................................................................... 29
Dạng 5. Giải hệ phương trình bằng phương pháp thế - phương pháp cộng ........................................................ 30
Dạng 6. Giải bài toán bằng cách lập phương trình – hệ phương trình ................................................................... 35
Chương 2. PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN ....................................... 39
Bài 1. Phương trình quy về phương trình bậc nhất một ẩn ..................................................................... 39
A. KIẾN THỨC CẦN NHỚ .......................................................................................................................................................... 39
B. BÀI TẬP MẪU ............................................................................................................................................................................ 39
C. BÀI TẬP TỰ LUẬN .................................................................................................................................................................. 40
Dạng 1. Giải phương trình ax + b = 0 và phương trình đưa được về dạng ax + b = 0 ...................................... 40 A(x) = 0
Dạng 2. Phương trình tích: A( x).B ( x) = 0
......................................................................................... 43 B ( x) . = 0
Dạng 3. Phương trình chứa ẩn ở mẫu...................................................................................................................................... 45 TRANG: 1
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
Dạng 4. Toán thực tế .................................................................................................................................................................... 48
Bài 2. Bất đẳng thức và tính chất ................................................................................................................... 54
A. KIẾN THỨC CƠ BẢN .......................................................................................................................................................... 54
B. BÀI TẬP MẪU ........................................................................................................................................................................ 54
Bài 3. Bất phương trình bậc nhất một ẩn ..................................................................................................... 56
A. KIẾN THỨC CƠ BẢN .......................................................................................................................................................... 56
B. BÀI TẬP MẪU ........................................................................................................................................................................ 57
C. BÀI TẬP TỰ LUẬN .............................................................................................................................................................. 57
PHƯƠNG TRÌNH CHỨA DẤU GIÁ TRỊ TUYỆT ĐỐI (BỔ TÚC THÊM)............................................................ 63
Bài tập cuối chương.......................................................................................................................................... 64
Dạng 1. Phương trình tích ........................................................................................................................................................ 64
Dạng 2. Phương trình chứa ẩn ở mẫu ................................................................................................................................. 65
Chương 3. CĂN THỨC .......................................................................................................................................... 70
Bài 1. Căn bậc hai và căn thức bậc 2 .............................................................................................................. 70
A. KIẾN THỨC CƠ BẢN .......................................................................................................................................................... 70
B. BÀI TẬP MẪU ........................................................................................................................................................................ 70
C. BÀI TẬP TỰ LUẬN .............................................................................................................................................................. 73
Bài 3. Khai căn bậc hai với phép nhân và phép chia .................................................................................. 76
A. KIẾN THỨC CƠ BẢN .......................................................................................................................................................... 76
B. BÀI TẬP MẪU ........................................................................................................................................................................ 76
C. BÀI TẬP TỰ LUẬN .............................................................................................................................................................. 77
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai ........................................................................ 81
A. KIẾN THỨC CƠ BẢN .......................................................................................................................................................... 81
B. BÀI TẬP MẪU ........................................................................................................................................................................ 81
C. BÀI TẬP TỰ LUẬN .............................................................................................................................................................. 82
Bài 10. Căn bậc ba và căn thức bậc 3 ............................................................................................................. 85
A. KIẾN THỨC CƠ BẢN .......................................................................................................................................................... 85
B. BÀI TẬP MẪU ........................................................................................................................................................................ 85
C. BÀI TẬP TỰ LUẬN .............................................................................................................................................................. 86
Bài tập trắc nghiệm cuối chương ................................................................................................................... 89
Dạng 1. Căn bậc hai – Biến đổi đơn giản biểu thức chứa căn ..................................................................................... 89
Dạng 2. Căn bậc ba .....................................................................................................................................................................101
Phần HÌNH HỌC VÀ ĐO LƯỜNG HÌNH HỌC PHẲNG ............................................................................... 103
Chương 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG ...................................................................... 103
Bài 1. Tỉ số lượng giác của góc nhọn ........................................................................................................... 103
A. KIẾN THỨC CƠ BẢN ........................................................................................................................................................103
B. BÀI TẬP MẪU ......................................................................................................................................................................104
C. BÀI TẬP TỰ LUẬN ............................................................................................................................................................105
Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông ................................................................................ 108 TRANG: 2
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
A. KIẾN THỨC CƠ BẢN ........................................................................................................................................................108
B. BÀI TẬP MẪU ......................................................................................................................................................................108
C. BÀI TẬP TỰ LUẬN ............................................................................................................................................................110
Bài tập trắc nghiệm cuối chương ................................................................................................................. 126
1. Một số hệ thức về cạnh và đường cao trong tam giác vuông ..............................................................................126
2. Tỉ số lượng giác của góc nhọn ..........................................................................................................................................129
3. Một số hệ thức về cạnh và góc trong tam giác vuông .............................................................................................131
4. Ứng dụng thực tế tỉ số lượng giác của góc nhọn ......................................................................................................134
Chương 5. ĐƯỜNG TRÒN .................................................................................................................................. 137
Bài 1. Đường tròn ........................................................................................................................................... 137
A. KIẾN THỨC CƠ BẢN ............................................................................................................................................................137
B. BÀI TẬP MẪU ..........................................................................................................................................................................137
1. Đường tròn - Tính đối xứng của đường tròn .............................................................................................................137
2. Đường kính và dây cung.....................................................................................................................................................137
C. BÀI TẬP TỰ LUẬN ................................................................................................................................................................138
1. Đường tròn - Tính đối xứng của đường tròn .............................................................................................................138
2. Đường kính và dây cung.....................................................................................................................................................139
Bài 14. Cung và dây của một đường tròn ................................................................................................... 141
A. KIẾN THỨC CƠ BẢN ............................................................................................................................................................141
B. BÀI TẬP MẪU ..........................................................................................................................................................................141
C. BÀI TẬP TỰ LUẬN ................................................................................................................................................................143
Bài 15. Độ dài cung tròn. Diện tích hình quạt tròn và hình vành khuyên ............................................ 147
A. KIẾN THỨC CƠ BẢN ............................................................................................................................................................147
B. BÀI TẬP MẪU ..........................................................................................................................................................................148
1. Độ dài cung tròn ....................................................................................................................................................................148
2. Hình quạt tròn ........................................................................................................................................................................148
3. Hình vành khuyên .................................................................................................................................................................149
C. BÀI TẬP TỰ LUẬN ................................................................................................................................................................150
1. Độ dài cung tròn ....................................................................................................................................................................150
2. Hình quạt tròn ........................................................................................................................................................................153
3. Hình vành khuyên .................................................................................................................................................................156
Bài 16. Vị trí tương đối giữa đường thằng và đường tròn ..................................................................... 162
A. KIẾN THỨC CƠ BẢN ............................................................................................................................................................162
B. BÀI TẬP MẪU ..........................................................................................................................................................................163
1. Vị trí tương đối của đường thẳng và đường tròn ....................................................................................................163
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn .........................................................................................................163
C. BÀI TẬP TỰ LUẬN ................................................................................................................................................................165
1. Vị trí tương đối của đường thẳng và đường tròn ....................................................................................................165
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn .........................................................................................................166 TRANG: 3
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
3. Tính chất hai tiếp tuyến cắt nhau ...................................................................................................................................169
Bài 17. Vị trí tương đối của hai đường tròn .............................................................................................. 173
A. KIẾN THỨC CƠ BẢN ............................................................................................................................................................173
B. BÀI TẬP MẪU ......................................................................................................................................................................174
C. BÀI TẬP TỰ LUẬN ................................................................................................................................................................174
Bài tập cuối chương........................................................................................................................................ 176
1. Đường tròn – Tính đối xứng của đường tròn .......................................................................................................176
2.Đường kính và dây cung ......................................................................................................................................................179
3.Góc ở tâm – Cung – Số đo cung .........................................................................................................................................181
4.Độ dài cung tròn .....................................................................................................................................................................184
5.Hình quạt tròn – Hình vành khuyên ...............................................................................................................................185
6.Vị trí tương đối của đường thẳng và đường tròn......................................................................................................187
7.Dấu hiệu nhận biết tiếp tuyến của đường tròn ..........................................................................................................190
8.Tính chất hai tiếp tuyến cắt nhau ....................................................................................................................................194
9.Vị trí tương đối của hai đường tròn ...............................................................................................................................196 TRANG: 4
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
Phần SỐ VÀ ĐẠI SỐ
Chương 1. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
Bài 1 & 2. Phương trình bậc nhất hai ẩn – Hệ phương
trình bậc nhất hai ẩn – Giải hệ phương trình bậc nhất hai ẩn
A. KIẾN THỨC CẦN NHỚ
1. Phương trình bậc nhất hai ẩn
• Là phương trình có dạng: ax + by = c. Trong đó a, b, c là các số cho trước, a ≠ 0 hoặc b ≠ 0.
• Nếu cặp số thực (x0; y0) thỏa mãn ax0 + by0 = c thì nó được gọi là nghiệm của phương trình ax + by = c.
• Trong mặt phẳng tọa độ Oxy, mỗi nghiệm (x0; y0) của phương trình ax + by = c được biểu diễn
bởi điểm có tọa độ (x0; y0).
2. Hệ phương trình bậc nhất hai ẩn ax + by = c (1)
• Hệ phương trình bậc nhất hai ẩn là hệ phương trình có dạng
a ' x + b ' y = c ' (2)
Trong đó a, b, a’, b’ là cá số thực cho trước và a2 + b2 ≠ 0; a’2 + b’2 ≠ 0, x và y là ẩn số.
• Nếu hai phương trình (1) và (2) có nghiệm chung (x0; y0) thì (x0; y0) được gọi là nghiệm của hệ
phương trình. Nếu hai phương trình (1) và (2) không có nghiệm chung thì hệ phương trình vô nghiệm.
• Giải hệ phương trình là tìm tất cả các nghiệm của nó.
3. Giải hệ phương trình bậc nhất hai ẩn
a. Giải hệ phương trình bằng phương pháp thế
Bước 1. Từ một phương trình của hệ phương trình, biểu diên một ẩn bằng ẩn còn lại, sau đó thế vào phương
trình còn lại, ta được phương trình mới chỉ còn một ẩn.
Bước 2. Giải phương trình một ẩn vừa có, rồi từ đó suy ra nghiệm của hệ phương trình đã cho.
Chú ý: Để lời giải được đơn giản, ở bước 1, ta thường chọn phương trình có các hệ số có giá trị
tuyệt đối không quá lớn (thường là 1 hoặc -1).
b. Giải hệ phương trình bằng phương pháp cộng đại số
Bước 1. Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một
ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau;
Bước 2. Cộng hay trừ từng vế hai phương trình của hệ phương trình để thu được một phương trình một ẩn;
Bước 3. Giải p/trình một ẩn vừa thu được từ đó suy ra nghiệm của hệ phương trình đã cho. TRANG: 5
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025 Lưu ý:
- Khi các hệ số của cùng một ẩn đối nhau thì ta cộng vế theo vế của hệ.
- Khi các hệ số của cùng một ẩn bằng nhau thì ta trừ vế theo vế của hệ.
- Khi hệ số của cùng một ẩn không bằng nhau cũng không đối nhau thì ta chọn nhân với số thích
hợp để đưa về hệ số của cùng một ẩn đối nhau (hoặc bằng nhau).
4. Các bước giải bài toán bằng cách lập hệ phương trình
Bước 1. Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp cho các ẩn số.
- Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.
- Lập hệ phương trình biểu thị sự tương quan giữa các đại lượng.
Bước 2. Giải hệ phương trình vừa thu được.
Bước 3. Kết luận
- Kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thỏa mãn điều kiện của ẩn. - Kết luận bài toán. B. BÀI TẬP MẪU
Dạng 1. Nhận dạng và xác định hệ số a, b, c của phương trình bậc nhất hai ẩn Bài 1.
Trong các phương trình sau, phương trình nào là phương trình bậc nhất hai ẩn? Xác định các
hệ số a, b, c của phương trình bậc nhất hai ẩn đó.
a) 3x + 5y = −3 b) 0x − 2y = 7 c) 4 − x + 0y = 5 d) 0x + 0y = 8
Dạng 2. Kiểm tra điểm M(xo;yo) có phải là nghiệm của phương trình bậc nhất hai ẩn Bài 2.
Kiểm tra cặp số sau có phải là nghiệm của phương trình 2x − y −1 = 0 hay không? a) (1;1) ; b) (0,5;3) . Bài 3.
Trong các cặp số (2;1) , (3; 1
− ) , (0;5) cặp số nào là nghiệm của phương trình x + 2y − 4 = 0
Dạng 3. Biểu diễn nghiệm của phương trình bậc nhất hai ẩn trên mặt phẳng Oxy Bài 4.
Biểu diễn tất cả các nghiệm của mỗi phương trình sau trên mặt phẳng tọa độ Oxy
a) 3x − y − 2 = 0 ;
b) 0x + 2y = 3 .
Dạng 4. Nhận dạng hệ phương trình bậc nhất hai ẩn Bài 5.
Trong các hệ phương trình sau, hệ phương trình nào là phương trình bậc nhất hai ẩn? x + 3y = 3 0x + 0y = 5 − 2x + 0y = 0 a) b) c) 2x + y = 4 − 2x + 7 y = 3 0x − 3y =1
Dạng 5. Kiểm tra điểm M(xo;yo) có phải là nghiệm của hệ phương trình bậc nhất hai ẩn Bài 6.
Hãy kiểm tra xem mỗi cặp số sau có là nghiệm của hệ phương trình tương ứng không? TRANG: 6
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
1 x −2y = 12 − 3x − 5y = 7 − a ) ( 1 ; 2 ) v à 2 ; b ) (2, 1) và 2x + y = 4 1 7 x + y = − 3 3 Hướng Dẫn: a) Có; b) Không
Dạng 6. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp đồ thị Bài 7.
Cho ba đường thẳng: dl : x + 2y = 5,d2 : 2x + y = 4.
a) Vẽ hai đường thẳng d1 và d2 trên cùng một hệ trục tọa độ.
b) Từ đổ thị của d1 và d2 tìm tọa độ giao điểm của hai đường thẳng đã cho.
c) Hỏi giao điểm đó có phải là nghiệm của hệ phương trình gồm hai đường thẳng d1 và d2 không?
Hướng Dẫn: a) Học sinh tự vẽ hình; b) (1; 2);
Dạng 7. Giải hệ phương trình bằng phương pháp thế Bài 8.
Giải các hệ phương trình sau bằng phương pháp thế 4x + 5y = 3 7x − 2y =1 5 x + 3y =1 a) b) c)
x − 3y = 5. 3 x + y = 6 2x + y = 1 − ĐS: a) ( ; x y) = (2; 1 − ) b) ( ; x y) = (1;3) c) ( ; x y) = ( 4 − ;7)
Dạng 8. Giải hệ phương trình bằng phương pháp cộng đại số Bài 9.
Giải các hệ phương trình sau bằng phương pháp cộng đại số. x − 3y =1 2x − y = 3 3 x + 4y =18 a) b) c) 2x + 3y =11 x − y =1 4x − 3y = 1 − ĐS: a) ( ; x y) = (4;1) b) ( ; x y) = (2;1) c) ( ; x y) = (2;3)
Bài 10. Xác định hệ số a và b để đồ thị hàm số y = ax + b đi qua hai điểm A(2; - 2) và B(-1; 3).
Dạng 9. Toán thực tế (Giải toán bằng cách lập hệ phương trình)
Dạng 9.1. Toán số học, phần trăm
• Biểu diễn số có hai chữ số: ab =10a + b trong đó a là chữ số hàng chục và 0 a 9 , a , b
là chữ số hàng đơn vị và 0 b 9,b .
• Biểu diễn số có ba chữ số: abc =100a +10b + c trong đó a là chữ số hàng trăm và 0 a 9,
a , b là chữ số hàng chục và 0 b 9,b ,c là chữ số hàng đơn vị và 0 c 9,c
Bài 11. Tìm hai số tự nhiên biết rằng hiệu của số lớn với số nhỏ bằng 1814 và nếu lấy số lớn chia số
nhỏ thì được thương là 9 và số dư là 182. Giải x y 1814
Đặt số lớn là x và số nhỏ là y. Theo đề bài, ta có hệ phương trình: . x 9y 182 TRANG: 7
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
ĐS: Vậy hai số cần tìm là 204 và 2018 .
Bài 12. Một người mua hai loại hàng và phải trả tổng cộng 2,17 triệu đồng, kể cả thuế giá trị gia tăng
(VAT) với mức 10% đối với loại hàng thứ nhất và 8% đối với loại hàng thứ hai. Nếu thuế VAT là
9% đối với cả hai loại hàng thì người đó phải trả tổng cộng 2,18 triệu đồng. Hỏi nếu không kể thuế
VAT thì người đó phải trả bao nhiêu cho mỗi loại hàng? Giải
Đặt x và y là giá của hai loại hàng không kể thuế VAT. x 0.10x y 0.08y 2.17
Theo đề bài, ta có hai phương trình sau: . x 0.09x y 0.09y 2.18
Giải hệ ta được: x = 0,5 (triệu đồng) và y = 1,5 (triệu đồng)
ĐS : Vậy loại thứ nhất 0,5 triệu đồng, loại thứ hai 1,5 triệu đồng.
Dạng 9.2. Toán năng suất công việc
• Năng suất được tính bằng tỉ số giữa khối lượng công việc và thời gian hoàn thành.
Bài 13. Trên một cánh đồng cấy 60 ha lúa giống mới và 40 ha lúa giống cũ. Thu hoạch được tất cả
460 tấn thóc. Hỏi năng suất mỗi loại lúa trên 1 ha là bao nhiêu biết rằng 3 ha trồng lúa mới thu hoạch
được ít hơn 4 ha trồng lúa cũ là 1 tấn. Giải
Đặt x là năng suất trên một ha của lúa giống mới và y là năng suất trên một ha của lúa giống cũ. 60x 40y 460
Theo đề bài, ta có hai phương trình sau:
. Giải hệ ta được x = 5; y = 4. 3x 4y 1
ĐS: Vậy năng suất 1 ha giống lúa mới là 5 tấn, năng suất 1 ha giống lúa cũ là 4 tấn.
Bài 14. Trong tháng đầu hai tổ sản xuất được 800 chi tiết máy. Sang tháng thứ 2 tổ 1 làm vượt mức
15%, tổ 2 vượt mức 20% do đó cuối tháng hai cả hai tổ sản xuất được 945 chi tiết máy. Hỏi trong
tháng đầu mỗi tổ sản xuất được bao nhiêu chi tiết máy. Giải
Đặt x là số chi tiết máy tổ 1 sản xuất trong tháng đầu và y là số chi tiết máy tổ 2 sản xuất trong tháng đầu. x y 800
Theo đề bài, ta có hai phương trình sau: x 0.15x y 0.20y 945
Giải hệ ta được: x = 300 (chi tiết) và y = 500 (chi tiết)
ĐS: Vậy trong tháng đầu tổ 1 sản xuất được 300 chi tiết máy, tổ 2 sản xuất được 500 chi tiết máy.
Dạng 9.3. Toán chuyển động
Một số lưu ý khi giải bài toán về chuyển động:
• Có ba đại lượng tham gia là quãng đường s , vận tốc v và thời gian t . TRANG: 8
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
• Ta có công th ức liên hệ giữa ba đại lượng s,v và t là s = vt .
Bài 15. Mỗi ngày ba của bạn An chở bạn ấy từ nhà đến trường mất 30 phút. Vì hôm nay là ngày thi
tuyển sinh nên ba bạn ấy muốn con mình đến trường sớm hơn, do đó ông ấy đã tăng vận tốc xe lên
15 (km/h) và đến sớm hơn thường ngày là 10 phút. Hỏi quãng đường từ nhà của bạn An đến trường là bao nhiêu km ? Giải
Đặt x km/h là tốc độ thường ngày ba An chở An đến trường. Ta có S = x.1/2 = x/2
Hôm nay, ngày thi tuyển sinh nên ba An đi với tốc độ (x + 15) km/h với thời gian là 20 phút
tương ứng 1/3 giờ. Ta có S = (x + 15).1/3
Theo đề bài, ta có phương trình: (x + 15).1/3 = x/2. Giải phương trình ta được: x = 30 km/h
Quãng đường từ nhà đến trường là x/2 = 30/2 = 15 km
ĐS: Vậy quãng đường từ nhà của bạn An đến trường là 15 km.
Bài 16. Một ô tô đi quãng đường AB với vận tốc 50 km/h rồi đi tiếp quãng đường BC với vận tốc 45
km/h. Biết quãng đường tổng cộng dài 165 km và thời gian ô tô đi trên quãng đường AB ít hơn thời
gian đi trên quãng đường BC là 30 phút. Tính thời gian ô tô đi trên mỗi đoạn đường. Giải
Gọi x là thời gian ô tô đi từ A đến B và y là thời gian ô tô đi từ B đến C.
Tổng quãng đường AB và BC là 165 km: AB + BC = 165
Thời gian đi trên quãng đường AB ít hơn thời gian đi trên quãng đường BC là 30 phút: y = x + 0.5 (giờ)
Áp dụng công thức vận tốc, ta có các phương trình sau: 50x = AB và 45y = BC.
Từ đó, ta có: AB + BC = 50x + 45y = 165 y x 0.5
Theo đề bài, ta có hai phương trình sau:
, ta được: x = 1,5 và y = 2. 50x 45y 165
ĐS: Vậy thời gian ô tô đi hết quãng đường AB là 1,5 giờ. Thời gian ô tô đi hết quãng đường BC là 2 giờ.
Bài 17. Một ôtô dự định đi từ A đến B trong một thời gian nhất định. Nếu xe chạy mỗi giờ nhanh hơn
10 km thì đến nơi sớm hơn dự định 3 giờ, còn nếu xe chạy chậm lại mỗi giờ 10 km thì đến nơi chậm
mất 5 giờ. Tính vận tốc của xe lúc ban đầu, thời gian dự định và chiều dài quãng đường AB. Giải
Gọi V, t là vận tốc và thời gian dự định ban đầu của oto đi từ A đến B. Ta có S = V.t
Vận tốc khi ôtô chạy nhanh hơn 10km/h là (V + 10)km/h; thời gian ôtô định chạy nhanh hơn dự
định là (t - 3) giờ. Ta có: S = (V + 10)*(t - 3)
Vận tốc khi ôtô chạy chậm hơn 10km/h là (V - 10)km/h; thời gian khi ôtô chạy chậm hơn dự
định là (t + 5) giờ. Theo công thức vận tốc, ta có: S = (V - 10)*(t + 5) S V 10 . t 3 3V 10t 30
Từ (1) và (2), ta có hệ phương trình: . S V 10 . t 5 5V 10t 50
Ta được: V = 40; t = 15 TRANG: 9
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
ĐS: Vậy vận tốc xe lúc đầu là 40km / h . Quãng đường AB dài 4015 = 600km .
Dạng 9.4. Toán có các yếu tố hình học Kiến thức cần nhớ:
• Diện tích hình chữ nhật: S = .
x y ( x là chiều rộng, y là chiều dài) 1
• Diện tích tam giác S = a h (h là chiều cao, a là cạnh đáy tương ứng). 2
• Độ dài cạnh huyền: 2 2 2
c = a + b (c là cạnh huyền; a,b là các cạnh góc vuông)
Bài 18. Một hình chữ nhật có chu vi bằng 28 cm. Tính chiều dài và chiều rộng của chữ nhật, biết rằng
nếu tăng chiều dài thêm 1 cm và tăng chiều rộng thêm 2 cm thì diện tích hình chữ nhật đó tăng thêm 2 25cm . Giải
Gọi chiều dài của hình chữ nhật là x và chiều rộng là y.
Chu vi của hình chữ nhật là 28 cm, ta có phương trình: 2x + 2y = 28 hay x + y = 14
Tăng chiều dài thêm 1 cm và tăng chiều rộng thêm 2 cm, diện tích của hình chữ nhật tăng thêm
25 cm2. Điều này có thể biểu diễn bằng phương trình: (x + 1) * (y + 2) = xy + 25 hay 2x + y = 23 x y 14
Ta có hệ phương trình: , x = 9 và y = 5. 2x y 23
ĐS: Vậy chiều dài của hình chữ nhật là 9 cm, chiều rộng của hình chữ nhật là 5 cm.
Bài 19. Một sân trường hình chữ nhật có chu vi 340 m. Biết 3 lần chiều dài hơn 4 lần chiều rộng là 20
m. Tính chiều dài và chiều rộng của sân trường. Giải
Gọi chiều dài của sân trường là x và chiều rộng là y. x y 170
Theo đề bài, ta có hệ phương trình:
, giải được x = 100 và y = 70 3x 4y 20
ĐS: Vậy chiều dài của sân trường là 100 m và chiều rộng là 70 m.
Dạng 9.5. Toán việc làm chung làm riêng
Những kiến thức cần nhớ:
• Có ba đại lương tham gia là: toàn bộ công việc, phần công việc làm được trong một đơn vị thời
gian (năng suất) và thời gian 1
• Nếu một đội làm xong công việc trong x giờ thì một ngày đội đó làm được công việc. x TRANG: 10
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
Bài 20. Hai đội xe chở cát để san lấp một khu đất. Nếu hai đội cùng làm thì trong 18 ngày xong công
việc. Nếu đội thứ nhất làm trong 6 ngày, sau đó đội thứ hai làm tiếp 8 ngày nữa thì được 40% công
việc. Hỏi mỗi đội làm một mình thì bao lâu xong công việc ? Giải
Gọi x, y (ngày) lần lượt là thời gian mà mỗi đội làm 1 mình thì xong công việc. Do đó năng suất
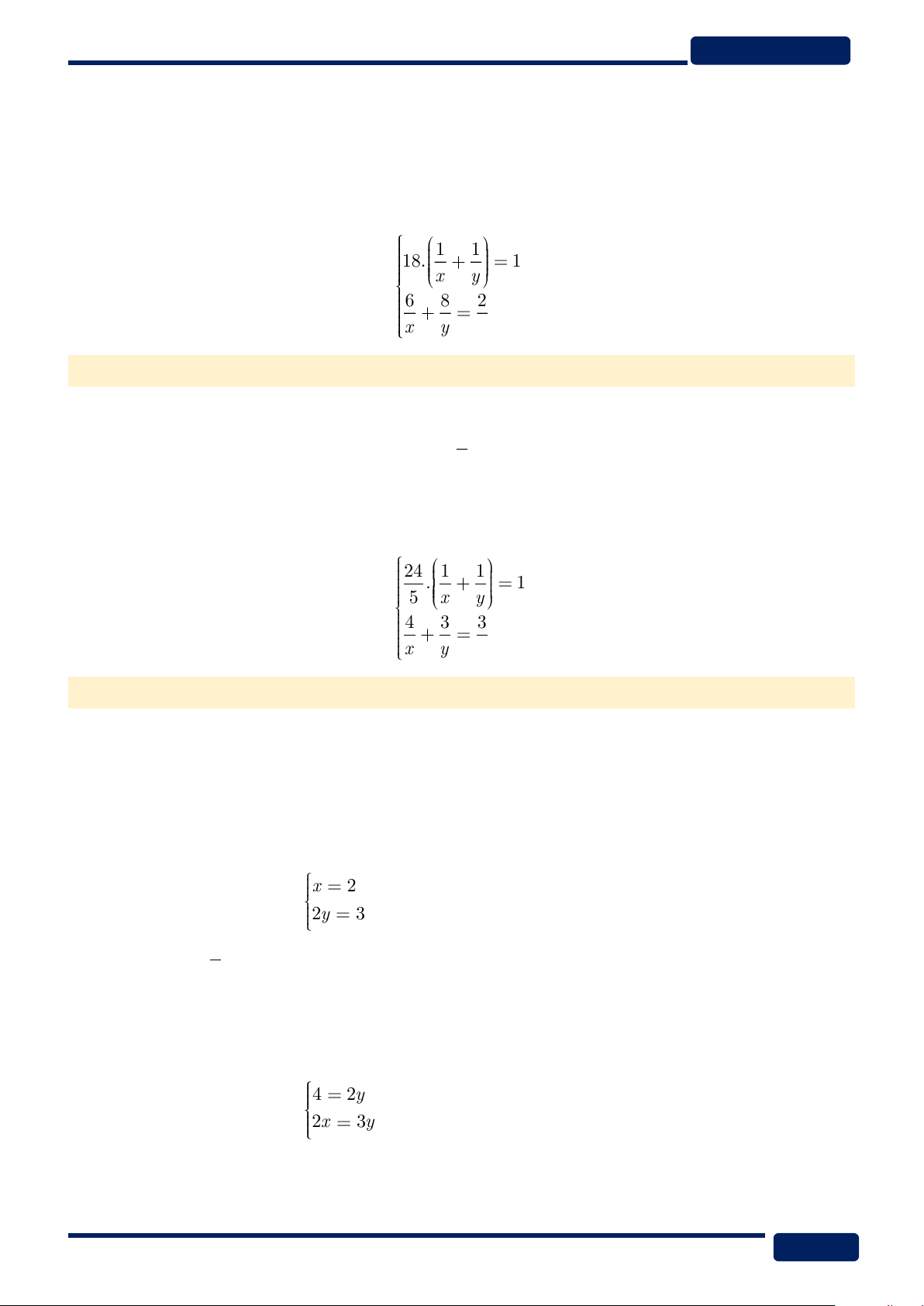
làm việc của mỗi đội trong một ngày lần lượt là 1/x và 1/y. 1 1 18. 1
Theo đề bài, ta có hệ phương trình: x y
, giải được x = 45 và y = 30 6 8 2 x y 5
ĐS: Vậy đội một làm 45 ngày và đội hai làm 30 ngày.
Bài 21. Hai vòi nước cùng chảy vào một bể thì sau 4 giờ 48 phút bể đầy. Nếu vòi I chảy trong 4 giờ, 3
vòi II chảy trong 3 giờ thì cả hai vòi chảy được bể. Tính thời gian mỗi vòi chảy một mình đầy bể. 4 Giải
Gọi x, y (giờ) lần lượt là thời gian mà mỗi vòi chảy 1 mình thì đầy bể. Do đó năng suất làm việc
của mỗi vòi trong 1 giờ lần lượt là 1/x và 1/y. 24 1 1 . 1
Theo đề bài, ta có hệ phương trình: 5 x y
, giải được x = 8 và y = 12. 4 3 3 x y 4
ĐS: Vậy thời gian vòi một chảy đầy bể là 12 giờ và vòi hai chảy đầy bể là 8 giờ.
Dạng 9.6. Cân bằng phương trình phản ứng hóa học
Bài 22. (SGK CTST) Cân bằng phương trình hóa học sau bằng phương pháp đại số: Al + O → Al O 2 2 3 Giải
Gọi x, y lần lượt là hệ số cân bằng tại Al và O2 ta được: xAl + yO → Al O 2 2 3 x 2
Ta có hệ phương trình:
, giải được x = 2 và y = 3/2. 2y 3 3
Vậy 2Al + O → Al O 2 2 3 2
Bài 23. (SGK KNTT) Tìm hệ số x, y trong phản ứng hóa học đã được cân bằng sau: 4Al + O x 2 → A y l2 3 O Giải 4 2y
Ta có hệ phương trình:
, giải được x = 3 và y = 2. 2x 3y Vậy 4Al + 3O2 → 2Al2 3 O
Bài 24. (SGK C Diều) Tìm các hệ số x, y để cân bằng phương trình phản ứng hóa học: F x 3 e O4 + O2 → F y e2 3 O TRANG: 11
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025 Giải 3x 2y
Ta có hệ phương trình:
, giải được x = 4 và y = 6. Vậy 4Fe O + O → 6Fe O 4x 2 3y 3 4 2 2 3
Bài 25. (SGK CKP) Tìm các hệ số x, y để cân bằng phương trình phản ứng hóa học: Z x n + 4 H y NO3 → Z x n(NO3)2 + 2NO + 2 H y 2O Giải
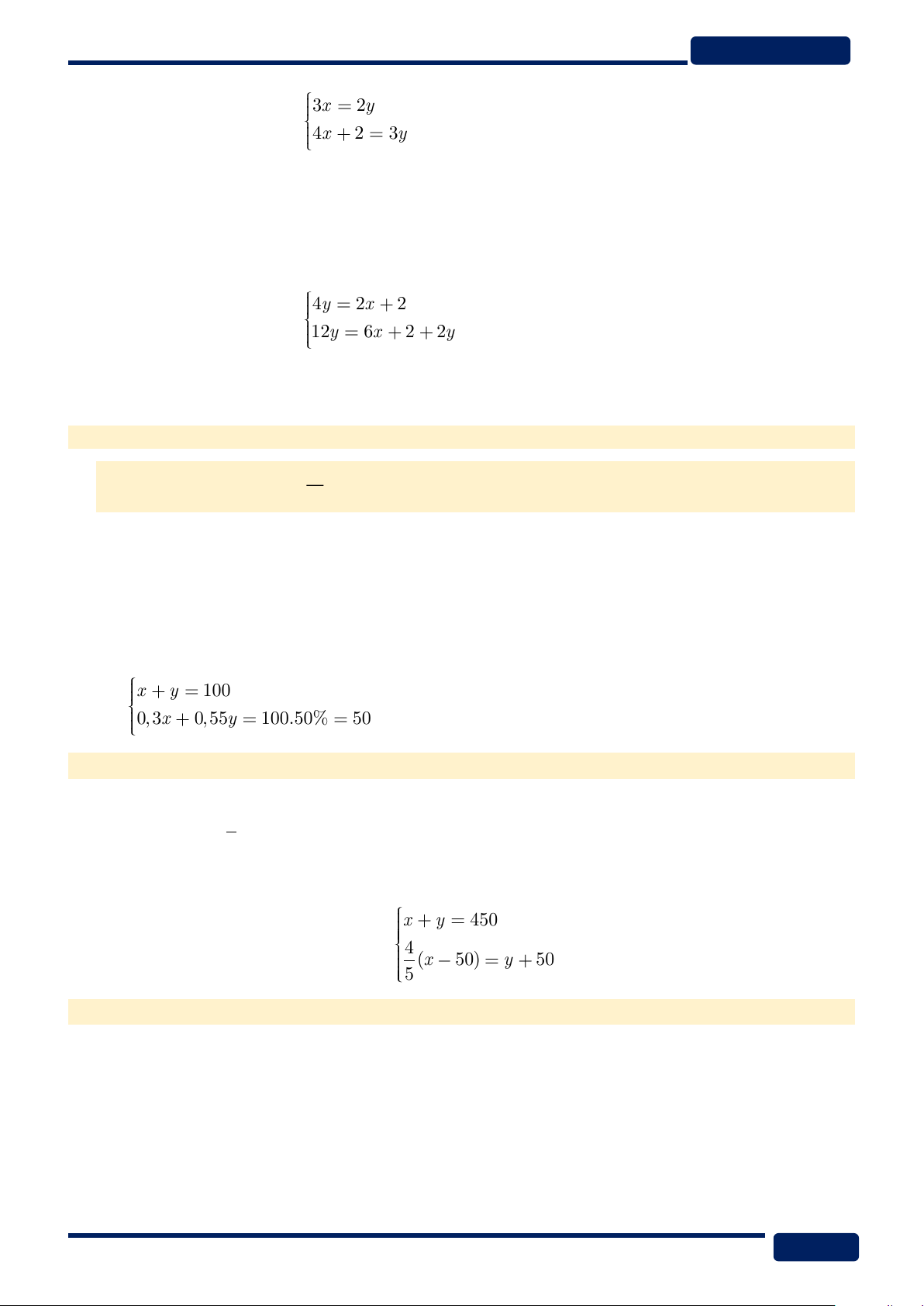
Vì chỉ số Zn và H ở hai bên phương trình phản ứng bằng nhau nên ta chỉ quan tâm đến chỉ số của N và O. 4y 2x 2
Ta có hệ phương trình:
, giải được x = 3 và y = 2. 12y 6x 2 2y
Vậy 3Zn + 8HNO3 → 3Zn(NO3)2 + 2NO + 4H2O
Dạng 9.7. Dạng toán khác
Những kiến thức cần nhớ: • m
Thể tích dung dịch V =
( V là thể tích dung dịch, m là khối lượng, D là khối lượng riêng). D
Bài 26. Một dung dịch chứa 30% axit nitơric (tính theo thể tích) và một dung dịch khác chứa 55% axit
nitơric. Cần phải trộn thêm bao nhiêu lít dung dịch loại 1 và loại 2 để được 100 lít dung dịch 50% axit nitơric? Giải
Gọi x là lượng dung dịch 30% cần sử dụng và y là lượng dung dịch 55% cần sử dụng. Bạn muốn
tạo ra 100 lít dung dịch 50% axít nitơric, vì vậy chúng ta có hệ phương trình: x y 100
, giải được x = 20 lít và y = 80 lít 0, 3x 0, 55y 100.50% 50
ĐS: Vậy lượng dung dịch loại 1 là 20 lít và loại 2 là 80 lít.
Bài 27. Hai giá sách có 450 cuốn. Nếu chuyển 50 cuốn từ giá thứ nhất sang giá thứ hai thì số sách trên 4
giá thứ hai bằng số sách giá thứ nhất. Tính số sách trên mỗi giá. 5 Giải
Gọi x, y (số sách) lần lượt là số sách trên hai giá. x y 450
Theo đề bài, ta có hệ phương trình: 4
, giải được x = 300 và y = 150. (x 50) y 50 5
ĐS: Vậy số sách ở giá thứ nhất là 300 cuốn, ở giá thứ hai là 150 cuốn.
Bài 28. Hai anh Quang và Bình góp vốn cùng kinh doanh. Anh Quang góp 13 triệu đồng, anh Bình
góp 15 triệu đồng. Sau một thời gian kinh doanh lãi được 7 triệu đồng. Lãi được chia đều theo tỉ lệ
góp vốn. Tính số lãi mỗi anh được hưởng. Giải
Tổng vốn đầu tư là 13 triệu đồng (anh Quang) + 15 triệu đồng (anh Bình) = 28 triệu đồng.
Tỷ lệ góp vốn của anh Quang là 13/28 = 0.464, và tỷ lệ góp vốn của anh Bình là 15/28 = 0.536.
Vì lợi nhuận được chia theo tỷ lệ vốn góp, nên:
Anh Quang nhận được 7. 0,464 = 3.25 triệu đồng. TRANG: 12
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
Anh Bình nhận được 7.0,536 = 3.75 triệu đồng.
ĐS: Vậy anh Quang được lãi 3750000 đồng và anh Bình được lãi 3250000 đồng.
C. BÀI TẬP TỰ LUẬN
Dạng 1. Kiểm tra điểm M(xo;yo) có phải là nghiệm của phương trình bậc nhất hai ẩn Bài 1.
Trong các cặp số (12; 1), (1; 1), (2; - 3), (1; -2), cặp số nào là nghiệm của phương trình bậc
nhất hai ẩn 2x – 5y = 19.
Hướng Dẫn: Cặp số (1; 1) không là nghiệm, (2; -3) là nghiệm, (1; -2) không là nghiệm của phương trình. Bài 2.
Cặp số (-2; 3) là nghiệm của phương trình nào trong các phương trình sau: a) x – y = 1; b) 2x + 3y = 5; c) 2x + y = -4; d) 2x – y = -7; e) x – 3y = -10; f) 2x – y = 2.
Hướng Dẫn: (-2; 3) là nghiệm của các phương trình b) và d). Bài 3.
Trong các cặp số (0;2), (-1; -8), (1; 1), (3; -2), (1; -6), cặp số nào là nghiệm của phương trình 3x – 2y = 13 ?
Hướng Dẫn: (-1; -8), (3; -2)
Dạng 2. Biểu diễn nghiệm của phương trình bậc nhất hai ẩn trên mặt phẳng Oxy Bài 4.
Biểu diễn tập nghiệm của các phương trình sau trên mặt phẳng tọa độ Oxy a) 2x – 3y = 5; b) 4x + 0y = 12; c) 0x – 3y = 6. x x = 3 x Hướng Dẫn:a) 2 5 b) c) y = x − y y = 2 − 3 3 Bài 5.
Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của các phương trình sau trên mặt phẳng tọa độ: a) 2x – y = 3; b) 5x + 0y = 20; c) 0x – 8y = 16. x x = 4 x Hướng Dẫn: a) b) c) y = 2x − 3 y y = 2 − Bài 6.
Viết công thức nghiệm tổng quát và biểu diễn tập nghiệm của các phương trình sau trên mặt phẳng tọa độ: a) x – 3y = 6; b) 3y – 2x = 3; c) 7x + 0y = 14; d) 0x – 4y = 8; e) 2x – y = 5; f) 3y + x = 0. x x x = 2 Hướng Dẫn: a) x ; b) 2 c) y = − 2 y = x +1 y 3 3 x x x d) ; e) f) 1 y = 2 − y = 2x − 5 y = − x 3 TRANG: 13
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
Dạng 3. Kiểm tra điểm M(x
o;yo) có phải là nghiệm của hệ phương trình bậc nhất hai ẩn Bài 7.
Kiểm tra xem cặp số (-4; 5) là nghiệm của hệ phương trình nào trong các hệ phương trình sau đây: 1 − = − x 2y 12 2x + y = 3 − a) 2 ; b) . 3 − x + 2y = 21 1 7 x + y = − 3 3
Hướng Dẫn: a) không là nghiệm. b) là nghiệm. Bài 8.
Hãy kiểm tra xem mỗi cặp số sau có là nghiệm của hệ phương trình tương ứng không?
1 x −2y = 12 − 3x − 5y = 7 − a ) ( 1 ; 2 ) v à 2 ; b ) (2, 1) và 2x + y = 4 1 7 x + y = − 3 3 Hướng Dẫn: a) Có; b) Không Bài 9.
Hãy kiểm tra xem mỗi cặp số sau có là nghiệm của hệ phương trình tương ứng không: 2 − x + y = 3 2x + y = 3 − a) (1, 1) và ; b) (-2; 1) và . x + y = 7 x + 3y =1 Hướng Dẫn: a) Không b) Có
Dạng 4. Giải hệ phương trình bậc nhất hai ẩn bằng phương pháp đồ thị
Bài 10. Cho hai phương trình đường thẳng: d1 : 2x – y = 5 và d2 : x – 2y = 1.
a) Vẽ hai đường thẳng d1 và d2 trên cùng một hệ trục tọa độ.
b) Từ đổ thị của d1 và d2 tìm tọa độ giao điểm của hai đường thẳng đã cho.
c) Hỏi giao điểm đó có phải là nghiệm của hệ phương trình gồm hai đường thẳng d1 và d2 không?
Hướng Dẫn: a) Học sinh tự vẽ hình. b) (3; 1) c) là nghiệm
Bài 11. Cho ba đường thẳng: dl : x + 2y = 5,d2 : 2x + y = 4.
a) Vẽ hai đường thẳng d1 và d2 trên cùng một hệ trục tọa độ.
b) Từ đổ thị của d1 và d2 tìm tọa độ giao điểm của hai đường thẳng đã cho.
c) Hỏi giao điểm đó có phải là nghiệm của hệ phương trình gồm hai đường thẳng d1 và d2 không?
Hướng Dẫn: a) Học sinh tự vẽ hình. b) (1; 2) c) là nghiệm
Bài 12. Cho hai đường thẳng d1 : 2x + y = 3 và d2 : x - 4y = 6.
a) Vẽ hai đường thẳng d1 và d2 trên cùng một hệ trục tọa độ.
b) Từ đổ thị của d1 và d2 tìm tọa độ giao điểm của hai đường thẳng đã cho. TRANG: 14
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
c) Hỏi giao điểm đó có phải là nghiệm của hệ phương trình gồm hai đường thẳng d 1 và d2 không?
Hướng Dẫn: a) Học sinh tự vẽ hình. b) (2; -1) c) là nghiệm
Dạng 5. Giải hệ phương trình bằng phương pháp thế - phương pháp cộng
Bài 13. Giải các hệ phương trình sau bằng phương pháp THẾ: x − 2 y = 1 7x − 2y = 1 x + y = 3 a. b. c. 2x + y = 7 3x + y = 6 x − 2y = 0
2x + y − 4 = 0
2x + 3y − 7 = 0 5 x + 6y =17 d. e. f.
x + 2y − 5 = 0
x + 2y − 4 = 0 9 x − y = 7 5 x − 3y = 4 5 x − 3y = 4 4x − 2y = 4 g. h. i. x + 2y = 3 x + 2y = 3 x + 5y =17,5 2x − y =1 3 x + 5y =1 2x − 3y = 1 − j. k. l. 4 − x + 2y = 2 2x − y = 8 − x + y = 8 x − 2y =1 3 x − y = 5 2x + y = 7 m. n. o. 2x − y = 4 5 x + 2y = 28 −x + 4y =10 3 − x + 2y = 3 2x − 3y = 1 − x − 2y =1 p. q. r. 2x + y = 5 x + y = 8 2x − y = 4
Bài 14. Giải các hệ phương trình sau bằng phương phấp CỘNG: 4x − 2y = 3 2x + 3y = 5
3x − 4y + 2 = 0 a. b. c. 6x − 3y = 5 4x + 6y = 10 5x + 2y = 14 2x + 5y = 3 2x − y =1 4x − 2y = 4 d. e. f.
3x − 2y = 14 4 − x + 2y = 2 x + 5y =17,5 3 x − 4y = 7 − 3 x + 3y =1 3 x − y = 5 g. h. i. 3 x + 4y = 7
−x +1,5y = 0 − ,5 5 x + 2y = 28 3 x + 5y =1 2x − 3y = 1 − x − 2y =1 j. k. l. 2x − y = 8 − x + y = 8 2x − y = 4 5
x 3 + y = 2 2 , 0 2x + 1 , 0 y = 3 , 0
0,75x − 3, 2y =10 m. n. o.
x 6 − y 2 = 2 3x + y = 5
x 3 − y 2 = 4 3 2x + y = 7
2x + y − 4 = 0
2x + 3y − 7 = 0 p. q. r.
−x + 4y = 10
x + 2y − 5 = 0
x + 2y − 4 = 0 TRANG: 15
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
Bài 15. Giải các hệ phương trình sau:
− x + 3y = −10 2x + y = 4 2x + y = 7 1) 2) 3) x − 5y =16
2x + 0y − 6 = 0
− x + 4y =10 2x + y = 5 x − 2y = 2
3x − 5y = −18 4) 5) 6) x + 7y = 9 2x − 4y = 1 x + 2y = 5
5x + 3y = −7
− 2x + y = −3 2x − y = 2 7) 8) 9)
3x − y = −8 3x + 4y = 10
4x − 2y − 4 = 0
2x − y = x + 3y + 3 x + y = 2 x + 2y = 4 10) 11) 12) 3x − 3y = 9 x + 3y = 6 2x + 9y = 18 2x − 4y = 3
x − 2y = −5
− 2x + y = −3 13) 14) 15) − x + 2y =1
3x + 4y = −5 x + y = 3 3x − 2y =12 2x − y =10 x − y = 0 16) 17) 18) 4x + y = 5 5x + 2y = 6 2x + y = −5 3x + y = −2 2x + y = 0 − x + y = 3 20) 21) 22)
− 9x − 3y = 6 x − 4y = 0 x + 2y = 3
− x + 3y = −10
2x + y = −3x − 20 x − y = 2 23) 24) 25) 2x + y = −1
4x + y = x − 2y −12 3x − 2y = 9 5x − y = 1 3x + y = 2 2x − y = 3 26) 27) 28)
10x − 2y = 0 6x + 2y = 3 3x + y = 7 2x + y = 7 x + 2y = −2
x − 2y = −5 29) 30) 31)
− x + 2y = −5 2x − y = 1 3x + 2y =1 2x + y = 5 2x + y = 5 x + y = −1 32) 33) 34) x − y = 1 3x − y = 15
3x − 2y = −8 0x + y = 3 3 x − 2y = 5 3 x + 2y = 7 35) 36) 37)
x − 2y = −4 2x + y = 8 2x + y = 4 2x − y = 3 x − y =1 3x − y = 5 38) 39) 40) ; 3 x + y = 7 3 x + 2y = 3 5 x + 2y = 23 3 x + 5y =1 3
x − 4y + 2 = 0 x − y = 3 41) ; 42) 43) ; 2x − y = 8 − 5 x + 2y =14 3 x − 4y = 2 3x + = 2 y 0 x + 5y = 7 x y − = 1 44) 2 45) 2 3 . 46) 3x − 2y = 4 x + y 2y 5 5 x −8y = 3 − = 2 3 2 TRANG: 16
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
( 2 −1)x − y= 2
−x − 2y = 3 x + 7 = 2 − 3 47) . 48) . 49) .
x + ( 2 +1)y =1
2x + 2y = − 6 2 − x − 2 7 y = 11
Bài 16. Giải hệ phương trình: ( x + y )+(x + 2y) = 2 − 3
(y − 5) + 2(x − 3) = 0 a) . b) ; 3 − + + − − =
( x + y) + ( x − 2y) = 1
7(x 4) 3(x y 1) 14 0
(x +1)(y −1) = (x − 2)(y +1) −1 5
(x + 2y) − 3(x − y) = 99 c) . d) .
2(x − 2)y − x = 2xy − 3
x − 3y = 7x − 4y −17
(x +1)(y −1) = xy −1
2(x + y) + 3(x − y) = 4 e) . f) ;
(x − 3)(y − 3) = xy − 3
(x + y) + 2(x − y) = 5
(x +1)(y −1) = xy −1 3 x − 2 (2y − )1 = 0 g) . h) .
(x − 3)(y + 3) = xy − 3 3 x + 2y = 2 (7 − x) x
( y + 5) + 2y = xy + 9 3
(x +1) + 2(x + 2y) = 4 i) ( . j) 3x + + − + = ) 1 (2y − ) 1 = 6xy
4(x 1) (x 2y) 9 3 1 x + y 2 x + y = + = 3 3 3 k) 4 2 l) 3 4x − y x x + y = 1 + = 1 4 6 4 5
(x + 2y) − 3(x − y) = 99 4x − 3 m) ; x + y =
x − 3y = 7x − 4y −17 n) 5 ; 15 − 9y x + 3y = 14
2(x + y) + 3(x − y) = 9
(x −1)(y + 3) = xy + 27 o) ; p) . 5
(x + y) − 7(x − y) = 8
(x − 2)(y +1) = xy + 8 5
(x + 2y) = 3x −1 q)
2x + 4 = 3(x − 5y) −12. ĐS: a) 1 ; 1 − . b) (3; 5) c) 17 4 ; d) (4; 7) e) (2; 2) f) 1 13 − ;− g) Vô 2 11 11 2 2 10 4 − x = 4 nghiệm h) (2;2) . i) (1;2) . j) (1; ) 1 − . k) ( ; ) l) (2; 5) m) 7 7 y = 7 29 33 −
n) (12; − 3) o) (2; 1); p) (10; 0) q) ; 8 40
Bài 17. Xác định hệ số a và b để đồ thị hàm số y = ax + b đi qua hai điểm A và B trong mỗi trường hợp sau: a) A(2; 3) và B(5; 4). b) A(1; 2) và B3; 8). c) A(2; 1) và B(4; - 2). d) A(- 2; - 1) và B(4; 5). e) A(1 ; 1), B(2 ; -1) f) A(1; - 2) và B(4; 2). g) A(1; - 3) và B(2; 1). h) A(4; - 3) và B(2; - 1). i) A(1; 4) và B( - 2; 1). TRANG: 17
TOÁN 9 (KNTT) - HK1 - TÀI LIỆU HỌC TẬP NĂM HỌC: 2024 - 2025
j) Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 5 và cắt trục hoành tại điểm có hoành độ bằng -2
Dạng 6. Toán thực tế (Giải toán bằng cách lập hệ phương trình)
Dạng 6.1. Toán số học, phần trăm
Bài 18. Cho một số có hai chữ số. Nếu đổi chỗ hai chữ số của nó thì được một số lớn hơn số đã cho là
63. Tổng của số đã cho và số mới tạo thành bằng 99. Tìm số đã cho.
ĐS: Vậy số cần tìm là 18.
Bài 19. Tìm 2 số biết tổng của chúng bằng 1006, nếu lấy số lớn chia cho số bé được thương là 2 và số dư 124.
ĐS: số lơn là 712, số bé là 294.
Bài 20. (SGK CTST – KNTT) Tìm hai số nguyên dương biết tổng của chúng bằng 1006, nếu lấy số
lớn chia cho số bé được thương là 2 và dư là 124.
Bài 21. (SGK KNTT) Tìm số tự nhiên N có hai chữ số, biết rằng tổng của hai chữ số đó bằng 12, và
nếu viết hai chữ số đó theo thứ tự ngược lại thì được một số lớn hơn N là 36 đơn vị.
Bài 22. (SGK KNTT) Tìm số tự nhiên N có hai chữ số, biết rằng nếu viết thêm chữ số 3 vào giữa hai
chữ số của N thì được một số lớn hơn số 2N là 585 đơn vị, và nếu viết hai chữ số của N theo thứ tự
ngược lại thì được một số nhỏ hơn số N là 18 đơn vị.
Bài 23. Tìm số tự nhiên có hai chữ số, biết hiệu giữa chữ số hàng chục và chữ số hàng đơn vị là 5 .
Nếu lấy số đã cho chia cho số viết theo thứ tự ngược lại ta được thương là 3 và số dư là 13.
ĐS: Vậy số cần tìm là 61 .
Bài 24. Tìm một số có hai chữ số, biết rằng tổng các chữ số của số đó bằng 9 và viết các chữ số theo 2
thứ tự ngược lại thì được một số bằng số ban đầu. 9
ĐS: Vậy số cần tìm là 81 .
Bài 25. (SGK CTST) Trong tháng thứ nhất, hai tổ sản xuất được 800 chi tiết máy. So với tháng thứ
nhất, trong tháng thứ hai, tổ một sản xuất vượt 15%, tổ hai sản xuất vượt 20% nên trong tháng này,
cả hai tổ sản xuất được 945 chi tiết máy. Hỏi trong tháng thứ nhất mỗi tổ sản xuất được bao nhiêu chi tiết máy?
Bài 26. (SGK CTST) Nhân kỉ niệm ngày Quốc khánh 2/9, một nhà sách giảm giá mỗi cây bút bi là
20% và mỗi quyển vở là 10% so với giá niêm yết. Bạn Thanh vào nhà sách mua 20 quyển vở và 10
cây bút bi. Khi tính tiền, bạn Thanh đưa 175000 đồng và được trả lại 3000 đồng.Tính giá niêm yết
của mỗi quyển vở và mỗi cây bút bi, biết rằng tổng số tiền phải trả nếu không được giảm giá là 195000 đồng.
Bài 27. (SGK CTST) Nhà máy luyện thép hiện có sẵn loại thép chứa 10% carbon và loại thép chứa
20% carbon. Giả sử trong quá trình luyện thép các nguyên liệu không bị hao hụt. Tính khối lượng
thép mỗi loại cần dùng để luyện được 1000 tấn thép chưa 16% carbon từ hai loại thép trên. TRANG: 18




