Các dạng toán hệ thức lượng trong tam giác vuông

Tài liệu gồm 35 trang, phân loại và hướng dẫn giải các dạng toán hệ thức lượng trong tam giác vuông, giúp học sinh lớp 9 tham khảo khi học chương trình Toán 9 (tập 1) phần Hình học chương 1. Mời bạn đọc đón xem.

76 38 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 1: Hệ thức lượng trong tam giác vuông

Môn: Toán 9

Thông tin:

35 trang 3 tháng trước

Tác giả:

Profile Hà Việt Anh
MỤC LỤC
VẤN ĐỀ 1. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG (PHẦN
1) 3
A. TÓM TẮT LÝ THUYẾT ....................................................................................................... 3
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ......................................................................................... 3
C.BÀI TẬP VỀ NHÀ ...................................................................................................................... 4
VẤN ĐỀ 2. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG (PHẦN
II) ............................................................................................................................................................ 6
A. TÓM TẮT LÝ THUYẾT ............................................................................................................ 6
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ........................................................................................... 6
Dạng 2. Chứng minh các hệ thức liên quan đến tam giác vuông ....................................... 6
VẤN ĐỀ 3 : LUYỆN TẬP HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC
VUÔNG ................................................................................................................................................ 8
A. TÓM TẮT LÝ THUYẾT ............................................................................................................ 8
B. BÀI TẬP TỰ LUYỆN ................................................................................................................. 8
C. BÀI TẬP VỀ NHÀ ..................................................................................................................... 9
VẤN ĐỀ 4. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN I) ............................................... 10
A. TÓM TẮT LÝ THUYẾT .......................................................................................................... 10
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ......................................................................................... 10
Dạng 1. Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc ...................................... 10
C. BÀI TẬP VỀ NHÀ ................................................................................................................... 11
VẤN ĐỀ 5. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN II) ............................................. 13
A. TÓM TẮT LÝ THUYẾT ..................................................................................................... 13
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ....................................................................................... 13
Dạng 2. Sắp thứ tự dãy các tỉ số lượng giác ......................................................................... 13
Dạng 3.Dựng góc nhọn
α
biết tỉ số lượng giác của nó là
.
m
n
.......................................... 14
C. BÀI TẬP VỀ NHÀ : ................................................................................................................. 15
VẤN ĐỀ 6. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG (PHẦN
I). .......................................................................................................................................................... 16
A. TÓM TẮT LÝ THUYẾT. ......................................................................................................... 16
B. BÀI TẬP VÀ CÁC DẠNG TOÁN. ........................................................................................ 16
Dạng 1. Giải tam giác vuông .................................................................................................. 16
Dạng 2. Tính cạnh và góc của tam giác ................................................................................ 17
C. BÀI TẬP VỀ NHÀ ................................................................................................................... 17
VẤN ĐỀ 7. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG (PHẦN
II) .......................................................................................................................................................... 19
A. TÓM TẮT LÝ THUYẾT .......................................................................................................... 19
1
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ......................................................................................... 19
Dạng 3. Toán ứng dụng thực tế ............................................................................................. 19
Dạng 4. Toán tổng hợp ............................................................................................................ 20
C. BÀI TẬP VỀ NHÀ ................................................................................................................... 20
ÔN TẬP CHỦ ĐỀ 3 .......................................................................................................................... 21
A. TÓM TẮT LÝ THUYẾT .......................................................................................................... 21
B. BÀI TẬP TỰ LUYỆN ............................................................................................................... 22
HƯỚNG DẪN GIẢI ......................................................................................................................... 26
VẤN ĐỀ 1. ..................................................................................................................................... 26
VẤN ĐỀ 2 ...................................................................................................................................... 26
VẤN ĐỀ 3 ...................................................................................................................................... 27
VẤN ĐỀ 4 ...................................................................................................................................... 28
VẤN ĐỀ 5 ...................................................................................................................................... 29
VẤN ĐỀ 6. ..................................................................................................................................... 31
VẤN ĐỀ 7 ...................................................................................................................................... 32
ÔN TẬP CHỦ ĐỀ 3 ................................................................................................................. 32
2
7
5
y
x
H
C
B
A
CHỦ ĐỀ 3. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
VẤN ĐỀ 1. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
(PHẦN 1)
A. TÓM TẮT LÝ THUYẾT
Cho tam giác
vuông tại
A
, đường cao
AH
. Khi đó ta có các hệ thức sau:
•
2
.AB BH BC=
hay
2
.'c ac=
•
2
.AC CH BC=
hay
2
'b ab=
•
..AB AC BC AH=
hay
cb ah=
•
2
.HA HB HC=
hay
2
''h cb=
•
222
1 11
AH AB AC
= +
hay
2 22
111
hcb
= +
.
•
222
BC AB AC= +
(Định lí Pitago).
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Tính độ dài các đoạn thẳng trong tam giác vuông
Phương pháp giải: Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Nếu biết độ dài
hai trong sáu đoạn thẳng
, ,, ,,AB AC BC HA HB HC
thì ta luôn tính được độ dài bốn
đoạn thẳng còn lại.
• Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Tính
,xy
trong mỗi hình vẽ sau:
y
x
6
8
H
C
B
A
20
12
y
x
H
C
B
A
Hình 1 Hình 2 Hình 3
Bài 2. Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
a) Cho biết
3, 4.AB cm AC cm= =
Tính độ dài các đoạn thẳng
,,BH CH AH
và
.BC
b) Cho biết
9 , 16BH cm ch cm= =
. Tính độ dài các đoạn thẳng
,,AB AC BC
và
.AH
Bài 3. Cho tam giác
ABC
vuông tại
A
,
AH BC⊥
(
H
thuộc BC ). Cho biết
: 3:4AB AC =
và
15 .BC cm=
Tính độ dài các đoạn thẳng
BH
và
.CH
Bài 4. Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
Cho biết
: 3:4AB AC =
và
6.AH cm=
Tính độ dài các đoạn thẳng
BH
và
.CH
* Học sinh tự luyện tập các bài tập sau tại lớp :
Bài 5. Tính
,xy
trong các hình vẽ sau :
b
c
c'
b'
a
H
C
B
A
3
y
x
1
4
H
C
B
A
Hình 4
y
13
H
C
B
A
Hình 5
x
5
4
H
C
B
A
Hình 6
Bài 6. Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
a) Cho biết
3, 5.AB cm BC cm= =
Tính độ dài các đoạn thẳng
,,BH CH AH
và
.AC
b) Cho biết
60 , 144 .AH cm CH cm= =
Tính độ dài các đoạn thẳng
,,AB AC BC
và
.BH
c) Cho biết
60
12 , .
13
AC cm AH cm= =
Tính độ dài các đoạn thẳng
,,AB BC BH
và
.CH
Bài 7. Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
Cho biết
5
6
AB
AC
=
và
122 .BC cm=
Tính độ dài các đoạn thẳng
,.BH CH
Bài 8. Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
Cho biết
: 3:4AB AC =
và
12 .AH cm=
Tính độ dài các đoạn thẳng
,.BH CH
C.BÀI TẬP VỀ NHÀ
Bài 9. Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
Cho biết
4 , 7,5 .AB cm BC cm= =
Tính
độ dài các đoạn thẳng
,.BH CH
Bài 10. Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
a) Biết
6 , 4,5 .AH cm BH cm= =
Tính
,,,.AB AC BC HC
b) Biết
6, 3.AB cm BH cm= =
Tính
,,.AH AC CH
Bài 11. Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
Tính diện tích tam giác
ABC
, biết
12 , 9 .AH cm BH cm= =
Bài 12. Cho tam giác
,ABC
biết
7,5 , 4,5 , 6 .BC cm CA cm AB cm= = =
a) Tính độ dài đường cao
AH
của tam giác
.ABC
b) Tính độ dài các đoạn thẳng
,.BH CH
Bài 13. Cho tam giác vuông với các cạnh góc vuông là 7 và 24. Kẻ đường cao ứng với cạnh
huyền. Tính độ dài đường cao và các đoạn thẳng mà đường cao đó chia ra trên cạnh huyền.
Bài 14. Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
Biết
5
, 15 .
7
AB
AH cm
AC
= =
Tính độ dài
các đoạn thẳng
HB
và
.HC
4
Bài 15. Cho ABCD là hình thang vuông tại
A
và
.D
Đường chéo
BD
vuông góc với
.BC
Biết
12 , 25 .AD cm DC cm= =
Tính độ dài
,AB BC
và
.BD
5
VẤN ĐỀ 2. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
(PHẦN II)
A. TÓM TẮT LÝ THUYẾT
Nhắc lại lý thuyết : Cho tam giác
ABC
vuông tại
A
, đường cao
.AH
Khi đó có các hệ thức
sau :
•
2
.AB BH BC=
hay
2
.'c ac=
•
2
.AC CH BC=
hay
2
.'b ab=
•
..AB AC BC AH=
hay
.cb a h=
•
2
.HA HB HC=
hay
2
''h cb=
•
222
1 11
AH AB AC
= +
hay
222
111
hcb
= +
•
222
BC AB AC= +
( Định lí Pitago)
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 2. Chứng minh các hệ thức liên quan đến tam giác vuông
Phương pháp giải : Sử dụng các hệ thức về cạnh và đường cao một cách hợp lý theo hướng :
Bước 1. Chọn các tam giác vuông thích hợp chứa các đoạn thẳng có trong hệ thức.
Bước 2. Tính các đoạn thẳng đó nhờ hệ thức về cạnh và dường cao.
Bước 3. Liên kết các giá trị trên để rút ra hệ thức cần chứng minh.
* Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 1. Cho tam giác
CDE
nhọn, đường cao
.CH
Gọi
,MN
theo thứ tự là hình chiếu của
H
lên
,.CD DE
Chứng minh :
a)
. .;CD CM CE CN=
b) Tam giác
CMN
đồng dạng với tam giác
.CED
Bài 2. Cho hình vuông
.ABCD
Gọi
I
là một điểm nằm chính giữa
A
và
.B
Tia
DI
và tia
CB
cắt nhau ở
.K
Kẻ đường thẳng qua
D
, vuông góc với
DI
, cắt đường thẳng
BC
tại
L
.
Chứng minh :
a) Tam giác
DIL
là tam giác cân ;
b) Tổng
22
11
DI DK
+
không đổi khi
I
thay đổi trên cạnh
.AB
* Học sinh tự luyện tập các bài tập sau tại lớp :
Bài 3. Cho tam giác
ABC
có ba góc nhọn và
AH
là đường cao.
h
b
c
c'
b'
a
H
C
B
A
6
a) Chứng minh
2222
;AB CH AC BH+=+
b) Gọi
,MN
theo thứ tự là hình chiếu của
H
lên
,.AB AC
Chứng minh :
. ..AM AB AN AC=
Bài 4. Cho hình thoi
ABCD
có hai đường chéo cắt nhau tại
O
. Cho biết khoảng cách từ
O
tới mỗi cạnh của hình thoi là
, ,.h AC m BD n= =
Chứng minh :
22 2
111
.
4mn h
= +
C.BÀI TẬP VỀ NHÀ
Bài 5. Cho hình chữ nhật
ABCD
có
8 , 15 .AB cm BC cm= =
a) Tính độ dài đoạn thẳng
.BD
b) Vẽ
AH
vuông góc với
BD
tại H. Tính độ dài đoạn thẳng
.AH
c) Đường thẳng
AH
cắt
BC
và
DC
lần lượt tại
I
và
.K
Chứng minh
2
..AH HI HK=
Bài 6. Cho hình thang ABCD vuông tại A và D. Cho biết AB = 15cm, AD = 20cm, các đường
chéo AC và BD vuông góc với nhau ở O. Tính
a) Độ dài các đoạn thẳng OB và OD;
b) Độ dài đoạn thẳng AC ;
c) Diện tích hình thang ABCD.
Bài 7. Cho tam giác ABC vuông tại A. Đường cao AH, kẻ HE, HF lần lượt vuông góc với
AB, AC. Chứng minh :
a)

=


3
EB AB
FC AC
; b)
=
3
BC.BE.CF AH
.
Bài 8. Cho tam giác ABC cân tại A có AH và BK là hai đường cao. Kẻ đường thẳng vuông
góc với BC tại B cắt tia CA tại D. Chứng minh :
a) BD = 2.AH ; b)
22 2
11 1
BK BC 4HA
= +
.
7
VẤN ĐỀ 3 : LUYỆN TẬP HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC
VUÔNG
A. TÓM TẮT LÝ THUYẾT
Nhắc lại lý thuyết : Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các
hệ thức sau:
● AB
2
= BH. BC hay c
2
= a.c’
● AC
2
= CH. BC hay b
2
= a.b’
● AB. AC = BC. AH hay c.b = a. h
● HA
2
= HB. HC hay h
2
= c’. b’
●
222
1 11
AH AB AC
= +
hay
222
111
hcb
= +
● BC
2
= AB
2
+ AC
2
(Định lí Pitago)
B. BÀI TẬP TỰ LUYỆN
* Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 1. Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 4cm, CH = 9cm. Gọi D,
E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC.
a) Tính độ dài đoạn thẳng DE.
b) Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N. Chứng
minh
1
MN BC
2
=
.
c) Tính diện tích của tứ giác DENM.
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là hình chiếu
vuông góc của H trên AB, AC. Chứng minh
a)
2
2
AB HB
HC
AC
=
; b)
3
3
AB BD
EC
AC
=
;
c) DE
2
= BD. CE. BC; d)
3
33
2 22
BC BD CE= +
.
*Học sinh tự luyện các bài tập sau đây
Bài 3. Cho tam giác ABC vuông tại A, đường cao AH.
a) Cho biết AB = 6cm, AC = 8cm. Tính độ dài các đoạn thẳng BH, CH, AH và BC.
b) Cho biết AB = 6cm, BC = 10cm. Tính độ dài các đoạn thẳng BH, CH, AH và AC.
8
Bài 4. Tìm độ dài các cạnh của một tam giác vuông nếu đường cao ứng với cạnh huyền có
độ dài 48cm và hình chiếu của các cạnh góc vuông trên cạnh huyền theo tỉ lệ 9 : 16.
Bài 5. Cho tam giác ABC vuông tại A, phân giác AD, đường cao AH. Biết BD = 15cm, CD =
20cm. Tính độ dài các đoạn thẳng HB, HC.
Bài 6. Cho hình thang cân ABCD có độ dài cạnh đáy AB = 26cm và cạnh bên AD = 10cm.
Cho biết đường chéo AC vuông góc với cạnh bên BC. Tính diện tích hình thang
ABCD.
C. BÀI TẬP VỀ NHÀ
Bài 7. Cho tam giác ABC vuông tại A, đường cao AH.
a) Nếu BH = 2cm, CH = 8cm. Tính độ dài các đoạn AB, AC, BC, AH.
b) Nếu AH = 5cm, CH = 16cm. Tính độ dài các đoạn thẳng AB, AC, BC, BH.
Bài 8. Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 4 và AH =
12cm. Tính độ dài các đoạn thẳng BH và CH.
Bài 9. Cho tam giác ABC vuông tại A, phân giác AD, đường cao AH. Cho biết BD = 15cm,
CD = 20cm. Tính độ dài các đoạn thẳng HB và HC.
Bài 10. Cho tam giác ABC vuông tại A, đường cao AH. Tính chu vi của tam giác ABC biết
AH = 14cm,
HB 1
HC 4
=
.
Bài 11. Cho tam giác ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC biết
rằng AH = 12cm, BH = 9cm.
Bài 12. Cho tam giác ABC vuông tại C, đường cao CK.
a) Cho biết AB = 10cm, AC = 8cm. Tính BC, CK, BK và AK.
b) Gọi H và I theo thứ tự là hình chiếu của K trên BC và AC. Chứng minh CB. CH =
CA. CI
c) Gọi M là chân đường vuông kẻ từ K xuống IH. Chứng minh
= +
2 22
1 11
KM CH CI
.
d) Chứng minh
3
3
AI AC
BH
BC
=
.
9
VẤN ĐỀ 4. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN I)
A. TÓM TẮT LÝ THUYẾT
● Cho góc nhọn
( )
oo
0 90α <α<
. Dựng tam giác ABC vuông tại A sao cho
ABCα=
.
Từ đó ta có:
AB
cos
AC
α=
;
AC
sin
AB
α=
;
AC
tan
AB
α=
;
AB
cot
AC
α=
.
● Với góc góc nhọn
α
bất kì, ta luôn có:
0 <
sin α
< 1; 0 < cos
α
< 1
tan
α
=
sin
cos
α
α
; cot
tan
cos
α
α=
α
;
tan .cot 1α α=
;
sin
2
α
+ cos
2
α
= 1; 1 + tan
2
α
=
2
1
cos x
; 1 + cot
2
α
=
2
1
sin
−
α
.
●Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang
góc kia.
● Bảng tỉ số lượng giác các góc đặc biệt
α
Tỉ số
30
o
45
o
60
o
sin
α
1
2
2
2
3
2
cos
α
3
2
2
2
1
2
tan
α
3
3
1
3
cot
α
3
1
1
3
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Phương pháp giải:Sử dụng các kiến thức trong phần Tóm tắt lý thuyết ở trên.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Cho tam giác ABC vuông tại Ccó
= =1,2 , 0,9 .BC cm AC cm
Tính các tỉ số lượng giác
của góc B. Từ đó suy ra tỉ số lượng giác của góc A.
10
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Hãy tính
sin , sinBC
trong các trường
hợp sau (làm tròn kết quả đến chữ số thập phân thứ 4):
a)
= =13 , 0,5 ;AB cm BH dm
b)
= =4, 3.CH cm BH cm
Bài 3. Cho tam giác ABCcó
= = =5, 2, 3AB a AC a BC a
a) Chứng minh rằng ABC là tam giác vuông.
b) Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A.
Bài 4. Cho tam giác ABC vuông tại A. Hãy tính các tỉ số lượng giác của góc C biết rằng
=cos 0,6.B
Bài 5. Cho tam giác ABCvuông tại Acó
= = ⋅
5
5 , cot
8
AB cm B
Tính độ dài các đoạn thẳng AC
và BC.
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 6. Cho tam giác ABC vuông tại A có
= =1,6 , 1,2 .AB cm CA cm
Tính các tỉ số lượng giác
của góc B. Từ đó suy ra tỉ số lượng giác của góc C.
Bài 7. Cho tam giác ABCcó
= = =3, 2, 5.AB a AC a BC a
a) Chứng minh rằng ABC là tam giác vuông.
b) Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc C.
Bài 8. Cho tam giác ABC vuông tại A. Cho biết
=cos 0,8.B
Hãy tính các tỉ số lượng giác của
góc C.
Bài 9. Cho tam giác ABCvuông tại Acó
= = ⋅
5
6 , tan
12
AB cm B
Tính độ dài các đoạn thẳng
AC và BC.
C. BÀI TẬP VỀ NHÀ
Bài 10. Cho tam giác ABC vuông tại A có
= =60 , 8 .AB mm CA cm
Tính các tỉ số lượng giác của
góc B. Từ đó suy ra tỉ số lượng giác của góc C.
Bài 11. Cho tam giác ABCvuông tại Acó
= = ⋅
5
30 , tan
12
AB cm B
Tính độ dài các đoạn thẳng
AC và BC.
Bài 12. Tính
αααsin , cot , tan
biết
α= ⋅
1
cos
5
Bài 13. Cho tam giác ABCvuông tại A. Tính độ dài các đoạn thẳng AC và BC biết:
a)
= = ⋅
3
12 , tan
4
AB cm B
b)
= = ⋅
5
15 , cos
13
AB cm B
11
Bài 14. Cho tam giác ABC vuông ở A,
= =
30 , 10 .C BC cm
a) Tính AB, AC.
b) Kẻ từ A các đường thẳng AM, AN lần lượt vuông góc với các đường phân giác
trong và ngoài của góc B. Chứng minh MN sog song với BC và MN = BC.
c) Chứng minh các tam giác MAB và ABC đồng dạng. Tìm tỉ số đồng dạng.
12
VẤN ĐỀ 5. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN II)
A. TÓM TẮT LÝ THUYẾT
• Cho góc nhọn
( )
0 90α <α<

. Dựng tam giác ABC vuông tại A sao cho
ABCα=
. Từ
đó ta có :
cos ; sin ; tan ; cot
AB AC AC AB
BC BC AB AC
α= α= α= α= ⋅
• Với góc nhọn
α
bất kỳ, ta luôn có:
0sin 1;0cos 1.< α< < α<
sin cos
tan ; cot ; tan .cot 1.
cos sin
αα
α= α= α α=
αα
22 2 2
22
11
sin cos 1;1 tan ;
1 cot
cos si
n
α+ α= + α= + α= ⋅
αα
• Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang
góc kia.
• Bảng tỉ số lượng giác của các góc đặc biệt:
α
Tỉ số
30
o
45
o
60
o
sin
α
1
2
2
2
3
2
cos
α
3
2
2
2
1
2
tan
α
3
3
1
3
cot
α
3
1
1
3
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 2. Sắp thứ tự dãy các tỉ số lượng giác
Phương pháp giải: Để sắp thứ tự dãy các tỉ số lượng giác cho trước ta cần làm được hai
bước sau:
Bước 1: Đưa về các tỉ số lượng giác trong bài toán cùng loại bằng cách sử dụng tính chất
"Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc
kia"
Bước 2: Với góc nhọn
,,αβ
ta có:
13
sin sin ;
cos cos ;
tan tan ;
cot cot .
α< β⇔α<β
α< β⇔α>β
α< β⇔α<β
α< β⇔α>β
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Không dùng bảng số và máy tính, hãy so sánh
a)
sin20
và
sin70 .
b)
cos60
và
cos70 .
c)
tan73 20
′
và
tan45 .
d)
cot20
và
cot37 40 .
′
Bài 2. Sắp xếp các tỉ số lượng giác sau theo thứ tự từ lớn đến bé:
a)
tan42 , cot71 , tan38 , cot69 15 , tan28 ;
′

b)
sin32,cos51,sin39,cos7913,sin38.
′

* Học sinh tự luyện các bài tập sau tại lớp :
Bài 3. Không dùng bảng số và máy tính, hãy so sánh :
a)
0
sin40
và
0
sin70 ;
b)
0
cos80
và
0
cos50 ;
c)
0
tan73 20'
và
0
tan65 ;
d)
0
cot 53
và
0
cot 37 40'.
Bài 4. Sắp xếp các tỉ số lượng giác sau theo thứ tự từ bé đến lớn :
a)
00 00 0
tan12 ,cot61 ;tan 28 ;cot79 15';tan58 ;
b)
000 00
cos67 ,sin 56 ,cos63 41',sin74 ,cos85 .
Dạng 3.Dựng góc nhọn
α
biết tỉ số lượng giác của nó là
.
m
n
Phương pháp giải: Dựng một tam giác vuông có hai cạnh là
m
và
n
trong đó
m
và
n
là hai cạnh góc vuông hoặc một cạnh góc vuông và một cạnh huyền rồi vận dụng
định nghĩa tỉ số lượng giác để nhận ra góc
α
.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 5.Dựng góc nhọn
α
biết rằng :
a)
3
sin ;
5
α
=
b)
4
cos ;
7
α
=
c)
3
tan ;
2
α
=
d)
5
cot .
6
α
=
*Học sinh tự luyện ở lớp :
Bài 6.Dựng góc nhọn
α
biết rằng:
a)
2
sin ;
3
α
=
b)
2
cos ;
5
α
=
c)
3
tan ;
7
α
=
d)
4
cot .
5
α
=
14
C. BÀI TẬP VỀ NHÀ :
Bài 7.Cho tam giác
ABC
vuông tại
A
. Biết
5
30 , , tan =
12
AB cm B
αα
= =
. Tính cạnh
,.BC AC
Bài 8. Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Tính
sin ;sinBC
biết rằng:
a)
13; 5;AB BH= =
b)
3; 4.BH HC= =
Bài 9.Dựng góc nhọn
α
biết rằng:
a)
1
sin ;
2
α
=
b)
2
cos ;
3
α
=
c)
4
tan ;
5
α
=
d)
3
cot .
4
α
=
Bài 10. Sắp xếp các tỉ số lượng giác sau heo thứ tự từ bé đến lớn.
a)
0 00 00
sin35 ,cos28 ;sin34 72';cos62 ;sin45 ;
b)
00 0 00
cos37 ,cos65 30',sin72 ,cos59 ,sin47 .
Bài 11. Tính giá trị biểu thức :
a)
20 0 20 0
cos 52 sin45 sin 52 cos45 ;A = +
b)
0 20 20 0
sin45 cos 47 sin 47 cos45 .B = +
Bài 12. Tìm
cos ,tan ,cot
ααα
biết
1
sin .
5
α
=
Bài 13.Cho tam giác
ABC
vuông tại
A
,
0
30 , 10 .C BC cm= =
a) Tính độ dài các đoạn thẳng
,.AB AC
b) Kẻ từ
A
các đoạn thẳng
,AM AN
lần lượt vuông góc với các đường phân giác
trong và phân giác ngoài của góc
B
. Chứng minh
MN
song song với
BC
và
.MN BC=
c) Chứng minh tam giác
MAB
đồng dạng với tam giác
ABC
. Tìm tỉ số đồng dạng.
Bài 14.Không dùng bảng số và máy tính, hãy tính :
a)
202020202020
cos 20 cos 30 cos 40 cos 50 cos 60 cos 70 .A =+++++
b)
2020202020
sin 5 sin 25 sin 45 sin 65 sin 85 .A =++++
Bài 15. Cho tam giác
vuông tại
A
,
0
, 45AB AC C
α
<=<
, đường trung tuyến
AM
,
đường cao
AH
,
.MA MB MC a= = =
Chứng minh :
a)
sin2 2sin cos ;
α αα
=
b)
2
1 os2 2cos ;c
αα
+=
c)
2
1 os2 2sin .c
αα
−=
15
VẤN ĐỀ 6. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
(PHẦN I).
A. TÓM TẮT LÝ THUYẾT.
• Cho tam giác
ABC
vuông tại
A
có
, ,.BC a AC b AB c= = =
Ta có :
• Trong một tam giác vuông :
.sin .cos ;
.sin .cos ;
.tan .cot ;
.tan .cot .
ba Ba C
ca Ca B
bc Bc C
cb Cb B
= =
= =
= =
= =
• Cạnh góc vuông = (cạnh huyền ) x (sin góc đối)
= (cạnh huyền ) x (cosin góc kề)
• Cạnh góc vuông = (cạnh góc vuông ) x (tang góc đối)
= (cạnh góc vuông còn lại ) x (cotang góc kề).
B. BÀI TẬP VÀ CÁC DẠNG TOÁN.
Dạng 1. Giải tam giác vuông
Phương pháp giải:
1. Giải tam giác là tính độ dài các cạnh và số đo các góc dựa vào dữ kiện cho trước của bài
toán.
2. Trong tam giác vuông, ta dùng hệ thức giữa cạnh và các góc của một tam giác vuông và
sử dụng máy tính cầm tay hoặc bảng lượng giác để tính các yế tố còn lại.
3.Các bài toán về giải tam giác vuông bao gồm :
i) Giải tam giác vuông khi biết độ dài một cạnh và số đo một góc nhọn.
ii) Giải tam giác vuông khi biết độ dài hai cạnh.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Cho tam giác
ABC
vuông tại
A
, có
, ,.BC a AC b AB c= = =
Giải tam giác
, biết
rằng :
a)
0
10 ; 30 ;b cm C= =
b)
0
20 ; 35 .a cm B= =
Bài 2. Cho tam giác
ABC
vuông tại
A
, có
, ,.BC a AC b AB c= = =
Giải tam giác
, biết
rằng :
a)
15 ; 10 ;a cm b cm= =
b)
12; 7.b cm c cm= =
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 3. Cho tam giác
ABC
vuông tại
,A
có
, ,.BC a AC b AB c= = =
Giải tam giác
,ABC
biết
rằng:
c
b
a
A
C
B
16
a)
28 ; 21 ;b cm c cm= =
b)
10 ; 6 .a cm b cm= =
Bài 4. Cho tam giác
ABC
vuông tại
,A
có
, ,.BC a AC b AB c= = =
Giải tam giác
,ABC
biết
rằng:
a)
0
3,8 ; 51 ;c cm B= =
b)
0
11 ; 60 .a cm C= =
Dạng 2. Tính cạnh và góc của tam giác
Phương pháp giải: Làm xuất hiện tam giác vuông để áp dụng các hệ thức trên bằng
cách kẻ thêm đường cao.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 5. Cho tam giác
ABC
có
0
11 , 38BC cm ABC= =
và
0
30 .ACB =
Gọi
N
là chân đường
vuông góc hạ từ
A
xuống cạnh
.BC
Hãy tính:
a) Độ dài đoạn thẳng
;AN
b) Độ dài đoạn thẳng
.AC
Bài 6. Cho tam giác
,ABC
có
00
6 , 60 ; 40 .BC cm B C= = =
Hãy tính:
a) Chiều cao
CH
và cạnh
;AC
b) Diện tích tam giác
.ABC
*Học sinh tự luyện các bài tập sau tại lớp:
Bài 7. Cho tam giác
ABC
có
00
60 , 50 , 3,5 .B C AC cm= = =
Tính diện tích tam giác
ABC
(làm tròn đến hàng đơn vị).
Bài 8. Tứ giác
ABCD
có các đường chéo cắt nhau tại
O.
Cho biết
4, 5,AC cm BD cm= =
0
50 .AOB =
Tính diện tích tứ giác
.ABCD
C. BÀI TẬP VỀ NHÀ
Bài 9. Cho tam giác
ABC
vuông tại
,A
có
, ,.BC a AC b AB c= = =
Giải tam giác
,ABC
biết
rằng:
a)
0
5,4 , 30 ;b cm C= =
b)
0
10 , 45 .c cm C= =
Bài 10. Cho tam giác
ABC
vuông tại
,A
, ,.BC a AC b AB c= = =
Giải tam giác
,ABC
biết
rằng:
a)
15 , 10 ;a cm b cm= =
b)
12 , 7 .b cm c cm= =
Bài 11. Cho tam giác
ABC
vuông tại
,A
, ,.BC a AC b AB c= = =
Giải tam giác
,ABC
biết
rằng:
a)
0
40 , 8;A AC= =
b)
0
28 , 5;C AB= =
c)
8, 15.AB BC= =
Bài 12. Cho tam giác
ABC
có
00
60 , 50 , 35 .B C AC cm= = =
Tính diện tích tam giác
.ABC
17
Bài 13. Cho tứ giác
ABCD
có
00
90 , 40 , 4 , 3 .A D C AB cm AD cm= = = = =
Tính diện tích tứ
giác
.ABCD
Bài 14. Cho tam giác
ABC
vuông tại
,A
có đường cao
;AH
9 , 16 .HB cm HC cm= =
a) Tính
,,.AB AC AH
b) Gọi
D
và
E
lần lượt là hình chiếu vuông góc của
H
trên
AB
và
.AC
Tứ giác
ADHE
là hình gì?
c) Tính chu vi và diện tích của tứ giác
.ADHE
Bài 15. Cho tam giác
ABC
vuông tại
.A
Biết
3, 5.AB cm BC cm= =
a) Giải tam giác vuông
ABC
(số đo góc làm tròn đến độ).
b) Từ
B
kẻ đường thẳng vuông góc với
,BC
đường thẳng này cắt đường thẳng
AC
tại
D
. Tính độ dài các đoạn thẳng
,.AD BD
c) Gọi
,EF
lần lượt là hình chiếu của
A
trên
BC
và
.BD
Chứng minh :
. ..BF BD BE BC=
18
VẤN ĐỀ 7. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG
(PHẦN II)
A. TÓM TẮT LÝ THUYẾT
• Cho tam giác
vuông tại
A
có
, ,.BC a AC b AB c= = =
Ta có :
.sin .cos ;
.sin .cos ;
.tan .cot ;
.tan .cot .
ba Ba C
ca Ca B
bc Bc C
cb Cb B
= =
= =
= =
= =
• Trong một tam giác vuông
Cạnh góc vuông = (Cạnh huyền)
×
( sin góc đối)
= (Cạnh huyền)
×
( côsin góc kề)
Cạnh góc vuông = (Cạnh góc vuông)
×
(tang góc đối)
= (Cạnh góc vuông)
×
(cotang góc kề)
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 3. Toán ứng dụng thực tế
Phương pháp giải: Dùng hệ thức giữa cạnh và góc trong tam giác vuông để giải
quyết tình huống trong thực tế.
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Một cột đèn có bóng trên mặt đất dài
7,5 .m
Các tia nắng mặt trời tạo với mặt đất một
góc xấp xỉ bằng
0
42 .
Tính chiều cao của cột đèn.
Bài 2. Một cầu trượt trong công viên có độ dốc là
0
28
và có độ cao là
2,1 .m
Tính độ dài của
mặt cầu trượt (làm tròn đến chữ số thập phân thứ nhất).
*Học sinh tự luyện các bài tập sau tại lớp:
Bài 3. Một cột đèn có bóng trên mặt đất dài
5.m
Các tia nắng mặt trời tạo với mặt đất một
góc xấp xỉ bằng
0
50 .
Tính chiều cao của cột đèn.
Bài 4. Một cột đèn điện
AB
cao
6m
có bóng in trên mặt đất là
AC
dài
3,5 .m
Hãy tính góc
BCA
(làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất.
19
Dạng 4. Toán tổng hợp
Phương pháp giải: Vận dụng linh hoạt một số hệ thức giữa cạnh và góc trong tam giác
vuông để giải toán.
*Giáo viên hướng dẫn học sinh giải bài tập sau:
Bài 5. Cho tam giác
ABC
vuông tại
,A
có
.AC AB>
Đường cao
.AH
Gọi
,DE
lần lượt là
hình chiếu của
H
trên
,.AB AC
a) Chứng minh
..AD AB AE AC=
và tam giác
ABC
đồng dạng với tam giác
.AED
b) Cho biết
2 , 4,5 .BH cm HC cm= =
Tính dộ dài đoạn thẳng
.DE
c) Tính số đo góc
ABC
(làm tròn đến độ).
d) Tính diện tích tam giác
.ADE
*Học sinh tự luyện bài tập sau tại lớp:
Bài 6. Cho hình chữ nhật
.ABCD
Qua
B
kẻ đường thẳng vuông góc với đường chéo
AC
tại
.H
Gọi
,,EFG
theo thứ tự là trung điểm của
,,.AH BH CD
a) Chứng minh tứ giác
EFCG
là hình bình hành.
b) Chứng minh
0
90 .BEG =
c) Cho biết
,.BH h BAC
α
= =
Tính
ABCD
S
theo
h
và
.
α
d) Tính độ dài đường chéo
AC
theo
h
và
.
α
C. BÀI TẬP VỀ NHÀ
Bài 7. Cho tam giác
ABC
vuông tại
A
biết
21 , 40AB cm C= = °
.Tính độ dài đường phân
giác
BD
của góc
,ABD D
nằm trên cạnh
AC
.
Bài 8. Cho tam giác
ABC
vuông ở
A C BC cm=°=, 30 , 10
.
a) Tính
,AB AC
.
b) Kẻ từ
A
các đường thẳng
AM AN,
lần lượt vuông góc với các đường phân giác
trong và ngoài của góc
B
. Chứng minh
MN
song song với
BC
và
MN BC=2
.
c) Chứng minh tam giác
MAB
đồng dạng với tam giác
ABC
. Tìm tỉ số đồng dạng.
Bài 9. Cho tam giác
ABC
vuông tại
A
, có
AC AB>
, đường cao
AH
. Gọi
,DE
lần lượt là
hình chiếu của
H
trên
,AB AC
.
a) Chứng minh
..AD AB AE AC=
và tam giác
ABC
đồng dạng với tam giác
AED
.
b) Cho biết
2 , 4,5BH cm HC cm= =
.Tính :
i) Độ dài đoạn thẳng
DE
;
ii) Số đo
ABC
( làm tròn đến độ ) ;
iii) Diện tích tam giác
ADE
.
Bài 10. Chứng minh :
20
a) Diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn
tạo bởi các đường thẳng chứa hai cạnh ấy.
b) Diện tích của một hình bình hành bằng tích của hai cạnh kề nhân với sin của góc
nhọn tạo bởi các đường thẳng chứa hai cạnh ấy.
ÔN TẬP CHỦ ĐỀ 3
A. TÓM TẮT LÝ THUYẾT
1. Hệ thức về cạnh và đường cao trong tam giác vuông
Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Khi đó ta có các hệ thức sau :
•
2
.AB BH BC=
hay
2
.'c ac=
•
2
.AC CH BC=
hay
2
.'b ab=
•
..AB AC BC AH=
hay
..cb ah=
•
2
.HA HB HC=
hay
2
'. 'h cb=
•
222
1 11
AH AB AC
= +
hay
2 22
111
hcb
= +
•
222
BC AB AC= +
( Định lý Pitago )
2. Tỉ số lượng giác của góc nhọn
• Cho góc nhọn
(0 90 )
αα
°< < °
. Dựng tam giác
ABC
vuông tại
A
sao cho
ABC
α
=
. Từ đó
ta có :
cos ;sin ;tan ;cot
AB AC AC AB
BC BC AB AC
αα αα
= = = =
.
• Với góc nhọn
α
bất kỳ, ta luôn có :
22 2 2
22
0 sin 1; 0 cos 1;
sin cos
tan ;cot ;tan .cot 1;
cos sin
11
sin cos 1;1 tan ;1 cot .
cos sin
αα
αα
α α αα
αα
αα α α
αα
< << <
= = =
+=+= +=
• Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc
kia.
• Bảng tỉ số lượng giác của các góc đặc biệt :
α
Tỉ số
30°
45°
60°
1
2
2
2
3
2
cos
α
3
2
2
2
1
2
a
c
b
h
b'
c'
C
H
B
A
21
tan
α
3
3
1
3
3
1
3
3
3. Hệ thức về cạnh và góc trong tam giác vuông
• Cho tan giác
ABC
vuông tại
A
có
;;BC a AC b AB c= = =
. Ta có :
.sin .cos ;
.sin cos ;
.tan .cot ;
.tan .cot .
ba Ba C
ca Ca B
bc Bc C
cb Cb B
= =
= =
= =
= =
• Trong một tam giác vuông
Cạnh góc vuông = ( cạnh huyền ) x ( sin góc đối)
= ( cạnh huyền ) x ( cosin góc kề )
Cạnh góc vuông = ( cạnh góc vuông ) x ( tang góc đối )
= ( cạnh góc vuông còn lại ) x ( cotang góc kề )
B. BÀI TẬP TỰ LUYỆN
Bài 1. Cho tam giác
ABC
vuông tại
A
, đường cao
AH
. Trong các đoạn thẳng
, ,BC, , ,AB AC AH HB HC
, hãy tính độ dài các đoạn thẳng còn lại nếu biết :
a)
6AB cm=
và
9AC cm=
;
b)
15AB cm=
và
9HB cm=
;
c)
44AC cm=
và
55BC cm=
.
Bài 2. Cho tam giác
ABC
vuông tại
( )
A AB AC<
có đường cao
AH
và
12 ; 25AH cm BC cm= =
.
a) Tìm độ dài các đoạn thẳng
,,BH CH AB
và
AC
.
b) Vẽ trung tuyến
AM
. Tìm số đo của góc
AMH
.
c) Tính diện tích tam giác
AHM
.
Bài 3. Cho tam giác
ABC
có đường cao
CH
,
0
12 , 60BC cm B= =
và
0
40C =
.
a) Tính độ dài các đoạn thẳng
CH
và
AC
.
b) Tính diện tích tam giác
ABC
.
Bài 4. Cho tam giác
ABC
vuông ở
A
, đường cao
AH
,
3, 4AB cm AC cm= =
.
a) Tính độ dài các đoạn thẳng
BC
và
AH
.
b) Tính số đo các góc
,BC
.
c) Đường phân giác trong của góc
A
cắt cạnh
BC
tại
E
. Tính độ dài các đoạn thẳng
BE
và
CE
.
22
Bài 5. Cho tam giác nhọn
ABC
có đường cao
AH
. Từ
H
kẻ
HE
vuông góc với
AB
(
E
thuộc
AB
) và kẻ
HF
vuông góc với
AC
(
F
thuộc
AC
).
a) Chứng minh
. AF.AE AB AC=
.
b) Cho biết
4, 3AB cm AH cm= =
. Tính độ dài các đoạn thẳng
AE
và
BE
.
c) Cho biết
0
30HAC =
. Tính độ dài đoạn thẳng
FC
.
Bài 6. Tứ giác
MNEF
vuông tại
M
,
F
, có
EF
là đáy lớn, hai đường chéo
ME
và
NF
vuông góc với nhau tại
O
.
a) Cho biết
9MN cm=
và
12MF cm=
. Hãy :
i) Giải tam giác
MNF
.
ii) Tính độ dài các đoạn thẳng
MO
,
FO
.
iii) Kẻ
NH
vuông góc với
EF
tại
H
. Tính diện tích tam giác
FNE
. Từ đó tính diện
tích tam giác
FOH
.
b) Chứng minh
2
.MF MN FE=
.
Bài 7. Cho tam giác
EFD
biết
6DE cm=
,
8 , 10DF cm EF cm= =
.
a) Chứng minh rằng
là tam giác vuông.
b) Vẽ đường cao
DK
. Hãy tính
,DK FK
.
c) Giải tam giác vuông
EDK
.
d) Vẽ phân giác trong
DM
của tam giác
DEF
. Tính các độ dài các đoạn thẳng
,ME MF
.
e) Tính
sinF
trong các tam giác vuông
DFK
và
DEF
. Từ đó suy ra
. .EFED DF DK=
Bài 8. Cho tam giác
ABC
vuông tại
A
,
0
60B =
và
6BC cm=
.
a) Tính độ dài các cạnh
,AB AC
.
b) Trên tia đối của tia
BA
lấy điểm
D
sao cho
BD BC=
. Chứng minh
AB AC
BD CD
=
c) Dường thẳng song song với phân giác góc
CBD
kẻ từ
A
cắt
CD
tại
H
. Chứng minh
2 22
1 11
AH AC AD
= +
Bài 9. Cho hình vuông
ABCD
và điểm
E
tùy ý trên cạnh
BC
. Tia
Ax
vuông góc với
AE
tại
A
cắt
CD
kéo dài tại
F
. Kẻ trung tuyến
AI
của tam giác
AEF
và kéo dài cắt cạnh
CD
tại
K
.
a) Chứng minh
AE AF=
.
b) Chứng minh các tam giác
,
CAF
đồng dạng và
2
.AF KF CF=
23
c) Cho
3
4;
4
AB cm BE BC= =
. Tính diện tích tam giác
AEF
.
d)
AE
kéo dài cắt
CD
tại
J
. Chứng minh
22
11
AE AJ
+
không phụ thuộc vào vị trí điểm
E
.
Bài 10. Không dùng máy tính, sắp xếp các tỉ số lượng giác sau theo thứ tự từ bé đến lớn :
a)
0 00 00
sin 24 ,cos35 ,sin54 ,cos70 ,sin 78
.
b)
000 0
cot 24 ,tan16 ,cot 57 67',sin 78
.
Bài 11. Không dùng máy tính, sáp xếp các tỉ sô lượng giác sau theo thứ tự tăng dần :
a)
0 00 00
sin 40 ,cos28 ,sin 65 ,cos88 , os20c
b)
0000
tan32 48',cot 28 36',tan56 32',cot 67 18'
.
Bài 12. Cho góc
α
nhọn.
a) Tính
sin ,cot ,tan
ααα
biết
1
cos
5
α
=
.
b) Tính
os ,cot , tanc
ααα
biết
2
sin
3
α
=
.
c) Cho
tan 2
α
=
. Tính
sin
α
và
cot
α
.
d) Cho
cot 3
α
=
. Tính
sin ,cos
αα
và
tan
α
.
Bài 13. Một cột cờ cao
7m
có bóng trên mặt đất dài
4m
. Tính góc
α
mà tia sáng mặt trời tạo
với mặt đất ( làm tròn đến phút).
Bài 14. Một cột đèn có bóng trên mặt đất dài
6,5m
, các tia sáng mặt trời tạo với mặt đất một
góc xấp xỉ
0
44
. Tính chiều cao của cột đèn.
Bài 15.
a) Tính giá trị biểu thức
20202020
cos 20 cos 40 cos 50 cos 70A =+++
.
b) Rút gọn biểu thức
66 22
sin cos 3sin cosB
αα αα
=++ −
.
Bài 16. Cho
00
0 90x<<
. Chứng minh các đẳng thức sau :
a)
4 4 22
sin cos 1 2sin .cosx x xx+=−
.
b)
6 6 22
sin cos 1 3sin .cosx x xx+=−
.
c)
44 2
sin cos 1 2cosxx x−=−
.
Bài 17. Cho
00
0 90x<<
. Chứng minh các đẳng thức sau :
24
a)
1 cos sin
sin 1 cos
xx
xx
−
=
+
b)
sin 1 cos 2
1 cos sin sin
xx
xxx
+
+=
+
c)
sin cos 1 cos
1 cos sin cos 1
xx x
x xx
+−
=
− −+
25
HƯỚNG DẪN GIẢI
CHỦ ĐỀ 3. HỆ THỨC LƯỢNG
TRONG TAM GIÁC VUÔNG
VẤN ĐỀ 1.
Bài 1. Hình 1:
3,6; 6,4;xy= =
Hình 2:
7,2; 12,8;xy= =
Hình 3:
35 74
; 74.
74
xy= =
Bài 2. a)
1,8; 3,2;BH CH= =
2,4; 5;AH BC= =
b)
15; 20; 25; 12.AB AC BC AH= = = =
Bài 3.
5,4; 9,6.BH HC= =
Bài 4.
4,5; 8.BH CH= =
Bài 5.
5; 2 5.xy= =
Bài 6. a)
1,8; 3,2;BH cm CH cm= =
2,4; 4;AH cm AC cm= =
b)
65 ; 156 ;AB cm AC cm= =
169 ;BH 25 ;BC cm cm= =
c)
= 5AB cm
;
= 13BC cm
;
=
25
13
BH cm
;
=
144
13
CH cm
.
Bài 7.
= 50BH cm
;
= 72CH cm
.
Bài 8.
= 9BH cm
;
= 16CH cm
.
Bài 9.
=
32
17
BH cm
;
=
225
34
CH cm
.
Bài 10. a)
= 7,5AB cm
;
= 10AC cm
;
= 12,5BC cm
;
= 8HC cm
.
b)
= 33AH cm
;
= 63AC cm
;
= 9CH cm
.
Bài 11.
=
2
150S cm
.
Bài 12. a)
= 3,6AH cm
.
b)
= 4,8BH cm
;
= 2,7CH cm
.
Bài 13. Đường cao : 6,72 ; Độ dài hai đoạn
chia cạnh huyền : 1,96 ; 23,04.
Bài 14.
=
75
7
HB cm
;
= 21C H cm
.
Bài 15.
= 9AB cm
;
=
20BC cm
;
= 15BD cm
.
VẤN ĐỀ 2
Bài 1. a)
( )
= =
2
..CD CM CE CN CH
;
b)
( )
∆∆ ..CMN CDE c g c∽
vì
C
chung và
=
CM CN
CE CD
.
Bài 2. a)
( )
∆=∆ g.c.gADI CDL
⇒ = ⇒∆DI DL DIL
là tam giác cân ;
b)
+=+=
2222 2
1111 1
DI DK DL DK DC
Bài 3. a)
( )
+= +
22 2 2
AB CH BH AH
( )
+=+ +
2 2 22
CH BH AH CH
= +
22
BH AC
;
b) Làm tương tự câu a) bài 1, có
( )
= =
2
..AM AB AN AC AH
.
Bài 4.
+=+
22 2
1 1 14
BD
OA OB AC
⇒
đpcm.
Bài 5. a)
= 17BD
; b)
=
120
7
AH
;
c)
( )
∆∆.BHI IKC g g∽
⇒=HBI IKC
.
26
( )
⇒∆ ∆ .HKD HBI g g∽
⇒=
HK HD
HB HI
⇔= =
2
..HK HI HD DB AH
.
Bài 6. a)
( ) ( )
= =9 cm ; 16 cmOB OD
b)
= 12OA
;
=
100
3
AC
;
c)
( )
=
2
1250
cm
3
ABCD
S
.
Bài 7. a)
=
22
:
FB HB HC
FC AB AC

=


22
:.
AB AC AC
BC BC AB
 
= =
 
 
43
.
AB AC AB
AC AB AC
b)
=
22
. .CF BC. .
HB HC
BC BE
AB AC
( )
=
2
..
.
BC
HB HC
AB AC
= =
43
1
.AH AH
AH
Bài 8. a)
AH
là đường trung bình của
∆ ⇒=2BCD BD AH
.
b)
= +
222
111
BK BC BD
= +
22
11
4BC AH
.
VẤN ĐỀ 3
Bài 1. a)
= 6DE cm
; b) Chứng minh M là
trung điểm BH, N là trung điểm CH ; c)
=
2
19,5S cm
.
Bài 2. a)
= =
2
2
.
.
AB HB BC HB
HC BC BC
AC
b)
=
22
:
ED HB HC
EC AB AC

=


22
:.
AB AC AC
BC BC AB
 
= =
 
 
43
.
AB AC AB
AC AB AC
c)
=
22
.CF. . .BC
HB HC
BE BC
AB AC
( )
=
2
..
.
BC
HB HC
AB AC
= = =
4 33
1
.AH AH DE
AH
;
d)
= +
3
33
2 22
BC BD CE
⇔=+
22
33
22
1
BC BD
CE CE

⇔= +


2
2
3
2
1
BC AB
AC
CE
 
⇔ = ⇔=
 
 
23
2
3
2
BC BC BC BC
AC CE AC
CE

⇔=


3
AC CE
BC AC
⇔==
2
2
22
.
sin
CE AC HC
ABC
AC AC
=
2
cos ACB
(đpcm)
Bài 3. a)
= 3,6BH cm
;
= 6CH cm
;
= 4,8AH cm
;
= 10BC cm
.
b)
= 3,6BH cm
;
= 6,4CH cm
;
= 4,8AH cm
;
= 8AC cm
.
Bài 4. Cạnh huyền : 100 cm ; Các cạnh góc
vuông : 60 cm và 80 cm.
Bài 5.
= 22,4HB cm
;
= 12,6HC cm
.
27
Bài 6.
= ≈
2
34560
204,5
169
S cm
.
Bài 7. a)
= 4AB cm
;
= 25AB cm
;
= 45AC cm
;
=
10BC cm
.
b)
=
5 281
16
AB cm
;
= 281AC cm
;
=
281
16
BC cm
;
=
25
16
BH cm
.
Bài 8.
= 9BH cm
;
= 16BH cm
.
Bài 9. Tương tự Bài 3.
Bài 10.
( )
=+≈35 21 5 81.95P cm
.
Bài 11.
=
2
1500S cm
.
Bài 12. a)
= 6BC cm
;
= 4,8CK cm
;
= 3,6BK cm
;
= 6,4AK cm
.
b)
= =
2
..CB CH CK CA CI
.
c)
= +
2 22
1 11
KM HK KI
= +
22
11
CH CI
.
d)
=
22
:
AI KA KB
BH AC BC

=


22
:.
AC BC BC
AB AB AC
 
= =
 
 
43
.
AC BC AC
BC AC BC
.
VẤN ĐỀ 4
Bài 1.
=
3
sin B
5
;
= 41OK
;
= 3OH
.
Bài 2. a)
= ≈
12
sin B 0,9231
13
;
= ≈
5
sinC 0,3846
13
.
b)
= ≈
4
sin B 0,7559
7
;
= ≈
3
sinC 0,6547
7
.
Bài 3. a) Vì
= 22OK
.
b)
= =
10
sin cos
5
BA
;
= =
15
cos sin
5
BA
;
= =
6
tan cot
3
BA
;
= =
3
cot tan
6
BA
.
Bài 4.
=cos 0,8C
;
=sin 0,6C
;
=
4
cot
3
C
;
=
3
tan
4
C
.
Bài 5.
= 8AC
;
= 89BC
.
Bài 6.
= =
3
sin cosC
5
B
;
= =
4
cos sin
5
BA
;
= =
3
tan cot
4
BC
;
= =
4
cot tan
3
BC
.
Bài 7.a) Vì
=
18 13
13
HN
b)
= =
10
sin cos
5
BC
;
= =
15
cos sin
5
BC
;
= =
6
tan cot
3
BC
;
28
= =
3
cot tan
6
BC
.
Bài 8.
=cos 0,8C
;
=sin 0,6C
;
=
4
cot
3
C
;
=
3
tan
4
C
.
Bài 9.
=
5
2
AC
;
=
13
2
BC
.
Bài 10.
∈O Ay
.
Bài 11.
= 72AC
;
= 12 61BC
.
Bài 12.
α
=
26
sin
5
;
α
=tan 2 6
;
α
=
6
cot
12
.
Bài 13. a)
= 9AC
;
= 15BC
.
b) ANBM là hình chữ nhật vì AN // BM ;
AN = BM.
c)
( )
∆∆ .MAB ACB g g∽
.
VẤN ĐỀ 5
Bài 1. a)
<
00
sin20 sin70
;
b)
>
00
cos60 cos70
;
c)
>
00
tan73 20' tan45
;
d)
>
00
cot 20 cot 37 40'
.
29
Bài 2. a)
00
71 19=cot ( tan )
<=
<<<
00
000
cot69 15'( tan20 85')
tan28 tan38 tan42 ;
b)
00
79 13 10 87=cos ' sin '
00
00
32 36
51 39
<<
<=
sin sin
cos sin .
Bài 3. a)
<
00
sin40 sin70 ;
b)
<
00
cos80 cos50 ;
c)
00
73 20 65>tan ' tan ;
d)
<
00
cot 53 cot 37 40'.
Bài 4. a)
00
79 15 10 85=cot ' tan '
<<
<= <
00
00 0
tan12 tan 28
cot61 ( tan29 ) tan58 ;
b)
<=
000
cos85 cos67 ( sin23 )
<=
<<
00
00
cos63 41'( sin26 59')
sin56 sin74 .
Bài 5. Dựng một tam giác vuông có:
a) Độ dài cạnh góc vuông là 3, cạnh
huyền là 5, góc đối diện với cạnh
góc vuông đó là góc
α
;
b) Độ dài cạnh góc vuông là 4, cạnh
huyền là 7, góc giữa cạnh góc vuông
và cạnh huyền đó là
α;
c) Độ dài hai cạnh góc vuông là 3 và
2, góc đối diện với cạnh góc vuông
độ dài 3 là góc
α
;
d) Độ dài hai cạnh góc vuông là 5 và
6, góc đối diện với cạnh góc vuông
độ dài 6 là góc
α.
Bài 6. Dựng một tam giác vuông có:
a) Độ dài cạnh góc vuông là 2, cạnh
huyền là 3, góc đối diện với cạnh
góc vuông đó là góc
α
;
b) Độ dài cạnh góc vuông là 2, cạnh
huyền là 5, góc giữa cạnh góc vuông
và cạnh huyền đó là góc
α
;
c) Độ dài hai cạnh góc vuông là 3 và
2, góc đối diện với cạnh góc vuông
độ dài 3 là góc
α;
d) Độ dài hai cạnh góc vuông là 4 và
5, góc đối diện với cạnh góc vuông
có độ dài 5 là góc
α.
Bài 7.
= =32,5 ; 12,5BC cm AC cm
Bài 8. a)
= =
12 5
sin ; sin
13 13
BC
b)
= =
2 21
sin ;sin
7
7
BC
Bài 9. Dựng một tam giác vuông có:
a) Độ dài cạnh góc vuông là 1, cạnh
huyền là 2, góc đối diện với cạnh
góc vuông đó là góc
α
;
b) Độ dài cạnh góc vuông là 2, cạnh
huyền là 3, góc giữa cạnh góc vuông
và cạnh huyền đó là góc
α
;
c) Độ dài hai cạnh góc vuông là 4 và
5, góc đối diện với cạnh góc vuông
độ dài 4 là góc
α
;
d) Độ dài hai cạnh góc vuông là 3 và
4, góc đối diện với cạnh góc vuông
độ dài 4 là góc
α
.
Bài 10.a)
= <
00 0
cos62 ( sin28 ) sin34
<<
<=
00
00
sin 35 sin 45
cos28 ( sin62 );
b)
=
00
cos65 30'( sin 24 70')
<=
<< =
<
00
000
0
cos59 ( sin31 )
sin47 cos37 ( sin 53 )
sin72 .
Bài 11. a)
=
1
2
A
; b)
=
1
2
B
.
Bài 12.
α
=
26
cos
5
,
α
=
1
tan
26
,
30
α
=cot 2 6.
Bài 13. TươngtựBài 14. Vấnđề 4.
Bài 14. a)
= 3A
; b)
= 2,5.B
Bài 15.Góc
α
2
là góc
AMH
a)
α
= =
2
sin 2
AH AH
AM BC
αα
= =
2
.
2. 2sin cos ;
AB AC
BC
b)
α
+ =+=1 cos2 1
HM HC
AM AM
α
= = =
2
2
2
2 2 2cos ;
HC AC
BC
BC
c)
α
− =−=1 cos2 1
HM HB
AM AM
α
= = =
2
2
2
2 2 2 sin
HB AB
BC
BC
VẤN ĐỀ 6.
Bài 1. a)
= =
20 3 10 3
;.
33
ac
b)
= ≈
0
20.sin35 11,48;b
= ≈
0
20.cos35 16,38.c
Bài 2. a)
= =
2
115;sin
3
cB
⇒≈ ⇒≈
00
41,8 48,2 .BC
b)
= =
12
193;tan
7
aB
⇒≈ ⇒≈
00
59,7 30,3 .BC
Bài 3. a)
=≈≈
00
35; 53,1 ;C 36,9 ;aB
b)
=≈≈
00
8; 41,8 ; 48,2 .cB C
Bài 4. a)
≈≈ =
0
2,95; 4,69; 49 .baC
b)
≈==
0
9,53; 5,5; 30 .c bB
Bài 5.
≈≈3,65 ; 7,3 .AN cm AC cm
Bài 6. a)
= 33 ;CH cm
= ≈
0
3 3;sin80 5,28 .AC cm
b)
= ≈
2
1
.3 3.6,92 17,98 .
2
S cm
Bài 7.
≈
2
5,09 .S cm
Bài 8.
=
2
7,66 .S cm
Bài 9. a)
≈≈ =
0
3,12; 6,24; 60 .caB
b)
= 10 2.a
Bài 10. a)
= =
2
115;sin
3
cB
⇒≈ ⇒=
00
41,8 48,2 .BC
b)
= =
12
193;tanB
7
a
⇒≈ ⇒≈
00
59,7 30,3 .BC
Bài 11. a)
≈≈5,14 ; 6,13 ;a cm b cm
=
0
50 .C
b)
= ≈
0
62 ; 9,4 ;A a cm
= =
00
61;93 ; 28,07 .AC
Bài 12.
≈
2
509,08 .S cm
Bài 13.
3
24 9 3
.
2
S cm
+
=
Bài 14. a)
15 ; 20 ;AB cm AC cm= =
25 ; 12 ;BC cm AH cm= =
b)
ADHE
làhìnhchữnhật;
c)
2
69,12 ; 33,6 .S cm P cm= =
Bài 15. a)
0
4 ; 53,13 ;AC cm B= =
0
36,87C =
;
b)
2,25 ; 3,75 ;AD cm BD cm= =
31
c)
2
. ..BF BD BA BE BC= =
VẤN ĐỀ 7
Bài 1.Chiều cao
6,75 .m≈
Bài 2.Độ dài
0
2,1
4,5 .
sin28
m= ≈
Bài 3.Chiều cao
0
5.tan 50 5,96 .m= ≈
Bài 4.
0
59 44'.BCA ≈
Bài 5. a)
2
..AE AC AH AD AB= =
( )
c-g-c ;ABC AED⇒∆ ∆
b)
3.DE cm=
c)
0
56 ;ABC =
d)
2
54
.
13
ADE
S cm=
Bài 6. a) Vì
1
;
2
EF CG AB= =
;EF CG AB
b)
CF BE⊥
mà
EG CF
0
90 .EG BE BEG⇒ ⊥⇒ =
c)
2
;
sin .cos
ABCD
h
S =
αα
d)
.
sin .cos
h
AC =
αα
Bài 7.
0
21
22,73 .
cos22,5
BD cm= ≈
Bài 8. a)
5 ;AC 5 3 .AB cm cm= =
b)
AMBN
là hình chữ nhật
CBM ABM NMB⇒==
//MN BC⇒
(so le trong)
AMBN
là hình chữ nhật
1
.
2
MN AB BC⇒==
c)
1
2
CBM ABM ABC= =
0
30 ACB= =
( )
g-gMAB ABC⇒∆ ∆
Tỉ số đồng dạng :
1
.
2
AB
BC
=
Bài 9.Tương tự Bài 5.
Bài 10. a) Giả sử tam giác
ABC
có
0
90A <
,
kẻ đường cao
.BH
Ta có :
.sinBH AB A=
1
.
2
ABC
S BH AC
∆
⇒=
1
. .sin .
2
ABC
S AB AC A
∆
⇒=
b)
ABCD
là hình bình hành
có
0
90A <
,
,ABD CBD∆=∆
2
ABCD ABD
SS
∆
⇒=
. .sin .AB AD A=
ÔN TẬP CHỦ ĐỀ 3
32
Bài 9. a)
( )
..ABE ADF g c g∆=∆
AE AF⇒=
b)
0
, 45F chung FAK FCA= =
( )
2
.;
AKF CAF g g
AF CF
AF KF CF
KF AF
⇒∆ ∆ −
⇒=⇔ =
∽
c)
2
93
;
2
AEF
S cm
∆
=
Bài 12. a)
24
cos ;
5
α
=
1
tan ; cot 24
24
αα
= =
b)
52
cos ; tan ;
3
5
αα
= =
5
cot .
2
α
=
Bài 1. a)
3 13BC cm=
;
18 13
13
AH cm=
;
12 13
13
BH cm=
;
27 13
13
CH cm=
.
b)
25 ; 20 ;BC cm AC cm= =
16 ; 12 .HC cm AH cm= =
c)
132
33 ; ;
5
AB cm AH cm= =
99 176
; .
55
BH cm CH cm= =
Bài 2. a) Đặt
9 ; 16 ;BH cm CH cm= =
15 ; 20 .AB cm AC cm= =
b)
0
73,74 .AMH ≈
c)
2
84 .
AHM
S cm=
Bài 3.a)
63 ;CH cm=
0
63
10,55 ;
sin80
AC cm= ≈
b)
( )
2
1
6 3 6 1,83
2
40,69 .
ABC
S
cm
∆
= +
≈
Bài 4.a)
12
5 ;
5
BC cm AH cm= =
b)
00
53,13 ; 36,87BC≈≈
c)
15 20
; .
77
BE cm CE cm= =
Bài 5.a)
2
..AE AB AH AE AC= =
b)
97
;;
44
AE BE= =
c)
3
.
2
FC cm=
Bài 6. a) i)
15 ;NF cm=
00
48,59 ; 41,41 .MFN MNF≈=
ii)
36 48
; .
55
MO FO= =
iii)
2
96 .
FNE
S cm=
2
9
.
25
34,56 .
FOH
FNE
FOH
S
FO FH
S FN FE
S cm
∆
∆
∆
= =
⇒=
b)
( )
MFN FEM g g∆∆−∽
2
.
MF MN
MF MN FE
FE FM
⇒= ⇔ =
Bài 7. a) Vì
2 22
DE DF FE+=
b)
24 32
; .
55
DK cm FK cm= =
c)
0
18
; 90 ;
5
EK cm DKE= =
0 ' 0'
36 52 ; 53 8KDE KED≈=
d)
30 40
; .
77
ME cm MF cm= =
e)
sin , sin
DK DE
DFK DFE
DF E
F
= =
. ..
DK DE
DE DF DK EF
DF EF
⇒=⇔ =
Bài 8.a)
3 ; 6 3 .AB cm AC cm= =
b)
cos
AB AB
ABC
BD BC
= =
0
cos60 cos ;
AC
ACD
CD
= = =
c)
222
111
.
AH AC AD
= +
33
d)
22
11
AE AF
AE AJ
=⇒+
22 2
11 1
.const
AF AJ AD
= += =
Bài 10. a)
( )
00
cos70 sin20=
( )
00
000
sin 24 sin 54
cos35 sin55 sin78 ;
<<
<=<
b)
( )
00
tan16 cot74=
( )
0' 0
00 0
cot 57 67 cot30
cot 24 tan80 cot10 .
<<
<< =
Bài 11. a)
00
cos20 sin65<
( )
( )
00
000
cos25 cos28
sin40 cos50 cos88 .
= <
<= <
b)
( )
0' 0'
cot67 18 tan22 42=
( )
0' 0'
0' 0'
cot 28 36 tan61 24
tan32 48 tan56 32
<=
<<
c)
11
cot ;cos ;
2
5
αα
= = ±
2
sin
5
α
= ±
d)
11
tan ;sin ;
3
10
αα
= = ±
3
cos
10
α
= ±
Bài 13.
0'
7
tan 60 15
.
4
αα
=⇒≈
Bài 14.
6,28 .cm
Bài 15. a)
2.A =
b)
42
3sin sin .B
αα
= +
Bài 16. a)
44
sin cosxx+
( )
2
2 2 22
22
sin cos 2sin cos
1 2sin cos ;
x x xx
xx
=+−
= −
b)
66
sin cosxx+
( )
( )
3
22
22 2 2
22
sin cos
3sin cos sin cos
1 3sin cos .
xx
xx x x
xx
= +
−+
= −
c)
44
sin cosxx−
( )( )
2 22 2
2
sin cos sin cos
1 2cos .
xxx x
x
=−+
= −
Bài 17. a)
1 cos sin
sin 1 cos
xx
xx
−
=
+
( )( )
2
22
1 cos 1 cos sin
sin cos 1.
x xx
xx
⇔− + =
⇔+=
b)
( )
( )
2
2
sin 1 cos
sin 1 cos
xx
VT
xx
++
=
+
( )
2 2cos
;
sin 1 cos
x
VP
xx
+
= =
+
c) Biến đổi tương đương tương tự
câu a.
CHỦ ĐỀ 4. ĐƯỜNG TRÒN
VẤN ĐỀ 1.
Bài 1. a) Goi O là trung điểmcủa BC
O⇒
là tâm đườngtrònđi qua
Bài 4.
MNPQ
là hình chữ nhật tâm O
, , , MNPQ⇒
cùng thuộc
( )
;.O OM
Bài 5.Gọi
, , , EFPQ
lần lượt là trung điểm
của
, , , .MA MB MC MD
Chứng minh tứ giác
EFPQ
có hai góc đối
có tổng bằng
0
180 .
, , , EFPQ⇒
cùng thuộc một đường
tròn.
Bài 6. Trong hình thoi, đường chéo này là
Trung trực của đường chéo kia. Do đó,
điểm E là giao điểm hai đường trung trực
của hai cạnh
AB
và
AC
. Nên E là tâm
đường tròn ngoại tiếp
.ABC∆
Tương tự, F
là tâm đường tròn ngoại tiếp của
.ABD∆
Bài 7. a) Ta có:
0
90ACD C= ⇒
thuộcđường
trònđườngkính
AD
.
34
, , ;ABC
b)
1
2
OA OB OC OA BC==⇒=
ABC⇒∆
vuông tại
.A
Bài 2.Goi O là trung điểm BC.
Chứng minh:
, , , BCDE
nằm
trên
;.
2
BC
O



Bài 3. a)
IFEK
là hình bình hành tâm O có:
, //CH IK KE CH⊥
IK KE IFEK⇒⊥ ⇒
là hình chữ nhật
, , , IFEK⇒
cùng thuộc
( )
;.O OI
b) Chứng minh
KD DF⊥
KDF⇒∆
vuông.
Chứngminh
0
90ABD B= ⇒
thuộc đường
tròn đường kính
, AD B C⇒
cùng thuộc
đường tròn đường kính
AD
;
b)
10 .AD cm=
Bài8. a)Gọi O là trungđiểm BC.
Mà
1
;
2
D O BC

∈


OB OC OD⇒==
BDC⇒∆
vuông tại D.
CD AB⇒⊥
. Tương tự
;BE AC⇒⊥
b) Xét
ABC∆
có K là trực tâm
.AK BC⇒⊥
35
| 1/35
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

MỤC LỤC
VẤN ĐỀ 1. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG (PHẦN 1) 3 A.
TÓM TẮT LÝ THUYẾT ....................................................................................................... 3
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ......................................................................................... 3
C.BÀI TẬP VỀ NHÀ ...................................................................................................................... 4
VẤN ĐỀ 2. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG (PHẦN
II) ............................................................................................................................................................ 6
A. TÓM TẮT LÝ THUYẾT ............................................................................................................ 6
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ........................................................................................... 6
Dạng 2. Chứng minh các hệ thức liên quan đến tam giác vuông ....................................... 6
VẤN ĐỀ 3 : LUYỆN TẬP HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC
VUÔNG ................................................................................................................................................ 8
A. TÓM TẮT LÝ THUYẾT ............................................................................................................ 8
B. BÀI TẬP TỰ LUYỆN ................................................................................................................. 8
C. BÀI TẬP VỀ NHÀ ..................................................................................................................... 9
VẤN ĐỀ 4. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN I) ............................................... 10
A. TÓM TẮT LÝ THUYẾT .......................................................................................................... 10
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ......................................................................................... 10
Dạng 1. Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc ...................................... 10
C. BÀI TẬP VỀ NHÀ ................................................................................................................... 11
VẤN ĐỀ 5. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN II) ............................................. 13 A.
TÓM TẮT LÝ THUYẾT ..................................................................................................... 13
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ....................................................................................... 13
Dạng 2. Sắp thứ tự dãy các tỉ số lượng giác ......................................................................... 13
Dạng 3.Dựng góc nhọn α biết tỉ số lượng giác của nó là m .
n .......................................... 14
C. BÀI TẬP VỀ NHÀ : ................................................................................................................. 15
VẤN ĐỀ 6. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG (PHẦN
I). .......................................................................................................................................................... 16
A. TÓM TẮT LÝ THUYẾT. ......................................................................................................... 16
B. BÀI TẬP VÀ CÁC DẠNG TOÁN. ........................................................................................ 16
Dạng 1. Giải tam giác vuông .................................................................................................. 16
Dạng 2. Tính cạnh và góc của tam giác ................................................................................ 17
C. BÀI TẬP VỀ NHÀ ................................................................................................................... 17
VẤN ĐỀ 7. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG (PHẦN
II) .......................................................................................................................................................... 19
A. TÓM TẮT LÝ THUYẾT .......................................................................................................... 19 1
B. BÀI TẬP VÀ CÁC DẠNG TOÁN ......................................................................................... 19
Dạng 3. Toán ứng dụng thực tế ............................................................................................. 19
Dạng 4. Toán tổng hợp ............................................................................................................ 20
C. BÀI TẬP VỀ NHÀ ................................................................................................................... 20
ÔN TẬP CHỦ ĐỀ 3 .......................................................................................................................... 21
A. TÓM TẮT LÝ THUYẾT .......................................................................................................... 21
B. BÀI TẬP TỰ LUYỆN ............................................................................................................... 22
HƯỚNG DẪN GIẢI ......................................................................................................................... 26
VẤN ĐỀ 1. ..................................................................................................................................... 26
VẤN ĐỀ 2 ...................................................................................................................................... 26
VẤN ĐỀ 3 ...................................................................................................................................... 27
VẤN ĐỀ 4 ...................................................................................................................................... 28
VẤN ĐỀ 5 ...................................................................................................................................... 29
VẤN ĐỀ 6. ..................................................................................................................................... 31
VẤN ĐỀ 7 ...................................................................................................................................... 32
ÔN TẬP CHỦ ĐỀ 3 ................................................................................................................. 32 2
CHỦ ĐỀ 3. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
VẤN ĐỀ 1. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG (PHẦN 1) A. TÓM TẮT LÝ THUYẾT
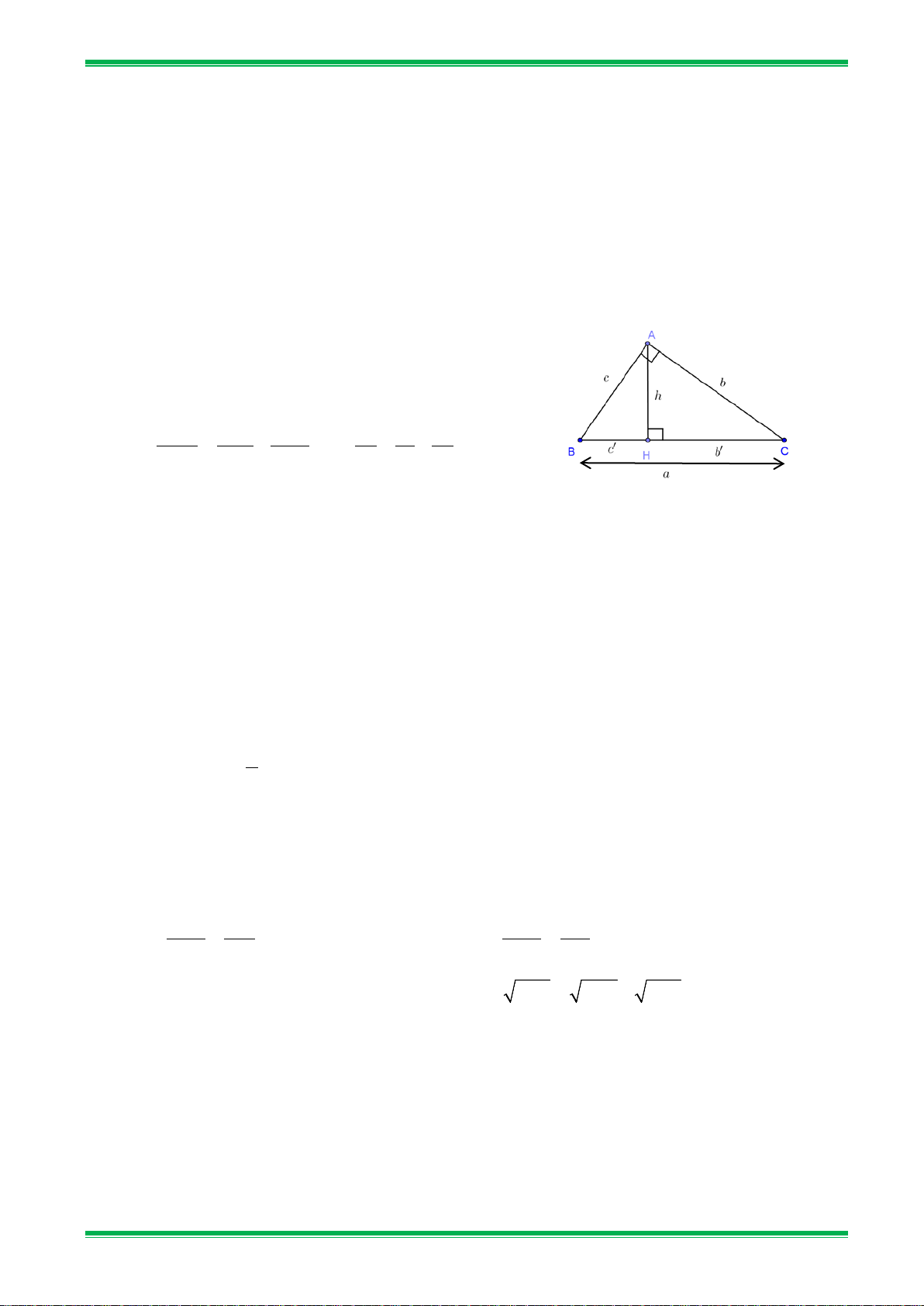
Cho tam giác ABC vuông tại A , đường cao AH . Khi đó ta có các hệ thức sau: • 2
AB = BH.BC hay 2 c = . a c' A • 2
AC = CH.BC hay 2 b = ab' • .
AB AC = BC.AH hay cb = ah c b • 2 HA = . HB HC hay 2 h = c'b' 1 1 1 1 1 1 c' b' • B C = + hay = + . 2 2 2 AH AB AC 2 2 2 h c b H • 2 2 2
BC = AB + AC (Định lí Pitago). a
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Tính độ dài các đoạn thẳng trong tam giác vuông
Phương pháp giải: Cho tam giác ABC vuông tại A , đường cao AH . Nếu biết độ dài
hai trong sáu đoạn thẳng AB, AC,BC,HA,HB,HC thì ta luôn tính được độ dài bốn đoạn thẳng còn lại.
• Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Tính x, y trong mỗi hình vẽ sau: A A A 12 7 5 6 8 x x y B C B C H H B C x H y 20 y Hình 1 Hình 2 Hình 3
Bài 2. Cho tam giác ABC vuông tại A , đường cao AH.
a) Cho biết AB = 3c , m AC = 4c .
m Tính độ dài các đoạn thẳng BH , CH , AH và BC.
b) Cho biết BH = 9c ,
m ch = 16cm . Tính độ dài các đoạn thẳng AB, AC, BC và AH.
Bài 3. Cho tam giác ABC vuông tại A , AH ⊥ BC ( H thuộc BC ). Cho biết AB : AC = 3: 4 và BC = 15c .
m Tính độ dài các đoạn thẳng BH và CH.
Bài 4. Cho tam giác ABC vuông tại A , đường cao AH. Cho biết AB : AC = 3: 4 và AH = 6c .
m Tính độ dài các đoạn thẳng BH và CH.
* Học sinh tự luyện tập các bài tập sau tại lớp :
Bài 5. Tính x, y trong các hình vẽ sau : 3 A A A 13 x 5 y B C H B C B C 1 H 4 y 4 H x Hình 4 Hình 5 Hình 6
Bài 6. Cho tam giác ABC vuông tại A , đường cao AH.
a) Cho biết AB = 3c , m BC = 5c .
m Tính độ dài các đoạn thẳng BH , CH , AH và AC.
b) Cho biết AH = 60c , m CH = 144c .
m Tính độ dài các đoạn thẳng AB, AC, BC và BH. c) Cho biết 60 AC = 12c , m AH = c .
m Tính độ dài các đoạn thẳng AB, BC, BH và CH. 13 Bài 7. Cho tam giác AB
ABC vuông tại A , đường cao AH.Cho biết 5 = và BC =122c . m AC 6
Tính độ dài các đoạn thẳng BH,CH.
Bài 8. Cho tam giác ABC vuông tại A , đường cao AH. Cho biết AB : AC = 3: 4 và AH = 12c .
m Tính độ dài các đoạn thẳng BH ,CH. C.BÀI TẬP VỀ NHÀ
Bài 9. Cho tam giác ABC vuông tại A , đường cao AH. Cho biết AB = 4c , m BC = 7, 5c . m Tính
độ dài các đoạn thẳng BH,CH.
Bài 10. Cho tam giác ABC vuông tại A , đường cao AH.
a) Biết AH = 6c , m BH = 4, 5c .
m Tính AB, AC, BC, HC.
b) Biết AB = 6c , m BH = 3c .
m Tính AH , AC, CH.
Bài 11. Cho tam giác ABC vuông tại A , đường cao AH.Tính diện tích tam giác ABC , biết AH = 12c , m BH = 9c . m
Bài 12. Cho tam giác ABC, biết BC = 7,5c , m CA = 4, 5c , m AB = 6c . m
a) Tính độ dài đường cao AH của tam giác ABC.
b) Tính độ dài các đoạn thẳng BH,CH.
Bài 13. Cho tam giác vuông với các cạnh góc vuông là 7 và 24. Kẻ đường cao ứng với cạnh
huyền. Tính độ dài đường cao và các đoạn thẳng mà đường cao đó chia ra trên cạnh huyền. Bài 14. Cho tam giác AB
ABC vuông tại A , đường cao AH.Biết 5 = , AH = 15c . m Tính độ dài AC 7
các đoạn thẳng HB và HC. 4
Bài 15. Cho ABCD là hình thang vuông tại A và .
D Đường chéo BD vuông góc với BC. Biết AD = 12c , m DC = 25c .
m Tính độ dài AB, BC và B . D 5
VẤN ĐỀ 2. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG (PHẦN II) A. TÓM TẮT LÝ THUYẾT
Nhắc lại lý thuyết : Cho tam giác ABC vuông tại A , đường cao AH. Khi đó có các hệ thức sau : • 2
AB = BH .BC hay 2 c = . a c ' • A 2
AC = CH .BC hay 2 b = . a b ' • A .
B AC = BC.AH hay cb = . a h • 2 b HA = . HB HC hay 2
h = c 'b ' c h • 1 1 1 1 1 1 = + hay = + 2 2 2 AH AB AC 2 2 2 h c b c' b' B C • 2 2 2
BC = AB + AC ( Định lí Pitago) H a
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 2. Chứng minh các hệ thức liên quan đến tam giác vuông
Phương pháp giải : Sử dụng các hệ thức về cạnh và đường cao một cách hợp lý theo hướng :
Bước 1. Chọn các tam giác vuông thích hợp chứa các đoạn thẳng có trong hệ thức.
Bước 2. Tính các đoạn thẳng đó nhờ hệ thức về cạnh và dường cao.
Bước 3. Liên kết các giá trị trên để rút ra hệ thức cần chứng minh.
* Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 1. Cho tam giác CDE nhọn, đường cao CH. Gọi M , N theo thứ tự là hình chiếu của
H lên CD, DE. Chứng minh : a) .
CD CM = CE.CN;
b) Tam giác CMN đồng dạng với tam giác CE . D
Bài 2. Cho hình vuông ABC .
D Gọi I là một điểm nằm chính giữa A và .
B Tia DI và tia CB
cắt nhau ở K. Kẻ đường thẳng qua D , vuông góc với DI , cắt đường thẳng BC tại L . Chứng minh :
a) Tam giác DIL là tam giác cân ; b) Tổng 1 1 +
không đổi khi I thay đổi trên cạnh A . B 2 2 DI DK
* Học sinh tự luyện tập các bài tập sau tại lớp :
Bài 3. Cho tam giác ABC có ba góc nhọn và AH là đường cao. 6 a) Chứng minh 2 2 2 2
AB + CH = AC + BH ;
b) Gọi M , N theo thứ tự là hình chiếu của H lên AB, AC. Chứng minh :
AM .AB = AN.AC.
Bài 4. Cho hình thoi ABCD có hai đường chéo cắt nhau tại O . Cho biết khoảng cách từ O
tới mỗi cạnh của hình thoi là 1 1 1 , h AC = , m BD = . n Chứng minh : = + . 2 2 2 m n 4h C.BÀI TẬP VỀ NHÀ
Bài 5. Cho hình chữ nhật ABCD có AB = 8c , m BC = 15c . m
a) Tính độ dài đoạn thẳng B . D
b) Vẽ AH vuông góc với BD tại H. Tính độ dài đoạn thẳng AH.
c) Đường thẳng AH cắt BC và DC lần lượt tại I và K. Chứng minh 2
AH = HI.HK.
Bài 6. Cho hình thang ABCD vuông tại A và D. Cho biết AB = 15cm, AD = 20cm, các đường
chéo AC và BD vuông góc với nhau ở O. Tính
a) Độ dài các đoạn thẳng OB và OD;
b) Độ dài đoạn thẳng AC ;
c) Diện tích hình thang ABCD.
Bài 7. Cho tam giác ABC vuông tại A. Đường cao AH, kẻ HE, HF lần lượt vuông góc với AB, AC. Chứng minh : EB  AB 3 a) =   ; b) = 3 BC.BE.CF AH . FC  AC 
Bài 8. Cho tam giác ABC cân tại A có AH và BK là hai đường cao. Kẻ đường thẳng vuông
góc với BC tại B cắt tia CA tại D. Chứng minh : a) BD = 2.AH ; b) 1 1 1 = + . 2 2 2 BK BC 4HA 7
VẤN ĐỀ 3 : LUYỆN TẬP HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
A. TÓM TẮT LÝ THUYẾT
Nhắc lại lý thuyết : Cho tam giác ABC vuông tại A, đường cao AH. Khi đó ta có các hệ thức sau:
● AB2 = BH. BC hay c2 = a.c’
● AC2 = CH. BC hay b2 = a.b’
● AB. AC = BC. AH hay c.b = a. h
● HA2 = HB. HC hay h2 = c’. b’ ● 1 1 1 1 1 1 = + hay = + 2 2 2 AH AB AC 2 2 2 h c b
● BC2 = AB2 + AC2 (Định lí Pitago)
B. BÀI TẬP TỰ LUYỆN
* Giáo viên hướng dẫn học sinh giải các bài tập sau :
Bài 1. Cho tam giác ABC vuông tại A, đường cao AH. Cho biết BH = 4cm, CH = 9cm. Gọi D,
E lần lượt là hình chiếu vuông góc của H trên các cạnh AB và AC.
a) Tính độ dài đoạn thẳng DE.
b) Các đường thẳng vuông góc với DE tại D và E lần lượt cắt BC tại M, N. Chứng minh 1 MN = BC . 2
c) Tính diện tích của tứ giác DENM.
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là hình chiếu
vuông góc của H trên AB, AC. Chứng minh 2 3 a) AB HB AB BD = ; b) = ; 2 AC HC 3 AC EC c) DE2 = BD. CE. BC; d) 3 2 3 2 3 2 BC = BD + CE .
*Học sinh tự luyện các bài tập sau đây
Bài 3. Cho tam giác ABC vuông tại A, đường cao AH.
a) Cho biết AB = 6cm, AC = 8cm. Tính độ dài các đoạn thẳng BH, CH, AH và BC.
b) Cho biết AB = 6cm, BC = 10cm. Tính độ dài các đoạn thẳng BH, CH, AH và AC. 8
Bài 4. Tìm độ dài các cạnh của một tam giác vuông nếu đường cao ứng với cạnh huyền có
độ dài 48cm và hình chiếu của các cạnh góc vuông trên cạnh huyền theo tỉ lệ 9 : 16.
Bài 5. Cho tam giác ABC vuông tại A, phân giác AD, đường cao AH. Biết BD = 15cm, CD =
20cm. Tính độ dài các đoạn thẳng HB, HC.
Bài 6. Cho hình thang cân ABCD có độ dài cạnh đáy AB = 26cm và cạnh bên AD = 10cm.
Cho biết đường chéo AC vuông góc với cạnh bên BC. Tính diện tích hình thang ABCD. C. BÀI TẬP VỀ NHÀ
Bài 7. Cho tam giác ABC vuông tại A, đường cao AH.
a) Nếu BH = 2cm, CH = 8cm. Tính độ dài các đoạn AB, AC, BC, AH.
b) Nếu AH = 5cm, CH = 16cm. Tính độ dài các đoạn thẳng AB, AC, BC, BH.
Bài 8. Cho tam giác ABC vuông tại A, đường cao AH. Cho biết AB : AC = 3 : 4 và AH =
12cm. Tính độ dài các đoạn thẳng BH và CH.
Bài 9. Cho tam giác ABC vuông tại A, phân giác AD, đường cao AH. Cho biết BD = 15cm,
CD = 20cm. Tính độ dài các đoạn thẳng HB và HC.
Bài 10. Cho tam giác ABC vuông tại A, đường cao AH. Tính chu vi của tam giác ABC biết AH = 14cm, HB 1 = . HC 4
Bài 11. Cho tam giác ABC vuông tại A, đường cao AH. Tính diện tích tam giác ABC biết rằng AH = 12cm, BH = 9cm.
Bài 12. Cho tam giác ABC vuông tại C, đường cao CK.
a) Cho biết AB = 10cm, AC = 8cm. Tính BC, CK, BK và AK.
b) Gọi H và I theo thứ tự là hình chiếu của K trên BC và AC. Chứng minh CB. CH = CA. CI
c) Gọi M là chân đường vuông kẻ từ K xuống IH. Chứng minh 1 1 1 = + . 2 2 2 KM CH CI 3 d) Chứng minh AI AC = . 3 BH BC 9
VẤN ĐỀ 4. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN I)
A. TÓM TẮT LÝ THUYẾT
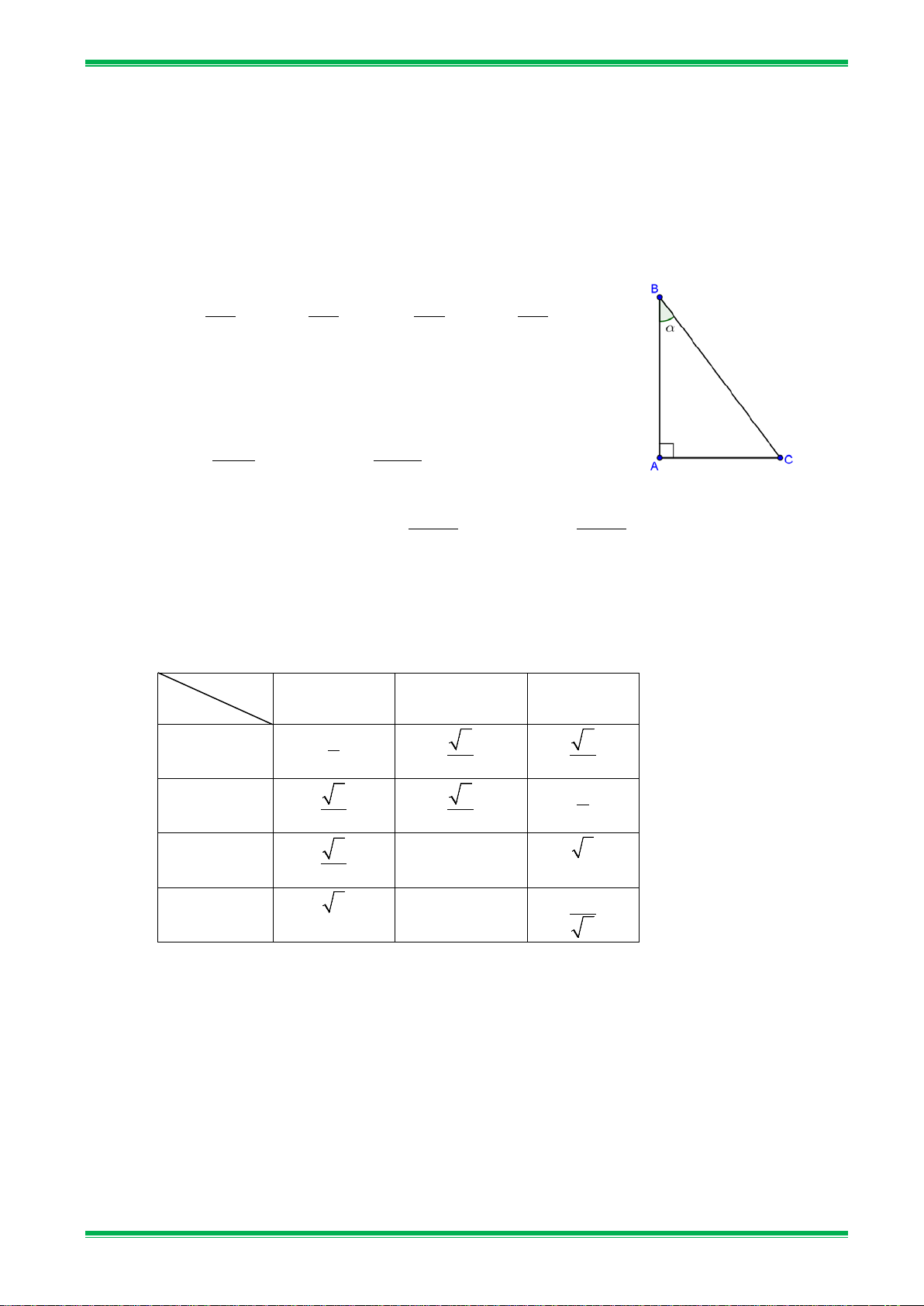
● Cho góc nhọn α ( o o
0 < α < 90 ) . Dựng tam giác ABC vuông tại A sao cho  α = ABC . Từ đó ta có: AB cosα = ; AC sin α = ; AC tan α = ; AB cot α = . AC AB AB AC
● Với góc góc nhọn α bất kì, ta luôn có:
0 < sin α < 1; 0 < cos α < 1 α tan α α = sin ; cot tan α = ; tan . α cot α = 1; cosα cosα sin 1 1 −
2 α + cos2 α = 1; 1 + tan2 α = ; 1 + cot2 α = . 2 cos x 2 sin α
●Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
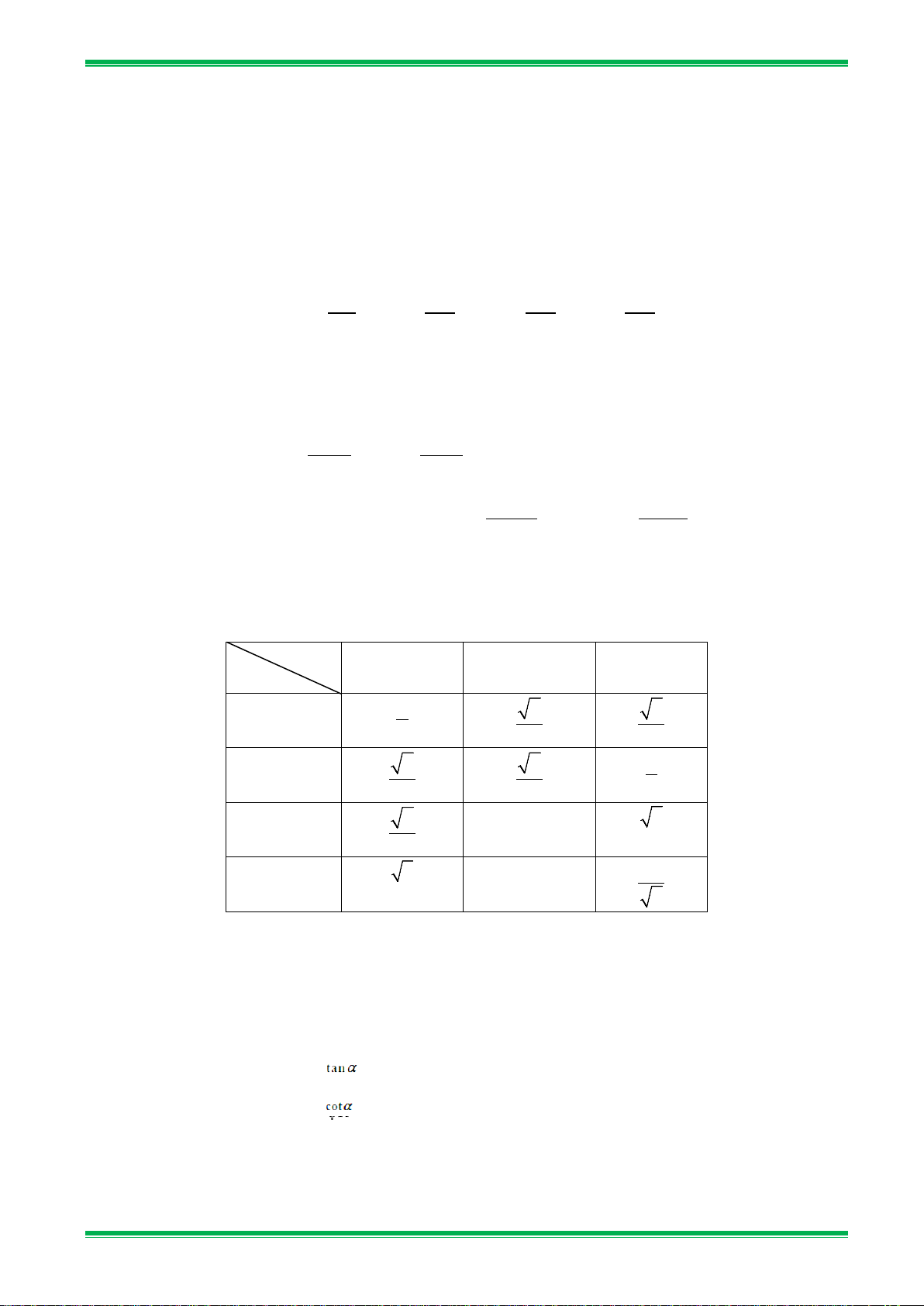
● Bảng tỉ số lượng giác các góc đặc biệt α 30o 45o 60o Tỉ số sin α 1 2 3 2 2 2 cosα 3 2 1 2 2 2 tanα 3 1 3 3 cot α 3 1 1 3
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 1. Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Phương pháp giải:Sử dụng các kiến thức trong phần Tóm tắt lý thuyết ở trên.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Cho tam giác ABC vuông tại Ccó BC = 1,2cm, AC = 0,9c .
m Tính các tỉ số lượng giác
của góc B. Từ đó suy ra tỉ số lượng giác của góc A. 10
Bài 2. Cho tam giác ABC vuông tại A, đường cao AH. Hãy tính sin B, sinC trong các trường
hợp sau (làm tròn kết quả đến chữ số thập phân thứ 4):
a) AB = 13cm,BH = 0,5dm;
b) CH = 4cm,BH = 3c . m
Bài 3. Cho tam giác ABCcó AB = a 5, AC = a 2,BC = a 3
a) Chứng minh rằng ABC là tam giác vuông.
b) Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc A.
Bài 4. Cho tam giác ABC vuông tại A. Hãy tính các tỉ số lượng giác của góc C biết rằng cosB = 0,6. Bài 5. 5
Cho tam giác ABCvuông tại Acó AB = 5cm, cot B = ⋅ Tính độ dài các đoạn thẳng AC 8 và BC.
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 6. Cho tam giác ABC vuông tại A có AB = 1,6cm, CA = 1,2c .
m Tính các tỉ số lượng giác
của góc B. Từ đó suy ra tỉ số lượng giác của góc C.
Bài 7. Cho tam giác ABCcó AB = a 3, AC = a 2,BC = a 5.
a) Chứng minh rằng ABC là tam giác vuông.
b) Tính các tỉ số lượng giác của góc B. Từ đó suy ra tỉ số lượng giác của góc C.
Bài 8. Cho tam giác ABC vuông tại A. Cho biết cosB = 0,8. Hãy tính các tỉ số lượng giác của góc C. Bài 9. 5
Cho tam giác ABCvuông tại Acó AB = 6 cm, tan B =
⋅ Tính độ dài các đoạn thẳng 12 AC và BC. C. BÀI TẬP VỀ NHÀ
Bài 10. Cho tam giác ABC vuông tại A có AB = 60mm, CA = 8c .
m Tính các tỉ số lượng giác của
góc B. Từ đó suy ra tỉ số lượng giác của góc C. Bài 11. 5
Cho tam giác ABCvuông tại Acó AB = 30 cm, tan B =
⋅ Tính độ dài các đoạn thẳng 12
AC và BC. Bài 12. 1
Tính sin α, cot α, tan α biết cos α = ⋅ 5
Bài 13. Cho tam giác ABCvuông tại A. Tính độ dài các đoạn thẳng AC và BC biết: a) 3 AB 5
= 12cm, tan B = ⋅
b) AB = 15cm, cosB = ⋅ 4 13 11
Bài 14. Cho tam giác ABC vuông ở A, C =  30 ,BC = 10 . cm a) Tính AB, AC.
b) Kẻ từ A các đường thẳng AM, AN lần lượt vuông góc với các đường phân giác
trong và ngoài của góc B. Chứng minh MN sog song với BC và MN = BC.
c) Chứng minh các tam giác MAB và ABC đồng dạng. Tìm tỉ số đồng dạng. 12
VẤN ĐỀ 5. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN II) A. TÓM TẮT LÝ THUYẾT
• Cho góc nhọn α (0 < α < 90) . Dựng tam giác ABC vuông tại A sao cho  α = ABC . Từ đó ta có : cos AB α = ; sin AC α = ; tan AC α = ; cot AB α = ⋅ BC BC AB AC
• Với góc nhọn α bất kỳ, ta luôn có:
0 < sinα < 1;0 < cosα < 1. sinα cos tan ; cot α α = α = ; tan . α cotα = 1. cosα sinα 2 2 2 1 2 1
sin α + cos α = 1;1+ tan α = ; 1+ cot α = ⋅ 2 2 cos α sin α
• Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
• Bảng tỉ số lượng giác của các góc đặc biệt: α 30o 45o 60o Tỉ số sin α 1 2 3 2 2 2 cosα 3 2 1 2 2 2 tan α 3 1 3 3 cot α 3 1 1 3 B.
BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 2. Sắp thứ tự dãy các tỉ số lượng giác
Phương pháp giải: Để sắp thứ tự dãy các tỉ số lượng giác cho trước ta cần làm được hai bước sau:
Bước 1: Đưa về các tỉ số lượng giác trong bài toán cùng loại bằng cách sử dụng tính chất
"Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia"
Bước 2: Với góc nhọn α,β, ta có: 13 sinα < sinβ ⇔ α < ; β cosα < cosβ ⇔ α > ; β tanα < tanβ ⇔ α < ; β cotα < cotβ ⇔ α > . β
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Không dùng bảng số và máy tính, hãy so sánh a) sin20 và sin70 . b) cos60 và cos70 .
c) tan7320′ và tan45 .
d) cot 20 và cot 3740 .′
Bài 2. Sắp xếp các tỉ số lượng giác sau theo thứ tự từ lớn đến bé:
a) tan42, cot71, tan38, cot69 15  ′, tan28;
b) sin32, cos51, sin39, cos79 1  3′, sin 38 .
* Học sinh tự luyện các bài tập sau tại lớp :
Bài 3. Không dùng bảng số và máy tính, hãy so sánh : a) 0 sin 40 và 0 sin70 ; b) 0 cos80 và 0 cos 50 ; c) 0 tan73 20' và 0 tan 65 ; d) 0 cot 53 và 0 cot 37 40'.
Bài 4. Sắp xếp các tỉ số lượng giác sau theo thứ tự từ bé đến lớn : a) 0 0 0 0 0
tan12 ,cot 61 ; tan 28 ;cot79 15'; tan 58 ; b) 0 0 0 0 0
cos67 ,sin 56 ,cos63 41',sin74 ,cos85 .
Dạng 3.Dựng góc nhọn α biết tỉ số lượng giác của nó là m . n
Phương pháp giải: Dựng một tam giác vuông có hai cạnh là m và n trong đó m và n
là hai cạnh góc vuông hoặc một cạnh góc vuông và một cạnh huyền rồi vận dụng
định nghĩa tỉ số lượng giác để nhận ra góc α .
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 5.Dựng góc nhọn α biết rằng : a) 3 sinα = ; b) 4 cosα = ; c) 3 tanα = ; d) 5 cotα = . 5 7 2 6
*Học sinh tự luyện ở lớp :
Bài 6.Dựng góc nhọn α biết rằng: a) 2 sinα = ; b) 2 cosα = ; c) 3 tanα = ; d) 4 cotα = . 3 5 7 5 14
C. BÀI TẬP VỀ NHÀ :
Bài 7.Cho tam giác ABC vuông tại A . Biết  5
AB = 30cm, B = α , tanα= . Tính cạnh 12 BC, AC.
Bài 8. Cho tam giác ABC vuông tại A , đường cao AH . Tính sin ;
B sinC biết rằng:
a) AB = 13; BH = 5;
b) BH = 3; HC = 4.
Bài 9.Dựng góc nhọn α biết rằng: a) 1 sinα = ; b) 2 cosα = ; c) 4 tanα = ; d) 3 cotα = . 2 3 5 4
Bài 10. Sắp xếp các tỉ số lượng giác sau heo thứ tự từ bé đến lớn. a) 0 0 0 0 0
sin 35 ,cos 28 ;sin 34 72';cos62 ;sin 45 ; b) 0 0 0 0 0
cos 37 ,cos65 30',sin72 ,cos59 ,sin 47 .
Bài 11. Tính giá trị biểu thức : a) 2 0 0 2 0 0
A = cos 52 sin 45 + sin 52 cos 45 ; b) 0 2 0 2 0 0
B = sin 45 cos 47 + sin 47 cos 45 .
Bài 12. Tìm cosα ,tanα ,cotα biết 1 sinα = . 5
Bài 13.Cho tam giác ABC vuông tại A ,  0
C = 30 ,BC = 10 . cm
a) Tính độ dài các đoạn thẳng AB, AC.
b) Kẻ từ A các đoạn thẳng AM, AN lần lượt vuông góc với các đường phân giác
trong và phân giác ngoài của góc B. Chứng minh MN song song với BC và MN = BC.
c) Chứng minh tam giác MAB đồng dạng với tam giác ABC . Tìm tỉ số đồng dạng.
Bài 14.Không dùng bảng số và máy tính, hãy tính : a) 2 0 2 0 2 0 2 0 2 0 2 0
A = cos 20 + cos 30 + cos 40 + cos 50 + cos 60 + cos 70 . b) 2 0 2 0 2 0 2 0 2 0
A = sin 5 + sin 25 + sin 45 + sin 65 + sin 85 .
Bài 15. Cho tam giác ABC vuông tại A ,  0
AB < AC,C = α < 45 , đường trung tuyến AM ,
đường cao AH , MA = MB = MC = .a Chứng minh : a) sin 2α = 2sinα cosα; b) 2 1+ os c 2α = 2cos α; c) 2 1− o c s2α = 2sin α. 15
VẤN ĐỀ 6. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG (PHẦN I). A. TÓM TẮT LÝ THUYẾT.
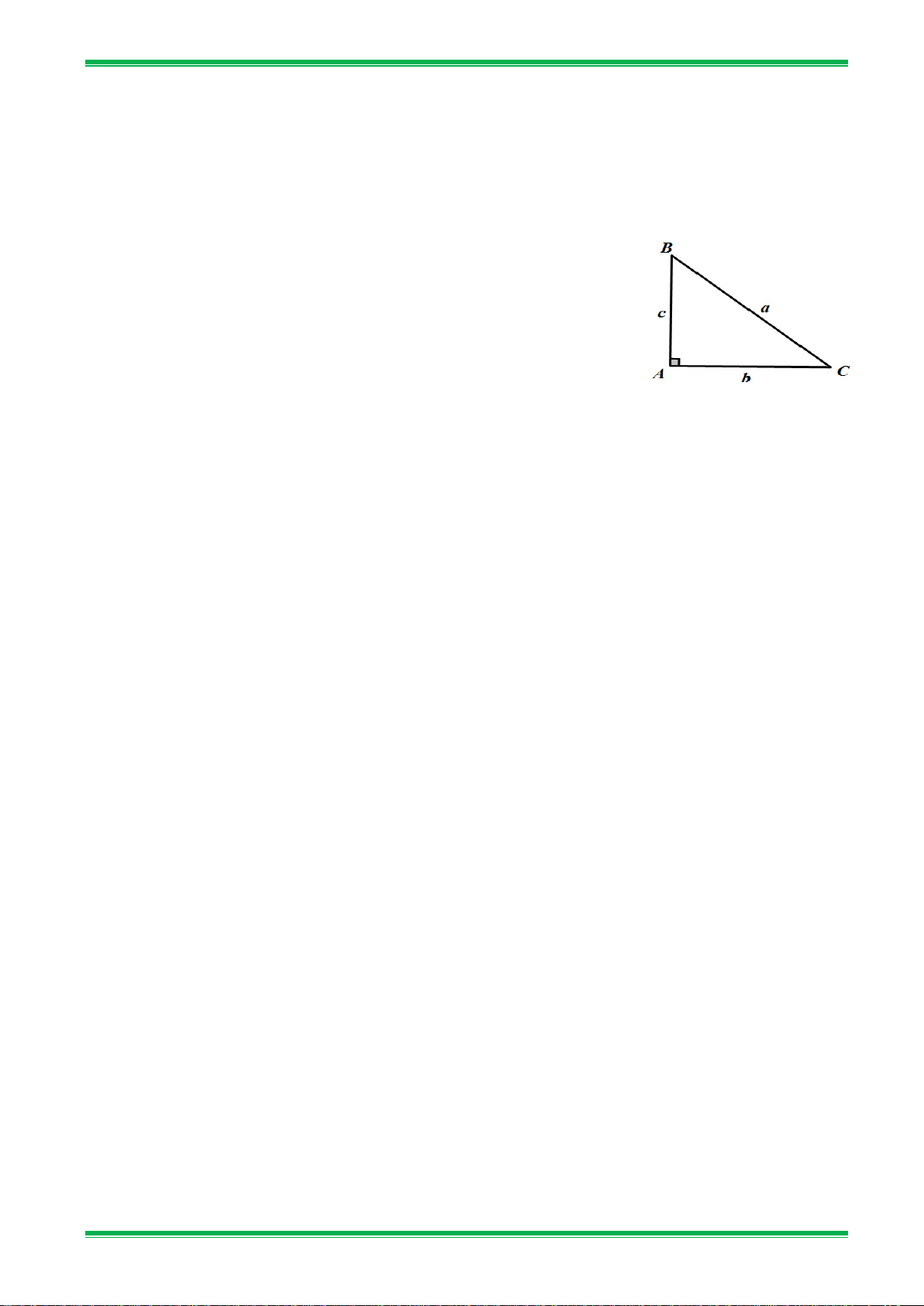
• Cho tam giác ABC vuông tại A có
BC = a, AC = b, AB = .c Ta có : B
• Trong một tam giác vuông : a b = .s a in B = .c a osC; c c = .s a inC = .c a os ; B
b = .ctan B = .ccotC; b A C c = . b tanC = . b cot . B
• Cạnh góc vuông = (cạnh huyền ) x (sin góc đối)
= (cạnh huyền ) x (cosin góc kề)
• Cạnh góc vuông = (cạnh góc vuông ) x (tang góc đối)
= (cạnh góc vuông còn lại ) x (cotang góc kề).
B. BÀI TẬP VÀ CÁC DẠNG TOÁN.
Dạng 1. Giải tam giác vuông Phương pháp giải:
1. Giải tam giác là tính độ dài các cạnh và số đo các góc dựa vào dữ kiện cho trước của bài toán.
2. Trong tam giác vuông, ta dùng hệ thức giữa cạnh và các góc của một tam giác vuông và
sử dụng máy tính cầm tay hoặc bảng lượng giác để tính các yế tố còn lại.
3.Các bài toán về giải tam giác vuông bao gồm :
i) Giải tam giác vuông khi biết độ dài một cạnh và số đo một góc nhọn.
ii) Giải tam giác vuông khi biết độ dài hai cạnh.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Cho tam giác ABC vuông tại A , có BC = a, AC = b, AB = .c Giải tam giác ABC , biết rằng : a)  0
b = 10cm; C = 30 ; b)  0
a = 20cm; B = 35 .
Bài 2. Cho tam giác ABC vuông tại A , có BC = a, AC = b, AB = .c Giải tam giác ABC , biết rằng :
a) a = 15cm; b = 10cm;
b) b = 12cm;c = 7c . m
* Học sinh tự luyện các bài tập sau tại lớp:
Bài 3. Cho tam giác ABC vuông tại A, có BC = a, AC = b, AB = .c Giải tam giác ABC, biết rằng: 16
a) b = 28cm;c = 21cm;
b) a = 10cm;b = 6c . m
Bài 4. Cho tam giác ABC vuông tại A, có BC = a, AC = b, AB = .c Giải tam giác ABC, biết rằng: a) c = cm  0 3,8 ; B = 51 ; b) a = cm  0 11 ;C = 60 .
Dạng 2. Tính cạnh và góc của tam giác
Phương pháp giải: Làm xuất hiện tam giác vuông để áp dụng các hệ thức trên bằng
cách kẻ thêm đường cao.
* Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 5. Cho tam giác ABC có BC = cm  0 11 , ABC = 38 và  0
ACB = 30 . Gọi N là chân đường
vuông góc hạ từ A xuống cạnh BC. Hãy tính:
a) Độ dài đoạn thẳng AN;
b) Độ dài đoạn thẳng AC.
Bài 6. Cho tam giác ABC, có BC = cm  0 B =  0 6 ,
60 ;C = 40 . Hãy tính:
a) Chiều cao CH và cạnh AC;
b) Diện tích tam giác ABC.
*Học sinh tự luyện các bài tập sau tại lớp:
Bài 7. Cho tam giác ABC có  0 B =  0
60 ,C = 50 , AC = 3,5c .
m Tính diện tích tam giác ABC
(làm tròn đến hàng đơn vị).
Bài 8. Tứ giác ABCD có các đường chéo cắt nhau tại O. Cho biết AC = 4cm,BD = 5cm,  0
AOB = 50 . Tính diện tích tứ giác ABC . D C. BÀI TẬP VỀ NHÀ
Bài 9. Cho tam giác ABC vuông tại A, có BC = a, AC = b, AB = .c Giải tam giác ABC, biết rằng: a) b = cm  0 5,4 ,C = 30 ; b) c = cm  0 10 ,C = 45 .
Bài 10. Cho tam giác ABC vuông tại A, BC = a, AC = b, AB = .c Giải tam giác ABC, biết rằng:
a) a = 15cm,b = 10cm;
b) b = 12cm,c = 7c . m
Bài 11. Cho tam giác ABC vuông tại A, BC = a, AC = b, AB = .c Giải tam giác ABC, biết rằng: a)  0 A = 40 , AC = 8; b)  0 C = 28 , AB = 5;
c) AB = 8,BC = 15.
Bài 12. Cho tam giác ABC có  0 B =  0
60 ,C = 50 , AC = 35c .
m Tính diện tích tam giác ABC. 17
Bài 13. Cho tứ giác ABCD có A =  0 D =  0
90 ,C = 40 , AB = 4cm, AD = 3c .
m Tính diện tích tứ giác ABC . D
Bài 14. Cho tam giác ABC vuông tại A, có đường cao AH; HB = 9cm,HC = 16c . m
a) Tính AB, AC, AH.
b) Gọi D và E lần lượt là hình chiếu vuông góc của H trên AB và AC. Tứ giác ADHE là hình gì?
c) Tính chu vi và diện tích của tứ giác A . DHE
Bài 15. Cho tam giác ABC vuông tại .
A Biết AB = 3cm,BC = 5c . m
a) Giải tam giác vuông ABC (số đo góc làm tròn đến độ).
b) Từ B kẻ đường thẳng vuông góc với BC, đường thẳng này cắt đường thẳng AC
tại D. Tính độ dài các đoạn thẳng AD,B . D
c) Gọi E,F lần lượt là hình chiếu của A trên BC và B . D Chứng minh :
BF.BD = B . E BC. 18
VẤN ĐỀ 7. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG (PHẦN II)
A. TÓM TẮT LÝ THUYẾT
• Cho tam giác ABC vuông tại A
có BC = a, AC = b, AB = .c Ta có : b = .s a in B = .c a osC; c = .s a inC = .c a os ; B
b = .ctan B = .ccotC; c = . b tanC = . b cot . B
• Trong một tam giác vuông
Cạnh góc vuông = (Cạnh huyền) × ( sin góc đối)
= (Cạnh huyền) × ( côsin góc kề)
Cạnh góc vuông = (Cạnh góc vuông) × (tang góc đối)
= (Cạnh góc vuông) × (cotang góc kề)
B. BÀI TẬP VÀ CÁC DẠNG TOÁN
Dạng 3. Toán ứng dụng thực tế
Phương pháp giải: Dùng hệ thức giữa cạnh và góc trong tam giác vuông để giải
quyết tình huống trong thực tế.
*Giáo viên hướng dẫn học sinh giải các bài tập sau:
Bài 1. Một cột đèn có bóng trên mặt đất dài 7,5 .
m Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 0
42 . Tính chiều cao của cột đèn.
Bài 2. Một cầu trượt trong công viên có độ dốc là 0 28 và có độ cao là 2,1 .
m Tính độ dài của
mặt cầu trượt (làm tròn đến chữ số thập phân thứ nhất).
*Học sinh tự luyện các bài tập sau tại lớp:
Bài 3. Một cột đèn có bóng trên mặt đất dài 5 .
m Các tia nắng mặt trời tạo với mặt đất một góc xấp xỉ bằng 0
50 . Tính chiều cao của cột đèn.
Bài 4. Một cột đèn điện AB cao 6m có bóng in trên mặt đất là AC dài 3,5 . m Hãy tính góc 
BCA (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất. 19
Dạng 4. Toán tổng hợp
Phương pháp giải: Vận dụng linh hoạt một số hệ thức giữa cạnh và góc trong tam giác vuông để giải toán.
*Giáo viên hướng dẫn học sinh giải bài tập sau:
Bài 5. Cho tam giác ABC vuông tại A, có AC > .
AB Đường cao AH. Gọi D,E lần lượt là
hình chiếu của H trên AB, AC. a) Chứng minh . AD AB = .
AE AC và tam giác ABC đồng dạng với tam giác AE . D
b) Cho biết BH = 2cm,HC = 4,5c .
m Tính dộ dài đoạn thẳng . DE c) Tính số đo góc 
ABC (làm tròn đến độ).
d) Tính diện tích tam giác AD . E
*Học sinh tự luyện bài tập sau tại lớp: Bài 6.
Cho hình chữ nhật ABC .
D Qua B kẻ đường thẳng vuông góc với đường chéo AC
tại H. Gọi E,F,G theo thứ tự là trung điểm của AH,BH,C . D
a) Chứng minh tứ giác EFCG là hình bình hành. b) Chứng minh  0 BEG = 90 .
c) Cho biết BH = h, 
BAC = α. Tính S theo h và α. ABCD
d) Tính độ dài đường chéo AC theo h và α. C. BÀI TẬP VỀ NHÀ
Bài 7. Cho tam giác ABC vuông tại A biết =  AB 21c ,
m C = 40° .Tính độ dài đường phân
giác BD của góc 
ABD, D nằm trên cạnh AC .
Bài 8. Cho tam giác ABC vuông ở  A,C = °
30 , BC = 10cm .
a) Tính AB, AC .
b) Kẻ từ A các đường thẳng AM , AN lần lượt vuông góc với các đường phân giác
trong và ngoài của góc B . Chứng minh MN song song với BC và 2MN = BC .
c) Chứng minh tam giác MAB đồng dạng với tam giác ABC . Tìm tỉ số đồng dạng.
Bài 9. Cho tam giác ABC vuông tại A , có AC > AB , đường cao AH . Gọi D, E lần lượt là
hình chiếu của H trên AB, AC . a) Chứng minh A .
D AB = AE.AC và tam giác ABC đồng dạng với tam giác AED .
b) Cho biết BH = 2cm, HC = 4,5cm .Tính :
i) Độ dài đoạn thẳng DE ; ii) Số đo 
ABC ( làm tròn đến độ ) ;
iii) Diện tích tam giác ADE .
Bài 10. Chứng minh : 20
a) Diện tích của một tam giác bằng nửa tích của hai cạnh nhân với sin của góc nhọn
tạo bởi các đường thẳng chứa hai cạnh ấy.
b) Diện tích của một hình bình hành bằng tích của hai cạnh kề nhân với sin của góc
nhọn tạo bởi các đường thẳng chứa hai cạnh ấy. ÔN TẬP CHỦ ĐỀ 3 A. TÓM TẮT LÝ THUYẾT
1. Hệ thức về cạnh và đường cao trong tam giác vuông
Cho tam giác ABC vuông tại A , đường cao AH . Khi đó ta có các hệ thức sau : • 2
AB = BH .BC hay 2 c = a.c ' A • 2
AC = CH .BC hay 2 b = a.b' • A .
B AC = BC.AH hay . c b = a.h b • 2 HA = . HB HC hay 2
h = c '.b' c h 1 1 1 1 1 1 • = + hay = + 2 2 2 AH AB AC 2 2 2 h c b b' c' B C • 2 2 2 H
BC = AB + AC ( Định lý Pitago ) a
2. Tỉ số lượng giác của góc nhọn
• Cho góc nhọn α ( 0° < α < 90 )
° . Dựng tam giác ABC vuông tại A sao cho  α = ABC . Từ đó ta có : cos AB α = ;sin AC α = ; tan AC α = ;cot AB α = . BC BC AB AC
• Với góc nhọn α bất kỳ, ta luôn có :
0 < sinα < 1;0 < cosα < 1; sinα cos tan = ;cot α α α = ; tanα.cotα = 1; cosα sinα 2 2 2 1 2 1
sin α + cos α = 1;1+ tan α = ;1+ cot α = . 2 2 cos α sin α
• Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
• Bảng tỉ số lượng giác của các góc đặc biệt : α 30° 45° 60° Tỉ số sinα 1 2 3 2 2 2 cosα 3 2 1 2 2 2 21 tanα 3 1 3 3 cotα 3 1 3 3
3. Hệ thức về cạnh và góc trong tam giác vuông
• Cho tan giác ABC vuông tại A có BC = a; AC = b; AB = c . Ta có : b = .s a in B = .c a os C;
c = a.sin C = a cos B; b = . c tan B = . c cot C; c = . b tan C = . b cot . B
• Trong một tam giác vuông
Cạnh góc vuông = ( cạnh huyền ) x ( sin góc đối)
= ( cạnh huyền ) x ( cosin góc kề )
Cạnh góc vuông = ( cạnh góc vuông ) x ( tang góc đối )
= ( cạnh góc vuông còn lại ) x ( cotang góc kề ) B. BÀI TẬP TỰ LUYỆN
Bài 1. Cho tam giác ABC vuông tại A , đường cao AH . Trong các đoạn thẳng
AB, AC , BC, AH , HB, HC , hãy tính độ dài các đoạn thẳng còn lại nếu biết :
a) AB = 6cm và AC = 9cm ;
b) AB = 15cm và HB = 9cm ;
c) AC = 44cm và BC = 55cm .
Bài 2. Cho tam giác ABC vuông tại A( AB < AC) có đường cao AH và
AH = 12 cm; BC = 25 cm .
a) Tìm độ dài các đoạn thẳng BH ,CH , AB và AC .
b) Vẽ trung tuyến AM . Tìm số đo của góc  AMH .
c) Tính diện tích tam giác AHM .
Bài 3. Cho tam giác ABC có đường cao CH , =  0 BC 12c , m B = 60 và  0 C = 40 .
a) Tính độ dài các đoạn thẳng CH và AC .
b) Tính diện tích tam giác ABC .
Bài 4. Cho tam giác ABC vuông ở A , đường cao AH , AB = 3c , m AC = 4cm .
a) Tính độ dài các đoạn thẳng BC và AH .
b) Tính số đo các góc   B, C .
c) Đường phân giác trong của góc A cắt cạnh BC tại E . Tính độ dài các đoạn thẳng BE và CE . 22
Bài 5. Cho tam giác nhọn ABC có đường cao AH . Từ H kẻ HE vuông góc với AB ( E
thuộc AB ) và kẻ HF vuông góc với AC ( F thuộc AC ).
a) Chứng minh AE.AB = AF.AC .
b) Cho biết AB = 4c ,
m AH = 3cm . Tính độ dài các đoạn thẳng AE và BE . c) Cho biết  0
HAC = 30 . Tính độ dài đoạn thẳng FC .
Bài 6. Tứ giác MNEF vuông tại M , F , có EF là đáy lớn, hai đường chéo ME và
NF vuông góc với nhau tại O .
a) Cho biết MN = 9cm và MF =12cm . Hãy : i) Giải tam giác MNF . ii)
Tính độ dài các đoạn thẳng MO , FO . iii)
Kẻ NH vuông góc với EF tại H . Tính diện tích tam giác FNE . Từ đó tính diện tích tam giác FOH . b) Chứng minh 2
MF = MN.FE . Bài 7. Cho tam giác E
D F biết DE = 6cm , DF = 8c , m EF = 10cm .
a) Chứng minh rằng DEF là tam giác vuông.
b) Vẽ đường cao DK . Hãy tính DK, FK .
c) Giải tam giác vuông EDK .
d) Vẽ phân giác trong DM của tam giác DEF . Tính các độ dài các đoạn thẳng ME, MF .
e) Tính sinF trong các tam giác vuông DFK và DEF . Từ đó suy ra E . D DF = DK.EF
Bài 8. Cho tam giác ABC vuông tại A ,  0
B = 60 và BC = 6cm .
a) Tính độ dài các cạnh AB, AC .
b) Trên tia đối của tia BA lấy điểm D sao cho BD = BC . Chứng minh AB AC = BD CD
c) Dường thẳng song song với phân giác góc 
CBD kẻ từ A cắt CD tại H . Chứng minh 1 1 1 = + 2 2 2 AH AC AD
Bài 9. Cho hình vuông ABCD và điểm E tùy ý trên cạnh BC . Tia Ax vuông góc với AE tại
A cắt CD kéo dài tại F . Kẻ trung tuyến AI của tam giác AEF và kéo dài cắt cạnh CD tại K .
a) Chứng minh AE = AF .
b) Chứng minh các tam giác AKF , CAF đồng dạng và 2
AF = KF.CF 23 c) Cho 3 AB = 4c ; m BE =
BC . Tính diện tích tam giác AEF . 4 d) 1 1
AE kéo dài cắt CD tại J . Chứng minh +
không phụ thuộc vào vị trí điểm 2 2 AE AJ E .
Bài 10. Không dùng máy tính, sắp xếp các tỉ số lượng giác sau theo thứ tự từ bé đến lớn : a) 0 0 0 0 0
sin 24 , cos 35 , sin 54 , cos 70 , sin 78 . b) 0 0 0 0
cot 24 , tan16 , cot 57 67 ', sin 78 .
Bài 11. Không dùng máy tính, sáp xếp các tỉ sô lượng giác sau theo thứ tự tăng dần : a) 0 0 0 0 0
sin 40 , cos 28 , sin 65 , cos 88 , os c 20 b) 0 0 0 0
tan 32 48 ', cot 28 36 ', tan 56 32 ', cot 67 18 ' .
Bài 12. Cho góc α nhọn.
a) Tính sinα,cotα, tanα biết 1 cosα = . 5 b) Tính o
c sα , cot α , tan α biết 2 sin α = . 3
c) Cho tanα = 2 . Tính sinα và cotα .
d) Cho cotα = 3 . Tính sinα,cosα và tanα .
Bài 13. Một cột cờ cao 7m có bóng trên mặt đất dài 4m . Tính góc α mà tia sáng mặt trời tạo
với mặt đất ( làm tròn đến phút).
Bài 14. Một cột đèn có bóng trên mặt đất dài 6,5m , các tia sáng mặt trời tạo với mặt đất một góc xấp xỉ 0
44 . Tính chiều cao của cột đèn. Bài 15.
a) Tính giá trị biểu thức 2 0 2 0 2 0 2 0
A = cos 20 + cos 40 + cos 50 + cos 70 . b) Rút gọn biểu thức 6 6 2 2
B = sin α + cos α + 3sin α − cos α . Bài 16. Cho 0 0
0 < x < 90 . Chứng minh các đẳng thức sau : a) 4 4 2 2
sin x + cos x = 1− 2 sin . x cos x . b) 6 6 2 2
sin x + cos x = 1− 3sin . x cos x . c) 4 4 2
sin x − cos x = 1− 2 cos x . Bài 17. Cho 0 0
0 < x < 90 . Chứng minh các đẳng thức sau : 24 a) 1− cos x sin x = sin x 1+ cos x b) sin x 1+ cos x 2 + = 1+ cos x sin x sin x
c) sin x + cos x −1 cos x = 1− cos x
sin x − cos x +1 25
AH = 2,4; BC = 5; HƯỚNG DẪN GIẢI
b) AB = 15; AC = 20; BC = 25; AH = 12.
CHỦ ĐỀ 3. HỆ THỨC LƯỢNG
Bài 3. BH = 5,4; HC = 9,6. TRONG TAM GIÁC VUÔNG
Bài 4. BH = 4,5;CH = 8. VẤN ĐỀ 1.
Bài 1. Hình 1: x = 3,6; y = 6,4;
Bài 5. x = 5; y = 2 5.
Hình 2: x = 7,2; y = 12,8;
Bài 6. a) BH = 1,8cm;CH = 3,2cm;
AH = 2,4cm; AC = 4cm; Hình 3: 35 74 x = ; y = 74. 74
b) AB = 65cm; AC = 156cm;
Bài 2. a) BH = 1,8;CH = 3,2;
BC = 169cm; BH = 25cm;
c) AB = 5cm; BC = 13cm ; 25 BH 144 = cm ;CH = cm. VẤN ĐỀ 2 13 13
Bài 1. a) CD CM = CE CN (= 2 . . CH ) ;
Bài 7. BH = 50cm ; CH = 72cm. b)
∆CMN ∽ ∆CDE ( .cg.c)vì
Bài 8. BH = 9cm ; CH = 16cm .  CM CN C chung và = . Bài 9. 32 BH 225 = cm ; CH = cm . CE CD 17 34
Bài 2. a) ∆ADI = ∆CDL (g.c.g)
Bài 10. a) AB = 7,5cm;
AC = 10cm ; BC = 12,5cm; HC = 8cm .
⇒ DI = DL ⇒ ∆DIL là tam giác cân ; b) AH = 3 3cm ; b) 1 1 1 1 1 + = + = 2 2 2 2 2
AC = 6 3cm ;CH = 9cm . DI DK DL DK DC 2 2 2 2 Bài 11.S = 2 150cm .
Bài 3. a) AB + CH = (BH + AH )
Bài 12. a) AH = 3,6cm . + 2 = 2 + ( 2 + 2 CH BH AH CH )
b) BH = 4,8cm; CH = 2,7cm . = 2 + 2 BH AC ;
Bài 13. Đường cao : 6,72 ; Độ dài hai đoạn
chia cạnh huyền : 1,96 ; 23,04.
b) Làm tương tự câu a) bài 1, có AM AB = AN AC (= 2 . . AH ). Bài 14. 75 HB =
cm ; CH = 21cm . 7 Bài 4. 1 1 1 4 + = + ⇒ đpcm. 2 2 2
Bài 15. AB = 9cm; BC = 20cm ; BD = 15cm. OA OB AC BD Bài 5. a) 120
BD = 17 ; b) AH = ;
c) ∆BHI ∽ ∆IKC ( . g g) 7   ⇒ HBI = IKC . 26
⇒ ∆HKD ∽ ∆HBI (g.g)  2 2 AB AC AC =  : . BC BC AB HK HD   ⇒ = HB HI
AB 4 AC AB 3 = . =    
⇔ HK HI = HD DB = 2 . . AH .
AC AB AC
Bài 6. a) OB = 9 (cm); OD = 16 (cm) 2 2 b) . .CF HB HC BC BE = BC. . AB AC b) OA = 12 ; 100 AC = ; BC 3 = (HB HC)2 . . . AB AC c) 1250 S = . 1 ABCD ( 2 cm ) 3 = 4 .AH = 3 AH AH 2 2
Bài 7. a) FB HB HC = : FC AB AC
Bài 8. a) AH là đường trung bình của 2 2 BC BD
∆BCD ⇒ BD = 2AH . ⇔ 3 = 3 + 1 2 2 CE CE b) 1 1 1 1 1 = + = + . BCAB 2 2 2 2 2 BK BC BD 2 2 BC 4AH ⇔ 3 = + 1 2   CEAC VẤN ĐỀ 3 2 3 2
Bài 1. a) DE = 6cm ; b) Chứng minh M là BCBC BC BC  ⇔ 3 = ⇔ = 2    
trung điểm BH, N là trung điểm CH ; c) CEAC CE AC S = 2 19,5cm .  3 AC CE ⇔ = 2   Bài 2. a) AB . HB BC HB BC AC = =   2 AC HC.BC BC  2 2 . 2 2 ⇔ sin CE AC HC ABC = = b) ED HB HC 2 2 = : AC AC EC AB AC  = 2 cos ACB (đpcm)  2 2 AB AC AC =  : .
Bài 3. a) BH = 3,6cm; CH = 6cm ;  BC BC AB
AH = 4,8cm ; BC = 10cm .
AB 4 AC AB 3 = . =    
b) BH = 3,6cm ; CH = 6,4cm;
AC AB AC
AH = 4,8cm ; AC = 8cm . 2 2 c) .CF. HB HC BE BC = . .BC
Bài 4. Cạnh huyền : 100 cm ; Các cạnh góc AB AC
vuông : 60 cm và 80 cm. BC = (HB HC)2 . .
Bài 5. HB = 22,4cm ; HC = 12,6cm. . AB AC 1 = 4 AH . = 3 AH = 3 DE ; AH d) 3 2 = 3 2 + 3 2 BC BD CE 27 Bài 6. 34560 S BC cm = ≈ 2 204,5cm . Bài 12. a) = 6 ; CK = 4,8cm ; 169
BK = 3,6cm ; AK = 6,4cm .
Bài 7. a) AB = 4cm ; AB = 2 5cm ; b) CB CH = 2 . CK = . CA CI .
AC = 4 5cm ; BC = 10cm . c) 1 1 1 = + 2 2 2 KM HK KI b) 5 281 AB =
cm; AC = 281cm; 16 1 1 281 = + . BC 25 = cm ; BH = cm . 2 2 CH CI 16 16 2 2 AI KA KB
Bài 8. BH = 9cm ; BH = 16cm . d) = : BH AC BC
Bài 9. Tương tự Bài 3.  2 2 AC BC BC =  : .
Bài 10. P = 35 + 21 5 ≈ 81.95(cm) .  AB AB AC 4 3 Bài 11.S = 2 1500cm .
AC BC AC  = . =     .
BC AC BC VẤN ĐỀ 4 Bài 4. cosC 4
= 0,8 ; sinC = 0,6 ; cotC = ; 3 Bài 1. 3
sin B = ; OK = 41 ; OH = 3 . 5 3 tanC = . 4 Bài 2. a) 12 sin B = ≈ 0,9231; 13
Bài 5. AC = 8 ; BC = 89 . 5 3 sinC = ≈ 0,3846 .
Bài 6. sin B = cosC = ; 13 5 4 b) 4 sin B = ≈ 0,7559 ;
cos B = sin A = ; 7 5 3 3 sinC = ≈ 0,6547 .
tan B = cotC = ; 7 4 4
Bài 3. a) Vì OK = 2 2 .
cot B = tanC = . 3 b) 10 sin B = cos A = ; 18 13 5
Bài 7.a) Vì HN = 13 15 cos B = sin A = ; 10 5
b) sin B = cosC = ; 5 6 tan B = cot A = ; 15 3 cos B = sinC = ; 5 3 cot B = tan A = . 6 6 tan B = cotC = ; 3 28 3 cot B = tanC = .
Bài 11. AC = 72 ; BC = 12 61 . 6 Bài 12. α 2 6 sin = ; tanα = 2 6 ; Bài 8. cosC 4
= 0,8 ; sinC = 0,6 ; cotC = ; 5 3 3 6 tanC = . cotα = . 4 12 Bài 9. 5 AC 13 = ; BC = . 2 2
Bài 10.O∈ Ay .
Bài 13. a) AC = 9 ; BC = 15.
b) ANBM là hình chữ nhật vì AN // BM ; AN = BM.
c) ∆MAB ∽ ∆ACB ( . g g). VẤN ĐỀ 5 Bài 1. a) 0 < 0 sin 20 sin70 ; b) 0 > 0 cos60 cos70 ; c) 0 > 0 tan73 20' tan 45 ; d) 0 > 0 cot 20 cot 37 40' . 29 Bài 2. a) 0 0 cot 71 (= tan19 )
c) Độ dài hai cạnh góc vuông là 3 và
2, góc đối diện với cạnh góc vuông < 0 cot 69 15'(= 0 tan 20 85')
độ dài 3 là góc α; < 0 tan 28 < 0 tan 38 < 0 tan 42 ;
d) Độ dài hai cạnh góc vuông là 4 và b) 0 0 cos79 13' = sin10 87'
5, góc đối diện với cạnh góc vuông
có độ dài 5 là góc α. 0 0 < sin32 < sin36 0 0 < cos
Bài 7. BC = 32,5cm; AC = 12,5cm 51 = sin 39 . Bài 3. a) 0 < 0 sin 40 sin70 ; Bài 8. a) 12 5 sin B = ;sinC = 13 13 b) 0 < 0 cos80 cos 50 ; 2 21 c) 0 0 tan 73 20' > tan 65 ; b) sin B = ;sinC = 7 7 d) 0 < 0 cot 53 cot 37 40'.
Bài 9. Dựng một tam giác vuông có: Bài 4. a) 0 0 cot 79 15' = tan10 85'
a) Độ dài cạnh góc vuông là 1, cạnh < 0 tan12 < 0 tan 28
huyền là 2, góc đối diện với cạnh < 0 cot 61 (= 0 tan 29 ) < 0 tan 58 ; góc vuông đó là góc α; b) 0
b) Độ dài cạnh góc vuông là 2, cạnh < 0 = 0 cos85 cos67 ( sin 23 )
huyền là 3, góc giữa cạnh góc vuông < 0 cos63 41'(= 0 sin 26 59')
và cạnh huyền đó là góc α; < 0 sin 56 < 0 sin74 .
c) Độ dài hai cạnh góc vuông là 4 và
Bài 5. Dựng một tam giác vuông có:
5, góc đối diện với cạnh góc vuông
a) Độ dài cạnh góc vuông là 3, cạnh độ dài 4 là góc α;
huyền là 5, góc đối diện với cạnh
d) Độ dài hai cạnh góc vuông là 3 và góc vuông đó là góc α;
4, góc đối diện với cạnh góc vuông
b) Độ dài cạnh góc vuông là 4, cạnh độ dài 4 là góc α.
huyền là 7, góc giữa cạnh góc vuông Bài 10.a) 0 = 0 < 0 cos62 ( sin 28 ) sin 34
và cạnh huyền đó là α; < 0 sin 35 < 0 sin 45
c) Độ dài hai cạnh góc vuông là 3 và < 0 cos 28 (= 0 sin 62 );
2, góc đối diện với cạnh góc vuông độ dài 3 là góc α; b) 0 = 0 cos65 30'( sin 24 70')
d) Độ dài hai cạnh góc vuông là 5 và < 0 cos 59 (= 0 sin 31 )
6, góc đối diện với cạnh góc vuông < 0 sin 47 < 0 cos 37 (= 0 sin 53 )
độ dài 6 là góc α. < 0 sin72 .
Bài 6. Dựng một tam giác vuông có:
a) Độ dài cạnh góc vuông là 2, cạnh 1 1
huyền là 3, góc đối diện với cạnh Bài 11. a) A = ; b) B = . góc vuông đó là góc α; 2 2
b) Độ dài cạnh góc vuông là 2, cạnh Bài 12. α 2 6 cos 1 = , tanα = ,
huyền là 5, góc giữa cạnh góc vuông 5 2 6
và cạnh huyền đó là góc α; 30 cotα = 2 6.
Bài 5. AN ≈ 3,65cm; AC ≈ 7,3c . m
Bài 13. TươngtựBài 14. Vấnđề 4.
Bài 6. a) CH = 3 3cm;
Bài 14. a) A = 3 ; b) B = 2,5. AC = 0 3 3;sin 80 ≈ 5,28c . m Bài 15.Góc α 2 là góc AMH b) 1 S = .3 3.6,92 ≈ 2 17,98cm . a) 2 α 2 sin 2 AH AH = = Bài 7. S ≈ 2 5,09cm . AM BC . AB AC Bài 8. S = 2 7,66cm . = 2. = 2sinα cosα; 2 BC Bài 9. a)  c ≈ a ≈ B = 0 3,12; 6,24; 60 . b) 1+ cos α 2 = 1 HM HC + = AM AM b) a = 10 2. 2 HC AC 2 = 2 = 2 = 2 2cos α;
Bài 10. a) c = 115;sin B = 2 BC BC 3  0  ⇒ B ≈ ⇒ C = 0 41,8 48,2 . c) 1− cos α 2 = 1 HM HB − = AM AM b) 12 a = 193; tanB = 2 HB AB 7 = 2 = 2 = 2 2sin α 2 BC BC  0  ⇒ B ≈ ⇒ C ≈ 0 59,7 30,3 . VẤN ĐỀ 6.
Bài 11. a) a ≈ 5,14cm;b ≈ 6,13cm; Bài 1. a) 20 3 10 3 a = ;c = . 3 3 C = 0 50 . b) A = 0
62 ; a ≈ 9,4cm; b) b = 0 20.sin 35 ≈ 11,48;  0  A = C = 0 61;93 ; 28,07 . c = 0 20.cos 35 ≈ 16,38. Bài 12.S ≈ 2 509,08cm . Bài 2. a) 2 c = 115;sin B = 24 + 9 3 3 Bài 13. 3 S = cm . 2  0  ⇒ B ≈ ⇒ C ≈ 0 41,8 48,2 .
Bài 14. a) AB = 15cm; AC = 20cm; b) 12 a = 193; tan B =
BC = 25cm; AH = 12cm; 7
b) ADHE làhìnhchữnhật;  0  ⇒ B ≈ ⇒ C ≈ 0 59,7 30,3 . c) 2
S = 69,12cm ; P = 33,6c . m Bài 3. a)  0  a = B ≈ ≈ 0 35; 53,1 ;C 36,9 ; Bài 15. a)  0
AC = 4cm; B = 53,13 ; b)  0  c = B ≈ C ≈ 0 8; 41,8 ; 48,2 .  0 C = 36,87 ; Bài 4. a)  b ≈ a ≈ C = 0 2,95; 4,69; 49 .
b) AD = 2,25cm; BD = 3,75cm; b)  c ≈ b = B = 0 9,53; 5,5; 30 . 31 c) 2
BF.BD = BA = B . E BC.
b) AMBN là hình chữ nhật VẤN ĐỀ 7   
⇒ CBM = ABM = NMB
Bài 1.Chiều cao ≈ 6,75 . m
⇒ MN / /BC (so le trong) 2,1 Bài 2.Độ dài = ≈ 4,5 . m
AMBN là hình chữ nhật 0 sin 28 1
⇒ MN = AB = BC. Bài 3.Chiều cao 0 = 5.tan 50 ≈ 5,96 . m 2 Bài 4.  0 BCA ≈ 59 44'. c)   1 
CBM = ABM = ABC 2 Bài 5. a) 2 . AE AC = AH = . AD AB 0  = 30 = ACB ⇒ AB ∆ C AE ∆ D(c-g -c); ⇒ M ∆ AB AB ∆ C (g-g) b) DE = 3c . m
Tỉ số đồng dạng : AB 1 = . c)  0 ABC = 56 ; BC 2
Bài 9.Tương tự Bài 5. d) 54 2 S = cm . ADE 13
Bài 10. a) Giả sử tam giác ABC có  0 A < 90 , Bài 6. a) Vì 1 EF BH = CG = ; AB kẻ đường cao . 2 Ta có :  BH = . AB sin A EF CG  ; AB 1
b) CF ⊥ BE mà EG CF ⇒ S = ∆ BH.AC ABC 2  0
⇒ EG ⊥ BE ⇒ BEG = 90 . 1  ⇒ S = ∆ . AB AC.sin . A ABC 2 2 c) h S = ; ABCD sinα.cosα
b) ABCD là hình bình hành có  0 A < 90 , A ∆ BD = C ∆ BD, d) h AC = . sinα.cosα ⇒ S = 2S  = . AB . AD sin . A ABCD AB ∆ D 21 Bài 7. BD = ≈ 22,73 . cm 0 cos 22,5
ÔN TẬP CHỦ ĐỀ 3
Bài 8. a) AB = 5cm; AC = 5 3 c . m 32 = Bài 1. a) c) 3 FC c . m BC = 3 13cm ; 2 18 13
Bài 6. a) i) NF = 15cm; AH = cm ; 12 13 BH = cm ; 13 13  0  0
MFN ≈ 48,59 ; MNF = 41,41 . 27 13 CH = cm . ii) 36 48 MO = ; FO = . 13 5 5
b) BC = 25cm; AC = 20cm; iii) 2 S = 96cm . FNE
HC = 16cm; AH = 12c . m S∆ FO FH FOH 9 = . = c) 132
AB = 33cm; AH = cm; S FN FE ∆ 25 5 FNE 2 ⇒ S = ∆ 34,56cm . 99 176 FOH BH = cm; CH = c . m 5 5 b) M ∆ FN ∽ F
∆ EM (g − g)
Bài 2. a) Đặt BH = 9cm; CH = 16cm; MF MN 2 ⇒ =
⇔ MF = MN.FE
AB = 15cm; AC = 20c . m FE FM b)  0 AMH ≈ 73,74 . Bài 7. a) Vì 2 2 2
DE + DF = FE c) 2 S = 84cm . AHM b) 24 32 DK = cm; FK = c . m 5 5
Bài 3.a) CH = 6 3cm; 18 6 3 c)  0 EK = cm; DKE = 90 ; AC = ≈ 10,55cm; 5 0 sin 80  0 '  0 '
KDE ≈ 36 52 ; KED = 53 8 1 S = + ∆ 6 3 ABC (6 1,83) b) 2 d) 30 40 ME = cm; MF = c . m 7 7 2 ≈ 40,69cm . e)  DK  sin = , sin DE DFK DFE = Bài 4.a) 12
BC = 5cm; AH = cm DF EF 5 DK DE ⇒ = ⇔ .
DE DF = DK.EF. b)  0  0
B ≈ 53,13 ; C ≈ 36,87 DF EF c) 15 20 BE = cm; CE = c . m
Bài 8.a) AB = 3cm; AC = 6 3c . m 7 7 AB AB Bài 5.a) 2 . AE AB = AH = . AE AC b)  = = cos ABC BD BC b) 9 7 AE = ; BE = ; 0  = cos60 = cos AC ACD = ; 4 4 CD c) 1 1 1 = + . 2 2 2 AH AC AD Bài 9. a) AB ∆ E = AD ∆ F ( . g .cg) Bài 12. a) 24 cosα = ; ⇒ AE = AF 5 b)    0 F , chung FAK = FCA = 45 1 tanα = ; cotα = 24 ⇒ AK ∆ F ∽ C
∆ AF (g − g) 24 AF CF 2 ⇒ =
⇔ AF = KF.CF; b) 5 2 cosα = ; tanα = ; KF AF 3 5 c) 93 2 S 5 = cotα = . ∆ cm ; AEF 2 2 33 d) 1 1 AE = AF ⇒ + c) 1 1 cotα = ;cosα = ± ; 2 2 AE AJ 2 5 1 1 1 2 = + = = const. sinα = ± 2 2 2 AF AJ AD 5 Bài 10. a) 0 ( 0 cos70 = sin 20 ) d) 1 1 tanα = ;sinα = ± ; 0 0 3 < sin 24 < sin 54 10 3 0 < cos 35 ( 0 = sin 55 ) 0 < sin78 ; cosα = ± 10 b) 0 ( 0 tan16 = cot74 ) Bài 13. 7 0 ' tanα = ⇒ α ≈ 60 15. 0 ' 0 < cot 57 67 < cot 30 4 Bài 14. 6,28c . m 0 0 < cot 24 < tan 80 ( 0 = cot10 ).
Bài 15. a) A = 2. Bài 11. a) 0 0 cos 20 < sin 65 b) 4 2 B = 3sin α + sin α. ( 0 = cos 25 ) 0 < cos 28 Bài 16. a) 4 4 sin x + cos x 0 < sin 40 ( 0 = cos 50 ) 0 < cos88 .
= (sin x + cos x)2 2 2 2 2 − 2sin xcos x b) 0 ' ( 0 ' cot 67 18 = tan 22 42 ) 2 2
= 1− 2sin xcos x; 0 ' < cot 28 36 ( 0 ' = tan 61 24 ) b) 6 6 sin x + cos x 3 2 2 0 ' 0 '
= (sin x + cos x) < tan 32 48 < tan 56 32 2 2 3
− sin xcos x( 2 2 sin x + cos x) 2 2 = 1− 3sin xcos . x c) 4 4 sin x − cos x = ( 2 2
sin x − cos x)( 2 2 sin x + cos x) 2 = 1− 2cos . x
Bài 17. a) 1− cos x sin x =
Bài 4. MNPQ là hình chữ nhật tâm O sin x 1+ cos x ⇒ M, N, ,
P Q cùng thuộc(O;OM).
⇔ (1− cos x)(1+ cos x) 2 = sin x
Bài 5.Gọi E, ,
F P, Q lần lượt là trung điểm 2 2
⇔ sin x + cos x = 1.
của MA, MB, MC, M . D x + ( + x)2 2 sin 1 cos b) VT
Chứng minh tứ giác EFPQ có hai góc đối = sinx(1+cosx) có tổng bằng 0 180 . 2 + 2cos x ⇒ E, ,
F P, Q cùng thuộc một đường = = x( + x) VP; sin 1 cos tròn.
c) Biến đổi tương đương tương tự
Bài 6. Trong hình thoi, đường chéo này là câu a.
Trung trực của đường chéo kia. Do đó,
điểm E là giao điểm hai đường trung trực
của hai cạnh ABvà AC . Nên E là tâm
CHỦ ĐỀ 4. ĐƯỜNG TRÒN
đường tròn ngoại tiếp AB ∆ C.Tương tự, F VẤN ĐỀ 1.
là tâm đường tròn ngoại tiếp của AB ∆ . D
Bài 1. a) Goi O là trung điểmcủa BC Bài 7. a) Ta có:  0
ACD = 90 ⇒ C thuộcđường
⇒ O là tâm đườngtrònđi qua
trònđườngkính AD. 34 A, , B C; Chứngminh  0
ABD = 90 ⇒ Bthuộc đường b) 1
OA = OB = OC ⇒ OA = BC
tròn đường kính AD ⇒ B, C cùng thuộc 2
đường tròn đường kính AD ; ⇒ AB ∆ C vuông tại . A b) AD = 10c . m
Bài 2.Goi O là trung điểm BC.
Bài8. a)Gọi O là trungđiểm BC. Chứng minh: B, , C D, Enằm Mà  1 D O; BC  ∈  trên ; BC O   .  2   2 
⇒ OB = OC = OD
Bài 3. a) IFEK là hình bình hành tâm O có: ⇒ B ∆ DC vuông tại D.
CH ⊥ IK,KE / /CH
⇒ CD ⊥ AB . Tương tự⇒ BE ⊥ AC;
⇒ IK ⊥ KE ⇒ IFEK là hình chữ nhật b) Xét AB ∆ C có K là trực tâm ⇒ I, , ,
F E K cùng thuộc(O;OI). ⇒ AK ⊥ BC.
b) Chứng minh KD ⊥ DF ⇒ K ∆ DF vuông. 35
Document Outline

  • VẤN ĐỀ 1. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG (PHẦN 1)
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 1. Tính độ dài các đoạn thẳng trong tam giác vuông
    • C.BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 2. HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG (PHẦN II)
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 2. Chứng minh các hệ thức liên quan đến tam giác vuông
  • VẤN ĐỀ 3 : LUYỆN TẬP HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP TỰ LUYỆN
    • C. BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 4. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN I)
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 1. Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
    • C. BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 5. TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN (PHẦN II)
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 2. Sắp thứ tự dãy các tỉ số lượng giác
      • Dạng 3.Dựng góc nhọn biết tỉ số lượng giác của nó là
    • C. BÀI TẬP VỀ NHÀ :
  • VẤN ĐỀ 6. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG (PHẦN I).
    • A. TÓM TẮT LÝ THUYẾT.
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN.
      • Dạng 1. Giải tam giác vuông
      • Dạng 2. Tính cạnh và góc của tam giác
    • C. BÀI TẬP VỀ NHÀ
  • VẤN ĐỀ 7. MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG (PHẦN II)
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP VÀ CÁC DẠNG TOÁN
      • Dạng 3. Toán ứng dụng thực tế
      • Dạng 4. Toán tổng hợp
    • C. BÀI TẬP VỀ NHÀ
  • ÔN TẬP CHỦ ĐỀ 3
    • A. TÓM TẮT LÝ THUYẾT
    • B. BÀI TẬP TỰ LUYỆN
  • HƯỚNG DẪN GIẢI
    • VẤN ĐỀ 1.
    • VẤN ĐỀ 2
    • VẤN ĐỀ 3
    • VẤN ĐỀ 4
    • VẤN ĐỀ 5
    • VẤN ĐỀ 6.
    • VẤN ĐỀ 7
      • ÔN TẬP CHỦ ĐỀ 3