Đề Thi Tuyển Sinh 10 Môn Toán Chung Sở GD Quảng Nam 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM ĐỀ CHÍNH THỨC Môn thi: TOÁN (chung)
Thời gian: 120 phút (không kể thời gian giao đề)
(Đề có 01 trang)
Câu 1 (2,0 điểm). a) Rút gọn biểu thức 2 1 A = 12 + ( 2 −1) −  3 − 2 1 2 x 1 b) Cho biểu thức B = + −
với x  0 và x  1. x + x
x −1 x − x
Rút gọn biểu thức B và tìm x để B = 8. 1
Câu 2 (2,0 điểm). Trong mặt phẳng tọa độ Oxy, cho parabol 2 (P) : y = x . 2 a) Vẽ parabol (P) .
b) Hai điểm A, B thuộc (P) có hoành độ lần lượt là 2; −1. Viết phương trình đường thẳng đi qua hai điểm A và B.
Câu 3 (2,0 điểm). a) Giải phương trình 4 2
x + 2x − 8 = 0 . b) Cho phương trình 2 2
x − (2m +1)x + m +1 = 0 (m là tham số).
Tìm giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt x , x sao cho 1 2 x x biểu thức 1 2 P = có giá trị nguyên. x + x 1 2
Câu 4 (3,5 điểm).
Cho hình vuông ABCD có cạnh bằng 6cm. Điểm N nằm trên cạnh CD sao cho DN = 2cm,
P là điểm nằm trên tia đối của tia BC sao cho BP = DN. a) Chứng minh A  BP = A
 DN và tứ giác ANCP nội tiếp đường tròn.
b) Tính độ dài đường tròn ngoại tiếp tứ giác ANCP.
c) Trên cạnh BC, lấy điểm M sao cho 0
MAN = 45 . Chứng minh MP = MN và tính diện tích tam giác AMN.
Câu 5 (0,5 điểm). Cho hai số thực x, y thỏa mãn x  3; y  3.  1   1 
Tìm giá trị nhỏ nhất của biểu thức T = 21 x + + 3 y +       y   x 
--------------- HẾT ---------------
Họ và tên thí sinh: .................................................................. Số báo danh: ........................... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM
Hướng dẫn chấm Môn TOÁN CHUNG
(Hướng dẫn chấm này có 4 trang) Câu Nội dung Điểm
Rút gọn biểu thức: 1 2 A = 12 + ( 2 −1) − 3 − 2
A = 4.3 + 2 −1 − ( 3 + 2) 1a 0,5
(1,0đ) (Nếu biến đổi đúng 2 trong 3 ý thì được 0,25)
A = 2 3 + 2 −1− 3 − 2 0,25 A = 3 −1. 0,25 1 2 x 1 Cho biểu thức: B = + −
với x  0, x  1. x + x
x −1 x − x
Rút gọn biểu thức 𝐵. Tìm tất cả các giá trị x để B = 8 . 1 2 x 1 B = + − x ( x + ) 1
( x + )1( x − )1 x( x − )1 0,25
(Nếu biến đổi đúng 2 trong 3 ý thì được 0,25) 1b
x −1+ 2 x x − ( x + ) 1 (1,0đ) = 0,25 x ( x + ) 1 ( x − ) 1 2( x − ) 1 2 = = 0,25 x ( x + ) 1 ( x − ) 1 x 2 1 B = 8  = 8  = x 1  x = x 4 16 0,25 1 Vậy để B = 8 thì x = . 16 1
Câu 2 Trong mặt phẳng tọa độ Oxy , cho parabol (𝑃): 2 y = x . 2 Trang 2
Vẽ parabol (𝑃)  1   1  2a
Parabol (P) đi qua 5 điểm (0;0) , 1;   , 1 − ;   , (−2; 2) , (2;2) 0,5  2   2  (1,0đ)
(Xác định đúng được 2 điểm được 0,25)
Vẽ đúng parabol (P) 0,5
Hai điểm A, B thuộc (P) có hoành độ lần lượt là 2; −1. Viết phương trình
đường thẳng đi qua hai điểm A và B.
x = 2  y = 2  ( A 2;2) 1 1 0,25 x = 1
−  y =  B( 1 − ; ) 2 2
Phương trình đường thẳng đi qua hai điểm A và B có dạng: y = ax + b 2b.  2 = 2a + b  0,25
(1,0đ) Lập được hệ 1 = −a + b 2  1 a =
Giải hệ ra kết quả:  2 0,25  b =1 1
Vậy phương trình đường thẳng đi qua hai điểm A và B là: y = x +1. 0,25 2 Câu 3
Giải phương trình: 𝑥4 + 2𝑥2 − 8 = 0.
Đặt 𝑥2 = 𝑡, điều kiện 𝑡 ≥ 0. Phương trình trở thành: 𝑡2 + 2𝑡 − 8 = 0. 0,25 𝑡 = −4 (loại) 3a ⇔ [ 0,25 𝑡 = 2 (nhận) (1,0đ) 𝑥 = √2
𝑡 = 2 ta có 𝑥2 = 2 ⇔ [ 0,25 𝑥 = −√2
Vậy phương trình đã cho có 2 nghiệm: 𝑥 = √2, 𝑥 = −√2. 0,25 Cho phương trình 2 2
x − (2m +1)x + m +1 = 0 (m là tham số). 3b
Tìm giá trị nguyên của m để phương trình đã cho có hai nghiệm phân biệt (1,0đ) x x
x , x sao cho biểu thức 1 2 P =
có giá trị nguyên. 1 2 x + x 1 2 Trang 3
Tính được  = 4m − 3 . 3 0,25
Pt có 2 nghiệm phân biệt khi ∆ > 0 ⇔ m  4
Theo định lý Viet, ta có: 2
 x + x = 2m +1 1 2  2 x x m +1 0,25 1 2  P = = . x x = m +1  1 2 x + x 2m +1 1 2 2m −1 5 5 P = +
 4P = 2m −1+ . 0,25 4 4(2m + ) 1 2m +1 3
Để 4P  Z thì 2m +1 là ước của 5. Mà m  5 nên 2m +1  4 2 0,25
Suy ra 2m +1 = 5  m = 2 .
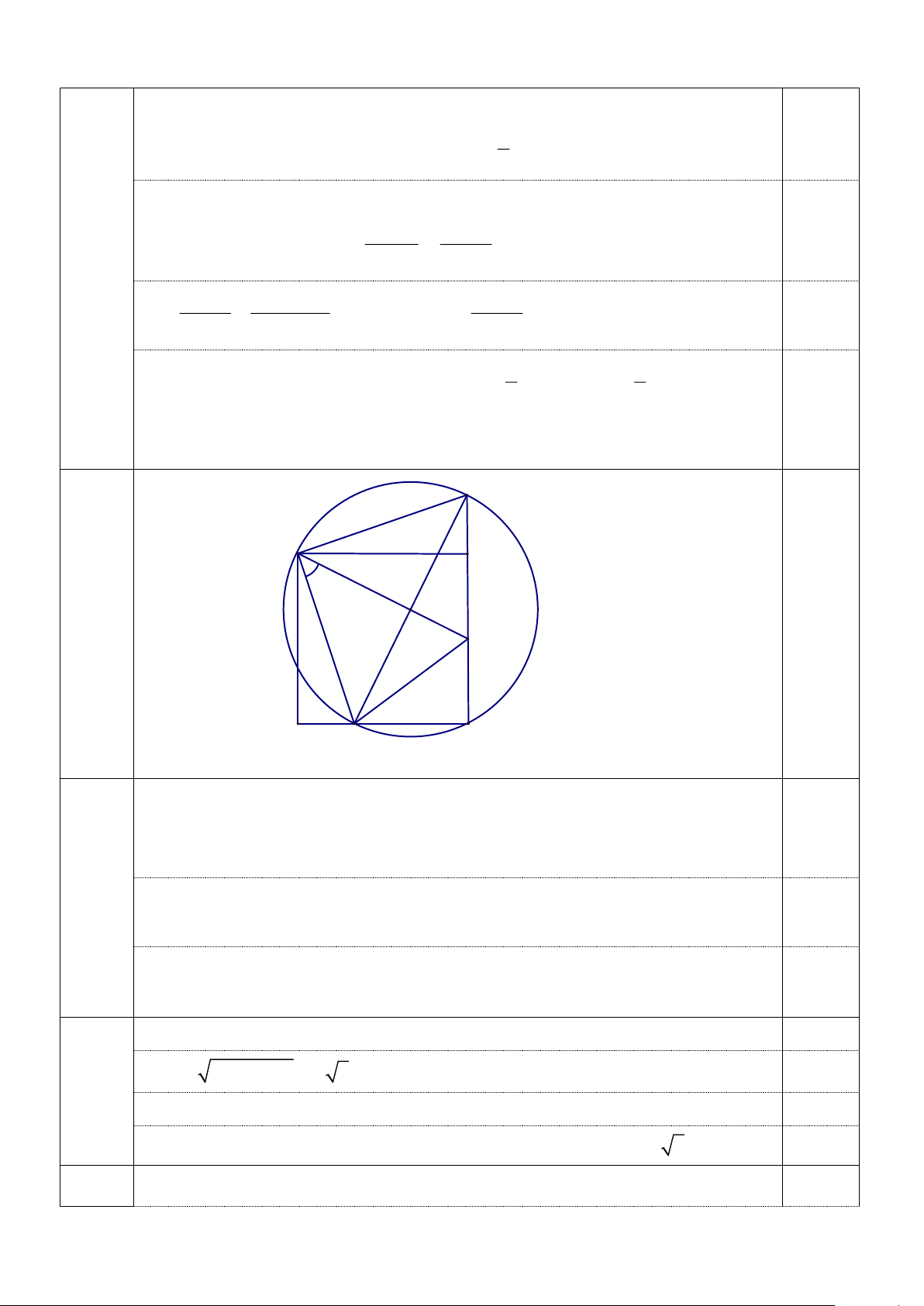
Thử lại m = 2 thì P = 1 (thỏa). Vậy m = 2 thỏa ycbt. P A B 450 Câu 4 0,5 (3,5đ) 6cm M
D 2cm C N
Hình vẽ phục vụ câu a đúng 0,25 đ; câu c đúng 0,25 đ.
+ Xét hai tam giác ADN và ABP có: 0
ADN = ABP = 90 , AD = AB, DN = BP Suy ra A  DN = A
 BP( c − g − c) 0,5
(Đúng hai trong 3 ý cho 0,25). 4a.  =   = (1,0đ) + ADN ABP PAB NAD 0,25 Suy ra 0
NAP = NAB + BAP = NAB + DAN = DAB = 90 . Suy ra 0 NAP + NCP = 180 0,25
Vậy tứ giác ANCP nội tiếp đường tròn.
Ta có: NC = 4 ; CP = 8 . 0,25 4b. 2 2 NP = NC +CP = 4 5 . 0,25
(1,0đ) Chỉ ra được NP là đường kính của đường tròn ngoại tiếp tứ giác ANCP 0,25
Suy ra độ dài đường tròn ngoại tiếp tứ giác ANCP: C =  d = 4 5 (cm). 0,25 4c. Chứng minh A  PM = A
 NM( c − g − c) Suy ra: MN = MP. 0,25 Trang 4 (1,0đ) 1 S = S = AB.MP. 0,25 AMN M A P 2 Đặt BM = x
Áp dụng định lý Pitago vào tam giác vuông NCM, ta có: 0,25 2 2 2
(x + 2) = (6 − x) + 4  x = 3 .
Tính được diện tích tam giác AMN bằng 15cm2. 0,25
Cho hai số thực x, y thỏa mãn x  3; y  3.  1   1 
Tìm giá trị nhỏ nhất của biểu thức T = 21 x + + 3 y +       y   x   1   1   7 21  x 3  2 62 Ta có: 21 x + + 3 y + = y + + + + y + x         0,25  y   x   3
y   3 x  3 3
Câu 5 Áp dụng bất đẳng thức Côsi, ta có: (0,5 đ) 7 21 7 21 x 3 x 3 y +  2 y = 14 ; +  2  = 2. 3 y 3 y 3 x 3 x 0,25  1   1  2 62
Mà x  3 ; y  3 nên T = 21 x + + 3 y + 14 + 2 + 3 + 3 = 80      y   x  3 3
Vậy giá trị nhỏ nhất của T bằng 80 khi x = y = 3 .
Ghi chú: Thí sinh có thể giải theo cách khác, giám khảo dựa trên đáp án để phân chia thang điểm hợp lý. Trang 5