Đề Thi Tuyển Sinh 10 Môn Toán Chuyên Tin Sở GD Quảng Nam 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM
Môn thi: TOÁN (chuyên Tin) ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề có 01 trang)
Câu 1 (1,5 điểm). x + x x Cho biểu thức A = −
với x  0 và x  1. x −1 x( x − ) 1
Rút gọn biểu thức A và tìm x để A = 3.
Câu 2 (1,0 điểm).
Tìm tất cả các cặp số tự nhiên (x; y) thỏa mãn x 2
2 − y + 2y + 3 = 0.
Câu 3 (2,0 điểm).
a) Giải phương trình 3 − x − x +1 = 0. 2 2
x + y + x + y = 4
b) Giải hệ phương trình 
2x + 2y − xy = 3.
Câu 4 (1,0 điểm). Cho parabol 2
(P): y = x và đường thẳng (d): y = m ( m là tham số). Tìm m để (d) cắt (P)
tại hai điểm phân biệt A, B sao cho tam giác OAB đều (với O là gốc tọa độ).
Câu 5 (3,5 điểm).
Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O) đường kính BC, tiếp tuyến của
đường tròn (O) tại A cắt đường thẳng BC tại D. Vẽ dây cung AE của đường tròn (O) vuông góc
với BC. Gọi H là giao điểm của AE và BC, K là hình chiếu vuông góc của A lên CE. Tia phân
giác của BAC cắt BC tại F.
a) Chứng minh AB.HC = AC.HA. b) Chứng minh CDE = CAK . c) Chứng minh 2 DF = DB.DC .
Câu 6 (1,0 điểm).
Cho ba số thực dương x, y, z. Tìm giá trị lớn nhất của biểu thức xy yz zx P = + + 
(2x + z)(2y + z)
(2y + x)(2z + x)
(2z + y)(2x + y)
--------------- HẾT ---------------
Họ và tên thí sinh: .................................................................. Số báo danh: ........................... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM HDC CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN: TOÁN (Chuyên Tin)
(Bản hướng dẫn này gồm 04 trang) Câu Nội dung Điểm x + x x Cho biểu thức A = −
, với x  0 và x  1. Rút gọn biểu thức A và tìm x −1 x( x − ) 1 1,5 x để A = 3. x( x +1) 1 A = −
(Đúng mỗi ý được 0,25đ) 0,5 ( x +1)( x −1) x( x −1) Câu 1 x 1 2 − + = − ( x) 1 x 1 = =
(đúng 2 ý sau, mỗi ý được 0,25đ) 0,5 (1,5) x −1 x( x −1) x( x −1) x x +1 A = 3  = 3  2 x =1. 0,25 x 1  x = 4 0,25 1
- Đối chiếu điều kiện suy ra x = là giá trị cần tìm. 4 Câu Nội dung Điểm
Tìm tất cả các cặp số tự nhiên (x; y) thỏa mãn x 2
2 − y + 2y + 3 = 0. 1,0 x 2
2 − y + 2y + 3 = 0  2x = ( y +1)( y − 3) (1) 0,25
* y +1 và y − 3 là hai số cùng chẵn, cùng lẻ và y +1  y − 3  0 . Do đó từ (1) ta có: y +1 = 2m 
( với m, n là hai số tự nhiên và m  n ). 0,25
y − 3 = 2n Câu 2 m n n m−n  − =  − = = (1,0) 2 2 4 2 (2 1) 4 4.1 (2) 2n = 4 n = 2 Suy ra:    . 0,25
2m−n −1 =1 m = 3 3 y +1= 2 Khi đó 
 y = 7  2x = (7 +1)(7 − 3)  x = 5 2 y − 3 = 2 0,25 Vậy ( ; x y) = (5;7). Trang 2 Câu Nội dung Điểm
a) Giải phương trình 3 − x − x +1 = 0. 1,0 x −1 0
3 − x − x +1 = 0  3 − x = x −1   2 3
 − x = (x −1) 0,25
(Nếu học sinh chỉ ghi được điều x  3 thì cho 0,25) x 1   0,25 2
x − x − 2 = 0 x 1   0,25 x = 1 − hoac x = 2
 x = 2 (thỏa điều kiện) 0,25
Vậy phương trình đã cho có một nghiệm x = 2 . 2 2
x + y + x + y = 4
Câu 3 b) Giải hệ phương trình  1,0
2x + 2y − xy = 3 (2,0) 2 2 2
x + y + x + y = 4 (
 x + y) − 2xy + (x + y) = 4    (*) 0,25
2x + 2y − xy = 3
2(x + y) − xy = 3
Đặt S = x + y, P = xy . Khi đó hệ (*) trở thành: 2
S − 2P + S = 4 S = 2 S =1 0,25    hoặc  2S − P = 3 P =1 P = 1 − S = 2 x + y = 2 x =1 • Với      0,25 P =1 xy =1 y =1  1− 5  + x = 1 5 x = • S = 1 x + y = 1 Với  2       hoặc 2  . 0,25 P = 1 − xy = −1  1+ 5  1− 5 y =  y =  2  2 Câu Nội dung Điểm Cho parabol 2
(P): y = x và đường thẳng (d): y = m ( m là tham số). Tìm m để (d) cắt (P) 1,0
tại hai điểm phân biệt A, B sao cho tam giác OAB đều (với O là gốc tọa độ). Câu 4 (1,0)
+ Phương trình hoành độ giao điểm của (P) và (d) là: 2 x =m .
+ Để (d) cắt (P) tại hai điểm phân biệt thì m 0. 0,25 x= m
Với điều kiện trên, ta có: 2 x = m  
. Khi đó ta có: A(− m; m), B( m; m). 0,25 x=− m Trang 3
Gọi H là trung điểm của AB.
Tam giác OAB cân tại O, do đó tam giác OAB đều khi: 3 OH = AB. 0,25 2 3 m=2 m. 2
 m =3m m=3 (vì m0 ). 2 0,25
Vậy m = 3 là giá trị cần tìm. Câu Nội dung Điểm
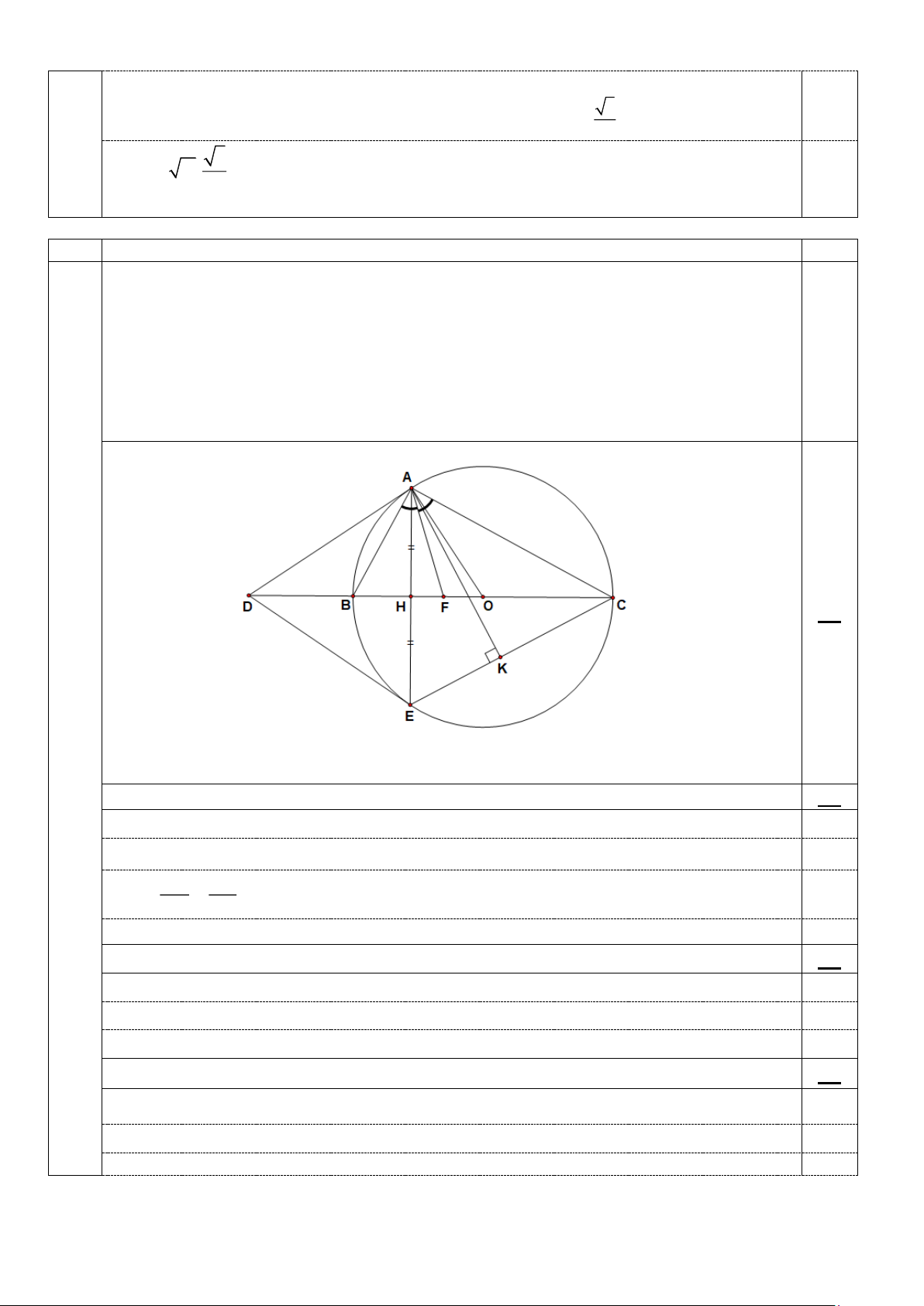
Cho tam giác ABC (AB < AC) nội tiếp đường tròn (O) đường kính BC, tiếp tuyến của đường
tròn (O) tại A cắt đường thẳng BC tại D. Vẽ dây cung AE của đường tròn (O) vuông góc với
BC. Gọi H là giao điểm của AE và BC, K là hình chiếu vuông góc của A lên CE. Tia phân
giác của BAC cắt BC tại F.
a) Chứng minh AB.HC = AC.HA.
b) Chứng minh CDE = CAK . c) Chứng minh 2 DF = DB.DC . 0,5 Câu 5 (3,5)
Hình vẽ phục câu b: 0,25
Hình vẽ phục cả hai câu b và c: 0,25
a) Chứng minh AB.HC = AC.HA. 1,0
Xét hai tam giác ABC và HAC có: 0 BAC = AHC = 90 , 0,25
ACB = HCA . Suy ra hai tam giác ABC và HAC đồng dạng. 0,25 AB AC Do đó = 0,25 HA HC  AB.HC = AC.HA . 0,25
b) Chứng minh CDE = CAK 1,0 0 0
CAK = 90 − ACE = 90 − EAD (đúng mỗi ý được 0,25) 0,5
+ Lập luận được tam giác ADE cân tại D nên EAD = AED 0,25 Suy ra 0 CAK = 90 − AED = CDE 0,25 c) Chứng minh 2 DF = DB.DC . 1,0
DAB = ACF (cùng chắn cung AB ), FAB = FAC (vì AF là phân giác của BAC ) 0,25
Suy ra: DAB + FAB = ACF + FAC  DAF = DFA . Suy ra tam giác ADF cân tại D. 0,25
+ Chứng minh được hai tam giác ABD và CAD đồng dạng. 0,25 Trang 4 AD BD Suy ra 2 =
 AD = DB.DC . Hơn nữa AD = DF nên 2 DF = DB.DC 0,25 CD AD Trang 5 Câu Nội dung Điểm
Cho ba số thực dương x, y, z. Tìm giá trị lớn nhất của biểu thức xy yz zx 1,0 A = + + .
(2x + z)(2y + z)
(2y + x)(2z + x)
(2z + y)(2x + y) 2 2
(2x + z)(2y + z)
4xy + 2z(x + y) + z
2z(x + y) + z = = 4 + 0,25 xy xy xy 2 2 2
2z(x + y) + z 
2z(x + y) + z  4(x + y + z)  4 + = 4 1+ =   Câu 6 2 2 2 (x + y) (x + y) (x + y)   0,25 (1,0) 4 xy x + y   0,25
(2x + z)(2y + z)
2(x + y + z) yz y + z zx z + x Tương tự:  ,  .
(2y + x)(2z + x)
2(x + y + z)
(2z + y)(2x + y)
2(x + y + z) 0,25
Suy ra A  1 (dấu ‘‘=’’ xảy ra khi x = y = z ).
Vậy giá trị lớn nhất của A bằng 1 khi x = y = z .
--------------- HẾT ---------------
* Lưu ý: Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số điểm
từng phần như hướng dẫn quy định. Trang 6