Đề Tuyển Sinh 10 Chuyên Môn Toán Chuyên Sở GD Quảng Nam 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM
Môn thi: TOÁN (Chuyên Toán) ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề thi có 01 trang) Câu 1. (2,0 điểm)
8 + x(1+ x − 2 x +1) x − 3 x
a) Rút gọn biểu thức A = +
(x − 4)(x − 2 x + 4) 2(x − x − 6)
(với x  1, x  4, x  9 )
b) Tìm tất cả bộ ba số nguyên tố p, q, r thỏa mãn pq = r +1 và ( 2 2 p + q ) 2 2 = r +1. Câu 2. (1,0 điểm) Cho parabol 2
(P): y = x và đường thẳng (d): y = (2−2m)x + m (m là tham số).
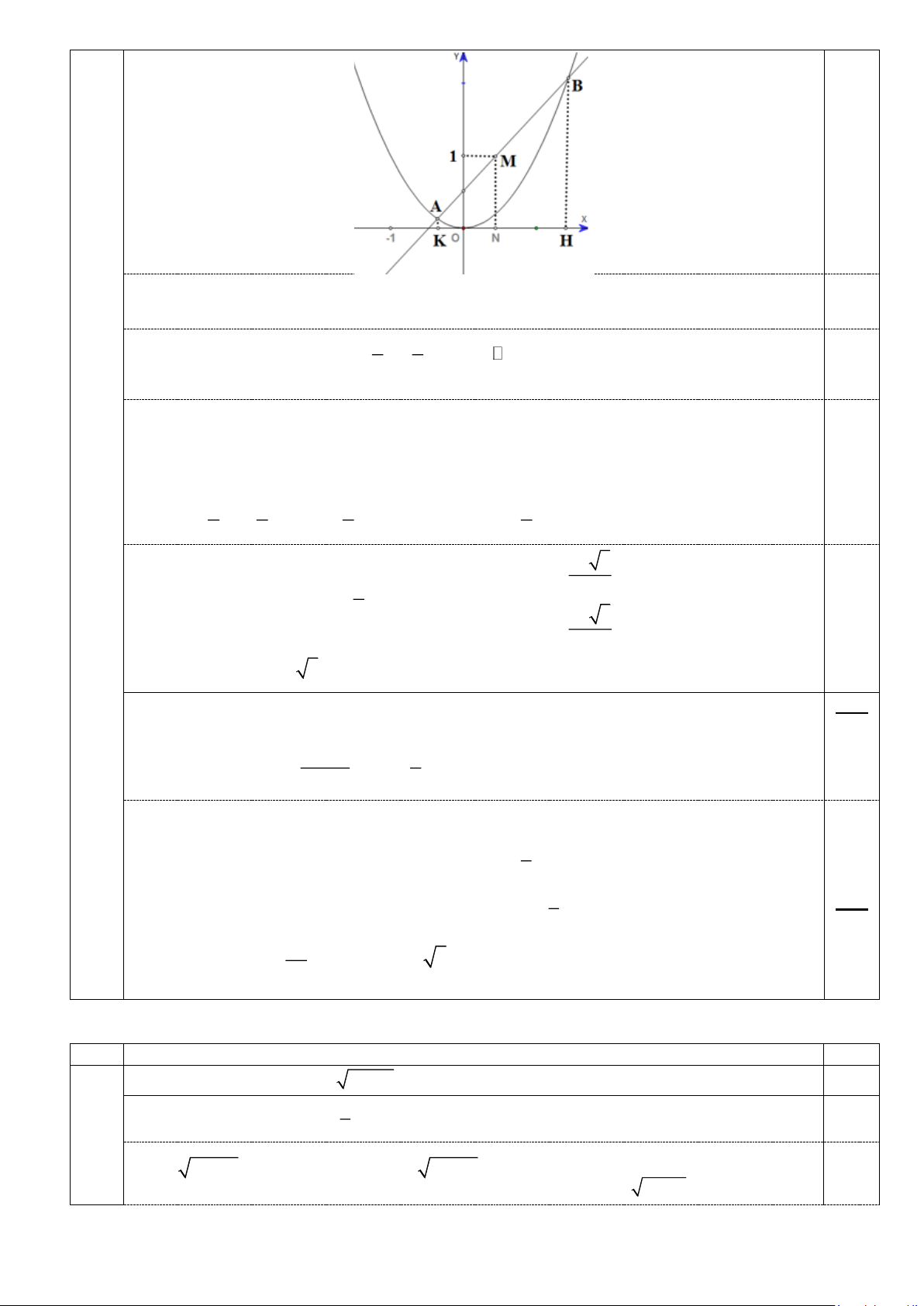
Chứng minh rằng (d) luôn cắt (P) tại hai điểm phân biệt với mọi giá trị của m. Khi đường  1
thẳng (d) cắt (P) tại hai điểm A, B sao cho  M ;1 
 là trung điểm của đoạn thẳng AB, hai  2 
điểm K, H lần lượt là hình chiếu vuông góc của A, B trên trục hoành. Tính độ dài đoạn thẳng KH. Câu 3. (2,0 điểm) a) Giải phương trình 2
(x −1) 7 − 2x = x − 3x + 2.
x + 2y − xy − 2 = 0 
b) Giải hệ phương trình  . 2 2 2 2
x − y + 2x y + 2xy +1 = 0 Câu 4. (2,0 điểm)
Cho hình vuông ABCD tâm O, điểm E nằm trên đoạn thẳng OB (E khác O, B), H là
hình chiếu vuông góc của C trên đường thẳng AE. Gọi F là giao điểm của AC và DH.
a) Chứng minh HD là tia phân giác của góc AHC .
b) Chứng minh diện tích hình vuông ABCD bằng hai lần diện tích tứ giác AEFD. Câu 5. (2,0 điểm)
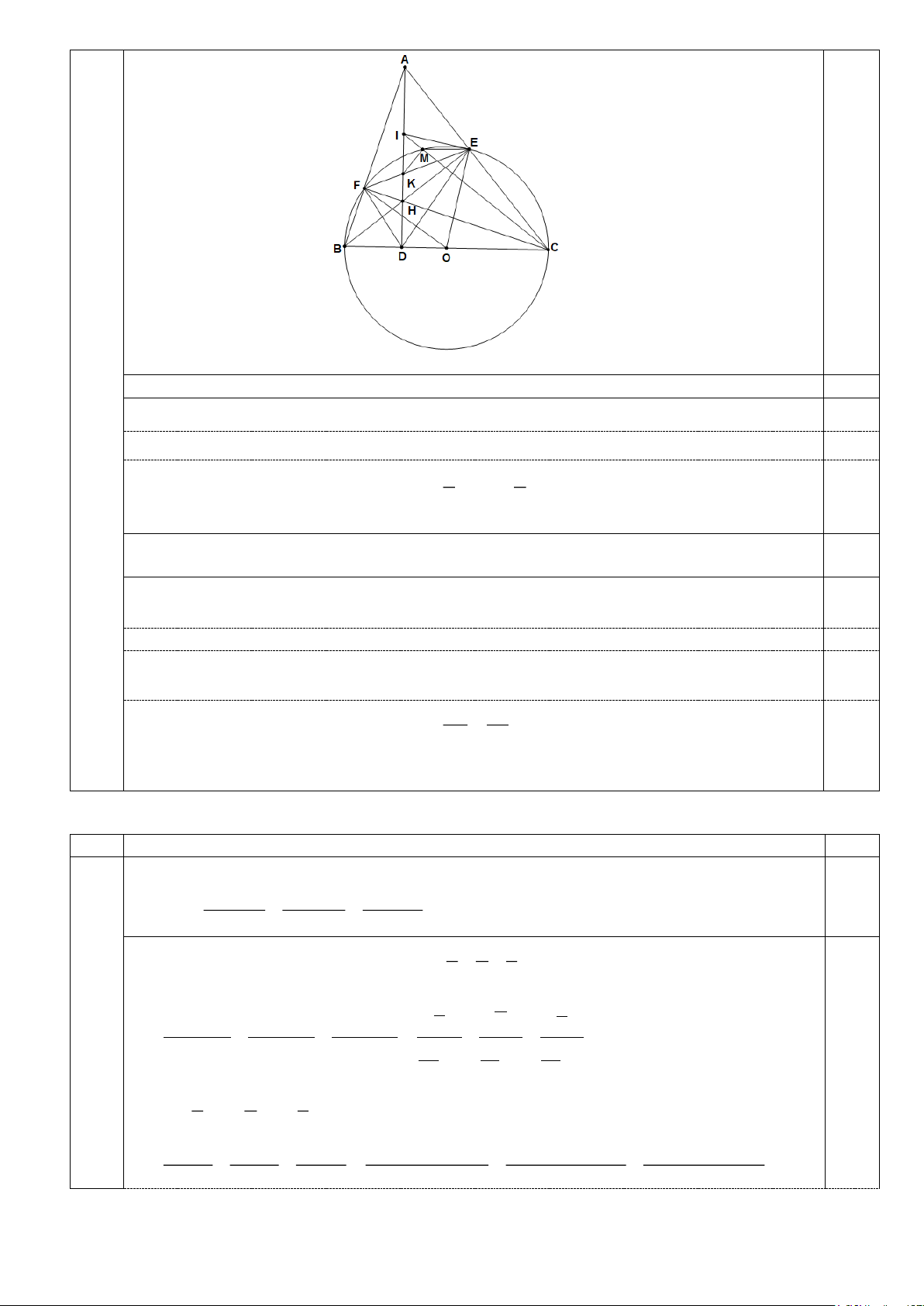
Cho tam giác nhọn ABC (AB < AC). Đường tròn (O) đường kính BC cắt AB, AC lần
lượt tại F, E. Gọi H là giao điểm của BE và CF, đường thẳng AH cắt BC tại D.
a) Chứng minh tứ giác ODFE nội tiếp đường tròn.
b) Gọi K là giao điểm của AH và EF, I là trung điểm của AH. Đường thẳng CI cắt
đường tròn (O) tại điểm M (M khác C). Chứng minh CI vuông góc với KM. Câu 6. (1,0 điểm)
Cho ba số thực dương x, y, z thỏa mãn xy + yz + zx = xyz. Tìm giá trị nhỏ nhất của 2 2 2 x y z biểu thức H = + +  2 2 2 9z + zx 9x + xy 9y + yz
--------------- HẾT ---------------
Họ và tên thí sinh:................................................................Số báo danh: ......................... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM HDC CHÍNH THỨC HƯỚNG DẪN CHẤM
MÔN: TOÁN (CHUYÊN TOÁN)
(Bản hướng dẫn này gồm 06 trang) Câu Nội dung Điểm
8 + x (1+ x − 2 x +1) −
a) Rút gọn biểu thức x 3 x A = +
( x  1, x  4, x  9 ) 1,0
(x − 4)(x − 2 x + 4) 2(x − x − 6)   + x + ( x −  )2 8 1 1  x   ( x −3) A = ( + 0,5
x − 2)( x + 2)(x − 2 x + 4) 2( x + 2)( x −3)
8 + x (1+ x − ) 1 x 1 x = ( + = + 0,25
x − 2)(x x +8) 2( x + 2)
x − 2 2( x + 2)
2( x + 2) + x ( x − 2) + x 4 = = 0,25
2( x + 2)( x − 2) 2(x − 4)
b) Tìm tất cả bộ ba số nguyên tố p, q, r thỏa mãn pq = r +1 và ( 2 2 p + q ) 2 2 = r +1 1,0
Câu 1 + Nếu p, q cùng là số lẻ  pq là số lẻ  r +1 là số lẻ  r là số chẵn  r =2
(2,0) Mà p, q lẻ nên p, q  3 = .
p q  9 . Khi đó r +1 = 2 +1  9 (không thỏa) 0,5
+ p, q khác tính chẵn lẻ, giả sử p = 2 , q là số nguyên tố lẻ. 2q = r +1 2 r = 3 − (loai) Khi đó, ta có  2 2
16 + (r +1) = 2r + 2  r − 2r −15 = 0  2 2  0,25 8
 + 2q = r +1 r = 5
r = 5 = q = 3 .
Vậy có hai bộ số thỏa yêu cầu là: ( p,q,r) = (2,3,5); ( p,q,r ) = (3;2;5). 0,25
Cách khác: Từ ( 2 2 p + q ) 2 2
= r +1suy ra r là số lẻ. 0.25
Suy ra pq = r +1 là số chẵn, nên pq chẵn, giả sử p chẵn, p nguyên tố nên p = 2 0.25 2q = r +1 2 r = 3 − (loai) Khi đó, ta có  2 2
16 + (r +1) = 2r + 2  r − 2r −15 = 0  2 2  0.25 8
 + 2q = r +1 r = 5
r = 5 = q = 3 . 0.25
Vai trò p,q như nhau nên có hai bộ số thỏa yêu cầu là: ( p, q, r) = (2,3,5);(3;2;5). Cho parabol 2
(P): y = x và đường thẳng (d): y = (2−2m)x + m (m là tham số). Chứng
minh rằng (d) luôn cắt (P) tại hai điểm phân biệt với mọi giá trị của m. Khi đường thẳng Câu 2  1  1,0
(1,0) (d) cắt (P) tại hai điểm A, B sao cho M ;1 
 là trung điểm của đoạn thẳng AB, hai  2 
điểm K, H lần lượt là hình chiếu vuông góc của A, B trên trục hoành, tính độ dài đoạn thẳng KH. Trang 2
- Phương trình hoành độ giao điểm của (P) và (d) là: 2 2 0,25
x = (2−2m)x + m x −2(1−m)x−m=0 (*) 2 2 1 2 3  '=(1− )
m +m=m −m 1
+ =(m− ) + 0, m   . 2 4 0,25
Suy ra pt (*) luôn có hai nghiệm phân biệt, hay (d) luôn cắt (P) tại hai điểm phân biệt.
+ Gọi x , x lần lượt là hai hoành độ của A,B (giả sử x  x ), khi đó x , x là hai nghiệm của 1 2 1 2 1 2 pt (*).
N là hình chiếu vuông góc của M lên trục hoành. 0,25
+ M là trung điểm của AB, khi đó N là trung điểm của KH. 1 1 1
x + x =2. (vì − x = x − 1 )  2(1−m) 1 = m= 1 2 2 1 2 2 2 2  1− 3 x= = x1 1 Khi đó pt(*) trở thành 2 2 2
x − x− =0 2x −2x 1 − =0  2  1+ 3 x= = x 0,25 2  2
Suy ra KH = x − x = 3 . 2 1 Cách khác: 0.25
Gọi x , x lần lượt là hoành độ của A,B, khi đó x , x là hai nghiệm của pt (*). 1 2 1 2 x + x 1 M trung điểm AB nên 1
2 = x =  x + x = 1 M 1 2 2 2
Ta có KH=|x − x | KH = ( x − x )2 = ( x + x )2 2 − 4x x 2 1 2 1 1 2 1 2  1 =  + = 2 − 2 =1 m x x m  Theo định lý Viet ta có 1 2  2    x x = −m 1  1 2 x x = − 0.25 1 2  2  1 −  Do đó 2 KH =1− 4 = 3  KH = 3    2  Câu Nội dung Điểm
a) Giải phương trình 2
(x −1) 7 − 2x = x − 3x + 2 1,0
Câu 3 Điều kiện: 7
7 − 2x  0  x  0,25 2 (2,0) x = 1 (th/m) 2
(x −1) 7 − 2x = x − 3x + 2  (x −1) 7 − 2x = (x −1)(x − 2)   0,25
 7 − 2x = x − 2 Trang 3 x  2 x − 2  0 
7 − 2x = x − 2    x = − (
1 loai) x = 3 0,25 2
7 − 2x = (x − 2)  x = 3
Vậy phương trình đã cho có hai nghiệm x = 1, x = 3 0,25
x + 2y − xy − 2 = 0 
b) Giải hệ phương trình  1,0 2 2 2 2
x − y + 2x y + 2xy +1= 0
* Cách 1: x + 2y − xy − 2 = 0  (x − 2)(1− y) = 0  x = 2 hoặc y = 1 0,25
+ Với x = 2 thay vào phương trình còn lại ta được:  =  = x 2 2 5 x 2 
3y + 8y + 5 = 0  y = 1
− hoặc y = − . Suy ra  ,  5 0,5 3 y = 1 − y = −  3
+ Với y = 1 thay vào phương trình còn lại ta được:  2 x = 0  = − 2 2 x
3x + 2x = 0  x = 0 hoặc x = − . Suy ra  ,  3 3
y =1 y =1 0,25 − −
Vậy hệ phương trình đã cho có 4 nghiệm: (x y) =     ( ( − ) 5 2 ; 0;1); 2; 1 ; 2; ; ;1      3   3 
* Lưu ý: Nếu học sinh làm đúng 1 trong 2 trường hợp trên (với x = 2, với y = 1) thì cho 0,5đ
x + 2y − xy − 2 = 0 
xy = x + 2y − 2 * Cách 2:     2 2 2 2 2 2
x − y + 2x y + 2xy +1= 0
x − y + 2xy(x + y) +1= 0 0,25 2 2
 x − y + 2(x + 2y − 2)(x + y) +1 = 0 2 2
 3x + 3y + 6xy − 4x − 4y +1 = 0 x + y = 1 2
 3(x + y) − 4(x + y) +1 = 0   1  0,25 x + y =  3
- Với x + y = 1  y = 1− x thay vào x + 2y − xy − 2 = 0 ta được: 2
x + 2(1− x) − x(1− x) − 2 = 0  x − 2x = 0  x = 0 hoặc x = 2 0,25 x = 0 x = 2 Suy ra  hoặc  y =1 y = 1 − 1 1
- Với x + y =  y = − x thay vào x + 2y − xy − 2 = 0 ta được: 3 3  1   1  2 2 x + 2 − x − x
− x − 2 = 0  3x − 4x − 4 = 0    
 x = 2 hoặc x = −  3   3  3 x = 2  2  x = − 0,25 Suy ra  5 hoặc  3 y = −  3 y =1 − −
Vậy hệ phương trình đã cho có 4 nghiệm: (x y) =     ( ( − ) 5 2 ; 0;1); 2; 1 ; 2; ; ;1      3   3  * Cách 3
x + 2y − xy − 2 = 0 
x + 2y − xy − 2 = 0    2 2 2 2
x − y + 2x y + 2xy +1= 0
(x + y)(x − y) + 2xy(x + y) +1 = 0 0,25
x + 2y − xy − 2 = 0
(x + y) − (xy − y) = 2     (*)
(x + y)[(x − y) + 2xy]+1 = 0 (
 x + y)[(x + y) + 2(xy − y)] = 1 − Trang 4 a − b = 2
+ Đặt a = x + y, b = xy − y . Hệ phương trình (*) trở thành:  (**)
a(a + 2b) = 1 −  5 a = − 0,25 a =1 
+ Giải hệ (**) tìm được: 3  ,  b  = 1 − 1 b  =  3 a =1
x = 0 x = 2 + Với  , giải tìm được  ,  . 0,25 b  = 1 − y =1 y = 1 −  5  = a = − x 2  2   x = − + Với  3  , giải tìm được  5 ,  3 . 1 y = − b  =  y =1   3  3 0,25 − −
Vậy hệ phương trình đã cho có 4 nghiệm: (x y) =     ( ( − ) 5 2 ; 0;1); 2; 1 ; 2; ; ;1      3   3  Câu Nội dung Điểm
Cho hình vuông ABCD tâm O, điểm E nằm trên đoạn thẳng OB (E khác O, B), H là hình
chiếu vuông góc của C trên đường thẳng AE. Gọi F là giao điểm của AC và DH. 0,25
(Hình vẽ phục vụ câu a: 0,25 điểm)
a) Chứng minh HD là tia phân giác của AHC . 0,75
Các điểm B, H, D cùng nhìn đoạn AC dưới 1 góc vuông nên 5 điểm A, B, H, C, D cùng 0,25
nằm trên đường tròn đường kính AC. Câu 4 (2,0) Suy ra 0 0
CHD = CAD = 45 , AHD = ABD = 45 . 0,25
 CHD = AHD. Vậy HD là phân giác AHC . 0,25
b) Chứng minh diện tích hình vuông ABCD bằng hai lần diện tích tứ giác AEFD 1,0 Ta có 2 A S BCD = AD (1) 0,25
Tứ giác AEFD có hai đường chéo vuông góc nhau nên 1 A S EFD = AF.DE (2) 2
Xét hai tam giác AFD và DAE có: + 0
AFD = AHD + HAC = 45 + HAC = DAE 0,5 + 0
AED = ABE + HAB = 45 + HDB = FDA
Suy ra hai tam giác AFD và DAE đồng dạng. Từ đó có tỉ lệ AF AD = hay 2 AD = AF.DE (3) DA DE 0,25
Từ (1), (2), (3) ta có SABCD = 2SAEFD (đpcm) Câu Nội dung Điểm
Câu 5 Cho tam giác nhọn ABC (AB < AC). Đường tròn (O) đường kính BC cắt AB, AC lần lượt tại
(2,0) F, E. Gọi H là giao điểm của BE và CF, đường thẳng AH cắt BC tại D. Trang 5
(Hình vẽ phục vụ câu a: 0,25 điểm)
a) Chứng minh tứ giác ODFE nội tiếp đường tròn. 0,75
+ Tứ giác CDHE nội tiếp đường tròn nên EDH = ECH = ECF 0,25
+ Tứ giác BDHF nội tiếp đường tròn nên FDH = FBH = FBE 0,25 1 1
 EDF = EDH + FDH = ECF + FBF = EOF + FOF = EOF 2 2 0,25
Vậy tứ giác ODFE nội tiếp đường tròn.
b) Gọi K là giao điểm của AH và EF, I là trung điểm của AH. Đường thẳng CI cắt đường 1,0
tròn (O) tại điểm M (M khác C). Chứng minh CI vuông góc với KM. 0 0
AEI + OEC = EAI + ECO = 90  IEO = 90 0,25
Suy ra IE là tiếp tuyến của đường tròn (O).
+ Chứng minh được hai tam giác IEM và ICE đồng dạng. Suy ra IE2 = IM.IC (1) 0,25
+ Tứ giác ABDE nội tiếp đường tròn nên ADE = ABE = IEK 0,25
Suy ra được hai tam giác IEK và IDE đồng dạng. Suy ra IE2 = IK.ID (2) IM IK
+ Từ (1) và (2) suy ra IM.IC = IK.ID hay =  ID IC 0,25
Suy ra được hai tam giác IMK và IDC đồng dạng.
Hơn nữa tam giác IDC vuông tại D nên tam giác IMK vuông tại M. Câu Nội dung Điểm
Cho ba số thực dương x, y, z thỏa mãn xy + yz + zx = xyz. Tìm giá trị nhỏ nhất của biểu 2 2 2 y z x 1,0 thức H = + +  2 2 2 9x + xy 9y + yz 9z + zx 1 1 1
Từ giả thiết, suy ra : xy + yz + zx = xyz  + + = 1 x y z 1 1 Câu 6 1 2 2 2 (1,0) y z x x y H z = + + = + + 2 2 2 x(9 + y )
y(9 + z ) z(9 + x ) 9 9 9 +1 +1 +1 2 2 2 y z x 0,25 1 1 1
Đặt a = , b = , c = , khi đó a, ,
b c  0 và a + b + c = 1. x y z 2 2 2 2 2 2 a b c
a(9b +1) − 9ab
b(9c +1) − 9bc
c(9a +1) − 9ca H = + + = + + 2 2 2 2 2 2
9b +1 9c +1 9a +1 9b +1 9c +1 9a +1 Trang 6 2 2 2  ab bc ca  2 2 2  ab bc ca 
= a + b + c − 9 + + =1− 9 + + 2 2 2  
9b +1 9c +1 9a +1   2 2 2
9b +1 9c +1 9a +1   2 2 2 2 2 2  ab bc ca   ab bc ca  3 9 + +   9 + +
 = (ab + bc + ca) 2 2 2
9b +1 9c +1 9a +1 6b 6c 6a 2     0,25 3
Suy ra H 1− (ab + bc + ca) 2 2
(a + b + c)
Chứng minh được ab + bc + ca  . 3 2
(a + b + c) Thật vậy: 2 2 2
ab + bc + ca 
 (a − b) + (b − c) + (c − a)  0 (đúng). 0,25 3 1 1
Suy ra ab + bc + ca  . Do đó H  . 3 2 1 1
Dấu bằng xảy ra khi a = b = c = hay x = y = z = 3 . Vậy giá trị nhỏ nhất của H bằng . 0,25 3 2 * Lưu ý:
Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số điểm
từng phần như hướng dẫn quy định. Trang 7