Đề Tuyển Sinh 10 Toán Chung Sở GD Quảng Nam 2025-2026 Có Lời Giải

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 VÀO TRƯỜNG TỈNH QUẢNG NAM THPT CHUYÊN
Môn thi: TOÁN (Chuyên) ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề gồm có 01 trang) Câu 1. (2,0 điểm)
a) Không dùng máy tính bỏ túi, hãy rút gọn biểu thức 6 2 A = 18 − + (1− 2) . 3 − + b) Rút gọn biểu thức x 4 x 2 x B = + với x  0 . x + 2 x Câu 2. (2,0 điểm)
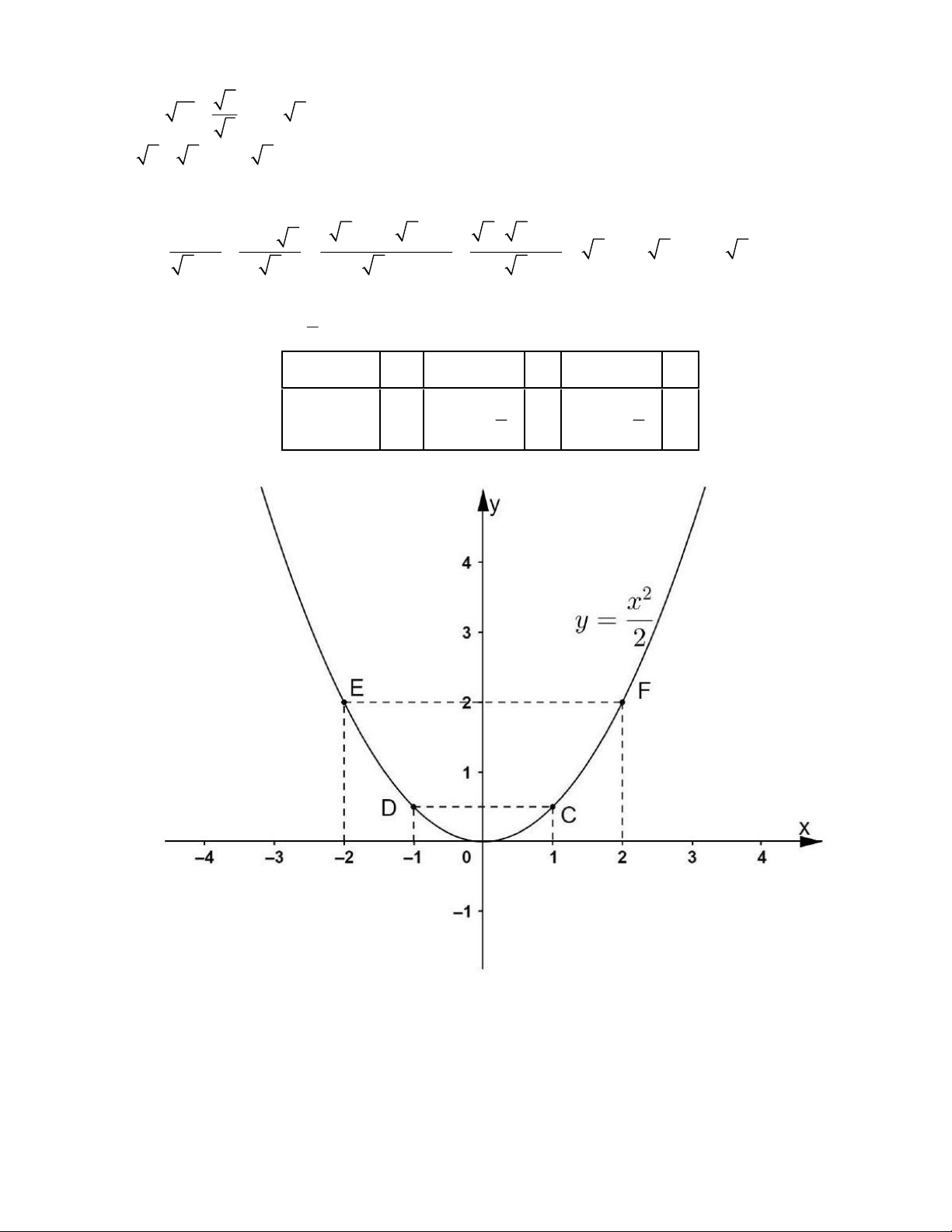
a) Vẽ đồ thị của hàm số 1 2 y = x . 2 3  x − y = 7
b) Giải hệ phương trình  . 2x + 3y =12 Câu 3. (2,0 điểm) a) Giải phương trình 4 2
2x − x −1 = 0 .
b) Xác định tất cả các giá trị của tham số m đế phương trình 2 2
x − 2mx + m + m − 3 = 0 có hai
nghiệm phân biệt x , x sao cho x − x = m . 1 2 1 2 Câu 4. (3,5 điểm)
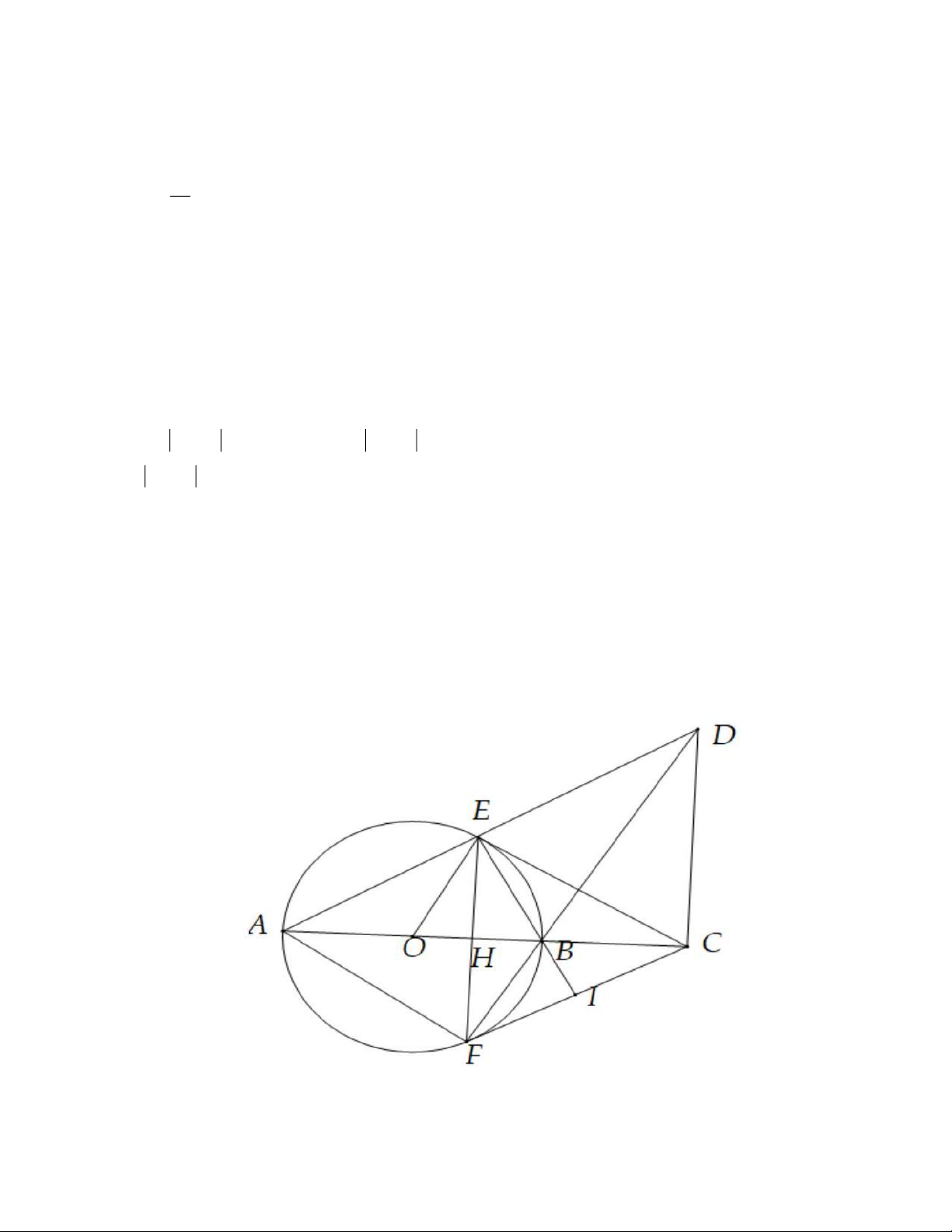
Cho đường tròn (O) có đường kính AB . Trên đường tròn (O) lấy điểm E (khác B) sao cho
tiếp tuyến của (O) tại E cắt tia AB tại điểm C . Gọi d là đường thẳng vuông góc với đường
thẳng AB tại C , D là giao điểm của đường thẳng AE và đường thẳng d, F là giao điểm thứ
hai của đường thẳng BD và đường tròn (O).
a) Chứng minh tứ giác BCDE nội tiếp đường tròn.
b) Chứng minh EF song song với đường thẳng d .
c) Gọi I là giao điểm của BE và CF, H là giao điếm cùa EF và AB .
Chứng minh BC.IF = 2IC.BH . Câu 4. (0,5 điểm)
Cho ba số thực dương a,b,c thỏa mãn a + b + c = 2 . Tìm giá tri lớn nhất của biểu thức
Q = 2a + bc + 2b + ca + 2c + ab. HƯỚNG DẪN GIẢI Trang 1 Câu 1. a) 6 2 A = 18 − + (1− 2) 3 = 3 2 − 2 + 3 − 2 2 = 3.
b) Với x  0 ta có: x − x + x
( x +2)( x −2) x( x +2 4 2 ) B = + = +
= x − 2 + x + 2 = 2 x. x + 2 x x + 2 x Câu 2.
a) Vẽ đồ thị hàm số 1 2 y = x 2 x -2 -1 0 1 2 y 2 1 0 1 2 2 2 b) 3
 x − y = 7 9
 x −3y = 21 11  x = 33 x = 3        2x + 3y = 12 2x + 3y = 12 2x + 3y = 12    y = 2
Vậy hệ phương trình có nghiệm ( ; x y) = (3;2) . Câu 3. Trang 2 a) Đặt 2
x = t (t  0) , ta có: 2
2t − t −1 = 0  (t − ) 1 (2t + ) 1 = 0 t = 1(TM )   −1 t = (L)  2 x =1 Với t =1   x = 1 −
Vậy phương trình có tập nghiệm S = 1;−  1 .
b) Để phương trình đã cho có hai nghiệm phân biệt thì: 2  = m − ( 2 Δ
m + m − 3) = 3− m  0  m  3
x + x = 2m Hệ thức Vi-et: 1 2  2
x x = m + m − 3  1 2
Ta có: x − x = m  m  0 (Vì x − x  0 ). Vậy 0  m  3 1 2 1 2
 ( x − x )2 = m  x + x − 2x x = m  (x + x )2 2 2 2 2 2
− 4x x = m (1) 1 2 1 2 1 2 1 2 1 2
Thay hệ thức Vi-et vào (1) ta có: 2 m − ( 2 m + m − ) 2 (2 ) 4 3 − m = 0 2 2 2
 4m − 4m − 4m +12 − m = 0
 (m + 6)(m − 2) = 0 m = 6 − (L)   m = 2  (TM ) Vậy m = 2 . Câu 4. Trang 3
a) Ta có: AEB = 90 (Góc nội tiếp chắn nửa đường tròn )  DEB = 90 mà DCB = 90 ( Giả thiết)
Suy ra tứ giác BCDE nội tiếp.
b) Ta có: BEC = BDC (Vì tứ giác BCDE nội tiếp)
Mặt khác: EFB = BEC (Góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn một cung)
Suy ra EFB = BDC , mà hai góc này ở vị trí so le trong nên EF / /DC hay EF / /d . EF / /CD c) Ta có: 
 EF ⊥ AB tại H AB ⊥ CD
 H là trung điểm EF (Quan hệ vuông góc giữa đường kính và dây)
BFE có BH vừa là đường cao vừa là đường trung tuyến nên BFE cân tại B Suy ra: FEB = BFE
CEF có CH là đường cao đồng thời là đường trung tuyến nên CEF cân tại C (dhnb)
 CEF = CFE mà EFB = BEC (cmt)(2)
Từ (1) và (2) suy ra BFI = FEB = FEB = BEC
Xét IEF và IFB có: FIE chung BFI = FEB (cmt)
Vậy IEF đông dạng với IFB (g-g) IE FE IF  = = IF FB IB
Mặt khác: FEB = BEC (cmt) suy ra Câu 5. Ta có:
2a + bc = (a + b + c)a + bc( Do a + b + c = 2)
a + b + a + c 2
= a + ab + bc + ac = (a + b)(a + c) ( ) ( ) 
(Áp dụng bất đẳng thức với hai 2
số dương a + b và a + c)
(a +b)+(a +c)
Vậy ta có: 2a + bc  2
Tương tự: (a+b)+(b+c) 2b + ca  2
(a +c)+(b +c) 2c + ab  2
Cộng (1), (2) và (3) theo vế ta được:
Q  2(a + b + c) = 4
Dấu "=" xảy ra khi và chỉ khi 2
a = b = c = 3 Trang 4
Suy ra giá trị lớn nhất của Q bằng 4 khi 2
a = b = c = . 3 Trang 5