Đề Tuyển Sinh 10 Toán Chuyên Sở GD Quảng Nam 2025-2026 Có Đáp Án

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM
Môn thi : TOÁN (Toán chuyên) ĐỀ CHÍNH THỨC
Thời gian : 150 phút (không kể thời gian giao đề)
Câu 1 (2,0 điểm). 3x 2x x − x
a) Cho biểu thức A = − +
với x  0 và x  1 .
2x + 3 x − 2 4x −1 ( x + 2)(4x − ) 1 4
Rút gọn biểu thức A và tìm x để A = 1 . 3x
b) Tìm tất cả các cặp số nguyên (a ; )
b thỏa mãn đẳng thức 2 a − a − 3 9 6 b = 0.
Câu 2 (2,0 điểm). a) Giải phương trình 2
2x + x( x + 3 − ) 1 − 3 = 0.  2 x + 2
y + x + y − xy = 3
b) Giải hệ phương trình   2 (x + 2
y )(xy +1) = 4 − (x − 2 ) y .
Câu 3 (1,0 điểm). Cho parabol P y = 2 ( ):
x và đường thẳng (d): y = ax + b . Tìm a và b để (d) cắt ( ) P
tại hai điểm phân biệt ,
A B sao cho A có hoành độ bằng 2 và khoảng cách từ A đến trục
tung bằng hai lần khoảng cách từ B đến trục tung.
Câu 4 (2,0 điểm). Cho hình vuông ABC ,
D điểm E nằm trên cạnh BC (E khác B, E khác ). C Hai
đường thẳng AE và CD cắt nhau tại F. 1 1 1 a) Chứng minh + = . 2 2 2 AE AF AB
b) Gọi G là trọng tâm của tam giác ACD và I là trung điểm của cạnh . AD Điểm M AD AC
di động trên đoạn thẳng ,
ID đường thẳng MG cắt AC tại N. Chứng minh + = 3; AM AN AM
trong trường hợp giá trị của tích AM.AN nhỏ nhất, tính tỉ số . AD
Câu 5 (2,0 điểm).
Cho tam giác nhọn ABC (AB  A )
C nội tiếp đường tròn ( )
O và có trực tâm H. Ba điểm , D ,
E F lần lượt là chân các đường cao vẽ từ , A ,
B C của tam giác AB . C Gọi M là trung điểm của cạnh ,
BC K là giao điểm của EF và .
BC Đường thẳng AK cắt đường tròn ( )
O tại điểm thứ hai là N.
a) Chứng minh tứ giác BFNK nội tiếp đường tròn và HK vuông góc với AM.
b) Lấy điểm L trên cung nhỏ BC của đường tròn ( ) O ( L khác ,
B L khác C ). Gọi P
là giao điểm của AL và ,
BE Q là giao điểm của BL và .
AD Chứng minh đường thẳng DE
cách đều hai điểm P và Q .
Câu 6 (1,0 điểm). Cho ba số thực dương , x ,
y z thỏa mãn x + y + z = 3.
Tìm giá trị lớn nhất của biểu thức P = 3 x yz+ 3 y zx + 3 z x . y
--------------- HẾT ---------------
Họ và tên thí sinh: ........................................................................................ Số báo danh: ...................................... Trang 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN QUẢNG NAM HDC CHÍNH THỨC
HƯỚNG DẪN CHẤM MÔN TOÁN CHUYÊN
(Bản hướng dẫn này gồm 05 trang) Câu Nội dung Điểm Câu 1 3x 2x x − x 1
(2,0) a) Cho biểu thức A = − +
với x  0 và x  .
2x + 3 x − 2 4x −1 ( x + 2)(4x − ) 1 4 1,0 1
Rút gọn biểu thức A và tìm x để A = . 3x − 3x 2x x x A = ( − + 0,25 2 x − )
1 ( x + 2) (2 x − ) 1 (2 x + ) 1
( x +2)(2 x − )1(2 x + )1 3x(2 x + )
1 − 2x( x + 2) + x − x 4x x − x x (4x − ) 1 = x ( = = = . 0,25 x + 2)(2 x − ) 1 (2 x + ) 1
( x +2)(4x− )1 ( x +2)(4x− )1 x +2 1 Với x
x  0 và x  : 1 1 A =  =
 3x x − x − 2 = 0 (*) 0,25 4 3x x + 2 3x
Đặt t = x (t  0, t 1/ 2) . Phương trình (*) trở thành: 0,25 3 2
3t − t − 2 = 0  (t −1)(3t + 3t + 2) = 0  t = 1  x = 1 (thỏa điều kiện).
b) Tìm tất cả các cặp số nguyên (a ; b) thỏa mãn đẳng thức 2 3
9a − 6a − b = 0. 1,0 2 3 2 3
9a − 6a − b = 0  9a − 6a +1 = b +1 2 3
 (3a −1) = b +1 (*) 0,25 Vì 2 (3a −1)  0 nên 3
b +1  0 hay b  −1. 1
+ Với b = −1 : Từ (*) suy ra: a = (không thỏa). 3 + Với b  0 : Vì 2
(3a −1) là số chính phương nên 3
b +1 là số chính phương. 0,25 2
 b − b +1  3 3 2 2 2 
b +1 = (b +1)(b − b +1) = (b +1) 
 = (b +1) b − 2 +    . b +1   b +1   3 .+ Do 3 b +1 và 2
(b +1) là các số chính phương khác 0 nên
 N  b0;  2 . 0,25 b +1
.+ Với b = 0  a = 0 (thỏa) 2 4
+ Với b = 2  a = − hoặc a = (cả 2 giá trị a không thỏa). 0,25 3 3
Vậy (a ; b) = (0;0) là cặp số duy nhất thỏa yêu cầu. * Cách khác: 2 3 2 3
9a − 6a − b = 0  9a − 6a +1 = b +1 2 3
 (3a −1) = b +1 (*) (0,25) Vì 2 (3a −1)  0 nên 3
b +1  0 hay b  −1.
+ Xét b = −1 không thỏa (*).
+ Xét b = 0 , từ (*) suy ra a = 0 . (0,25)
+ Xét b = 1 không thỏa (*).
+ Xét b  2 : Ta có: 2 3 2 2
(3a −1) = b +1  (3a −1) = (b +1)(b − b +1) Gọi d = ƯCLN 2
(b +1, b − b +1) . Vì 2
b − b +1 = b(b +1) − 2(b +1) + 3nên 3 d . (0,25) Hơn nữa 2
(3a −1) không chia hết cho 3 nên d  3 . Do đó d = 1 . Lại có 2 2
(3a −1) = (b +1)(b − b +1) nên b +1 và 2
b − b +1 đều là hai số chính phương. Mặt khác: 2 2 2
(b −1)  b − b +1  b (vì b  2 ) nên 2
b − b +1 không phải là số chính phương. (0,25)
Vậy (a;b) = (0;0) là cặp số duy nhất cần tìm. Trang 2 Câu Nội dung Điểm
Câu 2 a) Giải phương trình 2
2x + x( x + 3 − ) 1 − 3 = 0 (1). 1,0 (2,0) 2 2
(1)  2x − x − 3 + x x + 3 = 0  (x + 3) − x x + 3 − 2x = 0 (2) 0,25
Đặt t = x + 3 (t  0) , phương trình (2) trở thành: 2 2
t − xt − 2x = 0  t = −x hoặc t = 2x . 0,25 x  0 x  0   1− 13
Với t = −x thì x + 3 = −x      x = . 0,25 2 1 13
x + 3 = (−x) x = 2  2 x  0 x  0 Với 
t = 2x thì x + 3 = 2x      x = 1. 2
x + 3 = (2x)
x = 1 hoÆc x = −3/ 4 0,25 −
Vậy phương trình đã cho có hai nghiệm: 1 13 x =1, x = . 2
* Cách khác: Điều kiện: x  −3 . 2
(1)  2x + x x + 3 − x − 3 = 0 2
 2x − x x + 3 + 2x x + 3 − (x + 3) = 0  (0,5)
x(2x − x + 3) + x + 3 (2x − x + 3) = 0  (2x − x + 3)(x + x + 3) = 0
 2x − x + 3 = 0 hoặc x + x + 3 = 0
Giải phương trình 2x − x + 3 = 0 tìm được x = 1. (0,25) −
Giải phương trình x + x + 3 = 0 tìm được 1 13 x = và kết luận. (0,25) 2 2 2
x + y + x + y − xy = 3
b) Giải hệ phương trình  1,0 2 2 2
(x + y )(xy +1) = 4 − (x − y) . 2
(x + y) + x + y − 3xy = 3
Hệ phương trình đã cho tương đương với:  2 2  0,25
 (x + y) − 2xy (xy +1) = 4 − (x + y) + 4xy   2
S + S − 3P = 3 (1)
Đặt S = x + y, P = xy , hệ phương trình trên trở thành:  2 2
(S − 2P)(P +1) = 4 − S + 4P (2) 2 S + S − 3 (1)  P = (3) 0,25 3
Thay (3) vào (2) và biến đổi được: 4 3 2
S − S + S − 6S = 0 2
 S(S − 2)(S + S + 3) = 0  S = 0 hoặc S = 2 .
+ S = 0  P = −1. Giải được ( ; x y) = (1; 1 − ) hoặc ( ; x y) = ( 1 − ;1) . 0,25
+ S = 2  P = 1 . Giải được ( ; x y) = (1;1) . 0,25
Vậy hệ phương trình đã cho có 3 nghiệm: (1;1) , (1;−1) , (−1;1) . * Cách khác: Ta có: 2 2 2 2
(2)  (x + y )(xy +1) = 4 + 2xy − (x + y ) 2 2 2 2
 (x + y )(xy +1) + (x + y ) − 2(xy + 2) = 0 (0,5) 2 2
 (x + y )(xy + 2) − 2(xy + 2) = 0 2 2
 (xy + 2)(x + y − 2) = 0  xy = −2 hoặc 2 2 x + y = 2 .
+ Với xy = −2 ta có hệ: 2 2 2
x + y + x + y − xy = 3
(x + y) + (x + y) − 3xy = 3 2
(x + y) + (x + y) + 3 = 0      (vô nghiệm) (0,25) xy = 2 − xy = 2 − xy = 2 − + Với 2 2
x + y = 2 ta có hệ: 2 2
x + y + x + y − xy = 3 (x + y) − xy =1 
(x + y) − xy =1 
xy = (x + y) −1         2 2 2 2  2 2 x + y = 2 x + y = 2
(x + y) − 2xy = 2
(x + y) − 2(x + y) = 0 (0,25) x + y = 2 x + y = 0 x =1 x =1 x = 1 −   hoặc    hoặc  hoặc  . xy =1 xy = 1 −  y =1 y = 1 − y =1
Vậy hệ phương trình đã cho có 3 nghiệm: (1;1) , (1;−1) , (−1;1) . Trang 3 Câu Nội dung Điểm Câu 3 Cho parabol 2
(P): y = x và đường thẳng (d ): y = ax + b . Tìm a và b để (d ) cắt (P) tại hai
(1,0) điểm phân biệt ,A B sao cho A có hoành độ bằng 2 và khoảng cách từ A đến trục tung 1,0
bằng hai lần khoảng cách từ B đến trục tung.
+ A thuộc (P) và có hoành độ bằng 2 nên A(2;4).
d đi qua A(2;4) nên 4= 2a + b  b = 4 − 2a . Suy ra (d) : y =ax − 2a + 4 . 0,25
+ Phương trình hoành độ giao điểm của (P) và (d): 2
x − ax + 2a − 4 = 0  x = 2 hoặc x = a − 2
(d) cắt (P) tại hai điểm phân biệt khi: a − 2  2 hay a  4 . Hoặc: 0,25
+ Phương trình hoành độ giao điểm của (P) và (d): 2
x − ax + 2a − 4 = 0 (*)
(d) cắt (P) tại hai điểm phân biệt khi phương trình (*) có 2 nghiệm phân biệt 2
   0  (a − 4)  0  a  4 (được 0,25).
+ Khi đó hoành độ của A và B lần lượt là: x =2, x =a −2 A B . 0,25 d( ; A Oy) = 2d ( ;
B Oy)  x = 2 x  2 = 2 a − 2  a =1 A B hoặc a =3
Vậy a = 1; b = 2 hoặc a = 3; b = –2. 0,25 Câu Nội dung Điểm
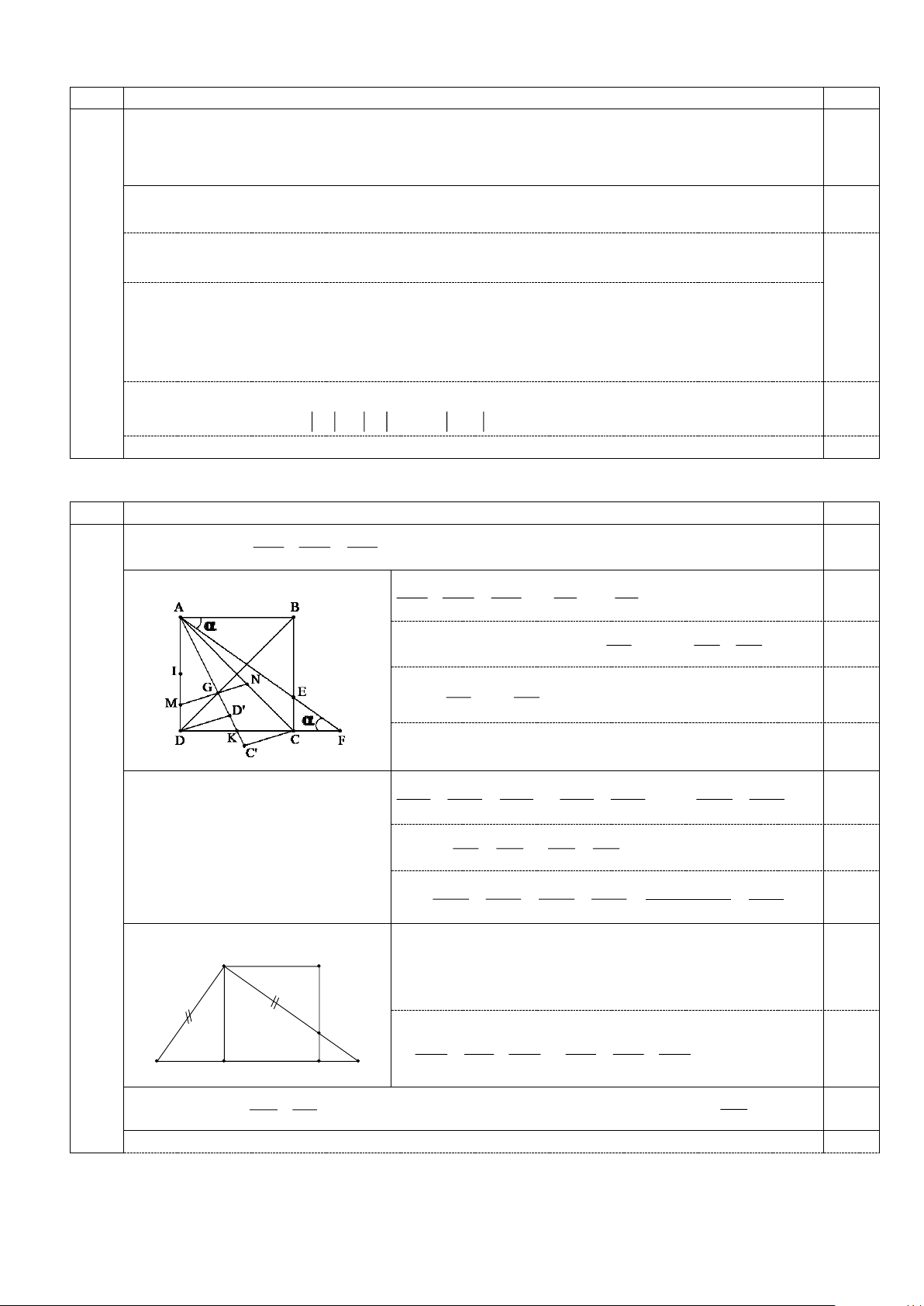
Câu 4 a) Chứng minh 1 1 1 + = . (2,0) 0,75 2 2 2 AE AF AB * Cách 1: 2 2 1 1 1  AB   AB  + =  + = 1. 0,25 2 2 2     AE AF AB  AE   AF  AB AB AD
Đặt BAE = AFD =  . Ta có: = cos, = = sin . 0,25 AE AF AF 2 2  AB   AB Vậy:  2 2 + = cos  + sin  =1     . 0,25  AE   AF 
Ghi chú: không có hình không chấm. * Cách 2: 2 2 1 1 1 AB AB 2 2 DC AD + =  + =1  + =1 . (0,25) 2 2 2 2 2 AE AF AB AE AF 2 2 AE AF AE DC DC DF Ta có: =  = . (0,25) AF DF AE AF 2 2 2 2 2 2 2 + Vậy: DC AD DF AD + = + DF AD AF = = =1. (0,25) 2 2 2 2 AE AF AF AF 2 2 AF AF * Cách 3:
Dựng đường thẳng qua A, vuông góc với AE và cắt A B
đường thẳng CD tại J. (0,5)
+ Chứng minh được hai tam giác ADJ và ABE bằng nhau. Suy ra AJ=AE.
+ Trong tam giác vuông AJF có: E 1 1 1 1 1 1 = +  = + . (0,25) 2 2 2 2 2 2 J D C F AD AJ AF AB AE AF b) Chứng minh AD AC +
= 3; trong trường hợp tích AM.AN nhỏ nhất, tính tỉ số AM . 1,25 AM AN AD
Hình vẽ phục vụ câu b (không có hình không chấm) 0,25 Trang 4 AD AC
* Khi M trùng I hoặc M trùng D ta có: + = 3 . AM AN
* Trường hợp M khác I và M khác D: 0,25
Gọi K là trung điểm của CD. Dựng CC’//MG, DD’//MG (C’, D’ thuộc AG). AD AD ' AC AC ' AD AC AD ' AC ' AD'+ AC ' Khi đó: = , = . Do đó + = + = . AM AG AN AG AM AN AG AG AG AD AC 2AK 3
Hai tam giác KDD’ và KCC’ bằng nhau nên KC’=KD’. Suy ra + = = 2. = 3 . 0,25 AM AN AG 2 4 Ta có: AD AC AD AC 3 = +  2. .
 AM.AN  .AD.AC (AD, AC không đổi). 0,25 AM AN AM AN 9 AD AC AM AG 2 Đẳng thức xảy ra khi =
 MN//DC hay MG//DC . Khi đó: = = . AM AN AD AK 3 0,25 AM 2
Vậy khi AM.AN nhỏ nhất thì = . AD 3 A B
* Chứng minh AD AC +
= 3 bằng cách khác: AM AN
Gọi H là giao điểm của MN và BC, P là trung điểm của MH. I N H (0,25) P G M AD MD AC NC HC = 1+ , = 1+ = 1+ AM AM AN AN AM AD AC MD HC MD + HC D K  + = 2 + + = 2 + C AM AN AM AM AM PK GK AD AC AM
MD + HC = 2PK = AM (vì 1 = = ). Suy ra + = 2 + = 3 . AM GA 2 AM AN AM (0,25)
Lưu ý: M trùng D hoặc I, ta vẫn có HC+MD=2PK. Câu Nội dung Điểm
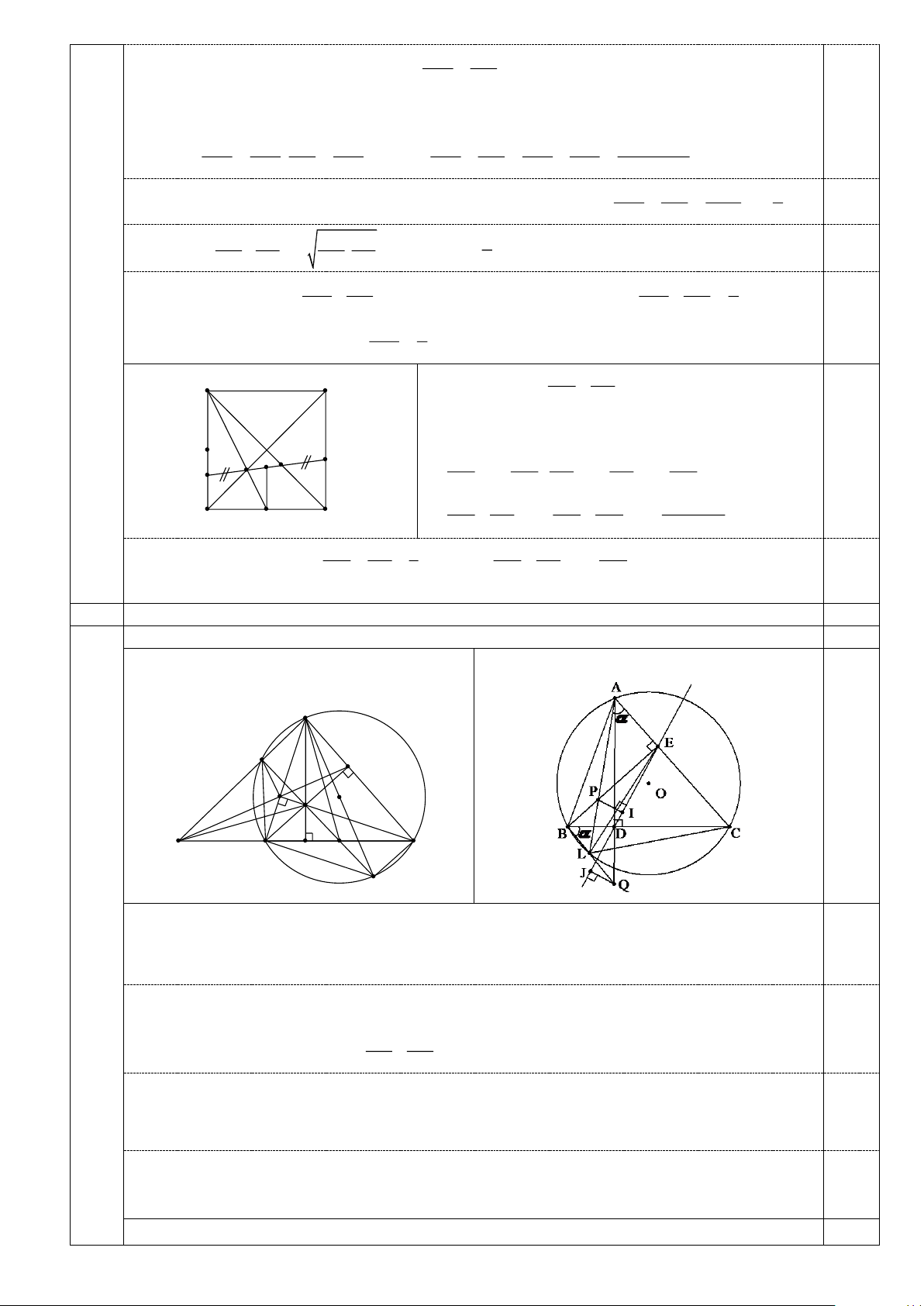
Câu 5 a) Chứng minh tứ giác BFNK nội tiếp trong đường tròn và HK vuông góc với AM . 1,25
(2,0) Hình vẽ phục vụ câu a (không tính điểm hình
vẽ câu b, không có hình không chấm) A N E 0,25 F O H K B D M C S
KNB=ACB (vì tứ giác ANBC nội tiếp)
KFB=ACB (vì tứ giác BCEF nội tiếp) 0,25
Suy ra KNB=KFB . Do đó tứ giác BFNK nội tiếp.
+ Hai tam giác KNB và KCA đồng dạng nên KN.KA = KB.KC
+ Hai tam giác KBF và KEC đồng dạng nên KF.KE = KB.KC 0,25 KN KE Suy ra KN.KA = KF.KE hay = . KF KA
Hơn nữa NKF=EKA . Do đó hai tam giác KNF và KEA đồng dạng.
Suy ra KNF=KEA . Do đó tứ giác ANFE nội tiếp. 0,25
Suy ra A, N, F, H, E nằm trên đường tròn đường kính AH. Do đó NH ⊥ AK .
+ Tia NH cắt đường tròn (O) tại S, AS là đường kính của (O).
+ Chứng minh được tứ giác BHCS là hình bình hành. Suy ra HS qua trung điểm M của BC. 0,25
Suy ra N, H, M, S thẳng hàng. Khi đó H là trực tâm của tam giác AKM. Vậy HK ⊥ AM .
b) Chứng minh đường thẳng DE cách đều hai điểm P và Q . 0,75 Trang 5
+ Hạ PI và QJ vuông góc với đường thẳng DE lần lượt tại I, J. Đặt LAC=LBC=α . 0,5
PI=EP.sinPEI=AE.tanα.sinBAD =(AB.cosA).tanα.cosB=AB.cosA.cosB.tanα .
QJ=QD.sinQDJ=BD.tanα.sinABE =(AB.cosB).tanα.cosA=AB.cosA.cosB.tanα . 0,25
Suy ra PI=QJ. Vậy P và Q cách đều đường thẳng DE.
Ghi chú: Nếu thí sinh xét 2 trường hợp và giải đúng trong trường hợp A, D, L thẳng hàng
thì được 0,25. Nếu không chia 2 trường hợp mà vẽ hình đặc biệt A, D, L thẳng hàng để giải thì không cho điểm.
Câu 6 Cho 3 số thực dương x, y, z thỏa x + y + z = 3 . Tìm giá trị lớn nhất của (1,0) 3 3 3 1,0
P = x yz + y zx + z x . y Ta có: 2
(a + b + c)  3(ab + bc + ca) với a, b, c là 3 số thực (dấu bằng xảy ra khi a=b=c).
Áp dụng bất đẳng thức trên với a = xy, b = yz, c = zx (x, y, z > 0) ta được: 0,25 2 2 2 2 2 2
(xy + yz + zx)
(xy + yz + zx)
(xy + yz + zx)  3( y zx + z xy + x yz)  xyz(x + y + z)   xyz  3 9 2
(xy + yz + zx) Ta có: 2 2 2 2 2 2
P = xyz(x + y + z ) 
(x + y + z ) 9 0,25 1 2 2 2
= (xy + yz + zx)(xy + yz + zx)(x + y + z ) 9 3 2 2 2 3 3
1 (xy + yz + zx) + (xy + yz + zx) + (x + y + z )  2 2
1 (x + y + z)  1  3     =   =   = 3 . 0,25 9  3     9  3   9 3   
P = 3  x = y = z =1. Vậy giá trị lớn nhất của P bằng 3 khi x = y = z =1. 0,25 * Lưu ý:
Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì vẫn cho đủ số điểm
từng phần như hướng dẫn quy định. Trang 6