

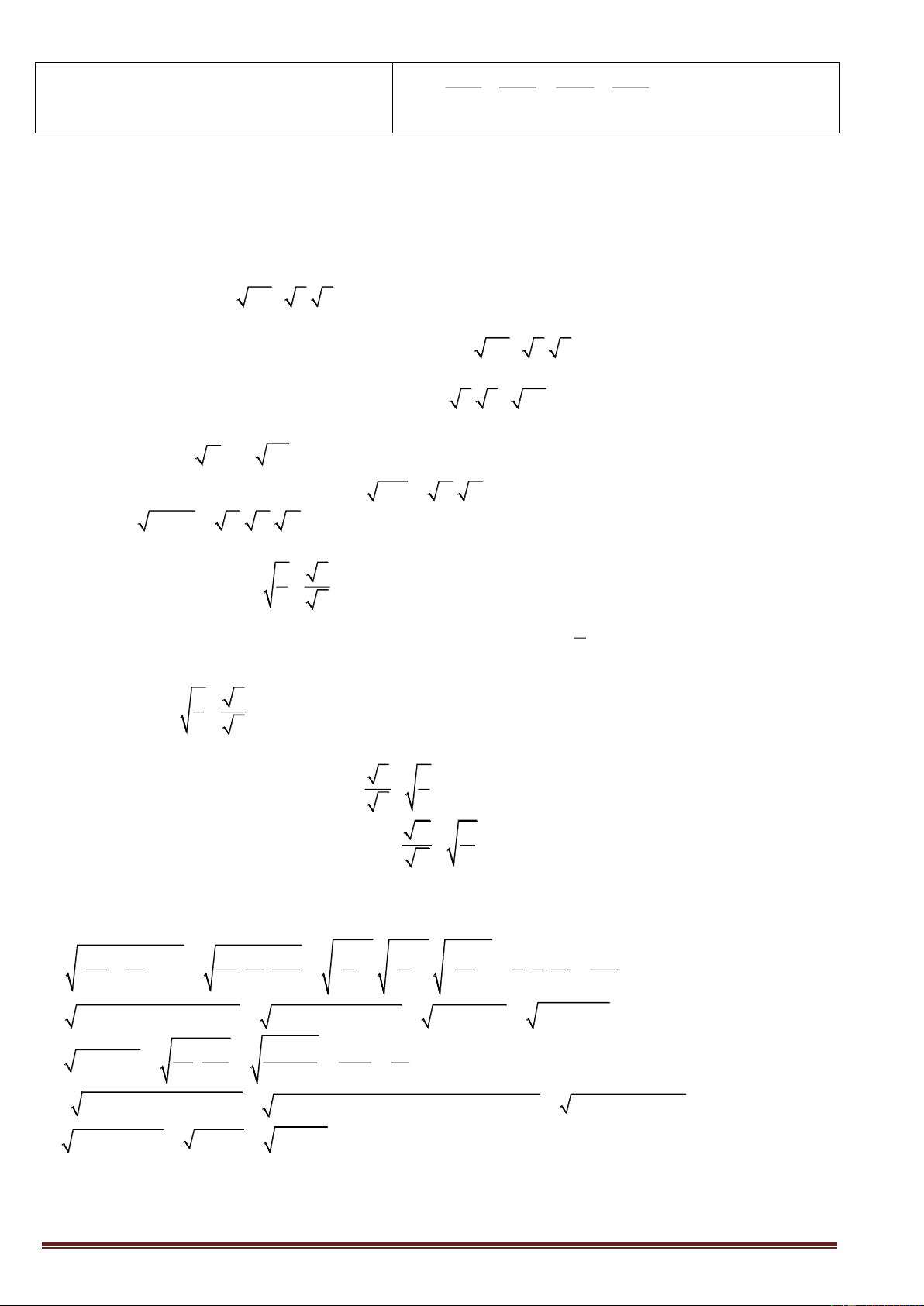



























Preview text:
Ngày dạy: ……………………..
CĂN BẬC HAI. CĂN THỨC BẬC HAI VÀ HẰNG ĐẲNG THỨC 2 A A
A./ Kiến thức cơ bản: 1. Căn bậc hai
- Định nghĩa: Căn bậc hai của số thực a là số x sao cho x2 = a. - Chú ý:
+ Mỗi số thực a > 0, có đúng 2 căn bậc hai là 2 số đối nhau: số dương: a , số âm: a
+ Số 0 có căn bậc hai là chính nó: 0 0
+ Số thực a < 0 không có căn bậc hai (tức a không có nghĩa khi a < 0). 2. Căn bậc hai số học
- Định nghĩa: Với a 0 thì số x a được gọi là căn bậc hai số học của a. Số 0 cũng được gọi là căn bậc hai số học của 0.
- Chú ý: Việc tìm căn bậc hai số học của 1 số không âm được gọi là phép khai phương.
- Định lý: Với a, b > 0, ta có:
+ Nếu a < b a b
+ Nếu a b a < b 3. Căn thức bậc hai
- Cho A là 1 biểu thức thì biểu thức
A được gọi là căn thức bậc hai của A ; A được gọi là biểu thức lấy
căn hay biểu thức dưới dấu căn.
- A có nghĩa (hay xác định hay tồn tại) A 0 4. Hằng đẳng thức 2 A A
- Định lý : Với mọi số thực a, ta có : 2 a a A nêu A 0
- Tổng quát : Với A là biểu thức, ta có : 2 A A -A nêu A<0
B./ Bài tập áp dụng
Dạng 1 : Tìm căn bậc hai, căn bậc hai số học * Phương pháp :
- Viết số đã cho dưới dạng bình phương của một số.
- Tìm căn bậc hai số học của số đã cho.
- Xác định căn bậc hai của số đã cho. 1
Bài 1 : Tìm căn bậc hai của các số sau : 121 ; 144 ; 324 ; ; 3 2 2 64 LG
+ Ta có CBHSH của 121 là : 2
121 11 11 nên CBH của 121 là 11 và -11 + CBHSH của 144 là : 2
144 12 12 nên CBH của 121 là 12 và -12 + CBHSH của 324 là : 2
324 18 18 nên CBH của 324 là 18 và -18 2 + CBHSH của 1 1 1 1 1 1 là : nên CBH của 1 là và 64 64 8 8 64 8 8 + Ta có : 2 3 2 2 2 2 2 1 2 1
2 1(vi 2 1 0) nên CBH của 3 2 2 là 2 1 và 2 1
Dạng 2 : So sánh các căn bậc hai số học * Phương pháp :
- Xác định bình phương của hai số.
- So sánh các bình phương của hai số.
- So sánh giá trị các CBHSH của các bình phương của hai số. Trang 1 Bài 2 : So sánh a) 2 và 3 b) 7 và 47 c) 2 33 và 10 d) 1 và 3 1 e) 3 à v 5- 8 g) 2 11 à v 3 5 LG
a) Vì 4 > 3 nên 4 3 2 3
b) Vì 49 > 47 nên 49 47 7 47
c) Vì 33 > 25 nên 33 25 33 5 2 33 10
d) Vì 4 > 3 nên 4 3 2 3 2 1 3 1 1 3 1 3 2 e) * Cách 1: Ta có:
3 8 5 3 5 8 8 3 * Cách 2: giả sử 2 2 3 5 8 3 8 5 3 8
5 3 2 24 8 25
2 24 14 24 7 24 49
Bất đẳng thức cuối cùng đúng do đó bất đẳng thức đầu tiên đúng. 2 3 g) Ta có: 2 11 3 5 11 5
Dạng 3: Tìm điều kiện để căn thức xác định: A xác định A 0
Bài 3: Tìm điều kiện của x để các biểu thức sau xác định: 2 1 1 x 2 2 a) x b) x 2 c) d ) 3x 5 3 5 2x 3 x 4 LG
Để các căn thức trên có nghĩa thì: 2 1 2 1 3 a) x
0 x x 3 5 3 5 10 b) Ta có: 2 2 x 2 0, x
x 2 xác định với mọi x 1 x 1 x 0 1 x 0 c) 0 hoặc 2x 3 2x 3 0 2x 3 0 x 1 1 x 0 + Với 3 3 x 2x 3 0 x 2 2 x 1 1 x 0 + Với 3 x 1 2x 3 0 x 2
Vậy căn thức xác định nếu 3 x hoặc x 1 2 3 x 5 0 5 3 x 5 0 x d) 2 3 x 4 0 x 4 0 x 4 x 4
Dạng 4 : Rút gọn biểu thức
Bài 4: Rút gọn các biểu thức sau:
a) A 4 2 3 4 2 3 c) 2
C 9x 2x (x 0)
b) B 6 2 5 6 2 5 d) 2
D x 4 16 8x x (x 4) LG Trang 2 2 2
a) Cách 1 : A 3 1 3 1 3 1 3 1 2 3 2
A 4 2 3 4 2 3 2 (4 2 3).(4 2 3) 8 2 16 12 8 2.2 12 Cách 2 : A 2 3 2 2 b) B 5 1 5 1 5 1 5 1 2 5
c) C x2 3
2x 3x 2x 3
x 2x 5
x (vi x 0) d) 2 2
D x 4 16 8x x x 4 (4 x) x 4 4 x x 4 x 4 2(x 4) ( i v x 4)
Dạng 5 : Tìm Min, Max Bài 5 : Tìm Min 2 x x 2 a) y x 2x 5 b) y 1 4 6 LG a) Ta có : 2 2 2
x 2x 5 (x 1) 4 4
x 2x 5 4 2
vậy Miny = 2. dấu ‘‘ = ’’ xảy ra khi và chỉ khi x – 1 = 0 => x = 1 2 2 2 x x x 1 35 35 x x 35 35 b) Ta có : 1 y 1 4 6 2 6 36 36 4 6 36 6 vậy Miny = 35 . Dấu « x x
= » xảy ra khi và chỉ khi 1 1 1
0 x 6 2 6 2 6 3
**************************************************
Ngày dạy: ……………………..
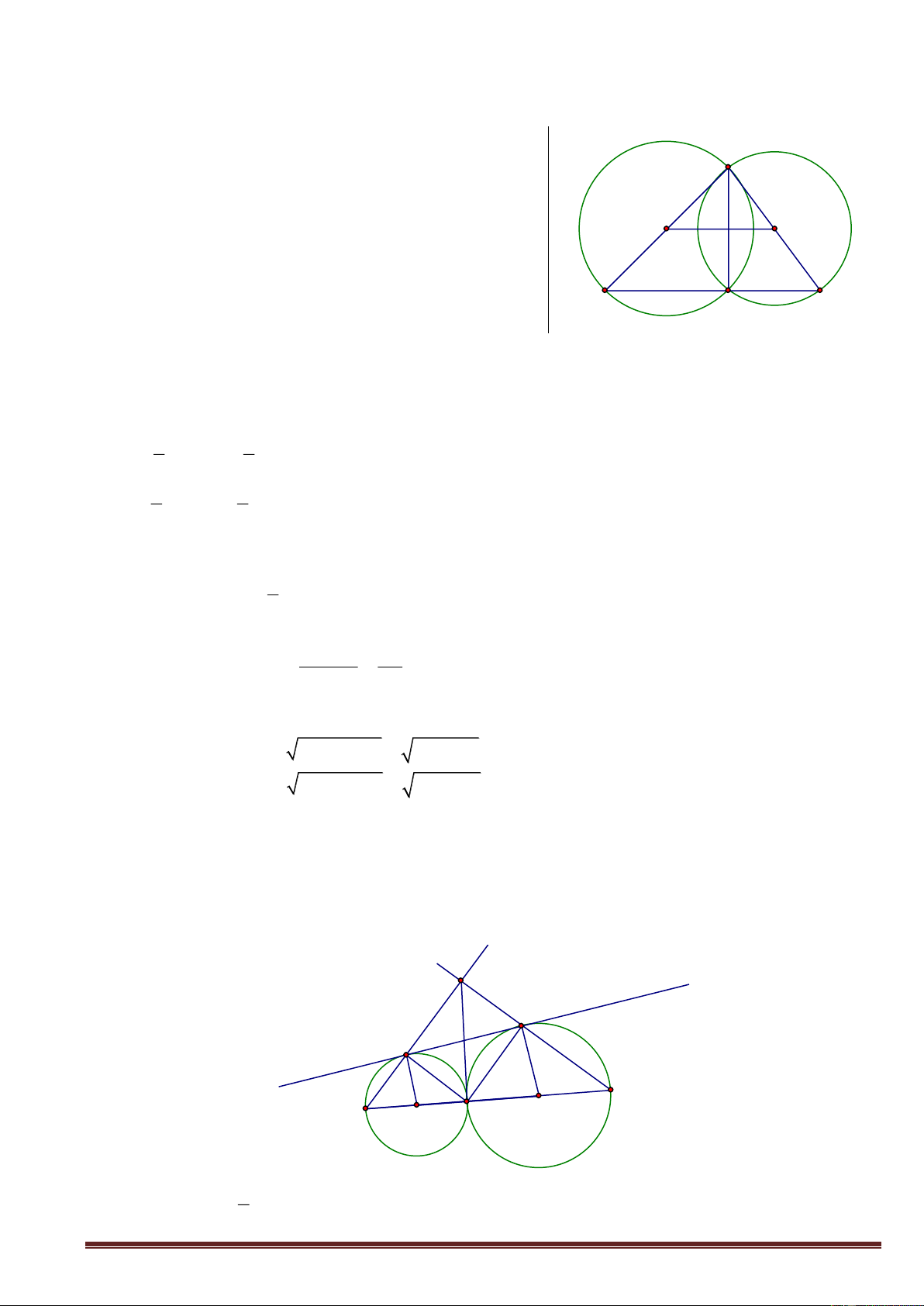
VẬN DỤNG CÁC HỆ THỨC VỀ CẠNH VÀ ĐƯỜNG CAO TRONG TAM GIÁC VUÔNG
A./ Kiến thức cơ bản
Cho tam giác ABC vuông tại A, đường cao AH sao cho ta có: ' ' AH ,
h BC a, AB , c AC ,
b BH c , CH b khi đó: 2 ' 2 ' 1) b . a b ; c . a c A 2 ' '
2) h b .c 3) . b c . a h b 1 1 1 c 4) h 2 2 2 h b c 2 2 2
5) a b c (Pitago) c' b' B H C a B./ Bài tập áp dụng
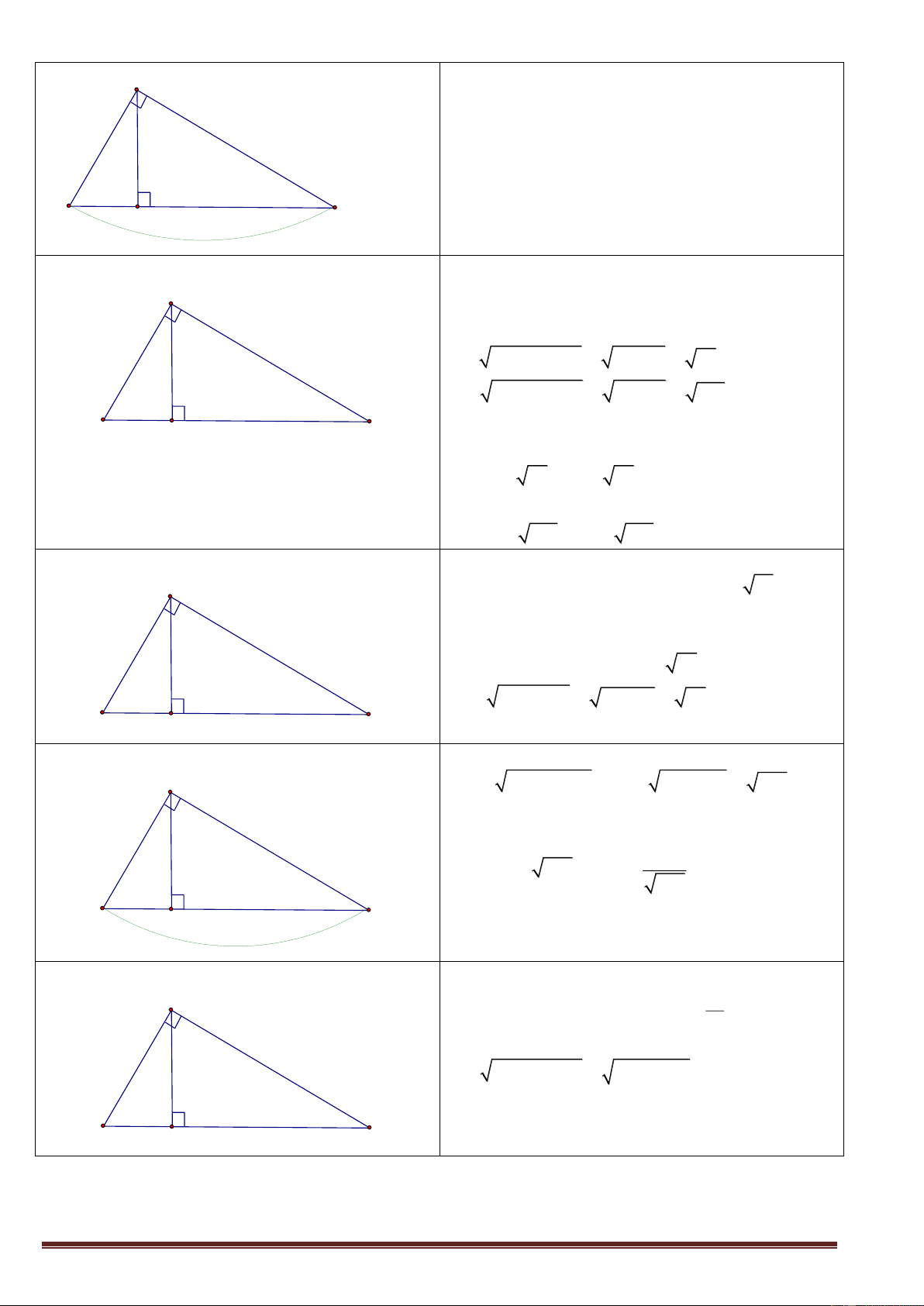
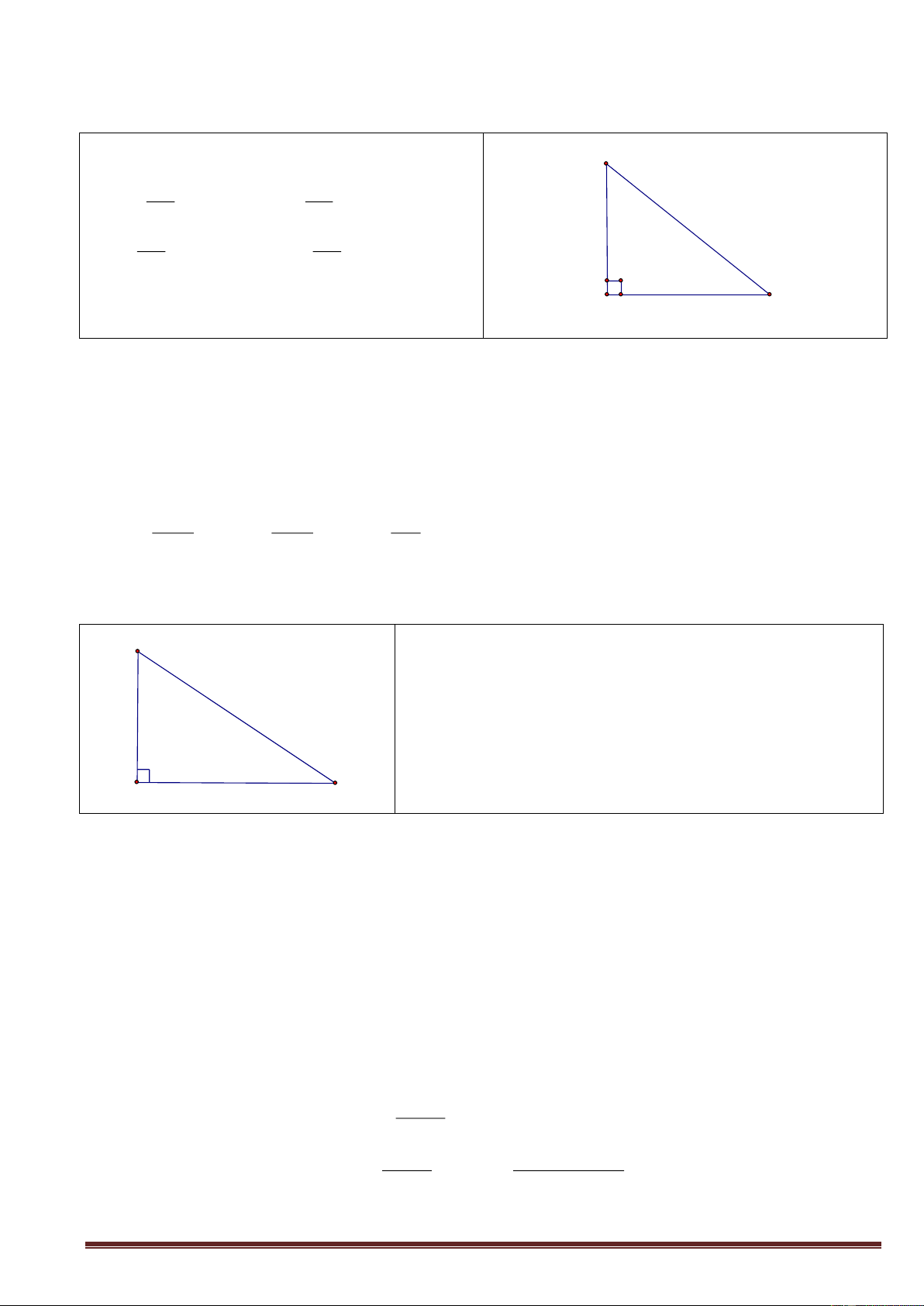
Bài 1 : Tìm x, y trong các hình vẽ sau: a) + ta có: A 2 2 BC
AB AC (Pitago) 2 2
BC 4 6 52 7,21 6 + Áp dụng định lý 1 4 : 2 2
AB BC.BH 4 52.x x 2, 22 x y 2 2
AC BC.CH 6 52.y y 4,99 B H C
Hay y = BC – x = 7,21 – 2,22 = 4,99 b)
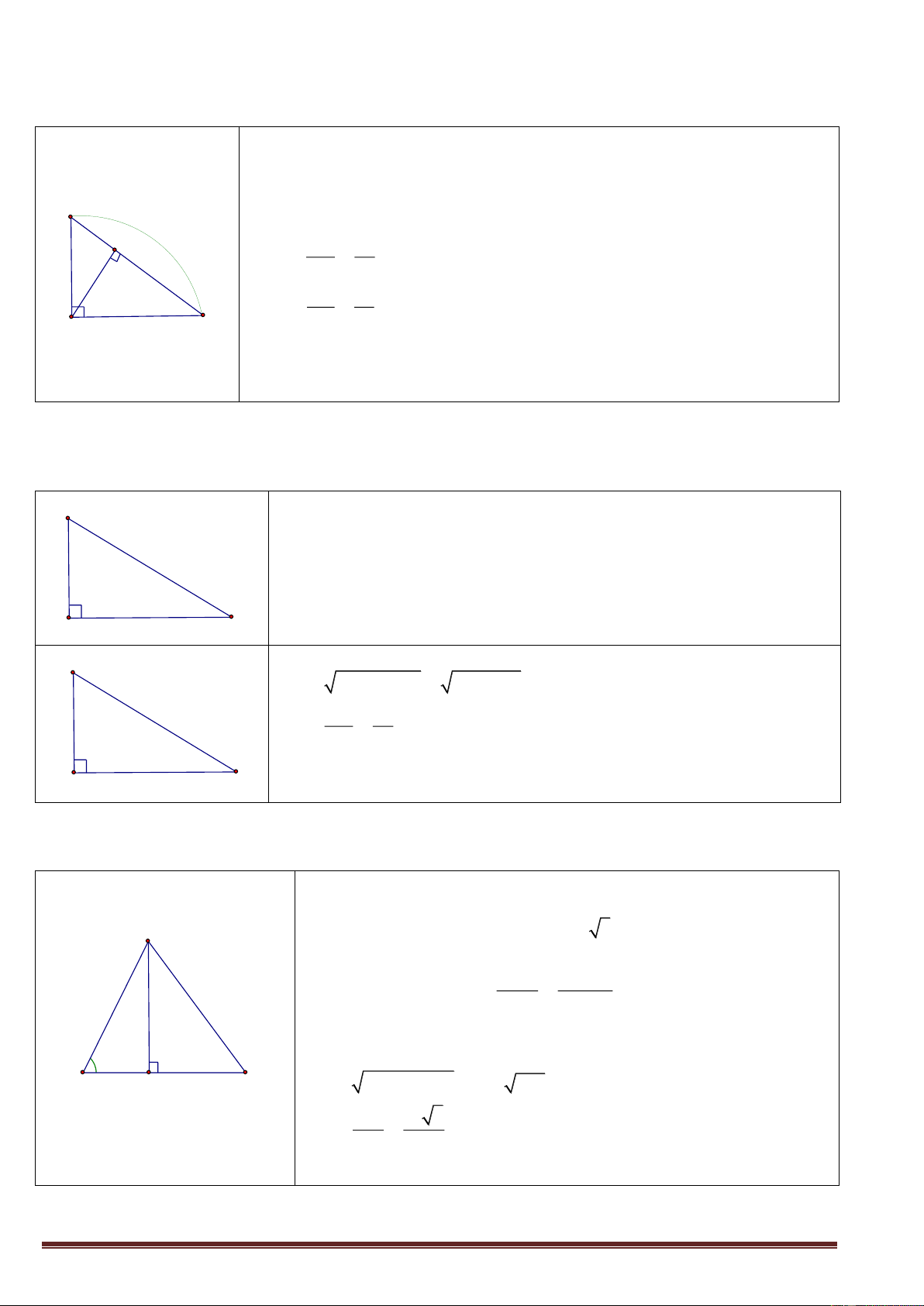
- Xét tam giác ABC vuông tại A. áp dụng định lý 1 ta có : Trang 3 2 2 A
AC BC.CH 12 18.y y 8
x BC y 18 8 10 12 x y B H C 18 c) * Cách 1 :
AH2 = BH.CH = 4.9 = 36 => AH = 6 A
Theo Pitago cho các tam giác vuông AHB; AHC ta có: y x 2 2 2 2 x BH AH 4 6 52 2 2 2 2
y CH AH 6 9 117 4 9 B
* Cách 2: Áp dụng định lý 1 ta có: H C 2
AB BC.BH (BH CH ).BH (4 9).4 52
AB 52 x 52 2
AC BC.CH (BH CH ).CH (4 9).9 117
AC 117 y 117 d)
Áp dụng định lý 2, ta có: 2 2 A
AH BH.CH x 3.7 21 x 21
Áp dụng định lý 1. ta có : 2 y AC BC.CH (BH CH ).CH x 2
y (3 7).7 70 y 70 2 2 ( y x CH 21 49 70) 3 7 B C H e) Theo Pitago, ta có : A 2 2 2 2 BC
AB AC y 13 17 458
Áp dụng định lý 3, ta có : A .
B AC BC.AH 17 13 x 221
13.17 458.x x 10,33 458 B C H y g)
Áp dụng định lý 2, ta có : 2 A 5 2 2
AH BH.CH 5 4.x x 6,25 4
Theo Pitago cho tam giác AHC vuông tại H, ta có : y 5 2 2 2 2 y
AH CH 5 6, 25 8 2 (D 1
L : y BC.x (4 6, 25).6, 25 y 8) x 4 B H C
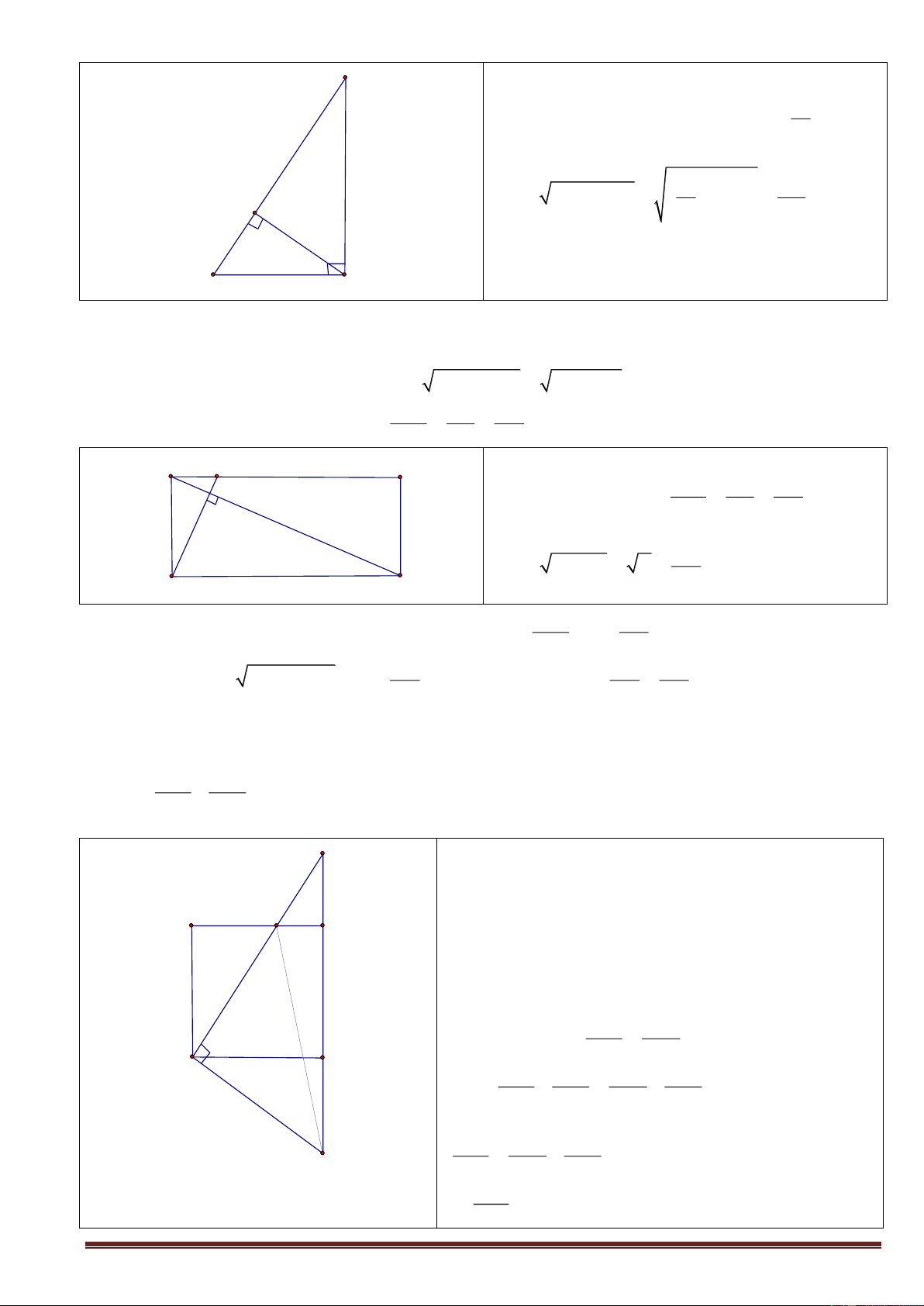
Bài 2 : Cho tam giác ABC vuông tại A, có các cạnh góc vuông AB = 15cm, AC = 20cm. Từ C kẻ đường
vuông góc với cạnh huyền, đường này cắt đường thẳng AB tại D. Tính AD và CD? LG Trang 4 µ 0 D B C ,
D C 90 ,CA BD . Theo định lý 3, ta có : 80 2 2 CA A .
B AD 20 15.AD AD 3 x
Theo Pitago trong tgiác ACD vuông tại A, ta có : 2 y 80 100 2 2 2 CD AD CA 20 A 3 3 20 15 B C
Bài 3: Cho hình chữ nhật ABCD có AB = 60cm, AD = 32cm. Từ D kẻ đường thẳng vuông góc với đường
chéo AC, đường thẳng này cắt AC tại E và AB tại F. Tính độ dài EA, EC, ED, FB, FD. LG
Xét tam giác ADC vuông tại D, ta có: 2 2 2 2 AC
AD CD 32 60 68 2 2 Theo định lý 1: AD 32 256 2
AD AC.AE AE AC 68 17 Theo định lý 1, ta có: A F 60 B 2 2 CD 60 900 2 E
CD AC.CE CE AC 68 17 32 Theo định lý 2, ta có: 480 DE
AE.EC ... 17 D C 2 AD 544
Xét tam giác DAF, theo định lý 1: 2
AD DF.DE DF ... DE 15 256 256 644 Theo Pitago: 2 2 AF
DF AD ....
FB AB AF 60 15 15 15
Bài 4: Cho hình vuông ABCD. Gọi E là một điểm nằm giữa A, B. Tia DE và tia CB cắt nhau ở F. Kẻ
đường thẳng qua D vuông góc với DE, đường thẳng này cắt đường thẳng BC tại G. Chứng minh rằng: a) Tam giác DEG cân. b) Tổng 1 1
không đổi khi E chuyển động trên AB. 2 2 DE DF LG ¶ ¶ F
a) Ta có: D D (cùng phụ với ¶ D ) 1 3 2 xét AD E à v C DG ta có : A E AD DC(gt) B D D cmt A DE C DG g. . c g 1 3 0 A C 90
DE DG D EG cân tại D 1 1 1 b) vì DE = DG 2 2 2 DE DG D C 3 1 1 1 1 ta có : 2 2 2 2 DE DF DG DF
xét tam giác DGF vuông tại D, ta có : 1 1 1 G (định lý 4) 2 2 2 CD DG DF 1 Vì
không đổi khi E chuyển động trên AB, suy ra 2 CD Trang 5 tổng 1 1 1 1 không đổi khi E thay 2 2 2 2 DE DF DG DF đổi trên AB.
*******************************************************
Ngày day: …………………..
CÁC PHÉP TÍNH VỀ CĂN BẬC HAI
A./ Kiến thức cơ bản :
1. Khai phương một tích. Nhân các căn bậc hai. a) Định lý : ; a b 0,ta ó c : a.b= a. b
b) Quy tắc khai phương một tích : Muốn khai phương một tích các số không âm, ta có thể khai phương
từng thừa số rồi nhân các kết quả với nhau ( ; a b 0,ta ó c : a.b= a. b )
c) Quy tắc nhân các căn bậc hai : Muốn nhân các CBH của các số không âm, ta có thể nhân các số dưới
dấu căn với nhau rồi khai phương kết quả đó ( ; a b 0: a. b= a.b ) d) Chú ý : - Với A > 0 ta có : 2 2 A A A
- Nếu A, B là các biểu thức : ; A B 0ta ó c : . A B . A B - Mở rộng : . A . B C . A B. C ( , A , B C 0)
2. Khai phương một thương. Chia các căn bậc hai a) Định lý a a
: a 0, b 0 ta ó: c = . b b
b) Quy tắc khai phương một thương : Muốn khai phương một thương a , trong đó số a không âm và số b b
dương, ta có thể lần lượt khai phương số a và số b, rồi lấy kết quả thứ nhất chia cho kết quả thứ hai a a
( a 0, b 0 ta ó: c = . ) b b
c) Quy tắc chia hai CBH : Muốn chia CBH của số a không âm cho số b dương, ta có thể chia số a cho số
b rồi khai phương kết quả đó ( a a
a 0, b 0 : = ) b b A A
d) Chú ý : Nếu A, B là biểu thức : A 0, B 0 : = B B
B./ Bài tập áp dụng : Dạng 1 : Tính
Bài 1 : Thực hiện phép tính: 2 2 2 24 1 49 81 1 7 9 1 7 9 1 63 a) 1 .5 .0, 01 . . . . . . 25 16 25 16 100 5 4 10 5 4 10 200 2 ) b
2, 25.1, 46 2, 25.0, 02 2, 25(1, 46 0, 02) 2, 25.1, 44 (1,5.1, 2) 1,5.1, 2 1,8 2 25 169 (5.13) 5.13 13 c) 2, 5.16, 9 . 2 10 10 10 10 2 2 2
d ) 117, 5 26, 5 1440 (117, 5 26, 5).(117, 5 26, 5) 1440 144.91144.10 2
144(9110) 144.81 (12.9) 108
Dạng 2 : Rút gọn các biểu thức
Bài 2 : Tính giá trị các biểu thức: Trang 6 1 9 64 4 441
a) A 0,1 0,9 6, 4 0, 4 44,1 10 10 10 10 10 1 3 8 2 2 35 35 10 7 10 10 10 10 10 10 10 10 2 2 3 7 2 3 7 6 14 2 b) B 2 3 28 2 3 2 7 2( 3 7) 2
3 54 33 54 3 3 5 3 5 c) C 4 3 4 3 4 34 3
12 3 3 4 5 15 12 3 3 4 5 15 24 2 15 16 3 13
Bài 3 : Rút gọn các biểu thức: 2
a) 9 x 5 x 5 3 x 5 3 x 5 2 b) 2
x . x 2 x 0 x . x 2 x 2 x x x 2 3 3 108x 108x c) x 0 2
9x 3 x 3x 12x 12x 4 6 4 6 13x y 13x y 1 1 1 1 d)
x 0; y 0 6 6 2 6 6 208x y 16x 4 x 4 x 4 208 x x y
Dạng 3 : Chứng minh
Bài 4 : Chứng minh các biểu thức sau: a) 6 35 . 6 35 1
VT (6 35).(6 35) 36 35 1 VP b) 9 17 . 9 17 8
VT (9 17 ).(9 17 ) 8117 64 8 VP c) 2 2 1 9 8
VT 2 2 2 1 3 2 2
VT VP 2
VP 3 2 .2 3 2 2
d ) 4 32 49 48 2 VT 4 2 12 3 7 2 2 .3 7 4 3
VT VP 2
VP 7 4 .3 7 4 3 e 2 ) 2 2 2 3 3 1 2 2 6 6 9
VT 4 2 6 6 1 4 2 8 6 6 9 VP g)
8 2 15 8 2 15 2 3
VT 5 2. 5. 3 3 5 2. 5. 3 3 5 32 5 32
5 3 5 3 5 3 5 3 2 3 VP
Dạng 4 : Giải phương trình Trang 7
Bài 5 : Giải các phương trình sau:
a) 2 2x 5 8x 7 18x 28 1 dk : x 0 28 784 392
1 2 2x 5.2. 2x 7.3. 2x 28 13 2x 28 2x 2x x tm 13 169 169 1 b) 4x 20 x 5 9x 45 4 2 3 1 2 4(x 5) x 5 9(x 5) 4
dk : x 5 0 x 5 3 1
2 x 5 x 5 .3 x 5 4 2 x 5 4 x 5 2 x 5 4 x 9 tm 3 2 x 3 x 2 0 3 2 3x 2 x 1 0 x 1 3x 2 x c) 3 (3) đk : 0 3 x 1 x 1 3 x 2 0 2 x x 1 x 1 0 3 x 1 3x 2 1 1 Ta có (3)
9 ... 6x 1 1 x thỏa mãn x 1 6 4 5x 4 5 x 4 0 x 4 d ) 2 (4) đk : 5 x x 2 x 2 0 5 x 2
(4) 5x 4 2 x 2 5x 4 4 x 2 ..... x 12 thỏa mãn Bài tập a b
: (bất đẳng thức Cauchy) : Cho 2 số a và b không âm. Chứng minh rằng ab . Dấu đẳng 2 thức xảy ra khi nào? LG * Cách 1 :
+ vì a 0;b 0 a; b xác định. a b
+ ta có : a b 2 0 a 2 ab b 0 a b 2 ab ab 2
+ dấu đẳng thức xảy ra khi và chỉ khi a = b * Cách 2 : ta có a b2 2 2 2 2 2 2
0 a 2ab b 0 a b 2ab a 2ab b 4ab 2 a b a b
4ab a b 2 ab ab 2
*******************************************************
Ngày dạy: …………………..
TỈ SỐ LƯỢNG GIÁC CỦA GÓC NHỌN A. Kiến thức cơ bản 1. Định nghĩa : Cho 0 0 ABC
(0 90 ) ta định nghĩa các tỉ số giữa các cạnh AB, BC, CA của tam
giác ABC vuông tại A như sau: Trang 8 AC AB sin ; cos C BC BC AC AB tg ; cot g Huyền AB AC Đối A B Kề
* Nhận xét : từ định nghĩa ta thấy : + tỉ số lượng giác của 1 góc nhọn luôn dương 1
+ 0 < sin, cos < 1 + cot g
;tg.cot g 1 tg
2. Tỉ số lượng giác của 2 góc phụ nhau.
- Định lý : nếu 2 góc phụ nhau thì sin góc này bằng cosin góc kia, tg góc này bằng cotg góc kia. Tức: nếu si n cos ; cos sin 0
90 thì ta có : t
g cot g;
cot g tg
3. Bảng các tỉ số lượng giác của các góc đặc biệt: 300 450 600 Tỉ số lượng giác Sin 1 2 3 2 2 2 Cos 3 2 1 2 2 2 tg 1 1 3 3 Cotg 3 1 1 3 * Nhận xét :
- Dựa vào bảng trên ta thấy: si
n sin ; tg tg với 0 0 1 2 1 2 0 ; 90 à v . 1 2 1 2
cos cos ; cot g cot g 1 2 1 2 Tức là :
+ góc lớn hơn thì có sin lớn hơn, nhưng lại có cosin nhỏ hơn.
+ góc lớn hơn thì có tg lớn hơn, nhưng lại có cotg nhỏ hơn.
Hay ta có thể phát biểu : 0 0 0 90 thì :
+ sin và tg đồng biến với góc .
+ cosin và cotg nghịch biến với góc .
4. Các hệ thức cơ bản: sin 1 tg ;
3 tg.cot g 1; cos cos 2 cotg ; 4 2 2 sin cos 1 sin B. Bài tập áp dụng
Bài 1 : Cho biết sin = 0,6. Tính cos, tg và cotg? + ta có: 2 2 2 2
sin cos 1 cos 1 sin 1 0, 6 0,8 sin 0, 6 3 cos 0,8 4 + tg ; cotg cos 0,8 4 sin 0, 6 3 Bài 2: Trang 9
1. Chứng minh rằng: 1 1 2 2 4 4 2
a) tg 1
; b) cotg 1
; c) cos sin 2 cos 1 2 2 cos sin
2. Áp dụng: tính sin, cos, cotg, biết tg = 2 LG 1. a) ta có: 2 2 sin sin sin 2 2 tg tg tg 1 1 2 2 cos cos cos 2 2 sin cos 1 2 tg 1 2 2 cos cos 2 2 2 cos cos sin 1 b) 2
VT cot g 1 1 VP 2 2 2 sin sin sin c) 4 4
VT cos sin 2 2 cos sin . 2 2 cos sin 2 2 cos sin 2 cos 2 1 cos 2 2 2
cos 1 cos 2cos 1 VP 2. Ta có: tg 2 ê n n a 1 1 1 2 2 2 1 cos cos ; 2 cos 5 5 1
tg 2 cotg ; 2 2 b 1 1 1 5 4 2 5 2 1
sin sin 2 2 2 sin sin 4 5 5
Bài 3: Biết tg = 4/3. Tính sin, cos, cotg? LG
+ ta có: tg = 4/3 nên cotg = ¾ 1 9 3 + mà 2 2 tg 1 cos cos ; 2 cos 25 5 2 + mặt khác: 3 4 2 2 2 sin cos 1 sin 1 co s 1 5 5
Bài 4: Dựng góc trong các trường hợp sau: 1 2 a) sin ; b) cos ; c) tg 3;
d ) cot g 4 2 3 LG a)* Cách dựng y
- dựng góc xOy = 900 . Lấy đoạn thẳng làm đơn vị
- trên Oy lấy điểm B sao cho OB = 1
- vẽ cung tròn tâm B, bán kính bằng 2, cung này cắt Ox tại A.
- nối A với B BAO cần dựng B * Chứng minh: 2 OB 1 1 - ta có: sin sin BAO đpcm AB 2 x O A Trang 10 b)* Cách dựng y
- dựng góc xOy = 900 . Lấy đoạn thẳng làm đơn vị
- trên Ox lấy điểm A sao cho OA = 2. B
- vẽ cung tròn tâm A, bán kính bằng 3, cung này cắt Oy tại B.
- nối A với B BAO cần dựng 3 * Chứng minh: OA 2
- ta có: cos cos BAO đpcm AB 3 x 2 O A c) * Cách dựng: y
- dựng góc xOy = 900 . Lấy đoạn thẳng làm đơn vị.
- trên Ox lấy điểm A sao cho OA = 3
- trên Oy lấy điểm B sao cho OB = 1 O
BA cần dựng.
* Chứng minh: - thật vậy, ta có: B OA 3 tg tg O BA 3 đpcm OB 1 1 x O 3 A d) * Cách dựng y
- dựng góc xOy = 900 . Lấy đoạn thẳng làm đơn vị
- trên Ox lấy điểm A sao cho OA = 4
- trên Oy lấy điểm B sao cho OB = 1 O
AB cần dựng
* Chứng minh: - thật vậy, ta có: B OA 4
cotg cotg O AB 4 đpcm OB 1 1 x O 4 A
Bài 5: Cho tam giác ABC có AB = 5; BC = 12; AC = 13 a) CMR tam giác ABC vuông.
b) Tìm tỉ số lượng giác của góc A và góc C. LG a) Ta có: 2 2 2 2 2 2 2 2 2
AB BC 12 5 169 13 AC AB BC AC
theo định lý Pytago đảo, suy ra tam giác ABC vuông tại B. b) - vì 0 A C 90 ; A C là 2 góc phụ nhau A - do đó: 12 5 13
sin A cos C ;
cos A sin C 5 13 13 12 5 C
tgA cot gC ;
cot gA tgC 5 12 B 12
********************************************************* Trang 11
Ngày dạy: ……………………….
BIẾN ĐỔI ĐƠN GIẢN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI A. Kiến thức cơ bản
1. Đưa thừa số ra ngoài dấu căn:
A B (A 0;B 0) 2 A B A B
A B (A 0;B 0)
2. Đưa thừa số vào trong dấu căn: 2
A 0; B 0 : A B A B 2
A 0; B 0 : A B A B
3. Khử mẫu của biểu thức lấy căn A . A B : .
A B 0; B 0 : B B
4. Trục căn thức ở mẫu: A A B a) B 0 : B B C A B C 2
b) A 0; A B : 2 A B A B C A B C c) ,
A B 0; A B : A B A B * Chú ý:
- Các căn bậc hai đồng dạng là các căn bậc hai có cùng biểu thức dưới dấu căn.
- Biểu thức liên hợp: 2 biểu thức chứa căn thức được gọi là liên hợp với nhau nếu tích của chúng không chứa căn thức.
- Quy tắc trục căn thức ở mẫu: muốn trục căn thức ở mẫu của 1 biểu thức ta nhân tử và mẫu của biểu thức
đó với biểu thức liên hợp của mẫu.
B. Bài tập áp dụng
Dạng 1: Đưa nhân tử ra ngoài, vào trong dấu căn
Bài 1: Đưa nhân tử ra ngoài dấu căn:
a) 125x x 0
5x2 .5x 5x 5x 4 b) 80 y 4y 2 2 2 .5 4 y 5 c) 51 2 2
1 2 . 5 2 1 5 1 2 0 d ) 27 2 5 2 2
2 5 . 3.3 5 2.3. 3 2 5 0 2 10 3 2 10 3 2 2 2 e) 2 10 3 2
3 10 10 3 10 3. 10 3 3 10 10 9 Trang 12 2 5 1 3 5 1 3 5 3 1 g) 1 3 0 4 2 2
Bài 2: Đưa thừa số vào trong dấu căn và so sánh: a) 3 5 à v 5 3 ta có: 2 3 5 3 .5 45
do 75 45 75 45 5 3 3 5 2 5 3 5 .3 75 b) 4 3 à v 3 5 ta có: 2 4 3 4 .3 48
do 48 45 48 45 4 3 3 5 2 3 5 3 .5 45 c) 7 2 à v 72 ta có: 2
7 2 7 .2 98 do 98 72 98 72 7 2 72 d) 5 7 à v 4 8 ta có: 2 5 7 5 .7 175
do 175 128 175 128 5 7 4 8 2 4 8 4 .8 128
Bài 3: Đưa nhân tử vào trong dấu căn và rút gọn: a 2a a) 2 a 2 a 2
2a a 22
2a a 2 2 a 0 a 2 x
b) x 5 0 x 5 2 25 x x 5 x2 x 5 x x
5 x.5 x 5 x 5 0 a b 3a c) 0 a b 2 2 b a
3a a b2
3a b a2
3a b a a b 0 2 2 b a
b a.b a b a
Dạng 2: Thực hiện phép tính và rút gọn biểu thức
Bài 4: Thực hiện phép tính:
a) 125 4 45 3 20 80 ... 5 5 12 5 6 5 4 5 5 5 27 48 2 75 3 4 2 5 7 b) 2 ... 2. 3 3 . 3 ... 3 4 9 5 16 2 3 5 4 6 9 49 25 3 1 1 5 1 7 1 7 2 c) 2 ... 2. . 7. . ... . 8 2 18 2 2 2 3 2 3 2 6 Trang 13 1 1 2 2 d ) 5 20 3 12 15 4 27
5 4 5.2 5 3.2 3 15. 5 4.3 3 5 4.54 5 5
10 5 6 3 3 5 12 3
9 13 5 18 3 3 13 5 17 3 e)
7 4 3 28 10 3 2 32 5 32 2 3 5 3 7
Bài 5: Rút gọn biểu thức với giả thiết các biểu thức chữ đều có nghĩa: x x y y a) xy
x 0; y 0 x y x
y . x xy y
xy x xy y xy x 2 xy y x y 2 x y a a b a ab a b) ;ab 0 b ab
b b a b
x y y x. x y c)
x 0; y 0 xy
xy. x y . x y
x y . x y x y xy d ) A
x 2 2 x 2 x 2 2 x 2 x 2 x 2. 2 x 2 x 2. 2
x 2 2 x 2. 2 2 x 2 2 x 2. 2 2
x 2 22 x 2 22 x 2 2 x 2 2
- nếu x 2 2 x 2 2 x 4
A x 2 2 x 2 2 2 x 2
- nếu x 2 2 x 2 2 x 4
A x 2 2 x 2 2 2 2
Dạng 3: Trục căn thức ở mẫu
Bài 6: Trục căn thức ở mẫu 12.3 3 12.3 3 12 a) 3 3 3 3.3 3 2.3 3 9 3 8. 5 2 8. 5 2 8 b) 5 2 5 2. 5 2 8. 5 2 5 4 14. 10 3 14. 10 3 14 c) 10 3
10 3. 10 3 2. 10 3 10 3 7 35 11.8 37 11 7 3 5 11
16849 3340 33385 9 33217 d) 8 3 7 11
8 37 11.8 37 11 192 539 3 37 Trang 14 3 52 2.2 5 3 2 3 5 2 2
309 10 4 10 12 185 10 e) 2 5 3 2
2 5 3 2.2 5 3 2 20 18 2
Bài 7: Trục căn thức ở mẫu và thực hiện phép tính: 5 1 6 7 5 a) 4 11 3 7 7 2 2 5.4 11 6. 7 2 3 7 7 5
4 11.4 11 3 7 .3 7 7 2. 7 2 2 5.4 11 6. 7 2 5. 4 11 6. 7 2 3 7 7 5 3 7 7 5 16 11 9 7 7 4 2 5 2 3 2 3 7 7 5 4 11
2 7 2 4 11 4 7 2 7 4 4 11 3 7 2 4 3 2 3 1 b) 5 2 5 2 3 2 6 4 5 2 3. 5 2 2. 3 2 3 1
5 2 . 5 2 5 2. 5 2 3 2. 3 2 6
4 5 2 3. 5 2 2. 3 2 4 5 2 3 1 3 1 3. 5 2 2. 3 2 5 2 5 4 3 4 6 3 6
8 5 2 18. 5 2 12. 3 2 3 1 8 5 8 2 18 5 36 12 3 24 3 1 6 6 26 5 8 2 13 3 59 6
***********************************************************
Ngày dạy: ………………………..
RÚT GỌN BIỂU THỨC CHỨA CĂN THỨC BẬC HAI.
ÔN TẬP ĐẠI SỐ - CHƯƠNG I A. Kiến thức cơ bản
Để rút gọn biểu thức có chứa căn thức bậc hai, ta cần vận dụng thích hợp các phép biến đổi đã biết. B. Bài tập áp dụng Bài 1: Tính 2 2
a) 3 2 2 6 4 2 2 1
2 2 2 12 2 2 2 1 b) 5 3 29 12 5
5 3 2 5 32 5 3 2 5 3 5 6 2 5 5 5 2 1 5 5 1 1 c)
6 2 5 29 12 5 6 2 5 2 5 3 9 3 d ) 2 5 13 48 2 5 13 4 3 2 5 2 3 2 1 2 5 2 3 1
2 4 2 3 2 3 2 1 2 3 1 1 3 Trang 15
Bài 2: Thực hiện phép tính, rút gọn kết quả
a) 2 20 45 3 18 3 32 50 4 5 3 5 9 2 12 2 5 2 5 16 2 1 1 1 2 1 17 10 b) 32 0,5 2 48 4 2 2 3 2 4 3 ... 2 3 3 8 2 3 4 4 3 1 1 c)
4,5 12,5 0,5 200 242 6 1 24,5 2 8 1 9 25 1 9 49 2 2 2 10 .2 11 .2 6 2 2 2 2 8 2 1 3 5 3 7 2 2 2 5 2 11 2 6. 2 2 2 2 2 4 2 1 3 5 3 7 13 5 11 6. 2 2 2 2 2 4 2 2 3 2 3 2 d ) 6 2 4 .3 12 6 2 3 2 3 3 2 1 6 6 2 6 . 6 2 3 6 6. 2 3 3 2 3 6
Bài 3: Chứng minh đẳng thức a b a b 2b 2 b a) 2 a 2 b 2 a 2 b b a a b
Biến đổi vế trái ta được: a b a b 2b a b a b 2b VT 2 a 2 b 2 a 2 b b a
2 a b 2 a b a b . a b
a b2 a b2 4b a2 ab ba2 ab b4b 4 ab 4b
2 a b a b
2 a b a b
2 a b a b
4 b a b 2 b VP
2 a b a b a b 2 3 6 216 1 3 b) . 8 2 3 6 2
Biến đổi vế trái ta được: 6 2 1 2 3 6 216 1 6 6 1 VT . 8 2 6 2 2 . 3 1 3 6 6 1 3 1 3 2 6 . 6. VP 2 6 2 6 2
a b2 4 ab a b b a
Bài 4: Cho biểu thức A a b ab
a) Tìm điều kiện để A có nghĩa
b) Chửng tỏ rằng giá trị của biểu thức A không phụ thuộc vào a LG
a) đk: a > 0; b > 0; a khác b b) ta có: Trang 16
a b2 4 ab 2 4 ab a b a b b a a ab b ab A a b ab a b ab 2 2
a b a b a ab b
a b a b a b 2 b a b a b x x x
Bài 5: Cho biểu thức 2 1 1 B : x x 1 x 1 x x 1 a) Tìm đk xác định b) Rút gọn biểu thức B LG
a) đk: x 0; x 1 b) Ta có: 2 x x 1 x 1 2 x x 1 x 1 B : x x x x x x
1 x x : 1 1 1 1 x 1 x x 1
2 x x x x 1 x x 1 x 1 1 1 x
1 x x . . 1 x 1 x 1 x 1 x 1 x x x x x
Bài 6: Cho biểu thức 3 3 2 9 C 1 : x 9 2 x 3 x x x 6
a) Tìm đk để C có nghĩa b) Rút gọn C c) Tìm x để C = 4 LG
a) đk: x 0; x 4; x 9 b) Ta có:
x 3 x x 3 x 2 9 x C 1 : x 9 2 x 3 x x x 6
x x 3 3 x x 2 9 x 1
x 3 x 3 : x 2 x 3
x 2 x 3
3 x 3 x x 22 9 x 9 x x 22 9 3 x x x x 1 x 3 :
x 2 x 3 : x 3
x 2 x 3
x 2 x 3 3 3 . x 3 x 2 x 2 2 3 3 11 121 c) C = 4
4 x 2 x x x 2 4 4 16 x x x
Bài 7: Cho biểu thức 9 3 1 1 D : 3 x 9 x x 3 x x a) Tìm đk b) Rút gọn c) Tìm x sao cho D < -1 LG a) đk: x > 0; x khác 9 b) Ta có: Trang 17 x
x 9 3 x 1 1 x x 9 3 x 1 1 D : 3 x x x 3 x x 3 x
3 x3 x : 9 x
x 3 x
x 3 x x 9 2 x x x x 2 3 1 3 3 9
x x : x x
x x : 3 3 3 3 3
x x 3 3 x 3 x x 3 3 x 3
x 3 x . 2 x 2 2 x 4 3 x c) D 1 1
3 x 2 x 4 x 4 x 16 2 x 4 0 2 x 4
********************************************************
Ngày dạy: ……………………..
HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG A. Kiến thức cơ bản 1. Các hệ thức
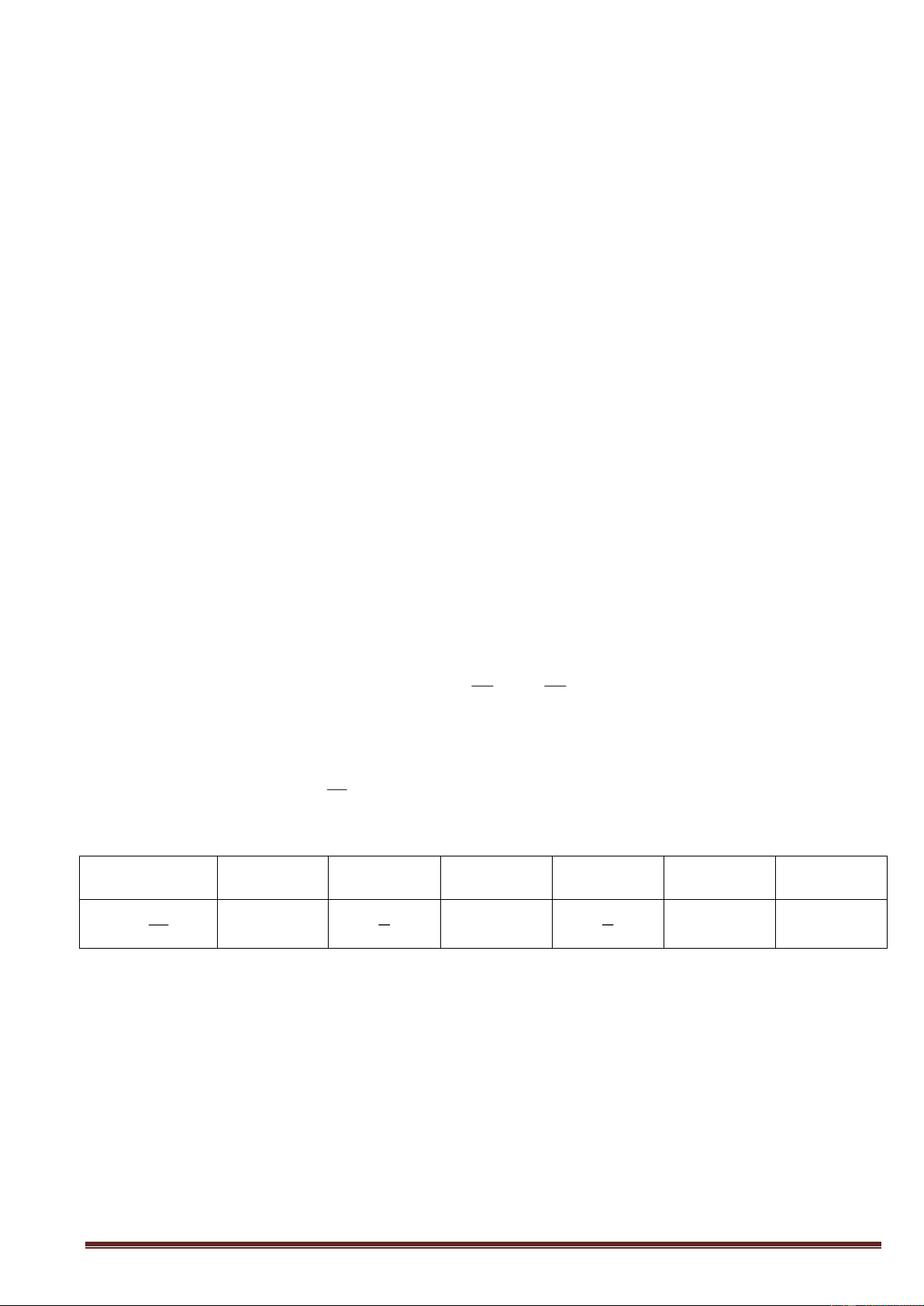
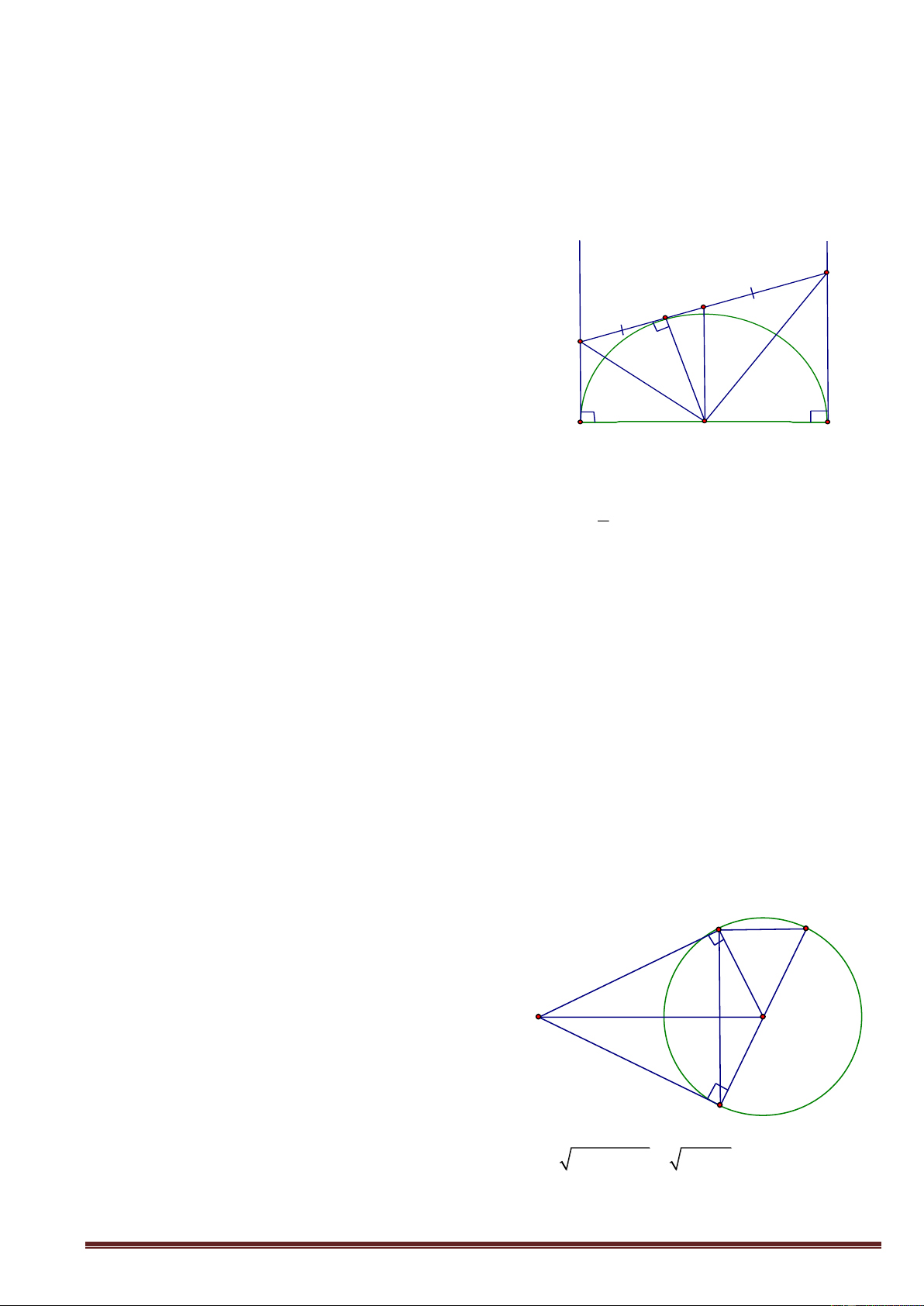
* Định lý: Trong 1 tam giác vuông, mỗi cạnh góc vuông bằng: C
- Cạnh huyền nhân Sin góc đối hoặc Cosin góc kề
- Cạnh góc vuông kia nhân Tang góc đối hoặc Cotg góc kề
(trong tam giác ABC vuông tại A, BC = a; AB = c; AC = b, ta a b có: b . a sin B . a cos C b . c tgB . c cot gC 1 2 c . a sin C . a cos B c . b tgC . b cot gB B A c
2. Áp dụng giải tam giác vuông
* Giải tam giác vuông: là tìm tất cả các yếu tố của một tam giác vuông (các cạnh, các góc) nếu biết trước
2 yếu tố trong đó có ít nhất 1 yếu tố về cạnh và không kể góc vuông
* Một số trường hợp giải tam giác vuông thường gặp
a) Biết 2 cạnh góc vuông
- Tính cạnh huyền (theo Pi-ta-go)
- Tính một góc nhọn (tg hoặc cotg)
- Tính góc nhọn còn lại (2 góc phụ nhau)
b) Biết cạnh huyền và 1 góc nhọn
- Tính góc nhọn còn lại (2 góc phụ nhau)
- Tính các cạnh góc vuông (hệ thức về cạnh và góc – hệ thức (1))
c) Biết cạnh góc vuông và góc nhọn kề
- Tính góc nhọn còn lại
- Tính cạnh góc vuông còn lại và cạnh huyền (hệ thức về cạnh và góc – hệ thức (1); (2))
B. Bài tập áp dụng
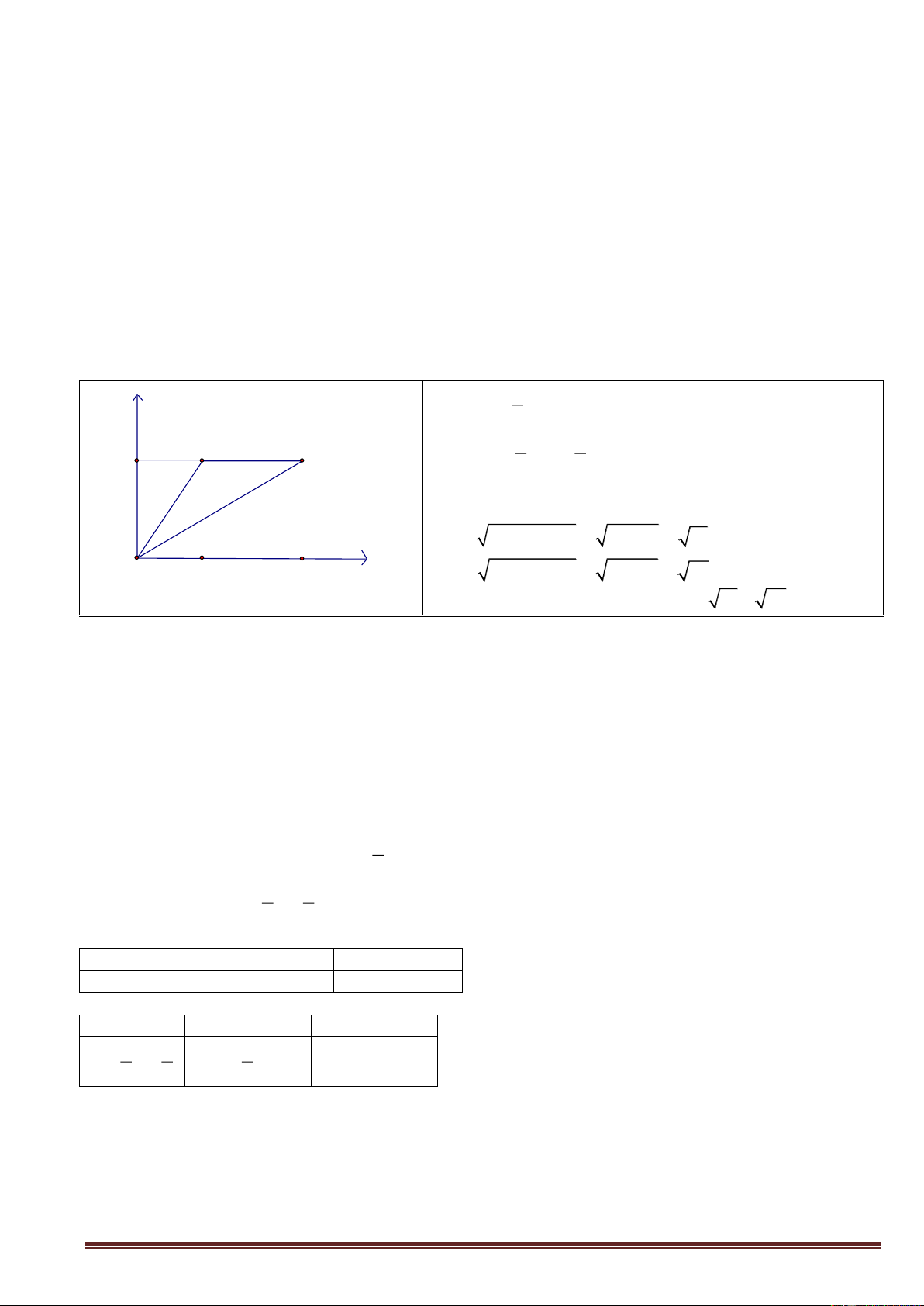
Bài 1: Cho tam giác ABC vuông tại A, biết 4 tgB và BC = 10. Tính AB; AC 3 B 4 - 0 ' tgB B 53 07 3 10
- theo hệ thức về cạnh và góc trong tam giác vuông 0 '
AB BC cos B 10.cos 53 07 6 0 ' A C
AC BC.sin B 10.sin 53 07 8
Bài 2: Cho tam giác ABC cân tại A; AB = AC = 17; BC = 16. Tính đường cao AH và góc A, góc B của tam giác ABC Trang 18 A A 1 2 A
+ tam giác ABC cân, có AH BC BC BH CH 8 2 1 2
+ xét tam giác AHC, vuông tại H 17 17 - ta có: 2 2 2 2 AH
AC CH 17 8 15 CH 8 - mặt khác: 0 ' 0 ' sin A A A 28 04 A
2A 56 08 2 2 1 2 AC 17 B C
+ xét tam giác AHB vuông tại H, ta có: 16 0 0 0 ' 0 ' B 90 A 90 28 04 61 56 1
Bài 3: Cho tam giác ABC có AB = 11, 0 0 A
BC 38 ; A
CB 30 . Gọi N là chân đường vuông góc kẻ từ A đến BC. Tính AN; AC
- xét tam giác ANB vuông tại N, theo hệ thức về cạnh và góc A
trong tam giác vuông ta có: 0 AN A .
B sin B 11.sin 38 6, 77 11
- xét tam giác ANC vuông tại N, theo hệ thức về cạnh và góc 380 300 B C N
trong tam giác vuông ta có: AN 6, 77
AN AC.sin C AC 13,54 0 sin C sin 30
Bài 4: Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 9; HC = 16. Tính góc B, góc C? A
- xét tam giác ABC vuông tại A, theo hệ thức về cạnh và đường
cao trong tam giác vuông , ta có: 2
AH BH .CH 9.16 144 AH 12
- xét tam giác AHB, vuông tại H, ta có: AH 12 0 ' tgB B 53 7 BH 9 - mà 0 0 ' B C 90 C 36 53 9 B H 16 C
Bài 5: Cho tam giác ABC có 0 B
60 , các hình chiếu vuông góc của AB và AC lên BC theo thứ tự bằng
12 và 18. Tính các góc và đường cao của tam giác ABC A
- xét tam giác AHB vuông tại H 1 0 0 1 2 B 60 A 30 BH AB 2
AB 2BH 2.12 24 2 2 2 2
AH AB BH 24 12 20,8
- xét tam giác AHC, theo hệ thức lượng… 600 AH 20,8 B 12 H 18 C 0 ' tgC C 49 06 HC 18 0 A 180 B C 0 ' 70 54
- theo hệ thức về cạnh và góc, ta có: HC 18
HC AC.cos C AC 27,5 0 ' cos C cos 49 06
Bài 6: Cho hình thang ABCD, có 0 A
D 90 , đáy nhỏ AB = 4, đáy lớn CD = 8, AD = 3. Tính BC, B , C ? Trang 19
- kẻ BH vuông góc với CD, suy ra AD = BH = 3; A 4 B
AB = DH = 4, do đó: CH = 8 – 4 = 4
- xét tam giác BHC vuông tại H, ta có: 3 2 2 2 2 BC
BH CH 3 4 5 BH 3 0 sin C C 37 H D C BC 5 8
- vì ABCD là hình thang nên: 0 0 0 0 0 B C 180 B 180 C 180 37 143
Bài 7: Giải các tam giác vuông sau, tam giác ABC vuông tại A biết: a) a = 18; b = 8 B b) b = 20; 0 C 38 3 c) tgB ; c 4 a c 4 b C A a) a = 18; b= 8 AC 8 0 ' 0 0 ' 0 ' sin B B 23 23 C 90 23 23 63 37 BC 18 0 '
AB BC.sin C 18.sin 63 37 16,1 b) b = 20; 0 C 38 AC 20 0 0 0 C 38 B 52 ;
AB AC.tgC 20.tg38 15, 6; BC 25, 4 0 sin B sin 52 3 c) tgB ; c 4 4 3 2 2 2 2
AC ABtgB 4. 3; BC
AB AC 3 4 5 4 c 4 0 ' 0 ' sin C
0,8 C 53 08 B 36 52 a 5
*********************************************************
Ngày dạy: ……………………………
ÔN TẬP HÌNH HỌC – CHƯƠNG I A. Kiến thức cơ bản
1. Các hệ thức về cạnh và đường cao trong tam giác vuông
Cho tam giác ABC vuông tại A, đường cao AH sao cho ta có : ' ' AH ,
h BC a, AB , c AC ,
b BH c , CH b khi đó : 2 ' 2 ' 1) b . a b ; c . a c 2 ' ' A
2) h b .c 3) . b c . a h b c h 1 1 1 4) 2 2 2 h b c c' b' B 2 2 2
5) a b c (Pitago) H C a
2. Định nghĩa các tỉ số lượng giác của góc nhọn Trang 20 Cho 0 0 ABC
(0 90 ) ta định nghĩa các tỉ số giữa các cạnh AB, BC, CA của tam giác ABC vuông tại A như sau : C AC AB sin ; cos BC BC Huyền AC AB Đối tg ; cot g AB AC A B Kề
3. Một số tính chất của các tỉ số lượng giác si n cos ; cos sin - Nếu 0
90 thì ta có : t
g cot g;
cot g tg - Cho 0 0 0 90 . Khi đó + 0 < sin, cos < 1 + 2 2 sin cos 1 sin cos 1 + tg ; cot g ; cot g
;tg.cot g 1 cos sin tg
4. Các hệ thức về cạnh và góc trong tam giác vuông
- Cho tam giác ABC vuông tại A, BC = a; AB = c; AC = b, ta C có: b . a sin B . a cos C b . c tgB . c cot gC 1 2 a c . a sin C . a cos B c . b tgC . b cot gB b B A c B. Bài tập áp dụng
Bài 1 : Chứng minh rằng : với là góc nhọn tương ứng trong tam giác ABC, 0 A 90 thì: 4 4 2
a) cos sin 2 cos 1 2 3
b) sin sin .cos sin 2 2 2 2
c) tg sin .tg sin 2 2 2
d ) cos tg .cos 1 LG a VT 2 2 2 2 2 2 2 2 2 ) cos sin . cos sin cos sin cos 1 cos
2cos 1 VP
b) VT sin . 2 1 cos 2 3
sin.sin sin VP 2 sin 2 2 2 2 2 2
c) VT tg .(1 sin ) tg .cos
.cos sin VP 2 cos
d ) VT cos .1 tg 2 2 2 sin cos sin 2 2 2 2 cos .1 cos . 1 VP 2 2 cos cos
Bài 2 : Cho tam giác ABC, biết AB = 21 ; AC = 28 ; BC = 35 Trang 21
a) Chứng minh rằng tam giác ABC vuông
b) Tính sinB, sinC, góc B, góc C và đường cao AH vủa tam giác ABC LG 2 2 2 2
AB AC 21 28 1225 2 2 2 a) ta có:
BC AB AC do đó theo 2 2 BC 35 1225
định lý đảo của định lý Pi-ta-go tam giác ABC vuông tại A B b) H AC 28 35 0 sin B 0,8 B 53 21 BC 35 AB 21 0 sin C 0,6 C 37 BC 35 28 C A
Xét tam giác AHB vuông tại H, áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có: 0 AH A .
B sin B 21.sin 53 21.0,8 16,8 (hoặc AH.BC = AB.AC)
Bài 3: Giải tam giác vuông tại A, biết a) a = 12; 0 B 42 b) b = 13; c = 20 LG - ta có: C 0 0 0 0 C 90 B 90 42 48 0 12
AB BC.cos B 12.cos 42 9 0
AC BC.cos C 12.cos 48 8 420 B A - ta có: C 2 2 2 2 BC AB AC 20 13 23,85 AC 13 13 0 tgB 0,65 B 33 AB 20 0 0 C 90 B 57 B A 20
Bài 4: Cho tam giác ABC có 0 B
60 các hình chiếu vuông góc của AB, AC lên BC theo thứ tự bằng
12; 18. Tính các cạnh, các góc và đường cao của tam giác ABC LG
+ ta có: BC = BH + CH = 12 + 18 = 30
+ xét tam giác AHB vuông tại H A - ta có : 0
AH BH.tgB 12.tg60 12 3 - mặt khác : 1 2 BH 12 BH A .
B cos B AB 24 0 cos B cos 60 0 0 0 0 A 90 B 90 60 30 1 600
+ xét tam giác AHC vuông tại H, ta có : B 12 H 18 2 2 C AC
AH CH ... 756 27, 5 AH 12 3 0 tgC C 49 HC 18 + xét ABC, tcó: 0 A B C 0 180 71
*********************************************************** Trang 22
Ngày dạy: …………………………..
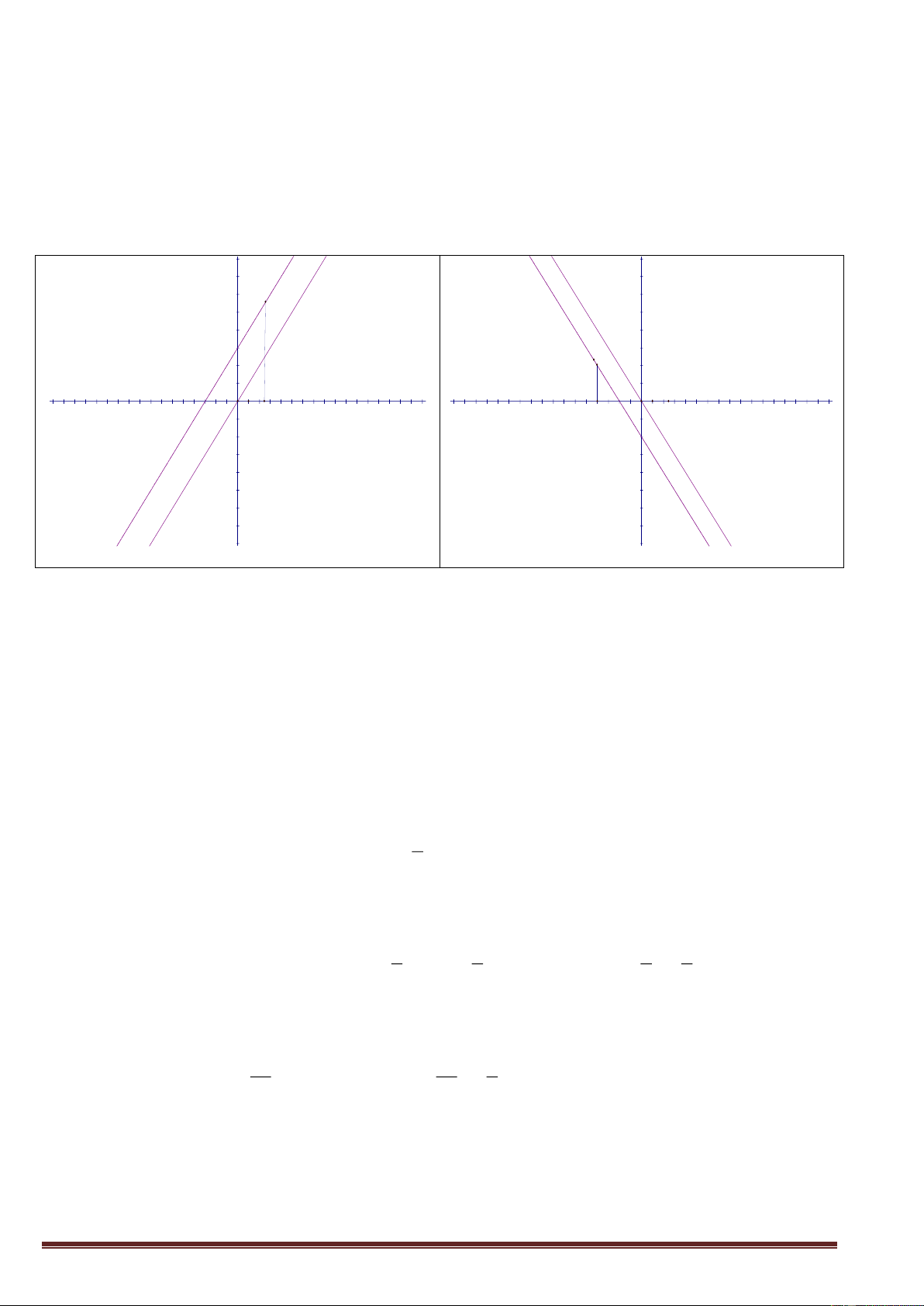
HÀM SỐ BẬC NHẤT. ĐỒ THỊ CỦA HÀM SỐ y ax b a 0 A. Kiến thức cơ bản
1. Định nghĩa hàm số bậc nhất
- Hàm số bậc nhất là hàm số được cho bởi công thức y ax b a 0 , trong đó a, b là các số cho trước
2. Tính chất của hàm số bậc nhất : Hàm số bậc nhất y ax b a 0 xác định với mọi x thuộc R và có tính chất sau :
a) Đồng biến trên R, khi a > 0
b) Nghịch biến trên R, khi a < 0
3. Đồ thị của hàm số y ax
- Đồ thị của hàm số y ax là 1 đường thẳng đi qua gốc tọa độ O - Cách vẽ
+ Cho x 0 y a A0;a
+ Đường thẳng đi qua gốc tọa độ O và A(0 ; a) là đồ thị hàm số y = ax
4. Đồ thị của hàm số y ax b a 0
- Đồ thị của hàm số y ax b a 0 là 1 đường thẳng
+ Cắt trục tung tại điểm có tung độ bằng b
+ Song song với đường thẳng y = ax nếu b khác 0; trùng với đường thẳng y = ax nếu b = 0
- Chú ý : Đồ thị của hàm số y ax b a 0 còn được gọi là đường thẳng y ax b a 0 b được
gọi là tung độ gốc của đường thẳng * Cách vẽ : 2 bước
- Bước 1 : Tìm giao của đồ thị với 2 trục tọa độ
+ Giao của đồ thị với trục tung : cho x 0 y b A0;b
+ Giao của đồ thị với trục hoành b b
: cho y 0 x B ; 0 a a
- Bước 2 : Vẽ đường thẳng đi qua 2 điểm A ; B ta được đồ thị hàm số y ax b a 0
B. Bài tập áp dụng
Bài 1 : Cho hàm số y f x 1
x 3 . Tính f(0) ; f(1) ; f(-1) ; f(2) ; f(-2) ; f(8) 2 LG
- Lập bảng giá trị tương ứng của x và f(x) -2 -1 0 1 2 8 x -4 7 3 5 2 -1 f x 1 x 3 2 2 2
Bài 2: Biểu diễn các điểm sau trên mặt phẳng tọa độ? A(-3; 2), B(1; 4), C(-5; 0), D(0; 3), E(-1; -4) LG Trang 23 y B 4 D 3 A 2 1 C -1 x -5 -3 O 1 2 -2 E -4
Bài 3: Tìm m để hàm số sau là hàm số bậc nhất?
a) y m 4 x 2009
b) 2m 3 x 2m 1 m 2 c) y x 4
d ) y 3 m.x 5 3 m m 2 LG
a) ...... m 4 0 m 4 3
b) ...... 2m 3 0 m 2 m 2 m 2 0 m 2 c) ...... 0 m 2 m 2 0 m 2
d ) ...... 3 m 0 3 m 0 m 3
Bài 4: Cho hàm số y = (m – 5)x + 2010. Tìm m để hàm số trên là a) hàm số bậc nhất
b) hàm số đồng biến, nghịch biến LG
a) ...... m 5 0 m 5
b) hàm số đồng biến m – 5 > 0 m > 5
- hàm số nghịch biến m – 5 < 0 m < 5
Bài 5 : Cho hàm số y 2
m 5m 6 x 2 . Tìm m để
a) hàm số trên là hàm số bậc nhất
b) hàm số đồng biến, nghịch biến
c) đồ thị hàm số đi qua điểm A(1 ; 4) LG m 2 0
a) hàm số đã cho là hàm số bậc nhất 2
m 5m 6 0 m 2m 3 0 m 3 0 m 2 0 m 2 m 3 0 m 3 m 3 b) hàm số đồng biến 2
m 5m 6 0 m 2m 3 0 m 2 0 m 2 m 2 m 3 0 m 3 *) hàm số ngh.biến Trang 24 m 2 0 m 2 m 3 0 m 3 2 m 3 2
m 5m 6 0 m 2m 3 0 m 2 0 m 2 kotm m 3 0 m 3
c) vì đồ thị hàm số đi qua A(1 ; 4) nên : 2 m m 2 4 5
6 .1 2 m 5m 4 0 m 1 m 4 0 m 1 0 m 1 m 4 0 m 4
Bài 6 : Vẽ tam giác ABO trên mặt phẳng tọa độ Oxy. Biết O(0 ; 0) , A(2 ; 3), B(5 ; 3)
a) Tính diện tích tam giác ABO b) Tính chu vi tam giác ABO LG y 1 a) S A .
B OD trong đó OD = 3; AB = 3 ABO 2 1 9 D A B S .3.3 3 ABO 2 2
b) xét tam giác AOD và tam giác BOD. Theo Pi-ta-go ta có: 1 2 2 2 2
OA OD AD 3 2 13 x O 2 5 E 2 2 2 2
OB OD BD 3 5 34 Chu vi: C
AB AO BO 3 13 34 ABO
Bài 7: Cho hàm số y = (m-1).x + m
a) Xác định m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2
b) Xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3
c) Vẽ đồ thị của 2 hàm số ứng với giá trị của m vừa tìm được ở câu a) và b) trên cùng mặt phẳng tọa độ Oxy LG
a) hàm số y = (m-1).x + m có tung độ gốc b = m
- vì đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2, nên m = 2
- hàm số có dạng : y = x + 2
b) vì đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng -3, nên tung độ của điểm này bằng 0, ta có :
m 3 0 1
3 m 2m 3 m 2 1 3
- hàm số có dạng : y x 2 2 c) x 0 -2 y = x + 2 2 0 x 0 -3 1 3 3 0 y x 2 2 2 Trang 25 8 6 3 3 f x = x+ 2 2 4 2 -15 -10 -5 5 10 15 -2 gx = x+2 -4 -6 -8
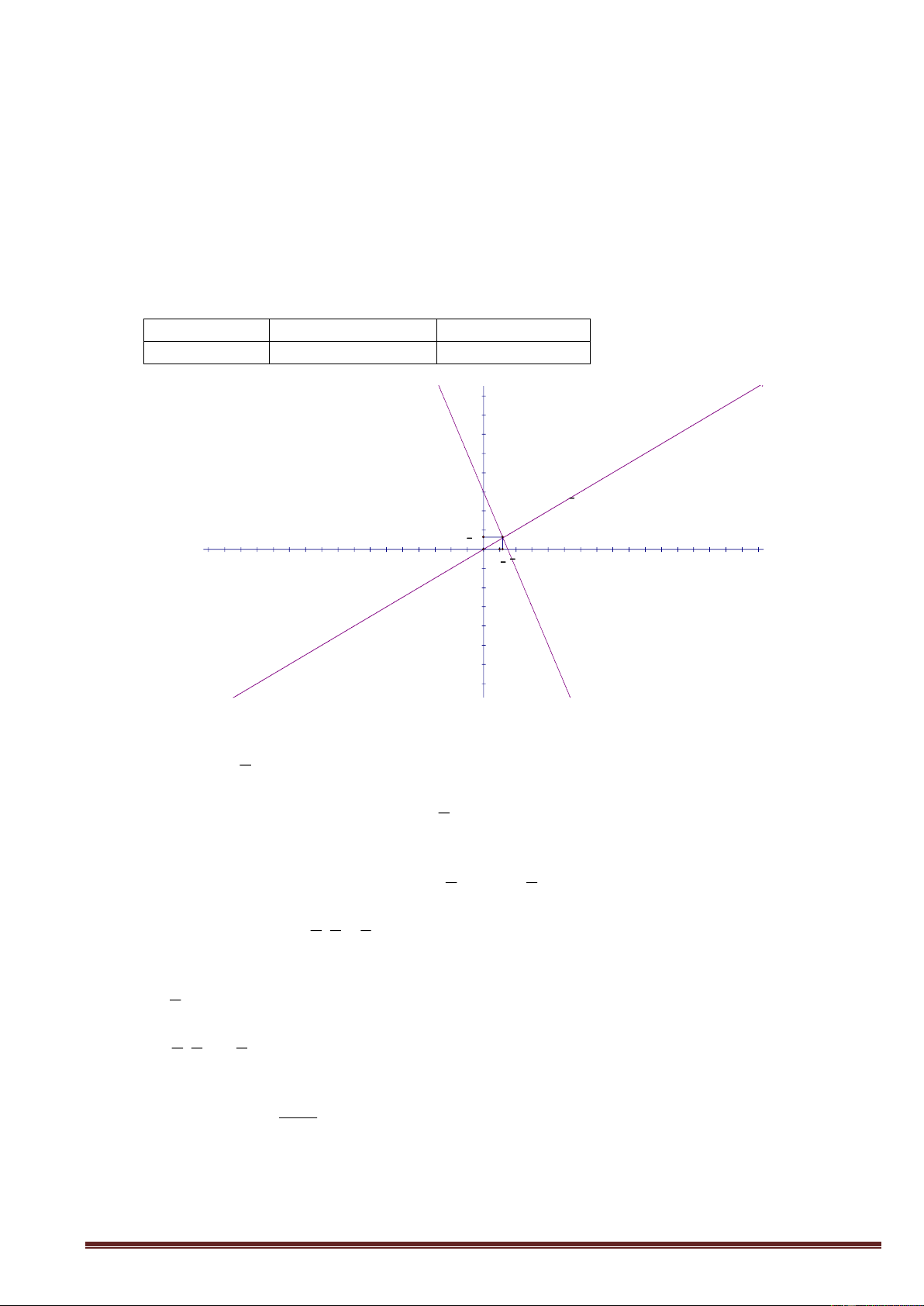
Bài 8 : Cho các hàm số : y = x + 4 ; y = -2x + 4
a) Vẽ 2 đồ thị hàm số trên cùng mặt phẳng tọa độ
b) 2 đường thẳng y = x + 4 ; y = -2x + 4 cắt nhau tại C và cắt trục hoành theo thứ tự tại A và B. Tính chu
vi và diện tích của tam giác ABC LG
a) Vẽ 2 đồ thị hàm số trên cùng mặt phẳng tọa độ
* Bảng các giá trị của x và y là : +) hàm số y = x + 4 x 0 -4 y = x + 4 4 0 +) hàm số y = -2x + 4 x 0 2 y = -2x + 4 4 0 8 6 gx = -2x+4 f x = x+4 4 C 2 A B -20 -15 -10 -5 5 10 -4 2 -2 -4 -6 1 b) S A .
B CO trong đó AB = 6; CO = 4 1 S .6.4 12 ABC 2 ABC 2
xét tam giác vuông AOC và tam giác vuông BCO. Theo Pi-ta-go, ta có: 2 2 2 2
AC OA OC 4 4 4 2 2 2 2 2
BC OB OC 2 4 2 5 Chu vi: C
AB AC BC 6 4 2 2 5 ABO
***************************************************** Trang 26
Ngày dạy: …………………………….
SỰ XÁC ĐỊNH ĐƯỜNG TRÒN. TÍNH CHẤT ĐỐI XỨNG CỦA ĐƯỜNG TRÒN A. Kiến thức cơ bản
1. Định nghĩa của đường tròn: Đường tròn tâm O, bán kính R, ký hiệu: (O; R) là tập hợp các điểm cách O một khoảng bằng R.
2. Vị trí tương đối của 1 điểm đối với đường tròn: Cho (O; R) và 1 điểm M trong cùng 1 mặt phẳng
- điểm M nằm trên (O) OM = R
- điểm M nằm bên trong (O) OM < R
- điểm M nằm bên ngoài (O) OM > R
3. Sự xác định đường tròn
- Định lý: Qua 3 điểm không thẳng hàng ta vẽ được 1 và chỉ 1 đường tròn. - Chú ý:
+ tâm của đường tròn đi qua 3 điểm không thẳng hàng là giao điểm của các đường trung trực của tam giác
ABC. Đường tròn đi qua 3 điểm không thẳng hàng A, B, C được gọi là đường tròn ngoại tiếp tam giác
ABC ay tam giác ABC nội tiếp đường tròn.
+ không vẽ được đường tròn nào đi qua 3 điểm thẳng hàng.
+ để chứng minh nhiều điểm cùng nằm trên 1 đường tròn, ta chứng minh các điểm ấy cùng cách đều 1
điểm cố định. Điểm cố định ấy là tâm của đường tròn, khảng cách đều ấy là bán kính của đường tròn. B. Bài tập áp dụng
Bài 1: Cho tam giác ABC vuông tại A. Trên AB, AC lần lượt lấy các điểm D, E. Goik M, N, P, Q lần lượt
là trung điểm của DE, EB, BC, CD. CMR: 4 điểm M, N, P, Q cùng thuộc 1 đường tròn. LG A D M E N Q B P C + Xét tam giác EDB, ta có: ME MD
MN là đường trung bình của EDB, suy ra MN // = ½ B (1) hay MN//AB NE NB
+ Xét tam giác BCD, ta có : QC QD
PQ là đường trung bình của tam giác BCD, suy ra PQ // = ½ BD (2) PC PB
+ Từ (1) và (2) => MN // = PQ => tứ giác MNPQ là hình bình hành (*)
+ Xét tam giác CDE, ta có : MD ME
MQ là đường trung bình của CDE, suy ra MQ // CE => MQ // AC QD QC MQ / / AC + Ta có : 0 MN / / AB
MQ MN M 90 (**) à m AC AB
+ Từ (*) và (**) => tứ giác MNPQ là hình chữ nhật, gọi O là giao điểm của MP và NQ => OM = ON =
OP = OQ => 4 điểm M, N, P, Q cùng thuộc 1 đường tròn.
Bài 2 : Chứng minh định lý sau :
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu 1 tam giác có 1 cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông. LG Trang 27 A A B C B O C O
Vì tam giác ABC nọi tiếp đường tròn tâm O có
Xét tam giác ABC vuông tại A. Gọi O là trung đường kính BC => OA = OB = OC
điểm của BC => OA = OB = OC (vì AO là trung => OA = ½ BC
tuyến của tam giác) => O là tâm của đường trong => tam giác ABC vuông tại A. ngoại tiếp tam giác ABC.
Bài 3 : Cho tam giác ABC nhọn, vẽ đường tròn (O ; ½ BC) cắt các cạnh AB, AC theo thứ tự tại D và E
a) Chứng minh rằng : CD vuông góc với AB ; BE vuông góc với AC.
b) Gọi K là giao điểm của BE và CD. Chứng minh rằng : AK vuông góc với BC. LG A E D K B C O
a) Theo bài 2, tam giác BCD và tam giác BCE có cạnh BC là đường kính => tam giác BCD vuông tại D
(=> CD vuông góc với AB) và tam giác BCE vuông tại E (=> BE vuông góc với AC)
b) Xét tam giác ABC, ta có : BE AC CD AB
K là trực tâm của tam giác ABC => AK vuông góc với BC à
m BE CD K
Bài 4 : Cho tam giác ABC, góc A > 900. Gọi D, E, F theo thứ tự là chân các đường cao kẻ từ A, B, C. Chứng minh rằng:
a) Các điểm A, D, B, E cùng nằm trên 1 đường tròn.
b) Các điểm A, D, C, F cùng nằm trên 1 đường tròn.
c) Các điểm B, C, E, F cùng nằm trên 1 đường tròn. LG F E A N M D I C B
a) gọi M là trung điểm của AB 1 xét tam giác ADB, 0 D
90 MA MB MD AB (1) 2 1 xét tam giác AEB, 0 E
90 MA ME MB AB (2) 2 Trang 28
từ (1) và (2) => MA = MB = MD = ME => các điểm A, D, B, E cùng nằm trên 1 đường tròn.
b) gọi N là trung điểm của AC.
xét tam giác ADC vuông tại D và tam giác AFC vuông tại F, ta có: DN, FN lần lượt là trung tuyến ứng
với cạnh huyền BC => NA = ND = NC = NF => A, D, C, F cùng nằm trên 1 đường tròn.
c) gọi I là trung điểm của BC.
(chứng minh tương tự)
Bài 5: Cho tam giác ABC có AB = AC nội tiếp đường tròn tâm O, đường cao AH của tam giác cắt đường tròn (O) tại D.
a) Chứng minh rằng AD là đường kính của đường tròn tâm O. b) Tính góc ACD?
c) Cho BC = 12cm, AC = 10cm. Tính AH và bán kính của đường tròn tâm O. LG
a) + vì AB = AC => tam giác ABC cân tại A, mà AH vuông góc A
với BC => AH là đường trung trực của BC => AD cũng là trung trực của BC. (1)
+ do tam giác ABC nội tiếp đường tròn tâm O => O thuộc đường trung trực của BC (2) O
+ từ (1) và (2) => O thuộc AD => AD là đường kính của đường tròn (O) B C H
b) theo bài 2 tam giác ACD nội tiếp đường tròn (O) có AD là
đường kính => góc ACD = 900 D 1 1
c) + vì AD BC BH CH BC .12 6 cm 2 2
+ xét tam giác AHC vuông tại H, ta có: 2 2 2 2 2
AC AH CH AH 10 6 8 cm
+ xét tam giác ACD vuông tại C, áp dụng hệ thức về cạnh và đường cao trong tam giác 2 2 AC 10 vuông ta có: 2 AC A . D AH AD
12,5cm => bán kính của đường tròn (O) là AH 8 1 1 R AD .12, 5 6, 25cm 2 2
******************************************************* Trang 29
Ngày dạy: ………………………………
HỆ SỐ GÓC CỦA ĐƯỜNG THẲNG.
ĐƯỜNG THẲNG SONG SONG, ĐƯỜNG THẲNG CẮT NHAU
A. Kiến thức cơn bản
1. Góc tạo bởi đường thẳng y = ax + b (a khác 0) và trục Ox
- Góc tạo bởi đường thẳng y = ax + b (a khác 0) và trục Ox là góc tạo bởi tia Ax và tia AT, trong đó A
là giao điểm của đường thẳng y = ax + b với trục Ox; T là điểm thuộc đường thẳng y = ax + b và có tung độ dương 8 8 6 6 T 4 4 T 2 2 A -15 -10 -5 5 10 15 -15 -10 -5 5 10 15 A y=ax+b y=ax y=ax -2 -2 y=ax+b -4 -4 -6 -6 -8 -8 Trường hợp a > 0 Trường hợp a < 0 - với a > 0 0 0
0 90 , a càng lớn thì càng lớn - với a < 0 0 0
90 180 , a càng lớn thì càng lớn
2. y = ax + b (a khác 0) thì a được gọi là hệ số góc của đường thẳng
3. Với 2 đường thẳng d y ax b v ' d ' '
y a x b ' : à : ; a a 0 , ta có:
d 'd ' '
a a b b
d 'd ' ' / / ;
a a ;b b
d 'd ' a a
d 'd ' . a a 1
- Chú ý: khi a khác a’ và b = b’ thì 2 đường thẳng có cùng tung độ gốc, do đó chúng cắt nhau tại 1 điểm
trên trục tung có tung độ là b B. Bài tập áp dụng
Bài 1: Xác định hệ số góc k của đường thẳng y = kx + 3 – k trong mỗi trường hợp sau:
a) Đường thẳng song song với đồ thị hàm số 2 y x 3
b) Cắt trục tung tại điểm có tung độ bằng 2
c) Cắt trục hoành tại điểm có hoành độ bằng 3 LG
a) Vì đt y = kx + 3 – k song song với đths 2 y 2 x k ptđt có dạng: 2 7 y x 3 3 3 3
b) Vì đths y = kx + 3 – k cắt trục tung tại điểm có tung độ là b = 3 – k, mà theo giả thiết đths cắt trục tung
tại điểm có tung độ bằng 2 nên 3 k 2 k 1ptđt có dạng: y = x+2
c) Vì đt y = kx + 3 – k cắt trục hoành tại đểm có hoành độ bằng 3, nên tung độ tại điểm này bằng 0 3 3 9
ta có : 0 3k 3 k k
ptđt có dạng : y x 2 2 2
Bài 2 : Cho hs bậc nhất : y = ax – 4 (1). Xác định hệ số a trong mỗi trường hợp sau
a) đths (1) cắt đường thẳng y = 2x – 1 tại điểm có hoành độ bằng 2
b) đths (1) cắt đường thẳng y = -3x + 2 tại điểm có tung độ bằng 5 LG
a) Gọi M là giao điểm của đths (1) và đt y = 2x – 1 => tọa độ điểm M thỏa mãn đồng thời cả 2 đt trên
- tung độ của điểm M là y = 2.2 – 1 = 3 => M(2 ; 3) Trang 30
- vid đths (1) đi qua điểm M(2 ; 3), nên ta có : 3 = 2.a – 4 => a = 7/2
b) Gọi N là giao điểm của đths (1) và đt y = -3x + 2 => tọa độ điểm N thỏa mãn đồng thời cả 2 đt trên
- hoành độ của diểm N là 5 = -3x + 2 => x = -1 => N(-1 ; 5)
- vì đths (1) đi qua N(-1 ; 5), nên ta có : 5 = a.(-1) – 4 => a = - 9
Bài 3 : Cho hs : y = -2x + 3 a) Vẽ đths trên
b) Xác định hs có đthị là đt đi qua gốc tọa độ và vuông góc với đt y = -2x + 3
c) Tìm tọa độ giao điểm A của đt y = -2x + 3 và đt tìm được ở câu b)
d) Gọi P là giao điểm của đt y = -2x + 3 với trục tung. Tìm diện tích tam giác OAP LG a) Vẽ đths y = -2x + 3 x 0 3/2 y = -2x + 3 3 0
=> đths y = -2x + 3 đi qua 2 điểm P(0 ; 3), Q(3/2 ; 0) 8 6 fx = -2x+3 4 P 1 g x = x 2 2 A 3 H 5 3 -15 -10 -5 5 10 15 O 6 2 5 -2 -4 -6
b) đt qua gốc tọa độ O có dạng y = ax (a khác 0)
- vì y = -2x + 3 và y = ax vuông góc với nhau nên : -2a = 1 => a = -1/2 1
=> hs có dạng : y x 2
c) tìm tọa độ giao điểm của y = 1 -2x + 3 và y x 2
- gọi A là giao điểm của 2 đt trên => tọa độ điểm A thỏa mãn cả 3 đt trên 1 6
- hoành độ điểm A là nghiệm của pt : 2
x 3 x x 2 5 1 6 3
- tung độ của điểm A là : y . 2 5 5
Vậy giao điểm A của 2 đt trên có tọa độ : A(6/5 ; 3/5) 1 d) S
AH.OP trong đó : AH = 6/5 ; OP = 3 AOP 2 1 6 9 S . .3 (đvdt) AOP 2 5 5 BTVN: m 1
Bài 4 : Cho hàm số : y x m 2 (1) m 1
a) Với gtr nào của m thì (1) là hsbn?
b) Với gtr nào của m thì (1) là hs đồng biến?
c) Với gtr nào của m thì đths (1) đi qua điểm A(1; 2)? LG Trang 31 m 1 m 1 0 a) hs (1) là hsbn 0 m 1 m 1 m 1 0 m 1 0 m 1 m 1 0 m 1 m 1 b) hs (1) đồng biến 0 m 1 m 1 0 m 1 m 1 m 1 0
c) vì đths (1) đi qua A nên tọa độ điểm A thỏa mãn hs (1), ta có: m 1 2
m 2 2(m 1) m 1 m 1 m 2 2
m 2m 1 0 m 1
m 2 m m m 1 2 1 2 0 1 2 1
2 0 m 1 2 Bài 5:
a) Vẽ đt các hs sau trên cùng mặt phẳng tọa độ:
y = 2x (1); y = 0,5x (2); y = - x + 6 (3)
b) Gọi các giao điểm của các đt có pt (3) với 2 đt có pt (1) và (2) theo thứ tự là A và B. Tìm tọa độ của 2 điểm A và B
c) Tính các góc của tam giác OAB LG a) vẽ đt 8 E 6 A 4 B C 2 1 D F -15 -10 -5 O 2 4 5 6 10 15 -2 -4 -6
- đths (1) đi qua điểm O và C(1; 2)
- đths (2) đi qua điểm O và D(2; 1)
- đths (3) đi qua điểm E(0; 6) và F(6; 0)
b) Tìm tọa độ điểm A và B
- hoành độ điểm A thỏa mãn pt: 2x = -x + 6 => x = 2
Thay x = 2 vào (1) ta đc y = 4 => A(2; 4)
- hoành độ điểm B thỏa mãn pt : 0,5x = -x + 6 => x = 4
Thay x = 4 vào (2) ta đc y = 2 => B(4 ; 2) 2 2 OA 2 4 20 c) ta có :
OA OB O AB cân tại O 2 2 OB 2 4 20
Ta lại có : AOB AOx BOx trong đó : 4 2 1 0 ' 0 ' tan AOx
2 AOx 63 26 ; tan BOx BOx 26 34 2 4 2 0 0 ' 180 36 52 0 ' 0 ' 0 ' 0 '
AOB 63 26 26 34 36 52 A B 71 34 2 Trang 32
************************************************** Trang 33
Ngày dạy: ……………………………………
VỊ TRÍ TƯƠNG ĐỐI CỦA ĐƯỜNG THẲNG VÀ ĐƯỜNG TRÒN. A. Kiến thức cơ bản
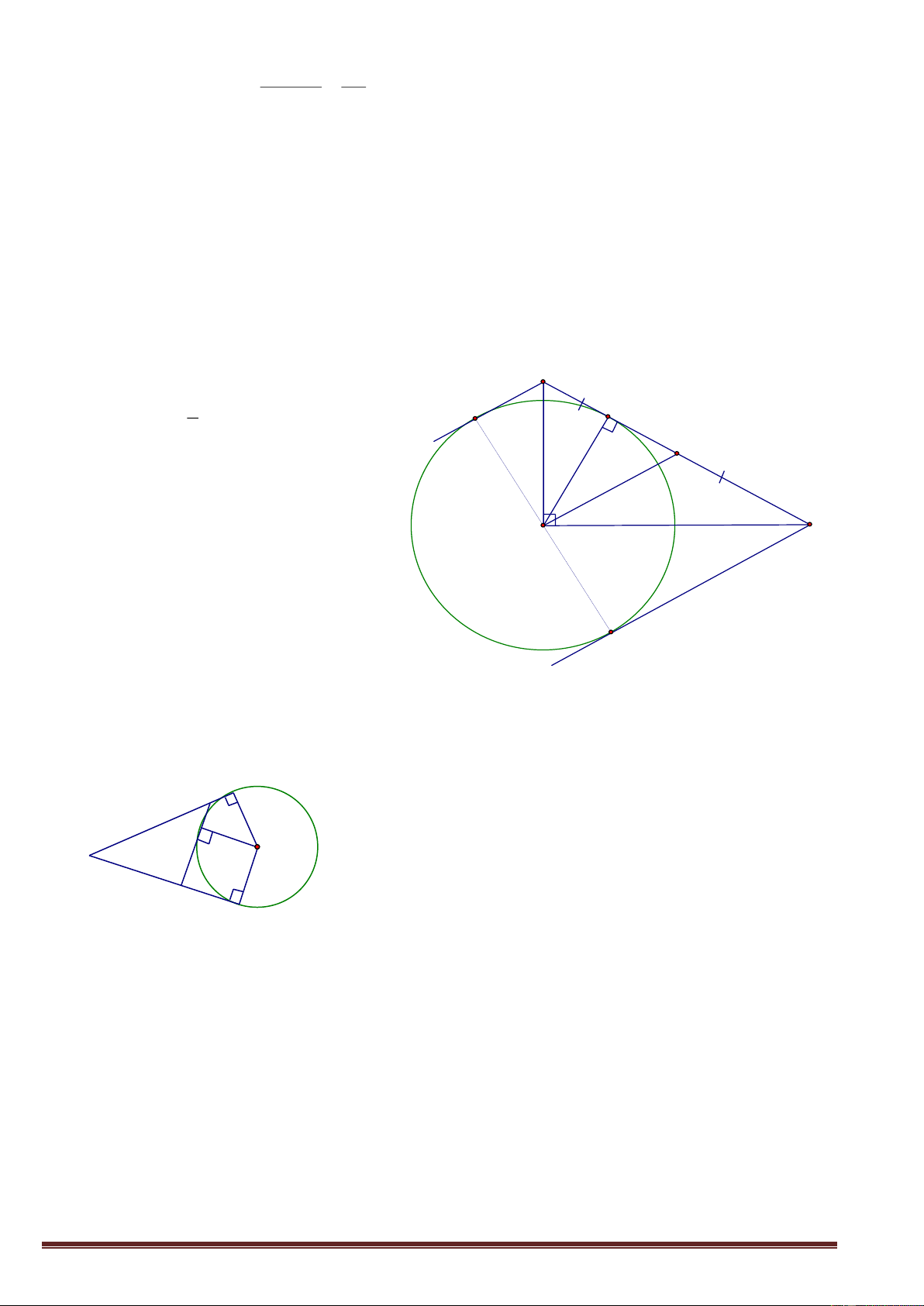
1. Vị trí tương đối của đường thẳng và đường tròn.
Gäi OH =d lµ kho¶ng c¸ch tõ t©m O ®Õn ®-êng th¼ng a.
a; a c¾t (0) 2 ®iÓm chung db; a tiÕp xóc (0) 1 ®iÓm chung d = R
c; a kh«ng giao (0) kh«ng cã ®iÓm chung d >R
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn
Đường thẳng a là tiếp tuyến của đtr (O ; R) d = R (d : là khoảng cách từ tâm O đến a)
Nếu đt a đi qua 1 điểm của đtr và vuông góc với bán kính đi qua điểm đó thì đt a là 1 tiếp tuyến của đtr
3. Tính chất hai tiếp tuyến cắt nhau
Nếu 2 tiếp tuyến của đtr cắt nhau tại một điểm thì :
- điểm đó cách đều hai tiếp điểm
- tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến
- tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua 2 tiếp điểm
4. Đường tròn nội tiếp tam giác
- đtr nội tiếp tam giác là đtr tiếp xúc với 3 cạnh của tam giác
- tâm của đtr nội tiếp tam giác là giao điểm của 3 đường phân giác của các góc trong tam giác
4. Đường tròn bàng tiếp tam giác
- đtr bàng tiếp tam giác là đtr tiếp xúc với 1 cạnh của tam giác và tiếp xúc với phần kéo dài của hai cạnh còn lại
- tâm của đtr bàng tiếp tam giác là giao điểm của 2 đường phân giác các góc ngoài tại hai đỉnh của tam giác
- mỗi tam giác có 3 đtr bàng tiếp B. Bài tập áp dụng Bµi 1:
Cho ®-êng trßn t©m 0 vµ ®iÓm I n»m trong (0)
C / m r»ng d©y AB vu«ng gãc víi OI t¹i I ng¾n h¬n mäi d©y kh¸c ®i qua I Gi¶i:
GV h-íng dÉn : VÏ d©y CD bÊt k× qua I (Kh¸c d©y AB )
ta c/m AB Muèn so s¸nh hai d©y ta so s¸nh ®iÒu g× ? A O
( Ta so s¸nh hai kho¶ng c¸ch tõ t©m ®Õn 2 d©y ; Dïng tÝnh
chÊt trong tam gi¸c vu«ng th× c¹nh huyÒn lµ c¹nh lín nhÊt )
Bài 2 : Từ 1 điểm A nằm bên ngoài đtr (O), kẻ các tiếp tuyến AB và AC với C đtr H (B ; C Klà cá c tiế D p điểm).
Qua điểm M thuộc cung nhỏ BC, kẻ tt với đtr (O), tt này cắt các tt AB, AC
theo thứ tự tại D và E. Chứng
minh rằng chu vi tam giác ADE bằng 2.AB LG B Trang 34
Theo tính chất 2 tt cắt nhau, ta có : B D DM = DB (1) ; EM = EC (2) M A O Chu vi tam giác ADE là : E C AD AE DE AD AE DM EM (3) A DE C Từ (1) ; (2) và (3) : C
AD AE DB EC
AD DB AE EC AB AC 2AB (vì AB = AC) ADE
Bài 3 : Cho đtr (O), điểm I nằm bên ngoài đtr (O). Kẻ các tt IA và IB với đtr (A, B là các tiếp điểm). Gọi
H là giao điểm của IO và AB. Biết AB = 24cm ; IA = 20cm
a) Tính độ dài AH ; IH ; OH
b) Tính bán kính của đtr (O) LG
- Theo tính chất của 2 tt cắt nhau, ta có: IA = IB A
= 20cm; IO là phân giác của góc AIB
- Tam giác IAB cân tại I, có IH là phân giác =>
IH cũng đồng thời là đường cao và là đg trung H tuyến 1 1
AH BH AB .24 12cm I O 2 2
- Xét tam giác AHI vuông tại H B ta có : 2 2 2 2 2 2
IH IA AH 20 12 16 IH 16cm (theo Pytago)
- Xét tam giác AIO, vuông tại A, áp dụng hệ thức về cạnh và đg cao trong am giác vuông ta có : 2 2 AH 12 2
AH HI.HO HO 9 HI 16 2 AO I .
O OH IH OH .OH 16 9.9 225 AO 15cm
Bài 4 : Cho nửa đtr (O ; R) đg kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đtr cùng
thuộc nửa mp có bờ là AB). Lấy M thuộc Ax, qua M kẻ tt với nửa đtr, cắt By tại N a) Tính góc MON b) CMR : MN = AM + BN c) CMR: AM.BN = R2 LG
a) - theo tc của 2 tt cắt nhau, ta có: y 1 O O
AOH ; MA MH 1 2 2 (1) N x 1 O O
BOH ; NB NH 3 4 2 - ta có: 1 1 H
MON O O AOH BOH 0 0 .180 90 2 3 2 2 b) do MN = MH + NH (2) M
=> từ (1) và (2) : MN = MA + NB
c) Xét tam giác MON vuông tại O, theo hệ thức về
cạnh và đg cao trong tam giác vuông, ta có : 3 2 4 1 R B A O 2
OH MH.NH AM .BN 2
AM.BN R à m OH R Trang 35 BTVN.
Bài 5: Cho đtr (O; R) và 1 điểm A nằm cách O 1 khoảng bằng 2R. Từ A vẽ các tt AB, AC với đtr (B, C là
các tiếp điểm). đg thg vuông góc với OB tại O cắt AC tại N, đg thg vuông góc với OC tại O cắt AB tại M a) CMR: AMON là hình thoi
b) Đthg MN là tt của đtr (O)
c) Tính diện tích hình thoi AMON LG
a) + vì AB, AC là 2 tt của đtr (O) B AB O ; B AC OC + mà ON O ; B OM OC M
Nên AB // ON, AC // OM => tứ giác AMON là Hình bình hành (1) 1 H A O
+ mặt khác : A A (tc 2 tt cắt nhau) (2) 2 1 2
+ từ (1) và (2) => tứ giác AMON là hình thoi
b) + vì AMON là hình thoi MN OA (3) N C + mặt khác 1 1 : HO AH OA .2R R (4) 2 2
+ từ (3) và (4) => MN là tt của đtr (O) OB R 1
c) + xét tam giác ABO, vuông tại B ta có : 0 sin A A 30 1 1 OA 2R 2
+ xét tam giác AHM vuông tại H, ta có : 3 3 2R 3 0
MH AH . tan A . R tan 30 . R
MN 2.MH 2. . R 1 3 3 3 2 + do đó 1 1 2R 3 2R 3 : S .MN.AO . .2R (đvdt) AMON 2 2 3 3
******************************************************** Trang 36
Ngày dạy: ………………………………….
ÔN TẬP ĐẠI SỐ + HÌNH HỌC I. ĐẠI SỐ
Bài 1: Thực hiện phép tính
a) 50 3 45 2 18 5 20 5 2 9 5 6 2 10 5 2 5
82 23 2 2 2 3 2 1 2 8 2 2 2 3 2 2 3 2 2 1 2 3 23 2 2 1 21 2 b) 28 14 2
2 3 2 2 4 2 2 2 3 2 2 1 7 7 7 1 3 1 7 7 7 3 21 1 . 2 1 . 2 1 7.1 7 2 c) 1 7 3 1 7 3 1 7. 1
7 7 1 . 7 1 7 2 2 1 7 1 6
10 2 3 2 29 12 5 10 2 3 2 20 2.2 5.3 9 10 2 3 2 2 5 32 d)
10 2 3 22 5 3 10 2 3 4 5 6 10 2 5 2.2. 5 4 10 2 5 22 2 10 2 5 2 10 2 5 4 6 2 5 5 2 5 1 5 1 5 1 x x x
Bài 2: Cho biểu thức 2 1 1 B 1: x x 1 x x 1 x 1 a) RG biểu thức B b) So sánh B với 1 LG
a) đk: x 0; x 1. Ta có: x 2 x 1 x 1 B 1: x
1 x x 1 x x 1
x 1 x 1 x 2 x 1 1 1: x
1 x x
1 x x 1 x 1
x 2 x 1 . x
1 x x 1
x 2 x 1 x x 1 1:
x x x 1: 1 1
x 1x x 1 x. x x x 1 x x x 1 1: x
1 x x 1: 1
x 1x x 1: 1 x x 1 x b) xét hiệu: x x x x x x x x 2 1 1 1 2 1 B 1 1 0 x x x x
B 1 0 B 1 Trang 37
2.x 2 x x x x x 1 1 1
Bài 3: Cho biểu thức: P : x x x x x 1 a) RG bth P b) Tìm x để P < 0
c) Tìm x nguyên để P nguyên LG a) Đk: 0 < x #1. Ta có:
2. x 2 x x x x x 1 1 1 P : x x x x x 1 x
1x x 1 x 1x x 1 2. x 2 1 x x x x : 1 1 x 1 x 1
x x 1 x x 1 2. x 1 2 x x 1 x 1 : x x x . 1 x 2. x 1 x 1 x 1 b) P 0
0 x 1 0 vi x 1 0 x 1 x 1 0 x 1 x 1 x 1 x 1 2 2 c) Ta có: P 1 x 1 x 1 x 1 2 P Z
Z 2 x 1 x 1 Ư(2), mà Ư(2) = 1 ; 2 x 1
) x 1 1 x 2 x 4 tm ) x 1 1
x 0 x 0 tm
) x 1 2 x 3 x 9 tm ) x 1 2 x 1 loai 3 3 x 1 x 2
Bài 4: Cho bth: P : x 1 x x 2 x 1 a) Đk? b) RG bth P
c) Tìm x nguyên để P nguyên LG
a) đk: x 0; x 1; x 4 b) Ta có:
3 x 3 x 1
x 1 x 1 x 2 x 2 3
x 1 x 4 P
x x :
x x
x x : 1 2 1 1
x 2 x 1
x 2 x 1 x 2 3
x x . 1 3 x
c) Tìm x nguyên để P nguyên Trang 38 x 2 2 P 1
Z x U 1;2 (2) x x
) x 1 x 1loai
) x 2 x 4 loai
) x 1loai
) x 2loai
Bài 5: Thực hiện phép tính M 6 2 2. 3
2 12 18 128 6 2 2. 3 2 12 18 8 2 M 6 2 2. 3
2 12 4 2 2 6 2 2. 3 2 2 3 4 2
M 6 2 2. 3 2 3 4 6 2 2. 3 3 2 1 6 2 2. 3 3 1
M 6 2 2. 2 3 6 2. 4 2 3 6 2. 3 2 1 6 2. 3 1
M 6 2 3 2 4 2 3 3 2 1 3 1 Bài 6:
a) Với gtr nào của m thì hsbn: y 4m 3 x 5 đồng biến
b) Với gtr nào của m thì hsbn: y 2m 5 x 14 nghịch biến LG a) hsđb 3
4m 3 0 m 4 5
b) hsnb 2m 5 0 m 2
Bài 7: Tìm gtr của m để đường thẳng:
y m 3 x m 1, m 3 và đường thẳng
y 2 m x 3, m 2 cắt nhau tại 1 điểm trên trục tung LG
- Xét y m 3 x m 1, m 3 (1)
Ta có: a = m – 3; b = m + 1
- Xét y 2 m x 3, m 2 (2)
Ta có: a’ = 2 – m; b’ = - 3
- Để đth (1) và đth (2) cắt nhau tại 1 điểm trên trục tung khi và chỉ khi ' a a
m 3 2 m 2m 5 m 4 ' b b m 1 3 m 4
Bài 8 : Cho 2 hsbn : y m 3 x 1 1 à
v y 1 2m x 5
2. Với gtr nào của m thì đồ thị 2 hs trên là 2 đg thg a) Song song ; b) Cắt nhau ; c) Trùng nhau LG
Xét (1), ta có : a = m + 3 ; b = -1
Xét (2), ta có : a’ = 1 – 2m ; b’ = 5 Trang 39 ' a a
m 3 1 2m 2 a) (1) // (2) 3m 2 m ' b b 1 5 3 b) (1) cắt (2) 2 '
a a m 3 1 2m 3m 2 m 3 ' 2 a a
m 3 1 2m m c) (1) trùng (2)
3 không tồn tại m thỏa mãn ' b b 1 5 1 5 2
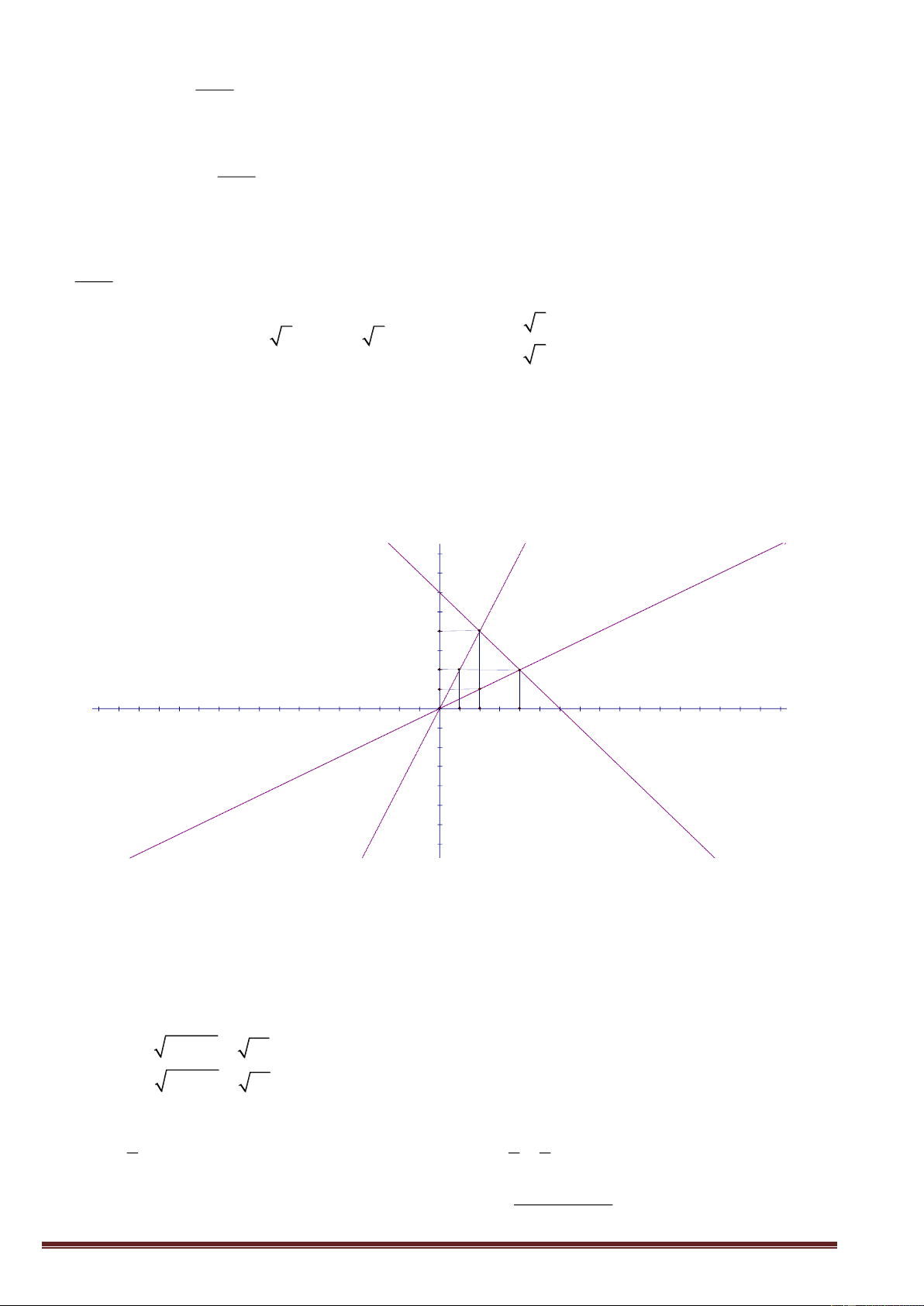
Bài 9 : Vẽ đthị 2 hs sau trên cùng 1 hệ trục tọa độ : y
x 2 (1); y 2x 2 2 . Gọi A ; B là giao 3
điểm của (1) và (2) với trục hoành ; và giao điểm của 2 đg thg là C. Tìm tọa độ giao điểm A, B, C. Tính diện tích tam giác ABC LG
* Bảng các giá trị của x và y : x 0 - 3 x 0 -1 2 y 2x 2 2 0 y x 2 2 0 3 * Đồ thị hs 2 y
x 2 (1) đi qua điểm A(-3 ; 0) và điểm C(0 ; 2). Đồ thị hs y 2x 2 (2) đi qua điểm 3
B(-1 ; 0) và điểm C(0 ; 2) 8 6 f x = 2x+2 4 2 g x = x+2 3 2 C A -15 -10 -5 -3 B -1 0 5 10 15 -2 -4 -6
* diện tích tam giác ABC là : 1 1 S . AB CO .2.2 2 (đvdt) ABC 2 2
Bài 10 : Cho x ab 2 a 2 b 2 2 1 1
; y a 1 b b 1 a . Hãy tính y theo x, biết (ab>0) LG Ta có :
x ab 1 a 1 b 2 2 2 2 2 2
a b 2ab 2 1 a 2 1 b 2 1 a 2 1 b 2 2
2a b 2ab 2 1 a 2 1 b 2 2 a b 1
y a 1 b b 1 a 2 2 2 2 2 a 2
1 b 2ab 2 1 a 2 1 b 2 b 2 1 a 2 2
2a b 2ab 2 1 a 2 1 b 2 2 a b Do đó : 2 2 2
y x 1 y x 1 Trang 40
II. HÌNH HỌC : (Ôn tập về tính chất của 2 tt cắt nhau)
Bài 1 : Cho nửa đtr (O ; R), đường kính AB, vẽ các tiếp tuyến Ax, By về nửa mp bờ AB chứa nửa đtr.
Trên Ax, By lấy theo thứ tự M và N sao cho góc MON bằng 900. Gọi I là trung điểm của MN. CMR :
a) AB là tt của đtr (I ; IO)
b) MO là tia phân giác của góc AMN
c) MN là tt của đtr đường kính AB LG
a) CMR : AB là tt của (I ; IO) x y
- ta có: AM // BN (cùng vuông góc với AB) => tứ giác ABNM là hình thang N AO BO I
- xét hình thang ABNM, ta có: IO là đường H MI NI
trung bình của hình thang ABNM M => IO // AM // BN
- mặt khác: AM AB IO AB O AB là tt của đtr (I; IO) A O B
b) CMR : MO là tia phân giác của góc AMN
- vì AM // IO => AMO = MOI (so le trong) (1)
- tam giác MON có O = 900, OI là trung tuyến 1
OI IM IN
MN => tam giác IMO cân tại I => 2 IMO = IOM (2)
- từ (1) và (2) => MOI = AMO = IMO => MO là phân giác của AMN
c) CMR: MN là tt của đtr đkính AB
- kẻ OH vuông góc với MN (3)
- xét tam giác MAO và tam giác MHO, ta có: 0 A H 90 MN : chung M AO M
HO CH GN => OA = OH = R (cạnh tương ứng) A MO H MO
=> OH là bán kính của đtr tâm O đkính AB (4)
- từ (3) và (4) => MN là tt của đtr đkính AB
Bài 2: Cho đtr (O), điểm A nằm bên ngoài đtr. Kẻ các tt AM, AN với đtr (M, N là các tiếp điểm)
a) CMR: OA vuông góc với MN
b) Vẽ đkính NOC. CMR: MC // AO
c) Tính độ dài các cạnh của tam giác AMN, biết OM = 3cm; OA = 5cm LG
a) ta có: OM = ON (= bán kính)
AM = AN (tính chất 2 tt cắt nhau) M C
=> AO là trung trực của đoạn thẳng MN => OA MN
b) gọi H là giao điểm của MN và AO - vì OA MN =>MH = NH H A O - xét tam giác MNC, ta có: ON OC
HO là đg trung bình của tam giác MH NH
MNC => HO // MC hay MC // AO N
c) xét tam giác AMO, M = 900, theo Pytago ta có : 2 2 2 2
AM A O OM 5 3 4 => AM = AN = 4cm
- mặt khác, áp dụng hệ thức về cạnh và đg cao trong tam giác vuông AMO, ta có: Trang 41 M . A MO 4.3 M .
A MO MH.OA MH 2,4cm OA 5
MN 2.MH 2.2,4 4,8cm
Bài 3: Cho tam giác ABC, A = 900, đg cao AH, vẽ đtr (A; AH), kẻ các tt BD, CE với đtr (D, E là các tiếp điểm khác H). CMR:
a) 3 điểm D, A, E thẳng hàng
b) DE tiếp xúc với đtr đkính BC LG
a) theo tc 2 tt cắt nhau, ta có:
- AB là phân giác của DAH => A1 = A2
- AC là phân giác của EAH => A3 = A4
- mà DAE = A1 + A2 + A3 + A4 = 2( A2 + A3) = 2.900 = 1800
=> 3 điểm D, A, E thẳng hàng
b) gọi M là trung điểm của BC B
- xét tam giác ABC A = 900, có AM là trung tuyến 1 H AM BC (1) D 2
- ta có: BD // CE (cùng DE) => tứ giác M BDEC là hthang 1 - xét hthang BDEC, ta có : 2 3 AD AE 4
AM là đường trung bình của C A MB MC
hình thang BDEC => MA // CE, mà CE DE => MA DE (2)
- từ (1) và (2) => DE tiếp xúc với đường tròn (M) đường kính BC E
Bài 4: Cho đtròn (O), điểm M nằm bên ngoài đtròn. Kẻ tiếp tuyến MD, ME với đtròn (D, E là các tiếp
điểm). Qua điểm I thuộc cung nhỏ DE, kẻ tiếp tuyến với đtròn, cắt MD và ME theo thứ tự tại P và Q. Biết
MD = 4cm. Tính chu vi tam giác MPQ LG
- Theo tính chất 2 tt cắt nhau, ta có: D P MD = ME; PI = PD; QI = QE
- Chu vi tam giác MPQ bằng: I
MP + PQ + MQ = MP + PI + QI + MQ O M = (MP + PD) + (QE + MQ) = MD + ME = 2.MD = 2.4 = 8cm Q E
Bài 5: Cho đtròn (O; 2cm), các tt AB và AC kẻ từ A đến đtròn vuông góc với nhau tại A (B, C là các tiếp điểm)
a) Tứ giác ABOC là hình gì? Vì sao?
b) Gọi M là điểm bất kỳ thuộc cung nhỏ BC. Qua M kẻ tt với đtròn, cắt AB và AC theo thứ tự tại D và E. Tính chu vi tam giác ADE. c) Tính số đo góc DOE? LG Trang 42
a) Tứ giác ABOC có 3 góc vuông nên là HCN, mà lại có 2
cạnh kề là OB và OC: OB = OC nên nó là Hình vuông
b) Tương tự BT4, ta có chu vi tam giác ADE bằng: 8cm
c) Theo tính chất tiếp tuyến ta có: 1 1 O O MO ; B O O MOC O B 1 3 2 4 3 2 2 1 2 1 1 4 O O MOB MOC .90 45 1 2 0 0 D 2 2 M 0 DOE 45 A E C
Bài 6: Cho đtròn (O; 5cm) điểm M nằm bên ngoài đtròn. Kẻ các tt MA, MB với đtròn (A, B là các tiếp
điểm). Biết góc AMB bằng 600.
a) CMR: tam giác AMB là tam giác đều b) Tính chu vi tam giác AMB
c) Tia AO cắt đtròn ở C. Tứ giác BMOC là hình gì? Vì sao? LG
a) theo tính chất 2 tt cắt nhau, ta có: MA = MB, do đó tam A giác AMB cân tại M + mặt khác: 0 AMB 60 1 O
Nên tam giác AMB là tam giác đều M 2
b) theo tch 2 tt cắt nhau, ta có: 1 0 M M AMB 30 1 2 2 C B + mà MA là tt nên 0
MAO 90 => tam giác MAO vuông tại A
+ xét tam giác MAO vuông tại A có 1 0
M 30 AO
MO MO 2.AO 2.5 10 cm 1 2 Theo Pytago: 2 2 2 2 MA
MO AO 10 5 75 5 3
+ Chu vi tam giác AMB bằng: MA + MB + AB = 3.MA = 3.5 3 15 3
c) Tam giác AMB đều có MO là phân giác nên MO cũng đồng thời là đường cao của tam giác
MO AB (1)
+ Tam giác ABC có trung tuyến BO bằng 1 AC nên tam giác ABC là tam giác vuông tại B BC AB 2 (2)
+ Từ (1) và (2) BC / / MO , do đó tứ giác BMOC là hình thang
**********************************************************
Ngày dạy: 08/01/20...
GIẢI HỆ PHƯƠNG TRÌNH BẰNG PHƯƠNG PHÁP THẾ A. Kiến thức cơ bản 1. Quy tắc thế
- từ một trong các phương trình của hệ biểu diễn x theo y (hoặc y theo x)
- dùng kết quả đó thế cho x (hoặc y) trong pt còn lại rồi thu gọn
2. Cách giải hệ phương trình bằng phương pháp thế
- dùng quy tắc thế biến đổi hệ phương trình đã cho để đc 1 hpt mới trong đó có 1 pt 1 ẩn
- giải pt 1 ẩn vừa tìm đc, rồi suy ra nghiệm của hpt đã cho
B. Bài tập áp dụng Trang 43
Bài 1: Giải các hpt sau bằng phương pháp thế
2x y 4 x 5 3
x 2y 5 x 11 3
x 2y 2 a) b) y hpt ô v nghiêm c) 13 2
x y 3 y 19 x 2 5
x 4y 1 y 2 2
2x y 6 x 4
x 2y 6 0 x 4
2x 3y 8 x 1 d ) e) g) 3
x 5y 22 y 2 5
x 3y 5 0 y 5 5
x 2y 1 y 2 109 x x y 1 x 2
2x 7 y 8 13
x 15y 48 x 9 106 h) i) k) 3
x 2y 8 y 1 12
x 11y 3 45
2x y 29 y 11 y 53 1 1 1 1
x 6y 17 x 5
x y 2 0 x 3
x y 0 x 10 l) ) m 3 4 n) 5 6 5
x y 23 y 2 y 4 y 12 5x y 11 5
x 4y 2
Bài 2: giải các hpt bằng phương pháp thế
5x y 5
3 1 x 3
2 3x 5y 2 6 15 x 2 a) b) y 5 3
x y 3 2 3 y 3 2 3x 3 5 y 21
x 2y 5 5 x 2 5
x 2y 7 x 7 c) d )
5x y 5 2 5 y 5
2x 7y 2 7 7 y 7 5 2
x y 3 5 x 0 e) y 3 5 x 2 y 6 2 5 4
2x y 3 3 x 2y 3 48 5
x 2y 45 x 7 f ) 3
3x 4y 3 44x 2y 9 48
25x 20y 75 y 5 x y 1 6
8 2x 3y
4x 9y 8 x g) 5
y x 4
5 3x 2y 8
x 3y 5 y 1 29 2 2
1 1, 5 3 2 6 x x y x
2x 3y 0,5 10 h) 11 ,5 4
3 x 2y 5 x 3
x 0,5 2y 5 21 y 10
Bài 3: Tìm các giá trị của m, n sao cho mỗi hpt ẩn x, y sau đây 2mx
1n y m n1 a) hpt
có nghiệm (2; 1); đáp số: 2 1 m ; n m
1 x m n y 3 9 3 2x m
1 y m 2n 1 b) hpt
có nghiệm (-3; 2); đáp số: m 1; n 1 nx
1m y 3 3
mx n 1 y 93 c) hpt
có nghiệm (1; -5); đáp số: m 1; n 17
nx 4my 3 m 2
x 5ny 25 d) hpt
có nghiệm (3; -1); đáp số: m 2; n 5 2mx
n 2 y 5
Bài 4: Tìm a, b trong các trường hợp sau:
a) đg thg d1: ax + by = 1 đi qua các điểm A(-2; 1) và B(3; -2)
b) đg thg d2: y = ax + b đi qua các điểm M(-5; 3) và N(3/2; -1) Trang 44
c) đg thg d3: ax - 8y = b đi qua các điểm H(9; -6) và đi qua giao điểm của 2 đường thẳng (d): 5x – 7y = 23; (d’): -15x + 28y = -62
d) đt d4: 3ax + 2by = 5 đi qua các điểm A(-1; 2) và vuông góc với đt (d’’): 2x + 3y = 1 Đáp số 8 5 a 56 a a 3 13 a 7 a) ; b) ; c) 3 ; d ) b 5 1 5 b b 120 b 13 7
**************************************************************** Trang 45
Ngày dạy: 11/12/20...
VỊ TRÍ TƯƠNG ĐỐI CỦA HAI ĐƯỜNG TRÒN.
TIẾP TUYẾN CHUNG CỦA HAI ĐƯỜNG TRÒN A. Kiến thức cơ bản
1. Ba vị trí tương đối của hai đtr
Xét đtr (O; R) và (O’; r) với '
R r;OO d , ta có: a) Hai đtr cắt nhau - số điểm chung: 2
- hệ thức: R – r < d < R + r b) hai đtr tiếp xúc nhau - số điểm chung: 1
- hệ thức:+ tiếp xúc trong: d = R – r > 0
+ tiếp xúc ngoài: d = R + r c) hai đtr không giao nhau - số điểm chung: 0
- hệ thức:+ 2 đtr ở ngoài nhau: d > R + r
+ 2 đtr đựng nhau: d < R – r + 2 đtr đồng tâm: d = 0
2. Tính chất đường nối tâm - Định lý:
a) Nếu 2 đtr cắt nhau thì 2 giao điểm đối xứng với nhau qua
đường nối tâm, tức là đường nối tâm là đường trung trực của A
dây chung (OO’ là đường trung trực của dây AB)
b) Nếu 2 đtr tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm O' O (A thuộc OO’) B A O' O
3. Tiếp tuyến chung của hai đường tròn
- Định nghĩa: tiếp tuyến chung của 2 đtr là đg thg tiếp xúc với cả 2 đtr đó d2 d1 d2
d1; d2 là tiếp tuyến chung ngoài: tiếp tuyến chung
ngoài không cắt đoạn nối tâm d1
d1; d2 là tiếp tuyến chung trong: tiếp tuyến chung
trong cắt đoạn nối tâm B. Bài tập áp dụng
Bài 1: Cho đường tròn (O; 4cm) và đường tròn (O’; 3cm) cắt nhau tại 2 điểm phân biệt A; B biết OO’ =
5cm. Từ B vẽ 2 đường kính BOC và BO’D
a) CMR: 3 điểm C, A, D thẳng hàng
b) Tam giác OBO’ là tam giác vuông Trang 46
c) Tính diện tích tam giác OBO’ và diện tích tam giác CBD
d) Tính độ dài các đoạn thẳng AB; CA; AD LG a) CMR: C; D; A thẳng hàng B
+ ta có: tam giác ABC nội tiếp đtr (O) có BC làm đkính =>
tam giác ABC vuông tại A => A1 = 900
+ lại có: tam giác ABD nội tiếp đtr (O’) có BD làm đkính => 4 3
tam giác ABD vuông tại A => A H 2 = 900 O O'
+ do CAD = A1 + A2 = … =1800 5
=> 3 điểm C, A, D thẳng hàng
b) CMR: tam giác OBO’ là tam giác vuông 1 2 D C A + ta có: '2 2 2 ' 2 2 2 '2 2 ' 2
OO 5 25; OB O B 4 3 25. OO OB O B 25
=> tam giác OBO’ vuông tại B ( theo định lý đảo của định lý Pytago)
c) Tính diện tích tam giác OBO’ và diện tích tam giác CBD ta có: 1 1 ' 2 S . OB O B .4.3 6 cm ' OBO 2 2 1 1 2 S C . B DB .8.6 24 cm OBD 2 2
d) Tính độ dài các đoạn thẳng AB; CA; AD
+ ta có: OO’ là đg trung trực của AB (theo tính chất đoạn nối tâm) 1 ' BH OO à v BH
AB hay AB 2.BH 2
+ xét tam giác OBO’, B = 900, theo hệ thức về cạnh và đường cao trong tam giác vuông ta có: ' O . B O B 4.3 ' ' O . B O B H . B OO BH 2, 4 cm ' OO 5
=> AB = 2. BH = 2 . 2,4 = 4,8 cm
+ áp dụng định lý Pytago cho tam giác vuông: 0 2 2 2 2
ABC, A 90 AC BC AB 8 4,8 6, 4 cm 0 2 2 2 2
ABD, A 90 AD BD AB 6 4,8 3,6 cm
Bài 2 (tương tự BT76SBT/139): Cho đtr (O) và (O’) tiếp xúc ngoài tại A, đg thg OO’ cắt đtr (O) và (O’)
lần lượt tại B và C (khác A). DE là tt chung ngoài (D thuộc (O), E thuộc (O’)), BD cắt CE tại M
a) CMR: DME = 900 b) Tứ giác ADME là hình gì? Vì sao?
c) MA là tt chung của cả 2 đtr d) MD.MB = ME.MC LG
a) ta có : O1 = B1 + D1 (góc ngoài của tam giác), mà B1 = D1 (tam giác cân) M E I D 1 3 1 2 2 1 1 1 1 1 C O' B O A 1
O 2B B O (1) 1 1 1 1 2 Trang 47 + lại có : '
O C E (góc ngoài của tam giác), mà C 1 1 1 1 = E1 (tam giác cân) 1 ' '
O 2C C O (2) 1 1 1 1 2 + từ (1) và (2) 1 B C 1 ' O O 0 0
.180 90 (theo tính chất hình thang) 1 1 1 1 2 2 0 0
BMC 90 hay DME 90
b) + tam giác ABD nt đtr (O) có AB là đkính => tam giác ABD vuông tại D
=> ADB = 900 => ADM = 900
+ tam giác ACE nt đtr (O) có AC là đkính => tam giác ACE vuông tại E
=> AEC = 900 => AEM = 900
+ tứ giác ADME có : ADM = DME = AEM = 900 => tứ giác ADME là hình chữ nhật
c) + gọi I là giao điểm của AM và DE => tam giác IAD cân tại I => A2 = D3 (3)
+ do tam giác OAD cân tại O nên suy ra: A1 = D2 (4)
+ từ (3) và (4) => A1 + A2 = D2 + D3 = 900 (tính chất tt tại D) => MA vuông góc với AB tại A
=> MA là tt của đtr (O) và cũng là tt của đtr (O’)
Bài 3: Cho đtr (O) và đtr (O’) tiếp xúc ngoài tại A, BC là tt chung ngoài của cả 2 đtr (B, C là các tiếp
điểm). tt chung trong của 2 đtr tại A cắt BC tại M
a) CMR: A, , C thuộc đtr (M) đường kính BC
b) Đường thẳng OO’ có vị trí ntn đối với đtr (M; BC/2)
c) Xác định tâm của đtr đi qua O, M, O’
d) CMR: BC là tt của đtr đi qua O, M, O’ LG
a) theo tính chất 2 tt cắt nhau, ta có: 1
MA MB MC
BC tam giác ABC vuông tại A C 2 M
=> a nằm trên đtr có đkính BC. Hay 3 điểm A, B, C B thuộc (M; BC/2)
b) và (O) và (O’) tiếp xúc ngoài tại A => A thuộc OO’
=> OO’ vuông góc với MA tại A thuộc (M; BC/2) => O' O I
OO’ là tt của đtr (M; BC/2) A
c) theo tính chất tt cắt nhau, ta có: 1 1 ' ' BMO AMO
AMB; CMO AMO AMC 2 2 1 1 '
AMO AMO AMB AMC 0 0 .180 90 2 2
=> tam giác OMO’ vuông tại M => tâm của đtr đi qua 3 điểm O, M, O’ là trung điểm I của cạnh OO’
d) + tứ giác BOO’C là hình thang vuông vì có BO // CO’ (cùng vuông góc với BC) BM MC
+ Xét hình thang BOO’C, ta có:
MI là đg trung bình của hthang BOO’C ' OI IO
=> IM // OB, mà BC OB => IM BC => BC là tt của đtr đi qua 3 điểm O, O’, M
Bài 4(BTVN): Cho đtr (O) đkính AB, điểm C nằm giữa A và O. Vẽ đtr (O’) đkính BC
a) xác định vị trí tương đối của đtr (O) và (O’)
b) kẻ dây DE của đtr (O) vuông góc với AC tại trung điểm H của AC. Tứ giác ADCE là hình gì? Vì sao?
c) gọi K là giao điểm của DB và (O’). CMR: 3 điểm E, C, K thẳng hàng
d) CMR: HK là tt của đtr (O’) LG Trang 48
a) ta có: OO’ = OB – O’B > 0 => (O) và (O’) tiếp xúc trong tại B D
b) + vì AB DE tại H => DH = EH + xét tứ giác ADCE, ta có K : DH EH 1 2 3
AH CH ADCE là hình thoi 1 A B AC DE H C O' O c) ta có : 1 1
OD OA OB AB AD
B vuông D AD BD 2 1 E ' ' ' O C O K O B BC CKB vuông K CK BD 2 => AD // CK (1)
+ mà ADCE là hình thoi nên AD // CE (2)
+ từ (1) và (2) => C, K, E thẳng hàng (theo Tiên đề Ơclit)
d) + vì KH là trung tuyến của tam giác DKE vuông tại K => HD = HK = HE => tam giác HKE cân tại H => K1 = E1 (*)
+ mà E1 = B1 (cùng phụ với BDE) (**)
+ từ (*) và (**) => K1 = B1 (3)
+ mặt khác: B1 = K3 (tam giác O’KB cân tại O’) (4)
+ từ (3) và (4) => K1 = K3 + do 0 0 '
K K 90 K K 90 HK O K HK là tt của đtr (O’) 2 3 1 3
************************************************************** Trang 49
Ngày dạy: ……………………………..
GIẢI HỆ PHƯƠNG TRÌNH BẰNG PHƯƠNG PHÁP CỘNG ĐẠI SỐ A. Kiến thức cơ bản
1. Quy tắc cộng đại số: gồm 2 bước
- Cộng hay trừ từng vế 2 pt của hpt đã cho để đc pt mới
- Dùng pt mới ấy thay thế cho 1 trong 2 pt của hệ (giữ nguyên pt kia)
2. Tóm tắt cách giải hệ phương trình bằng phương pháp cộng đại số
- Giải theo quy tắc: “Nhân bằng, đổi đối, cộng, chia
Thay vào tính nốt ẩn kia là thành” - Nghĩa là:
+ nhân cho hệ số của 1 ẩn trong hai phương trình bằng nhau
+ đổi dấu cả 2 vế của 1 pt: hệ số của 1 ẩn đối nhau
+ cộng vế với vế của 2 pt trong hệ, rút gọn và tìm 1 ẩn
+ thay vào tính nốt ẩn còn lại B. Bài tập áp dụng
Bài 1: Giải các hệ phương trình sau bằng phương pháp cộng đại số 1 x 5
x 2y 1
2x 3y 2 x 1 19 a) b) 3
x 5y 3 12 3
x 2y 3 y 0 y 19 7 x 3
x y 8 x 3
x 2y 5 3 c) d )
7x 2y 23 y 1 x y 1 4 y 3
Bài 2: Giải hệ phương trình bằng phương pháp cộng đại số
2x 2 3y 5 x 2 x 5 3
5x 4y 15 2 7 a) b) 9 3 7 3
2x 3y y 3
x 2y 3 y 2 2 2 29 5
2 3 1 x x y y
4x 5 y 1 2x 3 8 2 2 c) d )
h v nghi m B 2x 4 3
x 5y12 3
7x 2 52y ê ô ê 33 1 3x y 40 3 1 1 2 2x 1 3 y 2 6
x y 8 2x 3y 6x x x 2 2 e) 4 g) 5
y x 5 3x 2y 23 y
x y x 3 1 4 3 2 5 y 2 2
ài 3: Giải hpt bằng phương pháp cộng đại số x 2
1 x 22 9 y x 5 7 x
2 5 x2 6y x 0 a) b) y 2 y 2 y 3 x y 2 y2 y 4 3 2 5 2 6 4x
Bài 4: xác định a, b để đồ thị hs y = ax + b đi qua 2 điểm A và B trong các trường hợp sau:
a) A(4; 3), B(-6; -7). Đáp số: a = 1; b = -1
b) A(3; -1), B(-3; -2). Đáp số: a = 1/6; b = -3/2
c) A(2; 1), B(1; 2). Đap số: a = -1; b = 3
d) A(1; 3), B(3; 2). Đáp số: a = -1/2; b = 7/2 Trang 50
x 1 y 2 2x y
Bài 5: Tìm m để nghiệm của hệ phương trình: 3 4 5
cũng là nghiệm của phương x 3 y 3 2y x 4 3 trình: 3mx – 5y = 2m + 1
x 1 y 2 2x y
4x 9y 1 0 x 11 - ta có: 3 4 5 x 3 y 3 1
5x 28y 3 y 6 2y x 4 3
- thay x = 11; y = 6 vào phương trình ta đc: 3 .
m 115.6 2m 1 31m 31 m 1
Bài 6 : Tìm m để đường thẳng (d) : y = (2m – 5)x – 5m đi qua giao điểm của 2 đường thẳng (d1) : 2x + 3y = 7 và (d2) : 3x + 2y = 13 LG
- gọi A là giao điểm của đường thẳng (d1) và (d2). Tọa độ của điểm A là nghiệm của hpt :
2x 3y 7 x 5 => A(5 ; -1) 3
x 2y 13 y 1
- vì đg thg (d) đi qua điểm A nên tọa độ điểm A thỏa mãn đth (d). thay x = 5 ; y = -1 vào (d) ta đc : m 24 1 2
5 .5 5m 5m 24 m 5
Bài 7 : Tìm m để các đường thẳg sau đây đồng quy :
(d1) : 5x + 11y = 8 ; (d2) : 4mx + (2m – 1)y = m + 2 ; (d3) : 10x – 7y = 74 LG
- gọi A là giao điểm của đường thẳng (d1) và (d3). Tọa độ của điểm A là nghiệm của hpt : 5
x 11y 8 x 6 => A(6 ; -2) 10
x 7 y 74 y 2
- để 3 đg thg trên đồng quy thì đg thg (d2) phải đi qua điểm A, tức tọa độ điểm A thỏa mãn đth (d2). thay x = 6 ; y = -2 vào (d 2) ta đc : 4 . m 6 2m
1. 2 m 2 19m 0 m 0
******************************************************
Ngày dạy: …………………………
GIẢI BÀI TOÁN BẰNG CÁCH LẬP HỆ PHƯƠNG TRÌNH A. Kiến thức cơ bản
Để giải bài toán bằng cách lập hệ phương trình ta thực hiện theo 3 bước sau :
- bước 1 : lập hpt (bao gồm các công việc sau)
+ chọn ẩn và đặt điều kiện thích hợp cho ẩn)
+ biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết
+ lập hpt biểu thị tương quan giữa các đại lượng
- bước 2 : giải hpt vừa lập đc ở bước 1
- bước 3 : kết luận : so sánh nghiệm tìm đc với điều kiện đặt ra ban đầu
B. Bài tập áp dụng
Dạng 1: Toán tìm số
- Ta phải chú ý tới cấu tạo của một số có hai chữ số , ba chữ số …viết trong hệ thập phân. Điều kiện của các chữ số .
Bài 1: Tìm hai số biết rằng 4 lần số thứ hai cộng với 5 lần số thứ nhất bằng 18040, và 3 lần số thứ nhất
hơn 2 lần số thứ hai là 2002. LG
- gọi số thứ nhất là x, số thứ hai là y x, y N 5
x 4y 18040 x 2004 - theo bài ra, ta có : 3
x 2y 2002 y 2005 Trang 51
Bài 2. Tìm một số tự nhiên có hai chữ số, biết rằng số đó gấp 4 lần tổng các chữ số của nó. Nếu viết hai
chữ số của nó theo thứ tự ngược lại thì đc số mới lớn hơn số ban đầu 36 đơn vị. LG
- gọi số tự nhiên cần tìm có dạng: ab a,b N;0 a,b 9
ab 4(a b) a 4 - theo bài ra, ta có: ab 48 b 8 ba ab 36
Bài 3. Tìm một số có hai chữ số. Biết rằng nếu viết thêm số 1 vào bên phải số này thì được một số có ba
chữ số hơn số phải tìm 577 và số phải tìm hơn số đó nhưng viết theo thứ tự ngược lại là 18 đơn vị. LG
- gọi số tự nhiên cần tìm có dạng: ab a,b N;0 a 9;0 b 9 a 1 b ab 577 1
0a b 64 a 6 - theo bài ra, ta có: ab 64 a b 2 b 4 ab ba 18
Bài 4. Tìm một số có hai chữ số, biết rằng tổng hai chữ số của nó nhỏ hơn số đó 6 lần và thêm 25 vào tích
của hai chữ số đó sẽ được số viết theo thứ tự ngược lại với số phải tìm. LG
- gọi số tự nhiên cần tìm có dạng: ab a,b N;0 a,b 9 25 a loai
ab 6a b 5 4 4a 5b a b - theo bài ra, ta có: b 5 4
ab 25 ba
ab 25 ba 2 b 9b 20 0 a 5 thoa man b 4
- vậy số cần tìm là : 54
Dạng 2: Toán làm chung, làm riêng
- Ta coi toàn bộ công việc là 1 đơn vị, nếu gọi thời gian làm xong công việc là x thì trong một đơn vị thời
gian làm được 1 công việc . x
* Ghi nhớ : Khi lập pt dạng toán làm chung, làm riêng không được cộng cột thời gian, năng suất và thờ i gian của
cùng 1 dòng là 2 số nghịch đảo của nhau.
Bài 1: Hai vòi nước chảy cùng vào 1 bể không có nước thì trong 6 giờ đầy bể. Nếu vòi thứ nhất chảy 2
trong 2 giờ, vòi thứ 2 chảy trong 3 giờ thì được
bể. Hỏi mỗi vòi chảy bao lâu thì sẽ đầy bể? 5 LG * lập bảng V 1 V 2 Cả 2 V TGHTCV x y 6 Năng suất 1h 1 1 1 x y 6 Năng suất 2h 2 x 2 Năng suất 3h 3 5 y 1 1 1
x y 6 x 10 * ta có hpt: 2 3 2 y 15 x y 5 Trang 52
Bài 2: Hai tổ cùng làm chung công việc trong 12 giờ thì xong, nhưng hai tổ cùng làm trong 4 giờ thì tổ (I)
đc điều đi làm việc khác , tổ (II) làm nốt trong 10 giờ thì xong công việc. Hỏi mỗi tổ làm riêng thì trong bao lâu xong việc. * lập bảng Tổ 1 Tổ 2 Cả 2 tổ TGHTCV x y 12 Năng suất 1h 1/x 1/y 1/12 Năng suất 4h 4/12 = 1/3 Năng suất 10h 10/y 1 1 1
x y 12 x 60 * ta có hpt: 1 10 y 15 1 3 y
Bài 3: Hai vòi nước cùng chảy vào 1 bồn không có nước. Nếu vòi 1 chảy trong 3h rồi dừng lại, sau đó vòi
2 chảy tiếp trong 8h nữa thì đầy bồn. Nếu cho vòi 1 chảy vào bồn không có nước trong 1h, rồi cho cả 2
vòi chảy tiếp trong 4h nữa thì số nước chảy vào bằng 8/9 bồn. Hỏi nếu chảy 1 mình thì mỗi vòi sẽ chảy
trong bao lâu thì đầy bồn? * lập bảng Vòi 1 Vòi 2 Cả 2 vòi Thời gian chảy x y 1h 1/x 8/9 4h 4/x 4/y 3h 3/x 1 8h 8/y 3 8 1 x y x 9 * ta có hpt: 1 4 4 8 y 12 x x y 9
Bài 4: Hai vòi nước cùng chảy vào một bể cạn trong một giờ được 3 bể. Nếu vòi thứ nhất chảy trong 3 10
giờ, vòi thứ hai chảy trong 2 giờ thì cả hai vòi chảy được 4 bể. Tính thời gian mỗi vòi chảy một mình đầy 5 bể . * lập bảng Vòi 1 Vòi 2 Cả 2 vòi TGHTCV x y Năng suất 1h 1/x 1/y 3/10 Năng suất 2h 2/y 4/5 Năng suất 3h 3/x 1 1 3
x y 10 x 5 * ta có hpt: 3 2 4 y 10 x y 5
Dạng 3. Toán chuyển động
Bài 1. Quãng đường AC qua B dài 270km, một xe tải đi từ A đến B với vận tốc 60km/h rồi đi từ B đến C
với vận tốc 40km/h, tất cả hết 6giờ, Tính thời gian ô tô đi quãng đường AB và BC. * Lập bảng Thời gian Vận tốc Quãng đường x AB 60 60x Trang 53 y BC 40 40y 3 x x y 6
* Ta có hệ phương trình: 2
60x 40y 270 9 y 2
Bài 2. Một ô tô và một xe đạp chuyển động từ hai đầu một quãng đường sau 3 giờ thì gặp nhau. Nếu đi
cùng chiều và xuất phát tại cùng một điểm, sau 1 giờ hai xe cách nhau 28km. Tính vận tốc xe đạp và ô tô
biết quãng đường dài 180km * Sơ đồ: XD Gnhau XM A XD XM B * Lập bảng: V t (đi ngược chiều) S (đi ngược t (đi cùng chiều) S (đi cùng chiều) chiều) Xe đạp x 3 3x 1 x Xe máy y 3 3y 1 y 3
x 3y 180
x y 60 x 16
* Ta có hệ phương trình:
x y 28
x y 28 y 44
Bài 3: 1 ô tô đi qđ AB với vận tốc 50km/h, rồi đi tiếp qđ BC với vận tốc 45km/h. Biết tổng chiều dài qđ
AB và BC là 165km và thời gian ô tô đi qđ AB ít hơn thời gian ô tô đi qđ BC là 30ph. Tính thời gian ô tô đi trên mỗi qđ?
Gọi thời gian ô tô đi trên AB, BC lần lượt là x, y 5
0x 45y 165 3 x
Ta có hệ phương trình: 1 2 x y y 2 2
Bài 4: 1 ca nô xuôi dòng 1 quãng sông dài 12km, rồi ngược dòng quãng sông đó mất 2h30ph. Nếu cũng
trên quãng sông ấy, ca nô xuôi dòng 4km rồi ngược dòng 8km thì hết 1h20ph. Tính vận tốc riêng của ca
nô và vận tốc của dòng nước?
- gọi v ca nô là x, v dòng nước là y (km/h; x > y > 0) - v xuôi: x+y - v ngược: x-y 12 12 5
x y x y 2 - ta có hpt
giải hệ ta được x = 10 ; y = 2 (tmđk) 4 8 4
x y x y 3
Bài 5: Một ca nô chạy trên sông xuôi dòng 84 km và ngược dòng 44 km mất 5 giờ. Nếu ca nô xuôi dòng
112 km và ngược dòng 110 km thì mất 9 giờ.Tính vận tốc riêng của ca nô và vận tốc của dòng nước.
- gọi x, y lần lượt là vận tốc riêng của ca nô và vận tốc của dòng nước (km, 0 < y < x)
- vận tốc xuôi của ca nô: x + y
- thời gian xuôi dòng 84km là: 84/x+y
- thời gian xuôi dòng 112km là: 112/x+y
- vận tốc ngược của ca nô: x - y
- thời gian ngược dòng 44km là: 44/x-y
- thời gian ngược dòng 110km là: 110/x-y
- theo bài ra ta có hệ phương trình: Trang 54 84 44 5
x y x y đặt 1 1 ; a b 112 110 x y x y 9
x y x y
Dạng 4. Toán liên quan tới yếu tố hình học.
- Ta phải nắm được công thức tính chu vi; diện tích của tam giác, hình thang, hình chữ nhật, hình vuông, định lý Pi-ta-go.
Bài 1: 1 HCN có chu vi 80m. Nếu tăng chiều dài thêm 3m, tăng chiều rộng thêm 5m thì diện tích của
mảnh đất tăng thêm 195m2. Tính chiều dài, chiều rộng của mảnh đất
Gọi chiều dài là x, chiều rộng là y 2
x y 80 x 30 Ta có hpt x 3
y 5 xy 195 y 10
Bài 2: 1 thửa ruộng HCN, nếu tăng chiều dài thêm 2m và tăng chiều rộng thêm 3m thì diện tích tăng
thêm 100m2. Nếu cùng giảm cả chiều dài và chiều rộng đi 2m thì diện tích giảm đi 68m2. Tính diện tích của thửa ruộng đó? Gọi chiều dài HCN là x
Gọi chiều rộng HCN là y x 2
y 3 xy 100 x 22 Ta có hpt x 2
y 2 xy 68 y 14
Dạng 5. Toán năng suất * Chú ý:
- Năng suất (NS) là số sản phẩm làm được trong một đơn vị thời gian (t).
- (NS) x (t) = Tổng sản phẩm thu hoạch
Ngày dạy: …………………………..
CÁC GÓC VỚI ĐƯỜNG TRÒN A. Kiến thức cơ bản
1. Góc ở tâm. Số đo cung
a) Định nghĩa góc ở tâm: Góc có đỉnh trùng với tâm của đtròn đgl góc ở tâm b) Số đo cung:
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó
- Số đo của cung lớn bằng hiệu giữa 3600 và số đo của cung nhỏ (có chung 2 mút với cung lớn)
- Số đo của nửa đtr bằng 1800
c) Tính chất của số đo cung: Nếu C là một điểm nằm trên cung AB thì sđ AB =sđ AC +sđ CB
2. Liên hệ giữa cung và dây
a) Định lý 1: Với 2 cung nhỏ trong một đtròn hay trong 2 đtròn bằng nhau:
- 2 cung bằng nhau căng 2 dây bằng nhau
- 2 dây bằng nhau căng 2 cung bằng nhau
b) Định lý 2: Với 2 cung nhỏ trong 1 đtròn hay trong 2 đtròn bằng nhau:
- Cung lớn hơn căng dây lớn hơn
- Dây lớn hơn căng cung lớn hơn 3. Góc nội tiếp
a) Định nghĩa: Góc nội tiếp là góc có đỉnh nằm trên đtròn và 2 cạnh chứa 2 dây cung của đtròn đó. Cung
nằm trong góc gọi là cung bị chắn
b) Định lý: Trong 1 đtròn số đo của góc nội tiếp bằng nửa số đo của cung bị chắn Trang 55
c) Các hệ quả: Trong một đtròn
- Các góc nt bằng nhau chắn các cung bằng nhau
- Các góc nt cùng chắn 1 cung hoặc chắn các cung bằng nhau thì bằng nhau
- Góc nt (nhr hơn hoặc bằng 900) có só đo bằng nửa số đo của góc ở tâm cùng chắn một cung
- Góc nt chắn nửa đtròn là góc vuông
4. Góc tạo bởi tia tiếp tuyến và dây cung
a) Định nghĩa: Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh tại tiếp điểm, một cạnh là tiếp tuyến
và cạnh còn lại chứa dây cung
b) Định lý: Sđ của góc tạo bởi tia tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn
c) Định lý đảo: Nếu Ax B
có đỉnh nằm trên đtròn, một cạnh chứa dây cung AB, có sđ bằng nửa sđ cung
AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là 1 tia tiếp tuyến của đtròn
d) Hệ quả: Trong 1 đtròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn 1 cung thì bằng nhau
5. Góc có đỉnh ở bên trong đtròn. Góc có đỉnh ở bên ngoài đtròn
a) Góc có đỉnh ở bên trong đtròn
- Định lý: Sđ của góc ..... bằng nửa tổng sđ của 2 cung bị chắn
b) Góc có đỉnh ở bên ngoài đtròn
- Định lý: Sđ của góc ..... bằng nửa hiệu sđ của 2 cung bị chắn B. Bài tập áp dụng
Bài 1: Cho (O) và 1 điểm M cố định không nằm trên đtròn. Qua M kẻ 2 đường thẳng, đường thẳng thứ
nhất cắt đtròn (O) tại A và B, đường thẳng thứ hai cắt đtròn (O) tại C và D. CMR: MA.MB = MC.MD LG
* TH1: điểm M nằm bên trong đtròn (O) A
- Xét tam giác MAC và tam giác MDB, ta có: C
M M (đối đỉnh) 1 2 1
CAM BDM (góc nt chắn cung BC) M O 2 M AC M
DB (g.g) MA MC M .
A MB MC.MD MD MB D B
* TH2: điểm M nằm bên ngoài đtròn (O) C M
- Xét tam giác MAD và tam giác MCB, ta có: D 1 O M (chung)
D B (góc nt chắn cung AC) 1 1 M AD M
CB (g.g) 1 A MA MD B M . A MB MC.MD MC MB
Bài 2: Trên một đtròn lấy liên tiếp ba cung: AC, CD, DB sao cho sđ AC =sđ CD =sđ DB =600. hai đường
thẳng AC và BD cắt nhau tại E, hai tiếp tuyến của đtròn tại B và C cắt nhau tại T. CMR: a) AEB BTC
b) CD là tia phân giác của góc BCT? LG Trang 56 1 1 E a) Ta có: AEB
ABCD 0 0 180 60 0 60 T 2 2 1 BTC
BAC BDC 1 AB AC CD DB 2 2 C 1 D 1 0 0 0 0 180 60 60 60 0 2 60 2
Do đó: AEB BTC A B O 1 b) Ta có: 0 C
CD 30 (góc tạo bởi tia tiếp tuyến và dây cung) 1 2 1 0 C
DB 30 (góc nội tiếp) 2 2
C C . Do đó CD là phân giác của góc BCT 1 2
Bài 3: Cho tam giác ABC nội tiếp đtròn (O), tia phân giác của góc A cắt BC ở D và cắt đtròn ở M.
a) CMR: OM vuông góc với BC
b) Phân giác của góc ngoài tại đỉnh A của tam giác ABC cắt (O) ở N. CMR ba điểm M, O, N thẳng hàng.
c) Gọi K là giao điểm của NA và BC, I là trung điểm của KD. CMR: IA là tiếp tuyến của đtròn (O) LG x N 4 A 3 1 2 O 1 2 B D H K I C M
a) Ta có: A A BM CM BM CM 1 2 BM CM do
OM là trung trực của BC OM BC OB OC 1 1 b) Ta có: MAN BACCAx 0 0 .180 90 2 2
mà MAN là góc nội tiếp và 0
MAN 90 MN là đường kính. Do đó M, O, N thẳng hàng c) Do 0 0
MAN 90 DAK 90 DAK vuông tại A
mà IK = ID => IK = IA = ID => tam giác IAD cân tại I IAD D 1
IAD D (1) 2 D D 2 1
Mặt khác: tam giác OAM cân tại O OAM OMA (2)
Từ (1) và (2) IAD OAM D OMA IAO D OMA (3) 2 2
Do tam giác MHD vuông tại H (theo a) 0
D OMA 90 (4) 2 Từ (3) và (4) 0
IAO 90 IA là tiếp tuyến của đtròn (O) Trang 57
Bài 4: Cho nửa đtròn tâm O đường kính AB. Gọi C, D thuộc nửa đtròn (C thuộc cung AD). AD cắt BC
tại H, AC cắt BD tại E. Chứng minh rằng: a) EH vuông góc với AB
b) Vẽ tiếp tuyến với đtròn tại D, cắt EH tại I. Chứng minh rằng: I là trung điểm của EH LG E 1 I 1 D 2 C 2 H 1 A K O B a) Ta có: 0
ACB 90 (góc nt chắn nửa đtròn) AC BC 0
ADB 90 (góc nt chắn nửa đtròn) AD BD AE BC
Xét tam giác EAB, ta có: BE AD
H là trực tâm của tam giác EAB EH AB à
m AD BC H
b) Ta có: H B (cùng phụ F ); D B (cùng chắn cung AD) 2 1 2
H D IHD cân tại I => IH = ID (1) 2 2 0 E B 90 1 Mặt khác: 0
D D 90 E D I
ED cân tại I => ID = IE (2) 1 2 1 1 à m B D2
Từ (1) và (2) => IH = IE => I là trung điểm của EH
Bài 5: Cho (O), từ điểm M nằm ngoài đtròn (O) vẽ các tiếp tuyến MC, MD với (O) (C, D là các tiếp
điểm). Vẽ cát tuyến MAB không đi qua tâm O, A nằm giữa M và B. Tia phân giác của góc ACB cắt AB ở E a) CMR: MC = ME
b) DE là phân giác của góc ADB
c) Gọi I là trung điểm của AB. CMR 5 điểm O, I, C, M, D cùng nằm trên một đtròn
d) CMR: M là phân giác của góc CID LG C O M A E I 1 B D
a) + ta có: BCE ACE (gt)
CBA MCA (cùng chắn cung AC)
BCE CBA ACE MCA hay BCE CBA MCE (1) Trang 58
+ mặt khác: BCE CBA CEM (tính chất góc ngoài của tam giác) (2)
+ từ (1) và (2) MCE CEM M
CE cân tại M => MC = ME
b) + vì MC và MD là các tiếp tuyến => MC = MD, mà MC = ME => MD = ME => tam giác MDE cân tại
M MED MDE MDA ADE (1)
+ mặt khác: MED B BDE (tính chất góc ngoài của tam giác) (2) 1
+ (1); (2) MDA ADE B BDE (3) 1
+ lại có: MDA B (cùng chắn cung AD) (4) 1
+ (3); (4) ADE BDE DE là phân giác của góc ADB
c) + do MC, MD là các tiếp tuyến của (O) 0
OCM ODM 90 4 điểm O, C, D, M thuộc đtròn có đường kính OM (*)
+ lại có: I là trung điểm của AB IO AB (định lý đường kính và dây) => IO vuông góc với IM =>
tam giác IOM vuông tại I => 3 điểm I, O, M thuộc đtròn có đường kính OM (**)
+ (*) và (**) => 5 điểm 0, I, C, M, D cùng nằm trên một đtròn
d) + Xét đtròn đi qua 5 điểm: O, I, C, M, D có đường kính OM, ta có: 1 CIM sd CM ó g c nt 2 1 DIM d s DM ó g c nt
CIM DIM IM là phân giác của góc CID 2 à
m CM DM d s CM d s DM
Bài 6: Cho tam giác ABC nhọn nội tiếp đtròn (O), đường cao AH cắt đtròn ở D. Kẻ đường kính AE. CMR: a) BC song song với DE
b) Tứ giác BCED là hình thang cân LG A O H B C D E
a) Ta có: BC vuông góc với AD (gt) (1) + mà 0
ADE 90 (góc nt chắn nửa đtròn) => DE vuông góc với AD (2)
+ Từ (1) và (2) suy ra BC // DE (cùng vuông góc với AD)
b) HTC = HT + 2 góc ở 1 đáy bằng nhau (hoặc 2 đường chéo bằng nhau)
(Chú ý: Hình thang có 2 cạnh bên bằng nhau chưa chắc là HTC (VD: Hình bình hành là hình thang
có 2 cạnh bên bằng nhau nhưng không là HTC))
+ do BC // DE suy ra tứ giác BCED là hình thang (1) + lại có: BC // DE d s D B d
s CE (2 cung bị chắn giữa hai dây song song thì bằng nhau) d s D B d s DE d s CE d
s DE sd BE sdCD BE CD (liên hệ giữa cung và dây) (2)
+ từ (1) và (2) suy ra tứ giác BCED là Hình thang cân.
*************************************************************
Ngày dạy: …………………………………….. Trang 59 HÀM SỐ 2
y ax a 0. ĐỒ THỊ HÀM SỐ 2
y ax a 0 A. Kiến thức cơ bản 1. Tính chất hàm số 2
y ax a 0 a) Tính chất:
Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0
Nếu a < 0 thì hàm số nghịch biến khi x > 0 và đồng biến khi x < 0 b) Nhận xét:
Nếu a > 0 thì y > 0 với mọi x khác 0; y = 0 khi x = 0. giá trị nhỏ nhất của hàm số là y = 0.
Nếu a < 0 thì y < 0 với mọi x khác 0; y = 0 khi x = 0. giá trị lớn nhất của hàm số là y = 0.
2. Tính chất đồ thị hàm số 2
y ax a 0 Đồ thị hàm số 2
y ax a 0 là một đường cong đi qua gốc tọa độ và nhận trục Oy là trục đối
xứng. đường cong đó được gọi là một Parabol với đỉnh O.
Nếu a > 0 thì đồ thị nằm phía trên trục hoành, O(0;0) là điểm thấp nhất của đồ thị.
Nếu a < 0 thì đồ thị nằm phía dưới trục hoành, O(0;0) là điểm cao nhất của đồ thị. B. Bài tập áp dụng Bài 1: Cho hàm số 2 y 5 x
a) Lập bảng tính giá trị của y với các giá trị của x lần lượt bằng: 1 1 -2; -1; ; 0; ; 1; 2 2 2
b) Với giá trị nào của x thì hàm số nhận giá trị tường ứng bằng: 0; -7,5; -0,05; 50; -120 LG
a) Bảng các giá trị tương ứng của x và y là: x -2 -1 1 0 1 1 2 2 2 2 y 5 x -20 -5 5 0 5 -5 -20 4 4 b) + Với y = 0 ta có: 2 2 5
x 0 x 0 x 0 + Với y = -7,5 ta có: 2 2 5
x 7,5 x 1,5 x 1,5 + Với y = -0,05 ta có: 2 2 5 x 0
,05 x 0,01 x 0 ,1 + Với y = -7,5 ta có: 2 2 5
x 50 x 10 pt vô nghiệm + Với y = -7,5 ta có: 2 2 5 x 1
20 x 24 x 2 6 Bài 2: Cho hàm số 2 2 y m
m x . Tìm giá trị của m để:
a) Hàm số đồng biến với mọi x > 0
b) Hàm số nghịch biến với mọi x > 0 LG Ta có: 2
a m m . m m 1 m 0 m 0 m 1 0 m 1 m 1
a) Hàm số đồng biến với mọi x > 0 a 0 . m m 1 0 m 0
m 0 m 0 m 1 0 m 1
vậy m > 1 hoặc m < 0 thì hàm số đồng biến với mọi x > 0
b) Hàm số nghịch biến với mọi x > 0 m 0 m 0
a m m m 1 0 m 1 0 m 1 0 . 1 0 0 m 1 m 0
m 0 k ô h ng m m 1 0 m 1 Trang 60 Bài 3: Cho hàm số 2
y ax . Xác định hệ số a trong các trường hợp sau:
a) Đồ thị của nó đi qua điểm A(3; 12)
b) Đồ thị của nó đi qua điểm B(-2; 3) LG
a) Vì đồ thị hs đi qua điểm A nên tọa độ điểm A thỏa mãn hs, ta có: 4 2 12 .3 a a 3
b) Vì đồ thị hs đi qua điểm B nên tọa độ điểm B thỏa mãn hs, ta có: a 2 3 3 . 2 a 4 Bài 4: Cho hàm số 2 y ax
a) Xác định hệ số a, biết rằng đồ thị hàm số đi qua điểm A(2; 2)
b) Vẽ đồ thị hàm số với giá trị của a vừa tìm được LG
a) Vì đồ thị hs đi qua điểm A nên tọa độ điểm A thỏa mãn hs, ta có: 1 2 2 .2 a a 2
b) Với a = ½ ta có hàm số sau: 1 2 y x 2 14 12 10 1 8 fx = x2 2 6 4 2 -15 -10 -5 5 10 15 -2 Bài 5: Cho hàm số 2
y 0, 4x . Các điểm sau đây, điểm nào thuộc đồ thị hàm số, điểm nào không thuộc đồ
thị hàm số: A(-2; 1,6), B(3; 3,5), C( 5 ; 0,2) LG
PP: muốn kiểm tra xem 1 điểm thuộc hay không thuộc đồ thị hs ta làm như sau: thay hoành độ của điểm
đó vào hàm số, nếu giá trị của hs bằng với tung độ của nó thì điểm đó thuộc đồ thị hs; nếu giá trị của hs
không bằng với tung độ của nó thì điểm đó không thuộc đồ thị hs. - Điểm A(-2; 1,6)
Thay x = -2 vào hàm số ta có: y 2 0, 4 2
1,6 , do đó điểm A thuộc đồ thị hs - Điểm B(3; 3,5) Thay x = 3 vào hs ta có: 2
y 0, 4.3 3, 6 3,5 do đó điểm B không thuộc đồ thị hs - Điểm C( 5 ; 0,2)
Thay x = 5 vào hs ta có: y 2 0, 4. 5
2 0,2 do đó điểm C không thuộc đồ thị hs 1
Bài 6: Cho 2 hàm số 2 y x và y = 2x – 2 2
a) Vẽ đồ thị 2 hàm số trên trên cùng 1 mặt phẳng tọa độ
b) Tìm tọa độ giao điểm của 2 đồ thị LG a) Vẽ đồ thị Trang 61 14 12 10 8 1 fx = x2 g x = 2x-2 2 6 4 2 -15 -10 -5 5 10 15 -2
b) pt hoành độ giao điểm của 2 đồ thị: 1 2
x 2x 2 x x 2 1 2 2
thay x = 2 vào 1 trong 2 hs ta được: y = 2.2 – 2 = 2. Vậy tọa độ giao điểm của 2 đồ thị là M(2; 2) Bài 7: Cho hàm số 2 y ax
a) Xác định a biết rằng đồ thị hàm số cắt đường thẳng y = -3x + 4 tại điểm A có hoành độ bằng -2.
b) Với giá trị của a vừa tìm được, vẽ đồ thị 2 hàm số trên cùng mặt phẳng tọa độ
c) Tìm tọa độ giao điểm của 2 đồ thị LG
a) tung độ của điểm A là: y = -3.(-2) + 4 = 10. Vậy tọa độ điểm A(-2; 10) vì đồ thị hs 2
y ax đi qua điểm A nên tọa độ điểm A thỏa mãn hs, ta có: a 2 5 10 2 a . Khi đó 2 hs có dạng: 5 2 y x 2
b) vẽ đồ thị 2 hs trên cùng mặt phẳng tọa độ 10 8 6 5 h x = x2 2 4 2 q x = -3x+4 -10 -5 5 10 15 20 -2 -4 -6
c) pt hoành độ giao điểm của 2 đồ thị: 5 4 2 x 3
x 4 x ; x 2 1 2 2 5 + Với 4 4 8 x
y 3. 4 tọa độ điểm A( 4 8 ; ) 1 1 5 5 5 5 5 + Với x 2 y 3 . 2
4 10 tọa độ điểm B(-2; 10) 1 1 Bài 8: Cho hàm số 2 y ax
a) Xác định a biết rằng đồ thị hàm số cắt đường thẳng y = -2x + 3 tại điểm A có hoành độ bằng 1.
b) Với giá trị của a vừa tìm được, vẽ đồ thị 2 hàm số trên cùng mặt phẳng tọa độ
c) Tìm tọa độ giao điểm của 2 đồ thị. LG
a) tung độ của điểm A là: y = -2.1 + 3 = 1, do đó tọa độ của điểm A là A(1; 1) Trang 62 vì đồ thị hs 2
y ax đi qua điểm A nên tọa độ điểm A thỏa mãn hs, ta có: 2 1 .1 a
a 1. Khi đó hs có dạng: 2 y x
b) vẽ đồ thị 2 hs trên cùng mặt phẳng tọa độ 14 12 10 8 6 g x = -2x+3 4 f x = x2 2 -15 -10 -5 5 10 15 -2
c) pt hoành độ giao điểm của 2 đồ thị: 2 x 2
x 3 x 1; x 3 1 2
+ Với x 1 y 2
.1 3 1 tọa độ điểm A(1; 1) 1 1 + Với x 3 y 2 . 3
3 9 tọa độ điểm B(-3; 9) 1 1
Bài 9: Cho 2 hàm số (P): 2
y x và (d): y = 2x + 1.
a) Vẽ trên cùng mặt phẳng tọa độ đồ thị 2 hàm số trên
b) Xác định tọa độ giao điểm của (P) và (d)
c) Tìm hàm số (d1): y = ax + b biết rằng đồ thị của nó đi qua điểm A(-2; -1) và song song với (d). LG a) vẽ đồ thị 2 hs 6 4 2 q x = 2x+1 -15 -10 -5 5 10 15 -2 -4 hx = -x2 -6 -8 -10
b) pt hoành độ giao điểm của 2 đồ thị: 2
x 2x 1 x x 1 1 2 + Với x 1
y 2 1 1
tọa độ điểm A(-1; -1) 1 1
c) vì (d1) // (d) nên a = 2. khi đó (d1) có dạng: y = 2x + b
mặt khác (d1) đi qua A nên tọa độ của A thỏa mãn (d1), ta có: -1 = 2.(-2) + b => b = 3
vậy hàm số (d1): y = 2x + 3
Bài 10: Trên cùng 1 mặt phẳng tọa độ, cho Parabol (P): 2
y x và đường thẳng (d): y x 2 a) Vẽ (P) và (d)
b) Tìm tọa độ giao điểm của (P) và (d)
c) Tìm hàm số (d1): y = ax + b biết rằng đồ thị của nó song song với (d) và cắt (P) tại điểm M có hoành độ bằng 2 LG a) vẽ đồ thị Trang 63 14 12 10 8 6 4 r x = x2 2 s x = -x+2 -15 -10 -5 5 10 15 -2
b) pt hoành độ giao điểm của 2 đồ thị: 2
x x 2 x 1; x 2 1 2
+ Với x 1 y 2 1
1 tọa độ điểm A(1; 1) 1 1 + Với x 2 y 2
2 4 tọa độ điểm A(-2; 4) 1 1
c) vì d1 // d nên a = -1, do đó d1 có dạng: y = -x + b
+ tung độ của điểm M là: y = 22 = 4. Tọa độ điểm M(2; 4)
+ mặt khác d1 đi qua M nên ta có: 4 = -2 + b => b = 6 Vậy pt d1: y = -x + 6
*************************************************************
Ngày dạy: ……………………………………..
PHƯƠNG TRÌNH BẬC HAI MỘT ẨN A. Kiến thức cơ bản
1. Định nghĩa: pt bậc hai một ẩn là pt có dạng: 2
ax bx c 0a 0 (1), trong đó x là ẩn; a, b, c là các số cho trước. 2. Cách giải x 0 x 0
a) Khuyết c (c = 0): pt (1) trở thành: 2
ax bx 0 x ax b 0 b
ax b 0 x a
b) Khuyết b (b = 0): pt (1) trở thành: c 2 2 2
ax c 0 ax c x (2) a c - nếu
0 thì pt (2) vô nghiệm, suy ra pt (1) cung vô nghiệm a c c - nếu
0 x a a c) đầy đủ: 2
ax bx c 0a 0 Công thức nghiệm
Công thức nghiệm thu gọn 2
b 4ac ' '2
b ac
+ Nếu 0 thì pt có 2 nghiệm phân biệt: + Nếu '
0 thì pt có 2 nghiệm phân biệt: b b ' ' ' ' x ; x b b 1 2 x ; x 2a 2a 1 2 a a + nếu b '
0 thì pt có nghiệm kép: x x b 1 2 2a
+ nếu ' 0 thì pt có nghiệm kép: x x 1 2 a
+ nếu 0 thì pt vô nghiệm + nếu '
0 thì pt vô nghiệm d) Cho pt: 2
ax bx c 0a 0 . Điều kiện để phương trình: Trang 64 - Vô nghiệm: 0 ( ' 0 ) - Nghiệm kép: 0 ( ' 0 )
- Có 2 nghiệm phân biệt: 0 ( ' 0 ) hoặc a.c < 0 ' 0
- Có 2 nghiệm cùng dấu: x .x 0 1 2 ' 0
- Có 2 nghiệm cùng dấu âm: x .x 0 1 2 x x 0 1 2 ' 0
- Có 2 nghiệm cùng dấu dương: x .x 0 1 2 x x 0 1 2 ' 0
- Có 2 nghiệm khác dấu: x .x 0 1 2
3. Hệ thức Vi-ét và ứng dụng b x x 1 2 a - Định lý: Nếu x 2
1; x2 là 2 nghiệm của pt ax bx c 0a 0 thì c x .x 1 2 a
- Ứng dụng nhẩm nghiệm của hệ thức Vi-ét: + nếu pt 2 c
ax bx c 0a 0 có a b c 0 thì pt có 2 nghiệm là: x 1; x 1 2 a + nếu pt 2 c
ax bx c 0a 0 có a b c 0 thì pt có 2 nghiệm là: x 1 ; x 1 2 a
u v S + nếu
thì suy ra u, v là nghiệm của pt: 2
x Sx P 0 (điều kiện để tồn tại u, v là
u.v P 2
S 4P 0 ) B. Bài tập áp dụng
Bài 1: Giải các phương trình sau: 6 2 2 2 2
a) 5x 6x 0
x 0; x b) 2x 1 0 x ; x 1 2 1 2 5 2 2 5 3 2 2
c) 8x 5x 0 x 0; x
d ) 2x 3x 0 x 0; x 1 2 1 2 8 2 2
e) 2x 42 0
x 21;x 21 1 2
Bài 2: Giải các phương trình sau: 1 2 2
a) 3x 4x 1 0 x 1; x
b) x 10x 39 0
x 3; x 13 1 2 1 2 3 14 2
c) x 6x 55 0
x 11; x 5 2
d ) 3x x 70 0
x 5; x 1 2 1 2 3 1 2
e) 2x 5x 2 0 x 2; x 1 2 2
Bài 3: Giải các phương trình sau:
a) x x x 2 2 2 1 2 1 3
1 5x 6x 7 0 pt vô nghiệm Trang 65 2 10 b) 4x 1
2x x 6 2
1 0 14x 20x 0 x 0; x 1 2 7 11 c) 3x 1 x 2 2
20 3x 5x 22 0 x 2; x 1 2 3 15
d) x 44x 3 2
3 0 4x 19x 15 0 x 1; x 1 2 4
Bài 4: Chứng tỏ rằng với mọi m các phương trình sau luôn luôn có 2 nghiệm phân biệt. a) 2
x 21 m x m 0 2 1 3 Ta có: ' 2
... m m 1 m 0, m
, do đenta dương với mọi m nên pt có 2 nghiệm phân 2 4
biệt với mọi giá trị của m b) 2 2
x mx m 1 0 Ta có: ' 2 m 2 m 2 ... 4
1 ... 5m 4 0, m
, do đenta dương với mọi m nên pt có 2 nghiệm
phân biệt với mọi giá trị của m Bài 5: Cho pt 2
mx 2m
1 x 2 0 . Tìm m để pt có nghiệm kép Pt có nghiệm kép: m 0 a 0 m 0 3 2 2 3 2 2 m ; 3 2 2 3 2 2 m 1 2 2 0
4m 12m 1 0 m ; m 2 2 1 2 2 2 Bài 6: Cho 2 pt sau: 2 x mx 2 2 0 1 ;
x 2x m 0
2. Với giá trị nào của m thì 2 pt trên có 1 nghiệm chung m 2 2
- đk để pt (1) có nghiệm là: ' 2
m 8 0 (*) 1 m 2 2
- đk để pt (2) có nghiệm là: '
1 m 0 m 1 (**) 2
- từ (*) và (**) suy ra để cả 2 pt có nghiệm thì m 2 2
- giả sử x0 là 1 nghiệm chung của 2 pt trên, ta có : m 2 2 2
x mx 2 x 2x m
0 mx 2 2x m 0 m 2 x m 2 x 1 (vì m 0 0 0 0 0 0 0 0 m 2 khác 2 do m 2 2 ) - thay x
0 = 1 vào (1) hoặc (2) ta được: 2 1 m 2 0 m 3
Vậy m = -3 thì 2 pt trên có 1 nghiệm chung
Bài 7: Tìm m để 2 pt sau có nghiệm chung? 2
x m 4 x m 5 0 1 2
x m 2 x m 1 0 2 m 2 2 2
- đk để pt (1) có nghiệm là: 2
m 4m 4 0 (*) 1 m 2 2 2
- đk để pt (2) có nghiệm là: 2
m 0, m (**) 2 m 2 2 2
- từ (*) và (**) suy ra để cả 2 pt có nghiệm thì (***) m 2 2 2
- giả sử x0 là nghiệm chung của 2 pt trên, ta có : 2
x m 4 2
x m 5 x m 2 x m 1
0 m 4 m 2 x 4 x 2 0 0 0 0 0 0 - thay x 0 = 2 vào (1) ta được: 4 (m 4).2 m 5 0 m 1 (thỏa mãn (***))
Vậy m = 1 thì 2 pt trên có nghiệm chung. Trang 66
Bài 8: Tìm m để 2 pt sau có nghiệm chung? 2
2x mx 1 0 1 2
mx x 2 0 2
- đk để pt (1) có nghiệm là: 2
m 8 0, m (*) 1 1
- đk để pt (2) có nghiệm là: 1 8m 0 m (**) 2 8
- từ (*) và (**) suy ra để cả 2 pt có nghiệm thì 1 m (***) 8
- giả sử x0 là nghiệm chung của 2 pt trên, khi đó: 2 2
2x mx 1 mx x 2 0 m 2 2
x m 1 x 3 0 0 0 0 0 0 0 1 Ta có: m m m 2 2 10 25 5
0 m 5 5 m (vì m ), nên pt có 2 nghiệm phân biệt: 8
m 1 5 m 3
m 1 5 m 2m 4 2m 2 x ; x 1 0 0 1 2m 2 2 m 2 2m 2 2m 2 2m 2 3 - thay x vào (1) ta được: 1 0 m 2 2 3 3 2. . m 1 0 18 3m
m2m 22 2
0 m m 7 0 (phương trình vô nghiệm m 2 m 2 vì có 2 7 0 ) m
- thay x 1 vào (1) ta được: 2 2.1 .1
m 1 0 m 1 (thỏa mãn (***)) 02
Vậy m = -1 thì 2 pt trên có nghiệm chung. Bài 9: Cho pt 2
x 4x m 1 0
a) xác định m để pt có nghiệm
b) Tìm m để pt có 2 nghiệm thỏa mãn: 2 2 x x 10 1 2 LG a) Ta có: '
... 3 m . Pt có nghiệm '
0 3 m 0 m 3 x x 4
b) với m 3 giả sử pt có 2 nghiệm là x1 ; x2. theo Vi-ét ta có: 1 2 (*)
x .x m 1 1 2
lại có: x x 10 x x 2 2 2 2x x 10 (**) 1 2 1 2 1 2
thay (*) vào (**) ta được: 2 4 2m
1 10 m 2 (thỏa mãn điều kiện) 5 Bài 10: Cho pt 2
3x 5x m 0 . Xác định m để pt có 2 nghiệm thỏa mãn 2 2 x x 1 2 9
Ta có: ... 25 12m Pt có 2 nghiệm 25
0 25 12m m (*) 12 5 x x (1) 1 2 với 25 3 m
giả sử pt có 2 nghiệm là x1 ; x2. theo Vi-ét ta có: 12 m x .x 2 1 2 3 lại có: 5 5 5 5 1 2 2 x x x x x x x x
x x (3) 1 2 1 2 1 2 1 2 1 2 9 9 3 9 3 Trang 67 5 x x x 1 1 2 1
kết hợp (1) và (3) ta có hệ phương trình: 3 m 2 thay vào (2) ta được 2 1. m 2 1 x 3 3 2 x x 1 2 3 3 (thỏa mãn đk (*)) Bài 11: Cho pt 2
x 2mx 2m 1 0
a) Chứng tỏ rằng pt có nghiệm x1, x2 với mọi m b) Đặt A 2 2 2 x x 5x x 1 1 1 2 * CMR: 2
A 8m 18m 9 * Tìm m để A = 27
c) Tìm m để pt có nghiệm này bằng 2 lần nghiệm kia LG
a) ta có m m m 2 2 2 1 1 0, m
, do đó pt có 2 nghiệm với mọi giá trị của m
x x 2m
b) + với mọi m pt có nghiệm x1, x2. theo Vi-ét ta có: 1 2 (*)
x .x 2m 1 1 2
từ A 2x x 5x x A 2x x 2 2 2 9x x (**) 1 1 1 2 1 2 1 2
thay (*) vào (**) ta được: A m2 m 2 2 2 9 2
1 8m 18m 9 => đpcm + với A = 27 suy ra 3 2 2
8m 18m 9 27 8m 18m 18 0 m 3; m 1 2 4
c) giả sử x1 = 2.x2, kết hợp (*) ta có: 4m 4m x x 1 1 3 3 x 2x x 2x 1 2 1 2 2m 2m
x x 2m 3 x 2m x x 1 2 2 2 2 3 3
x .x 2m 1
x .x 2m 1 1 2 1 2 2 4m 2m 8
m 18m 9 0 . 2m 1 3 3 giải pt 3 3 2
8m 18m 9 0 m ; m 1 2 2 4
***************************************************
Ngày dạy: …………………………………….
CÁC GÓC VỚI ĐƯỜNG TRÒN – TỨ GIÁC NỘI TIẾP
A. Kiến thức cơ bản: Tứ giác nội tiếp
1. Định nghĩa: Tứ giác có 4 đỉnh nằm trên đtròn đgl tứ giác nội tiếp
2. Tính chất: Trong 1 tứ giác nội tiếp tổng số đo các góc đối diện bằng 1800
3. Dấu hiệu: Để chứng minh một tứ giác nội tiếp đtròn ta chứng minh:
- Tứ giác có 4 đỉnh nằm trên đtròn
- Tứ giác có tổng 2 góc đối diện bằng 1800
- Tứ giác có 2 góc bằng nhau cùng nhìn xuống 1 cạnh
B. Bài tập áp dụng:
Bài 1: Cho tam giác ABC vuông tại A, điểm M nằm trên AC, đtròn đường kính CM cắt BC tại E, BM cắt đròn tại D
a) CMR: tứ giác BADC nội tiếp
b) DB là phân giác của góc EDA
c) CMR 3 đường thẳng BA, EM, CD đồng quy Trang 68 B E M 1 A O C 1 2 D K a) ta có: 0 BAC 90 (gt) 0
BDC 90 (góc nt chắn nửa đtròn)
Suy ra tứ giác BADC nt đtròn đường kính BC
b) ta có: C D (cùng chắn cung ME) 1 1
vì tứ giác BADC nt C D (cùng chắn cung AB) 1 2
D D DB là phân giác của góc EDA 1 2
c) giả sử AB cắt CD tại K CK BK
xét tam giác KBC, ta có: BD CK
M là trực tâm của tam giác KBC KM BC
CA BD M
mặt khác ME BC (góc nt chắn nửa đtròn), suy ra đthẳng KM và ME trùng nhau
do đó 3 đthẳng AB, EM, CD đồng quy tại K
Bài 2: Cho tam giác ABC có 3 góc nhọn. Đường tròn tâm O đường kính BC cắt AB tại E, cắt AC tại F.
Các tia BE cà CE cắt nhau tại H. CMR: a) AH vuông góc với BC
b) Gọi K là giao điểm của AH và BC. CMR: FB là phân giác của góc EFK
c) Gọi M là trung điểm của BH. CMR: tứ giác EMKF nt A F 12 E H M1 2 1 2 2 1 C B K O a) ta có: 0
BEC 90 (góc nt chắn nửa đtròn) CE AB 0
BFC 90 (góc nt chắn nửa đtròn) BF AC CE AB
xét tam giác ABC, ta có: BF AC
H là trực tâm của tam giác ABC AH BC
BF CE H Trang 69 b) xét tứ giác CKHF, có: 0
K F 180 tứ giác CKHF nt C F (cùng chắn cung HK) 1 2
mặt khác: C F (cùng chắn cung BE) 1 1
suy ra F F , do đó FB là phân giác của góc EFK 1 2 c) xét tứ giác BKHE có 0
K E 180 tứ giác BKHE nt B K (cùng chắn cung HE) 1 1
mà: B C (cùng chắn cung EF) 1 2
mặt khác, do tứ giác CKHF nt K C (cùng chắn cung HF) 1 2
suy ra B K C K (1) 1 1 2 2 0 E 90 xét tam giác BEH, có:
BM HM ME B ME cân tại M BM HM
do đó EMF 2B (tính chất góc ngoài của tam giác) (2) 1
từ (1) và (2) EMF 2K 2K EKF tứ giác EMKF nt 1 2
Bài 3: Cho đtròn (O), điểm A nằm bên ngoài đtròn. Qua A kẻ 2 tiếp tuyến AB, AC với đtròn (B, C là các
tiếp điểm). M là một điểm trên dây BC, đthẳng qua M vuông góc với OM cắt tia AB và AC lần lượt tại D và E. CMR:
a) Các tứ giác: BDOM; ECOM nt
b) M là trung điểm của DE D B 1 1 M O A 1 1 E C
a) xét tứ giác BDOM, ta có: 0 DMO 90 (gt) 0
DBO 90 (tính chất tiếp tuyến)
Suy ra 4 điểm B, D, O, M nằm trên đtròn đường kính DO, do đó tứ giác BDOM nt xét tứ giác ECOM, ta có: 0 OME 90 (gt) 0
OCE 90 (tính chất tiếp tuyến) Suy ra 0
OME OCE 180 do đó tứ giác ECOM nt
b) vì tứ giác BDOM nt nên B D (cùng chắn cung MO) (1) 1 1
tứ giác ECOM nt nên C E (cùng chắn cung MO) (2) 1 1
mà B C (vì tam giác OBC cân tại O) 1 1
từ (1), (2) và (3) suy ra D E , do đó tam giác ODE cân tại O, lại có OM DE (gt), do đó OM là 1 1
đường cao đồng thời là đường trung tuyến ứng với cạnh DE => MD = ME. đpcm
Bài 4: Cho đtròn (O) và (O’) cắt nhau tại A và B (O và O’ thuộc 2 nửa mặt phẳng bờ AB). Qua B kẻ cát
tuyến vuông góc với AB cắt đtròn (O) ở C, căt đtròn (O’) ở D, tia CA cắt (O’) ở I, tia DA cắt (O) ở K. a) CMR: tứ giác CKID nt
b) Gọi M là giao điểm của CK và DI. Chứng minh 3 điểm M, A, B thẳng hàng Trang 70 M K I A O O' C D B a) vì 0
ABC 90 AC là đường kính của (O) 0
ABD 90 AD là đường kính của (O’) Ta có: 0
CKA 90 (góc nt chắn nửa đtròn (O)) 0
DIA 90 (góc nt chắn nửa đtròn (O’))
Do đó: CKA DIA tứ giác CKID nt đường tròn đường kính CD CI MD
b) xét tam giác MCD, ta có: DK MC
A là trực tâm của t.giác MCD MA CD (1)
CI DK A
mà AB CD (2)
từ (1) và (2) suy ra 3 điểm M, A, B thẳng hàng. đpcm
Bài 5: Cho đtròn (O) đường kính AB, M là 1 điểm trên đtròn; C là 1 điểm nằm giữa A và B. qua M kẻ
đthẳng vuông góc với CM, đthẳng này cắt các tiếp tuyến của (O) kẻ từ A và B lần lượt tại E và F. CMR:
a) Các tứ giác: AEMC, BCMF nt
b) Tam giác ECF vuông tại C E 1 M 1 F 2 2 1 1 A B C O a) xét tứ giác AEMC có: 0 0 0
A M 90 90 180 , mà góc A và góc M là 2 góc ở vị trí đối diện, do đó tứ giác AEMC nt
chứng minh tương tự ta cũng có tứ giác BCMF nt
b) vì tứ giác ACME nt A E (cùng chắn cung MC) (1) 1 1
tứ giác BCMF nt B F (cùng chắn cung MC) (2) 1 1 ta có: 0
AMB 90 (góc nt chắn nửa đtròn) 0
A B 90 (3) 1 1 từ (1); (2) và (3) 0
E F 90 1 1 xét tam giác ECF, có: 0 0
E F 90 ECF 90 ECF vuông tại C 1 1
Bài 6: Cho tam giác ABC nhọn nt đtròn (O), có 2 đường cao BB’ và CC
a) CMR: tứ giác BCB’C’ nt
b) Tia AO cắt đtròn (O) ở D và cắt B’C’ ở I. CMR: tứ giác BDIC’ nt
c) Chứng minh OA vuông góc với B’C’ Trang 71 A B' I O C' C D B
a) xét tứ giác BCB’C’ có ' ' 0
BB C BC C 90 tứ giác BCB’C’ nt
b) ta có: ACB ADB (cùng chắn cung AB) (1)
mặt khác do tứ giác BCB’C’ nt ' ' 0
BC B ACB 180 (2) từ (1) và (2) ' ' 0
BC B ADB 180 hay ' 0
BC I IDB 180 , suy ra tứ giác BDIC’ nt c) ta có: 0
ABD 90 (góc nt chắn nửa đtròn) ' 0 C BD 90 do tứ giác BDIC’ nt ' ' 0 ' 0 ' '
C BD C ID 180 C ID 90 AO B C
Bài 7: Cho hình vuông ABCD. Gọi M, N là 2 điểm lần lượt trên 2 cạnh BC và CD sao cho 0 MAN 45 .
AM và AN cắt đường chéo BD tại P và Q. Gọi H là giao điểm của MQ và NP. CMR: a) Tứ giác ABMQ nt b) Tam giác AQM vuông cân c) AH vuông góc với MN A B 1 2 450 P M H Q 1 2 D N C
a) vì ABCD là hình vuông có BD là đường chéo, nên BD là phân giác của góc ABC 1 0 0 0
B B .90 45 B QAM 45 tứ giác ABMQ nt 1 2 2 2 b) vì tứ giác ABMQ nt 0 0 0 0
ABM AQM 180 90 AQM 180 AQM 90 MQ AN 0 A 45 xét tam giác AQM, có:
AQM vuông cân tại Q 0 AQM 90
c) ta có: DB là đường chéo của hình vuông ABCD nên DB là phân giác của góc ADC 1 0 0
D D .90 45 1 2 2 tứ giác ADNP có 0
DAN D 45 tứ giác ADNP nt 2 0 0 0 0
ADN APN 180 90 APN 180 APN 90 NP AM MQ AN
Xét tam giác AMN, ta có: NP AM
H là trực tâm của tam giác AMN AH MN
MQ NP H
**************************************************************** Trang 72
Ngày dạy:……………………………..
PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC HAI
A. Kiến thức cơ bản:
1. Phương trình trùng phương. - dạng tổng quát: 4 2
ax bx c 0a 0
- cách giải: dùng phương pháp đặt ẩn phụ, đặt 2
x t t 0 . Khi đó ta có pt: 2
at bt c 0 (đây là pt bậc hai một ẩn)
2. Phương trình chứa ẩn ở mẫu: Các bước giải
- Tìm đk xác định của pt
- Quy đồng mẫu thức cả 2 vế của pt, rồi khử mẫu
- Giải pt vừa nhận được
- Kết luận: so sánh nghiệm tìm được với đk xác định của pt 3. Phương trình tích. - dạng tổng quát: A . B ... 0 x x A x 0 - cách giải: A B
x . x ... 0 B x 0
B. Bài tập áp dụng:
Bài 1: Giải phương trình. 4 2 4 2
a) x 5x 6 0
b) 4x 3x 1 0 4 2 4 2
c) x 29x 100 0
d ) x 13x 36 0
Bài 2: Giải phương trình. 2 1 3 1 2x 1 x 2 8x 3 a) b 2 x ) 2 2 1 x 1 4 18x 6 3x 1 9x 1 2 30 13 7 18x 7 x 4 3x 38 c) d ) 2 2 3 2 x 1 x x 1 x 1 x 1 2x 2 x 1
Bài 3: Giải phương trình.
a) x 3x
1 x 3x 2 2
b) x x 6 x 22 x 3 2 2 2 1
c) x 5 x 2 x 7 x 7 12x 23
d ) 2x 32 2 2 2 3
10x 15x 0 3 2 )
e x 5x x 5 0
Bài 4: Tìm m để pt ẩn x sau có 4 nghiệm: 4 2
x 6x m 0 (1) Đặt 2
x t t 0 . Khi đó pt (1) trở thành: 2
t 6t m 0 (2) '
9 m 0
Để pt (1) có 4 nghiệm thì pt (2) phải có 2 nghiệm phân biệt dương t
t 6 0 0 m 9 1 2
t .t m 0 1 2
Bài 5: Tìm m để pt có 2 nghiệm: 4
x m 2 2
1 x m 3 0 (1) Đặt 2
x t t 0 . Khi đó pt (1) trở thành: 2
t 2m
1 t m 3 0 (2)
Để pt (1) có 2 nghiệm thì pt (2) phải có 1 nghiệm dương (hay có 2 nghiệm trái dấu) 2 0 1 m2 ' m 3 3 7 2 0
m 3m 4 0 m 0 m 2 4 m 3 t .t 0 m 3 0 m 3 0 m 3 1 2 m 3 Bài 6: Cho pt: 4
mx m 2 2
3 x m 0 (1). Với giá trị nào của m thì pt có 4 nghiệm? Đặt 2
x t t 0 . Khi đó pt (1) trở thành: 2
mt 2m 3t m 0 (2) Trang 73
Để pt (1) có 4 nghiệm thì pt (2) phải có 2 nghiệm dương phân biệt: a m 0 m m 3 0 2 ' 2 m 0 m 0 m 3 3 6m 9 0 m m 0 2 3 2 2 t t 0 1 2 m 3 m 0 3 m 0 . 1 0 m t t 1 2
***************************************************************
Ngày dạy: …………………………………
GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH – HỆ PHƯƠNG TRÌNH
A. Kiến thức cơ bản:
- các bước giải bài toán bằng cách lập pt (hpt): 3 bước
B. Bài tập áp dụng:
Bài 1: Tìm 2 số biết tổng của chúng bằng 17 và tổng các bình phương của chúng là 157.
Gọi số thứ nhất là x (x < 17) Số thứ hai là: 17 – x
Theo bài ra ta có pt: x 17 x2 2 2
157 ... 2x 34x 132 0 x 11; x 6 1 2
Vậy 2 số cần tìm là: 11 và 6
Bài 2: Hai tổ đánh cá trong tháng đầu bắt được 590 tấn cá, tháng sau tổ 1 vượt mức 10%, tổ 2 vượt mức
15%, do đó cuối tháng cả hai tổ bắt được 660 tấn cá. Tính xem trong tháng đầu mỗi tổ bắt được bao nhiêu tấn cá. * Cách 1: lập pt Tháng đầu Tháng sau Tổ 1 x x 10%.x Tổ 2 590 x
590 x15%.590 x ……
Ta có pt: x 10%.x 590 x 15%.590 x 660 ...x 370
Vậy tổ 1: 370 tấn cá; tổ 2: 220 tấn cá * Cách 2: lập hê pt Tháng đầu Tháng sau Tổ 1 x
x 10%.x 1,1x Tổ 2 y
y 15%.y 1, 5 y ……….
x y 590 x 370 Ta có hpt: 1
,1x 1,5y 660 y 220
Bài 3: Lấy 1 số có 2 chữ số chia cho số viết theo thứ tự ngược lại thì được thương là 4 và dư 15. nếu lấy
số đó trừ đi 9 thì được 1 số bằng tổng bình phương của mỗi chữ số đó. Tìm số này?
Gọi số cần tìm là xy x, y N;0 x, y 9
Số viết theo thứ tự ngược lại là: yx
Vì lấy xy đem chia cho yx được thương là 4 và dư 15 nên ta có:
xy 4yx 15 2x 13y 5 (1)
Lấy xy trừ đi 9 được 1 số bằng tổng bình phương của mỗi chữ số, nên ta có: 2 2 2 2
xy 9 x y 10x y 9 x y (2) Trang 74
2x 13y 5 x 9
Từ (1) và (2) ta có hpt: ... xy 91 2 2 1
0x y 9 x y y 1
Bài 4: hai vòi nước cùng chảy vào 1 cái bể sau 1 thời gian thì đầy bể. Nếu vòi 1 chảy 1 mình thì lâu hơn
2h mới đầy bể so với cả 2 vòi, vòi 2 chảy 1 mình thì phải lâu hơn 4,5h mới đầy bể so với cả 2 vòi. Hỏi
nếu chảy 1 mình thì mỗi vòi chảy bao lâu mới đầy bể? Cả 2 vòi Vòi 1 Vòi 2 TGHTCV x x 2 x 4, 5 1h chảy được 1 1 1 x x 2 x 4, 5 1 1 1 Ta có pt: 2
... x 9 x 3 x 2 x 4,5 x
Nghiệm thỏa mãn là x = 3
Bài 5: 1 công nhân phải hoàn thành 50 sản phẩm trong 1 thời gian quy định. Do cải tiến kỹ thuật nên mỗi
giờ đã tăng năng suất thêm 5 sản phẩm vì thế người ấy hoàn thành kế hoaahj sớm hơn thời gian quy định
là 1h40ph. Tính số sản phẩm mỗi giờ người đó phải làm theo dự định.
Số sản phẩm mỗi giờ làm TGHTCV Dự định x 50 x Thực tế x 5 50 x 5 ……. Ta có pt: 50 50 5 2
..... x 5x 150 0 x x 5 3
x 10; x 1 5 1 2
Nghiệm thỏa mãn là x = 10
Bài 6: 1 chiếc thuyền khởi hành từ bến sông A. sau 2h40ph một ca nô chạy từ A đuổi theo và gặp thuyền
cách bến A 10km. Hỏi vận tốc của thuyền, biết rằng vận tốc ca nô hơn vận tốc của thuyền là 12km/h. S V T Ca nô 10 x 12 10 x 12 Thuyền 10 x 10 x ….. ta có pt: 10 10 8
30x 12 30x 8xx 12 2
.... 8x 96x 360 0 x x 12 3
x 3; x 1 5 1 2
Giá trị thỏa mãn là x = 3
Bài 7: khoảng cách giữa 2 bến sông A và B là 30km. 1 ca nô đi từ A đến B, nghỉ 40ph ở B, rồi lại trở về
A. thời gian kể từ lúc đi đến lúc trở về A là 6h. Tính vận tốc của ca nô khi nước yên lặng, biết vận tốc dòng nước là 3km/h. V S T Nước yên lặng x xuôi x 3 30 30 x 3 Ngược x 3 30 30 x 3 Ta có phương trình: 30 2 30 30 30 16 3 2 6
8x 90x 72 0 x 12; x 1 2 x 3 3 x 3 x 3 x 3 3 4 Trang 75
Bài 8: 1 phòng họp có 360 ghế được xếp thành các dãy và số ghế trong mỗi dãy đều bằng nhau. Nếu số
dãy tăng thêm 1 và số ghế trong mỗi dãy tăng thêm 1 thì thì phòng họp có 400 ghế. Tính số dãy ghế và số
ghế trong 1 dãy lúc ban đầu. Số dãy Số ghế trong 1 dãy Số ghế của cả phòng Ban đầu x y xy Sau khi thay đổi x 1 y 1
x 1 y 1 xy 360 xy 360 Ta có hpt:
x, y là nghiệm của pt bậc x 1 y 1 400
x y 39 hai: 2
t 39t 360 0 t 24; t 15 1 2
Vậy: - Nếu số dãy ghế bằng 24 thì số ghế trong một dãy là 15
- Nếu số dãy ghế bằng 15 thì số ghế trong một dãy là 24.
Bài 9: 1 xuồng máy xuôi dòng 30km, và ngược dòng 28km hết 1 thời gian bằng thời gian mà xuồng máy
đi 59,5km trên mặt hồ yên lặng. Tính vận tốc của xuồng khi đi trên hồ yên lặng, biết rằng vận tốc của nước là 3km/h V S T Nước yên lặng x 59,5 59, 5 119 x 2x xuôi x 3 30 30 x 3 Ngược x 3 28 28 x 3 ….. Ta có pt: 119 30 28
119x 3x 3 2 .x30.x 3 2 .x28.x 3 2x x 3 x 3 2 2
3x 12x 1071 0 x 4x 357 0 x 17; x 2 1 1 2
Bài 10: 1 lâm trường dự định trồng 75ha rừng trong một số tuần lễ. Do mỗi tuần trồng vượt mức 5ha so
với kế hoạch nên đã trồng được 80ha và hoàn thành sớm hơn 1 tuần. Hỏi mỗi tuần lâm trường dự định trồng bao nhiêu ha rừng?
1 tuần trồng được số ha TGHTCV Kế hoạch x 75 x Thực tế x 5 80 x 5 ….. Ta có pt: 75 80 2
1 x 10x 375 0 x 15; x 25 1 2 x x 5
Bài 11: 1 ca nô xuôi từ A đến B cách nhau 24km, cùng lúc đó cũng từ A đến B 1 bè nứa trồi với vận tốc
dòng nước là 4km/h. Khi đến B ca nô quay trở lại và gặp bè nứa tại điểm C cách A là 8km. Tính vận tốc thực của ca nô. A C B
Gọi vận tốc thực của ca nô là: x (km/h; x > 4)
Vận tốc xuôi: x + 4 (km/h)
Vận tốc xuôi: x - 4 (km/h)
Thời gian xuôi từ A đến B: 24 (h) x 4
Quãng đường BC: 24 – 8 = 16 (km)
Thời gian ngược từ B đến C: 16 (h) x 4 Trang 76
Thời gian bè nứa đi từ A đến C: 8 2 (h) 4 24 16 Ta có pt: 2
2 2x 40x 0 x 0; x 20 1 2 x 4 x 4 BÀI TẬP VỀ NHÀ:
Bài 1. Hai thành phố A và B cách nhau 50km. Một người đi xe đạp từ A đến B. Sau đó 1giờ 30phút một
xe máy cũng đi từ A và đến B trước người đi xe đạp 1 giờ .Tính vận tốc của mỗi người biết vận tốc của
người đi xe máy bằng 2,5 lần vân tốc người đi xe đạp . * Lập bảng Quãng đường Vận tốc Thời gian Xe đạp 50 50 x x Xe máy 50 2,5x 50 2, 5.x * Ta có phương trình: 50 50 3 1, nghiệm x = 12 x 2, 5.x 2
Bài 2: Một ô tô đi từ Hải Phòng về Hà Nội, đường dài 100km, người lái xe tính rằng nếu tăng vận tốc
thêm 10 km/h thì về đến Hà Nội sớm nửa giờ. Tính vận tốc của ô tô nếu không tăng. * Lập bảng Quãng đường Vận tốc Thời gian Không tăng 100 x 100/x Tăng 100 x + 10 100/x + 10 * Ta có phương trình: 100 100 1 x x 10 2
Bài 3. Một ô tô đi quãng đường AB dài 840km, sau khi đi được nửa đường xe dừng lại 30 phút nên trên
quãng đường còn lại, xe phải tăng vận tốc thêm 2km/h để đến B đúng hẹn. Tính vận tốc ban đầu của ô tô .
+ Gọi vân tốc ban đầu của ô tô là x (km/h, x > 0)
+ Thời gian đi hết quãng đường AB theo dự định là: 840 (h) x
+ Nửa quãng đường đầu ô tô đi hết: 420 (h) x
+ Vận tốc của ô tô trên nửa quãng đường còn lại là: x + 2 (km/h)
+ Thời gian của ô tô trên nửa quãng đường còn lại là: 420 (h) x 2
+ Theo bài ra ta có phương trình sau: 840 420 1 420
........... x 40; x 42 1 2 x x 2 x 2
Bài 4. Quãng sông từ A đến B dài 36km, một ca nô xuôi từ A đến B rồi ngược từ B về A hết tổng cộng 5
giờ. Tính vận tốc thực của ca nô biết vận tốc dòng nước là 3km/h V thực V nước V xuôi V ngược S t Xuôi x + 3 36/x+3 x 3 36 Ngược x – 3 36/x-3 36 36 * ta có pt sau:
5 x 15; x 0 ,6 x 3 x 3
Bài 5. Lúc 7 giờ một ô tô đi từ A đến B. Lúc 7giờ 30 phút một xe máy đi từ B đến A với vận tốc kém vận
tốc của ô tô là 24km/h. Ô tô đến B được 1 giờ 20 phút thì xe máy mới đến A. Tính vận tốc của mỗi xe ,
biết quãng đường AB dài 120km. * lập bảng V S T Ô tô x 120 120/x Trang 77 Xe máy x-24 120 120/x-24
- thời gian xe máy đi nhiều hơn ô tô là: 4 1 5 (h) 3 2 6 120 120 5 - ta có pt: 2
x 24x 3456 0 x 72; x 4 8 x 24 x 6
Bài 6: Một người đi đoạn đường dài 640 km với 4 giờ đi ô tô và 7 giờ đi tàu hỏa .Hỏi vận tốc cuả ô tô và
tàu hỏa biết rằng vận tốc cuả tàu hỏa hơn vận tốc cuả ô tô là 5 km/h. * lập bảng V T S ô tô x 4 4x Tàu hỏa x+5 7 7(x+5)
* ta có pt : 4x + 7(x + 5) = 640 => x = 55
Bài 7. Một ca nô xuôi từ A đến B, cùng lúc đó một người đi bộ đi từ dọc bờ sông về hướng B. Sau khi
chạy được 24km, ca nô quay trở lại và gặp người đi bộ tại C cách A là 8km. Tính vận tốc của ca nô khi
nước yên lặng , biết vận tốc người đi bộ và vận tốc dòng nước đều bằng 4km/h Toán năng suất * Chú ý:
- Năng suất (NS) là số sản phẩm làm được trong một đơn vị thời gian (t).
- (NS) x (t) = Tổng sản phẩm thu hoạch
Bài 1. Hai công nhân phải làm theo thứ tự 810 và 900 dụng cụ trong cùng một thời gian. Mỗi ngày người
thứ hai làm được nhiều hơn người thứ nhất là 4 dụng cụ. Kết quả người thứ nhất hoàn thành trước thời
hạn 3 ngày, người thứ hai hoàn thành trước thời hạn 6 ngày. Tính số dụng cụ mỗi người phải làm trong mỗi ngày. * Lập bảng
Tổng số sản phẩm cần làm Mỗi ngày làm được TGHTCV Người 1 810 x 810/x Người 2 900 y 900/y
y x 4 * Ta có hệ phtrình: 2 810 900
x 34x 1080 0 x 20; x 54 , sau đó tìm y 1 2 3 6 x y
Bài 2. Hai đội công nhân, mỗi đội phải sửa một quãng đường dài 20km, trong một tuần cả hai đội làm
tổng cộng được 9km. Tính xem mỗi đội sửa được bao nhiêu km trong một tuần, biết thời gian đội I làm
nhiều hơn đội II làm là một tuần . * Lập bảng
Tổng số quãng đường phải sửa Mỗi tuần làm được TGHTCV Đội 1 20 x 20/x Đội 2 20 9 – x 20/9 – x 20 20 * Ta có phtrình: 2
1 x 49x 180 0 x 45; x 4 x 9 x
Bài 3. Một đội công nhân dự định hoàn thành công việc với 500 ngày công thợ. Hãy tính số người của
đội, biết rằng nếu bổ sung thêm 5 công nhân thì số ngày hoàn thành công việc giảm 5 ngày . * Lập bảng Tổng số ngày công Số công nhân TGHTCV Lúc đầu 500 x 500/x Sau khi bổ sung 500 x + 5 500/ x + 5 500 500 * Ta có phtrình: 2
5 x 5x 500 0 x 2 5; x 20 x x 5
***************************************************************
Ngày dạy: …………………………. Trang 78 ÔN TẬP HÌNH HỌC
Bài 1: Từ 1 điểm M ở ngoài (O), vẽ 2 tiếp tuyến MA, MB với đtròn. Trên cung nhỏ AB lấy 1 điểm C. Vẽ
CD vuông góc với AB, CE vuông góc với MA, CF vuông góc với MB. Gọi I là giao điểm của AC và DE,
K là giao điểm của BC và DF. CMR:
a) Tứ giác AECD nt; tứ giác BFCD nt b) CD2 = CE.CF c) Tứ giác ICKD nt d) IK vuông góc với CD A 1 2 O 1 E I 2 D 1 2 C K 1 1 M 2 2 F B a) Ta có: 0
AEC ADC BDC BFC 90 (gt)
+ xét tứ giác AECD, ta có: 0
AEC ADC 180 , mà 2 góc này ở vị trí đối nhau suy ra tứ giác AECD nt
+ xét tứ giác BFCD, ta có: 0
BDC BFC 180 , mà 2 góc này ở vị trí đối nhau suy ra tứ giác BFCD nt
b) ta có: A B (cùng chắn cung AC) 1 1
+ do tứ giác BFCD nt F B (cùng chắn cung CD) 1 1
Suy ra: F A (1) 1 1
+ do tứ giác AECD nt A D (cùng chắn cung CE) (2) 1 1
Từ (1) và (2) suy ra: F D B 1 1 1
Mặt khác: A B (cùng chắn cung BC) 2 2
+ do tứ giác AECD nt A E (cùng chắn cung CD) 2 2
Suy ra: E B (3) 2 2
+ do tứ giác BFCD nt D B (cùng chắn cung CF) (4) 2 2
Từ (3) và (4) suy ra: E D A 2 2 2
Xét tam giác CDE và tam giác CDF, ta có: D F 1 1 CD CE CDE CFD g.g 2
CD CE.CF CF CD E D 2 2
c) Xét tứ giác ICKD, ta có: 0
ICK IDK ICK D D ACB B A 180 (tổng các góc của tam 1 2 1 2
giác ABC), mà ICK; IDK là 2 góc ở vị trí đối nhau, suy ra tứ giác ICKD nt
d) ta có tứ giác ICKD nt I D (cùng chắn cung CK), mà D A (cmt) 1 2 2 2
Suy ra I A , mà I ; A là 2 góc ở vị trí đồng vị nên IK // AB, lại do AB vuông góc với CD, nên IK 1 2 1 2 vuông góc với CD
Bài 2: Cho tam giác ABC cân tại A nt đtròn (O), điểm D thuộc tia đối của tia AB, CD cắt (O) tại E, tiếp
tuyến của (O) tại B cắt EA ở F. CMR: Trang 79 a) Tứ giác BFDE nt b) FD // BC D 1 F 2 A 1 E 2 O 2 1 1 B C
a) ta có: B E (cùng bù với E ) 1 1 2
mà B C (do tam giác ABC cân tại A) 1 1
suy ra: E C (1) 1 1
mặt khác: E C B (cùng chắn cung AB) (2) 2 1 2
từ (1) và (2) suy ra E B 2 đỉnh B, E cùng nhìn xuống cạnh DF dới 2 góc bằng nhau, suy ra tứ giác 1 2 BFDE nt
b) do tứ giác BFDE nt E D (cùng chắn cung BF), mà E 2 1
2 = B2 = C1 = B1, suy ra D1 =
B1 (2 góc ở vị trí so le trong) => FD // BC
Bài 3: Cho hình vuông ABCD, điểm M thuộc cạnh AD. Vẽ đtròn (O) đường kính MB, cắt AC tại E (khác
A). Gọi là giao điểm của ME và DC. CMR: a) Tam giác BEM vuông cân b) EM = ED
c) 4 điểm B, M, D, K thuộc cùng 1 đtròn
d) BK là tiếp tuyến của (O) A B 1 2 O M 1 2 E 2 1 2 1 1 C D K
a) vì tứ giác ABEM nt => BAM + BEM = 1800 => 900 + BEM = 1800 => BEM = 900 (1)
Mặt khác: A1 = A2 (tính chất của hình vuông) => sđ cung BE = sđ cung ME => BE=ME (2)
Từ (1) và (2) suy ra tam giác BEM vuông cân tại E
b) xét tam giác BCE và tam giác DCE, ta có: CE: chung
C1 = C2 (tính chất của hình vuông) CB = CD (gt) Trang 80 Do đó B CE D
CE (c.g.c) => BE = DE (cạnh tương ứng) (3)
Từ (2) và (3) => EM = ED (= BE) (4) 0 K M 90 1 1 c) ta có: 0 D D 90
K D E
DK cân tại E => ED = EK (5) 1 2 1 1 M D E DM â c n do EM ED 1 2
(4) và (5) => EB = EM = ED = EK => 4 điểm B, M, D, K thuộc cùng 1 đtròn có tâm E d) do tứ giác BKDM nt (E) 0 0
MDK MBK 180 ........ MBK 90 BK BM BK là tiếp tuyến của đtròn (O)
Bài 4: Cho tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên nội tiếp đtròn (O). Tiếp tuyến tại B và
C của đtròn lần lượt cắt tia AC và tia AB ở D và E. CMR: a) BD2 = AD.CD b) Tứ giác BCDE nt c) BC // DE A O j 1 1 C B 2 2 1 1 2 2 D E
a) ta có: A1 = B2 (cùng chắn cung BC)
xét tam giác ABD và tam giác BCD, ta có: A B 1 2 AD BD ABD BCD g.g 2 BD . AD CD : BD CD D chung 1 b) ta có: 1 E sd AC sd BC 1 2 1 D sd AB sd BC
D E 2 điểm D và E cùng nhìn xuống cạnh BC dưới 2 góc bằng 1 1 1 2 à
m AB AC sd AB sd AC nhau => tứ giác BCDE nt
c) ta có: B C (gt), mà tứ giác BCDE nt => BED = C 1 1 1 (cùng bù với BCD)
do đó B1 = BED (2 góc ở vị trí đồng vị) => BC // DE
Bài 5: Cho tứ giác ACBD nt đtròn (O), 2 đường chéo AB và CD vuông góc với nhau tại I. trung tuyến IM
của tam giác AIC cắt BD ở K, đường cao IH của tam giác AIC cắt BD ở N.
a) CMR: IK vuông góc với BD
b) Chứng minh N là trung điểm của BD
c) Tứ giác OMIN là hình gì? Tại sao? Trang 81 d) Chứng minh 1 1 OM B ; D ON AC 2 2 C 1 M O H 1 A 1 I B N K D
a) ta có: B1 = C1 (cùng chắn cung AD) (1)
+ do IM là trung tuyến của tam giác AIC => IM = MA => tam giác MAI cân tại M => A1= MIA
+ mà MIA = KIB (đối đỉnh) => KIB = A1 (2)
Từ (1) và (2) => B1 + BIK = C1 + A1 = 900 => IKB = 900 suy ra IK vuông góc với BD
b) ta có: CIH = DIN (đối đỉnh), mà CIH + C1 = 900, do đó: DIN + C1 = 900
+ mà C1 = B1 suy ra: DIN + B1 = 900 (*)
+ mặt khác: DIN + BIN = 900 (**)
(*) và (**) suy ra: B1 = BIN => tam giác BIN cân tại N => NB = NI (3) + lại có: IDN + B1 = 900 DIN + B1 = 900
Do đó: IDN = DIN => tam giác NID cân tại N => NI = ND (4)
(3) và (4) => NB = ND => N là trung điểm của BD
c) ta có: M, N lần lượt là trung điểm của AC và BD => OM vuông góc với AC; ON vuông góc với BD
=> OM // IN (cùng vuông góc với AC); ON // IM (cùng vuông góc vói BD)
Do đó tứ giác DMIN là hình bình hành (vì có các cạnh đối song song)
d) vì tứ giác OMIN là hình bình hành => OM = IN; ON = IM 1 1 1 1 mà IN ; BD IM AC nên OM B ; D ON AC 2 2 2 2 Trang 82




