Phương pháp giải bài tập ôn tập chương I hình học 9 (có đáp án và lời giải chi tiết)

ÔN TẬP CHƯƠNG I
A. KIẾN THỨC TRỌNG TÂM
Xem lại phần kiến thức trọng tâm của các bài đã học
 Hệ thức liên hệ giữa cạnh và đường cao trong tam giác.
 Tỉ số lượng giác của góc nhọn.
 Hệ thức liên hệ giữa cạnh và góc trong tam giác.
B. CÁC DẠNG BÀI TẬP VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: So sánh các tỉ số lượng giác
Ví dụ 1. Sắp xếp theo thứ tự tăng dần cos 72 , sin 65 , sin10 , cot 25 , sin 40 . Lời giải Ta có sin 65  cos 25 ;  sin10  cos80 ;  sin 40  cos50 .
Vì cos80  cos72  cos50  cos 25  cot 25 nên
sin10  cos72  sin 40  sin 75  cot 25 . Ví dụ 2. So sánh
a) sin 55 ; cos 55 ; tan 55 .
b) cot 20 ; sin 20 ; cos 20 . Lời giải
So sánh tương tự Ví dụ 1.
a) cos55  sin 55  tan 55;
b) sin 20  cos 20  cot 20 . Ví dụ 3. Cho 0  45   . Chứng minh rằng a) sin  cos . b) tan  cot  . Lời giải
a) Do 0    45 nên 90   45 suy ra   90  . Do đó
sin  sin 90    cos .
b) Tương tự câu a)   90 nên tan  tan 90    cot .
Ví dụ 4. Cho tam giác ABC vuông tại A có ˆ ˆ
B  C . Hãy sắp xếp theo thứ tự tăng dần sin B ,
cos B , tan B , sin C , cosC , cot C . Lời giải Ta có ˆ ˆ
B  C  90 nên sin C  cos B ; cosC  sin B ; tan B  cot C
Lại có B  C nên cos B  cosC . sin B Mà tan B   sin B . cos B Trang 1
Vậy sin C  cos B  cosC  sin B  tan B  cot C .
Dạng 2: Rút gọn và tính giá trị của biểu thức lượng giác
Ví dụ 5. Rút gọn các biểu thức 2 2 a) 2 2 2
sin   cot   cos  1 .
b) tan  cot   tan  cot  . c) 4 4 2 2
sin   cos   cos   3sin  . Lời giải 2 cos  a) 2 2 2 2 2 2 2
sin   cot   cos  1  sin  
 cos  1  cos   cos  1 1 . 2 sin  b) 2 2
(tan  cot  )  (tan  cot  ) 2 2           2 2 tan 2 tan cot cot
tan   2 tan  cot  cot    4   tan cot  4  . c) 4 4 2 2          2 2     2 2     2 2 sin cos cos 3sin sin cos sin cos  cos  3sin    2 2     2 2        2 2 1 sin cos cos 3sin
2 sin   cos    2  .
Ví dụ 6. Tính giá trị của biểu thức a)    2 sin 30 cos 60 tan 45 4 cos 30    . b) 2  2  2 cos 30 cot 60 tan 30   1. 2  2 cot 45  cos 45 c) . 2 2sin 60 Lời giải 2       1 1 3 a) 2
sin 30  cos 60  tan 45  4 cos 30   1 4   3   . 2 2 2   2 2 2          3 3 3 3 1 b) 2 2 2
cos 30  cot 60  tan 30 1          1  1        . 2 3 3 4 4       2  2  1   2  2 cot 45  cos 45 2   1 c)   . 2  2 2 sin 60   3 3 2   2  
Ví dụ 7. Tính giá trị của biểu thức     a) 2 2 2 2
cos 33  cos 41  cos 49  cos 57 .       b) 2 2 2 2 2 2
sin 35  sin 39  sin 43  sin 47  sin 51  sin 55 . Lời giải Trang 2 a) 2  2  2  2   2  2    2  2 cos 33 cos 41 cos 49 cos 57 cos 33 cos 57 cos 41 cos 49          2  2    2  2 cos 33 sin 33 cos 41 sin 41      11 2. b) 2  2  2  2  2  2 sin 35 sin 39 sin 43 sin 47 sin 51 sin 55       2  2    2  2    2  2 sin 35 sin 55 sin 39 sin 51 sin 43 sin 47         2  2    2  2    2  2 sin 35 cos 35 sin 39 cos 39 sin 43 cos 43        1113
Dạng 3: Tính độ dài đoạn thẳng, tính số đo góc
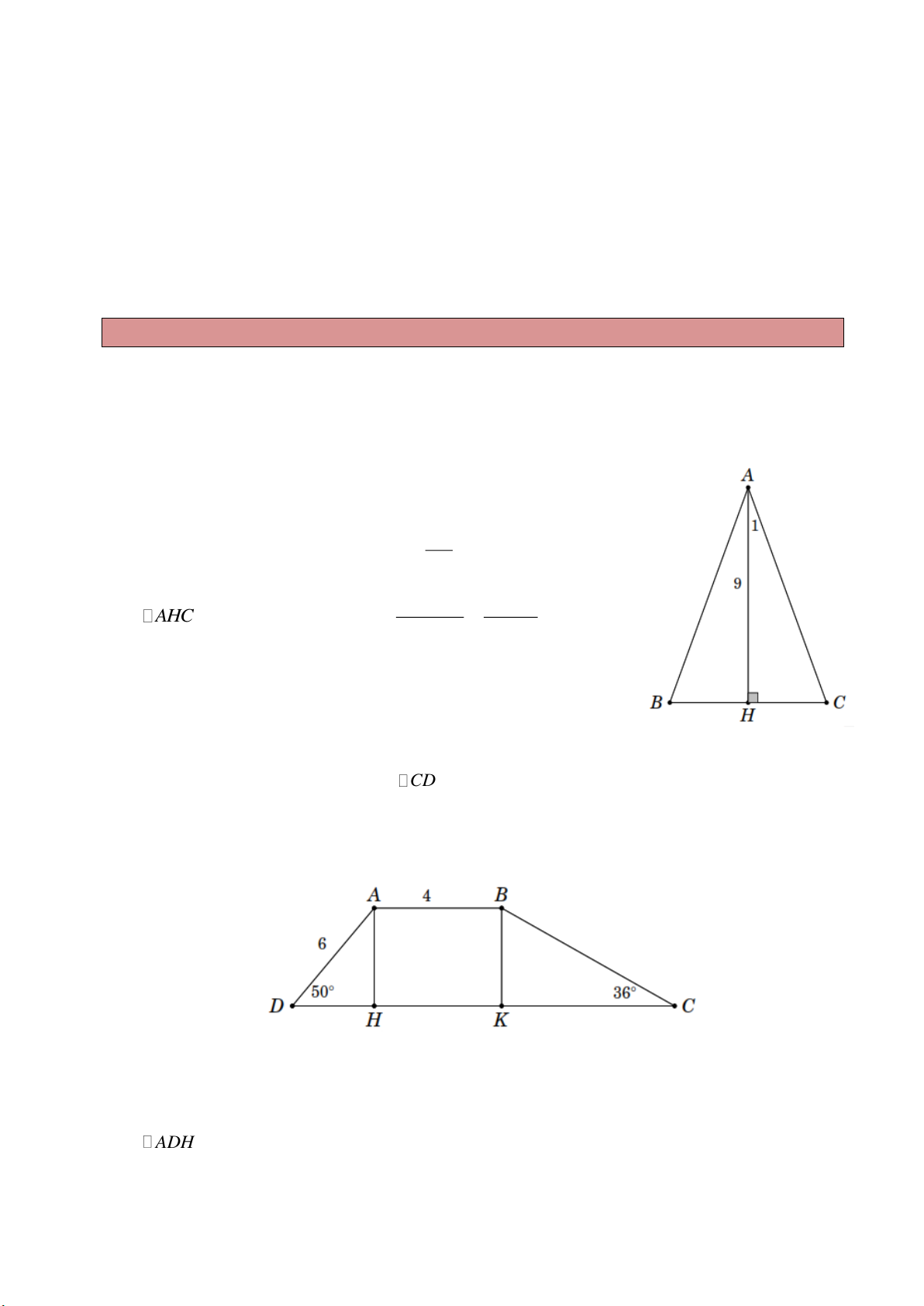
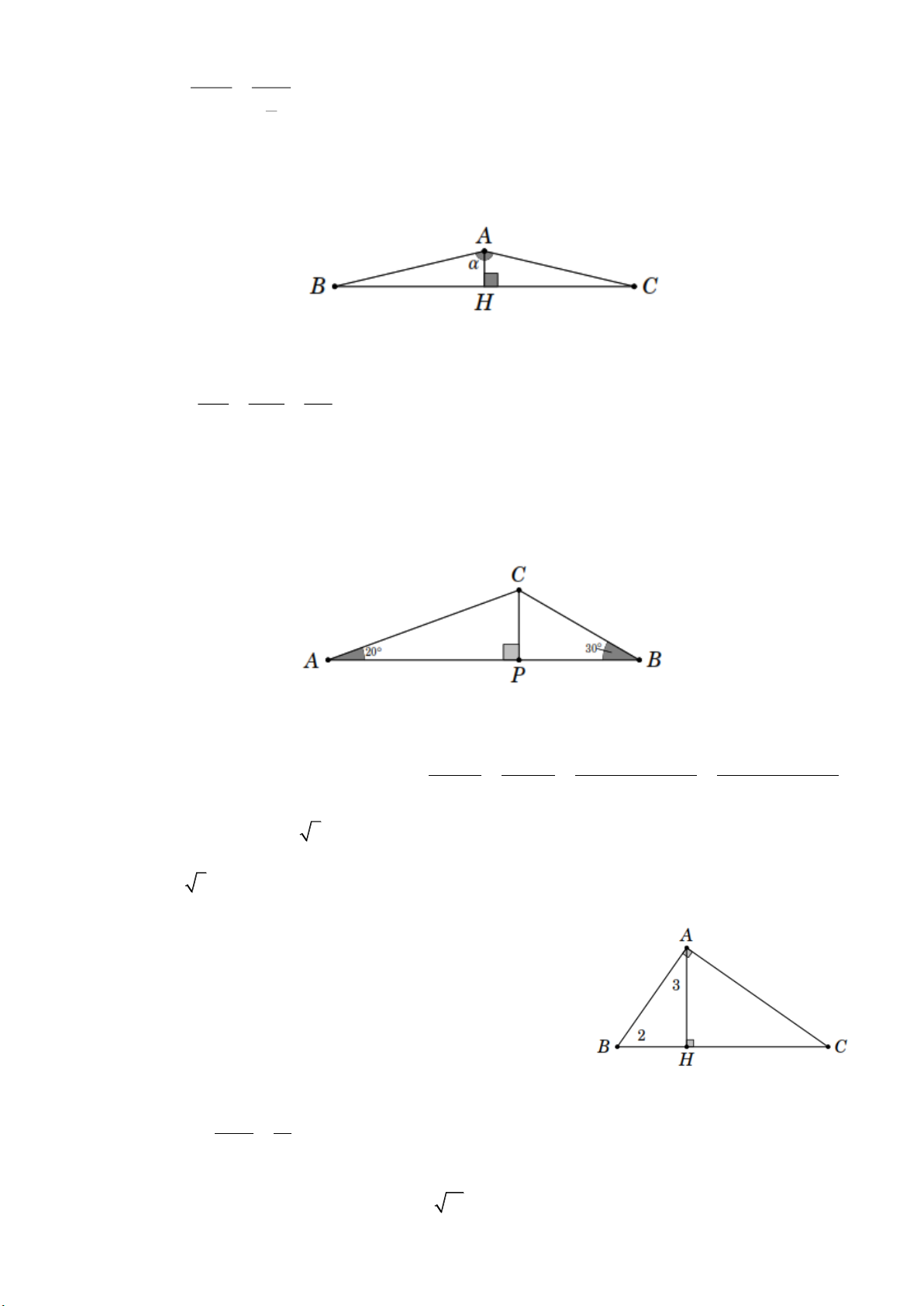
Ví dụ 8. Cho tam giác 
ABC cân tại A , đường cao AH . Biết ˆ
A  44 ; AH  9cm . Tính chu vi tam giác ABC . Lời giải
Do tam giác ABC cân đỉnh A , AH là đường cao nên AH cũng là
đường phân giác, đường trung tuyến. Do đó BC BAH CAH 22  
và HB  HC  . 2 AH 9
Xét AHC vuông tại H , ta có AC    9,7  cm cos HAC cos 22 và HC AH cot HAC 9 cot 22      3,  6 cm .
Do đó chu vi tam giác ABC là 29,7  3,6  26,  6 cm .
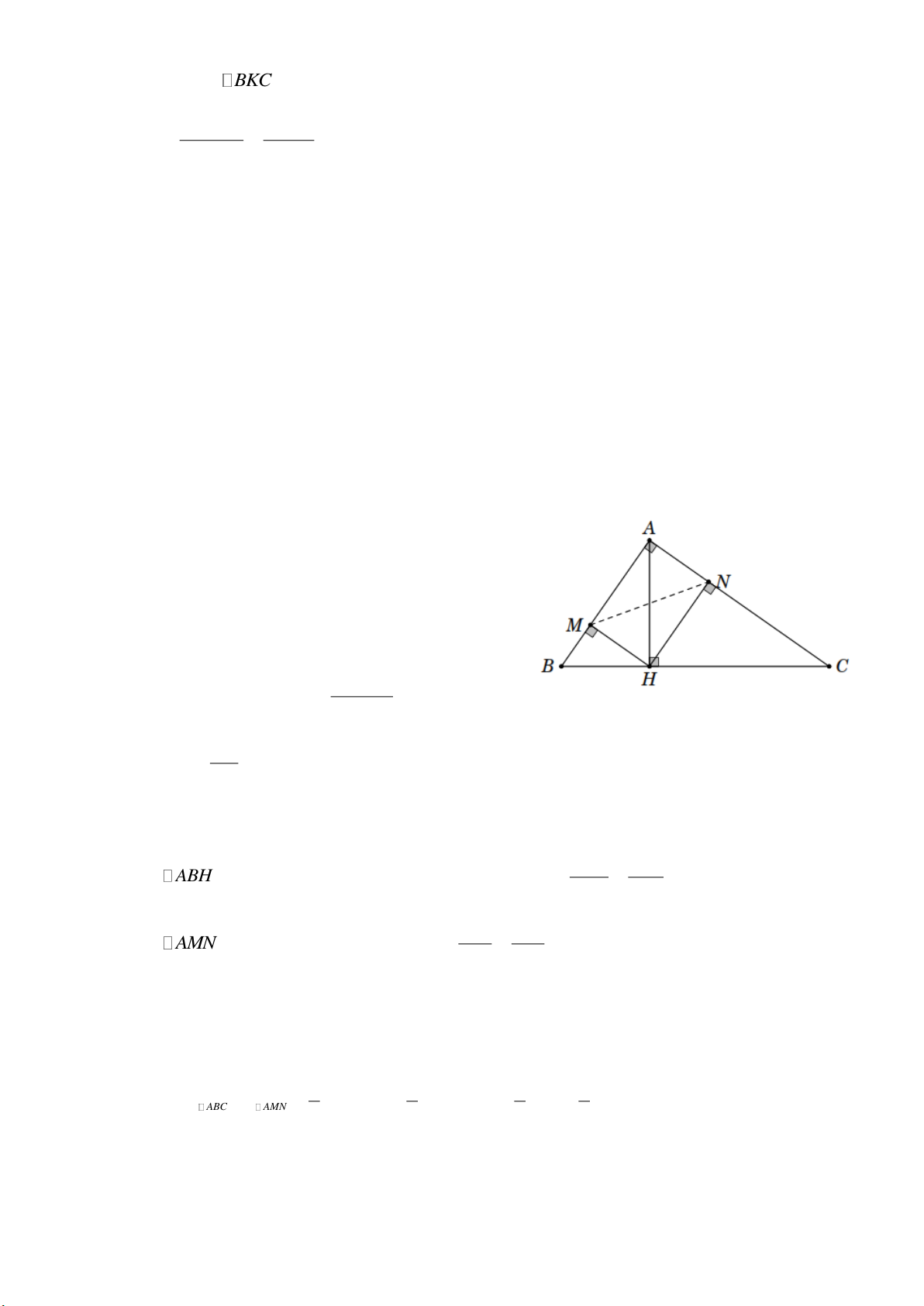
Ví dụ 9. Cho hình thang ABCD ( AB CD ), ˆ C 36  ; ˆ D 50 
. Biết AB  4cm , AD  6cm . Tính chu vi hình thang. Lời giải
Vẽ AH  CD và BK  CD , dễ thấy AHKB là hình chữ nhật.
Do đó AH  BK và AB  HK .
Xét ADH vuông tại H , ta có DH AD cos ADH 6 cos 50      4,  6 cm . Trang 3
Tương tự, xét BKC vuông tại K , ta có KC BK cot BCK 4,6 cot 36      6,  3 cm BK 4, 6 và BC    7,   8 cm. sin KCB sin 36
Ta có DC  DH  HK  KC  3,9  4  6,3  14,  2 cm .
Do đó chu vi của hình thang là 4  7,8 14, 2  614, 2  3  2 cm .
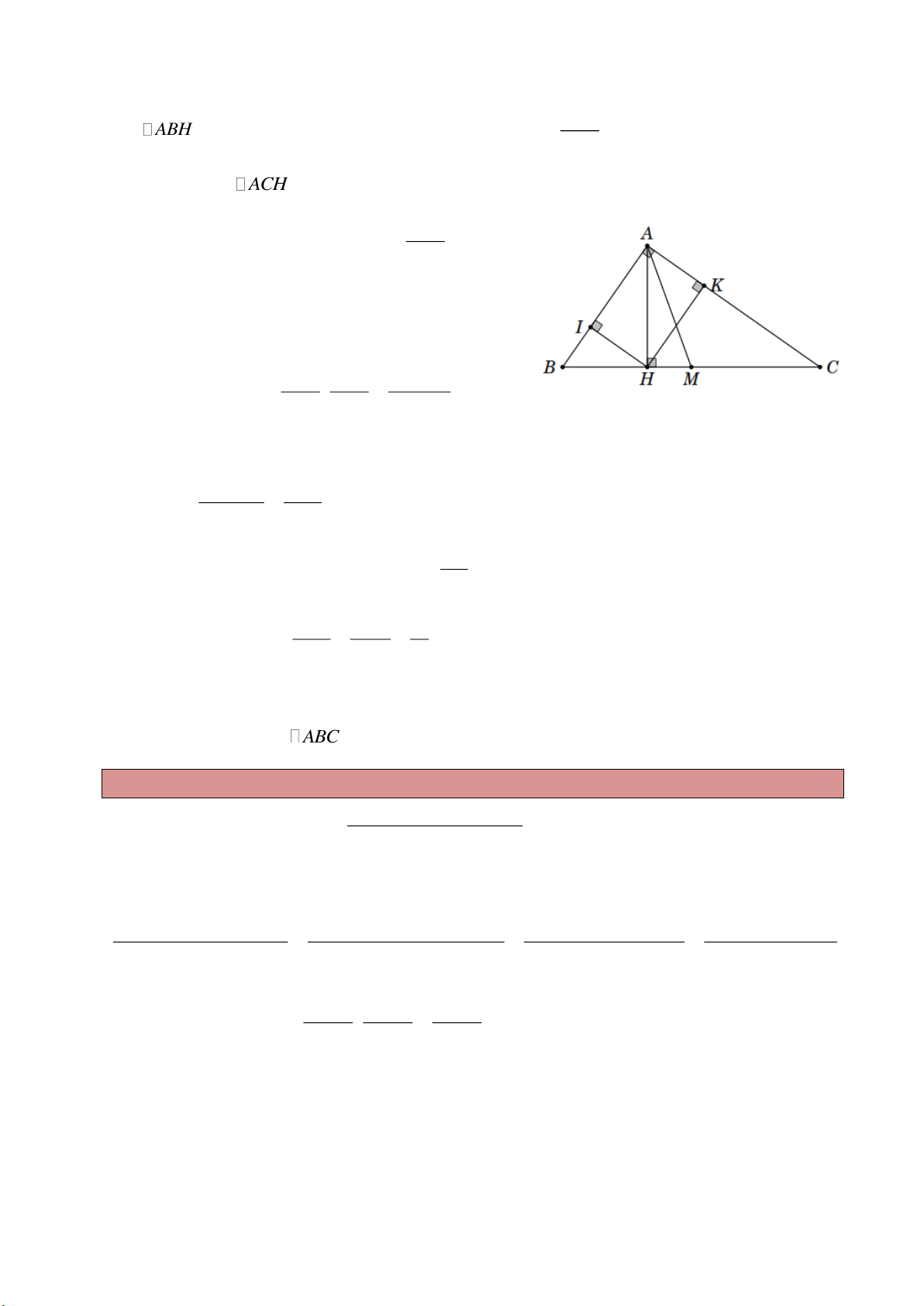
Ví dụ 10. Cho tam giác ABC vuông tại A , đường cao AH . Vẽ HM  AB ; HN  AC . Biết
AB  3cm ; AC  4cm .
a) Tính độ dài MN .
b) Tính số đo các góc của tam giác AMN .
c) Tính diện tích tứ giác BMNC . Lời giải
a) Áp dụng định lí Py-ta-go trong tam giác vuông ABC , ta có 2 2 2 2 2
BC  AB  AC  3  4  25 suy ra BC   5 cm .
Theo hệ thức lượng trong tam giác vuông ABC , ta có AB  AC
AH  BC  AB  AC  AH  BC 3 4 suy ra AH   2,  4 cm . 5
Dễ thấy AMHN là hình chữ nhật nên MN  AH nên MN  2, 4cm . 2 2 AH 2, 4
b) Xét ABH vuông tại H , ta có 2
AH  AM  AB  AM    1, 4  4 cm . AB 4 AN 1, 44 Ta xét 
AMN vuông tại A , ta có tan AMN  
 tan 3652 . Do đó AMN  36 52 . AM 1,92    
Mà ANM  90  AMN  90  36 52  53 8.
c) Gọi S là diện tích tứ giác BMNC . 1 1 1 1 Ta có S  S  S
  AB  AC   AM  AN  3 4  1,921, 44  4,6 . ABC AMN  2 cm  2 2 2 2
Vậy diện tích tứ giác BMNC là 2 4, 6cm .
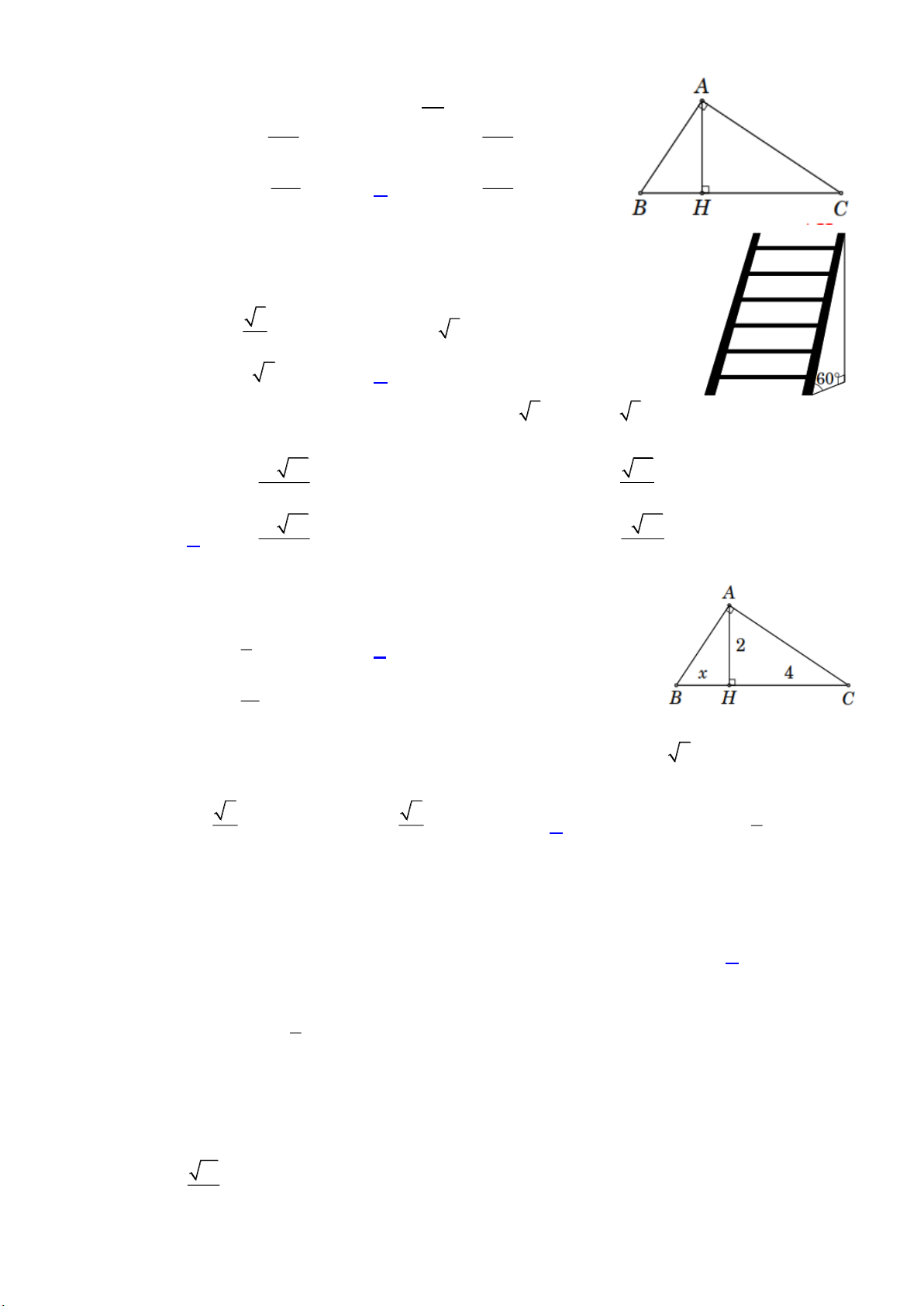
Ví dụ 11. Cho tam giác ABC vuông tại A , BC  4cm . Vẽ đường cao AH ; vẽ HI  AB ,
HK  AC . Tìm giá trị lớn nhất của diện tích tứ giác AIHK . Trang 4 Lời giải 2 AH
Xét ABH vuông tại H , ta có 2
AH  AI  AB suy ra AI  . AB
Tương tự, ta xét ACH vuông tại H , ta có 2 AH 2
AH  AK  AC suy ra AK  . AC
Gọi S là diện tích của tứ giác AIHK .
Do tứ giác AIHK là hình chữ nhật nên 2 2 4 AH AH AH
S  AI  AK    . AB AC AB  AC
Mặt khác theo hệ thức lượng trong tam giác vuông ABC ta có AB AC  AH  BC . 4 3 Khi đó AH AH S   . AH  BC BC BC
Gọi M là trung điểm của BC , ta có AM   2cm . 2 3 3 3 AH AM 2
Mà AH  AM nên S      2 2 cm  . BC BC 4
Dấu đẳng thức xảy khi AH  AM hay tam giác ABC vuông cân tại A . Vậy 2
max S  2cm khi ABC là tam giác vuông cân đỉnh A .
Dạng 4: Chứng minh hệ thức giữa các tỉ số lượng giác 2 2 4
cos   sin   sin 
Ví dụ 12. Chứng minh hệ thức 4  cot . 2 2 4
sin   cos   cos  Lời giải 2 2      cos   sin   2 1 sin   2     cos   2 2 2 4 2 2 2 1 sin cos sin sin cos sin cos      2 2 4 2 2
sin   cos   cos  sin   cos   2 1 cos   2 2 2 2 sin   cos  sin  sin   2 cos   2 2 4 cos  cos  cos  4     cot  . 2 2 4 sin  sin  sin 
Ví dụ 13. Chứng minh các đẳng thức sau a) 2
(1 cos )(1 cos )  sin  ; b) 2 2
sin  1 cos   2 ; c) 4 4 2 2
sin   cos   2 sin  cos   1; d) 2 3
sin   sin  cos   sin  . Lời giải Trang 5 a) 2 2
(1 cos )(1 cos )  1 cos   sin  ; b) 2 2 2 2
sin  1 cos   sin   cos  1  11  2 ; c)            2 4 4 2 2 2 2 2 sin cos 2sin cos sin cos 1 1; d) 2        2    2 3 sin sin cos sin 1 cos
 sin sin   sin  .
C. BÀI TẬP VẬN DỤNG
I. PHẦN TRẮC NGHIỆM Câu 1:
Cho tam giác ABC vuông tại A có AB  5 cm, AC 12 cm và BC 13 cm. Giá trị của sin C bằng 5 1 12 5 A. . B. . C. . D. . 12 13 13 13 Câu 2:
Cho tam giác ABC vuông tại A . Khẳng định nào sau đây đúng? AB AC AB AC A. cos B  . B. cos B  . C. cos B  . D. cos B  . BC AB AC BC Câu 3:
Cho tam giác ABC vuông tại A . Hệ thức nào sau đây đúng? AB AB AB AB A. sin B  . B. sin B  . C. tan B  . D. cos B  . BC AC AC AC Câu 4:
Khẳng định nào sau đây sai? A. cos 35 sin 40  . B. sin 35 cos 40  .     C. sin 35  sin 40 . D. cos 35  cos 40 . Câu 5:
Cho tam giác ABC vuông tại A , đường cao AH . Hệ thức nào đây sai? A. 2
AC  BC.HC . B. 2 AH  . AB AC . 1 1 1 C.   . D. 2 AH  H . B HC . 2 2 2 AH AB AC Câu 6: Cho ABC vuông tại ,
A đường cao AH. Biết BH  3, 2cm; BC  5cm thì độ đài AB bằng A. 8 cm. B. 16 cm. C. 1,8 cm. D. 4 cm.  Câu 7:
Cho tam giác ABC vuông tại A , ACB  30 , cạnh AB  5 cm. Độ dài cạnh AC là 5 5 2 A. 10 cm. B. cm. C. 5 3 cm. D. cm. 3 2 1 Câu 8:
Cho tam giác ABC vuông tại C. Biết sin B  , khi đó tan A bằng 3 2 2 1 A. . B. 3 . C. 2 2 . D. . 3 2 2  Câu 9:
Cho ABC cân tại A , BAC  120 , BC 12 cm . Tính độ dài đường cao AH .
A. AH  3 cm .
B. AH  2 3 cm .
C. AH  4 3 cm .
D. AH  6 cm . Trang 6
Câu 10: Cho tam giác ABC vuông tại A , đường cao AH (hình
bên). Đẳng thức nào sau đây là sai? AH BH A. sin B  . B. tan BAH  . AB AH HC AH C. cos C  . D. cot HAC  . AC AC
Câu 11: Một cái thang dài 4 cm đặt dựa vào tường, biết góc
giữa thang và mặt đất là 60 . Khoảng cách d từ chân thang đến
tường bằng bao nhiêu? 3 A. d  m .
B. d  2 3 m . 2
C. d  2 2 m . D. d  2 m .
Câu 12: Cho tam giác ABC vuông tại A và AB  2 5a , AC  5 3a . Kẻ
AK vuông góc với BC , với K nằm trên cạnh BC . Tính AK theo a . 19 57 95 A. AK  a . B. AK  a . 10 2 10 57 5 57 C. AK  a . D. AK  a . 19 19
Câu 13: Cho tam giác ABC vuông tại A , đường cao AH . Biết
AH  2 , HC  4 . Đặt BH  x (hình bên). Tính x . 1 A. x  . B. x 1. 2 16 C. x  . D. x  4 . 3 Câu 14: Cho xOy 45 
. Trên tia Oy lấy hai điểm A , B sao cho AB  2 cm. Tính độ dài hình
chiếu vuông góc của đoạn thẳng AB trên Ox . 2 2 1 A. cm. B. cm. C. 1 cm. D. cm. 2 4 2
Câu 15: Cho tam giác ABC vuông tại A , đường cao AH và đường trung tuyến AM (
H , M  BC ). Biết chu vi của tam giác là 72 cm và AM  AH  7 cm. Tính diện tích S của tam giác ABC .
A. S  48 cm 2 .
B. S 108 cm 2 .
C. S 148 cm 2 .
D. S 144 cm 2 . II. PHẦN TỰ LUẬN 1
Bài 1. Cho biết cos  . 4 a) Tính sin .
b) Chứng minh rằng tan  4sin . Lời giải 15 a) sin   . 4 Trang 7 sin  sin  b) tan     4sin . cos 1 4
Bài 2. Xem hình bên và tính góc tạo bởi hai mái nhà AB và AC , biết rằng mỗi máy nhà dài 2,34m và cao 0,8m. Lời giải AH 0,8 40 cos BAH   
 BAH  70  BAC  2BAH  2.70 140 . AB 2,34 117
Bài 3. Tam giác ABC có ˆ A 20  , ˆ B 30 
, AB  6cm. Đường vuông góc kẻ từ C đến AB cắt
AB tại P (hình vẽ bên). Hãy tìm a) AP , BP ; b) CP . Lời giải PA PB PA  PB 6
a) Ta có CP  A .
P tan 20  P . B tan 30     . tan 30 tan 20 tan 30  tan 20 tan 30  tan 20
Do đó PA  6.tan 30  2 3 cm ; PB  6.tan 20  2,18cm.
b) CP  2 3. tan 20  1, 26 cm .
Bài 4. Tính độ dài các cạnh và số đo các góc nhọn của tam
giác ABC vuông tại A trong hình bên Lời giải 2 2  AH 3 HC    4,5 . HB 2
 BC  BH  HC  2  4,5  6,5 .  2
BA  BH.BC  2.6,5 13  BA  13 . Trang 8  117 3 13 2
CA  CH .CB  4, 5.6, 5   AC  . 4 2  AH 3 tan B    B  59 19  ' . BH 2
 C  90  59 1  9'  30 4  1' .
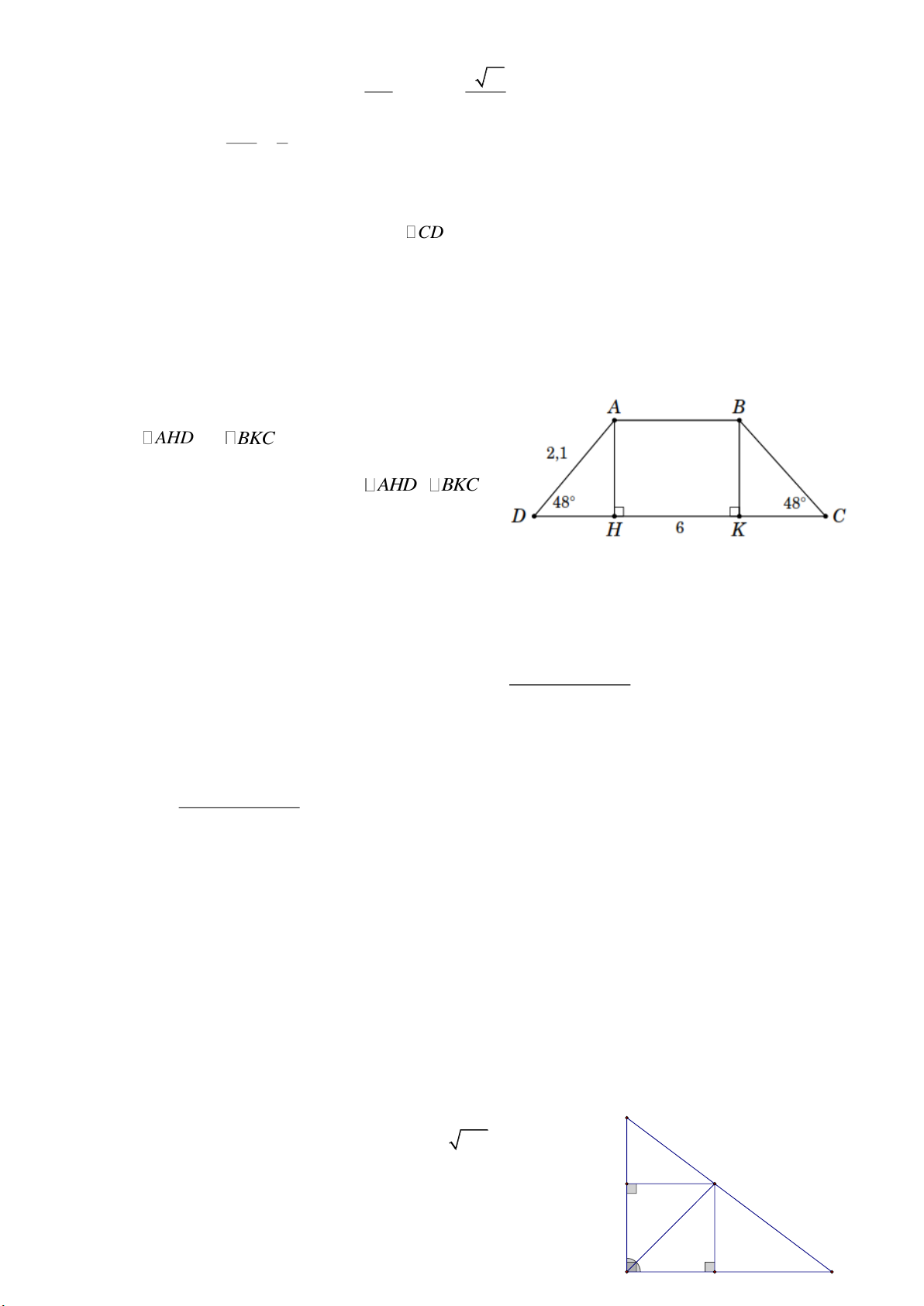
Bài 5. Cho hình thang cân ABCD ( AB CD ). Biết AD  2,1cm ; CD  6, 0cm và ˆ D 48  .
a) Tính độ dài AB .
b) Tính diện tích hình thang ABCD . Lời giải
a) Kẻ các đường cao AH  CD và BK  CD .
Dễ thấy ABKH là hình chữ nhật nên AB  HK .
Xét AHD và BKC , do giả thiết suy ra
AD  BC và ADH  BCK nên AHD  BKC .
Do đó DH  KC và HK  DC  2DH .
Xét tam giác vuông AHD ta có DH AB cos ADH 2,1 cos 48     1,  4 cm .
Suy ra AB  6, 0  2 1, 4  3,  2 cm .
AB CD AH
b) Gọi S là diện tích hình thang ABCD . Khi đó S  . 2
Xét tam giác vuông ADH ta có AH AB sin ADH 2,1 sin 48     1,5  6 cm . 3,2 6,01,56 Nên S   7,8  2 8 cm  . 2
Bài 6. Cho tam giác ABC vuông tại A , AB  6cm, AC  8 cm. a) Tính BC , ˆ B , ˆ C ; b) Phân giác của ˆ
A cắt BC tại D . Tính BD , CD .
c) Từ D kẻ DE và DF lần lượt vuông góc với AB , AC . Tứ giác AEDF là hình gì? Tính chu vi
và diện tích của tứ giác AEDF ? Lời giải
a) Theo định lý Py-ta-go, ta có B 2 2 2 2 2
BC  AB  AC  6  8  100  BC  100  10 cm . D E
Theo tỉ số lượng giác của góc nhọn trong tam giác ABC vuông tại A Trang 9 C A F AC 8 4 tan B 
   B  53 . AB 6 3
Do đó C  90  B  90  53  37.
b) Theo tính chất đường phân giác trong tam giác ta có DB AB DB DC DB  DC BC 10 5        . DC AC AB AC AB  AC 6  8 14 7 5 5
 DB  AB      5 5 6 4, 3 cm ; DC  AC  8  5,7cm . 7 7 7 7
c) Tứ giác AEDF có A  E  F  90 nên là hình chữ nhật. Mặt khác DE  DF (tính chất tia
phân giác của một góc) nên AEDF là hình vuông.
Theo hệ thức liên hệ giữa cạnh và góc trong BED  vuông tại E, ta có
DE  DB sin B  4,3sin 53  3, 43cm .
Chu vi của hình vuông AEDF : 4 3, 43  13, 72cm . 2
Diện tích hình vuông AEDF : S      2 3, 43 11, 7649 cm  . B AC
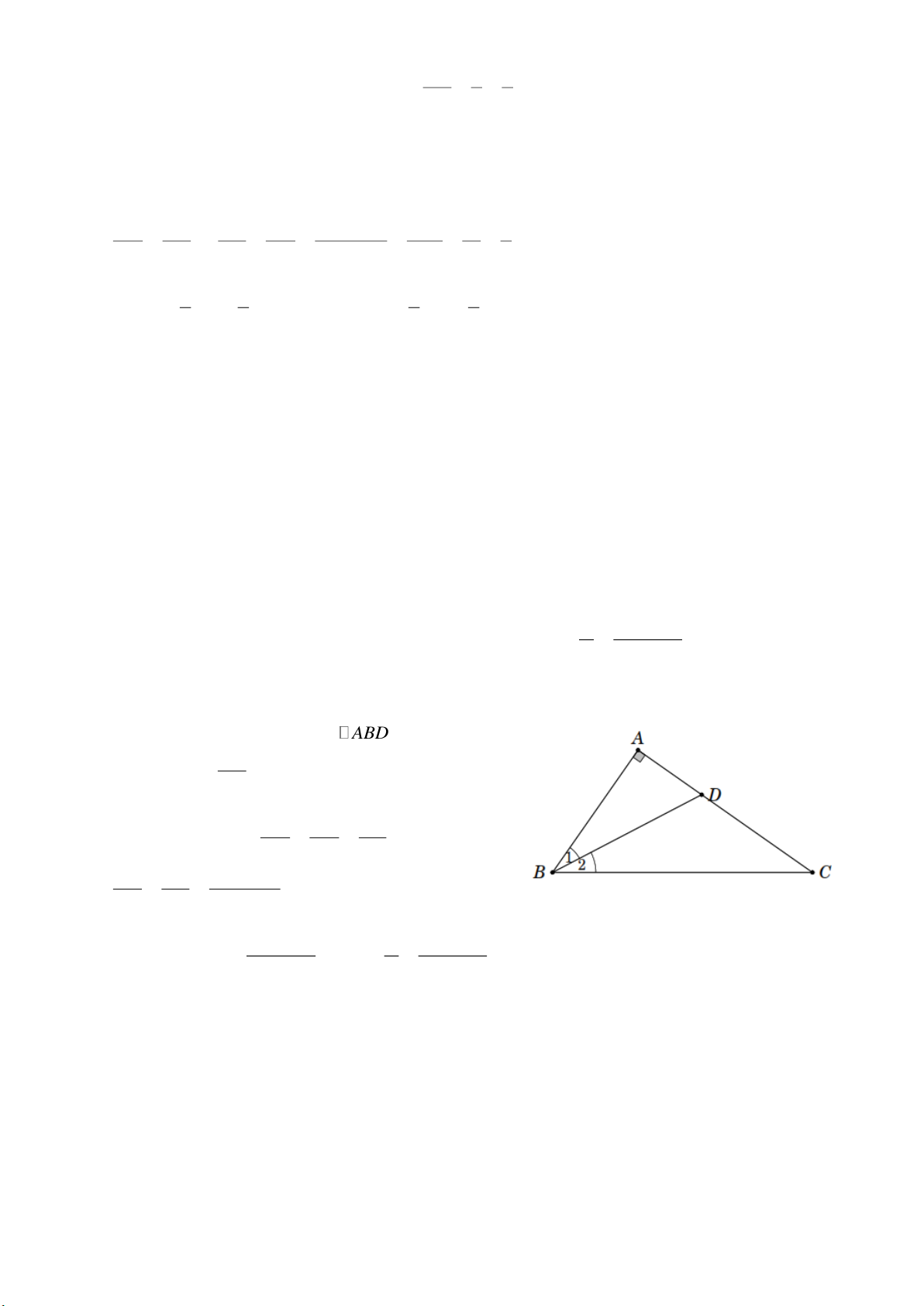
Bài 8. Cho tam giác ABC vuông tại A . Chứng minh rằng tan  . 2 AB  BC Lời giải
Vẽ đường phân giác BD . Xét ABD vuông tại A , ta AD có tan ABD  . AB AD AB AB Mặt khác   suy ra DC DC BC AD CD AD  CD   . AB BC AB  BC Do đó AC B AC tan ABD  hay tan  . AB  BC 2 AB  BC --- HẾT --- Trang 10