Phương pháp giải hệ thức giữa các tỉ số lượng giác (có đáp án và lời giải chi tiết)

Chuyên đề 4: HỆ THỨC GIỮA CÁC TỈ SỐ LƯỢNG GIÁC CỦA CÁC GÓC  VÀ 2 0    45 A. Đặt vấn đề
Trong chuyên đề này ta sẽ thiết lập các hệ thức liên hệ giữa các tỉ số lượng giác của góc  và góc 2 .
Nhờ đó mà ta tính được các tỉ số lượng giác của góc  khi biết tỉ số lượng giác của góc 2 và ngược lại B. Một số ví dụ
Ví dụ 1. Cho   45 , chứng minh rằng sin2  2sincos
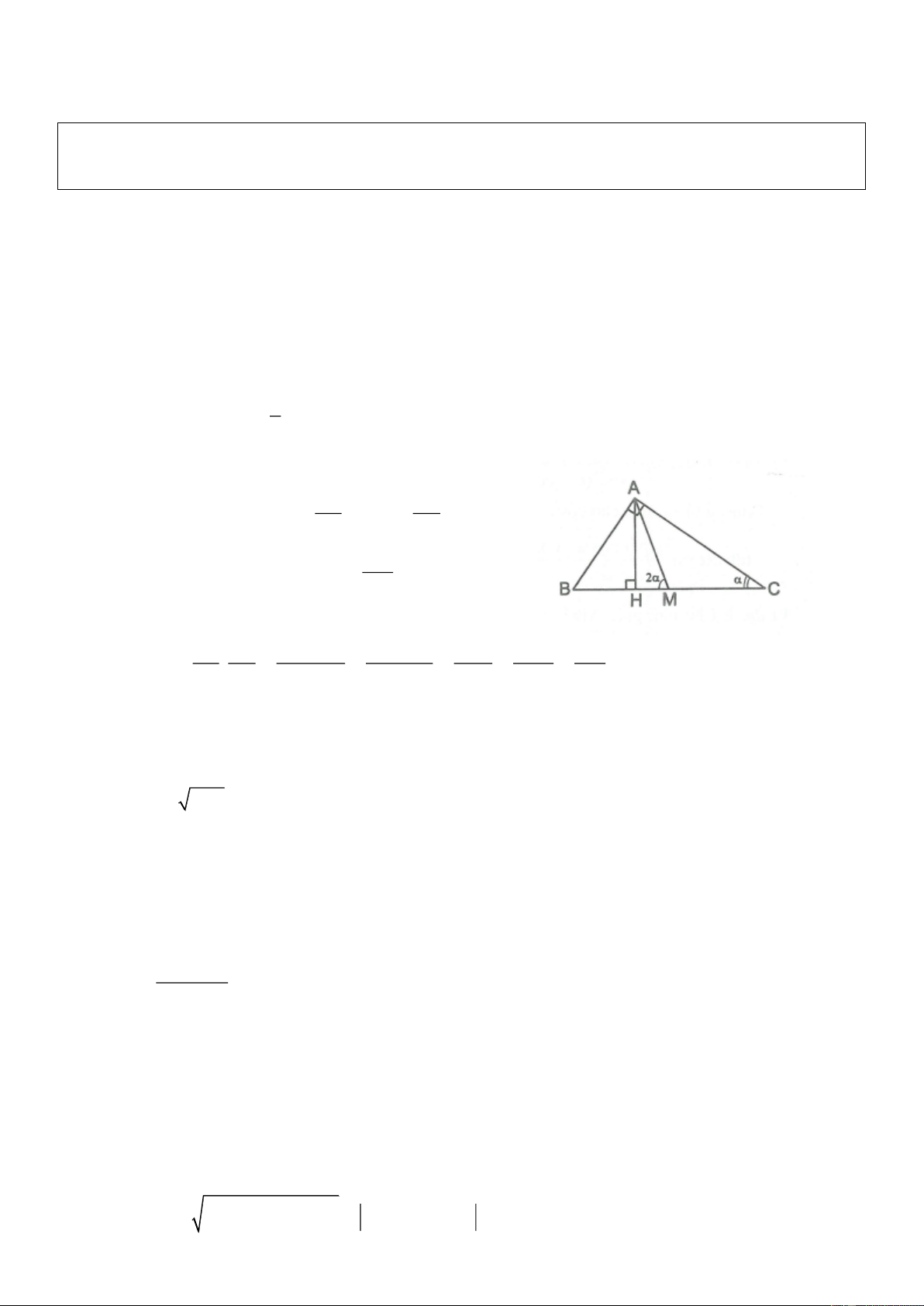
Áp dụng: Cho sin  0,6 tính sin2 Giải Xét A
 BCvuông tại A, C  45
Vẽ đường cao AH và đường trung tuyến AM. 1
Khi đó MA  MB  MC  BC 2 Ta có A
 MCcân tại M, do đó AMB  2C  2 AB AC A
 BCvuông tại A, ta có sin  ; cos  BC BC AH Xét A
 HM vuông tại H, ta có sin2    1 AM Ta có AB AC 2.A . B AC 2AH.BC 2AH 2AH AH 2sin .  cos  2 .      2 2 2 BC BC BC BC BC 2AM AM Từ  
1 và 2 suy ra sin2  2sincos
Áp dụng: Nếu sin  0,6 thì        2 2 2 cos 1 sin 1 0,6  0,64
Do đó cos  0,64  0,8. Vậy sin2  2sin .
 cos  2.0,6.0,8  0,96
Nhận xét: Việc xét A
 BC vuông tại A là để có sin và cos . Việc vẽ đường trung tuyến AM là để
xuất hiện 2 . Vẽ thêm đường cao AH để có thể tính sin2
Ví dụ 2. Cho   45 . Chứng minh các hệ thức sau: a) 2 2
cos2  cos   sin  2tan b) tan2  2 1 tan  Giải a) Ta có         2 2 2 2 2 cos 2 1 sin 2 1 2sin cos 1 4sin cos      2 2 2 2 2 cos sin  4sin  cos  4 2 2 4
 cos   2sin  cos   sin      2 2 2 cos sin Do đó:      2 2 2 cos2 cos sin 2 2  cos   sin  Trang 1
Vì   45 nên sin  cos (xem bài 2.26). Vậy 2 2
cos2  cos   sin 
Lưu ý: Tiếp tục biến đổi các hệ thức trên ta được các hệ thức sau 2 2 2        2   2 cos sin cos 1 cos  2cos  1 2 2      2   2 2 cos sin 1 sin  sin  1 2sin  Vậy 2 2 2 2
cos2  cos   sin   2cos   1 1 2sin  sin 2 2sin  cos b) Ta có tan 2   cos2 2 2 cos   sin  Chia cả tử và mẫu cho 2 cos  ta được: 2 2
2sin cos cos   sin  2sin 2tan tan2  :  :  2 1 tan   2 2 cos  cos  cos 2 1 tan 
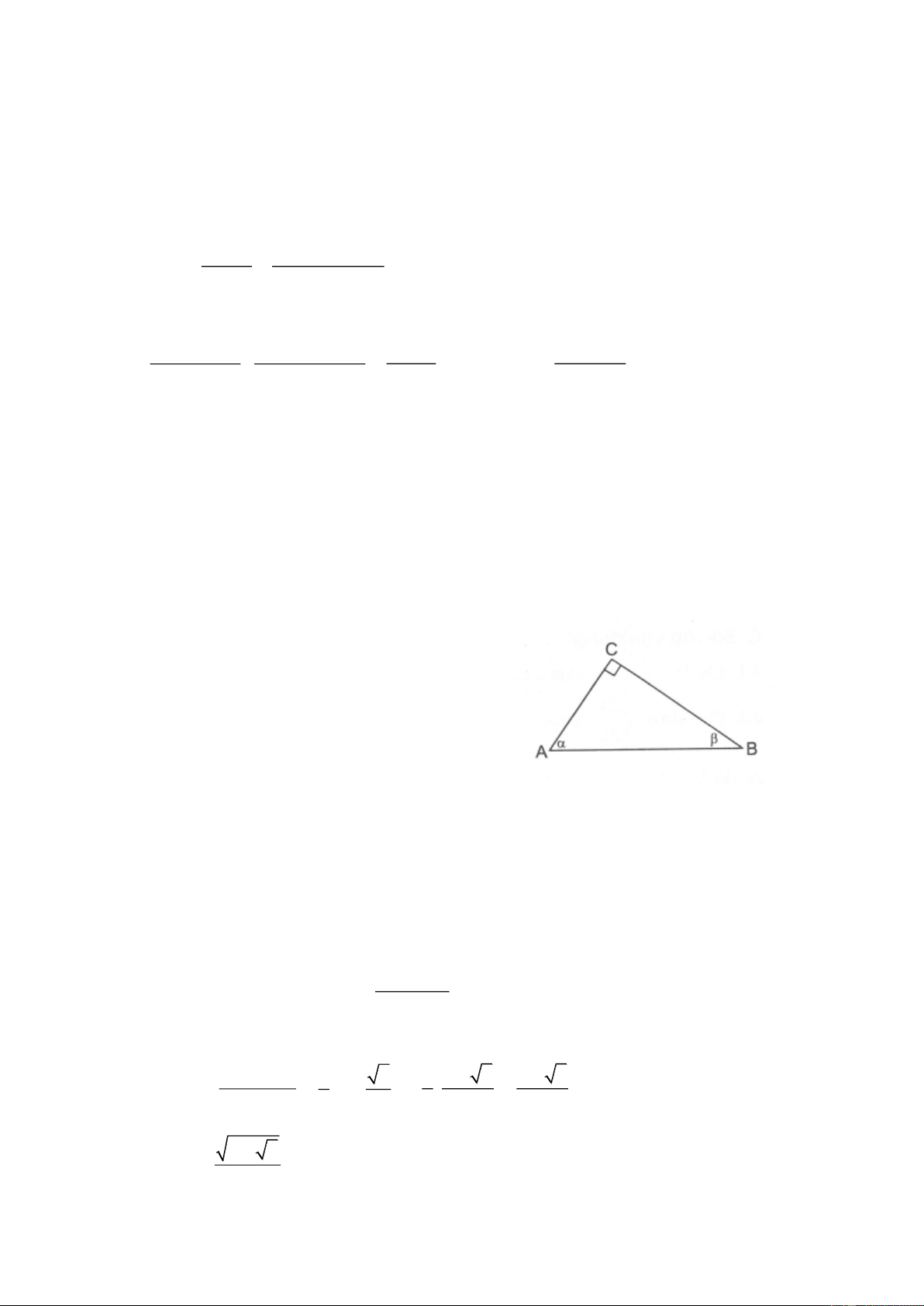
Ví dụ 3. Cho tam giác ABC vuông tại C, A   , B   với    . Chứng minh rằng:    2 sin sin  1 sin2 Giải A
 BCvuông tại C nên A B  90
Mặt khác, A  Bnên A    45
Ta có     90 nên sin  cos Do đó    2     2 sin sin sin cos 2 2
 sin   cos   2sin .
 cos 1 sin2
Ví dụ 4. Không dùng máy tính hoặc bảng số hãy tính: sin22 3  0 , cos22 3  0, tan22 3  0 Giải
 Tìm hướng giải Vì 22 3
 0 bằng một nửa của góc 45 , nên ta dùng công thức tỉ số lượng giác của góc nhân đôi để giải.
 Trình bày lời giải    1 cos2 Ta có 2 cos2  1 2sin  2  sin   2 Với   22 3
 0 , 2  45 ta được: 1 cos45   1 2  2  2   1 2 sin 2  2 3  0   1   2 2 .  2 2  2    2 2 4 2  2 Suy ra sin22 3  0  2 Trang 2    1 cos2 Ta có 2 cos2  2cos   1 2  cos   2 Với   22 3
 0 , 2  45 ta được: 1 cos45   1 2  2  cos22 3  0  1 2  1   2 2 .  2 2  2    2 2 4  Suy ra    2 2 cos22 30 2     2  2  2  2 1  sin22 30 2 2 2 2 tan22 3  0   :   cos22 3  0 2 2 2  2 2  2   1   2 2 1   2 1 1
C. Bài tập vận dụng
4.1. Cho 0    45 , chứng minh rằng 1 sin2  sin  cos 24 4.2. Cho sin   25 a) sin2  b) sin 2
4.3. Không dùng máy tính hoặc bảng số, hãy tính: sin15 , cos15 , tan15
4.4. Không dùng máy tính hoặc bảng số, hãy tính: sin75 , cos75 , tan75
4.5. Không dùng máy tính hoặc bảng số, hãy tính: sin67 3  0 , cos67 3  0, tan67 3  0
4.6. Không dùng máy tính hoặc bảng số, hãy tính: a) cos36
b) Từ đó hãy tính cos72 , cos18 , sin72 , sin18
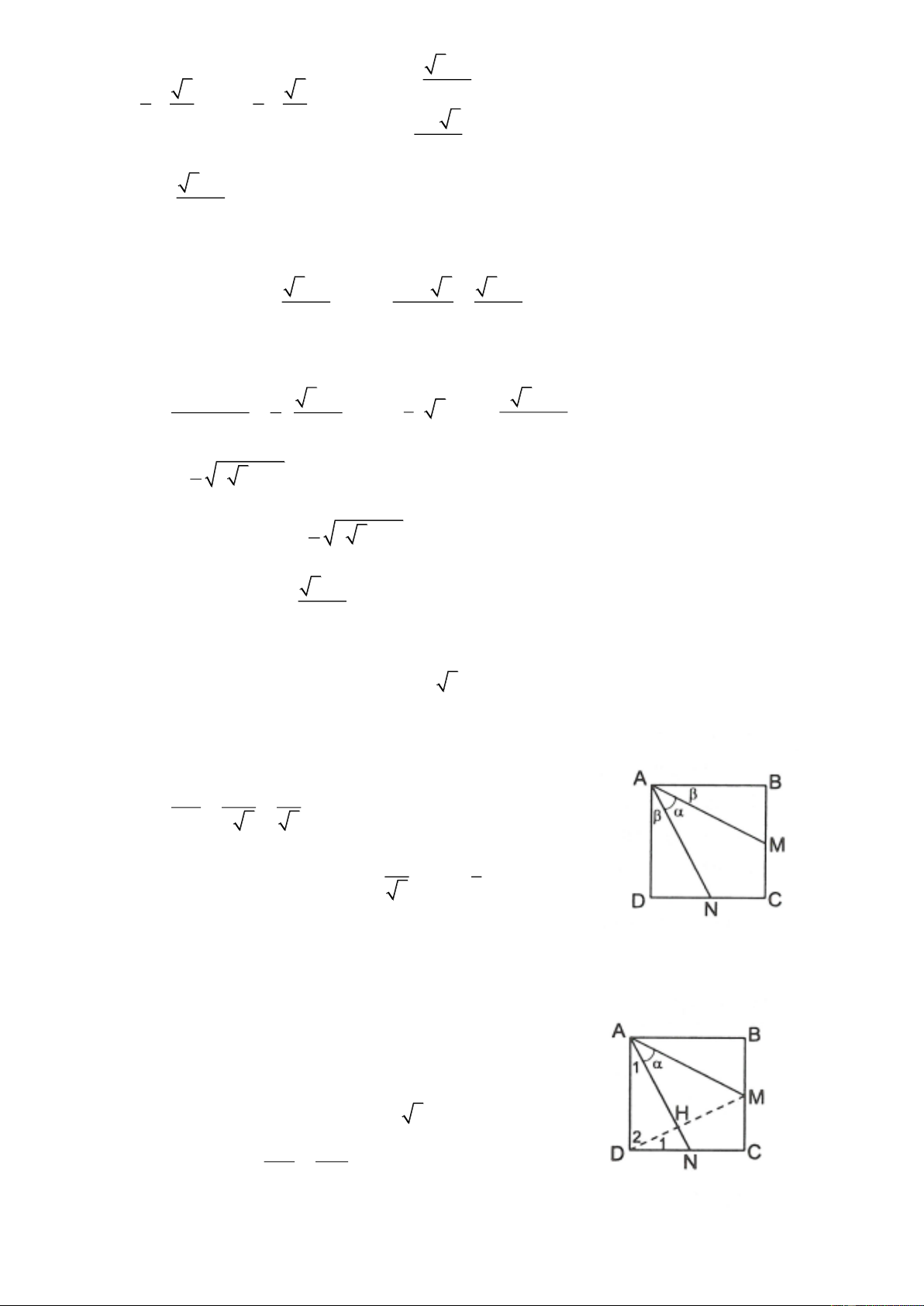
4.7. Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của BC và CD. Đặt MAN   , tính sin
4.8. Cho tam giác ABC vuông tại A, BC  a, C    45 . Vẽ đường trung tuyến AM. Qua A vẽ một 2  đườ a cos
ng thẳng vuông góc với AM cắt đường thẳng BC tại N. Chứng minh rằng: CN  2 2cos   1
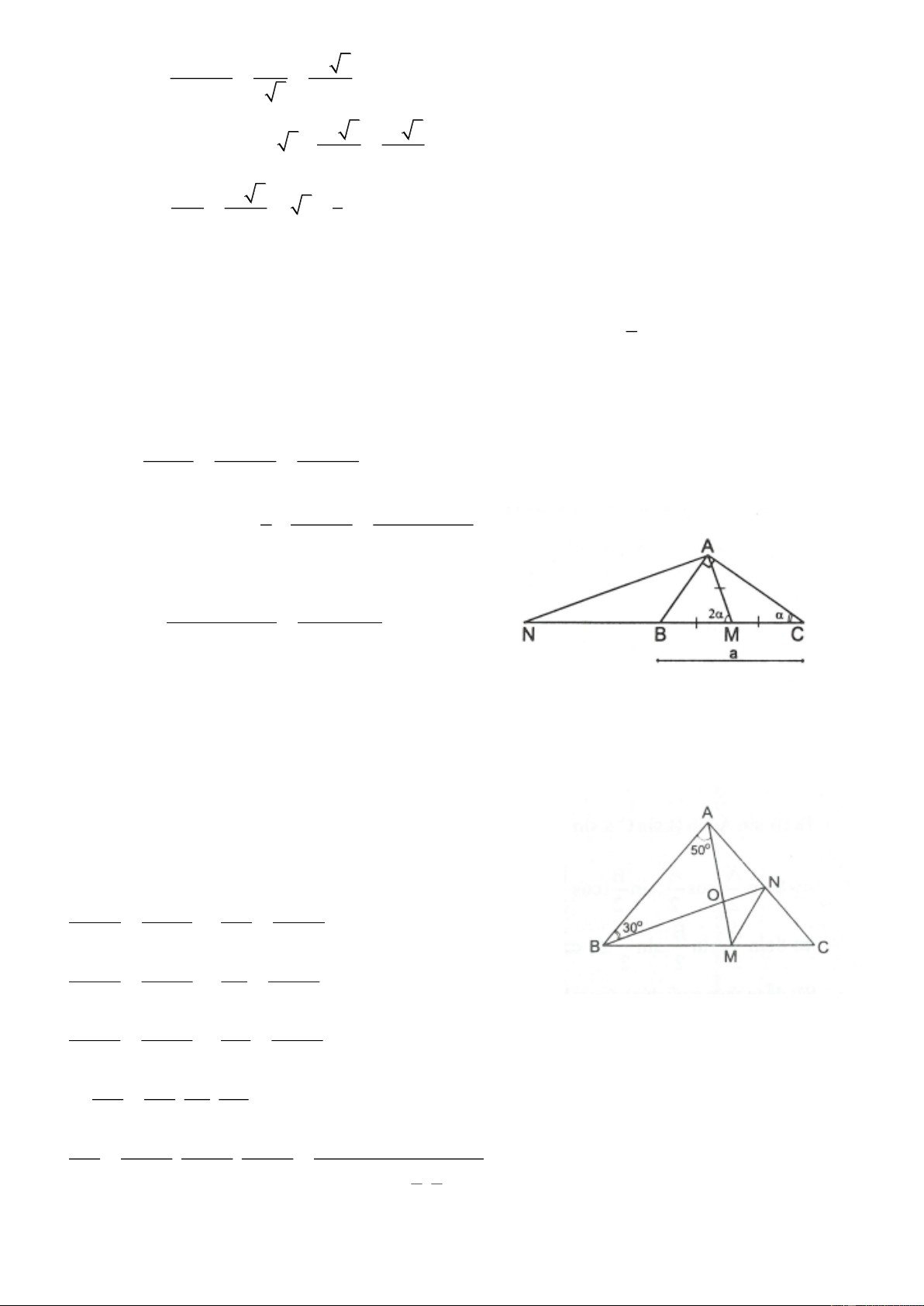
4.9. Cho tam giác ABC cân tại A, A  80 . Trên cạnh BC lấy điểm M, trên cạnh AC lấy điểm N sao cho
BAM  50, ABN  30 . Gọi O là giao điểm của AM và BN. Chứng minh rằng M
 ON là tam giác cân
4.10. Cho tam giác ABC nhọn. Chứng minh rằng: B  C C  A A  B sin . A sin . B sinC  sin .sin .sin 2 2 2 Trang 3
HƯỚNG DẪN GIẢI - ĐÁP SỐ
4.1. Ta có 1 sin2 2 2  sin   cos  2sin .  cos     2 sin cos Do đó 1 sin2     2 sin cos  sin  cos
Ta có sin  cos  0nên 1 sin2  sin  cos 4.2. 2  24  49 a) Ta có 2 2 sin   cos   1 2  cos   1     25 625 49 7 Do đó cos   625 25 24 7 336 Vậy sin2  2sin .  cos  2. .  25 25 625  b) Từ công thức 2
cos2  1 2sin  suy ra 2 cos  1 2sin 2  1 cos    3 Do đó 2 sin  7 9  1 : 2    . Vậy sin  2 2  25  25 2 5 1 cos2 4.3. Ta có 2 cos2  1 2sin  2  sin   2
Với   15 , 2  30 ta được:      3 2 1 cos30 1 3 2 3 4 2 3 2 sin 15   1  : 2    2  2  4 8 8   3  1 3  1 6  2 2  2 Do đó sin 15    8 2 2 4
Với   15 , 2  30 ta được:      3 2 1 cos30 1 3 2 3 4 2 3 2 cos 15   1  : 2    2  2  4 8 8     2 3 1 3  1 6  2 Do đó cos15    8 2 2 4 2  3   1  3 2 sin15 6  2 6  2 1 4  2 3 Ta có tan15   :     2  3 cos15 4 4    2 2 3 1 2 Trang 4
Cách giải khác: Tính trực tiếp theo định nghĩa tỉ số lượng giác.
 Cách thứ nhất Xét A
 BC vuông tại A, B  15 , AC  1
Để tính sin B, cosB, tanB ta cần phải biết AB, BC
Vẽ đường trung trực của BC cắt AB tại N. N
 BCcân tại N. Ta có ANC  2B  30 Xét A
 NC vuông tại A có ANC  30 , nên NC  2AC  2 AN  A .
C cot 30  1. 3  3; AB  AN  NB  AN  NC  2  3 Xét A
 BCvuông tại A có BC  AB  AC    2 2 2 2 2 2 3 1  8 4 3 2
Do đó BC  8 4 3  24 2 3  2 3   1  2  3  1 2  3   AC 1 1 6  2
Vậy sin15  sin B     BC    2.2 4 2 3 1 2   3 12 3 2 3  AB 6  2 cos15  cosB     BC    4 4 2 3 1 AC  tan15  tan B  1 2 3    2  3 AB 2  3 1
 Cách thứ hai Xét A
 BC vuông tại A, B  15 , BC  4
Vẽ đường trung tuyến AM và đường cao AH.
Ta có MA  MB  MC  2 M
 AB cân tại M, AMC  2B  30 1 Xét A
 MH vuông tại H, AMC  30nên AH  AM  1 2 3
Ta có HM  AM.cosM  2.cos30  2.  3 2
Suy ra HB  HM  MB  3  2 2 2 Ta có 2 2 2
AB  AH  HB 2  1   3  2
 8 4 3  24 2 3  22 3
 AB  2  3   1 2 2 2
AC  BC  AB    
          2 16 8 4 3 8 4 3 2 4 2 3 2 3 1
 AC  2  3   1 Trang 5 AC 6  2
Vậy sin15  sin B   BC 4 2  AB  3 1 6  2 cos15  cosB    BC 4 4   AC    2 2 3 1 3 1 tan15  tan B      AB    2 3 2 2 3 1
4.4. Dùng kết quả bài 4.3 ta được: 6  2 sin75  cos15  4 6  2 cos75  sin15  4 1 1 tan75  cot15    2  3 tan15 2  3
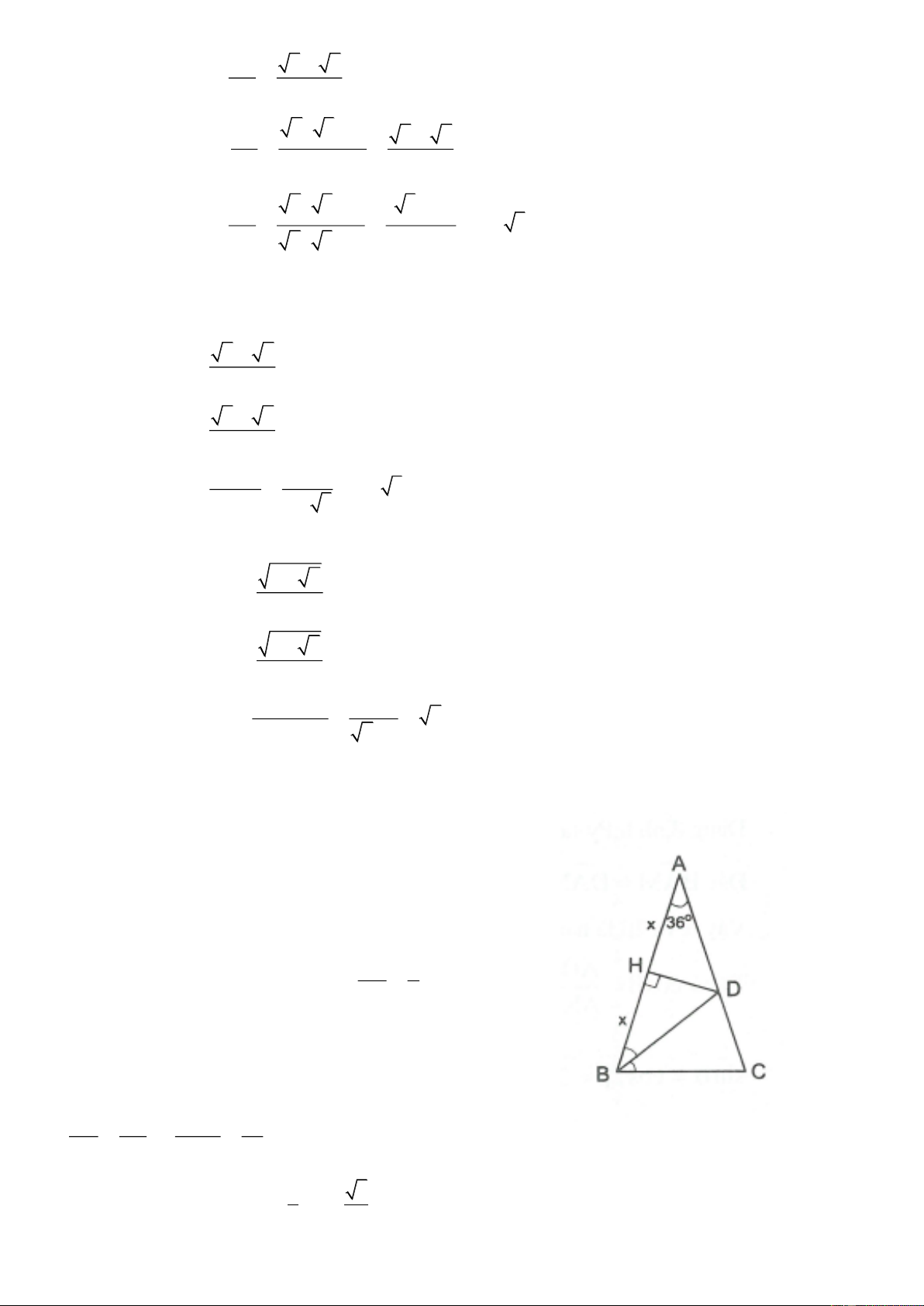
4.5. Dùng kết quả ví dụ 4 ta được: 2  2 sin67 3  0  cos22 3  0  2 2  2 cos67 3  0  sin22 3  0  2 1 1 tan67 3  0  cot 22 3  0    2 1 tan22 3  0 2  1 4.6. a) Vẽ A
 BCcân tại A, A  36 , BC  1. Khi đó B  C  72 Vẽ đường phân giác BD
Dễ thấy các tam giác BCD, ABD là những tam giác cân.
Do đó AD  BD  BC  1. Vẽ DH  AB thì HA  HB
Ta đặt HA  HB  x AH x Xét A
 DH vuông tại H, ta có cosA   AD 1
Do đó cos36  x Xét A
 BCcó AB  AC  2x; CD  2x 1
Vì BD là đường phân giác nên: DA AB 1 2x    DC AC 2x  1 1 2 2  1   5  2
 4x  2x 1 0  2x        0 2  2      Trang 6  5  1   x  (chän) 1 5   1 5    4 2x   2x     0    2 2   2 2      1 5 x   0 (lo¹i)  4 5  1 Vậy cos36  4 b) Vận dụng hệ thức 2
cos2  2cos   1 ta được 2  5 1 6  2 5 5 1 2
cos72  2cos 36 1  2.  1    4  8 4  
Cũng vận dụng hệ thức trên ta được 2 cos36  2cos 18 1 2 cos36  1 1  5  1  1 2 5  10 2  cos 18    1   5   5  2 2  4    8 16 1 Do đó cos18  2 5  10 4 1
Từ đó suy ra sin72  cos18  2 5  10 4 5  1 sin18  cos72  4
4.7. Ta đặt AB  2athì BM = DN = a
Dùng định lí Py-ta-go ta tính được AM  AN  a 5
Đặt BAM  DAN   , khi đó   90  2
Vậy  và 2 là hai góc phụ nhau AD 2a 2 Ta có cos    AN a 5 5 2  2  3 2
sin  cos2  2cos   1  2. 1     5  5 Cách giải khác
Gọi H là giao điểm của AN với DM A  ND  D  MC . c .
g c . Suy ra A  D 1 1
Ta có D  D  90 nên A  D  90 1 2 1 2
Suy ra AH  DH
Ta đặt AB  2a thì DN  a, DM  AM  a 5 D  HN  D  DH DN CM  . g  g   DC DM Trang 7 D . C DN 2 . a a 2a 5 Suy ra DH    DM a 5 5 Do đó 2a 5 3a 5
HM  DM  DH  a 5   5 5 HM 3a 5 3 Ta có sin   : a 5  AM 5 5 4.8. a A
 BC vuông cân tại A, AM là đường trung tuyến nên AM  MB  MC  2 A
 MCcân tại M  AMN  2 Xét A
 MN vuông cân ta có AM  M . N cos2 AM 2AM a  MN    cos2 2cos2 2cos2 a a acos2   1
Ta có CN  CM  MN    2 2cos2 2cos2 Vì 2
cos2  2cos   1 nên 2 cos2  1  2cos  2 2   Do đó . a 2cos . a cos CN   2 2 2cos    2 1 2cos   1 4.9. A
 BCcân tại A, A  80 nên B  C  50
Ta có BMA  180  50  50  80
CBN  50  30  20
ANB  NBC  C  20  50  70
CAM  80  50  30
Áp dụng định lí sin vào các tam giác OBM, OAB, OAN ta được: OM OB OM sin20    sin20 sin80 OB sin80 OB OA OB sin50    sin50 sin30 OA sin30 OA ON OA sin70    sin70 sin30 ON sin30 OM OM OB OA Vì  . . nên: ON OB OA ON OM sin20 sin50 sin70 sin20 .  cos40 .  cos20  . .  ON sin80 sin30 sin30 1 1 sin80 .  . 2 2 Trang 8 2sin20 .  cos20 .  2cos40 sin40 .  2cos40 sin80     1 sin80 sin80 sin80
Suy ra OM  ON do đó M
 ON cân tại O A A B B C C
4.10. Ta có sin A  2sin .cos ; sin B  2sin cos ; sinC  2sin cos 2 2 2 2 2 2 B  C 180  A  A  A sin  sin  sin 90   cos   2 2  2  2 C  A 180  B  B  B sin  sin  sin 90   cos   2 2  2  2 A  B 180  C  C  C sin  sin  sin 90   cos   2 2  2  2 B  C C  A A  B Ta có sin . A sin . B sinC  sin .sin .sin 2 2 2 A A B B C C A B C
 8sin .cos .sin .cos .sin .cos  cos .cos .cos 2 2 2 2 2 2 2 2 2 A B C  A B C 8sin .sin .sin  1 1  sin .sin .sin  2 2 2 2 2 2 8
Bất đẳng thức cuối đúng (xem bài 2.8). Do đó bất đẳng thức đã cho là đúng. Trang 9